Ultradilute self-bound quantum droplets in Bose–Bose mixtures at finite temperature*
Jia Wang(王佳), Xia-Ji Liu(劉夏姬), and Hui Hu(胡輝)
Centre for Quantum Technology Theory,Swinburne University of Technology,Melbourne,Victoria 3122,Australia
Keywords: Bose–Einstein condensation,quantum droplet
1. Introduction
The recent observation of an ultradilute self-bound droplet-like state[1]in single-component dipolar Bose–Einstein condensates (BECs)[2–5]and binary Bose–Bose mixtures[6–11]opens an entirely new direction to better understand the fascinating concept of quantum droplets – autonomously isolated quantum systems equilibrated under zero pressure in free space.Quantum droplets such as helium nanodroplets have already been intensively investigated in condensed matter community over the past few decades.[12–14]However, an in-depth understanding of helium nano-droplets is still lacking,due to the strong inter-particle interactions and the limited techniques to control and characterize the nanodroplets. These limitations could be overcome for ultradilute Bose droplets, owing to the unprecedented controllability in cold-atom experiments.[15]For example, the inter-particle interactions in Bose droplets can be tuned at will by using Feshbach resonances[16]and their structure and collective excitations can be accurately measured through in-situ or time-offlight absorption imaging.[15]In particular, the realization of a weakly interacting Bose droplet now allows us to develop quantitative descriptions and makes it possible to have testable theoretical predictions.[17–36]
In this respect, it is worth noting the seminal work by Petrov,[17]where the existence of a Bose droplet is proposed in binary Bose mixtures with attractive inter-species attractions.The mean-field collapse is surprisingly shown to be arrested by an effective repulsive force arising from Lee–Huang–Yang(LHY) quantum fluctuations.[38]This ground-breaking proposal is now successfully confirmed in several experimental setups, including the homonuclear39K–39K mixtures[6–9]and heteronuclear41K–87Rb[10]or23Na–87Rb mixtures.[11]Following Petrov’s pioneering idea,[17]numerous theoretical investigations have been recently carried out,[17–27,29–37]addressing various zero-temperature properties of Bose droplets.
The finite-temperature properties of Bose droplets in both dipolar BECs and binary Bose mixtures, however, do not receive too much attention. Ultradilute droplets of dipolar bosons at finite temperature have recently been considered in the presence of an external harmonic trap.[28]For Bose droplets in binary mixtures, only the bulk properties (of an infinitely large droplet) at nonzero temperature are addressed most recently.[39,40]As the effective repulsive force provided by the LHY fluctuation term can be easily neutralized by thermal fluctuations,it is not a surprise to find that a Bose droplet in binary mixtures can be completely destabilized above a threshold temperature Tth.[39]
The less interest in the finite temperature effect is probably due to the peculiar self-evaporation feature of quantum droplets. As a self-bound entity, the energy of elementary excitations of quantum droplets – either single-particle excitations or collective excitations – has to be bounded from above by the so-called particle-emission threshold,making the droplet essentially a low-temperature object. This is fairly evident in helium nano-droplets: once the nano-droplet is created, its temperature rapidly decreases to about 0.4 K in several milliseconds.[13]Afterward,however,the self-evaporation becomes not so efficient.[13]A Bose droplet in a binary mixture is similarly anticipated to be a low-temperature object.In particular, as predicted by Petrov from zero-temperature calculations,[17]for the number of particles in a certain range,there are no collective excitations below the particle-emission threshold. In other words, an excitation-forbidden region in the particle number exists. The Bose droplet then may automatically lose its thermal energy upon releasing the most energetic particles and reach exactly zero temperature.
In this work, we would like to argue that the selfevaporation efficiency of Bose droplets at low temperature could be much reduced, as in helium nano-droplets.[13]As a result, the experimentally observed Bose droplets might have a small but nonzero temperature in the realistic timescale of experiments.[6–9]We theoretically determine the finite-temperature structure and collective excitations of selfbound spherical Bose droplets with a finite number of particles, based on time-independent and time-dependent extended Gross–Pitaevskii equations (GPEs),[17]respectively.We find a rich phase diagram at finite temperature. In particular,the excitation-forbidden,self-evaporation region of the Bose droplet,found earlier by Petrov using a zero-temperature theory,[17]turns out to shrink with increasing temperature and disappears eventually. We also predict that the surface modes and compressional sound modes of the Bose droplet become softened at the droplet-to-gas transition upon increasing temperature. Our results could be experimentally examined in binary Bose mixtures if efficient thermometry can be established at low temperatures.
2. Extended Gross–Pitaevskii equation at finite temperature
To address the finite-temperature properties of a finitesize Bose droplet, we consider the finite-temperature version of the extended GPE

where Φ(x,t)can be treated as the wave-function of the Bose droplet with atomic mass m, μ is the chemical potential to be determined by the total number of particles N,and ?(n)is the local free energy functional(per unit volume V)depending on the local density n(x,t)=|Φ(x,t)|2.
The extended GPE in the form of Eq.(1)was first used by Petrov in his seminal work as an effective phenomenological theory to describe the low-energy dynamics of an LHY droplet at zero temperature.[17]In the studies of helium nano-droplets,such a density-functional description is widely adopted.[12]For an overview,we refer to the review paper.[13]The microscopic derivation of the extended GPE Eq.(1)is difficult,due to an intrinsic in-consistency in Petrov’s theory of the LHY droplet: one needs to artificially remove a small imaginary part in the LHY energy functional, which is related to the instability of mean-field collapse.[17]This difficulty was recently overcome by the present authors,with the consideration of the inter-species pairing of two bosons in different hyperfine states.[33,34]As a result of the correct description for the ground state, the extended GPE can be microscopically derived. This was demonstrated in our recent work for the zerotemperature case under the local density approximation.[35]The generalization of the derivation to the nonzero temperature T /=0 case is straightforward. We can simply replace the ground-state energy functional ?(n)at zero temperature used in our previous work[35]with a finite-temperature energy function ?(n)for free energy.
From the previous work for the finite-temperature bulk properties of the LHY droplet,[39]it is easy to show that the free energy functional per unit volume takes the form
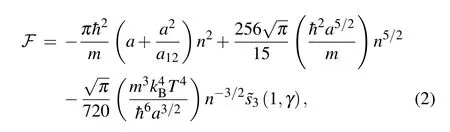


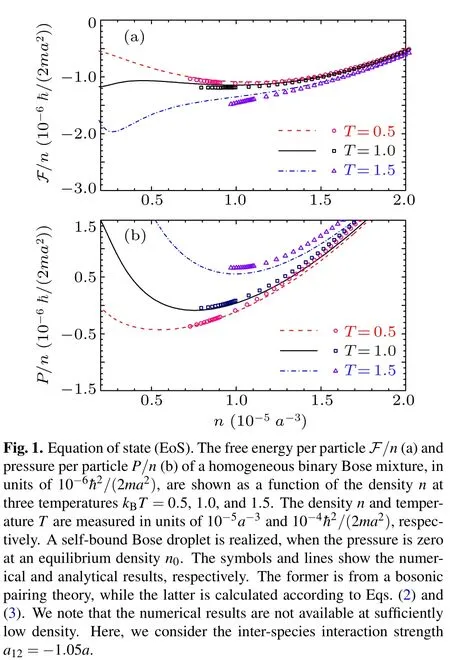


At zero temperature,where the last term in Eq.(13)is absent,Eq. (12) recovers the dimensionless extended GPE used earlier by Petrov.[17]The two temperature-dependent constants CTand BTare the functions of the ratio T/Tthonly and do not depend explicitly on the scattering lengths a and a12. Near the threshold temperature T ~Tth,both constants become significant, and we find that the LHY quantum-fluctuation term(∝|φ|5) in the free energy functional is largely compensated by the last thermal-fluctuation term. This eventually destabilizes a large Bose droplet at the threshold temperature Tth.[39]Let us now analyze how does this thermal destabilization occur for a Bose droplet with a finite(reduced)number of particles.
2.1. Time-independent GPE for the density distribution φ0

In this work, we solve the static GPE numerically via a gradient method, which improves the accuracy and efficiency from our previous work.[15,41,42]The details of our numerical method are described in Appendix A.
2.2. Bogoliubov equations for collective excitations
To study the collective excitations of the Bose droplet,we consider small fluctuation modes around the condensate wavefunction φ0(r)[15,32,42]


It should be noted that the wave-functions u(x)=+φ0(r)and v(x)=-φ0(r)are the zero-energy solution(i.e.,ωj=0)of the Bogoliubov equations. This is precisely the condensate mode of the Bose droplet and therefore should be discarded. To numerically solve the Bogoliubov equations,we follow the technique by Hutchinson,Zaremba,and Griffin.[43]The details of the numerical implementation can be found in Ref. [42] and Appendix A.
3. Results and discussion

3.1. Collective excitations at a given temperature
To start, let us briefly review the essential zerotemperature properties of a self-bound Bose droplet.[17]First,the chemical potential μ of the droplet has to be negative(μ <0), less than that of the surrounding vacuum (i.e., μvac=0).Otherwise, it is not energetically favorable for particles to be added into the droplet. For an infinitely large droplet, where the edge effect can be safely neglected,it is clear from the stationary GPE Eq.(16)that the condensate wave-function in the bulk is φ0=1 in the re-scale units and the chemical potential μ =-1/2. As we decrease the number of particles in the droplet,the wave-function φ0(r)will be smaller than unity and the chemical potential increases towards μ →0-. The droplet will eventually become unstable and experience a droplet-togas transition,when the zero-pressure condition for the droplet state is strongly violated at low density. The droplet-to-gas transition at the critical number of particles Nc?18.65 has been analyzed in detail by Petrov,[17]by considering the balance between the kinetic energy (i.e., from the Laplace operator -?2/2) and the interaction energy (i.e., ?(φ0)). The transition is clearly signaled by the softening of the breathing mode frequency ωl=0,n=0,which vanishes precisely at Nc.This is shown by blue circles in Fig.2(a),where we reproduce the lower panel of Fig. 1 in Ref. [17]. Petrov also predicted the existence of a metastable droplet state when the number of particles is slightly larger than the critical number, i.e.,Nc<N <Nm?22.55.[17]This metastable state has a positive total energy, i.e., -? <0 as shown in Fig. 2(a), so the particles in the droplet will eventually escape to the vacuum via tunneling through an energy barrier(created by the competing kinetic and interaction energies).
Another interesting zero-temperature feature of the Bose droplet is the existence of an excitation-forbidden window in the number of particles,[17]as we mentioned earlier. In Fig.2(a),there is no collective excitation in the stable droplet state below a threshold number of particles, N <Nth?94.2.All collective excitations are accumulated right above the particle-emission threshold |μ|, forming an unbounded collective excitation continuum.[42]The bounded collective excitations are only possible at N >Nth, where the quadruple mode frequency ωl=2,n=0first becomes smaller than|μ|,[17]as shown by the red empty squares. At sufficiently large number of particles(i.e.,N ~104),the Bose droplet is able to acquire a series of the surface modes and compressional sound modes with well-defined dispersion relations,[17,42]as we shall see later.

Fig. 2. The chemical potential -μ, free energy per particle -?/N,breathing mode frequency, and quadrupole mode frequency as a function of the number of particle at zero temperature(a)and at temperature T =0.6Tth (b). At zero temperature in (a), a metastable Bose droplet occurs when the number of particles decreases down to Nm ?22.55,when the free energy ? becomes positive(or-? becomes negative).
At finite temperature, the collective excitation spectrum can dramatically change. In Fig.2(b),we report the excitation spectrum at T = 0.6Tth. It is readily seen that the dropletto-gas transition now occurs at a much larger critical number of particles, Nc(T =0.6Tth)?30.9, where the breathing mode frequency drops to zero. At the same time, the free energy ? is always negative, indicating that the metastable droplet state found at zero temperature does not exist anymore. The threshold number of particle for the excitationforbidden window also significantly decreases and we find that Nth(T =0.6Tth)?66.2. For N >66.2, the quadruple mode frequency ω20decreases with increasing number of particles,while the breathing mode frequency ω00continuously follows the particle-emission threshold |μ| at the number of particles considered in the figure.
In Fig. 3, we show the excitation spectrum at an even higher temperature T = 0.8Tth. At this temperature, the excitation-forbidden window in the number of particles completely disappears. Both the breathing mode frequency and quadruple mode frequency appear to be bounded below the particle-emission threshold|μ|.
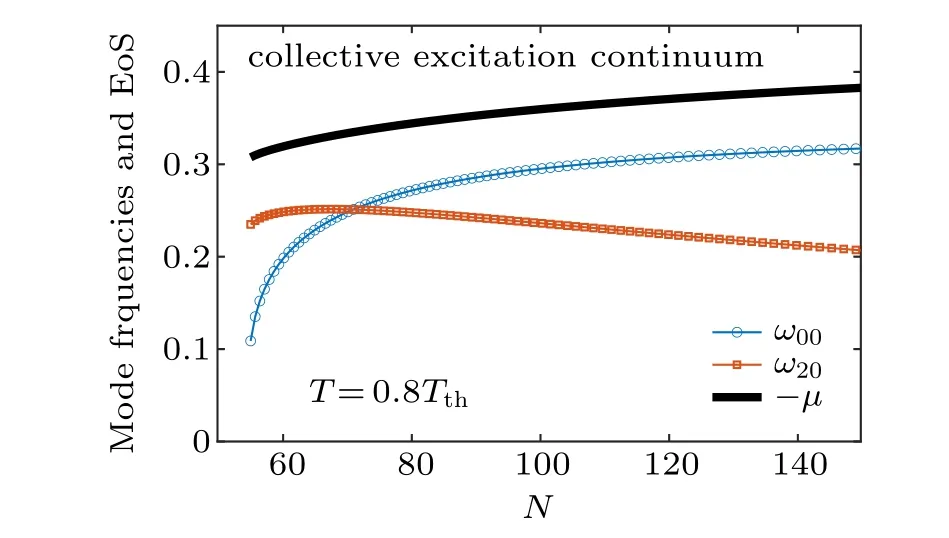
Fig. 3. The chemical potential -μ, breathing mode frequency, and quadrupole mode frequency as a function of the number of particle at temperature T =0.8Tth.
3.2. A finite-temperature phase diagram
We have calculated the excitation spectrum at different reduced temperatures and consequently have obtained a finitetemperature phase diagram,as reported in Fig.4.This presents the main result of our work. Here,the critical number of particle Nc(black solid curve)is determined by extrapolating the breathing mode frequency ω00to zero, and the critical number Nm(red dashed curve) is obtained by tracing the position where the free energy becomes positive. The two curves crosses with each other at about 0.24Tth,above which the window for a metastable droplet state closes. It is interesting to note that the critical number of particles Ncshows a sensitive temperature dependence. It increases very rapidly once the temperature is above about 0.4Tth. Approaching the bulk threshold temperature Tth,a Bose droplet with any number of particles becomes thermally unstable, as we already show in the previous work.[39]
On the other hand, the threshold number of particle Nth(blue dash-dotted curve) can be determined from the crossing point between the quadruple mode frequency ω20and the particle-emission threshold |μ|. It separates the phase space for a stable Bose droplet into two regimes: an excitationforbidden droplet regime without any bounded collective excitations below the particle-emission threshold and a standard droplet regime with at least one discrete collective excitation.With increasing temperature, we find that the Nth-curve terminates at about 0.73Tth(see, i.e., the solid circle symbol in the figure). Above this temperature, we always find standard Bose droplets, in which a small but nonzero temperature or entropy could be accommodated by the discrete bounded collective excitations. Therefore, the intriguing self-evaporation phenomenon predicted by Petrov, i.e., the emission of particles upon arbitrary excitations,[17]ceases to exist. The Bose droplets then fail to automatically reach zero temperature.

Fig. 4. The phase diagram of a finite-size Bose droplet as functions of the reduced number of particles N (horizontal axis) and of the reduced temperature T/Tth (vertical axis). At high temperature and small number of particles, the system is in the gas-like phase, while at low temperature and large number of particles, it is in the droplet state. A metastable droplet state also occurs at low temperature and relatively small number of particle.
3.3. The temperature-dependences of the density distribution and collective excitations
Let us now consider an idealized experimental situation.Initially, a Bose droplet is nearly in thermal equilibrium at a nonzero temperature.It then gradually reduces its temperature by emitting a very small portion of the most energetic particles. This slow self-evaporation might be treated as an adiabatic process.By taking the in-situ or time-of-flight absorption imaging of the Bose droplet,we may then experimentally extract the temperature-dependences of the density distribution and collective excitations of the Bose droplet at a nearly constant number of particles.
3.3.1. Large Bose droplets




Fig. 6. Excitation frequencies ωln (l ≤9 and n ≤2) of a large self-bound Bose droplet (N =3000), as a function of the reduced temperature T/Tth.The red dashed curves show the surface modes ωl≥2,n=0 and the blue dashdotted curves show the compressional bulk modes.The lowest surface mode ω20 (i.e, quadruple mode) and the lowest bulk mode (breathing mode) are highlighted by the red open squares and blue open circles,respectively. The black thick curve shows the threshold-μ.


3.3.2. Small Bose droplets
Let us now consider a Bose droplet with small reduced number of particles,which is more amenable to be created in the current experimental setups.[6,8]In Fig. 7, we show the density distribution of a N=100 Bose droplet at two temperatures: T =0 (solid curve) and T =0.7Tth(dashed curve).Compared with a large Bose droplet in Fig.5,the density distribution of a small droplet shows a more appreciable temperature dependence. In particular,the center density can change up to several tens of percent(see the inset),as we increase the temperature towards the threshold. This pronounced temperature dependence could be related to the loss of the flat-top structure in the density distribution due to the reduced number of particles. A small Bose droplet appears to be more easier to be altered than a large droplet.
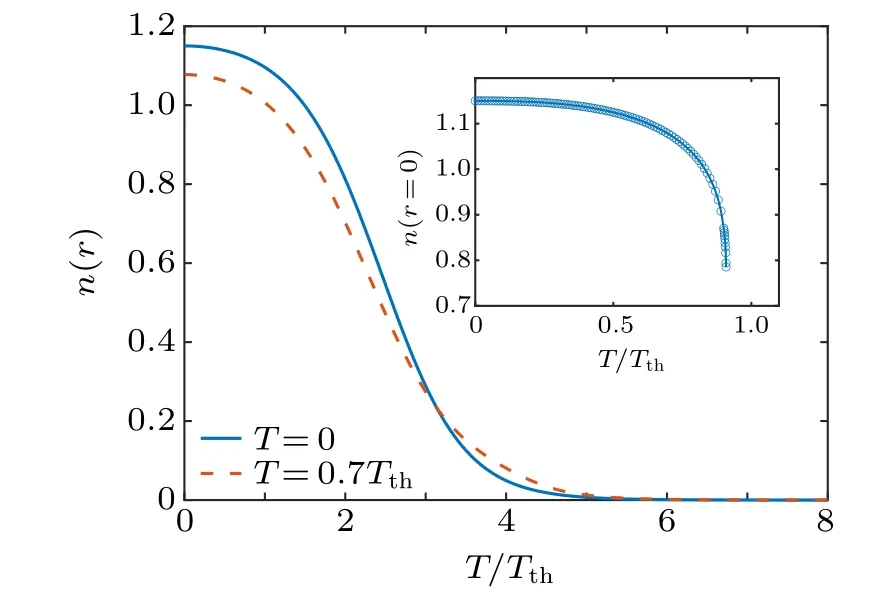
Fig.7. The density distribution n(r)of a small self-bound Bose droplet(N =100) at zero temperature (blue solid curve) and at the temperature T =0.7Tth (red dashed curve). The inset shows the temperature dependence of the center density at r=0.
In Fig.8,we report the temperature evolution of the collective excitation spectrum at N=100. At this number of particles and at zero temperature, only the lowest surface mode(i.e.,the quadruple mode ω20)is bounded below the particleemission threshold |μ|.[17]When we increase the temperature, the quadruple mode frequency decreases notably, presumably due to the increase of the droplet radius, since the droplet at this size acquires a more sensitive temperature dependence as we mentioned earlier. Interestingly, at about 0.7Tththe frequency of the lowest compression bulk mode,the breathing mode frequency, starts to fall off the particleemission threshold. It becomes increasingly softened towards the threshold temperature Tth. At an even higher temperature(i.e., T ~0.87Tth), more and more higher-order bulk modes fall off the the particle-emission threshold and become softened. This fall-off feature turns out to be very general,occurring also at smaller number of particles,as can be seen in the inset for the selected case of N=50.

Fig. 8. Excitation frequencies ωln (l ≤9 and n ≤2) of a small selfbound Bose droplet(N=100),as a function of the reduced temperature T/Tth. The red dashed curves show the surface modes ωl≥2,n=0 and the blue dash-dotted curves show the compressional bulk modes. The lowest surface mode ω20 (i.e, quadruple mode) and the lowest bulk mode(breathing mode)are highlighted by the red open squares and blue open circles,respectively. The black thick curve shows the threshold-μ. At this number of particles,most of the excitation modes enter the collective excitation continuum with a frequency ωln ?-μ. The inset shows the excitation spectrum at an even smaller number of particles,N=50.
The mode frequency softening, for both surface modes and compressional bulk modes in large and small Bose droplets,is therefore a characteristic feature of the thermallyinduced droplet-to-gas transition at finite temperature. The mode softening effectively removes the excitation-forbidden interval in the number of particles predicted by Petrov at zero temperature,[17]and opens the possibility to observe a small Bose droplet with non-zero temperature.
4. Conclusions
In summary,we have theoretically investigated the finitetemperature effects on the structure and collective excitations of an ultradilute quantum droplet in free space, formed in a binary Bose–Bose mixture with inter-species attractions near the mean-field collapse. Our calculations are based on the extended (time-dependent) Gross–Pitaevskii equation generalized to the finite-temperature case. The density distribution is determined by solving the static Gross–Pitaevskii equation,while the collective excitation spectrum is obtained by solving the coupled Bogoliubov equations.
We have found a rich finite-temperature phase diagram as a function of the number of particles in the droplet. In particular,the critical number of particles at the droplet-to-gas transition is found to depend sensitively on the temperature. The excitation-forbidden interval predicted by Petrov is shown to shrink with increasing temperature and disappears completely at about 0.73Tth, where Tthis the threshold temperature for thermally destabilizing an infinitely large Bose droplet.Above the temperature 0.73Tth,there is at least one discrete collective mode below the particle-emission threshold,which may block the self-evaporation of the Bose droplet and allow a small but nonzero temperature.
Our results could be experimentally examined, if we are able to overcome the difficulty of finding a useful thermometry to measure the temperature. Qualitatively, at the number of particles slightly below Nth(T =0)?94.2,the experimental observation of discrete quadrupole mode frequency or breathing mode frequency below the particle-emission threshold, i.e., ω20<|μ|or ω00<|μ|, would be a very strong evidence for the finite-temperature effect.
Appendix A:Numerical method

The B-spline basis has been extensively used in solving Schr¨oinger equations in two- and three-body problems with high accuracy.[45,46]The B-spline basis allows us to use an uneven grid, which might better represent the solution wavefunction.The B-spline basis also allows a higher order approximation of the derivative operator that appears in the kinetic energy term. The energy density functional ?/N then can be regarded as a non-linear function of coefficients cn,which can be minimized using the standard conjugate-gradient method via software package such as“minFunc”in Matlab.[47]
- Chinese Physics B的其它文章
- Numerical simulation on ionic wind in circular channels*
- Interaction properties of solitons for a couple of nonlinear evolution equations
- Enhancement of multiatom non-classical correlations and quantum state transfer in atom–cavity–fiber system*
- Protein–protein docking with interface residue restraints*
- Effect of interaction between loop bases and ions on stability of G-quadruplex DNA*
- Retrieval of multiple scattering contrast from x-ray analyzer-based imaging*