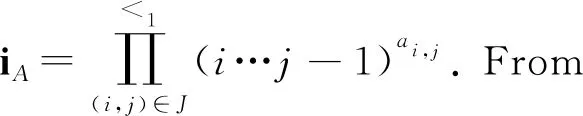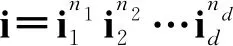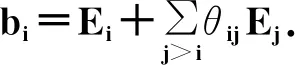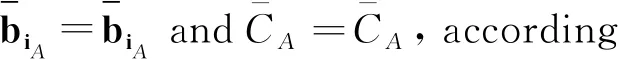The Bases for the Positive Part of Quantum Supergroup Uq(glm|n)
GU Haixia
(School of Science, Huzhou University, Huzhou 313000, China)
Abstract:In this article, the relations of the PBW bases and canonical bases for the positive partive of quantum supergroup Uq(glm|n) described by Du and the author based on the realization of Uq(glm|n), and by Clark, Hill and Wang in term of quantum shuffle are studied. We achieve that PBW bases and canonical bases are same up to sign respectively.
Keywords:quantum supergroup; quantum shuffle; PBW basis; canonical bases
0 Introduction
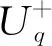
Here are some notations:
[1,m+n]=the set of integers from 1 tom+n;

M(m|n)+={A∈M(m|n)|aij=0 fori≥j};
1 Quantum supergroup Uq(glm|n)
Referring[8],quantum supergroupUq(glm|n) over the(q) is a2-graded algebra with quantum parameterq,i.ebracket multiplication is defined as following:
[x,y]=xy-(-1)p(x)p(y)yx,
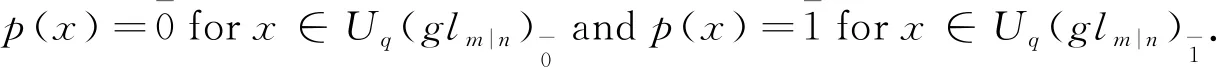
even generators:
Eh,h+1,Fh+1,h,Ki, forh=1,2,…,m+n-1,i=1,2,…,m+n,h≠m;
odd generators:
Em,m+1,Fm+1,m,
subject to some relations.Uq(glm|n) has a triangular decomposition. The subsuperalgebra generated byEh,h+1,h=1,2,…,m+n-1,h≠m,Em,m+1,is called the positive part ofUq(glm|n) and denoted denoted byUq+.
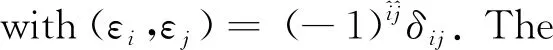
Q={εi-εj|1≤i≠j≤m+n} andQ+={εi-εj|1≤i and the set of simple positive roots is ∏={αi=εi-εi+1|1≤i≮m+n}. Obviously εi-εj=αi+αi+1+…+αj-1forεi-εj∈Q+. The root vector for positive rootεi-εjis denoted byEi,jwhich can be inductively defined by the following relations: According to [8], Ei,jEk,l=(-1)p(Ei,j)p(Ek,l)Ek,lEi,jfori There is an anti-involution denoted by-overUq(glm|n) such that Define the orders <1overJsuch that (i,j)<1(k,l) ifj>lorj=l,i Theorem1[4]The PBW basis {EA|A∈M(m|n)+},the bar involution, and the preorderdefine the uniquely canonical basesC+={CA|A∈M(m|n)+} of SetI={1,2,…,m+n-1}.F=F(I) is the free associative superalgebra over(q) generated byI, andi=(i1i2…id)=i1i2…id,which is called a word ofF(I). Fori∈Iandk∈N,use the notationWto be the set of words associated withI. Theq-quantum shuffle productq:F×F→Fis defined inductively by (xi)q(yi)=(xq(yj))i+(-1)(p(x)+p(y))p(j)q-(|x|+αi,αj)((xi)qy)j,xqφ=φqx=x, and [x,y]q=xy-(-1)p(x)p(y)q(|x|,|y|)yx, for homogenous elementsx,y∈Fandi,j∈I. LetW=(W,≤) be the ordered set with respect to the corresponding lexicographic orderi=(i1,…,id)<(j1,…,jk)=jif there exists an r such thatir In [5], The set of dominant words inWis denoted byW+, and the set of dominant Lyndon wordsL+=L∩W+.According to [5], for the caseglm|n,the set of dominant Lyndon words is L+={(i,…,j)|1≤i Theorem3[5]The mapi|i| defines a bijection fromL+to the set of the positive roots,andi∈W+if and only if its canonical factorization is of the formi=i1i2…ir, wherei1,i2,…,ir∈L+satisfyi1≥i2≥…≥ir∈L+andisappears only once whenever |is| is isotropic. Fori∈W+, {Ri|i∈W+}is the Lyndon basis of (F,). From the order overW, we can derive an order<1overJ={(i,j)|1≤i Theorem4 There is a one to one correspondence betweenW+andM(m|n)+. Fori∈L,call the decompositioni=i1i2the co-standard factorization ofiifi1,i2≠φ,i1∈Landi1is the maximal among all such decomposition. Wheni∈L+, define [i]+=iifi=i∈Iand otherwise, [i]+=[i1,i2]qwherei=i1i2is the co-standard factorization. For i=(i1i2…id), set |(i1i2…id)|=α1+…+αd. Theorem5 For anyi=(i,…,j)∈L+,Ψ(Ei,j+1)=Ri. ProofIn order to prove the assertion, we apply the induction to the length ofi.Fori=(i,i+1),from the definitionΨ(Ei,i+1)=Ri=Ri.Assume thatΨ(Ei,j)=Rifori=(i,…,j-1)∈L+.Now we showΨ(Ei,j+1)=Rifori=(i,…,j)∈L+. According to [5], fori=(i,…,j)∈L+,i=i1i2withi1=(i,…,j-1) andi2=(j) is the co-standard factorization ofi.Sincep(i1)p(j)=0,it yields [i]+=[i1]+j-q(|i1|,|j|)j[i1]+. According the definition, |i1|=εi-εj,|j|=εj-εj+1. Case1 Ifj Ψ(Ei,j+1)=Ψ(Ei,jEj,j+1-q-1Ej,j+1Ei,j)=Ri1Rj-q-1RjRi1=Ri. Case2 If and (εi-εj,εj-εj+1)=(εi-εm,εm-εm+1)=-1.Therefore [i]+=[i1]+j-q-1j[i1]+. Then we have Ψ(Ei,j+1)=Ψ(Ei,jEj,j+1-q-1Ej,j+1Ei,j)=Ri1Rj-q-1RjRi1=Ri. Case3 Ifj>m, then and(εi-εj,εj-εj+1)=1.Therefore[i]+=[i1]+j-qj[i1]+. Since we have Ψ(Ei,j+1)=Ψ(Ei,jEj,j+1-qEj,j+1Ei,j)=Ri1Rj-qRjRi1=Ri. In summary, for anyi=(i,…,j)∈L+,Ψ(Ei,j+1)=Ri. Theorem6 The basis {Ei|i∈W+} is the image of {EA|A∈M(m|n)+} over the action Ψ up to sign. ProofIn [4], we define an order <2overJ={(i,j)|1≤i As the first step, we need to prove From the definition of <1and <2, we know (i,j-1)<1(i,j)and(i,j-1)<2(i,j). For any (i′,j′)∈Jsuch that (i,j-1)<2(i′,j′)<1(i,j)and(i,j)<2(i′,j′), if we can deriveEijEi′j′=(-1)P(Ei,j)P(Ei′j′)Ei′j′Eij,then the equation (1) is shown. (Ⅰ) Since (i′,j′)<1(i,j), it yieldsi′ (Ⅱ) Since (i,j-1)<2(i′,j′), we havej′>j-1 orj′=j-1 andi (Ⅲ) Since (i,j)<2(i′,j′), it yieldsj Case1 Assumej′=j. According to (Ⅰ), in this casei>i′,however it yieldsi′>ifrom (Ⅲ). This is a contradiction. Case2 Assumej′=j-1. According to (Ⅱ), we havei′>i.As a result, we havei EijEi′j′=(-1)P(Ei,j)P(Ei′j′)Ei′j′Eij, thus we have The assertion is proved. Theorem7 The image of {CA|A∈M(m|n)+}overΨis same to{biA|A∈M(m|n)+}up to sign.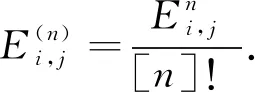
2 Quantum shuffle