TOEPLITZ OPERATORS WITH POSITIVE OPERATOR-VALUED SYMBOLS ON VECTOR-VALUED GENERALIZED FOCK SPACES ?
Jianjun CHEN ( 陳建軍 )
School of Mathematics and Statistics, Zhaoqing University, Zhaoqing 526061, China E-mail: chenarmy@foxmail.com
Xiaofeng WANG ( 王曉峰 ) ? Jin XIA ( 夏錦)
School of Mathematics and Information Science and Key Laboratory of Mathematics and Interdisciplinary Sciences of the Guangdong Higher Education Institute, Guangzhou University,Guangzhou 510006, China E-mail: wxf@gzhu.edu.cn; xiaj@cdut.edu.cn
Abstract In this article, we study some characterizations of Toeplitz operators with positive operator-valued function as symbols on the vector-valued generalized Bargmann-Fock spaces . Main results including Fock-Carleson condition, bounded Toeplitz operators, compact Toeplitz operators, and Toeplitz operators in the Schatten-p class are all considered.
Key words Toeplitz operator; operator-valued symbol; generalized Fock space
1 Introduction

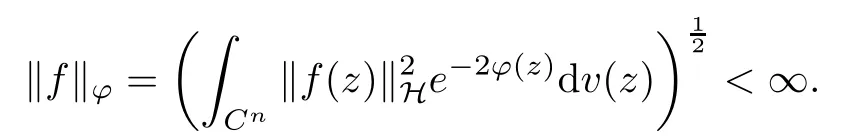
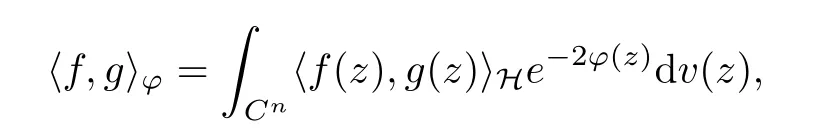
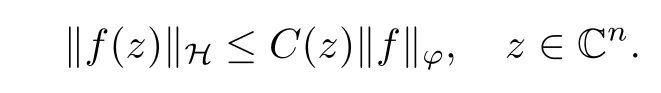
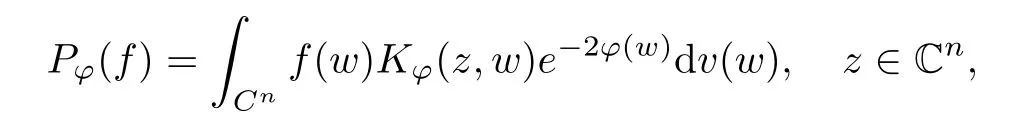
where (z,w) →K?(z,w) denotes the reproducing kernel of the scalar generalized Bargmann-Fock space(C). This formula is easily deduced from the reproducing formula of the scalar generalized Fock space(C) applied to z →〈p?f(z),e〉H, where e ∈H is arbitrary.
Something important is worthy being noticed that the reproducing formula is actually a Bochner integral, and it can make sense because
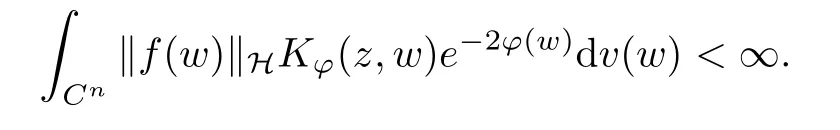
However, the Bochner’s theorem has revealed that alternative sufficiency is that f(z) must be strongly measurable for almost everywhere z ∈Cn. Fortunately, the Pettis’ theorem shows us that H-valued function f(z)is strongly measurable is equivalent to that it is weakly measurable and separably valued for almost everywhere z ∈Cn. That is the reason why we choose H is a separable Hilbert space. Under this assumption, all the Bochner integrals (in this article) will be considered as the Pettis integral because of the reflexivity of H. Now, it can be accounted for that why we can bravely apply z →〈pP?f(z),e〉H to the reproducing formula. More details about Bochner integral and Pettis integral are referred to [3] for example.
In what follows, L(H) will stand for the normed space of bounded linear operators on H with the norm. And B(L(H)) is referred to the Banach space of Bochner integral L(H)-valued functions G:Cn→L(H) with the norm defined by
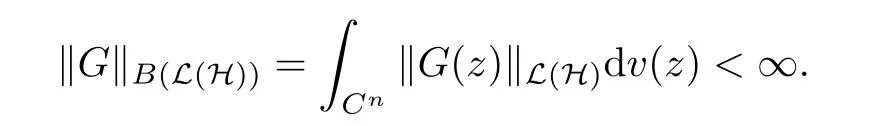
Then, we denote by T(L(H)) the space of all strongly positive measurable operator-valued functions G ∈B(L(H)) that satisfies
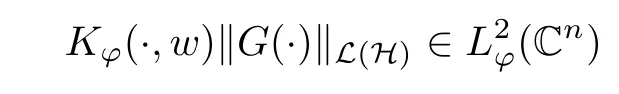
for any w ∈Cn. For a G ∈T(L(H)), we now define the Toeplitz operator with operator-valued function G on Cnas symbol by
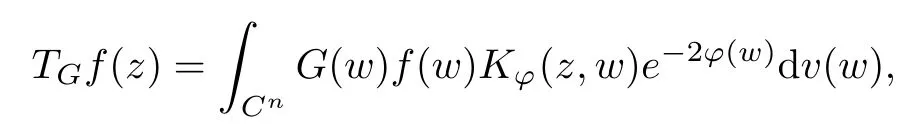
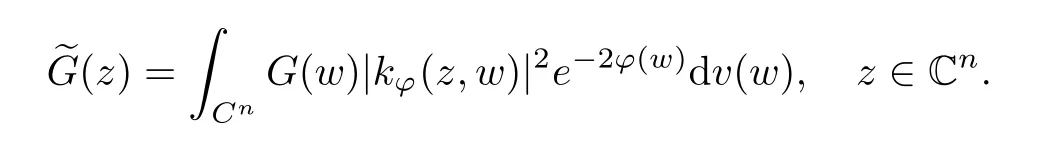
Additionally, the average function of G(z) in the Bochner integral sense is as follows:
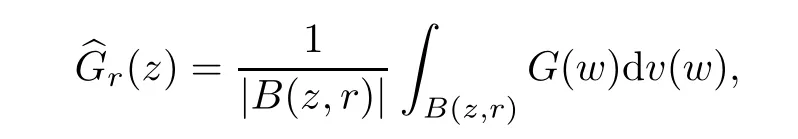
for any r > 0 and z ∈Cn. One more word about the average functionis mentioned by us that it is meaningful ifexists or G ∈T(L(H)) by Lemma 4 in [4].
In 2010, J.Isralowitz and K.Zhu [5] had taken the lead in characterizing the Toeplitz operators with positive measures symbols on the scalar Fock space. They had studied the boundedness, compactness, and Schatten-p class (0 < p ≤∞) of the Toeplitz operators. In the end of Introduction Part in [5], the authors had made a comment on that the results would be extended to higher dimension as long as one can handle the related lattices. Afterwards,Z.Hu,X.Lv [6] and T.Mengestie [7] had accomplished the goal, and moreover, they had researched the boundedness and compactness of Toeplitz operators on one Fock space to another in terms of the average function and t-Berezin transform. Furthermore,Z.Hu and X.Lv[8]had extended their results on the generalized Fock space. However, the rest about Schatten-p class was supplied by L.Xiao [9]. At last, X.Wang and R.Cho had used the same ideas to obtain the similar results on the Fock-Sobolev spaces [10] and Fock-Sobolev type spaces [11], respectively.
The well-informed reader will notice that nonnegative measure symbols of Toeplitz operators are considered by all described literatures above. Particularly in the scalar setting, if given a nonnegative measurable function f, we know that there exists a nonnegative measureμ such that dμ = fdv. Unfortunately, an important fact about the Bochner integral is that the Radon-Nikodym theorem fails to hold in general. See [3] for more details. In other words,we can not find a measure μ such that dμ=Gdv for an operator-valued function G generally.Therefore,our results would not be extended to the case of general measure symbols except the Radon-Nikodym property holds.
The organization of this article is as follows. In Section 2, we will consider the definitions and basic of the Fock-Carleson condition for vector-valued generalized Fock spaces, and then we also give some geometric equivalent conditions,from which we know that the results in[2, 5] remain valid in the vector-valued case. Section 3 will be dedicated to characterizing those positive operator-valued symbols G for which the induced Toeplitz operators TGare bounded or compact on. In the sequence, we will provide the similar characterizations of the Schatten class membership of these Toeplitz operators. Remember that unlike the classical Fock space setting for which one could use the explicit formulas for the reproducing kernel, we instead have to rely on some known estimates on the behavior of the reproducing kernel (see[2, 8] for more details). The proofs of our results would be divided into two cases, where it would be dealt with in Section 4 for p ≥1 and in Section 5 for 0 Throughout this article, we will write the notationfor two quantities A and B if there exists an unimportant constant C > 0 independent of the argument such that.Furthermore,is defined in the similar way. Then, we will writeif bothandhold at the same time. In this section, we are going to obtain some preliminary results which will be used in the subsequent sections. To the beginning, a L(H)-valued positive operator G(z) on Cnis said to satisfy the Fock-Carleson condition forH) if Theorem 2.1Suppose that G ∈T(L(H))andis the lattice in Cn. The following conditions are equivalent: (a) G satisfies the Fock-Carleson condition; (b) For all r >0 and z ∈Cn, G satisfies (c) For all r>0 and k>0, G satisfies ProofFor any f ∈(H), Cauchy-Schwarz inequality shows us that Because z →〈f(z),e〉H is holomorphic in(C) for any e ∈H, by Proposition 2.3 in [2], Together with the properties of lattice, we continue calculating that This shows that condition (c) implies (a). In order to obtain the fact that condition (a) implies (b), we take it into account that for any w ∈B(z,r) and a small enough r. Now, we use the same r to achieve that Note that the condition (a) implies that Lastly it is trivial that condition (b) implies (c). It is worthy of noting that condition (a) is independent of r. Thus, if condition (b) or condition (c) holds for some r >0, then it holds for every r >0. Similarly, we say that a L(H)-valued positive operator G(z) on Cnsatisfies the vanishing Fock-Carleson condition if whenever {fm} is a bounded sequence inthat converges to 0 uniformly on compact subsets of Cn. Theorem 2.2Suppose that G ∈T(L(H))andis the lattice in Cn. The following conditions are equivalent: (a) G satisfies the vanishing Fock-Carleson condition; (b) For all r >0, G satisfies The proof can easily be deduced from that of Theorem 2.1 and the details are omitted here. We will characterize boundedness and compactness of Toeplitz operators with positive operator-valued symbols and give several other equivalent conditions for a positive operatorvalued function to satisfy the Fock-Carleson condition. Theorem 3.1Suppose that G ∈T(L(H))andis the lattice in Cn. The following conditions are equivalent: (a) The Toeplitz operator TGis bounded on(H); (b) G satisfies the Fock-Carleson condition; (c) For any z ∈Cn, G satisfies ProofWe assume that Toeplitz operator TGis bounded on. Then we have We scoured12 the beach, enjoying the cool ocean breeze and the feel of the ocean mist on our bodies. Although we still exchanged no words, we became friends through our daily enterprise. for any unit element e ∈H, then we can see that It follows from the Cauchy-Schwarz inequality that the boundedness of TGimplies for all z ∈Cnand any unit element e. That means that condition(a)can deduce condition(c). In the sequence, according to the proof of Theorem D in [12] or Lemma 4 in [4], that is for all z ∈Cnand w ∈B(z,r), we have Therefore, the fact follows from that In view of Theorem 2.1, the condition (c) implies condition (b). Finally, we calculate the boundedness of Toeplitz operator that, for any f ∈(H), We concentrate our attentions to the integral by Cauchy-Schwarz inequality and obtain If the condition (b) holds, so does its equivalent condition (c) in Theorem 2.1. Therefore, Now the condition (a) follows. As a consequence of the characterization of vanishing Fock-Carleson condition in Theorem 2.1, we obtain several properties for compact Toeplitz operators, which gives additional characterizations for vanishing Fock-Carleson condition. Theorem 3.2Suppose that G ∈T(L(H))andis the lattice in Cn. The following conditions are equivalent: (a) The Toeplitz operator TGis compact on(H); (b) G satisfies the vanishing Fock-Carleson condition; (c) G satisfies We omit the proof of Theorem 3.2, because it can be easily adapted from the proof of Theorem 3.1. We want to determine when a Toeplitz operator TGon(H) belongs to the Schatten-p class Sp. This section is devoted to the case p ≥1, while the next describes the other case 0 Lemma 4.1Suppose that G ∈T(L(H)), andis an orthonormal basis of H.Then, TGis in the trace class S1if and only if G is finite on Cn. Moreover, ProofIf G is positive on Cn, so is TG. By Lemma 5.1 in [1], we have Together with the property of Toeplitz operator, we continue calculating that Sequently, the Fubini’s Theorem shows us that Thus, we conclude our results using Proposition 3.1 in [2]. Lemma 4.2Suppose that G ∈T(L(H)). TGandare both bounded on F2?(H) if ProofIf the sufficiency holds, an easy application of Theorems 2.1 and 3.1 gives us that both TGandare bounded. So, for any f ∈(H), we use Fubini’s theorem to obtain In particular, let f(w)=k?(w,z)e for any unit element e ∈H. The above comes into that where we use the fact that On the other side, For a small enough r, it follows from Proposition 2.3 in [2] that Therefore, this estimate gives us that Lemma 4.3Suppose that G ∈T(L(H)), andis an orthonormal basis of H. Then, TG∈Spif ProofTo the beginning, letbe an orthonormal basis of the scalar Fock space F2?(C). Then, it is clear that {Em,k(z)=fk(z)em}m,k≥1is an orthonormal basis of(H). For any m,k ≥1, we obtain Thus, for the case of p=∞, On the other side, when p=1, It implies that Lastly by the interpolation, we can obtain the desire results. We are now going to prove the main result of this section. Theorem 4.4Suppose that G ∈T(L(H)),is an orthonormal basis of H, andis the lattice in Cngenerated by r and ri. The following conditions are equivalent: (a) The operator TGis in the Schatten class Sp; ProofIn order to use Lemma 4.1,we choose another orthonormal basispossibly depending on z. Now, we can see that for any m, An application of triangle inequality tells us that We use Lemma 5.1 in [1] to have This implies that condition (a) deduces condition (b) because∈S1when TG∈Sp. That condition (b) implies condition (c) follows from the proof of Theorem 3.1 From now on, it is obtained that conditions (a), (b), and (c) are equivalent. To prove the equivalence of condition (b) and (d). we assume that condition (b) holds,which implies that Choose a positive integer N such that each point in Cnbelongs to at most N of the ball B(ak,r), For any m,k ≥1 and any z ∈B(ak,r), by triangle inequality, Therefore, This shows that condition (b) implies (d). On the other side,suppose that condition(d)holds,and letbe the lattice generated byand. Then, it is easy to see that In fact, for each point zjthat is not in the lattice, the ball B(zj,r) is covered by six adjacent ball B(ak,r). So, for any described zj, Now, condition (c) holds, with the equivalent of condition (b) and the proof is finished. In this section, we now focus our attentions to the case 0 Lemma 5.1Suppose that G ∈T(L(H)),is an orthonormal basis of H, andis the lattice in Cngenerated by r and ri. The following conditions are equivalent: ProofAccording to the proof of Theorem D in[12]or Lemma 4 in[4],we begin with the inequality Thus, that condition (a) implies condition (b) follows from Note that for any z ∈B(zj,), it implies that Thus, where condition (c) follows from condition (b). In order to finish the proof, we should use the estimate to straightly calculate that From now on, condition (a) has been deduced from if condition (c) holds for small enough r,ε>0. We are now ready to characterize Toeplitz operator TGin Spwith 0 Theorem 5.2Suppose that G ∈T(L(H)),is an orthonormal basis of H, andis the lattice in Cngenerated by r and ri. The following conditions are equivalent: (a) The operator TGis in the Schatten class Sp; ProofThe equivalence of condition (b), (c), and (d) was proved in Lemma 5.1. To the end, all we need is to obtain the fact that condition (b) implies condition (a) and condition(a)implies condition (d). It is easy to see that TGis positive because G is positive. As we all known, TGbelongs to Spif and only ifis trace class. By Lemma 5.1 in [1], we have the estimate for any 0 Here, condition (b) implies condition (a). In the sequence, we denote by χB(ξ,r)the vector-valued characteristic function of B(ξ,r),and letbe an orthonormal basis of the scalar Fock space(C). Then, it is clear that{Ej,m(z)=fj(z)em}j,m≥1is an orthonormal basis of F2?(H). We define a bounded linear operator A on(H) by AEj,m= k?(z,ξj)emfor any m,k ≥1, and hereis the sublattice ofin Cn. An application of Cauchy-Schwarz inequality promises that A makes sense,and it extends to a bounded operator on all of(H).In fact, for any f,g ∈(H), Now,fix a large enough R>0 such that R>2r,and partition{2ak}k≥1into N sublattices such that the Euclidean distance between any two points in each subsequence is at least R. Let{ξj}j≥1be such a subsequence, and let Because TG∈Spand G ≥U, then, TU∈Spand. Denoting T = A?TUA such that, we can split it as T = D+M, where D is the diagonal operator defined by and M is off-diagonal. It easily follows from the triangle inequality that, for any 0 Because M is a positive diagonal operator, we obtain As k?(z,ξj) ∈(H) from Proposition 3.3 in [2], there exits a small enough r > 0 such thatfor all z ∈B(ξj,r). Therefore, On the other hand, by Lemma 4.4 in [9], Noting that the definition of U(z), we continue calculating the Schatten norm of M Together with all above estimates, we deduce that Because this holds for each of the N subsequences of {ak}k≥1, we obtain for all positive operator G such that This proves that condition (a) implies (d), and the proof is finished.2 Fock Carleson Condition
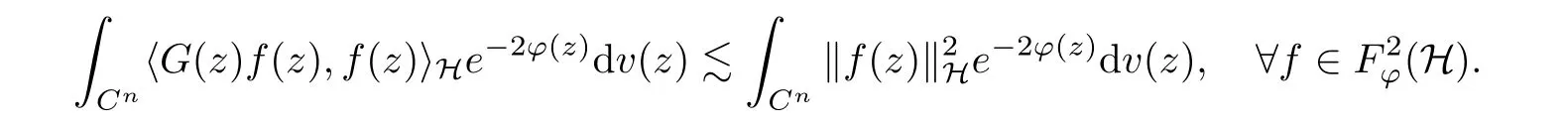
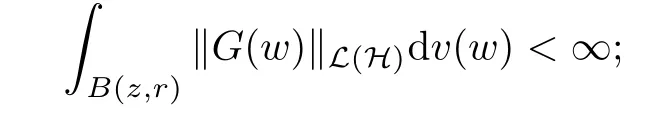
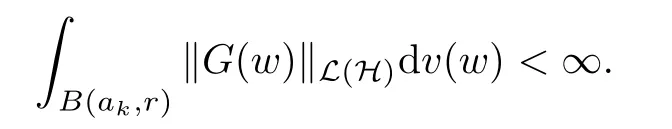
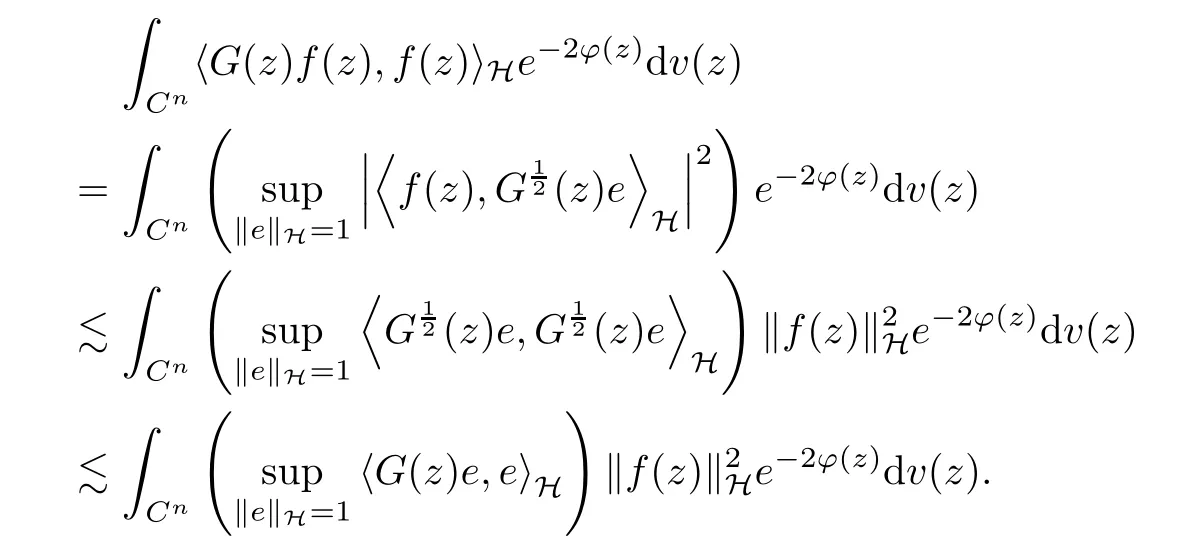
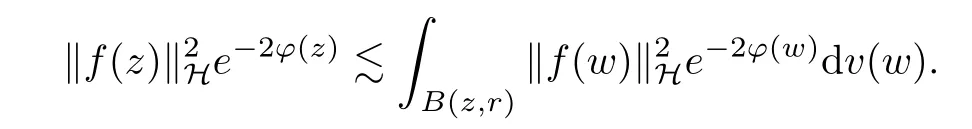
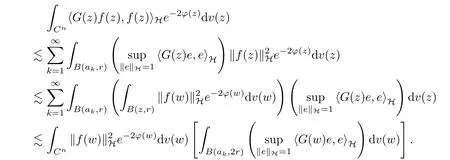
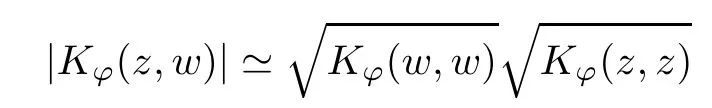
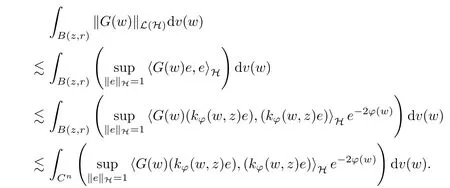
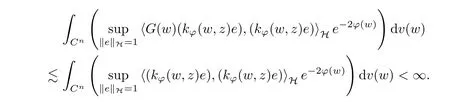
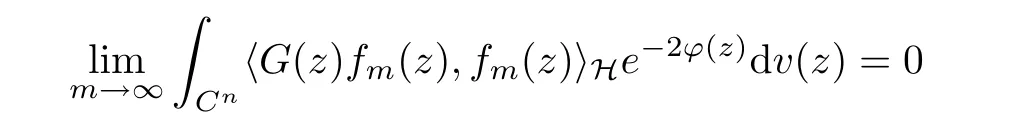
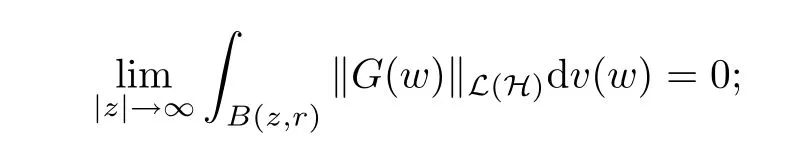
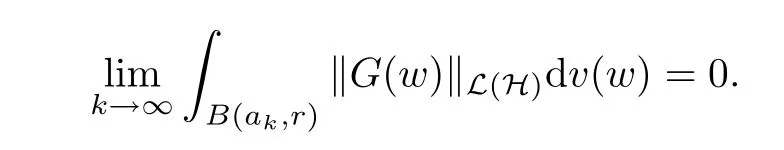
3 Boundedness and Compactness of Toeplitz Operators
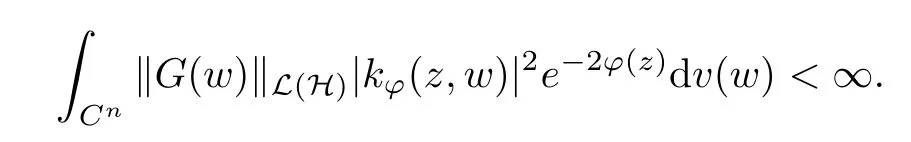
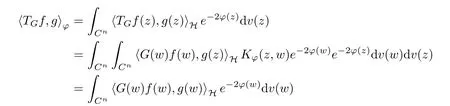
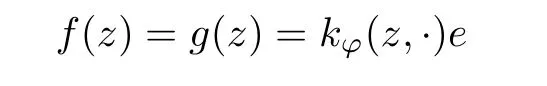
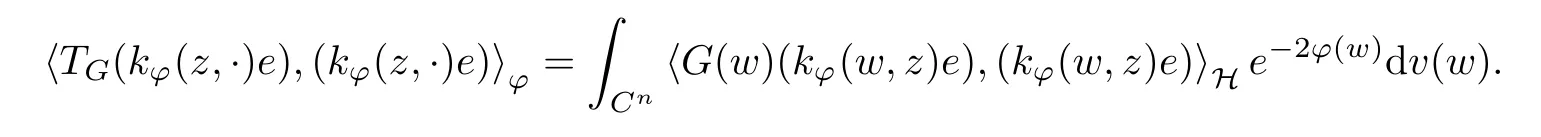
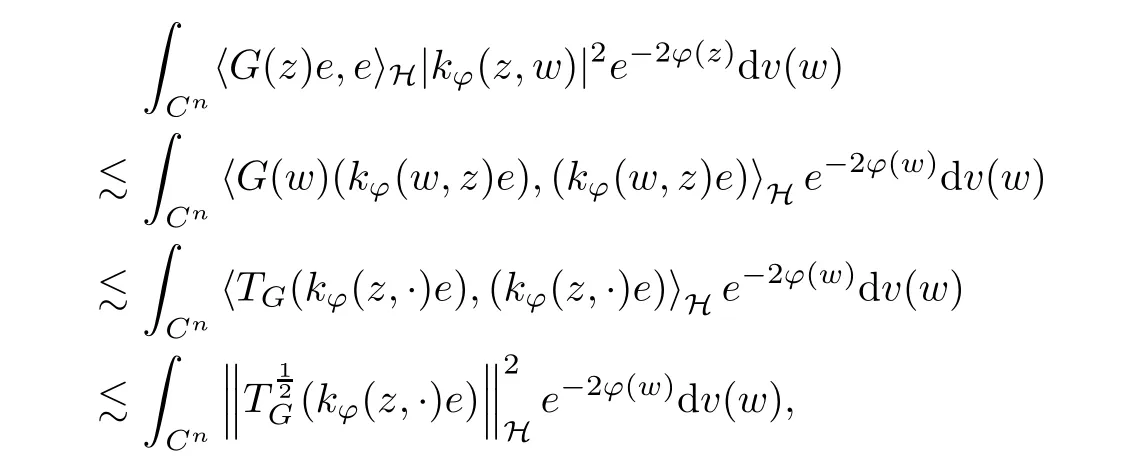
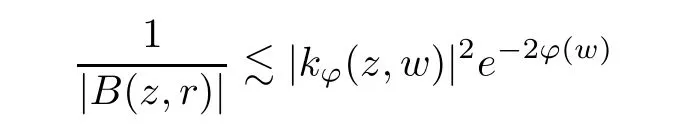
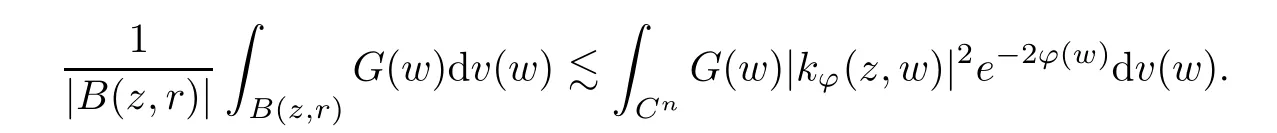
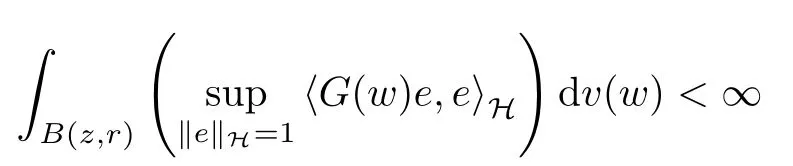
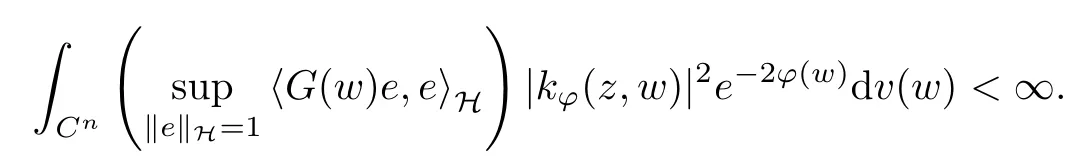
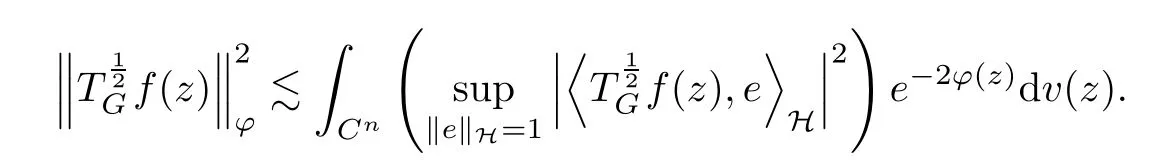
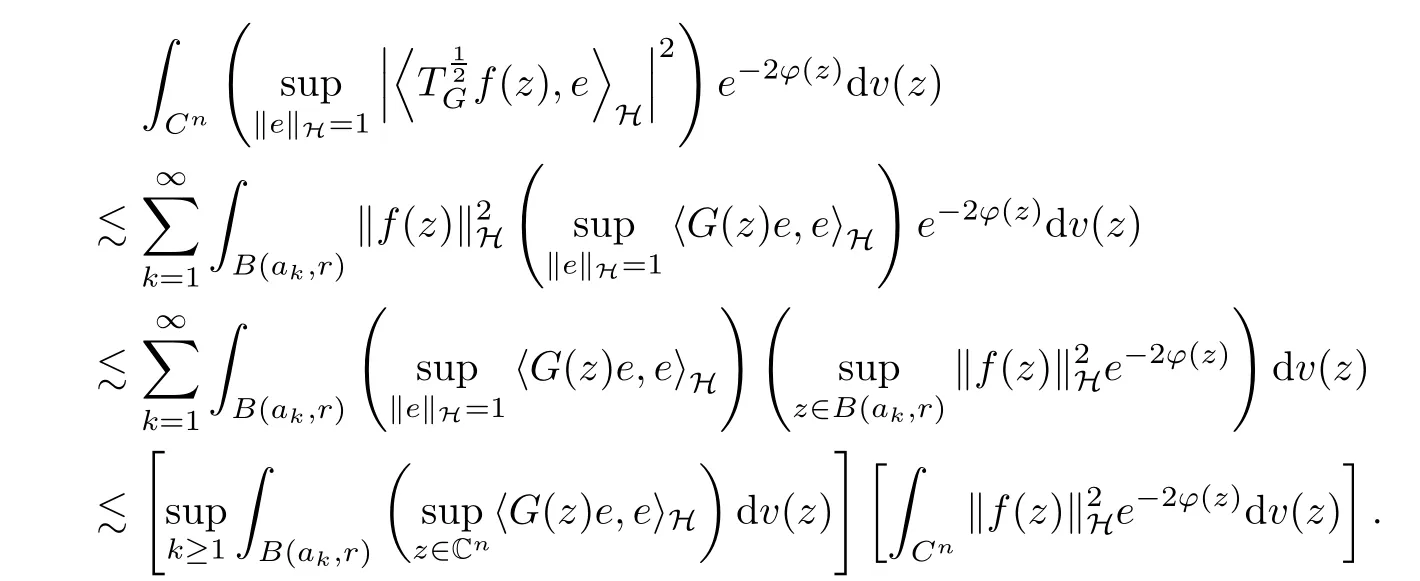
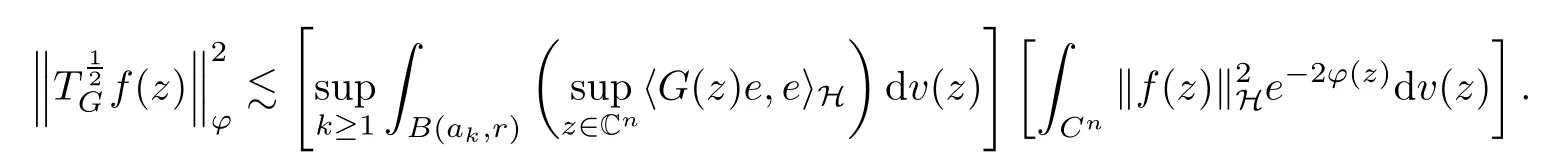
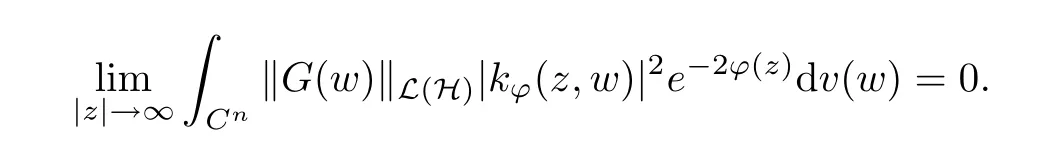
4 Toeplitz Operators in Sp With p ≥1
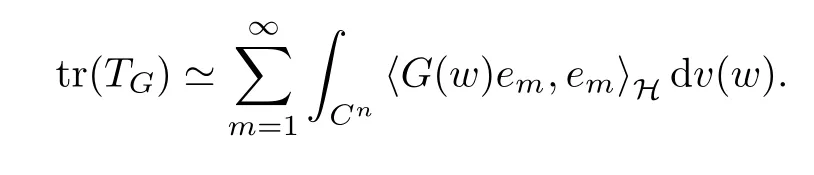
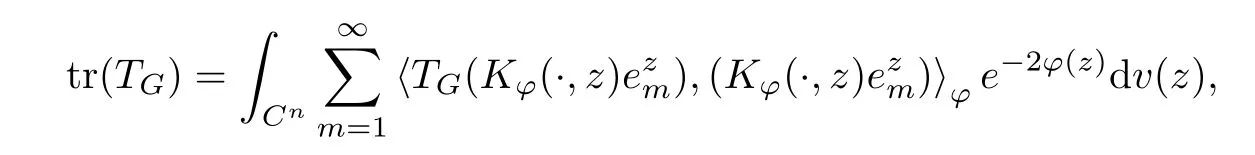
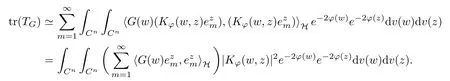
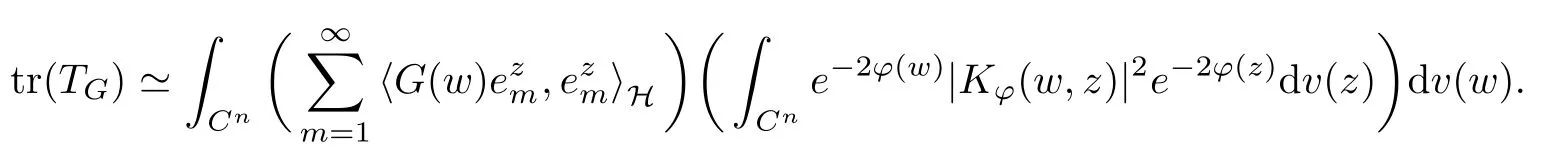
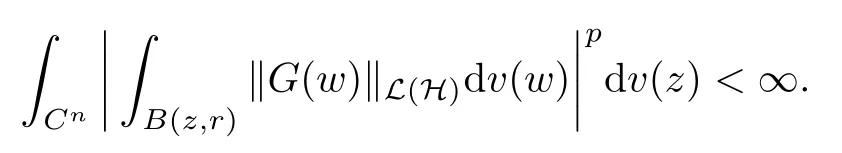
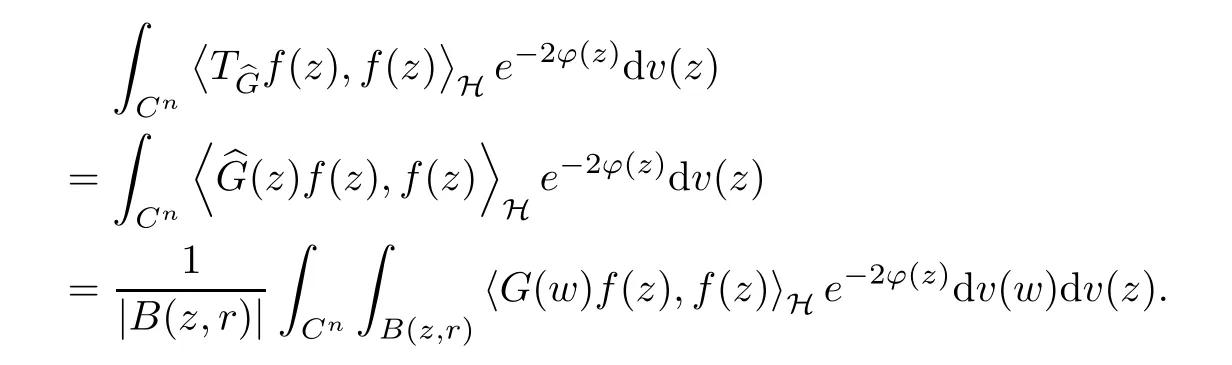
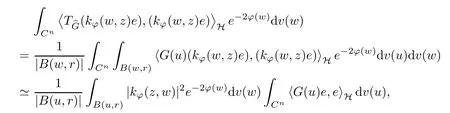
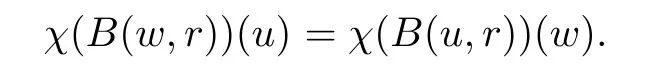
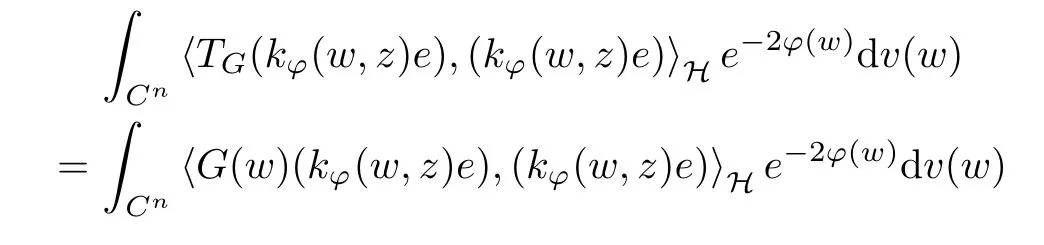
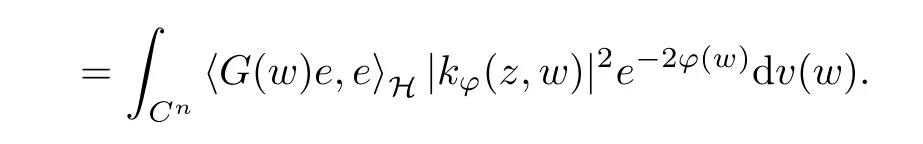
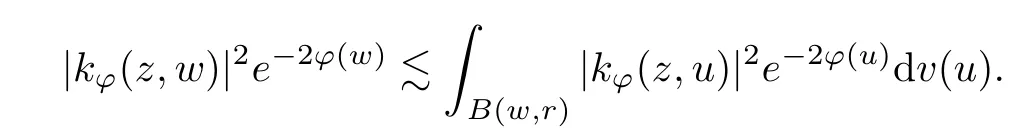
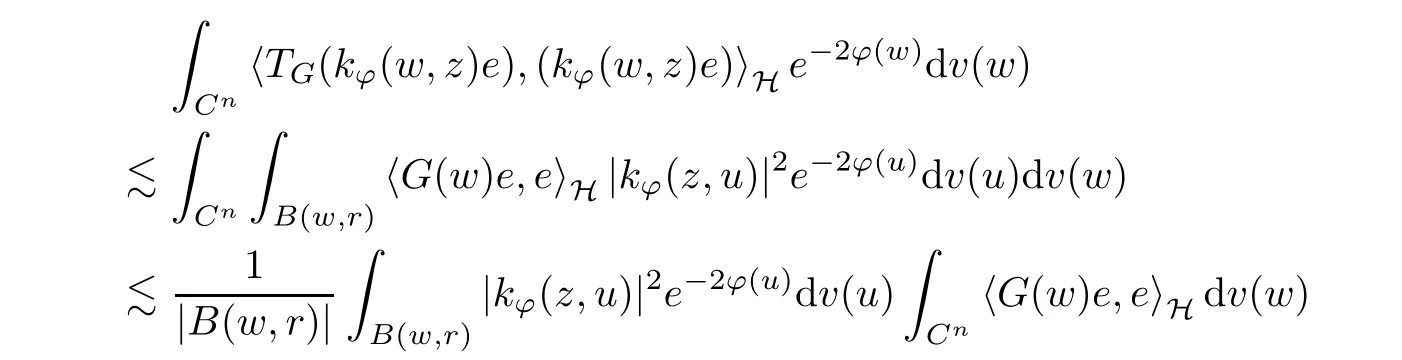
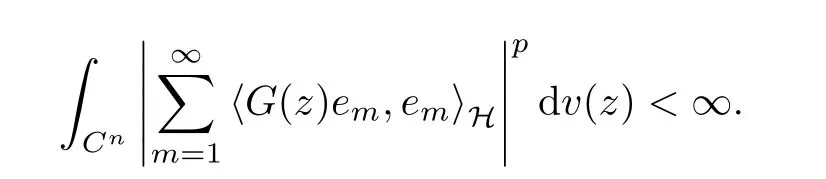
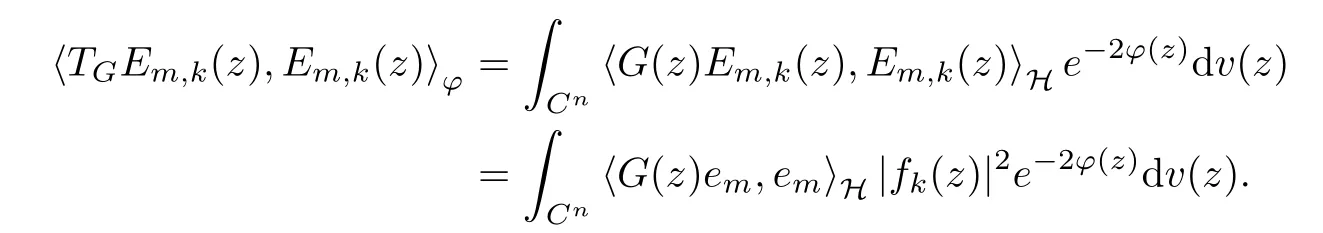
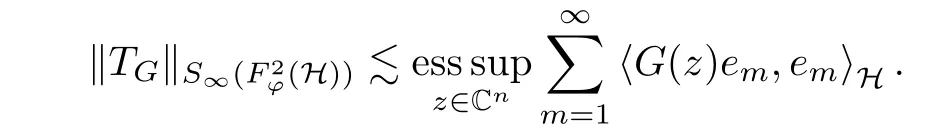
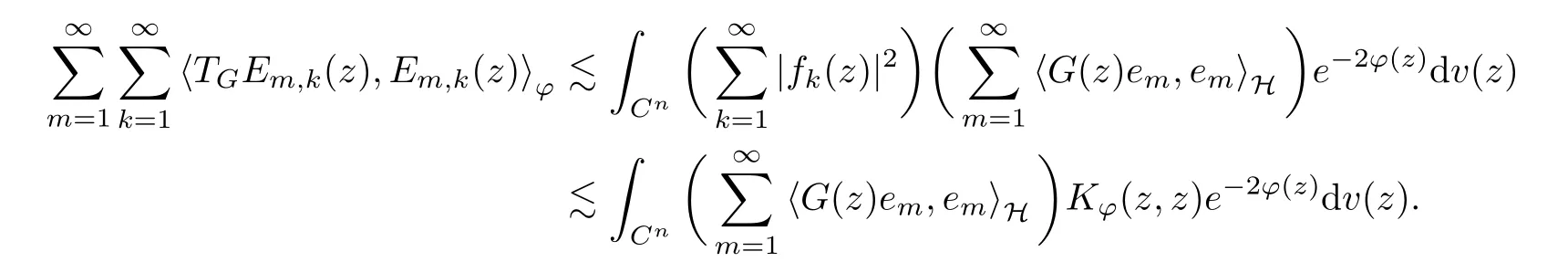
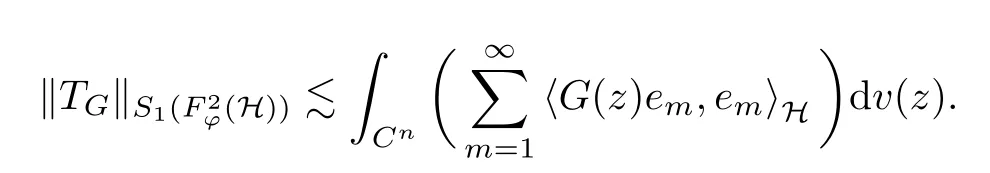
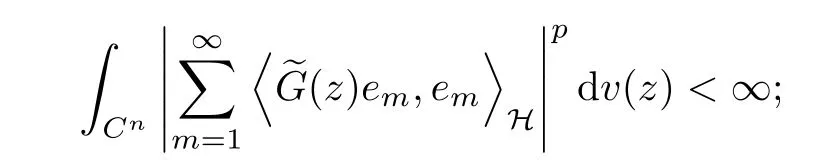
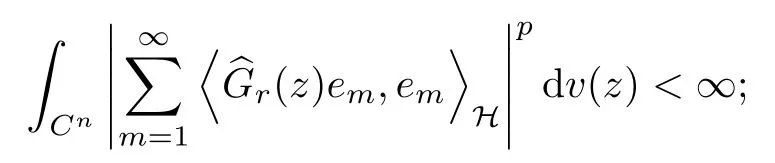
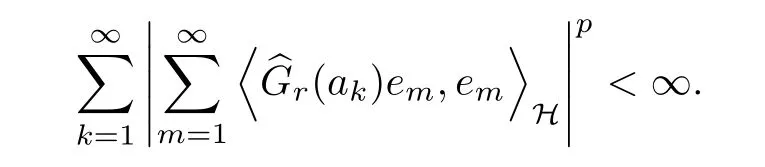
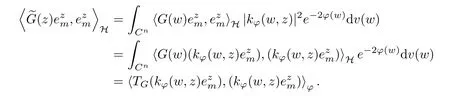
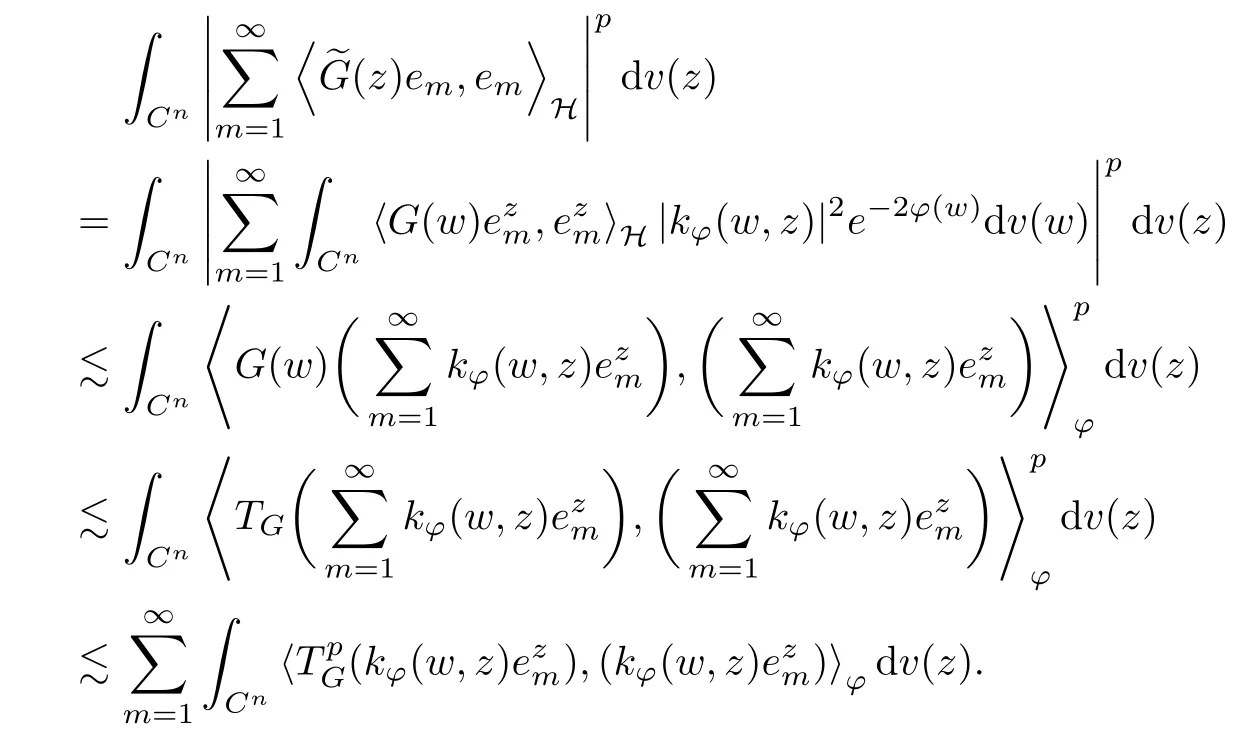
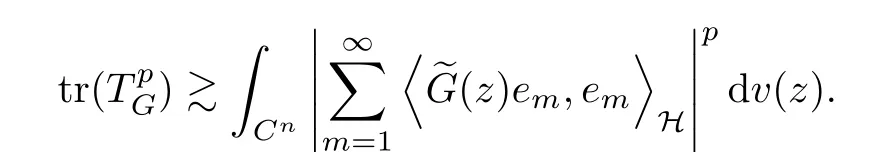
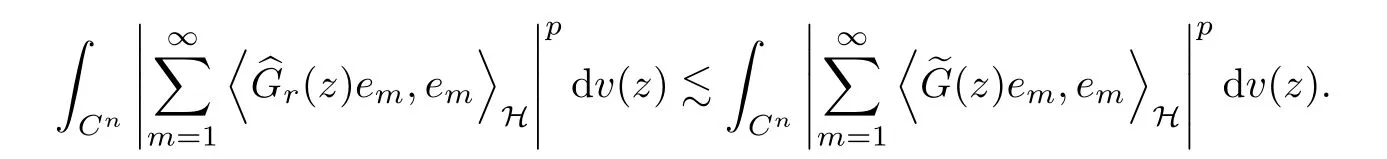
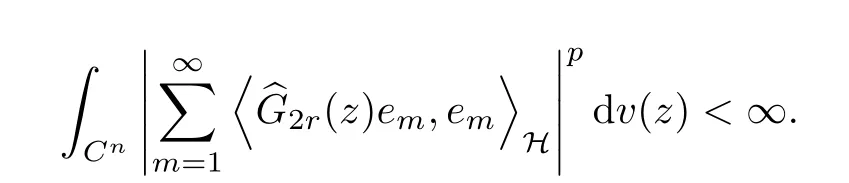
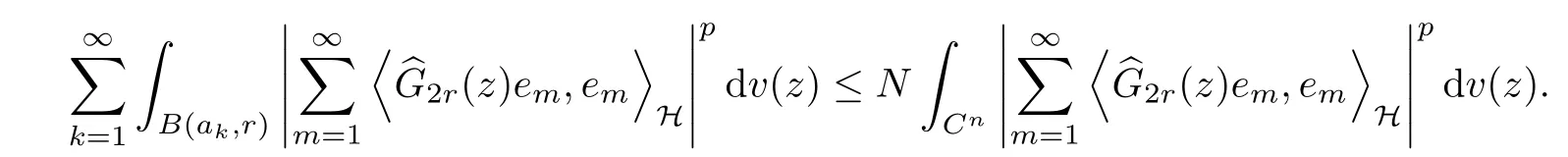
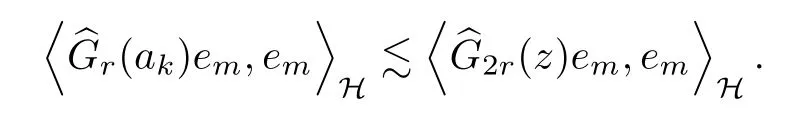
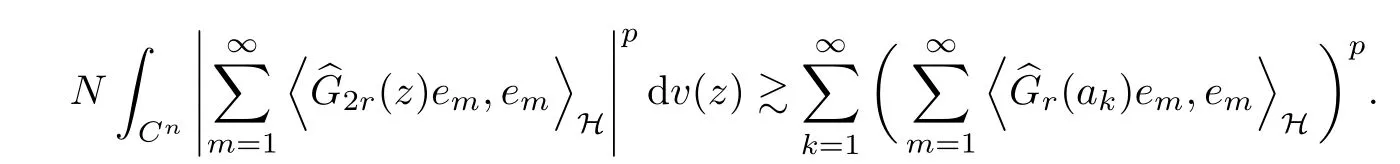
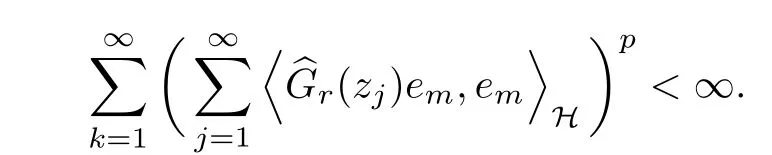
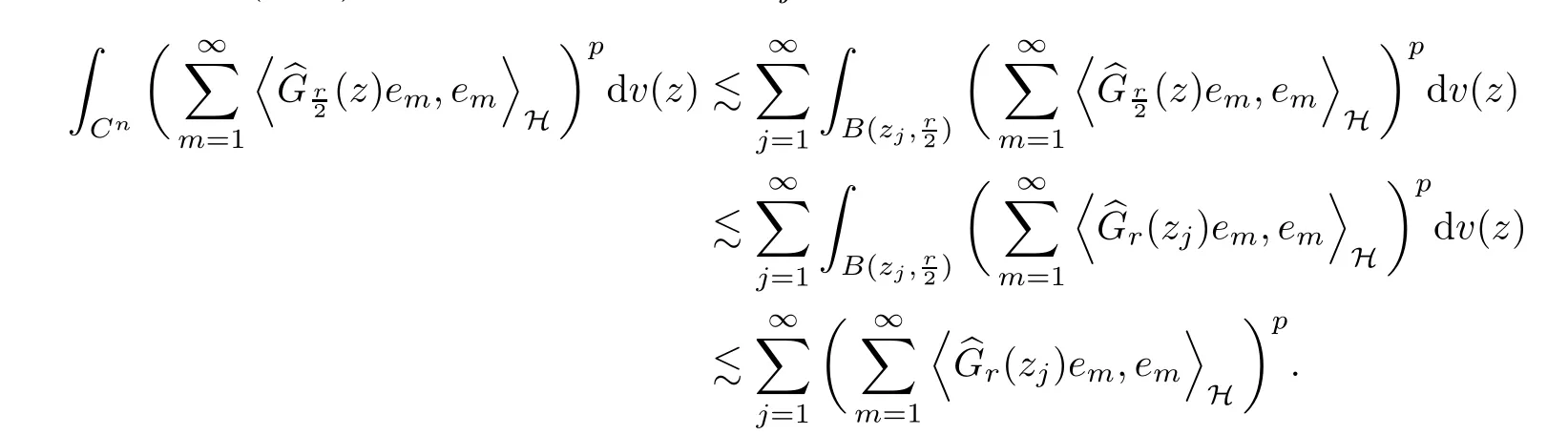
5 Toeplitz Operators in Sp With 0
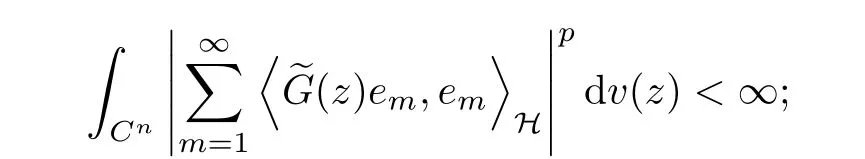
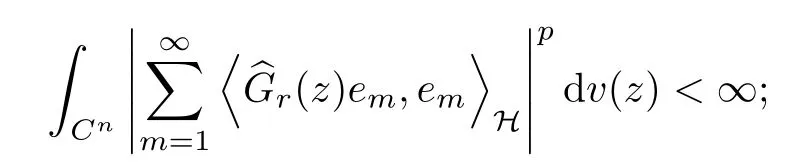
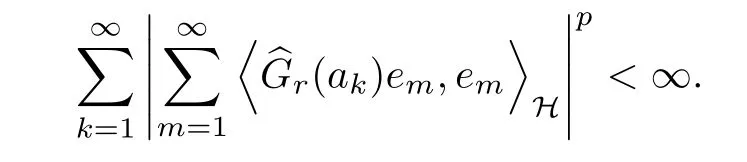
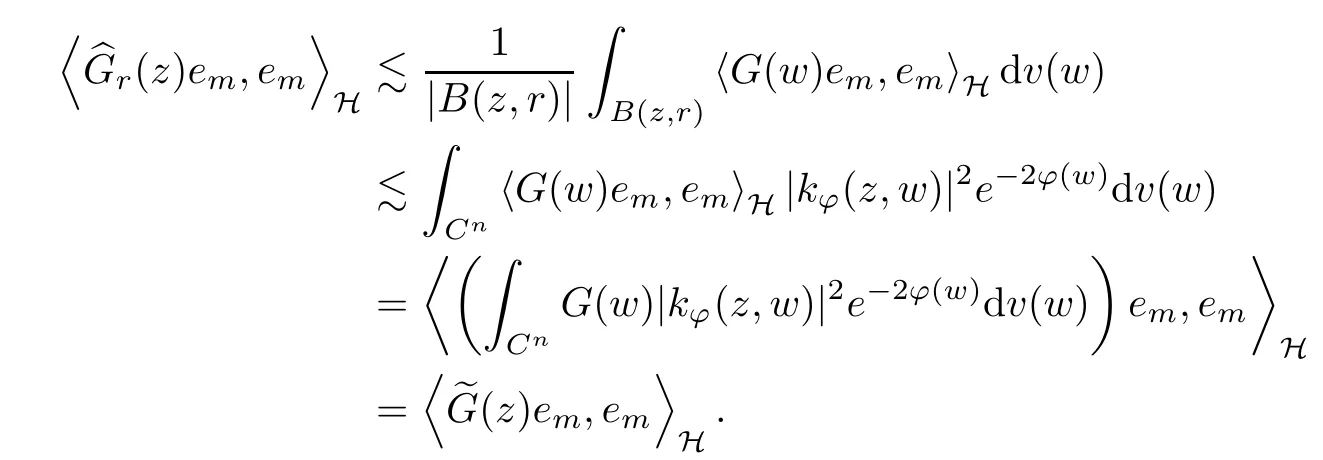
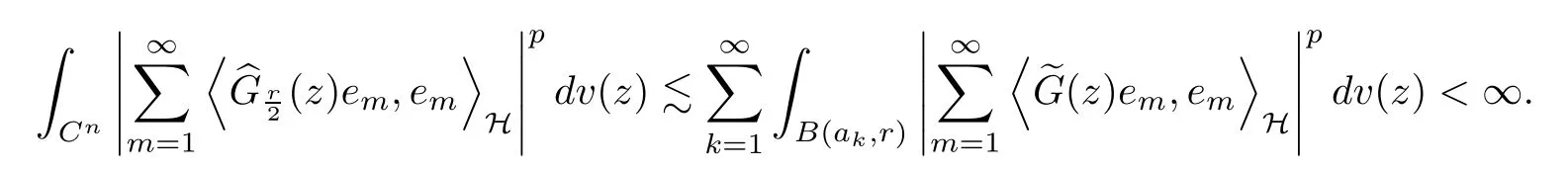
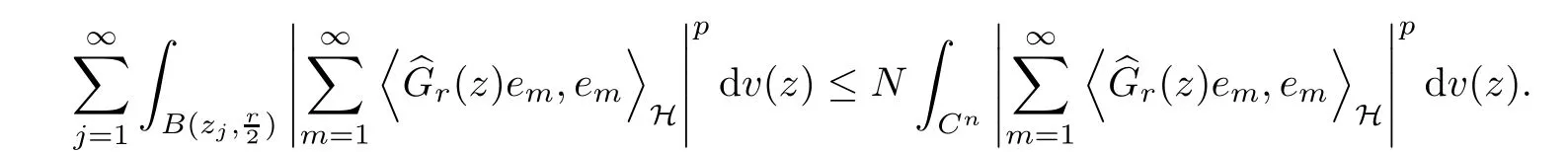
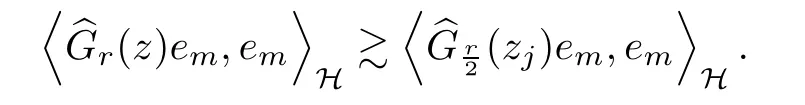
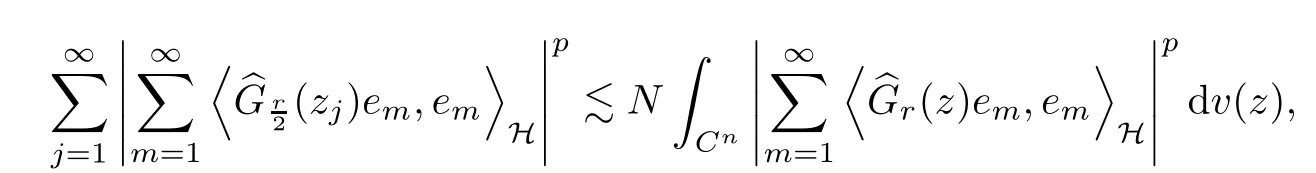
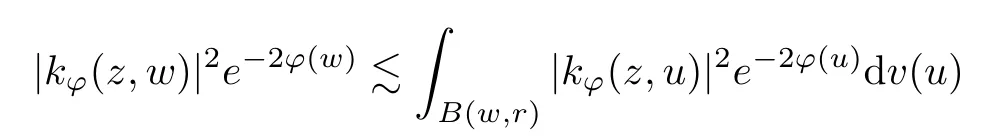
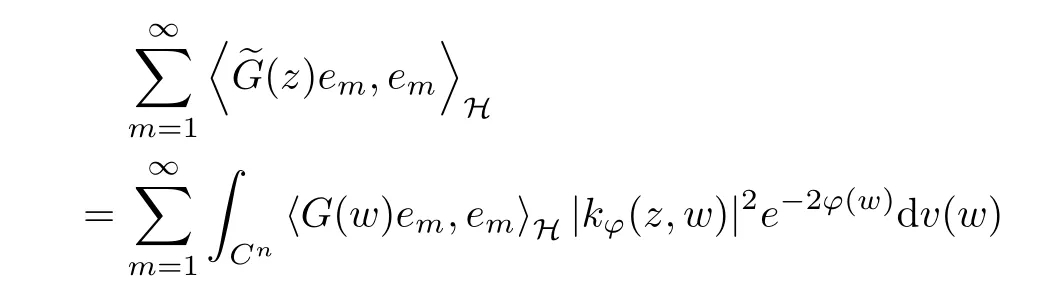
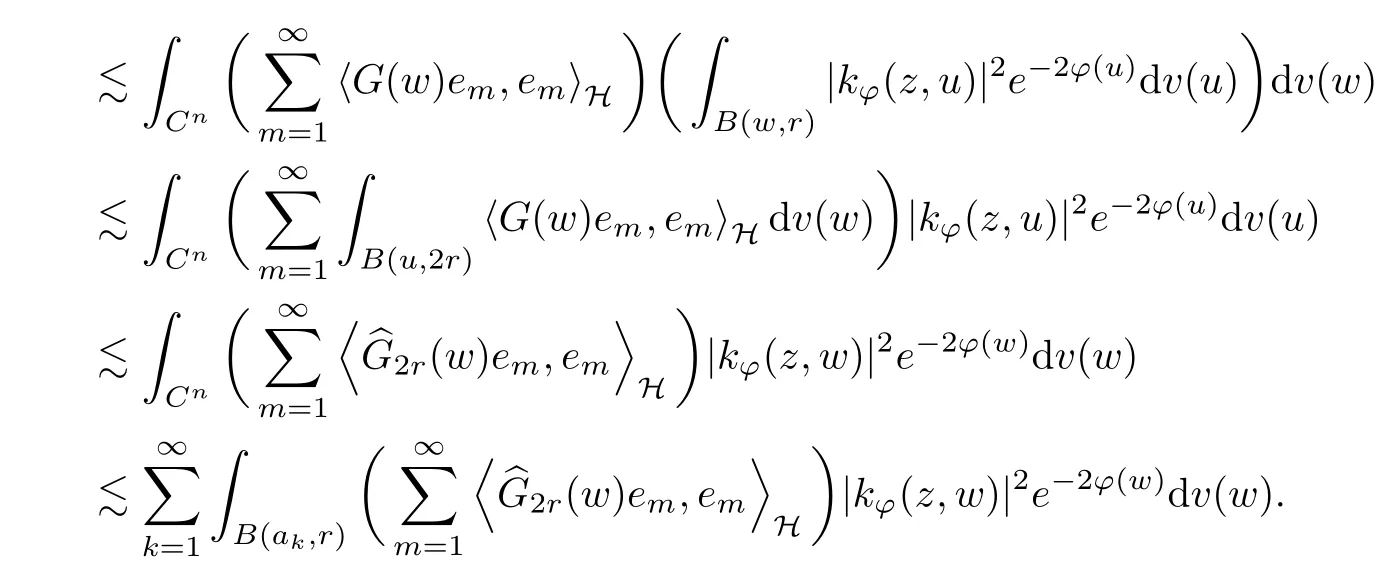
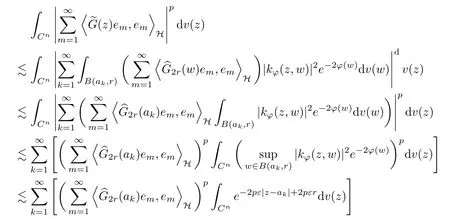
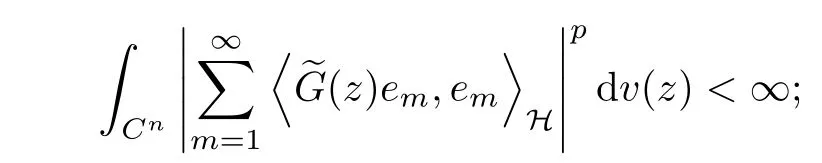
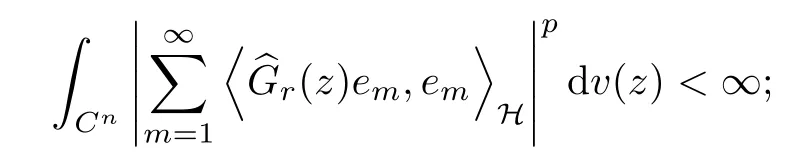
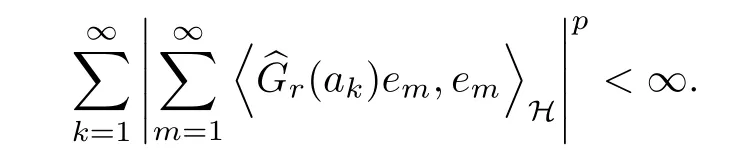
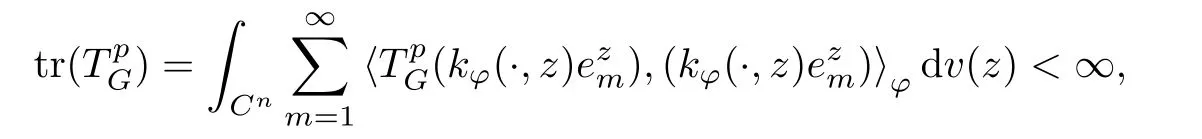
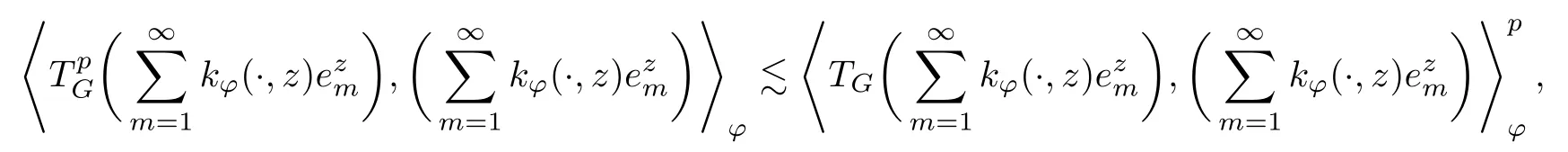
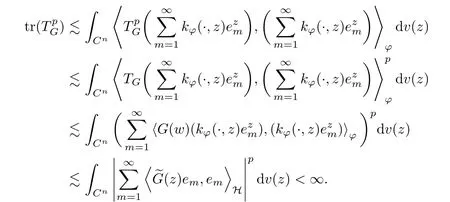
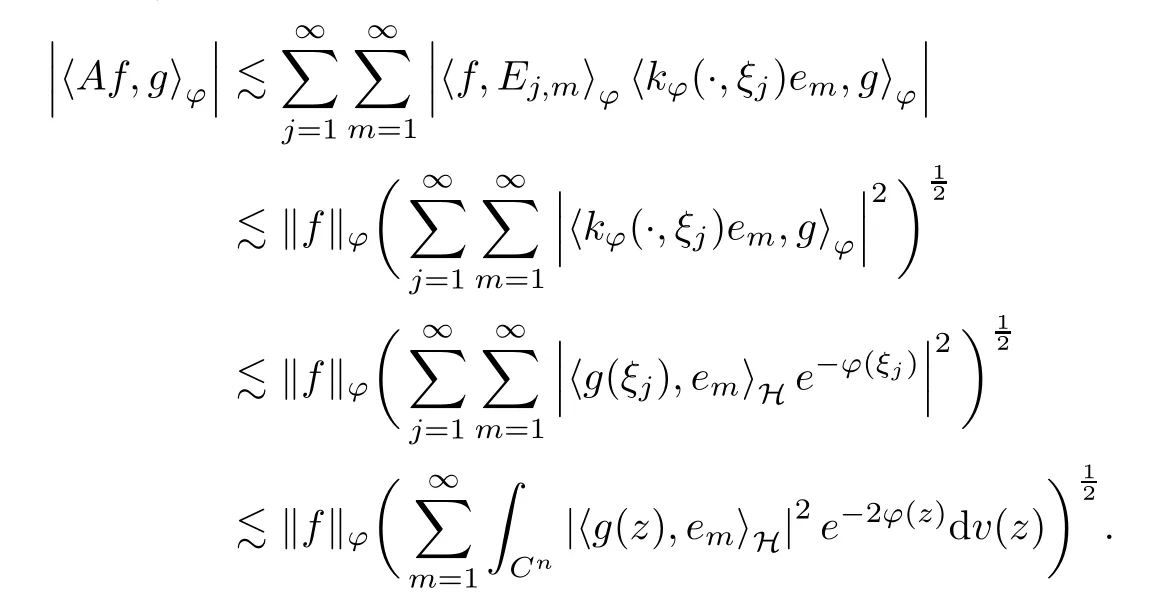
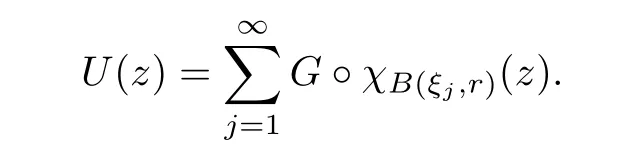
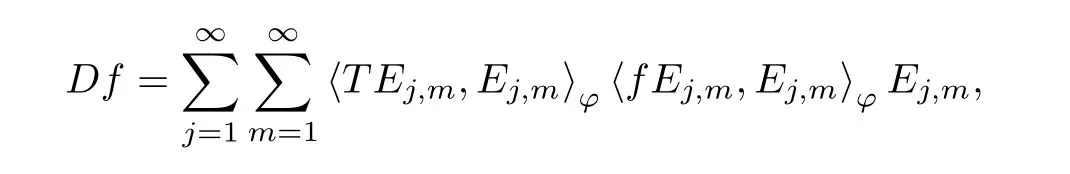
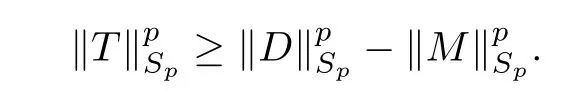

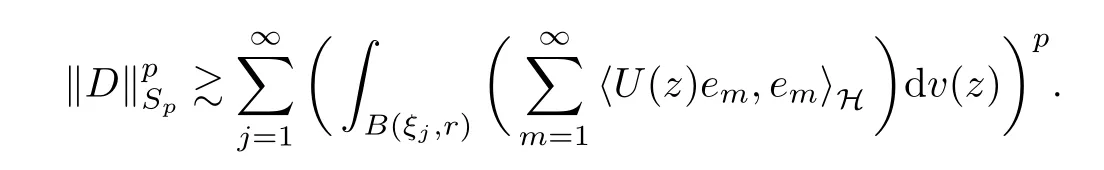
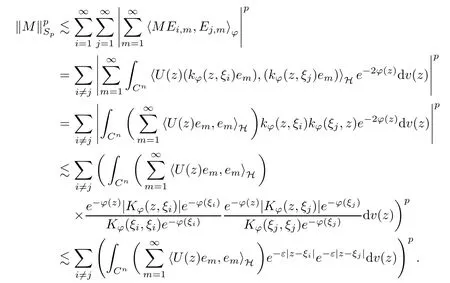
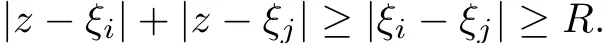
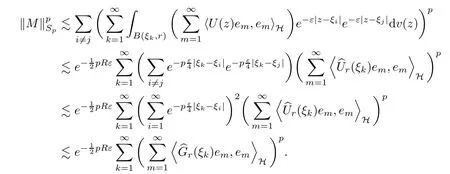
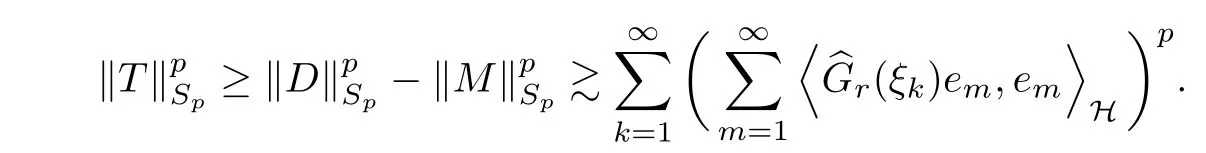
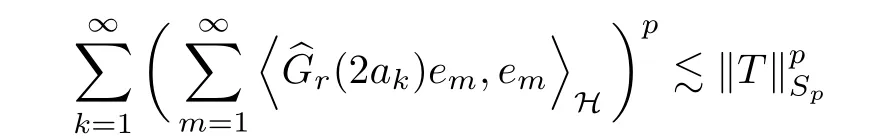
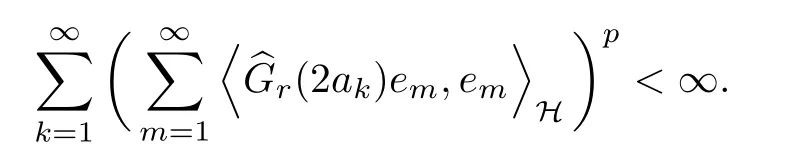
 Acta Mathematica Scientia(English Series)2020年3期
Acta Mathematica Scientia(English Series)2020年3期
