SYNCHRONIZATION OF SINGULAR MARKOVIAN JUMPING NEUTRAL COMPLEX DYNAMICAL NETWORKS WITH TIME-VARYING DELAYS VIA PINNING CONTROL?
K. S. ANAND
APS College of Engineering, Bangalore 560082, India
J. YOGAMBIGAI
MMES College of Arts and Science, Melvisharam, Tamilnadu, India
G. A. HARISH BABU
Reva Institute of Technology and Management, Bengaluru- 560064
M. SYED ALI
Department of Mathematics, Thiruvalluvar University, Vellore, Tamilnadu 632 115, India E-mail: syedgru@gmail.com
S. PADMANABHAN
RNS Institute of Technology, Channasandra, Bangalore 560098, India
Abstract This article discusses the synchronization problem of singular neutral complex dynamical networks (SNCDN) with distributed delay and Markovian jump parameters via pinning control. Pinning control strategies are designed to make the singular neutral complex networks synchronized. Some delay-dependent synchronization criteria are derived in the form of linear matrix inequalities based on a modified Lyapunov-Krasovskii functional approach. By applying the Lyapunov stability theory,Jensen’s inequality,Schur complement,and linear matrix inequality technique, some new delay-dependent conditions are derived to guarantee the stability of the system. Finally, numerical examples are presented to illustrate the effectiveness of the obtained results.
Key words Singular complex networks;synchronization;Lyapunov-krasovski method;markovian jump; pinning control; linear matrix inequality
1 Introduction
Over the past decade,complex networks have been studied intensively in various disciplines,such as sociology, biology, mathematics, and engineering [1–6]. A complex network is a large set of interconnected nodes, where the nodes and connections can be anything, and a node is a fundamental unit having specific contents and exhibiting dynamical behavior. There are two ways of connection between nodes: directed connection and undirected connection, and the connection relationship can be unweighted and weighted. According to different ways of connection and whether there are weights or not between nodes, we get some different kinds of complex networks, such as undirected unweighted network, directed weighted network, etc.A complex network can exhibit complicated dynamics which may be absolutely different from that of a single node.
The most well-known examples are electrical power grids, communication networks, internet, World Wide Web, metabolic systems, food webs, and so on. Hence, the investigation of complex dynamical networks is of great importance, and many systems in science and technology can be modeled as complex networks[8–10]. Time delay is encountered in many dynamical systems and often results in poor performance and even instability of control systems [11–13].Because delay is usually time-varying in many practical system, many approaches were developed to investigate the stability of systems with time-varying delay such as descriptor model transformation method; the improved bounding technique; free weighting matrices; and the properly chosen Lyapunov-Krasovskii functional (LKFs) (see [14–16] and references therein).
Synchronization is a kind of typical collective behaviors and basic motions in nature[17–19].Recently, one of the interesting and significant phenomena in complex dynamical networks is the synchronization of all dynamical nodes in a network. It is well known that there are many useful network synchronization phenomena in our real life, such as the synchronous transfer of digital or analog signals in communication networks [20]. More recently, adaptive synchronization in networks or coupled oscillators has received an increasing attention [21]. In particular,one of the interesting phenomena in complex networks is the synchronization, which is an important research subject with the rapidly increasing research, and there are amounts of results[22]. There are many different kinds of synchronization, such as generalized synchronization,phase synchronization, projective synchronization, cluster synchronization, and so on [23–27].Moreover, synchronization has some potential applications in real-world systems, such as synchronization phenomena on the Internet, synchronization related to biological neural networks.As we know the real-world complex networks normally have a large number of nodes. Therefore, it is usually difficult to control a complex network by adding the controllers to all nodes.To reduce the number of the controllers, a natural approach is to control a complex network by pinning part of nodes. In [28–32], the authors explored the controllability of complex networks via pinning. In [33], authors analyzed the synchronization of general complex dynamical network via pinning control.
Singular systems describe the physical systems better than the regular (nonsingular) ones.They have variety of physical processes such as power systems and circuit systems. These systems are sometimes called generalized systems, descriptor systems, differential-algebraic systems, or implicit systems. It has been noted that a considerable number of results of regular(nonsingular) systems were extended to singular systems (see references [34–37]). As pointed out in [38], singular systems can be introduced to improve the traditional complex networks to describe the singular dynamic behaviours of nodes.
Singular systems can be introduced to improve the traditional complex networks to describe the singular dynamic behaviors of nodes. Recently, there has been a growing interest in singular systems for their extensive application in control theory, circuits, economics, mechanical systems, and other areas, inspired by [39–42]. The neutral-type complex dynamic network of coupled identical nodes is described by a group of neutral functional differential equations, in which the derivatives of the past state variables are involved as well in the present state of the system [43]. Synchronization of neutral complex dynamical networks (NCDNs) with coupling time-varying delays is investigated in[44]. Synchronization of neutral complex dynamical networks with Markovian switching based on sampled-data controller is discussed in [45].
Motivated by the above, we investigate synchronization of Markovian jumping singular neutral complex dynamical network with time- delays via pinning control by utilizing a novel Lyapunov - Krasovskii functional. The novel delay dependent synchronization conditions are derived in terms of linear matrix inequalities, then synchronization problem is studied for the complex networks. By constructing a new Lyapunov-Krasovskii functional containing tripleintegral terms,employing Newton-Leibnitz formulation and linear matrix inequality techniques,and introducing free-weighting matrices,some robust global asymptotic stability criteria are derived in terms of linear matrix inequalities (LMIs). To the best of our knowledge, synchronization of singular neutral complex dynamical network with Markovian jumping and time delays via pinning control have received very little research attention, therefore, the main purpose of this article is to shorten such a gap. By employing some analysis techniques, less conservative sufficient conditions are derived in terms of LMIs. Finally, numerical example are provided to demonstrate the advantage and applicability of the proposed result.
NotationThe following notations are used throughout this article. Rndenotes the n dimensional Euclidean space and Rm×nis the set of all m×n real matrices. The superscript′T′denotes matrix transposition, and the notation X ≥Y (respectively, X < Y), where X and Y are symmetric matrices, means that X-Y is positive semidefinite (respectively, positive definite),anddenotes the Euclidean norm in Rn. If A is a square matrix,denote by λmax(A)(respectively, λmin(A)) means the largest(respectively, smallest) eigenvalue of A. Moreover, let(?,F,{Ft}t≥0,P)be a complete probability space with a filtration{Ft}t≥0satisfying the usual conditions (that is, the filtration contains all P-null sets and is right continuous). The asterisb?in a symmetric matrix is used to denote term that is induced by symmetry. Given a complete probability space{?,F,{Ft}t≥0,P},let a natural filtration{Ft}t≥0satisfy the usual conditions,where ? is the sample space, F is the algebra of events, and P is the probability measure defined on F. Let {r(t)(t ≥0)} be a right-continuous Markovian chain on the probability space (?,F,{Ft}t≥0,P) taking values in the finite space S = {1,2,··· ,m} with generator Π={πij}m×m(i,j ∈S) given by
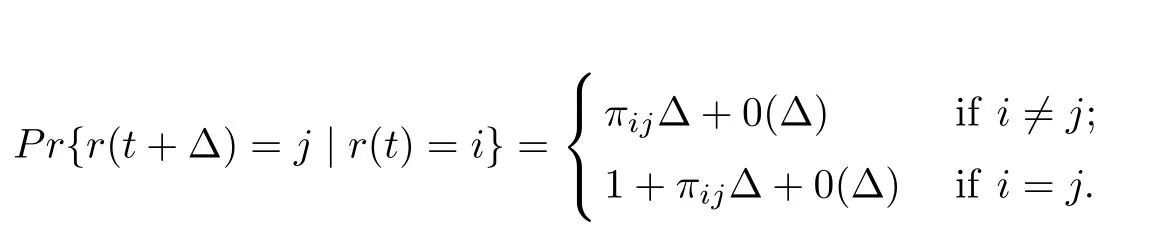
Here, ?>0 and πij≥0 is the transition rate from i to j ifwhile
2 Problem Formulation and Preliminaries
2.1 Problem description
Consider the following Markovian jumping singular neutral complex dynamical network with time varying distributed delay consisting of N identical nodes, in which each node is an n-dimensional dynamical subsystem:
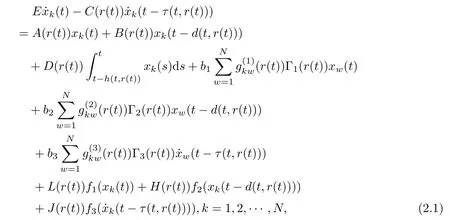
where E ∈Rn×nis a singular matrix and rank(E) = r(0 < r < n);xk(t) ∈Rnis the state variable of the node k ∈1,2,··· ,N;{r(t)(t ≥0)} is the continuous-time Markov process which describes the evolution of the mode at time t;A(r(t)),B(r(t)),C(r(t)),D(r(t)),L(r(t)),H(r(t)),and J(r(t))∈Rn×nare parametric matrices with real values in mode r(t);and f1,f2,f3:Rn→Rnare continuously nonlinear vector functions which are,with respect to the current state xk(t),the delayed state xk(t ?d(t,r(t))) and the neutral delay state(t ?τ(t,r(t))).
The nonlinear functions are globally Lipschitz,

where lk1,lk2, and lk3are non-negative constants.
Γ1(r(t)) ∈Rn×n, Γ2(r(t)) ∈Rn×n, and Γ3(r(t)) ∈Rn×nrepresent the inner-coupling matrices linking between the subsystems in mode r(t)., G(2)(r(t)) =andare the coupling configuration matrices of the networks representing the coupling strength and the topological structure of the SNCDN in mode r(t),in whichis defined as follows: if there exists a connection between kthandnodes, then, otherwise,and
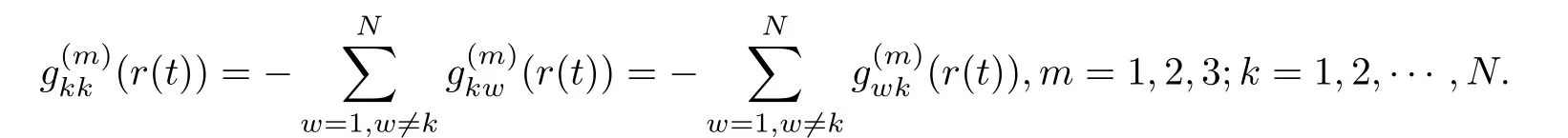
For simplicity of notations,we denote A(r(t)),B(r(t)),C(r(t)),D(r(t)),L(r(t)),H(r(t)),J(r(t)),G(m)(r(t)),Γm(r(t)),(m=1,2,3), by Ai,Bi,Ci,Di,Li,Hi,Ji,,Γmifor r(t)=i ∈s.
Remark 2.1The synchronization of Markovian jumping SNCDN (2.1) is investigated in this work, which is devoted to revealing the effect of pinning controller over the Markovian switching network topologies. The network topology switching is governed by a time homogenous Markov process, whose state space corresponds to all the possible topologies. However, a general complex network always has a fixed network topology, which can not describe the situation changing, so the research on the complex networks under randomly switching topologies,such as SNCDN (2.1), is very significant and important.
Assumption 1τ(t,r(t)),h(t,r(t)),and d(t,r(t))denote the mode-dependent time-varying neutral delay, distributed delay, and retarded delay, respectively. They are assumed to satisfy the followings:
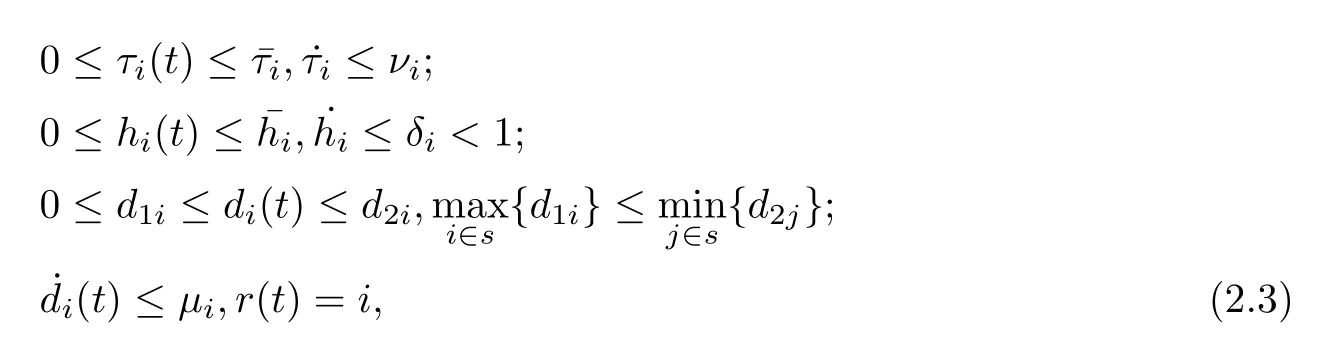
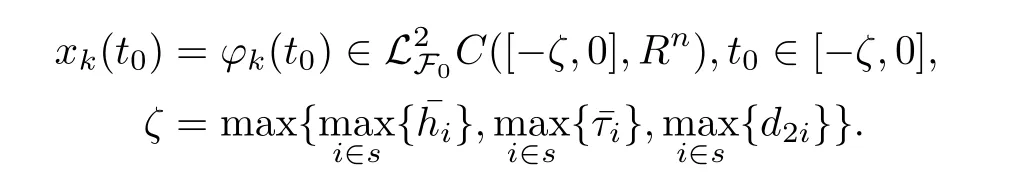
Correspondingly the response complex network with the control inputs uk(t) ∈RN(k =1,2,··· ,N) can be written as
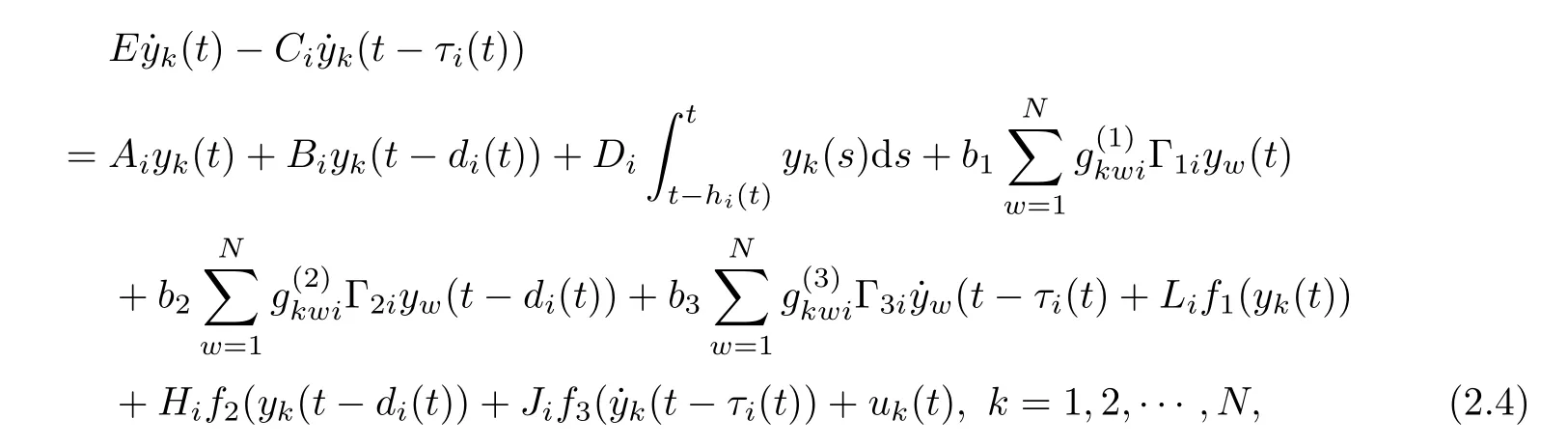
where uk(t) is defined by
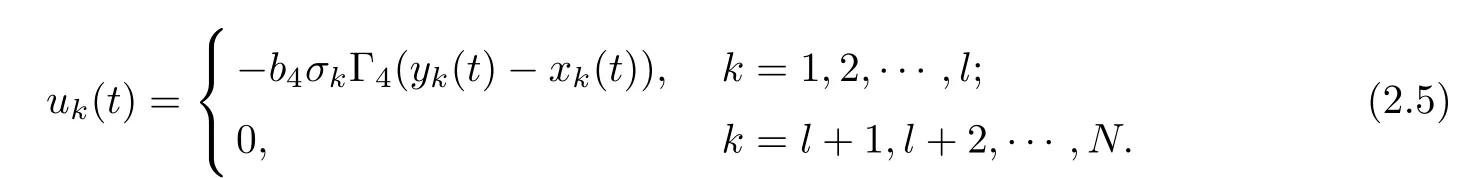
2.2 Basic ideas and Lemmas
In this section, we provide some definitions and lemmas which are absolutely necessary to derive the proposed synchronization criterion.
Definition 2.2([50]) Complex dynamical network (2.1) is said to be global (asymptotically) synchronized by pinning control, if
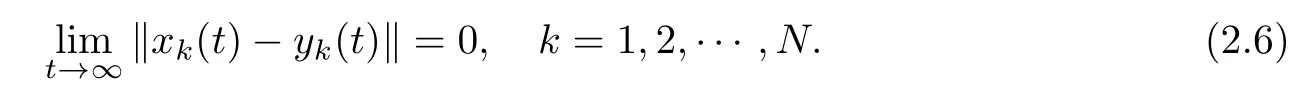
Definition 2.3([51]) The pair (E,Ai+b1Γ1iλk?b4σkΓ4) is said to be regular, if the det(aE ?(Ai+b1Γ1iλk?b4σkΓ4)), for some finite complex number a, is not identically zero.
Definition 2.4([51]) The pair (E,Ai+b1Γ1iλk?b4σkΓ4) is said to be impulse free, if deg(det(aE ?(Ai+b1Γ1iλk?b4σkΓ4)))=rank(E) for some finite complex number ‘a(chǎn)’.
Lemma 2.5([50]) The eigenvalues of an irreducible matrix G = (gkw) ∈RN×Nwithsatisfy the following properties:
(i) Real parts of all eigenvalues of G are less than or equal to 0 with multiplicity 1;
(ii) G has an eigenvalue 0 with multiplicity 1 and the right eigenvector (1,1,··· ,1)T.
Lemma 2.6([52]) The pair (E,Ai+b1Γ1iλk?b4σkΓ4) is regular and impulse free if and only if there exist matrices Pkisuch that the following inequalities hold for k =2,3,··· ,N :
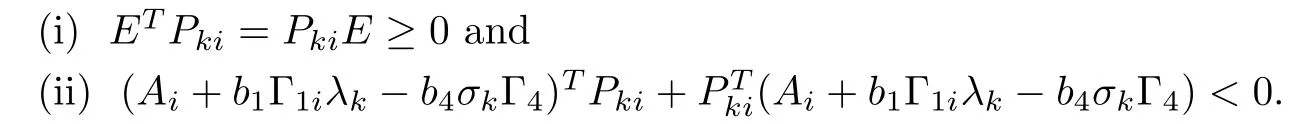
Lemma 2.7([53]) If for any constant matrix R ∈Rm×m,R=RT>0, scalar γ >0, and a vector function ? : [0,γ] →Rmsuch that the integrations concerned are well defined, the following inequality holds:
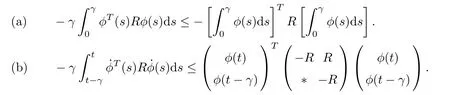
Let the error be ek(t) = yk(t)?xk(t). So, the error dynamics of Markovian jumping SNCDN(2.1) can be derived as follows:
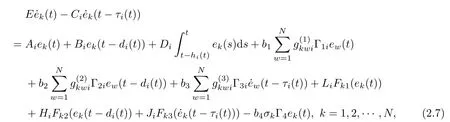
Remark 2.8The pinning controllers are applied to achieve synchronization of the Markovian jumping SNCDN (2.1). It can be seen that the synchronization problem of (2.1) is equivalent to the stabilization problem of the error dynamical systems (2.7) at the origin. The controller (2.5) accelerate each node to synchronizing with the target node according to the instantaneous state information, and the similar one also can be found in [28]. We only exert control actions on the pinned nodes to achieve the synchronization and reduce the number of controllers.
Remark 2.9The novelty of this article can be summarized as follows: (1) Synchronization of Markovian jumping singular neutral complex dynamical networks via pinning control is considered in this article; (2) A new Lyapunov-Krasovskii functional is constructed with triple-integral term.
3 Main Results
3.1 Asymptotic stability of complex dynamical systems
In this section,we derive delay-dependent stability criteria for the error dynamical network system (2.7). We also discuss the impact of additive time-varying delays on the stability of the system.
Denoting σk=0(k =l+1,l+2,··· ,N),then we may write the error system in its compact form as
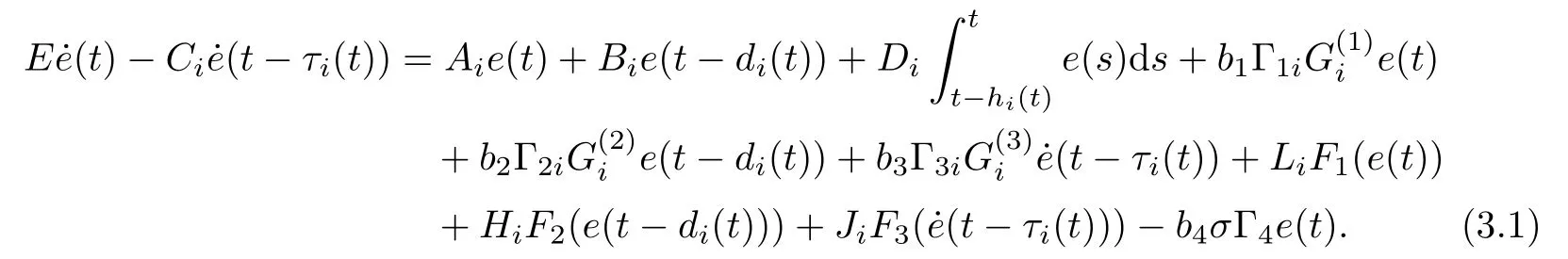
where e(t) = (e1(t),e2(t),··· ,eN(t)), F1(e(t)) = (F11(e1(t)),F21(e2(t)),··· ,FN1(eN(t))),F2(e(t ?di(t))=(F12(e1(t ?di(t)),F22(e2(t ?di(t)),··· ,FN2(eN(t ?di(t))), F3((t ?τi(t)))=(F13((t ?τi(t))),F23((t ?τi(t))),··· ,FN3((t ?τi(t)))), and σ =diag{σ1,σ2,··· ,σN}.
By the properties of the outer-coupling matrix(a=1,2,3), there exists a unitary matrix U =[U1,U2,··· ,UN]∈RN×Nsuch that UT=ΛiUTwith Λi=diag{λ1i,λ2i,··· ,λNi}(a = 1,2,3) and UUT= I. Using the nonsingular transform e(t)U = z(t) = [z1(t),z2(t),··· ,zN(t)]∈RN×N, from equation (3.1), it follows the matrix equation
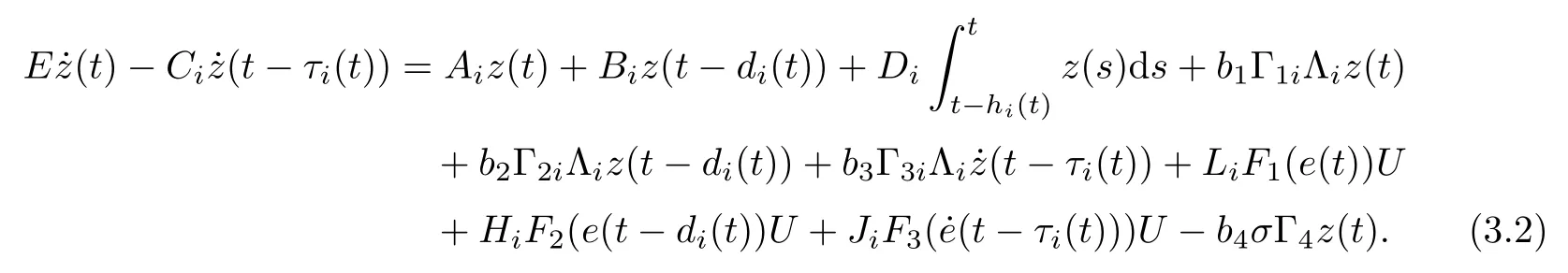
In a similar way, model (3.2) can be written as
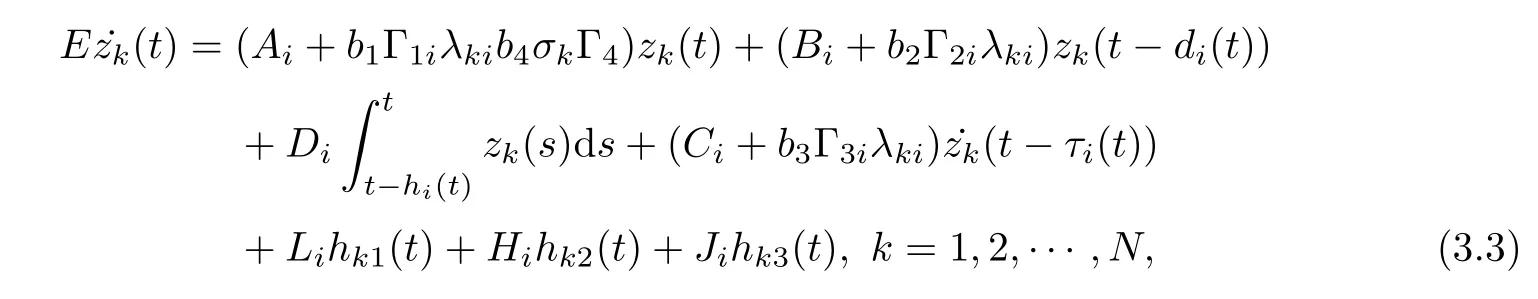
where hk1(t)=F1(e(t))Uk,hk2(t)=F2(e(t ?di(t))Uk, and hk3(t)=F3(˙e(t ?τi(t)))Uk.
So far, we transformed the synchronization problem of the singular complex dynamical networks (3.1) into the synchronization problem of the N pieces of the corresponding error dynamical network (3.3). From Lemma 2.5, λi1= 0 and z1(t) = e(t)U1= 0. Therefore, if the following (N ?1) pieces of the corresponding error dynamical network,
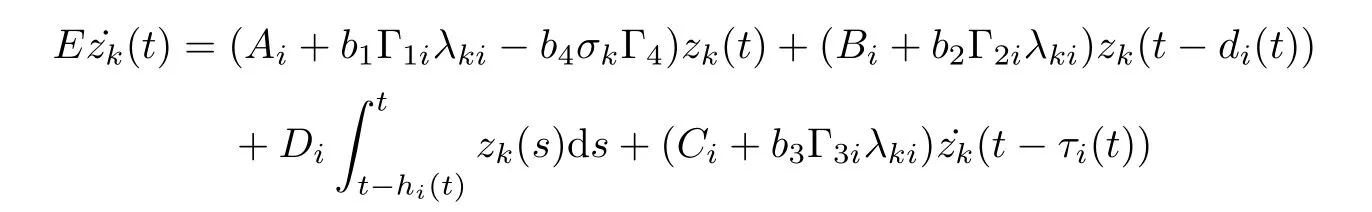

are asymptotically stable, which implies that the synchronized states (3.1) are asymptotically stable.
Let us define
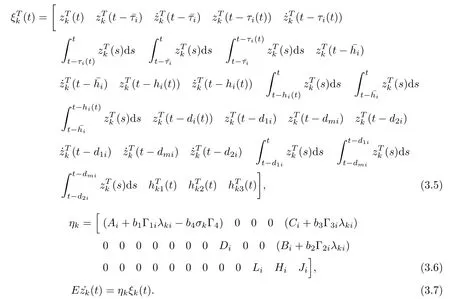
The inequality(2.2)and the Lipschitz continuity of hk1(t)can be used to make hk1(t)to satisfy

where ukwis the ω-th element of Ukand=max lk1. Therefore, the following inequality

holds, if the inequality
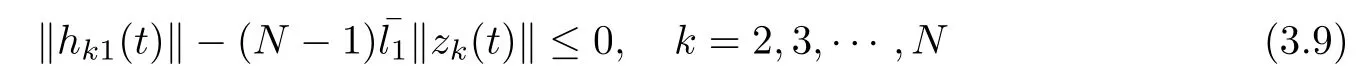
is satisfied. Similarly, the following inequalities holds:
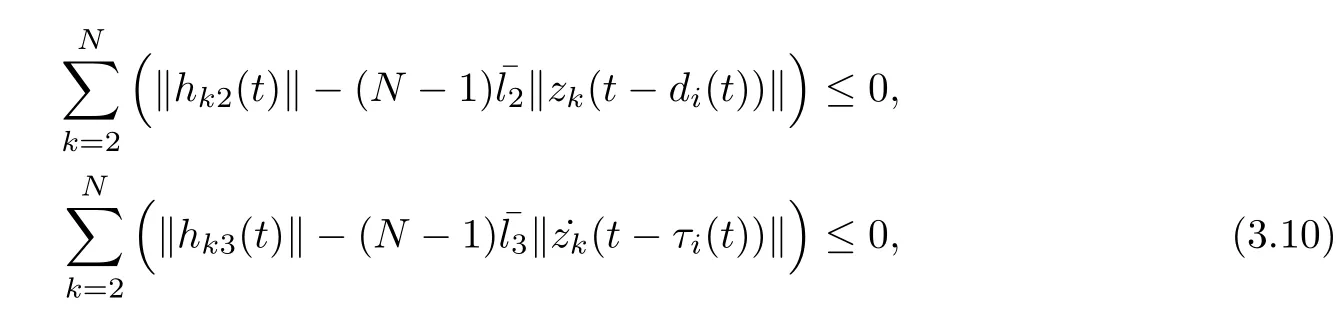
if the following inequalities are satisfied that
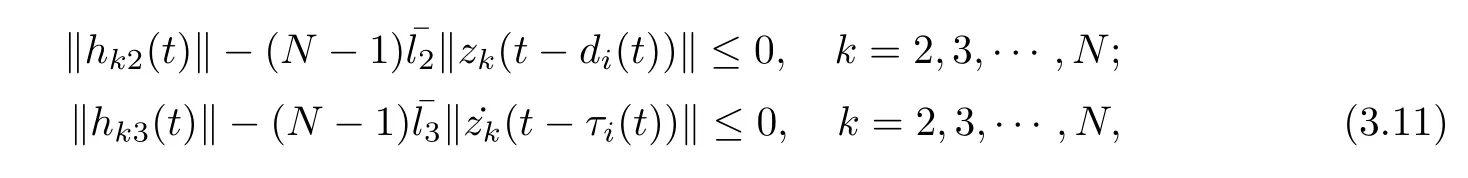

where
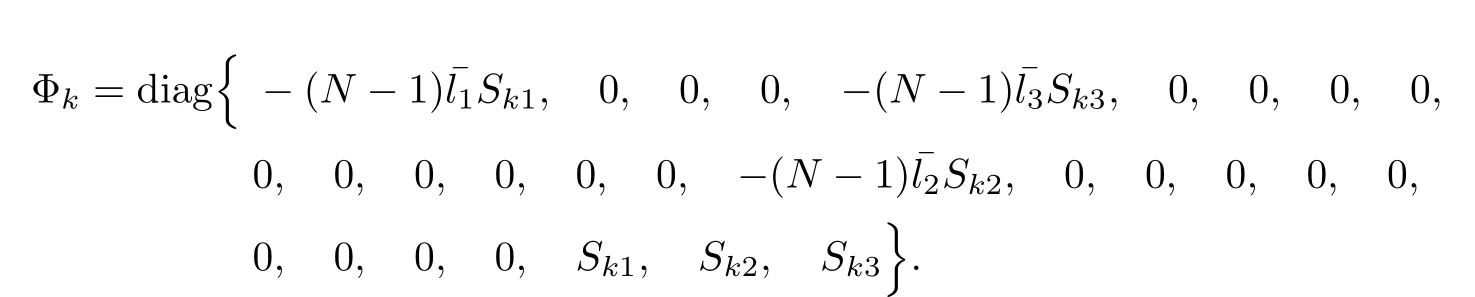
Theorem 3.1For given scalars,νi,,σi,d1i,d2i,μiand constant scalar dmisatisfying d1i< dmi< d2i, the Markovian jumping singular error dynamical network (3.4) is asymptotically stable if there exist positive constants αk, matrices Pki>0,Qk1i>0,Qk2i>0,Rk1i>0,Rk2i> 0, Tk1i> 0, Qkj> 0,Rkj> 0 (j = 3,4),Tkj> 0 (j = 2,3,4),Ukj> 0 (j = 1,2,3),Wkj> 0, Mkj> 0,Nkj> 0 (j = 1,2,3,4,5), and positive diagonal matrices Skj(j = 1,2,3)such that the following LMIs hold for all i ∈S:
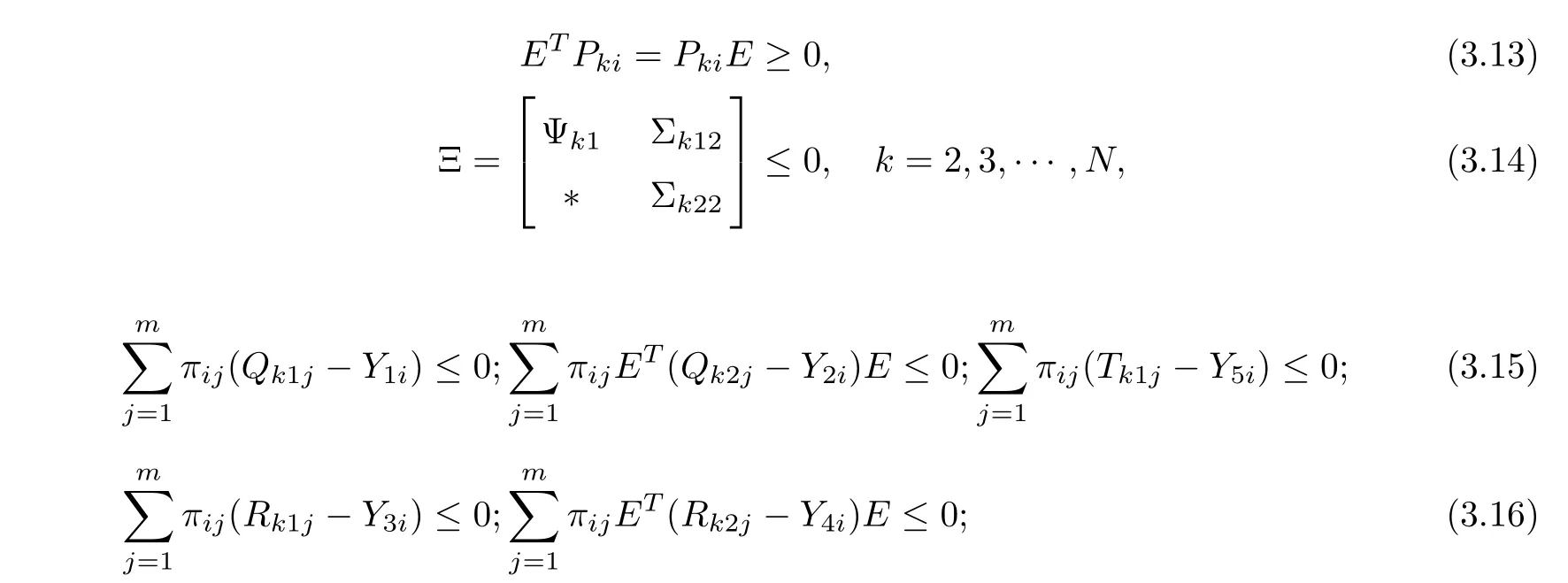
where


ProofConstruct the Lyapunov-Krasovskii functional:
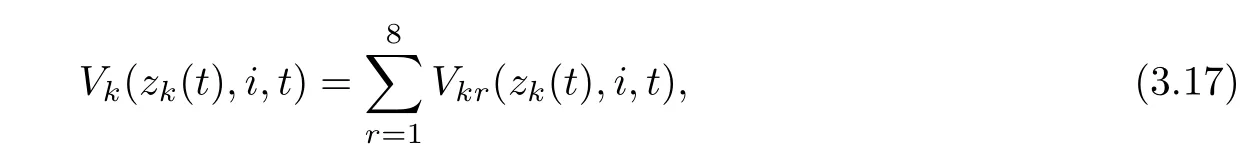
where
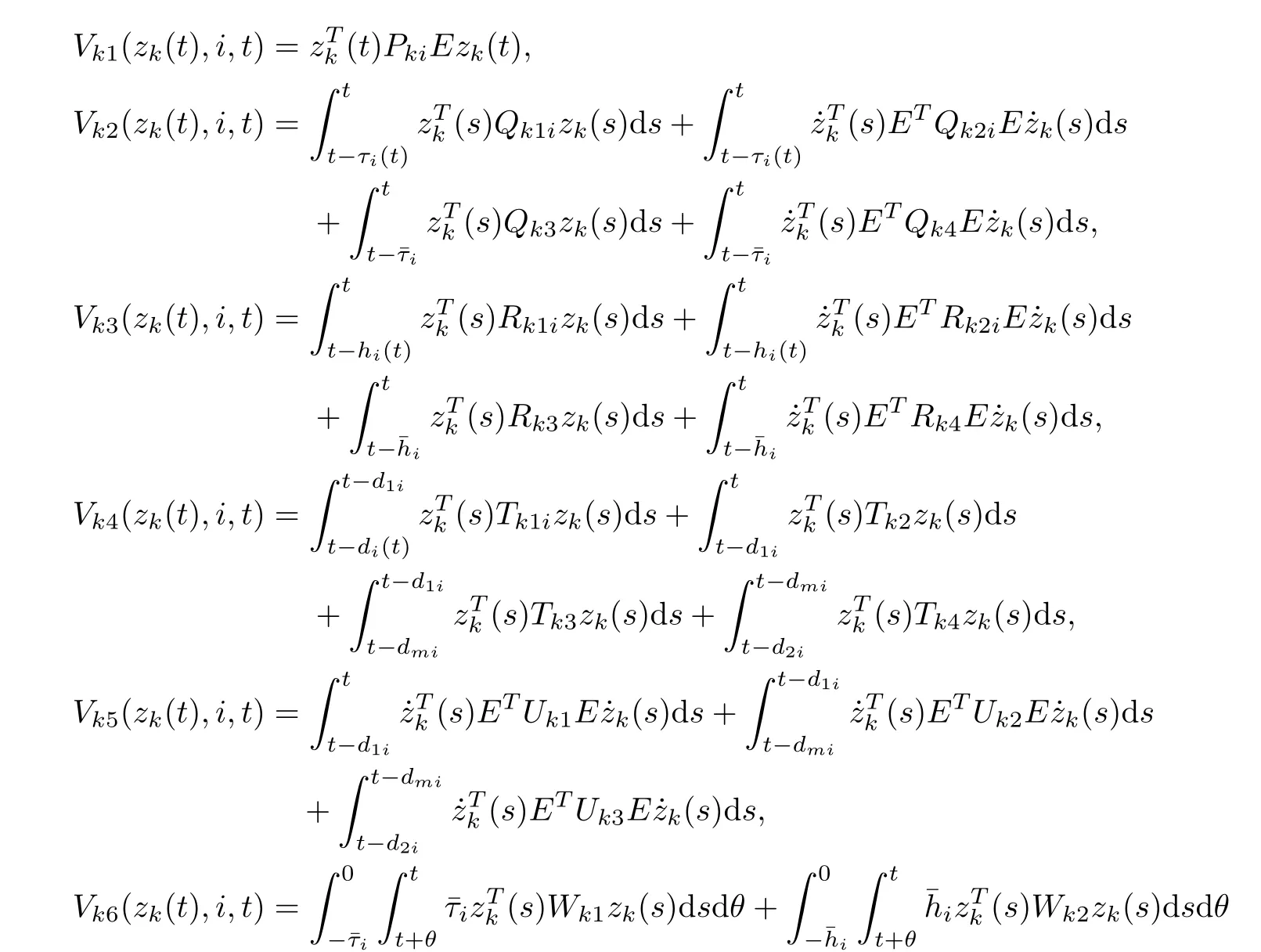

The derivative of Vkr(zk(t),i,t) along the trajectory of (3.4) with respect to t is given by
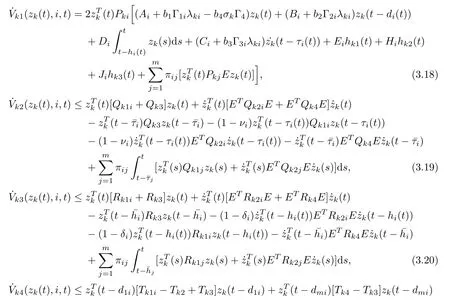

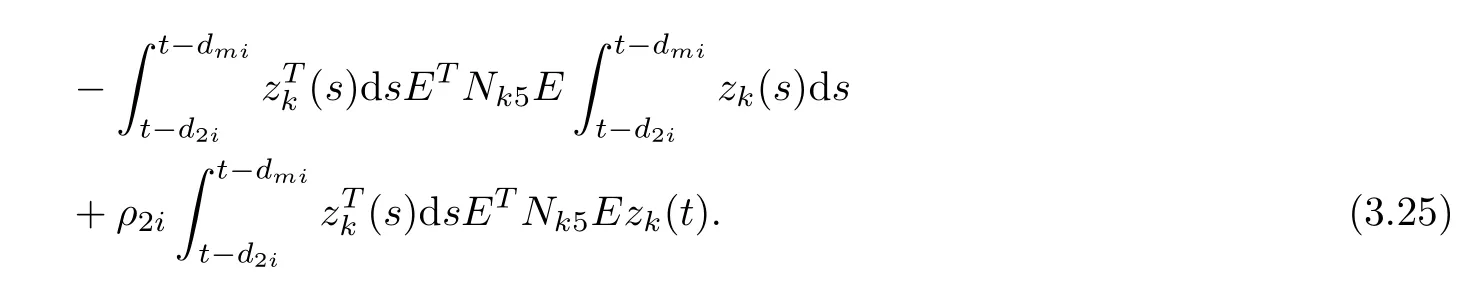
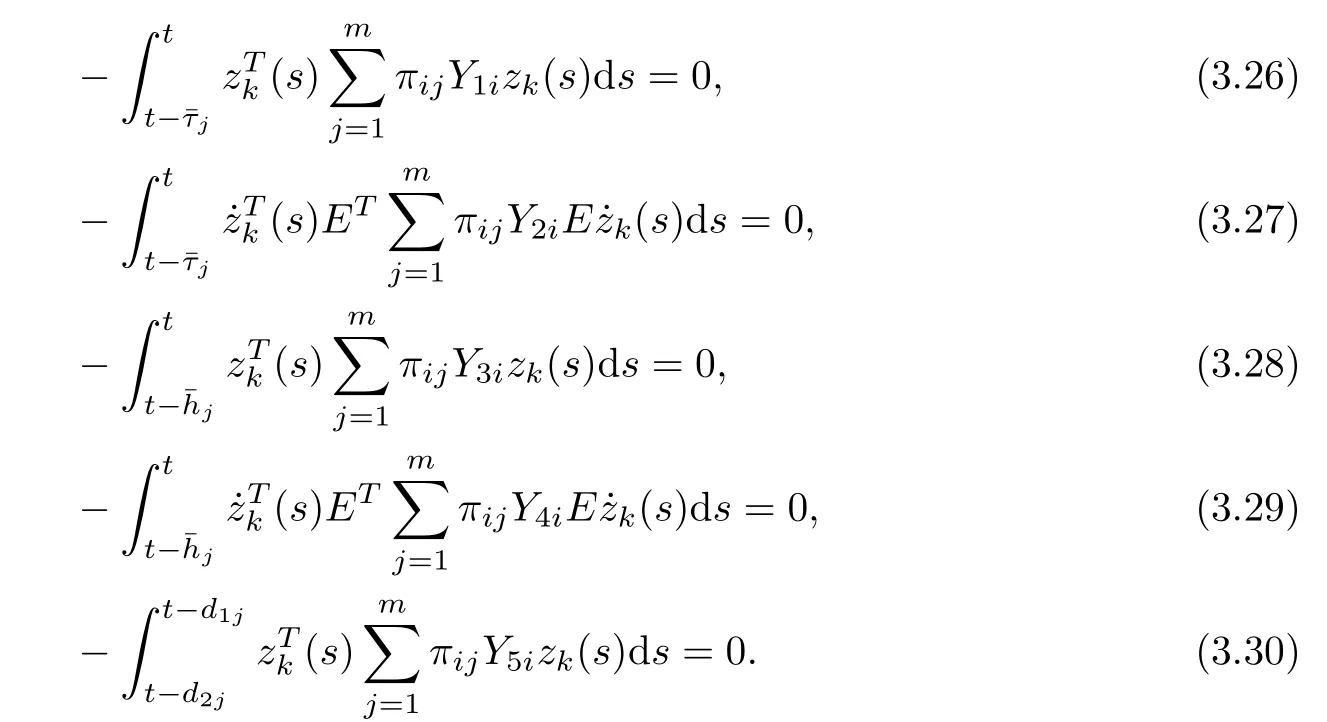
Notice (a) of Lemma 2.7, then,
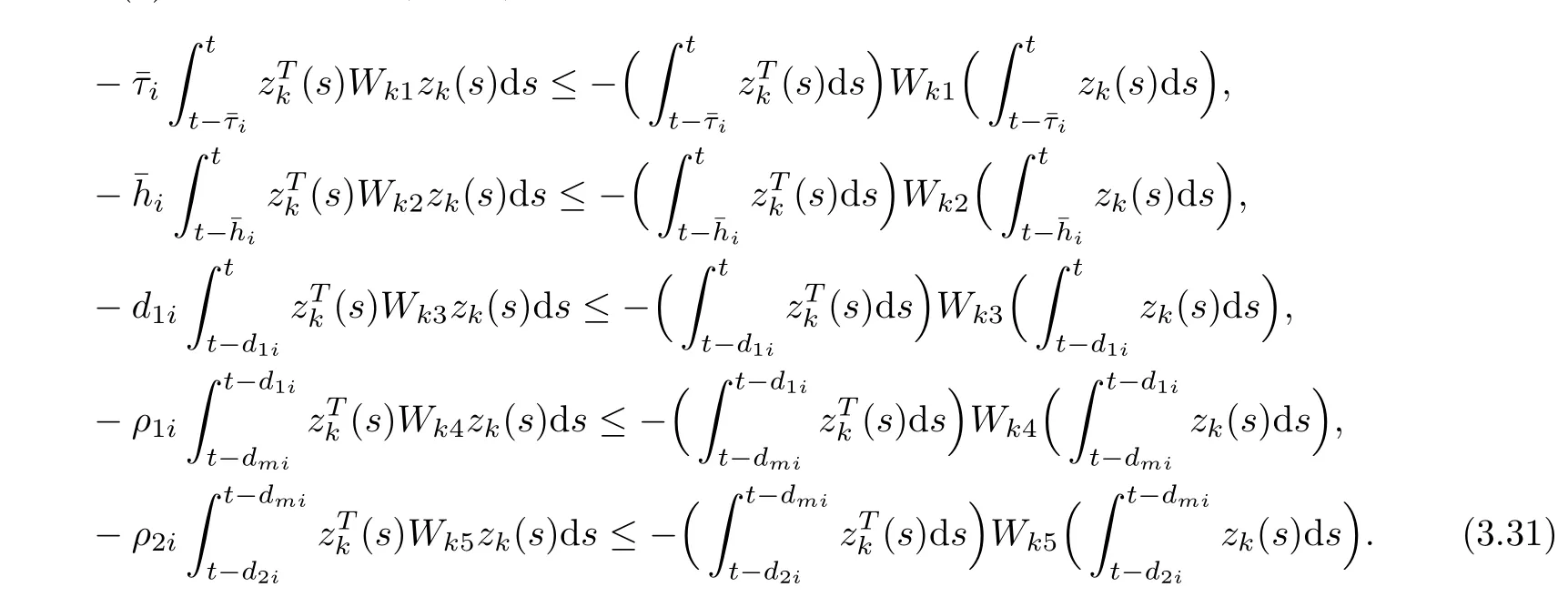
Notice (b) of Lemma 2.7, then,
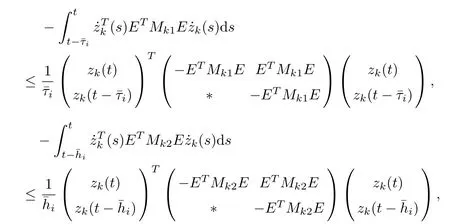
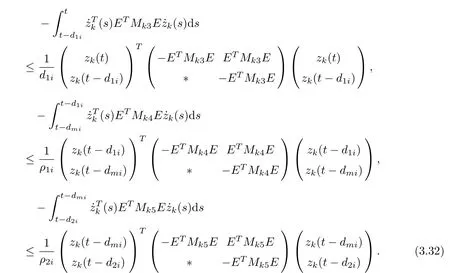
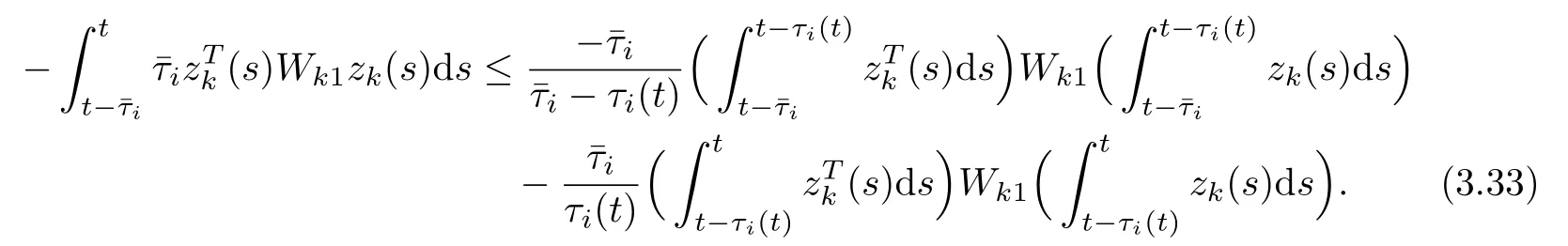
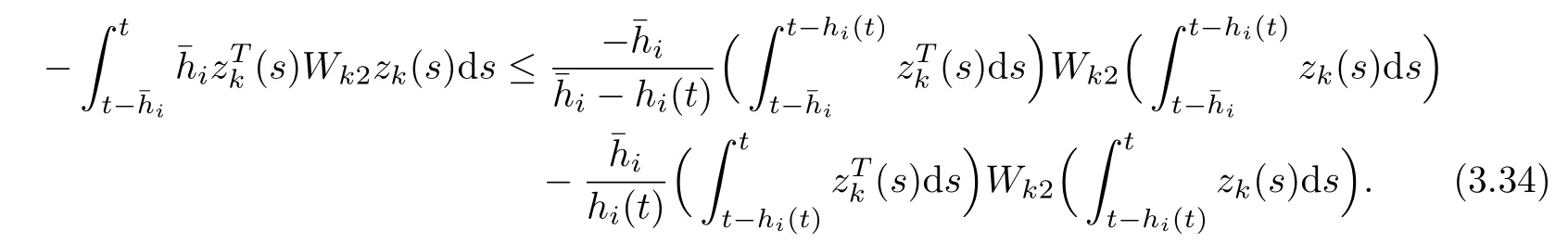
From equations (3.12) and (3.17)–(3.34), we obtain
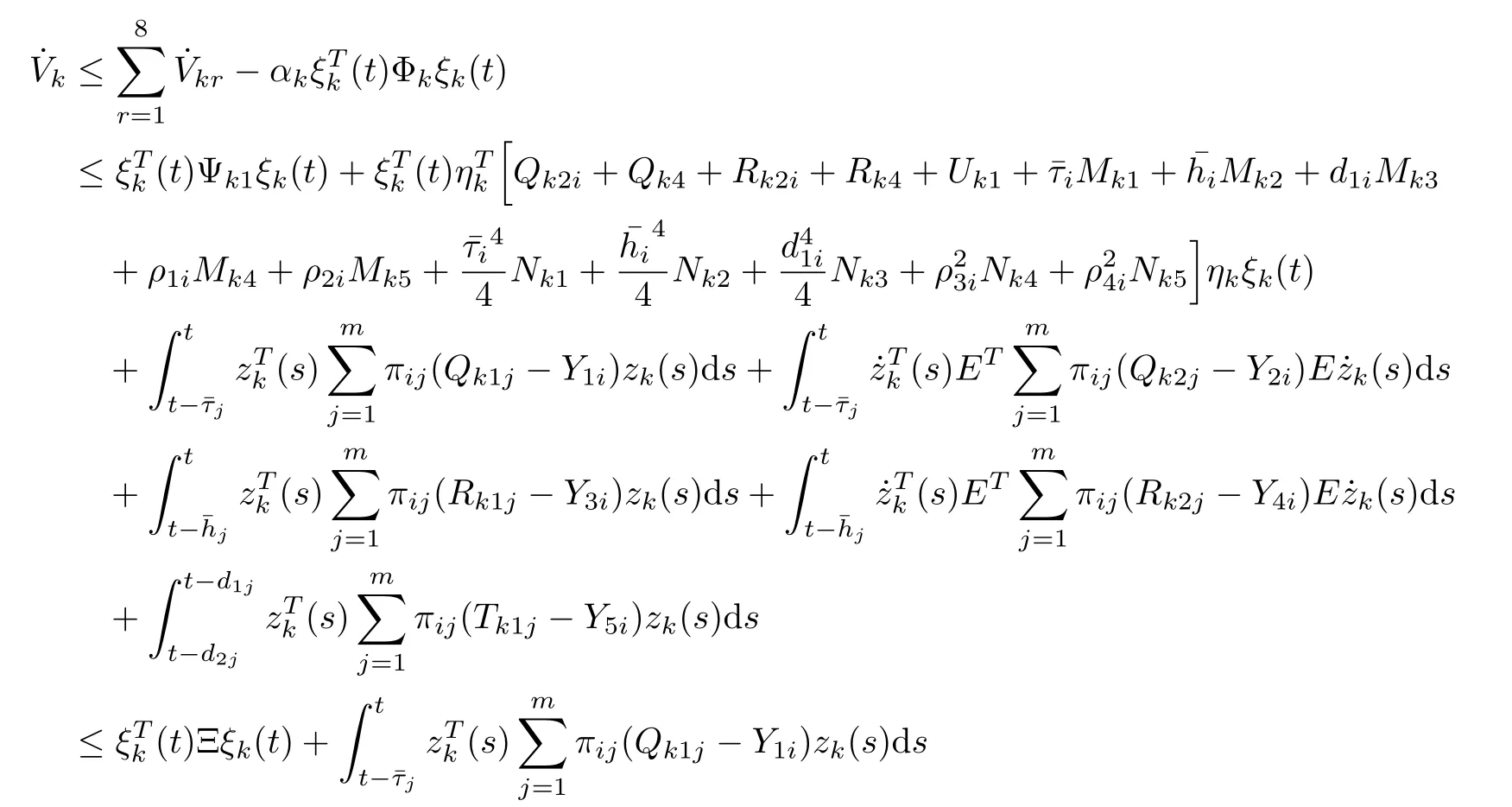
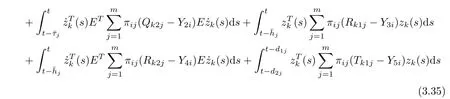
By Schur complement Lemma, we get (3.14), and

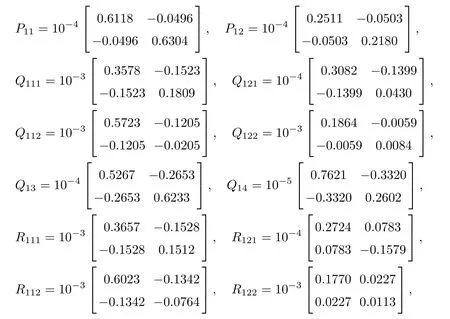
As ETPki=PkiE ≥0, the stable result cannot be obtained via the Lyapunov stability theory because the rank of ETPkiin the Lyapunov function Vk1(zk(t),i,t) is r By Lemma 2.6,it is clear that the pair(E,Ai+b1Γ1iλk?b4σkΓ4)is regular and impulse free whenever inequalities(3.13)–(3.16)hold. Then,the nonsingular matrices areand. The following decomposition holds: where Xk1∈Rr×n, Xk2∈R(n?r)×n, Yk1∈Rn×r,Yk2∈Rn×(n?r), and∈Rr×r, k =2,3,··· ,N. The network system (3.4) is equivalent to If we choose Wk,such that,which leads This completes the proof. Remark 3.2In the literature,the authors([2,5,7,13,20,21])investigated the problem of complex dynamical networks with time delay components. It is noted that unfortunately in the existing literature the problem of synchronization criteria for a class of singular neutral complex dynamical networks with distributed delay and Markovian jump parameters via pinning control has not been considered yet. Motivated by this,in this article we provided a sufficient condition to ensure that the SNCDN (3.1) is global (asymptotically) synchronized. Remark 3.3Synchronization of the Markovian jumping neutral complex dynamical networks is considered in[45]. In this article,Markovian jumping singular neutral complex dynamical networks with pinning control is employed. Synchronization conditions are established in the form of linear matrix inequalities(LMIs). The solvability of derived conditions depends not only on the pinned nodes but also on the initial values of the Markovian jumping parameter.It is pointed out that there is no useful term is ignored while maintaining our stability results. In this section, numerical examples are presented to demonstrate the effectiveness of the synchronization for pinning control. Example 4.1Consider the following time-varying delayed Markovian jumping SNCDN with 3-node and mode s=2, with (a = 1,2,3),Ji= Hi= 0,i = {1,2}. Let us consider b1= 1,b2= b3= 0.5,b4= 0.6, σ1= 0.4,σ2= 0.5, σ3= 0.3,== 0.2, ν1= ν2= 0.5,== 0.3, δ1= δ2= 0.6, d11= 0.4,d21= 0.6, dm1= 0.5,μ1= μ2= 0.4, and the eigenvalues ofare found to be λi1= 0,λi2= ?3 and λi3= ?3. By using Matlab LMI Toolbox, we solve the LMIs (3.13)–(3.16) in Theorem 3.1, we obtain the feasible solutions for N =3,k =1,i=1,2 as follows: Therefore, by Theorem 3.1, the Markovian jumping SNCDN with time-varying delays (3.1)achieve synchronization through the pinning controller uk(t) with the above mentioned parameters. Example 4.2Consider the following time-varying delayed Markovian jumping SNCDN with 5-node and mode s=2: with Ji= Hi= 0,i = {1,2}. Let us consider b1= 0.1,b2= b3= 0.3,b4= 0.2,σ1= 0.4, σ2= 0.5,σ3= 0.3,== 0.2, ν1= ν2= 0.5,== 0.3, δ1= δ2= 0.6, d11= 0.4, d21= 0.6,dm1= 0.5, μ1= μ2= 0.4. The eigenvalues ofandare found to be λ11= 0,λ12=λ13=λ14=?0.5, λ15=2.5, and λ21=0, λ22=λ23=λ24=λ25=?0.5. Using Matlab LMI Toolbox, we solve the LMIs (3.13)–(3.16) in Theorem 3.1, then we obtain the feasible solutions for N =5,k =1,i=1,2 as follows: Therefore, by Theorem 3.1, the Markovian jumping SNCDN with time-varying delays (2.1)achieve synchronization through the pinning controller uk(t) with the above mentioned parameters. Figure 1 State trajectories of the system in Example 2 In this article,some new synchronization stability criteria are proposed for a class of Markovian jumping SNCDNs with distributed delay and pinning control. On the basis of appropriate Lyapunov-Krasovskii functional which contains triple integral terms and bounding techniques,the novel delay dependent synchronization condition is derived in terms of linear matrix inequalities. We established some sufficiency conditions for synchronization, and the numerical results can demonstrate the effectiveness of the obtained result. In future,the preosed methods can be further extended to deal with some other problems on pinning control and synchronization for general stochastic dynamical networks, complex systems with impulsive perturbation,etc.
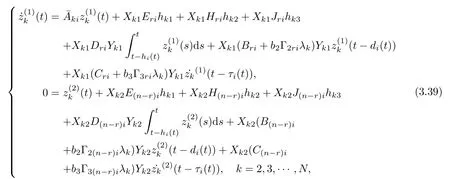

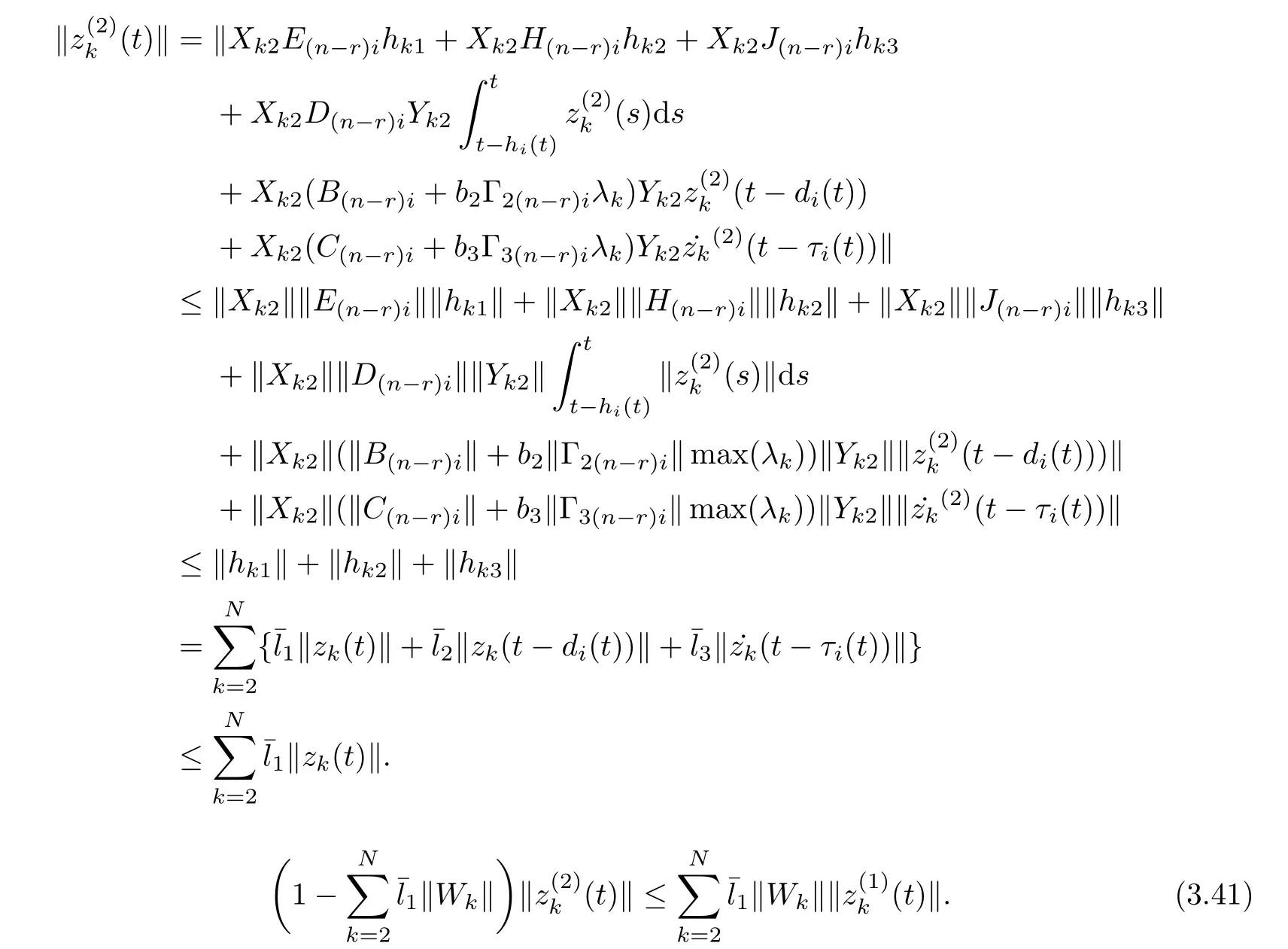
4 Numerical Examples
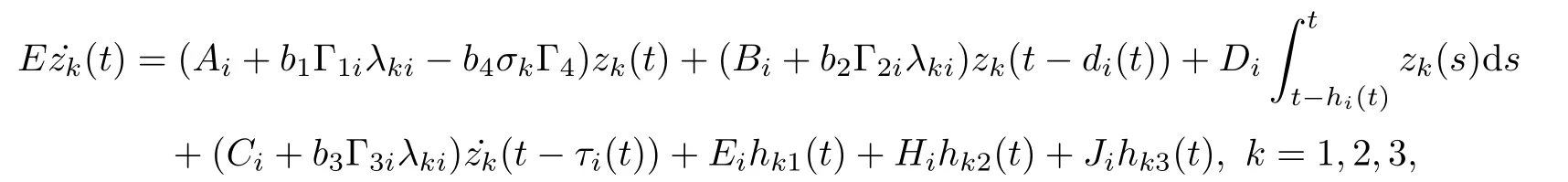
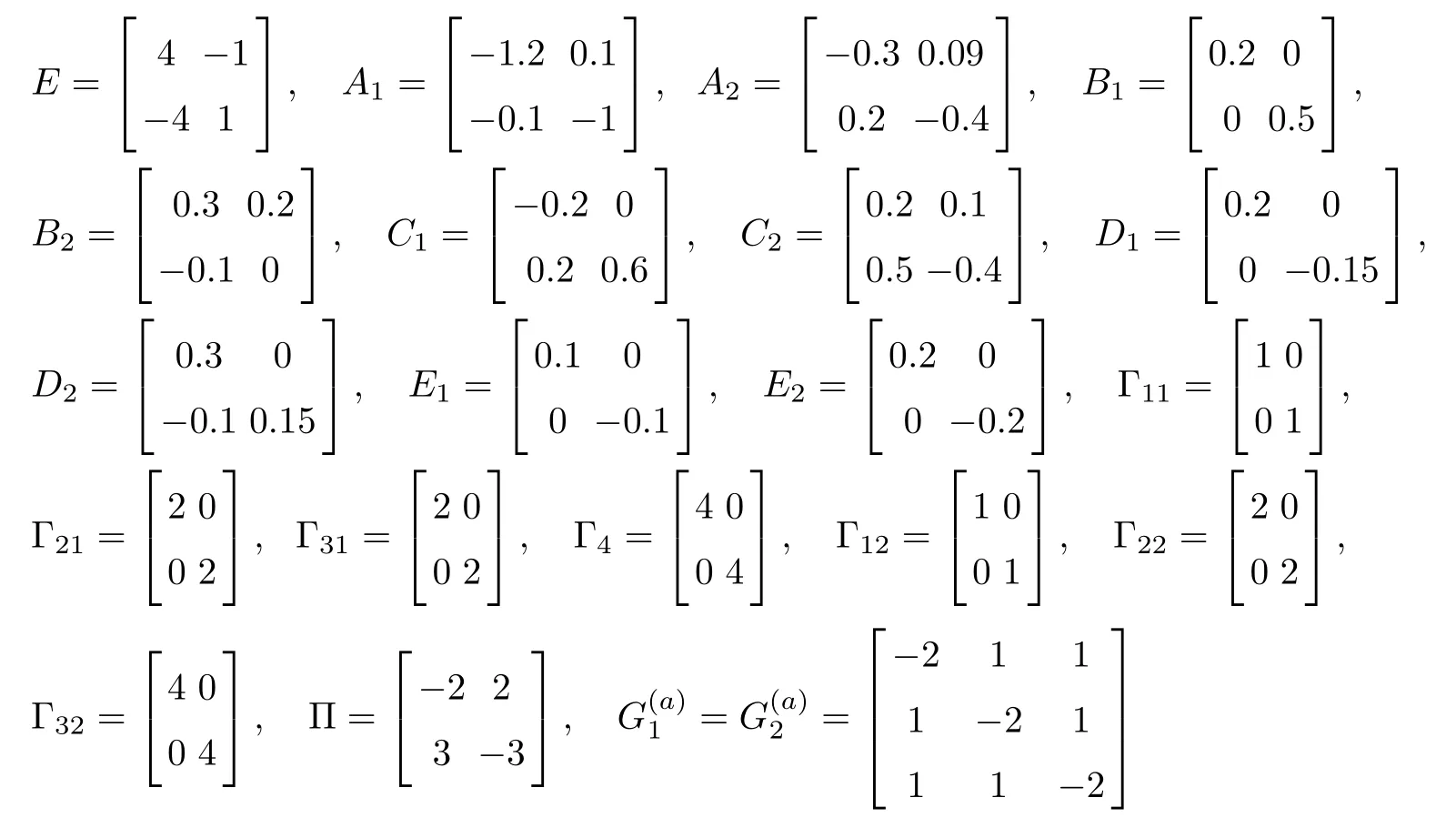

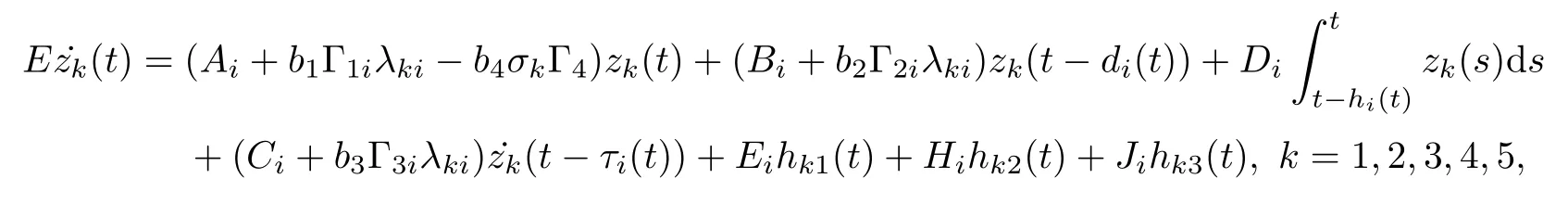

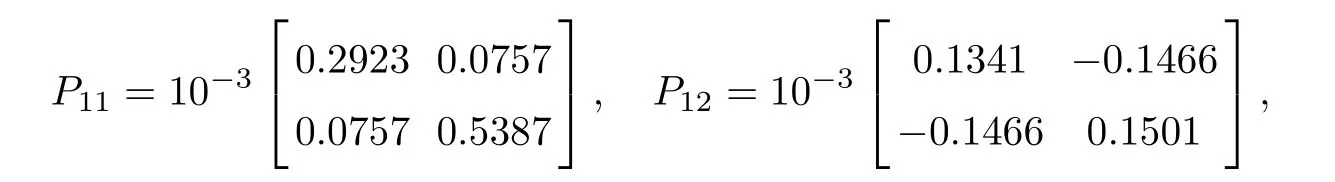


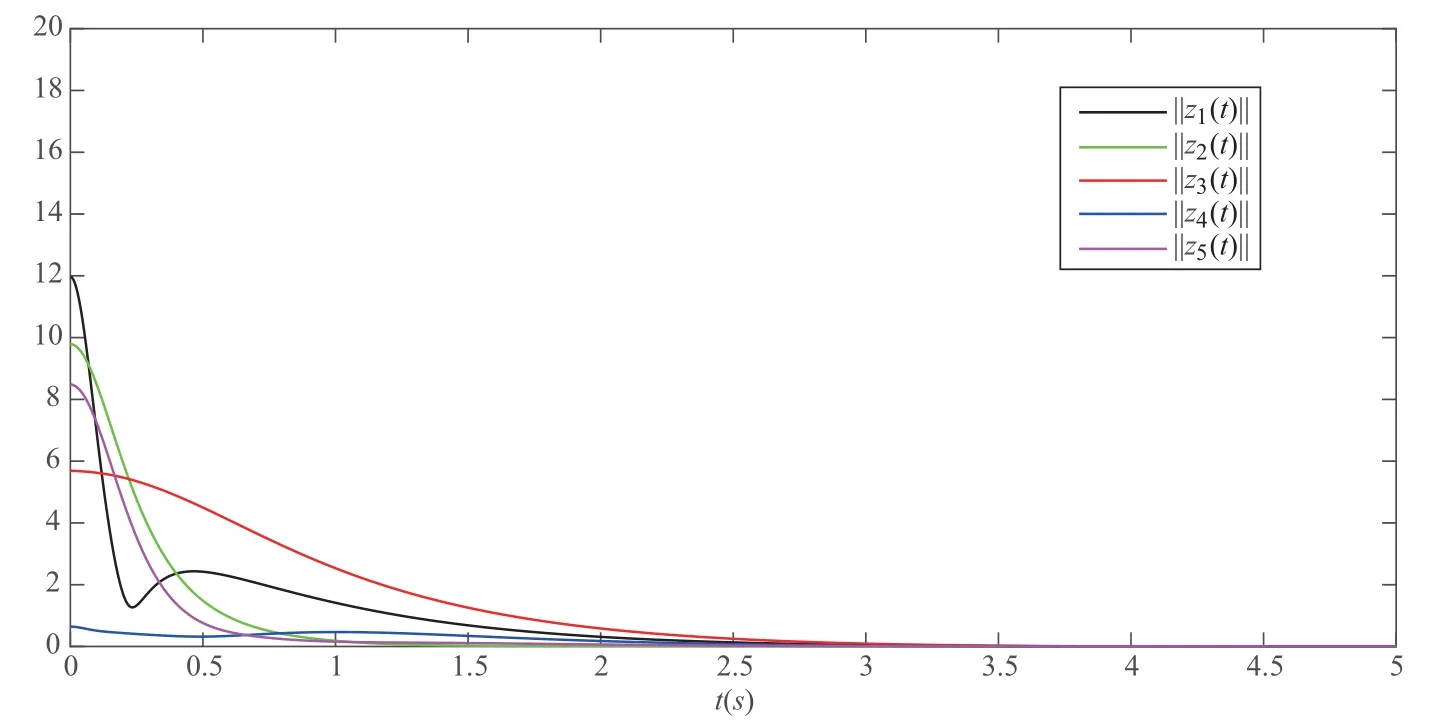
5 Conclusion
 Acta Mathematica Scientia(English Series)2020年3期
Acta Mathematica Scientia(English Series)2020年3期
- Acta Mathematica Scientia(English Series)的其它文章
- ARTIAL REGULARITY FOR STATIONARY NAVIER-STOKES SYSTEMS BY THE METHOD OF A-HARMONIC APPROXIMATION*
- ON BLOW-UP PHENOMENON OF THE SOLUTION TO SOME WAVE-HARTREE EQUATION IN d ≥ 5*
- THE QUASI-BOUNDARY VALUE METHOD FOR IDENTIFYING THE INITIAL VALUE OF THE SPACE-TIME FRACTIONAL DIFFUSION EQUATION ?
- ON APPROXIMATE EFFICIENCY FOR NONSMOOTH ROBUST VECTOR OPTIMIZATION PROBLEMS?
- ON THE ENTROPY OF FLOWS WITH REPARAMETRIZED GLUING ORBIT PROPERTY*
- ON NEW APPROXIMATIONS FOR GENERALIZED CAUCHY FUNCTIONAL EQUATIONS USING BRZDE?K AND CIEPLI′N(xiāo)SKI’S FIXED POINT THEOREMS IN 2-BANACH SPACES?
