一道解析幾何難題的巧解與推廣

湖北省宜都市一中 (443300)

艾昆侖

我校2019屆高三年級(jí)參加的十一月調(diào)研考試中解析幾何試題是一道難度極高的試題,許多同學(xué)由于方法不準(zhǔn)或計(jì)算失誤,導(dǎo)致第2問(wèn)不能得分.現(xiàn)給出一個(gè)較好解法,并對(duì)結(jié)論給出推廣.

(2)過(guò)點(diǎn)P(12,8)的兩條直線l1,l2分別交拋物線Γ于點(diǎn)C,D和E,F.線段CD和EF的中點(diǎn)分別為M,N.如果直線l1,l2的傾斜角互余,求證:直線MN經(jīng)過(guò)一定點(diǎn).

證明:(1)易得拋物線Γ的方程為y2=4x.

下面將題2結(jié)論推廣為:

過(guò)點(diǎn)P(m,n)的兩條直線l1,l2分別交拋物線Γ:y2=2px(p>0)于點(diǎn)C,D和E,F.線段CD和EF的中點(diǎn)分別為M,N.如果直線l1,l2的傾斜角互余,求證:直線MN經(jīng)過(guò)一定點(diǎn).

因直線CD和直線EF的傾斜角互余,故k1k2=1,即(y1+y2)(y3+y4)=4p2.

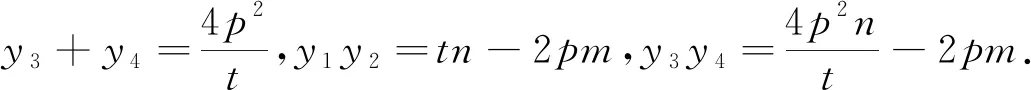
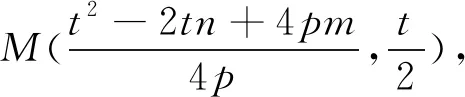
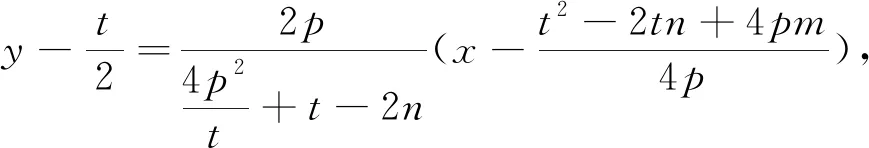
由上結(jié)論知,調(diào)考題答案為MN經(jīng)過(guò)定點(diǎn)(10,0).