TRANSPORTATION INEQUALITIES FOR THE FOURTH-ORDER STOCHASTIC HEAT EQUATIONS WITH FRACTIONAL NOISES
LI Yu-meng
(School of Statistics and Mathematics,Zhongnan University of Economics and Law,Wuhan 430073,China)
Abstract: In this paper,we study the fourth-order stochastic heat equations with fractional noises.By using the Girsanov transformation and the martingale representation theorem,we obtain a Talagrand transportation on the continuous paths space,which extends the result in[1].
Keywords: fourth-order stochastic heat equation;fractional noise;transportation inequality
1 Introduction
The purpose of this paper is to study the Talagrand’sT2-transportation inequality for the following fourth-order stochastic heat equation driven by a fractional noise:

It is well known that Talagrand’s transportation inequalities are related closed to the concentration of measure phenomenon,the log-Sobolev and Poincar′e inequalities,see for instance monographs[2–4].We also like to refer the readers to the survey[5]authored by Gozlan and references therein.
Recently,the problem of transportation inequalities and their applications to dif f usion processes was widely studied and was still a very active research area both from a theoretical and an applied point of view.Let us first recall the transportation inequality.
Let(E,d)be a metric space equipped with σ-field B such that d(·,·)is B×B measurable.Given p ≥ 1 and two probability measuresμ and ν on E,the Wassersetin distance is defined by

where the infimum is taken over all the probability measures π on E × E with marginal distributions μ and ν.The relative entropy of ν with respect to μ is defined as
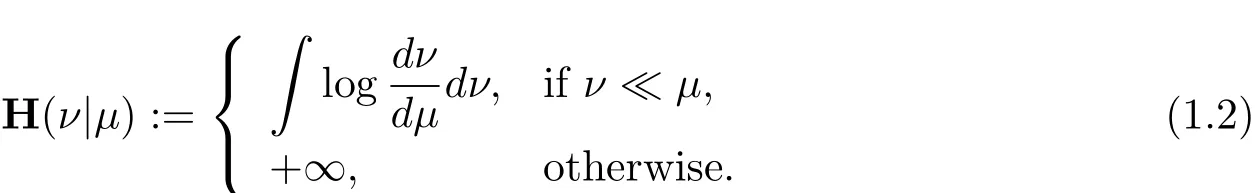
The probability measureμsatisfies the Lp-transportation inequality on(E,d)if there exists a constant C>0 such that for any probability measure ν on E,

As usual,we writeμ∈Tp(C)for this relation.The propertiesT1(C)andT2(C)are of particular interest.The phenomenon of measure concentration is related toT1(C)(see[3,6–8]).
The propertyT2(C)is stronger thanT1(C).It was first established by Talagrand[9]for the Gaussian measure,and it was brought into relation with the log-Sobolev inequality,Poincar′e inequality,Hamilton-Jacobi’s equation,the transportation-information inequality,see[8,10–13].The work of Talagrand on the Gaussian measure was generalized by Feyel and¨Ust¨unel[14]to the framework of an abstract Wiener space.
With regard to the paths of finite stochastic dif f erential equation(SDE for short),by means of Girsanov transformation and the martingale representation theorem,theT2(C)w.r.t.the L2and the Cameron-Martin distances were established by Djellout et al.[7];theT2(C)w.r.t.the uniform metric was obtained by Wu and Zhang[1].Bao et al.[15]established theT2(C)w.r.t.both the uniform and the L2distances on the path space for the segment process associated to a class of neutral function stochastic dif f erential equations.Saussereau[16]studied theT2(C)for SDE driven by a fractional Brownian motion,and Riedel[17]extent this result to the law of SDE driven by general Gaussian processes by using Lyons’rough paths theory.
For the infinite stochastic partial dif f erential equation(SPDE for short),Wu and Zhang[18]studied theT2(C)w.r.t.L2-metric by Galerkin’s approximation.By Girsanov’s transformation,Boufoussi and Hajji[19]obtained theT2(C)w.r.t.L2-metric for the stochastic heat equation driven by space-time white noise and driven by fractional noise.
Recently,the fourth-order stochastic heat equation driven by a fractional noise was actively studied,for example,Jiang et al.[20]proved the existence,uniqueness and regularity of the solution,and established the large deviation principle of the equation with a small perturbation;Yang and Jiang[21]obtained the moderate deviation principle;Liu et al.[22]proved a weak approximation for SPDE(1.1).
In this paper,we shall study theT2(C)w.r.t.the uniform metric for the fourthorder stochastic heat equation driven by a fractional noise.This gives a positive answer to Boufoussi and Hajji’s question in Remark 10 of[19].
The rest of this paper is organized as follows.In Section 2,we first give the definition of the fractional integral and the solution to eq.(1.1),and then state the main results of this paper.In Section 3,we prove the main result.
2 The Framework and Main Result
In this section,we first recall the fractional integral and give the known results about the solution of eq.(1.1),taking from Jiang et al.[20],and then state the main result of this paper.
2.1 The Fraction Noise and its Integral

with s,t∈ [0,T]and A,B ∈ B(D),λ is the Lebesgue measure.Denote by Ξ the set of step functions on[0,T]× D.Let Θ be the Hilbert space defined as the closure of Ξ w.r.t.the scalar product determined by
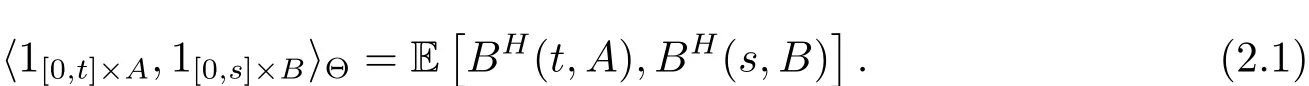
Note that the covariance kernel of the fractional Brownian motion
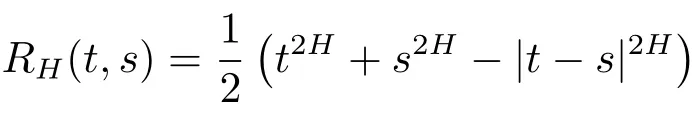
can be written as

where

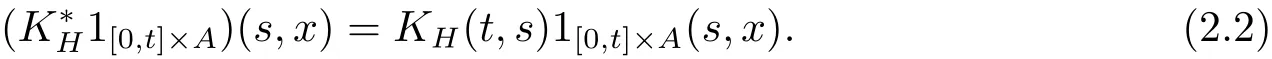
In particular,Then for any pair of step functions ? and ψ in Ξ,we have
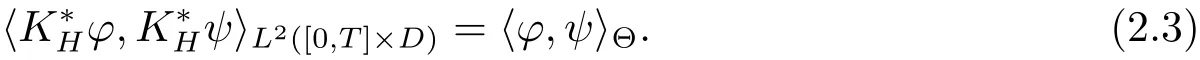

satisfying that

See Nualart[23]for more properties about the fractional noise.
2.2 The Solution of the Equation
Definition 2.1A random field u:={u(t,x),t∈[0,T],x∈D}is said to be a solution of eq.(1.1),if for any φ ∈ C∞0([0,T]×D),u satisfies that for any t∈ [0,T],

Let Gt(x,y)be the Green function ofwith Neuman boundary conditions.Then by Walsh’s theory[24],(2.6)is equivalent to the following form

for t∈[0,T]and x∈D,where the last term is defined by
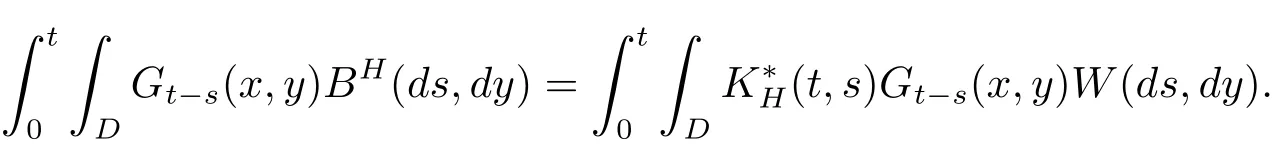
Assume that the coefficient f:R→R is Lipschitz continuous,i.e.,there exists a constant L>0 such that
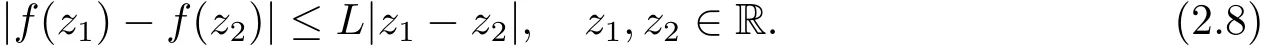
The existence and uniqueness of the solution of eq.(1.1)was established in Jiang et al.[20].
Theorem 2.2[20]Let H∈?Z(1/2,1).Und?er Lipschitzian condition(2.8),for any F0-adapted function u0such that<∞,eq.(1.1)has a unique adapted mild solution{u(t,x);(t,x)∈[0,T]×D},and moreover
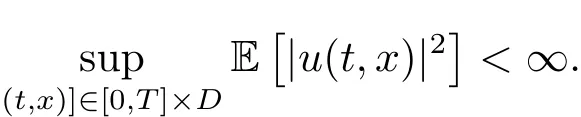
Remark 2.2The initial condition u0in Jiang et al.[20]is

In view of eq.(?3Z.5)in the pro?of Theorem 3.1 of[20],it follows that condition(2.9)can be replaced by E
Let C:=C([0,T]× D;R)be the space of all continuous functions on[0,T]× D,which is endowed with
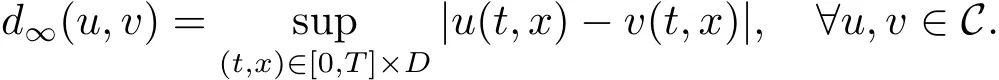
Let Pube the law of{u(t,x);(t,x)∈ [0,T]×D}on C.The main result of this paper is the following transportation inequality for Pu.
Theorem 2.3Let H∈(3/4,1).Under Lipschitzian condition(2.8),for any F0-adapted function u0such that E<∞,there exists some constant C>0 such that the probability measure Psatis fies T2(C)on the space C([0,T]×D)endowed with the metricd∞.
3 The Proof
By formula(2.5),we know that?Ft,where Ftis the filtration of the white-noise considered in(2.5).
ProofClearly,it is enough to prove the result for any probability measure Q on C such that Q?Puand H(Q|Pu)<∞.We divide the proof into two steps.
Step 1We shall closely follow the arguments in[7].Define
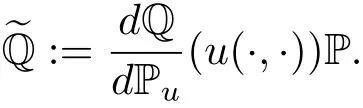
The process{u(t,x),(t,x)∈[0,T]×D}is adapted with respect to the white-noise filtration Ft=σ{W(s,A),s≤t,A∈B(D)}.Notice that(u(·,·))is an FT-measurable random variable.Since Q is a probability measure on C and the law of u under P is Pu,then
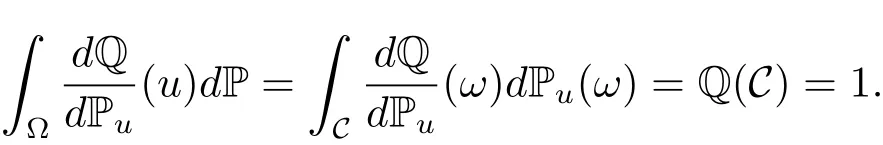
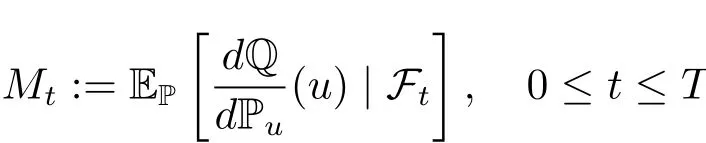
is an Ft-martingale.Let τ=inf{t∈ [0,T];Mt=0}∧T with the convention that inf?=+∞.Then τ is an(Ft)-stopping time andeQ(τ=T)=1.Thus,we can write
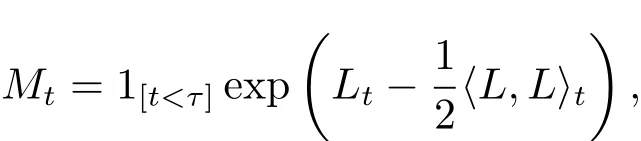
where
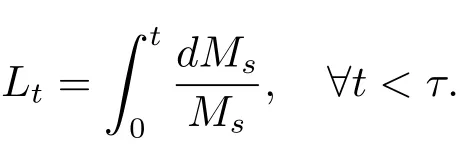
Following the argument as that in Djellout et al.[7],we have

On the other hand,consider
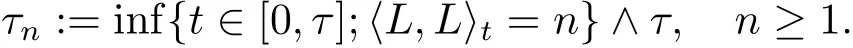
Then M is P?a.s.continuous and since τn↑ τ a.s.,we have,by(3.1),



and
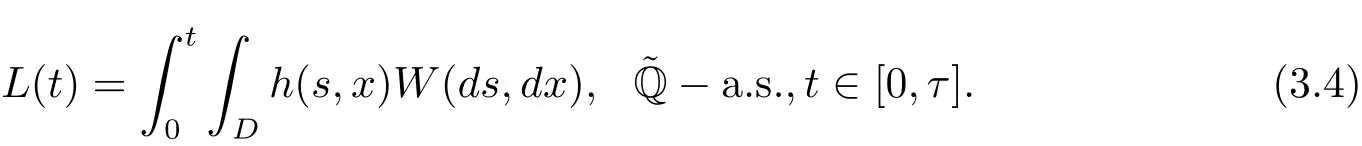
Combining(3.2)and(3.4),we obtain that

Step 2By Girsanov’s theorem for the Brownian sheet(see[26,Proposition 1.6]),under

is a space-time white noise,where W is the space-time noise considered in(2.5).Consider theeQ-fractional noisefWHassociated tofW defined by
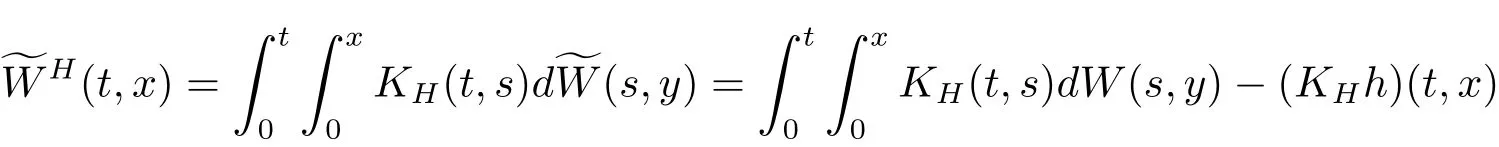
with
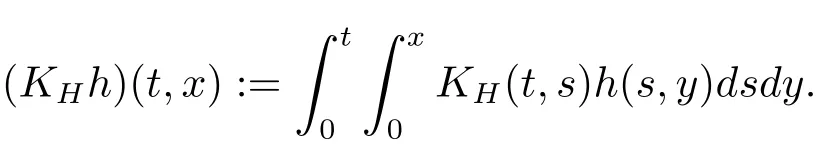
Since for any H>1/2,the kernel KH(t,s)is

by Fubini’s theorem,we have
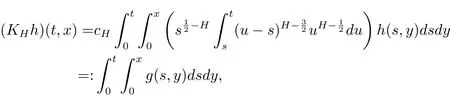
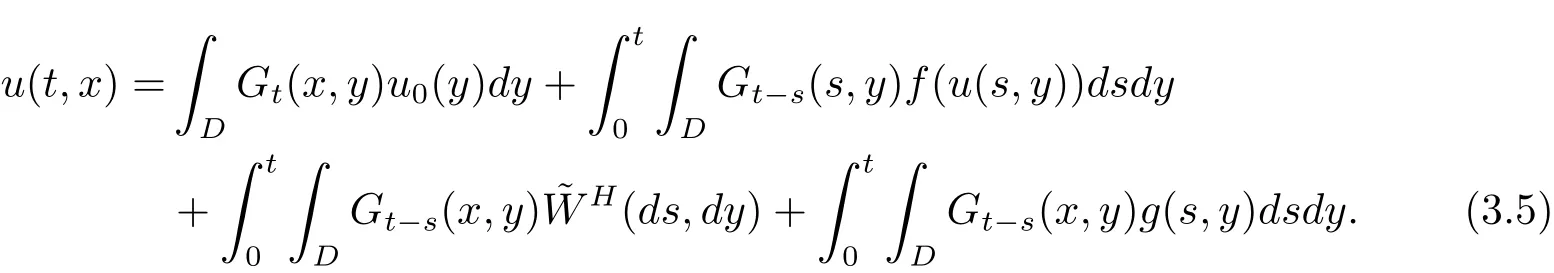
Now,consider{v(t,x),(t,x)∈ [0,T]×D}the solution of equation(1.1).By the uniqueness of the solution in Theorem 2.2,we know that the law of{v(t,x),(t,x)∈ [0,T]×D}is Pu.Thus,{(u(t,x),v(t,x)),(t,x)∈[0,T]×D}underis a coupling of(Q,Pu),which implies that

Next,we estimate the distance between u and v with respect to d∞-metric.For any(t,x)∈ [0,T]× D,
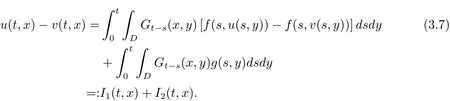
By(2.8)and H¨older’s inequality,we have
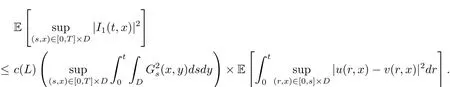
We use the approach in Boufoussi and Hajji[19]to estimate the second term I2:

By Lemma 1.2 of[27],we know that
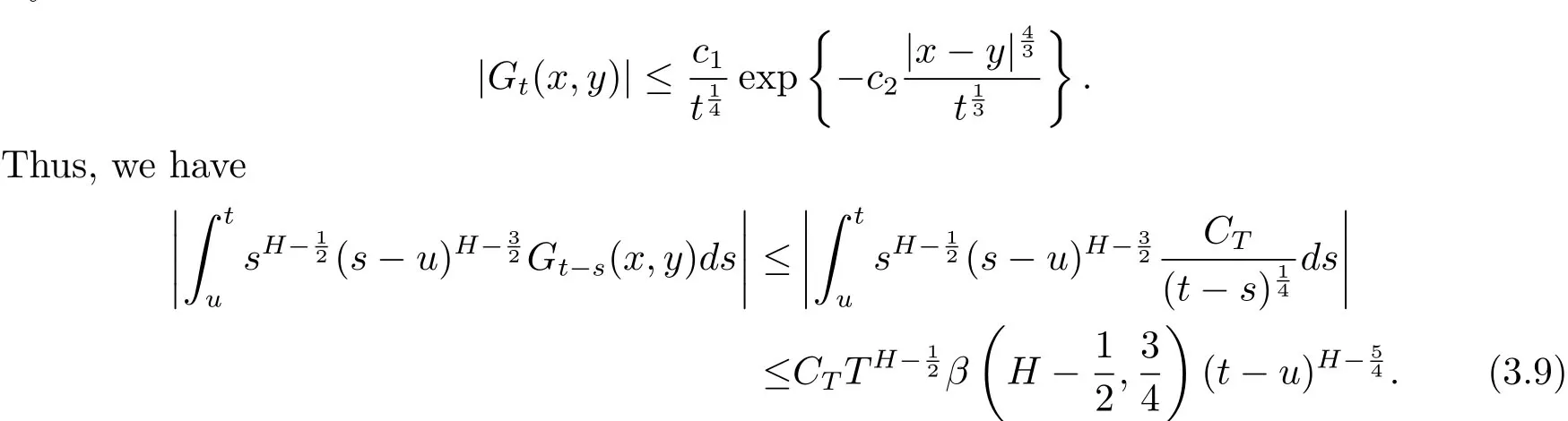
Putting(3.8)and(3.9)together,we have
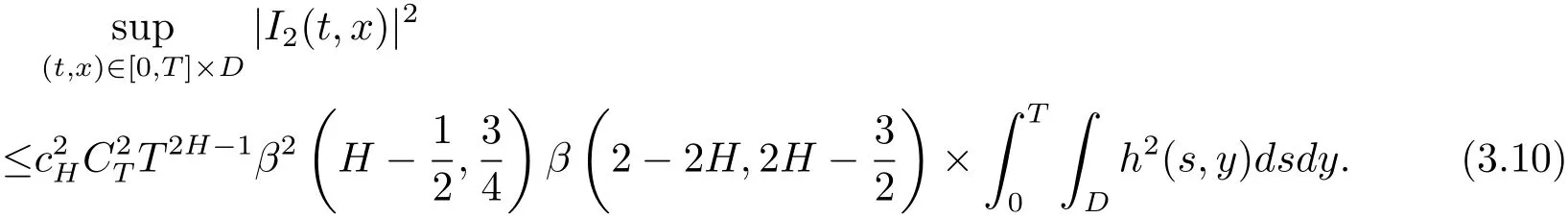
Putting(3.7),(3.8)and(3.10)together,
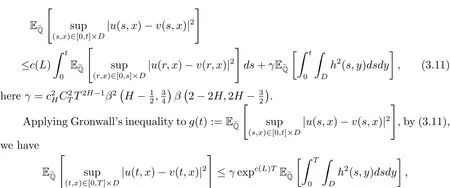
which is the desire result.
The proof is completed.

