Energy Conditions and Conservation Laws in LRS Bianchi Type I Spacetimes via Noether Symmetries?
Sumaira Saleem Akhtar and Tahir Hussain
Department of Mathematics, University of Peshawar, Khyber Pakhtunkhwa, Pakistan
(Received October 9, 2018; revised manuscript received November 2, 2018)
Abstract In this paper, we have completely classified the locally rotationally symmetric (LRS)Bianchi type I spacetimes via Noether symmetries(NS).The usual Lagrangian corresponding to LRS Bianchi type I metric is used to find the set of determining equations.To achieve a complete classification, these determining equations are generally integrated to find the components of NS vector field and the metric coefficients.During this procedure, several cases arise which give different Noether algebras of dimension 5,...,9, 11, and 17.A comparison is established between the obtained NS and the Killing and homothetic vectors.Corresponding to all NS generators, the conservation laws are stated by using Noether’s theorem.The metrics which we have obtained as a result of our classification are shown to be anisotropic or perfect fluids which satisfy certain energy conditions.
Key words: Bianchi type I model, Noether symmetry, conservation Laws, energy conditions
1 Introduction
The Einstein’s field equations(EFEs),Gab=kTab,are ten tensor equations in the Einstein’s theory of general relativity, which relate the spacetime curvature with the energy and momentum within spacetime.The termGabappearing in these equations expresses the curvature of spacetime and is known as the Einstein tensor.Moreover,ksignifies the gravitational constant andTabdenotes the stress-energy tensor,which gives the description of density and flux of energy and momentum in the spacetime.
An exact solution of the EFEs is a Lorentz metricgab,which is obtained by solving these equations in closed form and is conformable to a physically realisticTab.The study of the exact solutions of these equations is proved to be one of the important activities in different branches of physics.They describe the structure of spacetime including the inertial motion of objects in the spacetime.Moreover,these solutions lead to the prediction of black holes and different models of evolution of universe.The problem which one faces in finding the exact solutions of these equations is their highly nonlinear nature.These equations cannot be solved without some simplifying assumption,such as symmetry restriction ongab.Using such restrictions,there are numerous cases where the EFEs are solved completely.[1]
The most basic symmetry is expressed in terms of a Killing vector (KV)Xsatisfying the relationLXgab= 0,whereLdenotes the Lie derivative operator andgabis the metric tensor.The KVs are closely related to the conservation laws in a spacetime.For a detailed study of exact solutions of EFEs with the help of symmetry restrictions ongaband the corresponding conservation laws, we refer to Refs.[1–3].
Some other conventional symmetries, which have been studied in the literature include homothetic vectors (LXgab= 2ψgab);ψbeing a constant, curvature collineations (LXRabcd=0), Ricci collineations (LXRab=0)and matter collineations (LXTab=0).Recently, these collineations have been investigated for some physically important spacetimes.[4?9]
In 1918,Emmy Noether[10]proposed her work in terms of Noether theorem.As a result of this theorem, one can find the expression for conserved quantity for each continuous symmetry transformation that leaves the action invariant.NS are also called the variational symmetries and they are associated with mechanical systems possessing a Lagrangian.In particular, for a metric ds2=gabdxadxb,the associated Lagrangian is given byIn this expression, a dot denotes differentiation with respect to the geodesics parametersof the world line of a point particle moving in a spacetime.It is well known that every KV is an NS but there may exist some NS, which are not KVs.Thus the additional NS may yield some extra conservation laws.Homothetic vectors (HVs)are also closely related with NS.Corresponding to every homothetic vectorX,we have an NS,X+2ψs?s.Conversely,if the vector fieldX+2ψs?sis an NS, thenXis an HV provided thatXdoes not depend ons.[11]
In literature, NS, their relation will Killing and homothetic vectors and the corresponding conservation laws have been studied by many researchers,for details we refer to Refs.[11–19].
The termTabappearing in EFEs is crucial as it describes the physics of a spacetime.The exact solutions of these equations may not give physically interesting results unless the source ofTabis specified.For different sources,Tabhas some particular form.For example, for an anisotropic fluid,Tab=(ρ+p⊥)uaub+(p||?p⊥)nanb+p⊥gab;ρ,uaandnabeing energy density,four-velocity and spacelike unit vector respectively.The quantitiesp⊥andp||respectively represent the perpendicular and parallel pressures tona.Moreover,uaua=?1,nana= 1 anduana= 0.[20]Similarly, for a perfect fluid we have the same form ofTabwithp||=p⊥=p.
The positive energy condition is a relation satisfied by the componentT00of stress-energy tensor, which ensures that the energy density is non negative.The physical importance of this condition is evident from the fact that the empty vacuum may become unstable if both positive and negative energy regions are allowed.
There are some other energy conditions including weak, strong, null and dominant energy conditions, which generalize the conditionT00≥0 to the whole tensorTab.The weak energy condition states thatTabvavb ≥0, for any timelike vectorvaat a point of the spacetime manifold.For an anisotropic source, all the energy conditions take the form:
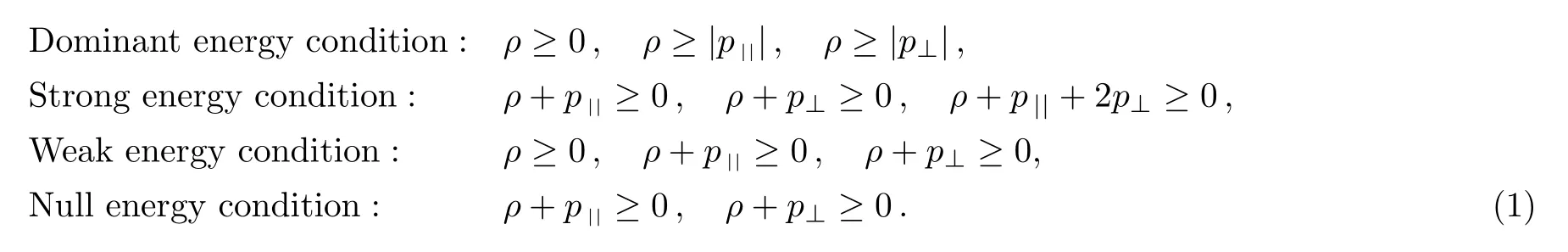
In particular, ifp||=p⊥, then these conditions reduce to the energy conditions for a perfect fluid.
According to the Bianchi classification of all the 3-dimensional real Lie algebras, there are nine types of Bianchi spatially homogeneous but not necessarily isotropic spacetimes.As a subclass, these models contain the isotropic Friedmann-Robertson-Walker (FRW)universes.The Bianchi type models are of vital importance because the physical variables in these models are dependent on time only.Consequently, the EFEs and other governing equations reduce to ordinary differential equations.
Among the Bianchi type models, the Bianchi type I spacetimes are those models for which the groupG3of translations of the 3-dimensional Euclidian space is Abelian.In the literature, Bianchi type I spacetimes have been thoroughly studied from the symmetry point of view.Paliathanasiset al.[21]presented the symmetry classification of the Klein-Gordon equation in Bianchi I spacetimes,which in turn related the Lie symmetries of this equation with the conformal Killing vectors (CKVs)of the underlying geometry.In the same analysis, it was also shown that the resulting Lie symmetries of the conformal algebra are also NS.Tsamparliset al.[22]studied the CKVs of Bianchi type I spacetimes and conjectured that there are only two conformally flat and two non conformally flat families of these spacetimes admitting CKVs.The same authors stated that for dynamical system whose equations of motion are of the formbeing an arbitrary function of its argument, the computation of Lie and NS reduce to the probelm of finding the special projective collieations.[23]These general results are then applied to the analytic computation of the Bianchi I metric.
In this paper, we present a complete classification of LRS Bianchi type I spacetimes via NS and the corresponding conservation laws.The bounds for energy conditions are also calculated for all the obtained models.In next section, we derive the list of determining equations for NS.In Secs.3–9, we present different metrics, their Noether generators and corresponding conservation laws.For each of the obtained model in these sections, a brief discussion on the energy conditions is provided.A conclusion of the present work is appended at the end of the paper.
2 Determining Equations
The metric of the LRS Bianchi type I spacetimes is given by:[1]
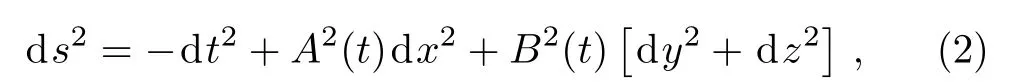
such thatA(t)≠0 andB(t)≠0.For this metric, the EFEs withk=1 give:
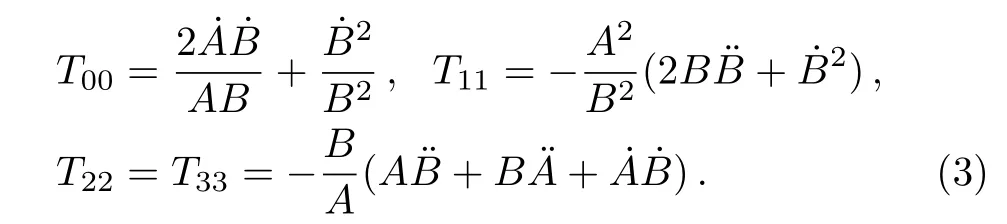
Here a dot onAandBdenotes differentiation with respect tot.For an anisotropic fluid, these components become:
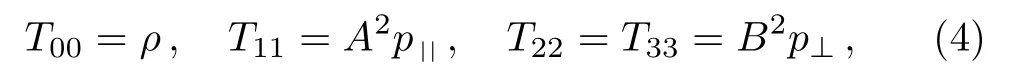
while for a perfect fluid, we have the same values ofTabwithp||=p⊥=p.Following is the Lagrangian corresponding to the metric (2):
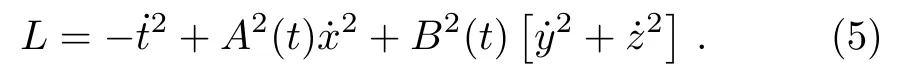
An NS vector fieldXis a vector field of the formX=ξ(?/?s)+Xj(?/?aj), satisfying the following condition:
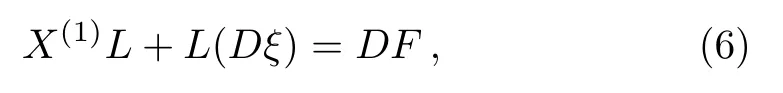
whereX(1)=X+Xjs(?/?˙aj)is the first prolongation ofXandXjs=DXj ?˙ajDξwithD=(?/?s)+ ˙aj(?/?aj).Moreover,ξ,Xjand the Gauge functionFall depend onsandaj, whereaj=(t,x,y,z)are depending variables ofssuch that ˙aj=?aj/?s.
Using the Noether’s theorem, the corresponding conservation law for each NS can be found with the help of the expression:

We may simplify Eq.(6)by using the Lagrangian (5)to get the following set of determining equations:

The componentsXaof the NS vector field, the Gauge functionFand the metric functionsAandBappearing in the above system can be found by decoupling and then integrating these equations systematically.In this way,we may get the exact form of LRS Bianchi type I metrics along with their NS.During this procedure, several cases arise which restrictAandBto satisfy certain conditions and give the exact form of LRS Bianchi type I metric admitting NS having dimension 5,...,9, 11, and 17.To avoid the repetition, we exclude to write the basic calculations and present the metrics along with their NS,conservation laws, Lie algebra and some physical implications in the upcoming sections.
3 Minimal Set of NS
The minimal set of NS admitted by LRS Bianchi Type I metric is found to be:
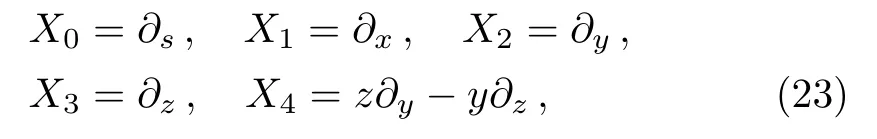
whereX0is the symmetry corresponding to the Lagrangian andX1,...,X4are the minimum KVs of the metric (2).The above minimal set of NS is obtained under the following restrictions on metric functions.

Table 1 Metrics admitting 5 NS
Using Eq.(7), the conservation laws for the above set of minimal NS are obtained as:
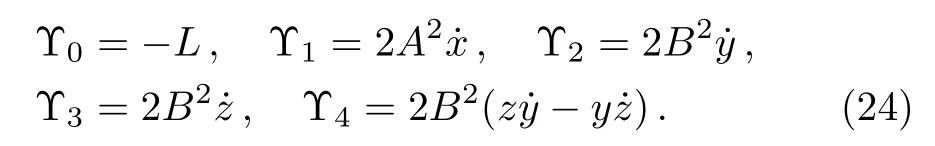
The corresponding Lie algebra for the generators given in Eq.(23)is:

The metrics 5a–5c are anisotropic fluids for which:

One may use these values in Eq.(1)to find the energy bounds for the metrics 5a-5c.For example, for the metric 5b, the energy conditions restrict the metric functionAas follows:
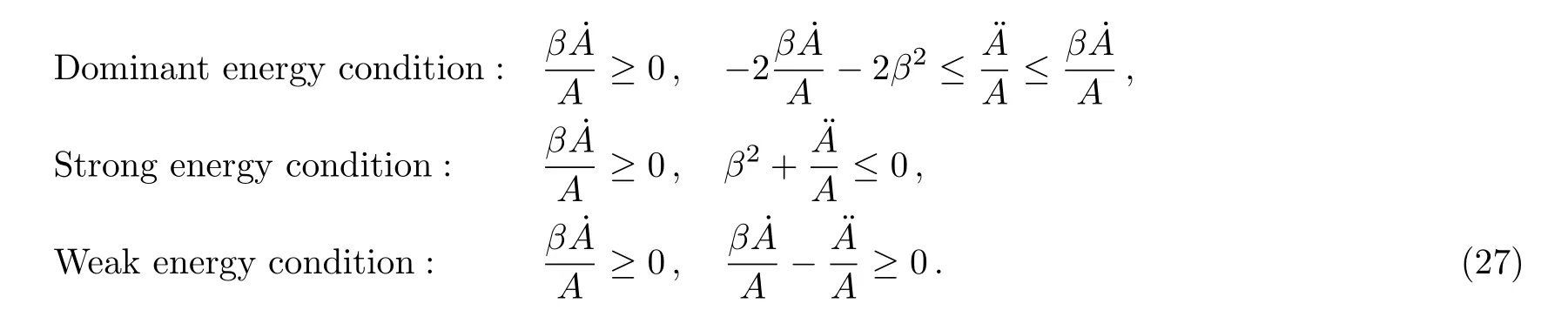
4 Six NS
IfA=α,whereαis a non zero constant andBsatisfies the conditions ¨B≠0 andB≠eβt,then the metric(2)becomes:
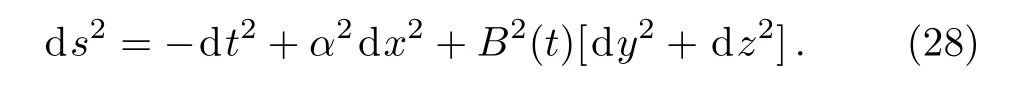
For this metric, we obtain six NS, out of which five are same as given in Eq.(23)and the sixth one is a proper NS,X5= (s/2α2)?x, with the Gauge functionF=x.The corresponding invariant for this Noether generator is Υ5=s˙x?xand the Lie algebra of these six NS generators is given by:
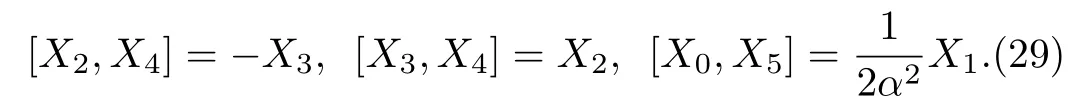
For the metric (28), being an anisotropic fluid, the physical terms are found to be:
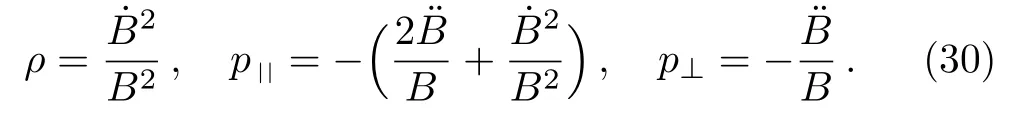
Here the dominant energy condition holds if/B+/B2≥0 and ¨B/B ≤0 and the remaining energy conditions are satisfied provided that ¨B/B ≤0.
5 Seven NS
In Table 2, we present some LRS Bianchi type I metrics each of which admits a 7-dimensional Lie algebra of NS.For each of these metrics, five NS are same as given in Eq.(23), while the extra two NS along with their conservation laws and Lie algebra are listed with each metric.

Table 2 Metrics admitting 7 NS.
For the metric 7a,X5is a KV andX6corresponds to a homothetic vector [(a1t+a2)/2a1]?twith the homothetic constant 1/2.In case 7b, bothX5andX6represent proper NS.Finally, bothX5andX6are KVs for the metrics 7c and 7d.
The metric in case 7a is an anisotropic fluid with:

The above expressions satisfy the dominant energy conditions ifc/b ≤1/2 and 3?4c/b ≥(b ?2c)2, while the weak energy conditions hold ifc/b ≤0.75 and 3?4c/b ≥?(b ?2c)2.Moreover, the strong energy conditions are satisfied whenc/b ≤1, 3?4c/b ≥ ?(b ?2c)2, and 2(1?c/b)≥?(b ?2c)2.
Similarly, the metric in case 7b is an anisotropic fluid whose energy density and parallel pressure vanish andp⊥=?¨A/A.Here the dominant energy condition is clearly failed, while the remaining energy conditions are satisfied provided that ¨A/A<0.
The energy momentum tensor components for the model 7c, being an anisotropic fluid, produces the following expressions:
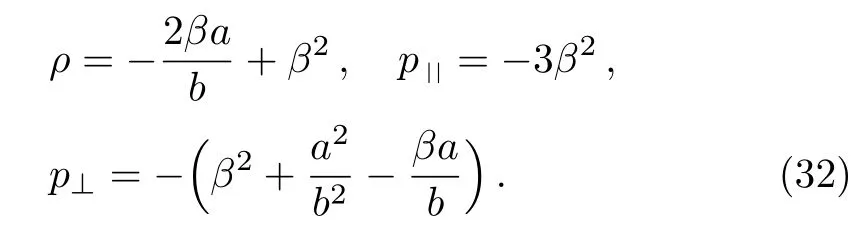
For the above values,the strong and dominant energy conditions are failed, while the weak energy conditions hold when 2βa/b ≤β2≤?βa/banda2/b2≤?βa/b.
Finally, for the metric 7d we have:
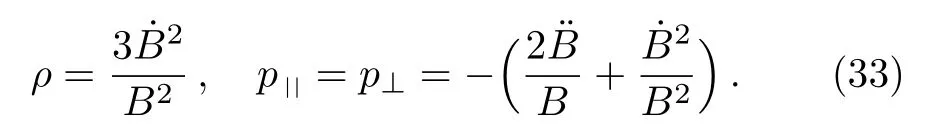
Here we have obtained a perfect fluid matter such that the dominant energy conditions hold if/B+/B2≥0 and/B2?/B ≥0,while strong and weak energy conditions respectively require/B ≤0 and/B2≥¨B/B.
6 Eight NS
In Table 3, we give all the LRS Bianchi type I metrics admitting eight NS,out of which five are same as given in Eq.(23).
For metric 8a,X5andX6are proper NS, whileX7corresponds to an HV [(a1t+a2)/2a1]?t+x/2?x.In case of metric 8b,X5corresponds to an HV (B/2 ˙B)?t;X6is a proper NS whileX7is a KV.Finally for case 8c,X5is an NS corresponding to the HV(A/2 ˙A)?tandX6,X7are KVs.
The metric 8a represents an anisotropic fluid with zero perpendicular pressure andρ=?p||=a21/(a1t+a2)2.All the energy conditions are satisfied here.Similarly,The metric 8b is also an anisotropic fluid for which we have:
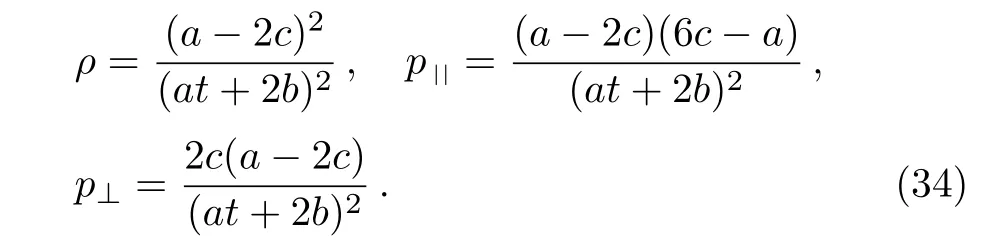
such that the strong and weak energy conditions hold if eithera ≥2c ≥0 ora ≤2c ≤0, while for dominant energy condition we must have (a ?2c)2≥|(a ?2c)(a ?6c)|and (a ?2c)2≥|2c(a ?2c)|.The physical terms for case 8c are given by:
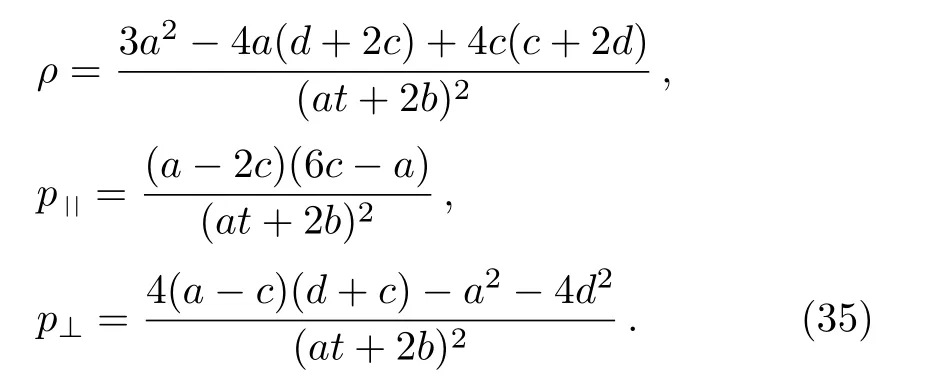
One may simplify the energy conditions using the above values, like the previous cases.

Table 3 Metrics admitting 8 NS.
7 Nine NS
There are nine metrics each of which possesses 9-dimensional algebra of NS.All such metrics and the four additional NS different from those given in Eq.(23)for each of these metrics along with their conservation laws and Lie algebra are presented in Table 4.
For the metric 9a,X5andX6represent KVs,X7is a proper NS whileX8is an NS corresponding to an HV(A/2a1)?t.In cases 9b–9f,X5andX6are KVs, whileX7andX8are proper NS.The metric given in case 9g admits three additional KVsX5,X6,andX7along with a proper Noether symmetryX8.For the metric 9h,X5is an NS which corresponds to an HV(A/2 ˙A)?t+(y/2)?y+(z/2)?z,X6is a KV whileX7andX8are proper NS.Finally, in case 9i, we have three additional KVsX6,X7,X8, and one NSX5corresponding to the HVA?t/2 ˙A.
The metric 9a represents a perfect fluid, while all the remaining cases give anisotropic fluids.For the metric 9a, we findp||=p⊥=?ρ/3=?a21/(a1t+a2)2, which satisfy all the energy conditions.For the models in cases 9b–9d, we getρ=p||= 0 andp⊥=?k2, which do not satisfy any energy condition except the positive energy condition,ρ ≥0.Similarly, for models 9e and 9f,we haveρ=p||= 0 andp⊥=k2.Here the dominant energy condition fails,while all the remaining energy conditions are trivially satisfied.For the model 9g,we obtainρ=?p⊥=β2andp||=?3β2, which do not satisfy any energy condition exceptρ ≥0.The metric given in 9h is an anisotropic fluid for whichρ=p||= 0 andp⊥= 2c(a ?2c)/(at+2b)2.The dominant energy condition is clearly failed,while the remaining energy conditions are satisfied provided thatc(a ?2c)≥0.The following physical terms for the metric 9i reveal that it represents a perfect fluid model:
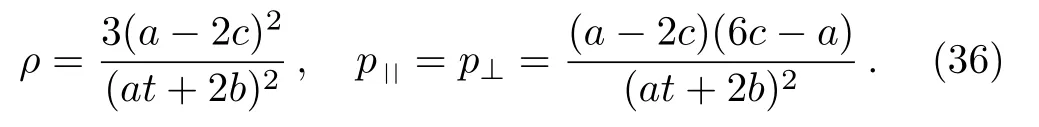
The corresponding weak energy conditions hold fora(a ?2c)≥0,whereas the strong energy conditions requirea ≥2c ≥0 ora ≤2c ≤0.Moreover, the dominant energy conditions are satisfied ifa(a ?2c)≥0, and(a ?2c)(a ?3c)≤0.
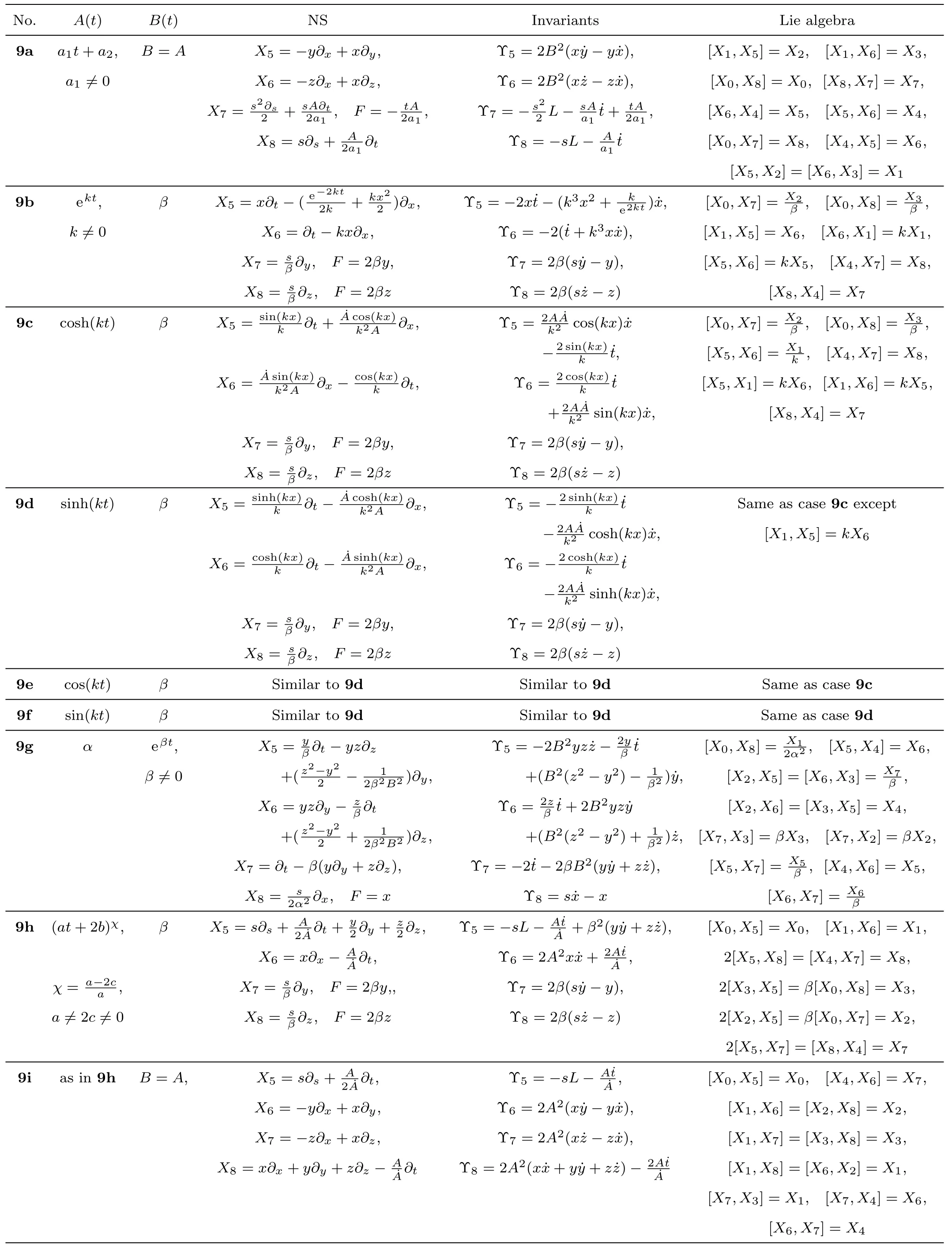
Table 4 Metrics admitting 9 NS.
8 Eleven NS
Following is the only one metric which admits eleven NS:

whereβ≠0.The set of eleven NS for the above metric contains the minimal set of NS and the extra six NS(KVs)are obtained as:

The Lie algebra for the above set of generators is found to be:
and the corresponding conservation laws are:

For the metric (37), we haveρ= 3β2andp=p||=p⊥=?3β2.Thus it gives a perfect fluid.Here the strong energy condition is violated while the remaining energy conditions are satisfied.
9 Maximal Set of NS
It is well known that the the dimension of Noether algebra for flat Minkowski metric is 17.Following is an another metric admitting 17 NS.

wherea1≠0 andβ≠0.Five NS of the above metric are same as given in Eq.(23), while the remaining twelve are given as follows:
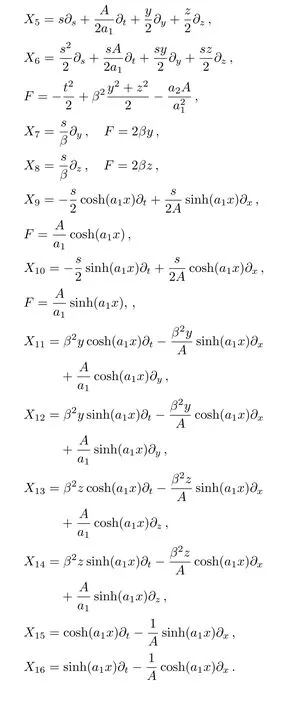
In the above set,X5is an NS and its corresponding HV is(A/2a1)?t+(y/2)?y+(z/2)?z.Moreover,X6,...,X10are proper NS andX11,...,X16are KVs.The Lie algebra for these generators is given by:
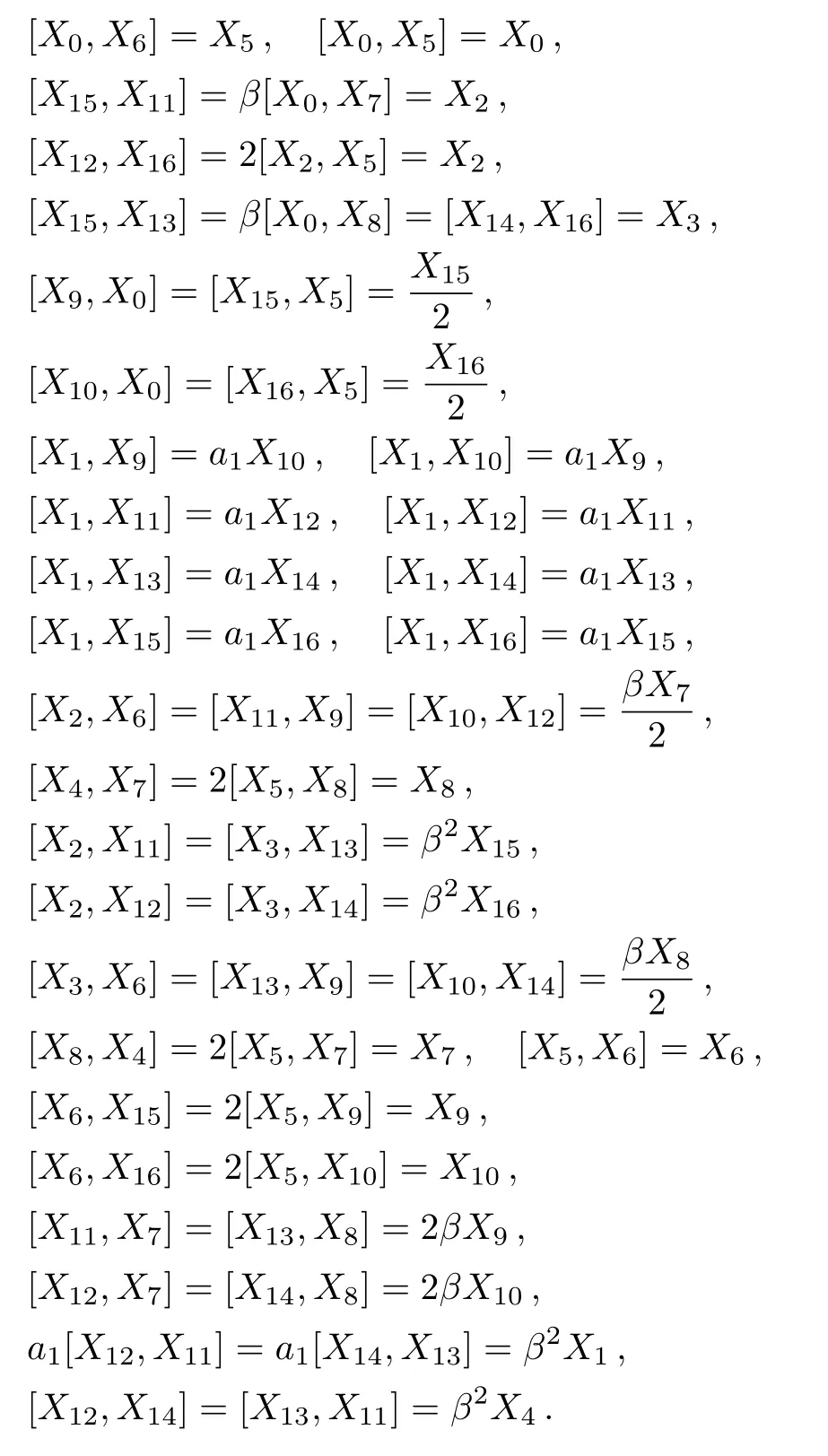
In this case, the conservation laws are obtained as:
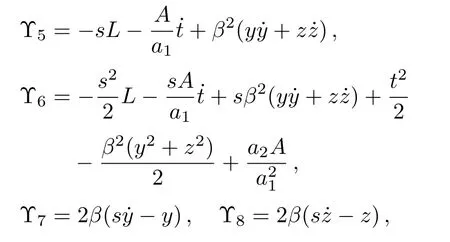

For the metric (40), we haveTab= 0.Thus it represents a vacuum solution.
10 Conclusion
In this paper, we have studied the NS of LRS Bianchi type I spacetimes.For a complete classification, the Noether determining equations are generally solved,which in result categorized the mentioned spacetimes metric into seven different classes according to the dimension of Noether algebra.The possible dimension of Lie algebra of Noether symmetry turned out to be 5, 6, 7, 8, 9, 11,and 17.These NS are compared with Killing and homothetic vectors and it is shown that the possible dimension of Killing algebra for LRS Bianchi type I spacetime is 4,5, 6, 7 or 10.Besides this, the conservations laws are presented for all the Noether symmetry generators by using the well known Noether’s theorem.Finally, it is observed that most of the obtained metrics are anisotropic or perfect fluids satisfying different energy conditions.
Acknowledgments
We are thankful to the referees for their useful suggestions on the manuscript.
 Communications in Theoretical Physics2019年3期
Communications in Theoretical Physics2019年3期
- Communications in Theoretical Physics的其它文章
- Entropy Quantization of Schwarzschild Black Hole
- Pull-in Instability Analysis of Nanoelectromechanical Rectangular Plates Including the Intermolecular, Hydrostatic, and Thermal Actuations Using an Analytical Solution Methodology
- Boundary Layer Flow over a Curved Surface Imbedded in Porous Medium
- Spin-Dependent Electron Tunneling in ZnSe/Zn1?xMnxSe Heterostructures with Double δ-Potentials
- Interaction of Wave Trains with Defects?
- Modulated Dust-Acoustic Wave Packets in an Opposite Polarity Dusty Plasma System
