Entropy Quantization of Schwarzschild Black Hole

M.Atiqur Rahman

Department of Applied Mathematics, Rajshahi University, Rajshahi 6205, Bangladesh

(Received October 4, 2018; revised manuscript received November 5, 2018)

Abstract The surface gravity of Schwarzschild black hole can be quantized from the test particle moving around different energy states analog to the Bohr’s atomic model.We have quantized the Hawking temperature and entropy of Schwarzschild black hole from quantization of surface gravity.We also have shown that the change of entropy reduces to zero when the boundary shrinks to very small size.

Key words: Hawking temperature, entropy, Schwarzschild black hole

1 Introduction

Black holes are one of the most fascinating objects in physics, which have been concerned to exist in our Universe.There are good observational evidences that black holes exist on scales from a solar mass in stellar binary systems up to million of solar masses in the center of galaxies and quasars.The theoretical studies of such objects, in particular the effects on their environment are of great importance to black hole candidate.In recent years, considerable attention has been concentrated on the study of the quantization of black holes.Black holes, however, are not objects of direct observing and so the quantization of black holes have remained esoteric, and there still exists no satisfactory solution yet.The quantization of black hole can be performed by considering the way of electron’s motion inside the atom from quantum theory like Bohr’s atomic model.It is therefore becomes one of the most important issues in physics.[1]

The unification of the general relativity(GR)with the quantum mechanics(QM)is one of the unsolved problems of the theoretical physics.The concern of the general relativity and gravitation depends on large scale structure in a fully classical ambit but the concern of QM depends on the small atomic or sub-atomic scale and remarkable understanding of the fundamental interactions.[2?4]The incongruity between the two theories comes from the couple of the quantum mechanics[3]with the classical one in modern physics in which the general relativity is embedded.For very small scale quantum properties of vacuum break the scale invariance of the classical approach.For the Planck-scale black hole quantum property of vacuum can be prevented by quantum effect due to smallest mass forming a black hole.Recently, Chiarelli and Cerrutiet al.have shown the way in passing from quantum to classical mechanics which is the decoherence of QM induced by fluctuations.[5?7]In this approach, the vacuum fluctuations is considered as never end and there is a certain ground state in which the mass of the black hole is nonzero produce the quantum decoherence, breaking the QM on large scale.[8?9]

The quantization of the horizon area of black holes was first discovered by Bekenstein.[10?12]The horizon area of a nonextremal black hole was discovered by Chirstodoulouet al.[13?14]Analyzing this work Bekenstein pointed out that reversible transformation of such type of horizon have an adiabatic nature.Of course, in accordance with the corresponding principle the quantization of an adiabatic invariant is perfectly natural.Later, Mukhanov[15]and Kogan[16]have discussed the quantization of black hole.Specially, Kogan was initiated this problem within string theory.

On the other side, the entropic framework developed by Verlinde[17]and He and Ma,[18]propose new way for quantizing gravity beyond classical physics.The quantization of gravity can be used to quantize the black hole.Within the framework of general relativity, gravitoelectromagnetism (GEM)has been discussed by many authors[19?34]in which the electric charge and the electric field of Maxwell electromagnetic theory play the role of the mass of the test particle and the gravitational acceleration, respectively.Following GEM it is possible to split the upper bound of energy without the quantization effects on energy level splitting in atoms and molecules[35]due to the hypothetical nature of the gravitipole.Considering GEM a new method has recently been developed in which the black hole energy can be quantized from the test particle moving around different circular orbits,[36?37]which is analog to the Bohr’s atomic model.

In this research,we have study Hawking radiation and Hawking temperature from quantization of surface gravity rather than using gravitational energy quantization method.The work studied here has the intention to contribute the development of the quantization of black hole by using thermodynamics law dM=(κ/8π)dA.It is believed that the quantum behavior of black holes could play a significant role as a testing ground for the quantum theory of gravity.So, our present research is very interesting and meaningful.

The remainder of this paper is as follows: In Sec.2,we have discussed the motion of a test particle in circular orbit around Schwarzschild black hole.The position of ground state with quantization process have been mentioned in Sec.3.In Sec.4, we have derived the quantization formula for surface gravity.The quantization of Hawking temperature,surface area and entropy have been given in Secs.5 and 6.Finally, we present the concluding remark in Sec.7.

2 Time-Like Geodesics

The line element of the Schwarzschild metric in terms of a spherical coordinates (t,r,θ,?)is given by

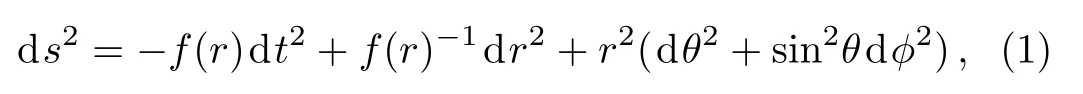
where the lapse functionf(r)is of the form

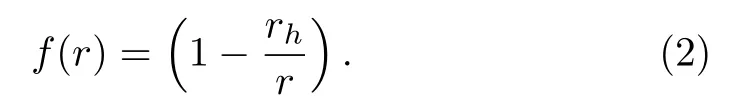
The position of the Schwarzschild black hole horizon is located atrh= 2M,Mbeing the gravitational mass.The geodesic structure of the particle can be formulated by using Euler-Lagrangian equation of motion for variational problem.The Lagrangian corresponding to the metric(1)is given by

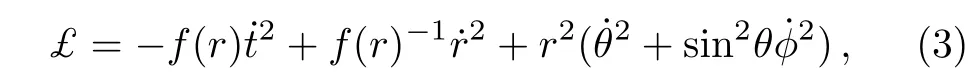
here dot indicates the differentiation with respect to the affine parameterτalong the geodesic.The Lagrangian equations of motion of the particle are

But the Lagrangian￡is independent of (t,?).Therefore,we have from Eqs.(4)and (7)

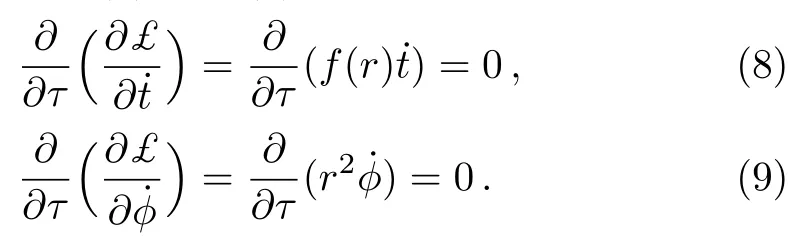
Since the corresponding conjugate momenta are conserved.Integrating Eqs.(8)and (9)we get

whereEandLare constants of integration respectively.The equation of motion forθ, Eq.(6)becomes

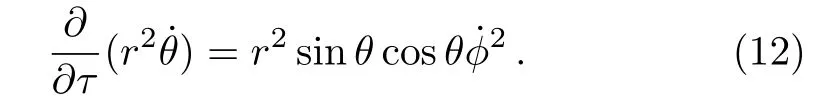
Here, we impose a restriction on the particle motion that the particle is moving in equatorial plane (θ=π/2)around different energy states.Then we have from Eq.(12)after integration

For simplicity, we choose constant=0 so that ˙θ=0.

The time-like geodesic equation corresponding to metric (1)can be written of the following form

Setting Eqs.(10), (11), and (13)into Eq.(14), we get

Therefore, the energy conservation equation for time-like geodesic can be obtained as

where

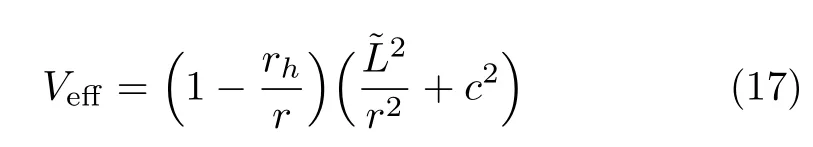
is defined as an effective potential.For a particle moving in a compact regionr=R, we have ˙r= 0, therefore Eq.(16)gives

and gives for the time-like circular geodesic

Therefore, from Eq.(19)the angular momentum of the test particle per unit mass can be derived and the smallest stable circular orbit (SSCO)can be calculated from the point of infection ofVeffusing the following equation

Introducing the energy and momentum of the test particle per unit rest mass according to Ref.[37] of the form

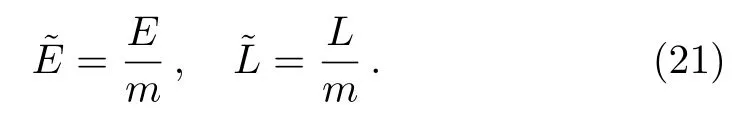
The SSCO equation can be obtained using Eqs.(19),(20),and (21)to the following form

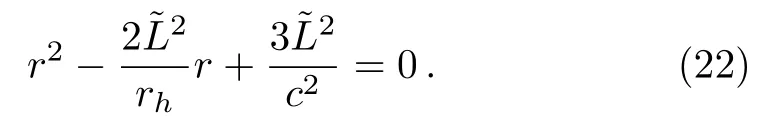
So the radius of each SSCO depends on both the Schwarzschild radiusrh, angular momentum of test particleL.So it is of course interesting to obtain the radius of SSCO equation to the form

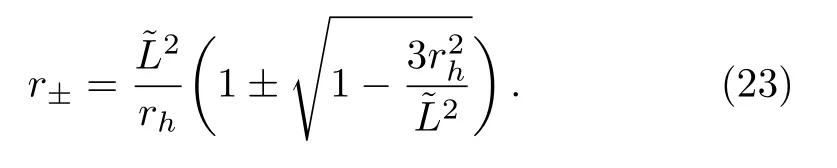
From Eq.(23)it is noted thatr±is real only when≥3r2h.Setting the square root term to zero the smallest stable circular orbit can be obtained when= 3r2h.For the other larger and largest stable circular orbits, we will set the conditions≥3r2hand?3r2hrespectively.

3 Ground State

We consider a test particle of massmorbiting around the black hole at the radius 3rh.The corresponding Compton radiusrc=/mc.Ifrh ?rc, the test particle behaves as a classical point mass moving in the potential given by Eq.(1).In this limit, the present semiclassical quantization approach is valid.[36?37]For possible circular orbits as mentioned before, we can write from Eq.(23)

with

Wilson[38]and Sommerfeld[39]have quantized the angular momentum of the test particleJ?using canonical momentumLconjugate to the angular variable of the form

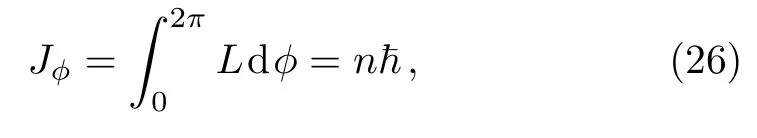
with

wherenis the label index of the orbit.Takingn0as the label index of the first circular orbit we have from Eq.(27)

In terms ofn0, Eq.(24)gives

The smallest radiusR0for ground state can be taken as

Sincerh ?rcwhenR0=rhwe haverh=n0rc, so thatn0?1.For other higher states we have

The quantize radius of different circular orbits have been mentioned in Ref.[36]and have shown that for large quantum number all the circular orbits coincide with one another.

4 Surface Gravity Quantization

The quantization formula of surface gravity can be performed from Eq.(30)interms of first index labeln0of the first circular orbit.Recalling Eq.(30), we have

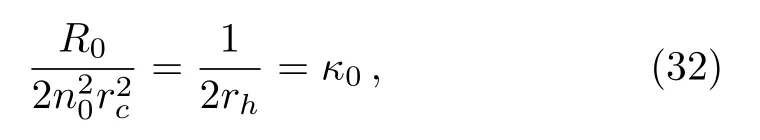
whereκ0is the surface gravity related to the smallest circular orbitR0.The surface gravity of the second circular orbit is

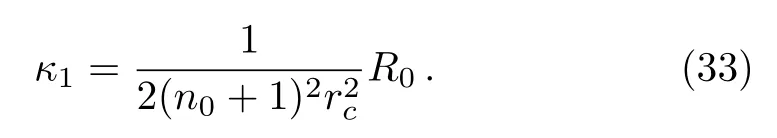
Sincerh ?rc,n0?1 and so (n0+1)2≈n20[1+2/n0],therefore Eq.(33)becomes

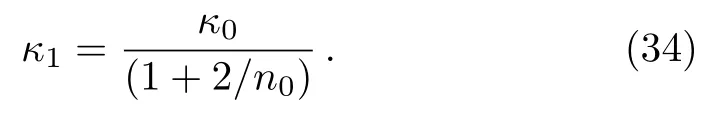
Replacingn+2 forn0, the surface gravity of the third circular orbit takes the form

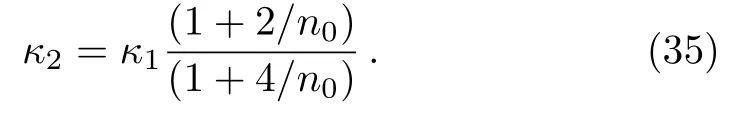
Using method of mathematical induction, the quantized formula of the surface gravity can be written as

Whenn0→∞,κn+1coincide withκn.Also when bothn →0 andn0→∞, we have from Eq.(36)

which is exactly surface gravity of the Schwarzschild black hole.

5 Hawking Temperature Quantization

The Hawking temperature for each of the energy state can be derived from dividing both sides of Eq.(36)by 2πto the following form

In the limiting case, whenn →0, Eq.(38)gives

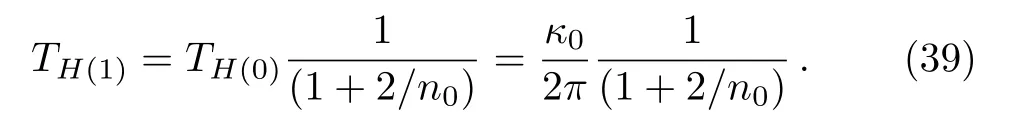
Again when the label index of the first circular orbit is very high, i.e., whenn0→∞, Eq.(39)is reduced to

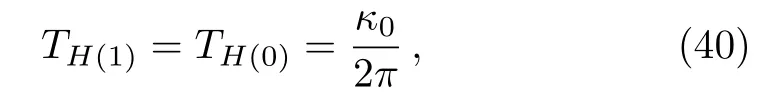
using Eq.(37)we have

i.e., the temperature reads as 1/8πMwhich is exactly Hawking temperature of Schwarzschild black hole.

6 Entropy Quantization

In this section, we quantize the entropy from quantization of surface gravity of Schwarzschild black hole.The quantize formula of the surface area for the higher states can be written with the help of Eq.(36)as

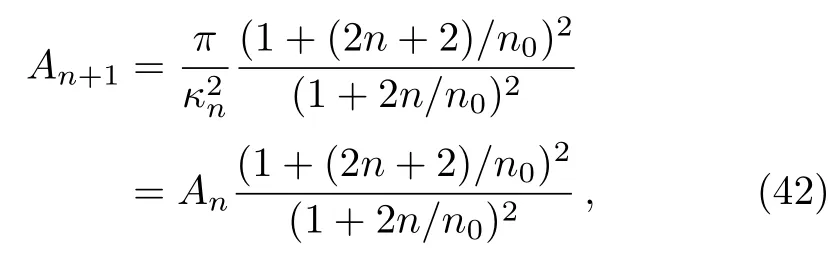
which shows that in the limiting case whenn0→∞, the surface area for higher energy states coincide.

The main task of the work is to develop entropy quantize formula.We consider the initial mass and radius of the Schwarzschild black hole asM0andrh=2M0respectively.During the evaporation process it losses mass until vanishing.A distance observer situated at spatial infinity will measure the Hawking temperature related to the remaining massMof the black hole byTH=1/4πrh.According to the first law of thermodynamics, the entropy related to the loses of an infinitesimal amount of internal energyUcan be written as

Using conservation of mass and energy,δE=?δM,Eq.(43)becomes

Integrating Eq.(44), the entropy of the whole of Hawking radiation emitted during the evaporation process can be written as

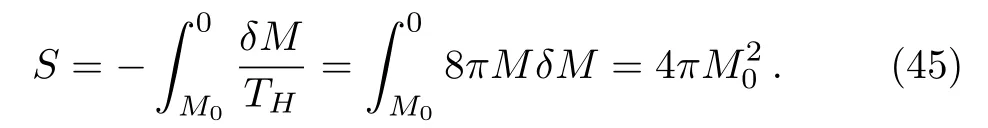
Therefore, the entropy of the initial black hole can be written using Eq.(45)as

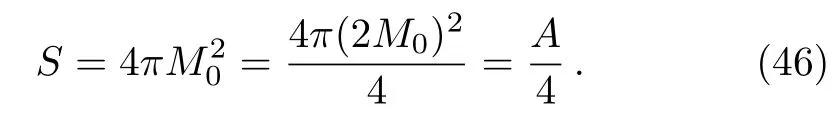
This result is exactly the Bekenstein-Hawking entropy of the initial black hole.Using Eq.(46)the quantize formula for Bekenstein-Hawking entropy yields

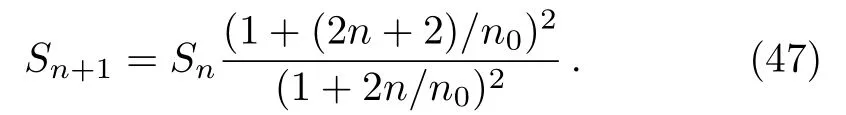
It is true from Eq.(47)thatSn+1=Snwhenn0→∞i.e., the change of entropy for all the energy states coincide.Again whenn →0, Eq.(47)gives

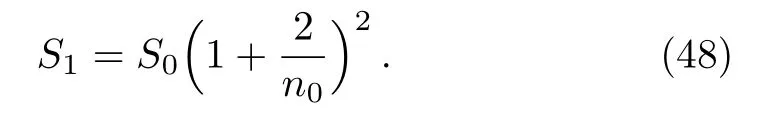
Butn0?1 impliesS1> S0, therefore, the entropy decrease with decrease of energy states.

IfA0denotes the surface area of the ground state then we haveA0=4πR20, which interms of first label indexn0becomes

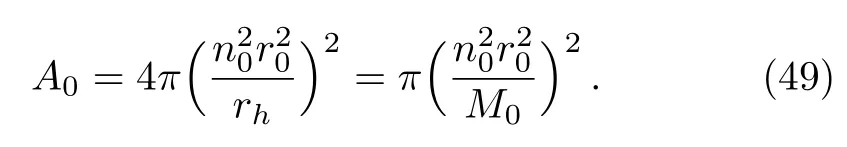
Equation(49)indicates that the ground state surface area never vanishes and it is not possible to convert all the mass into radiation i.e.,black holes cannot evaporate completely.The entropy corresponding to ground state surface area can be written by using Eq.(46)as

Setting Eq.(49)into Eq.(50)we get

which shows that during the evaporation process small amount of mass never vanishes.Mathematically,S0(M →0)→0 and agree with the result obtained by Sakalli’s.[40]The massM0of the black hole decrease due to Hawking radiation.WhenM0→0 the evaporation process further stop and the black hole becomes a remnant.The similar result has been shown in Refs.[41–44] when the effects of quantum gravity effects are taken into account.In another words,the surface area decreases with Hawking radiation.The decrease of surface area decrease energy states and when the surface area reduce to ground state the evaporation process stop.The black hole surface area shrinks to a very small size.

7 Concluding Remarks

In Ref.[36], we have developed the hawking radiation from energy quantized method.In this research,the same results have been shown by using quantization of surface gravity rather than energy and is more interesting and relevant in quantum theory.Our present work stringily supports the results of Bekenstein[10]that a black hole entropy is proportional to the horizon area of black hole.The present work shows that the different energy labels of black hole in the nature can be performed in the same way as that for the electron occupy different energy labels outside the atom like quantum theory,[41]however, it suggests a new idea to unify gravity with quantum theory.

We have shown some interesting properties of black holes from quantization of entropy, which was suggested in a previous work to unify the black hole entropy formula as entropic framework.[17,45]It indeed offers new perspectives on quantum properties of gravity.This suggests a way to unify gravity with quantum theory.