Quantum Fisher Information Gap for Systems with Nonlinear Hamiltonians?
Bo Liu(劉博),Yi-Xiao Huang(黃奕筱),and Xiao-Guang Wang(王曉光)
1Zhejiang Institute of Modern Physics,Department of Physics,Zhejiang University,Hangzhou 310027,China
2School of Physics,Changchun Normal University,Changchun 130032,China
3School of Science,Zhejiang University of Science and Technology,Hangzhou 310023,China
Abstract Quantum Fisher information(QFI)gap characterizes the stability of Qfito space directions.We study the Qfidistributions and Qfigap for quantum states generated from nonlinear Hamiltonians for both spin and bosonic systems.We find that the same spin-squeezing parameter(or principle squeezing parameter)corresponds to two different values Qfigap,and the locations of all extreme points of the Qfiare explicitly given.
Key words:quantum Fisher information,quantum metrology,nonlinear Hamiltonians
1 Introduction
The quantum Fisher information,[1]which is related to the quantum version of Cram′er-Rao inequality,[1?5]is the extension of classical Fisher information to quantum regime.[6]Moreover,Qfilies at the heart of the parameter estimation theory[7]and becomes a useful tool for evaluating the precision limits of quantum estimations.[8?15]A larger value of Qfimeans that we can estimate the parameter with a higher precision.For the past few years,this field has been developing rapidly,and a lot of useful and interesting results were discovered.[16?27]For instance,the researchers[28?29]obtained an alternative representation of Qfifor a unitary parametrization process in terms of a Hermitian generator H,and this representation is convenient to use for the applications of QFI.
In the scenario of quantum metrology,we apply a unitary evolution U(θ)to an input state ρ0,which is independent of θ.An output state ρθis given by ρθ=U(θ)ρ0U?(θ).The unitary evolution U(θ)can be expressed by the Hermitian generator H as U(θ)=exp(iθH).The generator H can be often written aswhere Akis an operator and n is the m-dimensional unit vector.The explicit expression for Qfiwith respect to θ is given by[29]
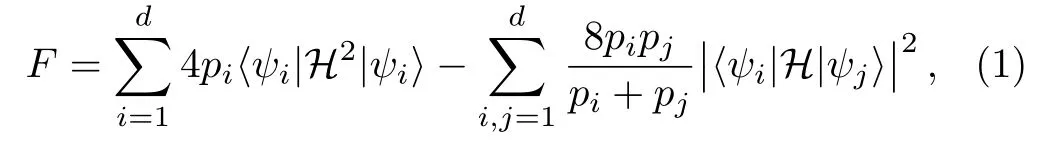
where piand|ψiare eigenvalues and eigenvectors of the initial density matrix,respectively.The eigenvalues here are non-zero.
In spin systems,the unitary operator U(θ)is expressed as

where J is the angular momentum operator J=(Jx,Jy,Jz)and n1is the unit vector given by n1=(sin?cosφ,sin?sinφ,cos?)Twith the polar angle ? and the azimuthal angle φ.While,in bosonic systems,U(θ)is expressed as

with X=(x,p)and n2=(cos?,sin?)T,where the dimensionless operators x and p are given by x=a+a?and p=(a? a?)/i.Here,a and a?are annihilation and creation operator of the boson,respectively.
From the above choices of unitary operators for both spin and bosonic systems,the Qfimust have a specific distribution over space directions.We can rewrite Qfias
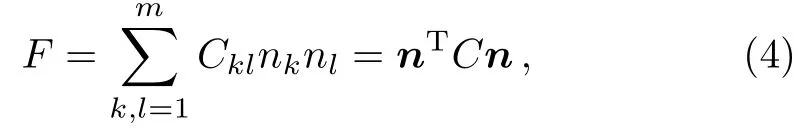
where C is a symmetric covariance matrix,and the matrix elements of C take the form as

It is very clear that Qfiis{nk}dependent.One question naturally arises is that how to characterize the sensitivity of Qfito space directions.Recently,we have established a definition of Qfigap,[30]which is the difference between the maximum and minimum values of Qfiover space directions,that is
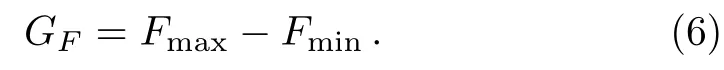
As discussed in Ref.[30],the matrix C can be diagonalized by an orthogonal transform as
where we can set E1≥ E2≥ E3≥ ···≥ Emand the rotated vector as n′=On.The rotated vector n′is also normalized and satisfies the conditionIt is easy to see that

In the appropriate spatial directions n′,we can obtain the maximal Qfias Fmax=E1,while the minimal Qfias Fmin=Em.Correspondingly,Qfigap is determined by the eigenvalues{Ek}of the symmetric covariance matrix C.
The QFI,which is{nk}dependent,has a specific distribution over space directions,and then,Qfigap can be used to optimize the choice of measurement direction.If the gap is large,the closer to the direction of maximum value,the better the measurement.The smaller the gap,the wider the measurement direction.Zero gap means that the Qfiis completely insensitive to the change of directions,and the bosonic coherent state is just belong to this situation.[30]Obviously,Qfigap characterizes the stability of Qfito space directions.
This paper is organized as follows.In Secs.2 and 3,we study Qfigap for several typical states generated from nonlinear Hamiltonians in spin and bosonic systems,respectively.As these states are often squeezed,we then investigate the relations between squeezing and Qfigap.Finally,a summary is provided in Sec.4.
2 Spin Systems
The Qfiis widely studied in spin systems.[31?36]Now we consider an ensemble of N spin-1/2 particles with ground state|↓and excited state|↑.The angular momentum operator Jγ(γ =x,y,z)are defined as Jγ=whereare Pauli matrices for the i-th qubit.Now,we discuss the Qfigap of one typical class of spin-squeezed state,i.e.,the one-axis twisted collective spin state.[37]This stateobtained by acting the unitary operator exp(?iζon the collective ground state
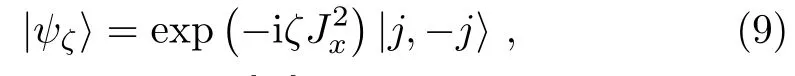
where ζ is a real parameter.[38]Here,the unitary operator is generated from the nonlinear Hamiltonian
Here,the Hermitian generator takes the form as H=J ·n1.The state|ψζwe investigated is a pure state,then the Qfiis just given by

It is just four times the variance of the generator H.Due to the parity symmetry,[39?40]we obtain the relevant expectation values,which determines the covariance matrix and the results are given in Table 1.Therefore,the Qfiof the state|ψζcan be obtained as

Table 1 The expectations of the operators(first column)under the collective ground state|j,?j(second column)and the one-axis twisted collective spin state|ψζ(last column).

Table 1 The expectations of the operators(first column)under the collective ground state|j,?j(second column)and the one-axis twisted collective spin state|ψζ(last column).
Expectations |j,?j ??ψζJz ?j ?j cos2j?1(ζ)J2z j2 14j(2j+1)+14j(2j? 1)cos2j?2(2ζ)J2y 12j 14j(2j+1)?14j(2j? 1)cos2j?2(2ζ)J2x 12j 12jJxJy+JyJx 0 j(2j ? 1)sinζ cos2j?2(ζ)
In Fig.1,we plot the Qfiover space directions.We can clearly observe F change periodically over space directions for fixed squeezing parameter ζ(ζ=1,2)in the cases of j=2,5/2.All maximal and minimal points are evident,and they also have a clear periodic structure.In fact,from Eq.(11),we can find locations of extreme value points at

or ? =mπ (m ∈ Z)and arbitrary φ.Thus,the locations of all the maximal and minimal points are explicitly given.
We now partition the parameter interval φ ∈ [0,2π]and ? ∈ [0,2π]into sub-intervals,respectively.Each subregion(φ ∈ [φi?δφi,φi],? ∈ [?j?δ?j,?j])is represented as a flake,which is tagged with a distinguished point.Each point corresponds to a value(height)of the QFI.According to this way,we may convert(a)and(d)in Fig.1 to be(a)and(b)in Fig.2,respectively.Then the width between the highest and the lowest line of the distribution of Qfiin Fig.2 is the Qfigap,which is similar to the concept of energy gap.It is obvious that the gap in Fig.2(b)is larger than that in Fig.2(a).
On the other hand,the maximal and minimal values of Qfias well as the Qfigap can be determined by the following covariance matrix,[17?18,30]


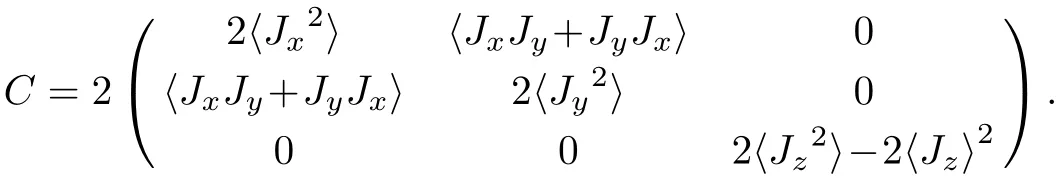
These three eigenvalues of C are given by

Therefore,from Eq.(6),the Qfigap is obtained as


Fig.1 (Color online)The Qfiof the one-axis twisted collective spin state as a function of the polar angle ? and the azimuthal angle φ for ζ(ζ=1,2)and j(j=2,5/2).

Fig.2 (Color online)Qfigap for different ζ and j.Representative values in(a)are selected with ζ=1 and j=2(corresponding to Fig.1(a)),and representative values in(b)are selected with ζ=2 and j=5/2(corresponding to Fig.1(d)).
Meanwhile,the so-called spin-squeezing parameter is obtained as[37,41]

From Table 1,we have also obtained the spin-squeezing parameter of this state as
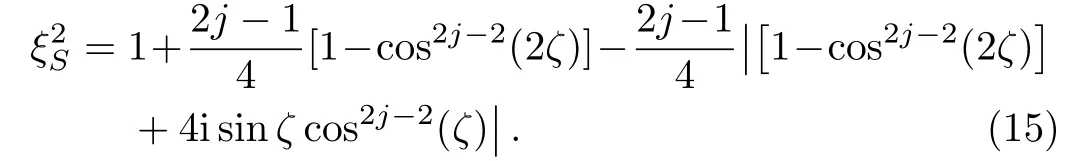
When ζ=0,the Qfigap and the spin-squeezing parameter of the one-axis twisted collective spin state return to the results of the collective ground statei.e.,GFJ=2j and=1.[30]Then the spin-squeezing parameteras the function of the parameter ζ is shown in Fig.3(a),Qfigap GFas the function of ζ is shown in Fig.3(b),and Qfigap GFas the function of the spin-squeezing parameteris shown in Fig.3(c),for different j(j=3/2,5/2,7/2),respectively.For a fixed ζ,the Qfigap always increases with increasing j,while the spin-squeezing parameter does not change monotonically with j.Both Qfigap and the spin-squeezing parameter change periodically with ζ,and the periods are both π.Within each period,the curves are axisymmetric for ζ=(2m+1)π/2(m ∈ Z).Moreover,it is interesting to see that the same spin-squeezing parameter can correspond to two different values of Qfigap.

Fig.3 (Color online)The spin-squeezing parameter ξ2S(a)and Qfigap GF(b)as the function of ζ for different j.These curves all change periodically with parameter ζ,and the curves in(b)increase sharply as j.(c)shows Qfigap GFas the function of the spin-squeezing parameter Representative values for j are selected with j=3/2(red),j=5/2(blue),j=7/2(orange),respectively.
3 Bosonic Systems
Now we turn to bosonic system.[42?49]The Hermitian generator for this system is H=X·n2.In the following,the state we investigated is obtained by acting the operator exp[?iβ(a?a)2]on the coherent state|α,i.e.,

where the coherent state is defined aswith α =|α|exp(i?). The nonlinear Hamiltonian is H ~(a?a)2.For a general state,the Qfiis given by[30]


It is evident from the above equation that the Qfitakes maximum at
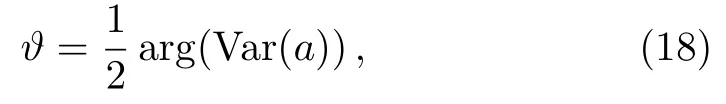
and takes minimum at
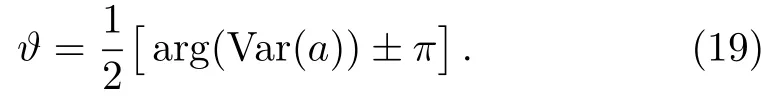
Thus,from the definition of the Qfigap in Eq.(6).we obtain

Meanwhile,the so-called principal squeezing parameter[50?52]is given by
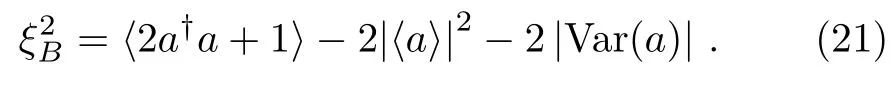
The relevant expectation values for the state|ψαare given in Table 2,from which one can obtain
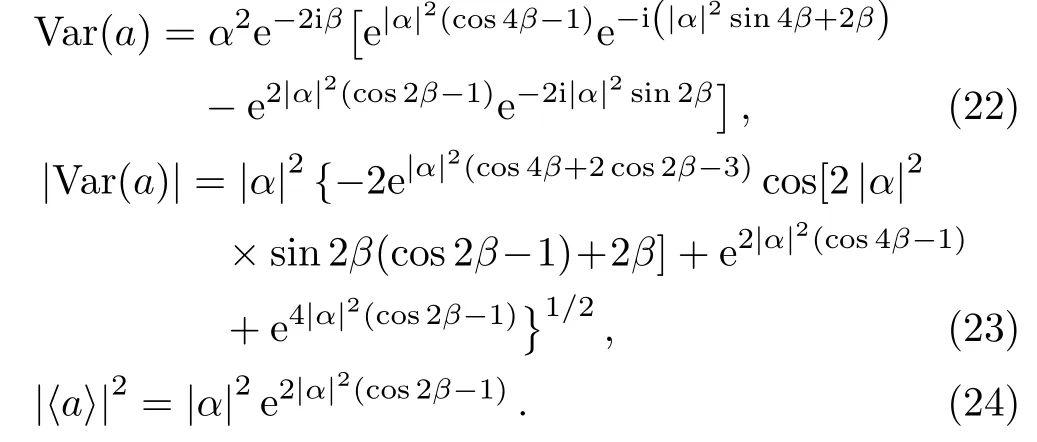
Table 2 The expectations of the operators(first column)under the coherent state second column)and under the bosonic states (last column).

Table 2 The expectations of the operators(first column)under the coherent state second column)and under the bosonic states (last column).
Expectations |α |ψαa α αexp[|α|2[exp(?2iβ)? 1]? iβ]a2 α2 α2exp[|α|2[exp(?4iβ)? 1]? 4iβ]a?a |α|2 |α|2
The Qfiof state|ψαas a function of the angle ? for α(α =1,3/2)and β (β =1,3/2)are shown in Fig.4.It is evident that the Qfichanges periodically.We also observe that the maximum and minimum are different for different parameters.According to Eqs.(18)and(19)and the value of arg(Var(a)),
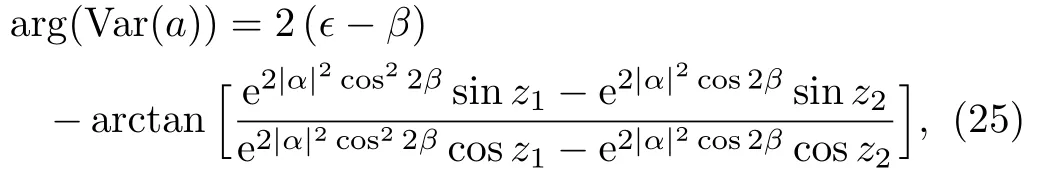
with z1=|α|2sin4β +2β and z2=2|α|2sin2β,then we can obtain all the locations of the maxima and minima.
In Fig.4,we plot the Qfiover space directions.We can clearly observe F change periodically over space directions for fixed squeezing parameter β (β =1,3/2)in the cases of α=1,3/2.All maximal and minimal points are evident.The curve of F,as a function of ?,is a periodic waveform with the period of π.The parameters α and β affect the amplitude,phase and height of the waveform,e.g.,the position of the waveform in Fig.4(b)is higher than that in Fig.4(a)on the ordinate,but the amplitude of the wave(corresponding to 1/2 of the gap)in Fig.4(b)is smaller than that in Fig.4(a).Thus,we can use these properties to select more appropriate measurements.
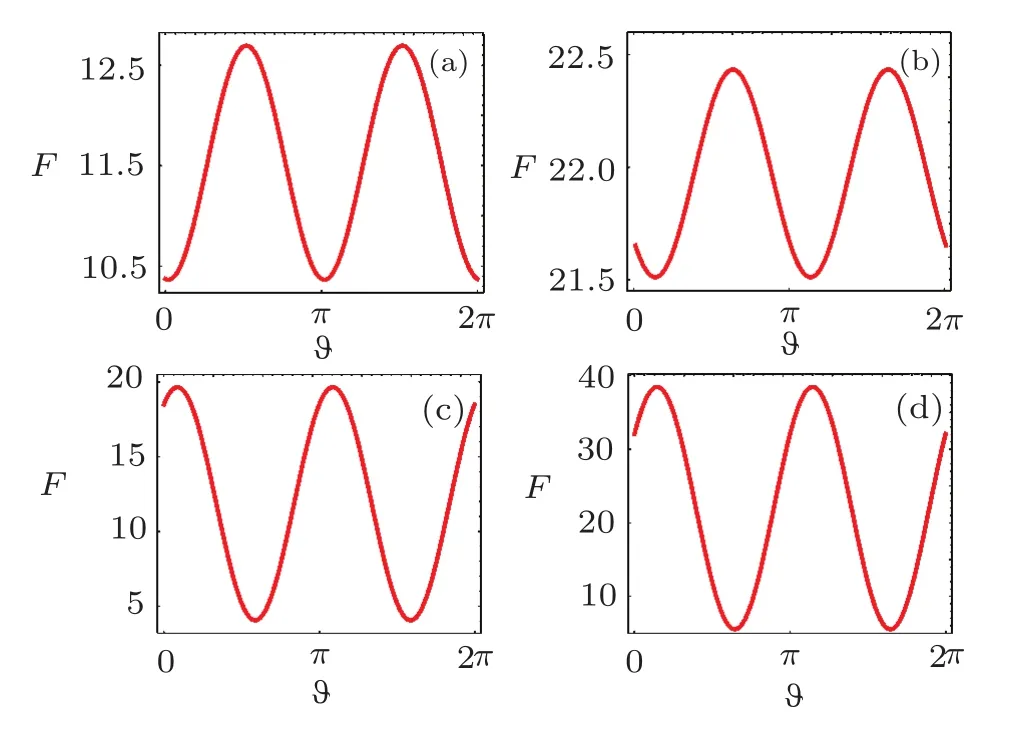
Fig.4 (Color online)The Qfiof the bosonic states|ψαas a function of the angle ? for α =1 and β =1(a),α =3/2 and β =1(b),α =1 and β =3/2(c),α =3/2 and β=3/2(d).
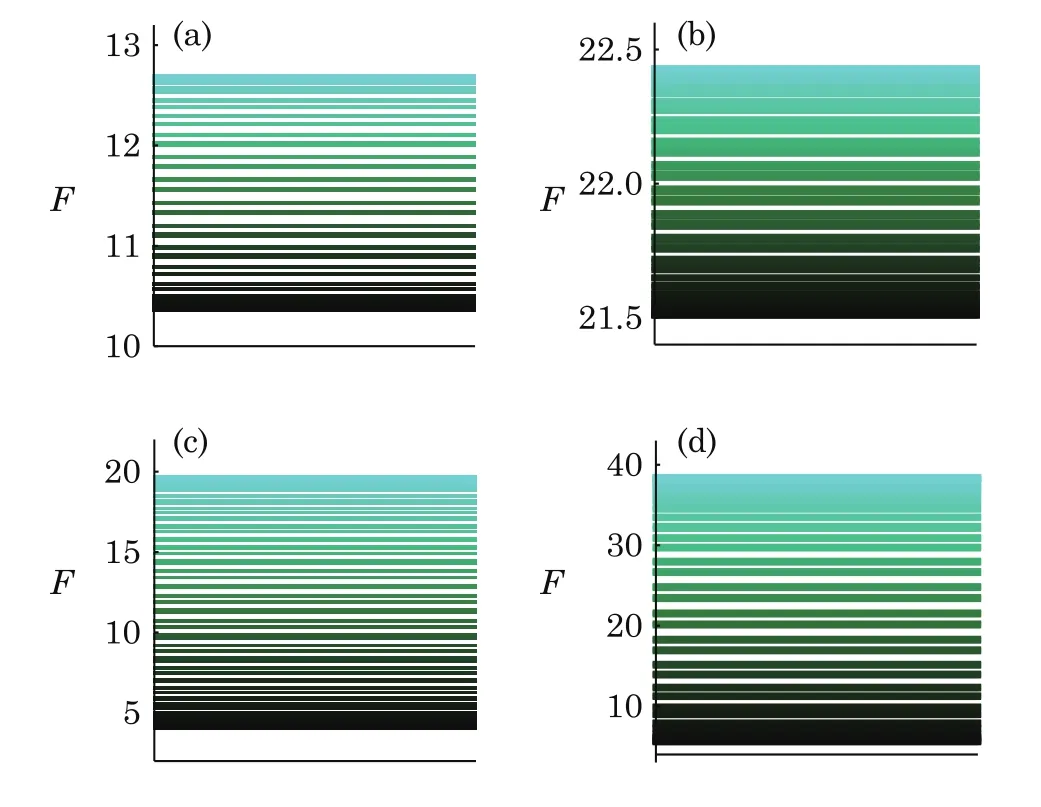
Fig.5 (Color online)Qfigap for different α and β.Representative values are selected with α=1,3/2 and β=1,3/2(corresponding to Fig.4 one-to-one)
We now partition the parameter interval ? ∈ [0,2π]into sub-intervals. Each curve in the sub-region(? ∈[?i? δ?i,?i])is represented as a line,which is marked with a unit line passing through the midpoint of the curve.The height of each line corresponds to a value(height)of the QFI.According to this way,we may convert Fig.4 to be Fig.5 in a one-to-one correspondence.Then the width between the highest and the lowest line of the distribution of Qfiin Fig.5 is the Qfigap.Comparing left and right charts in Fig.5,we can get the change of gap with α,and comparing up and down charts,we can get the dependence of gap on β.

Fig.6 (Color online)The principal squeezing parameter (a)and Qfigap GF(b)as the function of β for different α.(c)shows Qfigap GFas the function of the principal squeezing parameter Representative values for α are selected with|α|2=1(red),|α|2=2(blue),|α|2=3(orange),respectively.
The principal squeezing parameteras the function of β is shown in Fig.6(a),the Qfigap GFas the function of β is in Fig.6(b)and Qfigap GFas the function of the principal squeezing parameteris in Fig.6(c),for different α with|α|2=1(red),|α|2=2(blue)and|α|2=3(orange),respectively.The principal squeezing parameter and Qfigap change periodically with β,and the curves are axisymmetric in each period,but the period of the spin-squeezing is π/2 instead of π.When we compare Fig.3 and Fig.6,it is found that the trends of the curves are roughly similar.But the trend with β in the bosonic system is much more complicated than that in the spin system,especially near the point β=mπ/2,(m ∈ Z).In addition,just like the situation in spin systems,we can also observe that the same squeezing can correspond to two different values of Qfigap.
4 Conclusion
As a summary,we have obtained analytical results of the Qfigap for states generated from nonlinear Hamiltonians for both spin and bosonic system.Interestingly,the trends of the curves for the Qfigap as the function of the squeezing parameter ζ in spin system are roughly similar to those in bosonic systems.This is because that the SU(2)algebra can degenerate to Heisenberg-Weyl algebra under certain limits.We have also found that is the same spin-squeezing parameter(or principle squeezing parameter)corresponds to two different values of the Qfigap.The relations of nonlinearity and the Qfigap were investigated in our study and it is also interesting to study other Hamiltonian with nonlinearity,such as those in cold-atom systems.
——以“劇院運(yùn)營(yíng)與管理人才培訓(xùn)班”為例
 Communications in Theoretical Physics2019年1期
Communications in Theoretical Physics2019年1期
- Communications in Theoretical Physics的其它文章
- Kinetic Simulation of Nonequilibrium Kelvin-Helmholtz Instability?
- Nontrivial Effect of Time-Varying Migration on the Three Species Prey-Predator System?
- A One-Dimensional Discrete Boltzmann Model for Detonation and an Abnormal Detonation Phenomenon?
- Impact of Colored Noise on Population Model with Allee Effect?
- Improved Five-Parameter Exponential-Type Potential Energy Model for Diatomic Molecules?
- Dynamically Tunable and High-Contrast Graphene-Based Terahertz Electro-Optic Modulator?
