Path of Momentum Integral in the Skorniakov-Ter-Martirosian Equation?
Chao Gao(高超) and Peng Zhang(張芃)
1Department of Physics,Zhejiang Normal University,Jinhua 321004,China
2Department of Physics,Renmin University of China,Beijing 100872,China
3Beijing Computational Science Research Center,Beijing 10084,China
4Beijing Key Laboratory of Opto-electronic Functional Materials&Micro-nano Devices,Renmin University of China,Beijing 100872,China
AbstractThe Skorniakov-Ter-Martirosian(STM)integral equation is widely used for the quantum three-body problems of low-energy particles(e.g.,ultracold atom gases).With this equation these three-body problems can be efficiently solved in the momentum space.In this approach the boundary condition for the case that all the three particles are gathered together is described by the upper limit of the momentum integral,i.e.,the momentum cuto ff.On the other hand,in realistic systems,the three-body recombination(TBR)process can occur when all these three particles are close to each other.In this process two particles form a deep dimer and the other particle can gain high kinetic energy and then escape from the low-energy system.In the presence of the TBR process,the momentum-cuto ffin the STM equation would include a non-zero imaginary part.As a result,the momentum integral in the STM equation should be done in the complex-momentum plane.In this case the result of the integral depends on the choice of the integral path.Obviously,only one integral path can lead to the correct result.In this paper we consider how to correctly choose the integral path for the STM equation.We take the atom-dimer scattering problem in a specific ultracold atom gas as an example,and show the results given by different integral paths.Based on the result for this case we explore the reasonable integral paths for general case.
Key words:STM equation,integral path,atom-dimer scattering
1 Introduction
The three-body problems are important for various directions of quantum physics,e.g.,nuclear physics,[1?3]quantum chemistry,[4?5]condensed matter physics[6]and ultracold gases.[3,7]By solving these problems one can not only calculate the important parameters for the quantum systems,e.g.,the atom-dimer interaction intensity[8]and chemical reaction rate,[4]but also explore many interesting physical effects,e.g.,the E fimov effect,[9?11]which is induced by the scaling symmetry of three particles with resonant s-wave interactions.
In the previous research of quantum three-body problems,many attentions are paid to the low-energy systems where the de Broglie wavelength of the three particles are much larger than the characteristic length of the interparticle interaction potentials.Two examples are the ultracold atom gases and some low-energy nuclear systems.For these systems the physical properties are determined by a few parameters of the inter-particle interactions,such as the two-body scattering lengths,and are independent of the details of these interactions.[12]In another word,the physical properties of these systems are very universal.
Technically speaking,in the low-energy three-body problems the two-body interaction can be described by simple zero-range potentials or finite-range separable potentials.As a result,the three-body Schr?dinger equation can be re-expressed as an integral equation in the momentum space,i.e.,the Skorniakov-Ter-Martirosian(STM)equation,[13]which is easy to be solved numerically.The STM equation was initially developed by Skorniakov and Ter-Martirosian in 1957,and has been widely used for the three-body problems in various systems,e.g.,the ultracold gases or nuclear systems.
On the other hand,in the three-body problem with zero-range inter-particle potentials,there are two types of important boundary conditions.They are
(i)The “two-body short-range boundary conditions”for the cases that two of the three particles are close to each other,while the third one is far away from them.
(ii)The“three-body short-range boundary condition”for the case that all the three particles are gathered together.
In the STM equation,the two-body short-range boundary conditions are described by the parameters of two-body low-energy scattering,e.g.,the scattering length,while the three-body short-range boundary condition is described by the upper limit of the integrals over the three-body momentum,[14?17]i.e.the three-body momentum cuto ff.
Furthermore,in many realistic cases,e.g.,the ultracold atom gases,when the three particles come together,there occurs an inelastic scattering process,which is called as the three-body recombination(TBR).[18?19]Through this process,two particles can form a deep dimer while the third particle obtains high kinetic energy.As a result,the de Broglie wavelengths of all the three particles becomes pretty small,i.e.,the particles “escape” from the low-energy region.In the ultracold gases,with the help of the kinetic energy obtained from the TBR processes,the ultracold atoms can really loss from the trap.Accordingly,in the presence of TBR the momentum cuto ffin the STM equation becomes a complex number with nonzero imaginary part.As a result,the momentum integral in the STM equation must be done in the complex momentum plane,rather than just along the real axis.In this case,the result of the integral depends on the choice of the integral path.[16]Thus,there is a crucial question:which integration path is correct for the calculation of three-body problem via STM equation?
In this paper we try to investigate this problem by taking a typical atom-dimer scattering problem as an example.Explicitly,we consider the scattering between an ultracold bosonic atom and a shallow dimer,which is formed by one identical bosonic atom and another distinguishable atom(Fig.1),and compare the results given by different momentum integral paths.With the help of our result,we find the integral path,which may be always reasonable for various cases,i.e.,the path shown in Fig.5 and described in Sec.4 in detail.
The remainder of this paper is organized as follows.In Sec.2,we describe the physical system we study and show the STM equation.In Sec.3,we compare the results given by different integral paths.In Sec.4,we generalize them to the STM equations for more general cases.There are some summary in Sec.5.
2 System and STM Equation
As shown in Fig.1,we consider a three-body system consisted by two ultracold identical bosonic atoms(denoted by B),and another ultracold distinguishable atom(denoted by X),with intra-and inter-species scattering length aBBand aBX,respectively.Here we assume that the scattering length aBXbetween each bosonic atom and the atom X is positive and much larger than the range of the inter-species interaction potential,i.e.,the van der Waals length rvdW.For realistic ultracold atom gases this can be realized via the technique of Feshbach resonance.[20]In this case one bosonic atom and the atom X can form a shallow dimer with energy
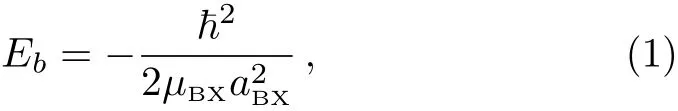
whereμBX=mBmX/(mB+mX)is the reduced mass of one bosonic atom and atom X,with mBand mXbeing their respective masses.In addition,for the convenience of our discussion,we further assume the absolute value of the scattering length between the two bosonic atoms,i.e.,|aBB|,is small enough so that the condition
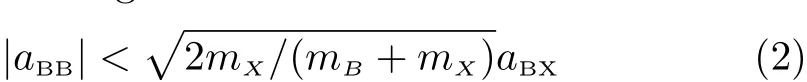
is satisfied.
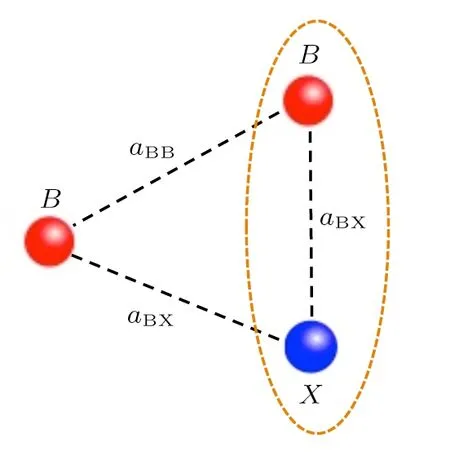
Fig.1 (Color online)Schematic of the three-body system studied in this work.We consider two bosonic atoms(denoted as B)and one extra atom(denoted as X),and assume the two-body scattering length aBXbetween B and X is positive and much larger than the van der Waals length,so that one bosonic atom and the atom X can form a shallow dimer.We calculate the scattering length between this shallow dimer and the other bosonic atom.
In this work we study how to calculate the scattering length aadbetween the shallow BX-dimer and the other bosonic atom.As shown above,for this system the inter-atomic interactions can be described by zero-range pseudo-potentials,and aadcan be calculated via the STM-equation approach.In Ref.[21]we derive the following STM equation for this problem from the corresponding Lippmann-Schwinger equation.We show that the STM equation can be expressed as the following equations for the functions{A(K,ε),η(K,ε)}(=mB=1):
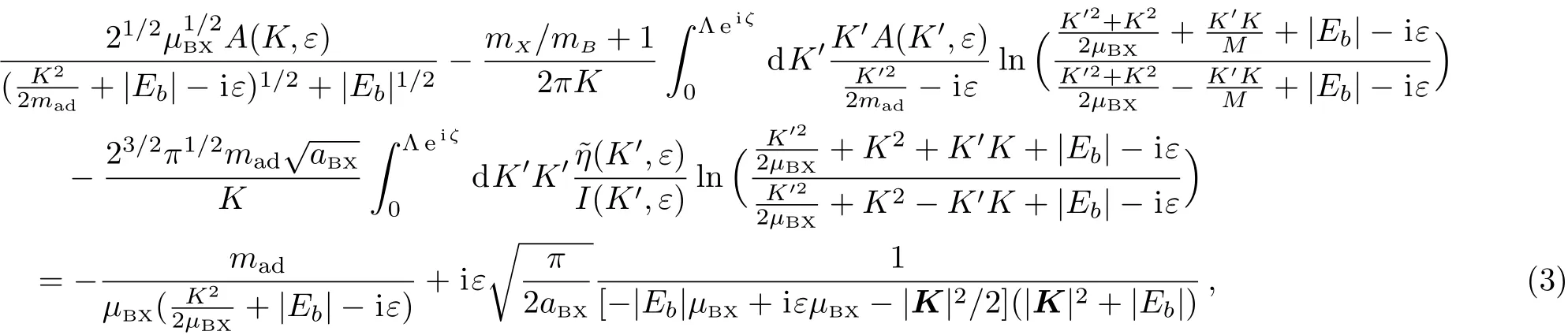
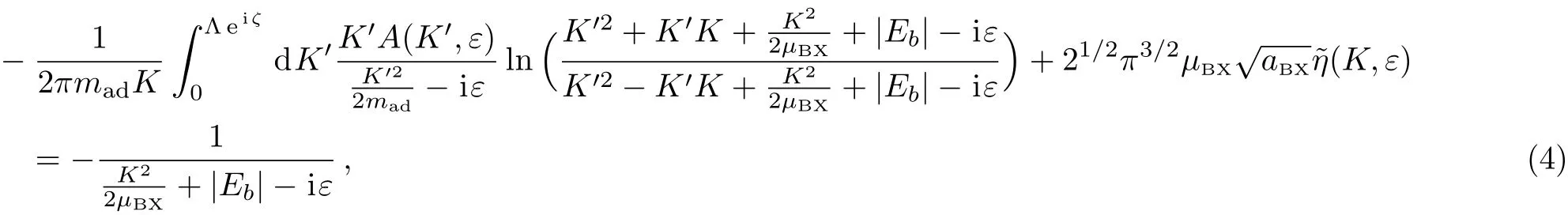
with mad=(mX/mB+1)/(mX/mB+2)being the value of the atom–dimer reduced mass in our natural unit,and the function I(K′,ε)in Eq.(3)being defined as
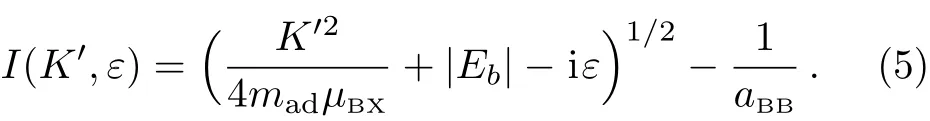
Here we take the complex angle Arg[z]of a complex number z to be in the region Arg[z]∈ (?π,+π].As we show in Ref.[21],the atom-dimer scattering length aadis given by
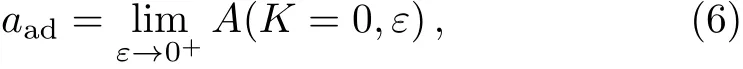
with A(K,ε)being the solution of Eqs.(3)and(4).
In the STM equation(3)and(4), Λeiζis the upper limit of the momentum integral,or the momentum cuto ff.Here the norm Λ is real and positive,and the real number ζ is the phase angle. ζ is non-zero in the presence of the TBR process.As shown in Sec.1,this upper limit describes the boundary condition for the case that all the three atoms are gathered together.For a realistic ultra-cold atom system,the exact values of Λ and ζ are determined by the short-range detail of the atom-atom interaction.Usually Λ is of the order of 1/rvdW,with rvdWbeing the van der Waals length,and ζ is small and positive.For instance,for41K-87Rb-87Rb system,ζ is suggested to be about 0.19.[22]
3 Results Given by Di ff erent Integral Paths
It is clear that the integraldK′plays a central role for the STM equation(3)and(4).Now we compare the results given by different paths of this integral.To be clear,we separately discuss the following three cases:Case 1 aBB<0,Case 2 0

In the following we will show the reason why we define the three cases as above.
Here we also emphasis that,as a result of the TBR process,the scattering length aadhas a non-zero imaginary part.Furthermore,using the optical theorem one can prove that the imaginary part of aadmust be negative,i.e.,

This is essentially due to the unitarity of the S-matrix of the atom-dimer scattering process.Physically speaking,the absolute value of Im(aad)is directly related to the TBR rate or the three-body loss rate K3via the relation
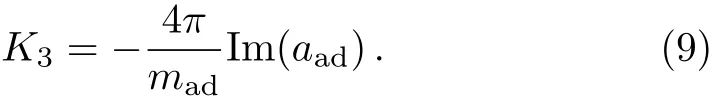
Equation(8)is the necessary condition for the physicallycorrect solution of the STM equation.
3.1 Case 1
For case 1 with aBB<0,there are the following two typical integral paths,as shown in Fig.2(a).Path-I is the straight line from K′=0 to K′= Λeiζ,while path-II consists of two straight lines(in blue color with arrow):from K′=0 to K′=Re[Λeiζ](denoted as path-IIa),and then from K′=Re[Λ eiζ]to K′= Λ eiζ(path-IIb).It is clear that for the integraldK′in the STM equation(3)and(4),the integrands have no pole in the region between these two paths in the limit ε→ 0+.As a result,the solutions of the STM equation with the two integration paths are the same.

Fig.2 (Color online)(a)Typical integration paths for case 1;(b)and(c):Re[aad]and Im[aad]as functions of aBB,for the systems of case 1.Here we take mB=mX,aBXΛ =100,and ζ=0.1,and show the results given by path-I(red dashed-dotted line)and path-II(blue open circles).The black dashed line in(c)indicates the positions with Im[aad]=0.
In Figs.2(b)and 2(c)we show the real and imaginary parts of the atom-dimer scattering length aadgiven by the STM equation with the two integral paths,for the cases with three equal-mass atoms with ζ=0.1.It is clearly illustrated that,as analyzed above,the two results are same with each other.In addition,as shown in Fig.2(c),the condition(8)is well satisfied by the results given by the integral path-I and path-II.
3.2 Case 2
Now we consider case 2 with 0

in our natural unit. According to our assumption in Eq.(2),we have>|Eb|,i.e.,the BB-dimer is a“deep dimer”whose binding energy is larger than the one of the shallow dimer formed by one bosonic atom and the atom X.
In this case,the equation I(K′,ε)=0 with the function I(K′,ε)being defined in Eq.(5),has one solution near the positive half of the real axis of the complex K′plane in the limit ε → 0+.Explicitly,we have
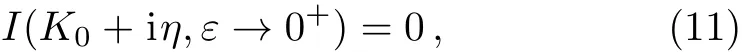
with
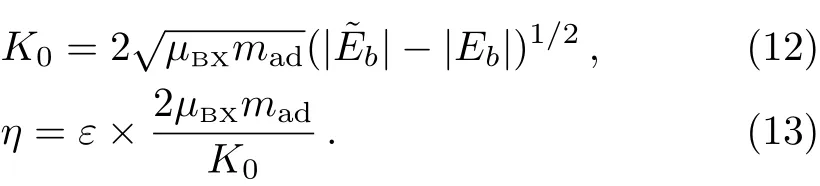
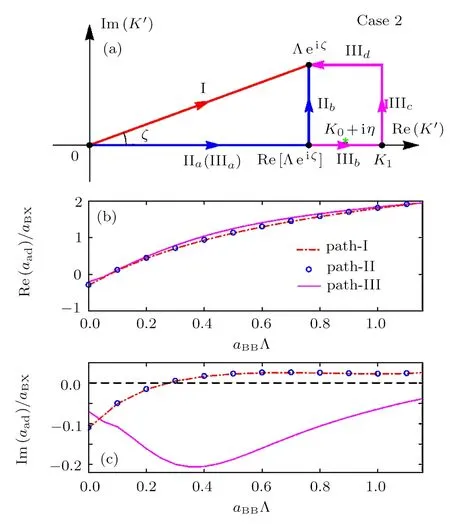
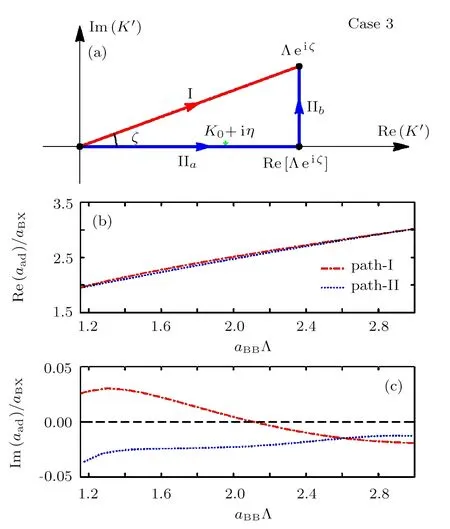
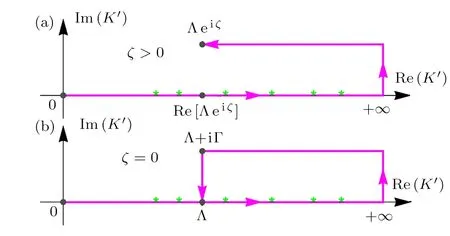
It is clear that K0+iη is a pole of the integrand of the integral∫Λeiζ0dK′in the STM equation(3).In addition,since in this case we have 0 Therefore,in this case there are three typical integral paths for the momentum integral in the STM equations,as shown in Fig.3(a).Path-I and path-II are defined as in the above case 1.In addition,path-III consists of four straight lines:the line from K′=0 to K′=Re[Λeiζ](path-IIIa,same to path-IIa),then from Re[Λeiζ]to K′=K1(path-IIIb),then from K′=K1to K′=K1+iIm[Λeiζ](path-IIIc),and finally from K′=K1+iIm[Λ eiζ]to K′= Λeiζ(path-IIId).Here K1can be an arbitrary real number larger than K0. Since no pole of the integrand of the STM equation appears in the area surrounded by path-I and path-II,and one pole(i.e.,K0+iη)appears in the area surrounded by path-II and path-III,the direct analysis yields that the the solution of the STM equation with momentum integral path-I and path-II would be same with each other,while the path-III would lead to a different solution.So,the question is:which path is reasonable? To answer this question,we calculate the atom-dimer scattering length aadwith the STM equation with these three integral paths,and show Re[aad]and Im[aad]in Figs.3(b)and 3(c),respectively.It is clearly shown that the necessary condition in Eq.(8)is well-satisfied by all the results from path-III,but violated by some results from path-I and path-II.Therefore,in this case the path-III is the reasonable integral path for the STM equation. Fig.3 (Color online)(a)Typical integration paths for case 2;(b)and(c):Re[aad]and Im[aad]as functions of aBB,for the systems of case 2.The parameters are same as in Fig.2.Here we show the results given by path-I(red dashed-dotted line),path-II(blue open circles),and path-III(magenta solid line). Now we consider case 3 with aBB>a?.Similar as in case 2,in this case the two bosonic atoms can also form a deep dimer with energygiven by Eq.(10).As a result,the pole K0+iη of the integrand of the integraldK′in the STM equation(3)can also appear near the positive half of the real axis of the complex K′plane. The only difference between the current case and case 2 is that,since aBB>a?,in the current we have Thus,as shown in Fig.4(a),now there are two typical momentum integral paths,i.e.,path-I and path-II,which have the same definitions as in the above cases 1 and 2.Nevertheless,the fact(15)yields that in the current case the pole K0+iη appears in the area surrounded by the two paths.Thus,the results given by these two integral paths would be different,and we should judge,which path is reasonable. In Figs.4(b)and 4(c)we show the real and imaginary parts of the atom-dimer scattering length aadgiven by the STM equation with these two integral paths.It is shown that the results given by the path-II can satisfy the necessary condition in Eq.(8),while the ones from path-I can violate this condition.Thus,in the current case path-II is reasonable. Fig.4 (Color online)(a)Typical integration paths for case 3;(b)and(c)Re[aad]and Im[aad]as functions of aBB,for the systems of case 3.The parameters are same as in Fig.2.Here we show the results given by path-I(red dashed-dotted line),path-II(blue dotted line). In the above section we study how to choose the reasonable momentum integral paths for the STM equation for the atom-dimer scattering problem introduced in Sec.2.Now we summarize the results obtained above to some principle,which can be generalized to other threebody problems. Our above analysis for the three cases 1,2,and 3 show that,the positions of some poles of the integrands of the integralin the STM equation is very important for the selection of the momentum integral path.Explicitly,the poles localized at the point K′=K?+iη?with K?>0 and η?→ 0+in the limit ε → 0+,with ε being the small positive imaginary part of the energy in the Green’s function,are very important.The reasonable integral path from K′=0 to K′= Λeiζshould go across below all of these poles.The reasonable paths for the above cases 1,2,and 3 all satisfy this condition. Thus,there is a special path,which would be always reasonable,i.e.,the path from K′=0 to K′=+∞,and then to K′=+∞ +iIm[Λeiζ]and then to K′= Λeiζ(the path shown in Fig.5(a)).Obviously,all the paths,which can be continuously deformed from this path without crossing any pole are also reasonable. In addition,there is an interesting particular case,i.e.,the case with ζ=0 and some poles with K?> Λ.This can be understood as the limit ζ→ 0 of the above cases.Thus,according to our above principle,as shown in Fig.5(b),for this case the reasonable integral path is not the path directly from K′=0 to K′=Λ.It would be the path from K′=0 to K′=+∞,and then to K′=+∞+iΓ,with Γ being any finite positive value,and then to K′= Λ +iΓ,and then to K′=Λ. It is clear that,the above principle for the choosing of the momentum integral path can be straightforwardly applied to the STM equations for other three-body problems. Fig.5 (Color online)Reasonable integration paths for general cases with ζ>0(a)and ζ=0(b). In this work we study how to choose the momentum integral path for the STM equation.By studying a typical atom-dimer scattering problem,we show that different integral path can lead to quite different solutions of the STM equation,especially for the imaginary part of the atom-dimer scattering length or the TBR rate K3. More importantly,we find that the necessary condition(8)can always be satisfied by the integral path,which the paths,which can be continuously deformed from the special path shown in Fig.5 without crossing any pole.This principle can be generalized to other three-body problems.Thus,our result is very helpful for the study of low-energy three-body problems in the presence of TBR. To our knowledge,so far the quantitative expression for the three-body short-range boundary condition in real space,which is mathematically equivalent to the momentum cuto ff Λeiζand the reasonable integral path shown above,has not been derived.In future we will try to explore this expression,so that the short-range physics can be described more clearly. Acknowledgments We thank Pascal Naidon,Hui Zhai,and Ren Zhang for helpful discussions and important suggestions.
3.3 Case 3

4 Generalization to Other Cases
5 Summary and Discussion
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
- Communications in Theoretical Physics的其它文章
- Electron Transport Properties of Graphene-Based Quantum Wires?
- Magnetic Properties of XXZ Heisenberg Antiferromagnetic and Ferrimagnetic Nanotubes?
- On the Singular Effects in the Relativistic Landau Levels in Graphene with a Disclination?
- Super-sensitivity in Dynamics of Ising Model with Transverse Field:From Perspective of Franck-Condon Principle?
- New Feedback Control Model in the Lattice Hydrodynamic Model Considering the Historic Optimal Velocity Di ff erence Effect?
- A Class of Rumor Spreading Models with Population Dynamics?
