Probing Nonclassicality of Two-Mode SU(2)Generator Based on Quantum Fisher Information?
Dan Zhang(張丹),Qiang Zheng(鄭強), and Xiao-Guang Wang(王曉光)
1School of Chemistry and Material Science,Guizhou Normal University,Guiyang 550001,China
2School of Mathematics,Guizhou Normal University,Guiyang 550001,China
3Quantum Physics and Quantum Information Division,Beijing Computational Science Research Center,Beijing 100084,China
4Zhejiang Institute of Modern Physics,Department of Physics,Zhejiang University,Hangzhou 310027,China
AbstractNonclassicality is an essential but still open question in quantum mechanics.Here,utilizing the maximum value of quantum Fisher information,we suggest a new version of the nonclassical criterion for SU(2)generator realized by two bosonic modes.As an application of the criterion,the system of two coupled nonlinear nanomechanical resonators is considered.And the nonclassicality of the phonon state in the dynamical evolution is explored.The system has a dynamical phase transition from the tunnelling phase to the self-trapping phase by tuning the coupling strength.It is found that for the tunnelling phase,the phonon state is nonclassical in the full time evolution.And for the self-trapping phase,the evolved phonon state is still nonclassical in the full time with a relatively large coupling strength,while it is nonclassical i n the most of time(but not all)with a small coupling strength.Quantum coherence has distinct different behaviors in the two phases.
Key words:quantum Fisher information,nonclassicality,coherence
1 Introduction
The nonclassicality is a basic feature of a quantummechanical system.[1?2]It is believed that the nonclassicality,as a resource for quantum information process,may be used to accomplish a task better than its classical counterpart.The well-known example is the quantum teleportation[3]achieved with the aid of the entangled state. Probing the nonclassicality of a given quantum state should be the first step to implement it as the resource of information processing. Lots of criteria have been proposed to detect the nonclassicality,such as the Mandel Q-factor,[4]the negativity of P-function,[5]and Wigner function,[6]the standard entanglement potentials,[7?8]the characteristic function,[9]just to mention a few.
At present,the nonclassicality of a quantum state is still an open question. There does not exist a simple and unified nonclassical criterion,just like the concurrence entanglement for two qubits,because a single criterion can only detect some quantum facets.For example,the Wigner function of a squeezed coherent state is positive,even it is generally considered as a nonclassical state.[10]And the photon statistics of the Schr?dinger’s cat state is Poissonian,but its Wigner function has the negative part.
In parallel to the nonclassicality,quantum Fisher information(QFI),[11]which describes the sensitivity of a state in terms of parameter change,plays a central role in quantum parameter estimation and quantum metrology.According to quantum Cramér-Rao inequality,[12]quantum Fisher information determines the upper bound of the parameter estimation precision.[13]Moreover,QFI is also related to entanglement,[14]squeezing,[15?16]quantum phase transition,[17]and quantum illumination.[18]Recently,a nonclassicality criterion of a quantum state based on QFI has been suggested.[19]The main idea behind Ref.[19]is that for an imaginary interferometer,a nonclassical state should produce a better resolution than a coherent state(with the same mean particle number).
At the same time,with the advance of the nano-technology, high quality-factor nanomechanical resonators[20?21]become a key element of precise measurement,such as detection of spin,[22]mass,[23]displacement,[24]etc.More importantly,nanomechanical resonators with the GHz resonance frequency are suitable candidates for testing the quantum mechanics in the mesoscopic scale.However,in the GHz frequency regime,the nonlinear(or anharmonic)behavior of nanomechanical resonators must be considered,[25]which has a nontriv-ial effect and provides new possibility realizing quantum coherent device.[26?27]
In this paper,based on the maximum value of quantum Fisher information,a new version of the nonclassical criterion for SU(2)generator with the two bosonic modes realization is proposed.This new criterion is exploited to explore the nonclassicality of two coupled nonlinear nanomechanical resonators in the dynamical evolution.The resonators have two dynamical phases:[28]the tunnelling phase and the self-trapping phase.It is demonstrated that in the tunnelling phase,the phonon state is nonclassical in the full time evolution.For the self trapping phase,the evolved phonon state is still nonclassical all the time with a relatively large coupling strength,while it is nonclassical in the most of time(but not all)with a small coupling strength.And it is found that quantum coherence has distinct different behaviors in the two phases.
The structure of this paper is as follows.Based on the maximum value of the QFI,in Sec.2 we propose a new version of the nonclassical criterion for SU(2)generator realized by two bosonic modes.In Sec.3 we investigate the system of two coupled nonlinear nanomechanical resonators.It has two phases:a tunnelling phase and self-trapping phase.The nonclassicality of the nanomechanical resonators is numerically studied in Sec.4.A conclusion is given in the last section.
2 Nonclassicality Criterion with Maximal QFI
Coherent state,defined as the eigenstate of the annihilation operator,is generally considered as an important class of quantum state.In this paper,we will explore the nonclassicality in the frame of quantum metrology.Usually,it is believed that the metrological resolution beyond the coherent state is the quantum effect.That is,a given state is nonclassical if it can provide a better resolution than coherent states with the same mean particle number.
In quantum metrology,the unitary transformation,as the most common situation,is described as
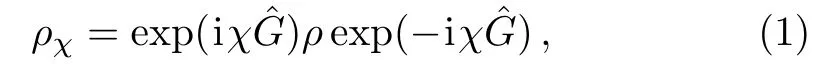
with χ being the parameter to be estimated,andthe generator of the unitary transformation.According to the quantum Cramér-Rao inequality,the variance of the unbiased estimatorsatisfies[29]

where M is the number of measurement,and Fχ=is quantum Fisher information with respect to the parameter χ,with the symmetric logarithmic derivative L determined by[29]
Specifically,let us focus on a two-mode SU(2)generator


The annihilation(creation)operatorssatisfy the commutatorsand
It should be stressed that it is not necessary to have a real rotation acting on ρ.The role of this fictitious transformation Eq.(3)is to probe the geometric structure of the quantum state ρ in the Hilbert space.

with Pclass(α)being a non-negative function no more singular than a Dirac delta function,and Fαbeing the QFI of the coherent state
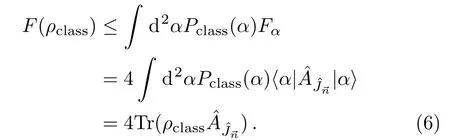
Here “::” denotes the normal order.
The violation of Eq.(6)provides a nonclassicality criterion:for a given state ρ,if it satisfies the inequality[19]
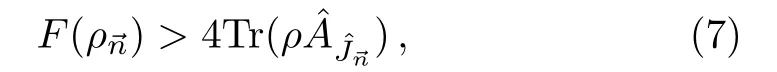
it is nonclassical.
The nonclassical criterion Eq.(7)is only valid for the linear detection scheme.With the nonlinear detection,a classical state still has the ability to produce a better metrological resolution than the coherent state.[31?32]
According to Eq.(3),there is a one-to-one correspondence between the QFI of a given state ρ and the unit vector.The state ρ is nonclassical,if there exists at least a unit direction ensuring that Eq.(7)is satisfied.It is obvious that with a larger QFI,the criterion can be hold more easily.To more sensitively detect the nonclassicality of a given state,we suggest a new version of the nonclassical criterion
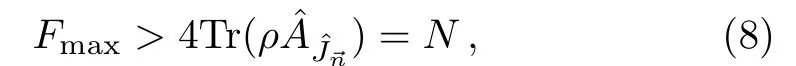
with Fmax≡ maxF(ρ)being the maximum value of the QFI with respect toandasis SU(2)equivalent to.Equation(8)is the main result of this paper.
Now,the remaining question is how to compute the maximum value of the QFI Fmax.For a pure state,which is closely relevant to the phonon state in Sec.3,the QFI equals to the variance of
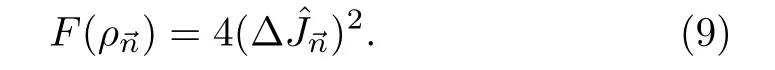
The variance can be rewritten as[33]

where O is an orthogonal matrix,is the rotated direction,andwith αibeing the eigenvalues of the symmetric covariance matrix C.The element of the matrix C is defined as[34]
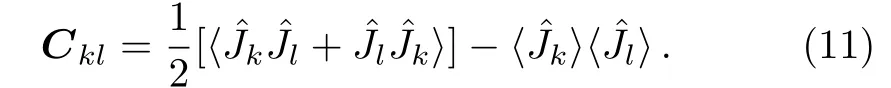
Making use of Eq.(10),the maximum value of the QFI can be obtained as Fmax=4α3,with α1≤ α2≤ α3.
To provide further evidence on the advantage of choosing Fmaxfor Eq.(8),√a simple example is given here.For the NOON statewhich is a typical nonclassical state,it is easy to obtain that

Similarly,here Fmin≡ minF(ρ)is the minimum value of the QFI with respect to.Equation(8)can successfully detect the nonclassicality of the NOON state for N≥2.However,it does not work for for any N if its left-side is replaced by Fmin.
3 Two Coupled Nonlinear Nanomechanical Resonators
Two coupled nonlinear nanomechanical resonators have the Hamiltonian in the following form[37](~=1)
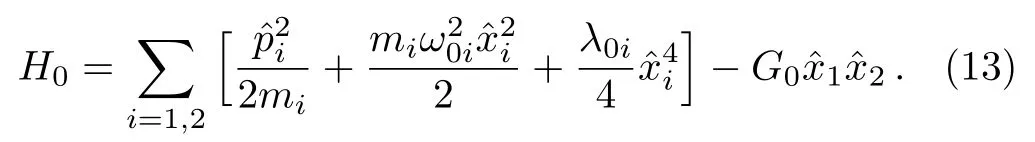
Here only their fundamental flexural modes ω0iare considered,and the interaction between two nanomechanical resonators can be implemented by piezoelectric or mechanical coupling.miis the effective mass of the i-th nanomechanical resonator with the associated displacement operatorand momentum operatordenotes the strength of nonlinearity,and the last term describes the coupling between two nanomechanical resonators with the strength
In the rotating frame with respect to ω01,the original Hamiltonian is changed into[38]

under the rotating wave approximation. Hereis the annihilation(creation)operator defined asfor the i-th nanomechanical resonator,withbeing the zero-point fluctuations.
In Eq.(14)the total phonon numberis a conserved quantity,thus H1is equivalent to the following Hamiltonian
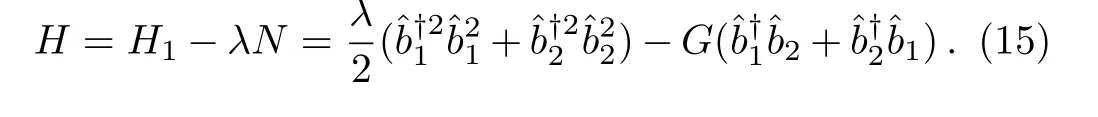
Here for simplicity we set?0=0 and λ1= λ2= λ.This is the phononic version of Josephson junction,[39?40]which has been also realized by BEC[41]and two coupled optical cavities.[42]
Taking the following facts into consideration that(i)the decoherent time of the nanomechanical resonators is relatively long with a very high quality-factor,and(ii)our new version of the nonclassicality criterion is only valid for the unitary evolution,the effect of the dissipation of the nanomechanical resonators will be omitted in this paper.The dynamics of the system is determined by the Schr?dinger equation

The wave function can be expanded in the Fock space

with n being the number of the phonons in the first nanomechanical resonator and(N?n)phonons in the second one.Note that the Fock basis?is also an eigenstate of
The Hamiltonian Eq.(15)has a classical counterpart(N→∞)[43]

with

Here the classical conjugated variables z and θ are defined as follows:Denoting the probability amplitudes of the phonons in the resonators asis the population(phase)difference difference,respectively.

4 Numerical Results and Discussions
Although the form of Hamiltonian Eq.(15)seems simple,it is difficult to solve its corresponding time-dependent Schr?dinger equation analytically.In this paper,Eq.(16)will be solved numerically by exact diagonalization.[44?45]And we are only interested in the system properties with the initial stateFor the initial statecorresponding to zi=?1,the critical value is gcr=2.And all the relevant parameters are scaled by λ=1.
In this section,we firstly investigate the nonclassical property of the two resonators based on the maximum value of the QFI,and then study the quantum coherence of the system.
4.1 Nonclassicality of Nanomechanical Resonators
Here our criterion Eq.(8)is adopted to investigate the nonclassicality of the nanomechanical resonators.Substituting the numerical solution of Eq.(16)into Eq.(8),the nonclassicality of the phonon state can be determined numerically.
According to Eq.(8),we define a ratio R(t)of the maximum value of the QFI Fmaxto N,
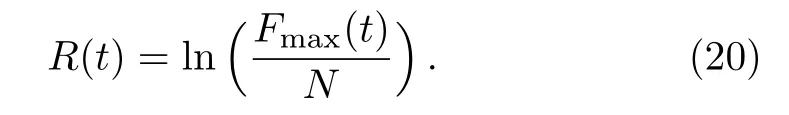
A given state is nonclassical if its corresponding ratio R>0.And a state is called a referring state if R=0.

Fig.1 (Color online)The time evolution of the ratio R(t).(a)corresponds to g=1.0 and 3.0,and(b)corresponds to g=8.0 and 20.0,respectively.The red-dashed line denotes the referring value R=0.The other parameter is N=500,and all the relevant parameter is scaled by λ=1.
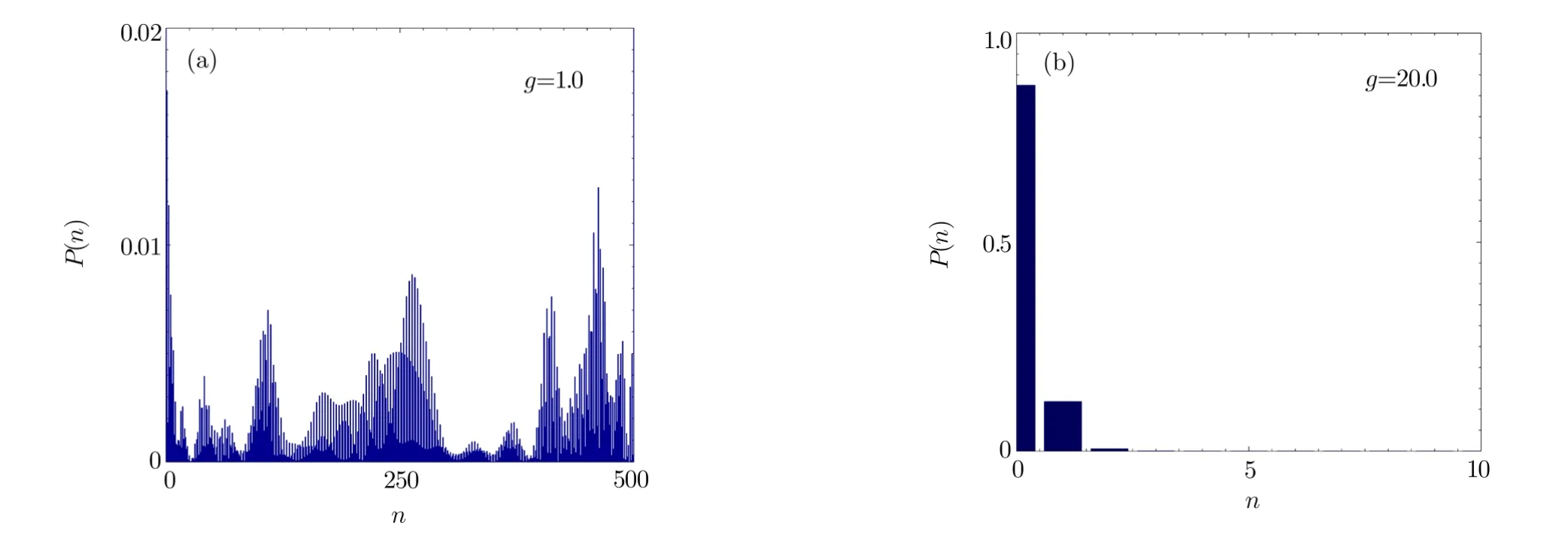
Fig.2 (Color online)The probability distribution of the phonon state in the Fock space at a fixed time t=25.(a)and(b)correspond to the nonclassical state with R>0 and the referring state with R≈0,respectively.All the relevant parameters are scaled by λ=1.
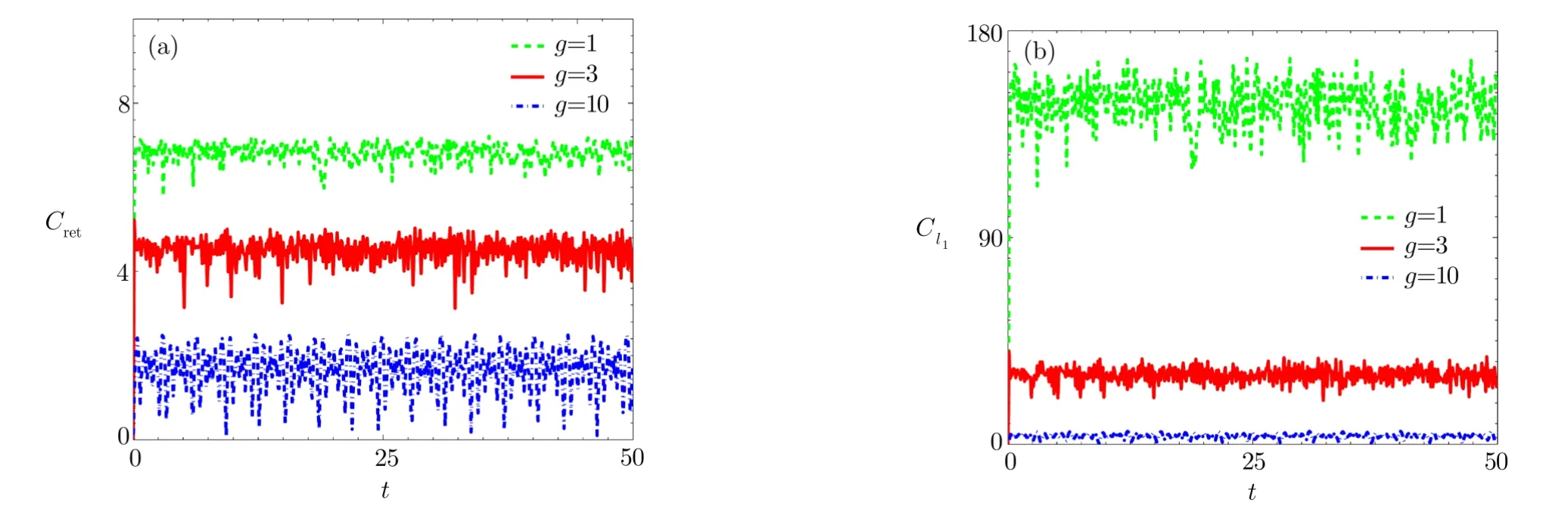
Figure 1 shows the time evolution of R(t)with different values of g.It displays that for g<20.0,the evolved phonon state is nonclassical all the time with R>0.With the increase of g,the values of R(t)decrease considerably at the same time.We also find that the long-time behavior of R(t)is also consistent with Fig.1(not shown here).That is,the phonon state in the tunnelling phase is nonclassical in the full time evolution,and for the selftrapping phase,the evolved phonon state is still nonclassical all the time with a relatively large coupling strength.
More interestingly,Fig.1(b)displays that for g=20.0,the phonon state is nonclassical in the most of the time(but not all),and in the other time it approaches the referring state with R=0.And in the limit g→ ∞,the evolved phonon state becomes to the referring state all the time R(t)≡0.
These results can be understood as follows.In the tunnelling phase with g To further gain some intuitive picture of these results,the probability distributionat a fixed representative time is shown in Fig.2.The value of R in Figs.2(a)and 2(b)isandrespectively.These values are extracted directly from Fig.1.Figure 2(a)clearly shows that as a nonclassical state,the probability distribution has a multi-peak non-Gaussian structure.And as displayed in Fig.2(b),the phonon state can be approximately expressed asIn this case,it is easy to obtainwith p0? p1.That is,?approaches a referring state. The quantum coherence of the two nanomechanical resonators has been investigated in Ref.[38],which is quantified by the mean fringe visibilityDifferent from Ref.[38],here we revisit this subject from quantum information perspective.[46]Our idea is in the following.In the tunnelling phase,the phonon state should have the distinct coherence to ensure that it can tunnel from one resonator to the other.And in the self-trapping phase,the phononic coherence is lost,which make them localize in one nanomechaical resonator. Fig.3 (Color online)The time evolutions of two kinds of quantum coherence with N=200.(a)and(b)correspond to the relative entropy coherence and l1-norm coherence defined in Eq.(21)and Eq.(22),respectively.All the relevant parameters are scaled by λ=1. Fig.4 (Color online)The time-averaged values of two kinds of quantum coherence as a function of g.(a)and(b)correspond to the relative entropy coherence and l1-norm coherence,respectively.All the relevant parameters are scaled by λ=1. The relative entropy coherence of the phonon stateis given as[47?48] The other kind of coherence,so-called l1-norm is defined as[49] It is just the sum of the norm of off-diagonal elements of the density matrix. Figure 3 presents the time evolution of the relative entropy coherence and l1-norm coherence.The behaviors of two kinds of quantum coherence are highly similar:both of them are rapidly oscillating functions of time.And the value of l1-norm coherence is larger than that of the relative entropy coherence.This is reasonable as the former is the sum of the norm of all off-diagonal elements.This figures also shows that at a fixed time the value of quantum coherence decreases with the increase of g.The numerical results are consistent with our argument at the beginning of Subsec.4.2:The system coherence in the tunnelling phase should be larger than that in the selftrapping phase. To well describe the property of the nanomechanical resonators,we also consider the time-averaged values of two kinds of quantum coherence Figure 4 plots(Cret)mand(Cl1)mas a function of g.For a small particle number,such as N=100,it seems that the transition between two dynamical phases is smooth.With the increase of N,the distinct different behaviors of(Cret)mand(Cl1)mpresent in the two phases.In the tunnelling phase with g In this paper,making use of the maximum value of the quantum Fisher information,we propose a new edition of the nonclassical criterion for the SU(2)generator realized by two bosonic modes.As an example,we apply our nonclassical criterion to the system of two coupled nonlinear nanomechanical resonators.The phonon state of the resonators has two dynamical phases:a tunnelling phase and a self-trapping phase.In the case of omitting the phononic dissipation,we find that for the tunnelling phase,the phonon state is nonclassical in the full time evolution.For the self-trapping phase,the evolved phonon state is still nonclassical all the time with a relatively large coupling strength,while it is nonclassical in the most of time(but not all)with a small coupling strength.And we also show that quantum coherence has distinct different behaviors in these two phases. In future,it is an interesting topic to explore the effect of the phononic dissipation on the nonclassicality.More importantly,extending our witness as a measure for the nonclassicality based on the quantum Fisher information should be more useful. Acknowledgements Q.Z.thanks the helpful discussion with Profs.Yong Li(CSRC)and Li-Bin Fu(IAPCM)and Drs.Y.X.Huang and W.H.Hu.4.2 Quantum Coherence in Two Phases

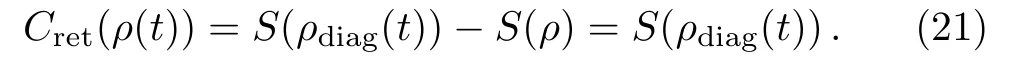



5 Conclusions
 Communications in Theoretical Physics2018年11期
Communications in Theoretical Physics2018年11期
