Numerical Study of Unsteady MHD Flow and Entropy Generation in a Rotating Permeable Channel with Slip and Hall Effects?
Z.H.Khan,O.D.Makinde,R.Ahmad,and W.A.Khan
1State Key Laboratory of Hydraulics and Mountain River Engineering,College of Water Resource&Hydropower,Sichuan University,Chengdu 610065,China
2Key Laboratory of Advanced Reactor Engineering and Safety,Ministry of Education,Tsinghua University,Beijing 100084,China
3Faculty of Military Science,Stellenbosch University Private Bag X2,Saldanha 7395,South Africa
4School of Mathematics and Physics,University of Queensland,St Lucia,Brisbane 4072,Queensland,Australia
5Faculty of Engineering Sciences,GIK Institute of Engineering Sciences and Technology,Topi,Swabi,KPK,Pakistan
6Department of Mechanical Engineering,College of Engineering,Prince Mohammad Bin Fahd University P.O.Box 1664,Al Khobar 31952,Kingdom of Saudi Arabia
AbstractThis article investigates an unbiased analysis for the unsteady two-dimensional laminar flow of an incompressible,electrically and thermally conducting fluid across the space separated by two infinite rotating permeable walls.The influence of entropy generation,Hall and slip effects are considered within the flow analysis.The problem is modeled based on valid physical arguments and the unsteady system of dimensionless PDEs(partial differential equations)are solved with the help of Finite Difference Scheme.In the presence of pertinent parameters,the precise movement of the flow in terms of velocity,temperature,entropy generation rate,and Bejan numbers are presented graphically,which are parabolic in nature.Streamline pro files are also presented,which exemplify the accurate movement of the flow.The current study is one of the infrequent contributions to the existing literature as previous studies have not attempted to solve the system of high order non-linear PDEs for the unsteady flow with entropy generation and Hall effects in a permeable rotating channel.It is expected that the current analysis would provide a platform for solving the system of nonlinear PDEs of the other unexplored models that are associated to the two-dimensional unsteady flow in a rotating channel.
Key words:unsteady flow,rotating permeable channel,MHD,slip,hall effects,entropy analysis, finite difference method
1 Introduction
Entropy generation determines the performance of thermal machines such as heat engines,power plants,heat pumps,refrigerators and air conditioners.It performs a significant part in the thermodynamics of irreversible processes,which is briefly explained by de Groot and Mazur.[1]In recent years,the analysis of entropy generation has widely been used for the investigation of thermal processes.Entropy forms the foundation of most of the formulations of thermodynamics.Entropy generation analysis appears as a powerful tool to optimize efficiency of various heat transfer and fluids engineering devices.Identification of various conditions for exergetic effectiveness enhancement to occur would serve as a useful theoretical tool for the design and thermodynamic efficiency characterization of such an integrated system.Bejan[1]studied the entropy generation in fundamental convective heat transfer and explored that in convective fluid flow,entropy generation is due to viscous shear stresses and heat transfer.One of the aims of entropy generation is to minimize the heat transfer irreversibility and viscous dissipation irreversibility.The process of irreversibility exists inside the cavity during the process of convection.To retain the energy,it is essential to vanish the process of irreversibility.[1?2]The combined effects of hydrodynamic slip,suction or injection and convective boundary conditions on the global entropy generation in a steady flow of an incompressible MHD fluid through a channel with permeable plates has been investigated by Guillermo.[3]Eegunjobi and Makinde[4]examined the analysis of entropy generation in a variable viscosity within the MHD flow with permeable walls and convective surface boundary conditions.Arikoglu et al.[5]explored the slip effects on entropy generation in MHD flow over a rotating disk by mean of a semi-numerical analytical solution technique.
Flows that are persuaded by the rotating disks are of considerable attention to the researchers and this is due to the physical phenomena of the flow within the rotating permeable or impermeable flow passages.The applications of such types of flows have emerged well in rotating machinery,lubrication,viscometer and crystal growth processes,etc.[3?8]Similarly,magnetic effects in lubrication have received a remarkable attention due to their substantial roles in industrial applications.Another significant factor within the MHD boundary layer analysis is the Hall effects.The Hall effects are substantial only when the applied magnetic field is very strong.Thus,the electric field as a result of polarization of charges and Hall effects becomes trivial.It has been briefly discussed by Ahmad.[9?11]A study in detail linked to Hall effects on free and forced convective flow in a rotating channel is investigated by Rao and Krishna.[12]Akbar and Khan[13]performed the entropy analysis for the Peristaltic flow of Cu-water nanofluid with magnetic field in a lopsided channel.Guria and Jana[14]examined the Hall effects on the hydromagnetic convective flow in a rotating channel.The unsteady two-dimensional MHD Couette flow in a rotating system with the Hall current and ion-slip current effects is examined by Jha and Apere.[15]Seth et al.[16]examined the combined free and forced convection Couette-Hartmann flow in a rotating channel with arbitrary conducting walls and Hall effects.Eegunjobi and Makinde[17]investigated the irreversibility in a variable viscosity Hartmann flow through a rotating permeable channel with Hall effects.Mabood et al.[18]investigated the MHD flow of a variable viscosity of the nanofluid in a rotating permeable channel with Hall effects.Makinde and Onyejekwe[19]found the numerical analysis of the two-dimensional MHD generalized Couette flow and heat transfer with variable viscosity.Makinde[20]solely performed the thermal decomposition of unsteady non-Newtonian MHD Couette flow with variable properties.Sheikholeslami et al.[21?22]have discussed interesting effects of non-uniform and variable magnetic fields on the flow of nanofluids.
In the above studies,the scholars have achieved numerous results,which are linked to the two-dimensional laminar boundary layer analysis of MHD flow with entropy generation in different permeable rotating flow passages.In all the above studies,they transformed the system of PDEs into a system of ODEs via similarity transformation and then solved the corresponding system of ODEs with suitable numerical or analytical technique.The coupled high order non-linear PDEs solutions in boundary layer analyses for the unsteady MHD flow and entropy generation in a rotating permeable microchannel are very rare and so far,it has not been explored.To cover the gap,it is essential to find the solution to the high order nonlinear PDEs for the current analysis as PDEs solution show us the exact trend of the fluid flow for any category of a flow in any flow microchannel.Practical application of the considered problem in the present study can be found in miniaturized electronic devices such as micromixers.Micromixing technology has experienced rapid development in the past few years.It is an essential component of integrated micro fluidic system for chemical,biological and medical purposes.A well-designed micromixer has rapid mixing and compact in size.The thermal management in such devices has become a taxing issue.Micro-scale heat transfer becomes a topical subject and innovative techniques are needed to improve the thermal performance of heat sinks.For this purpose,a system of nonlinear PDEs solution has been obtained by mean of Finite Difference Scheme.In the understanding of recent studies,It is expected that the current analysis would provide a platform for solving the system of nonlinear PDEs of the other unexplored and unattempted fluid flow models that are associated to the two-dimensional unsteady flow in a rotating channel.It is believed that the current study would also be beneficial in cooling of electronic devices and heat exchangers.
2 Problem Formulation
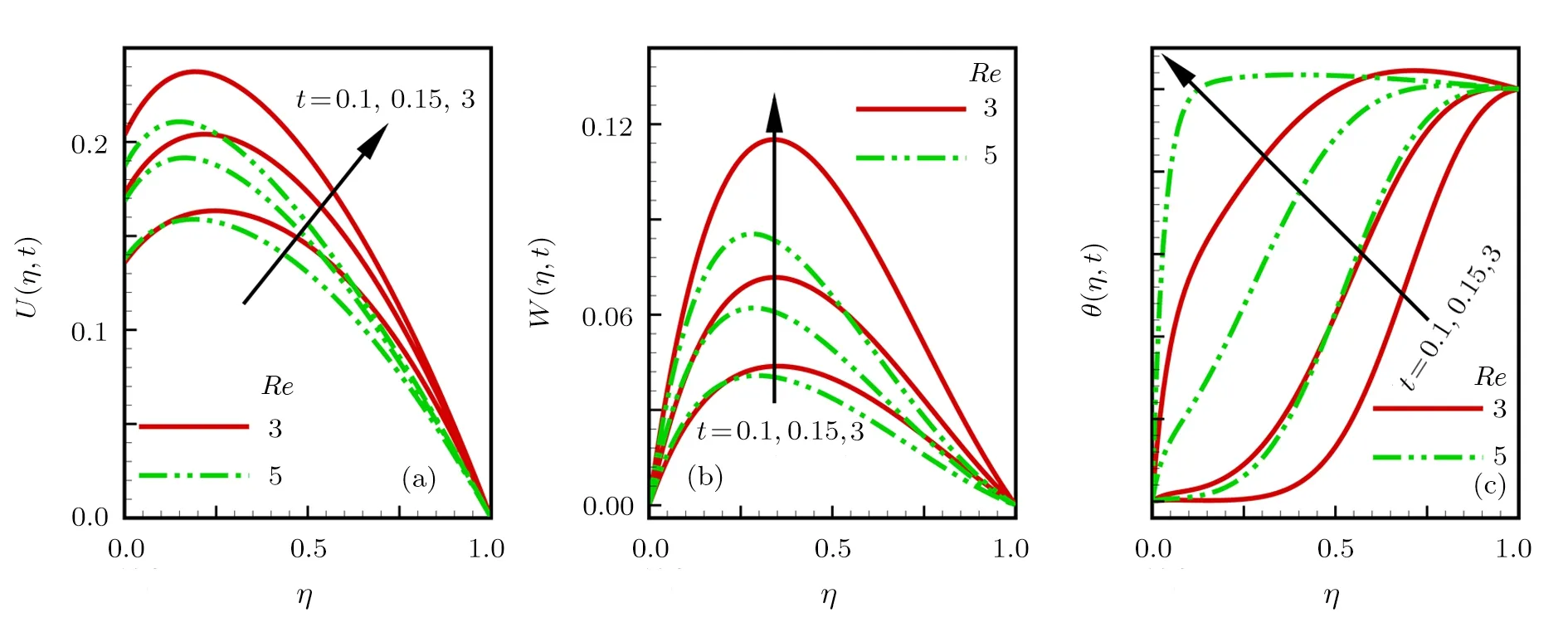
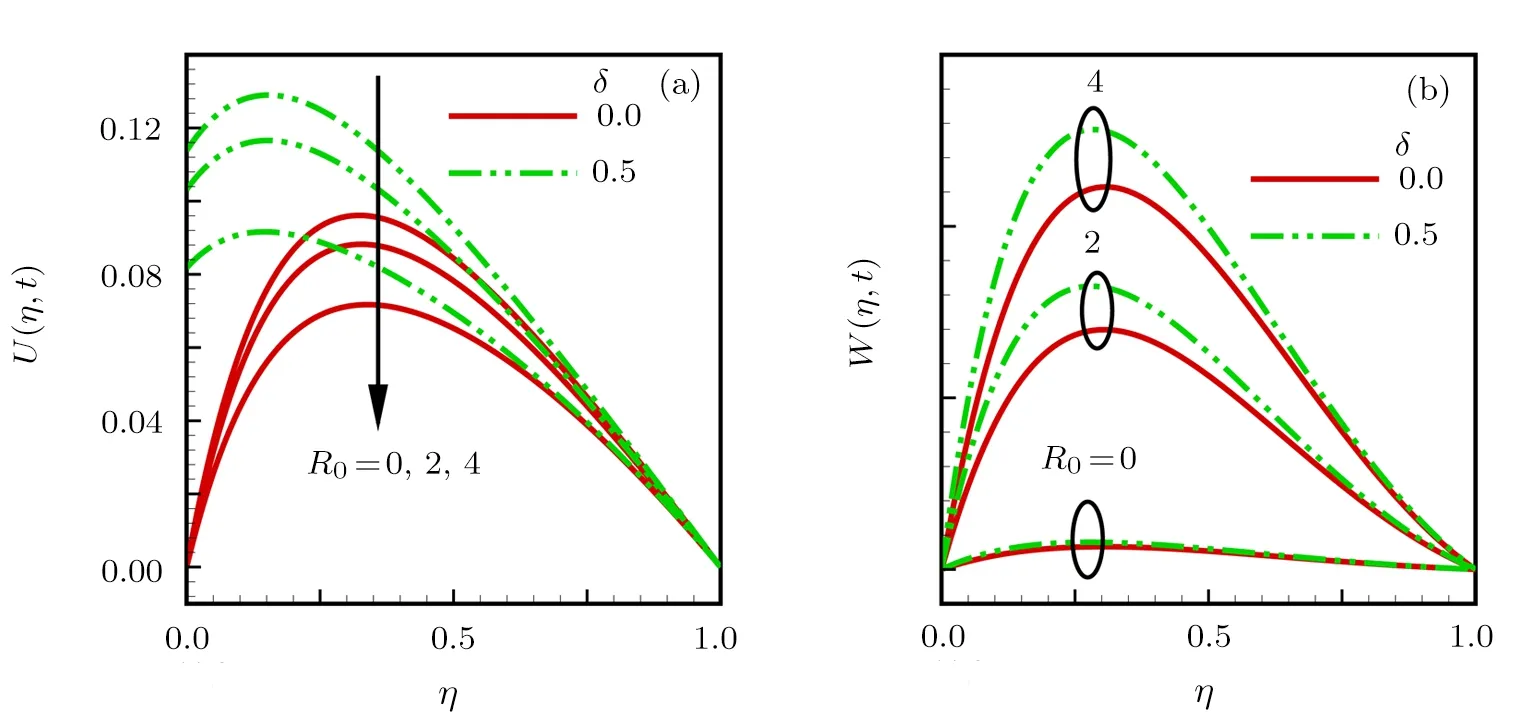
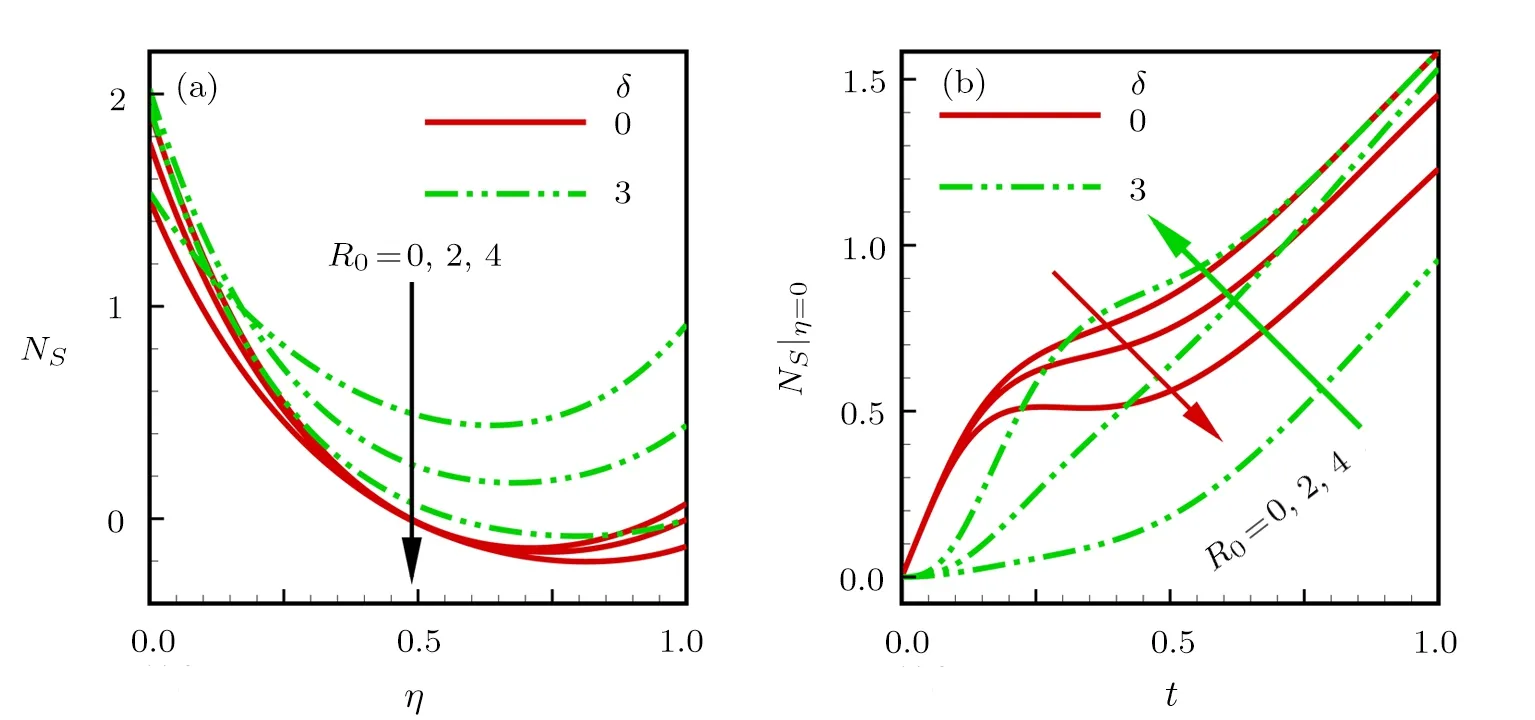
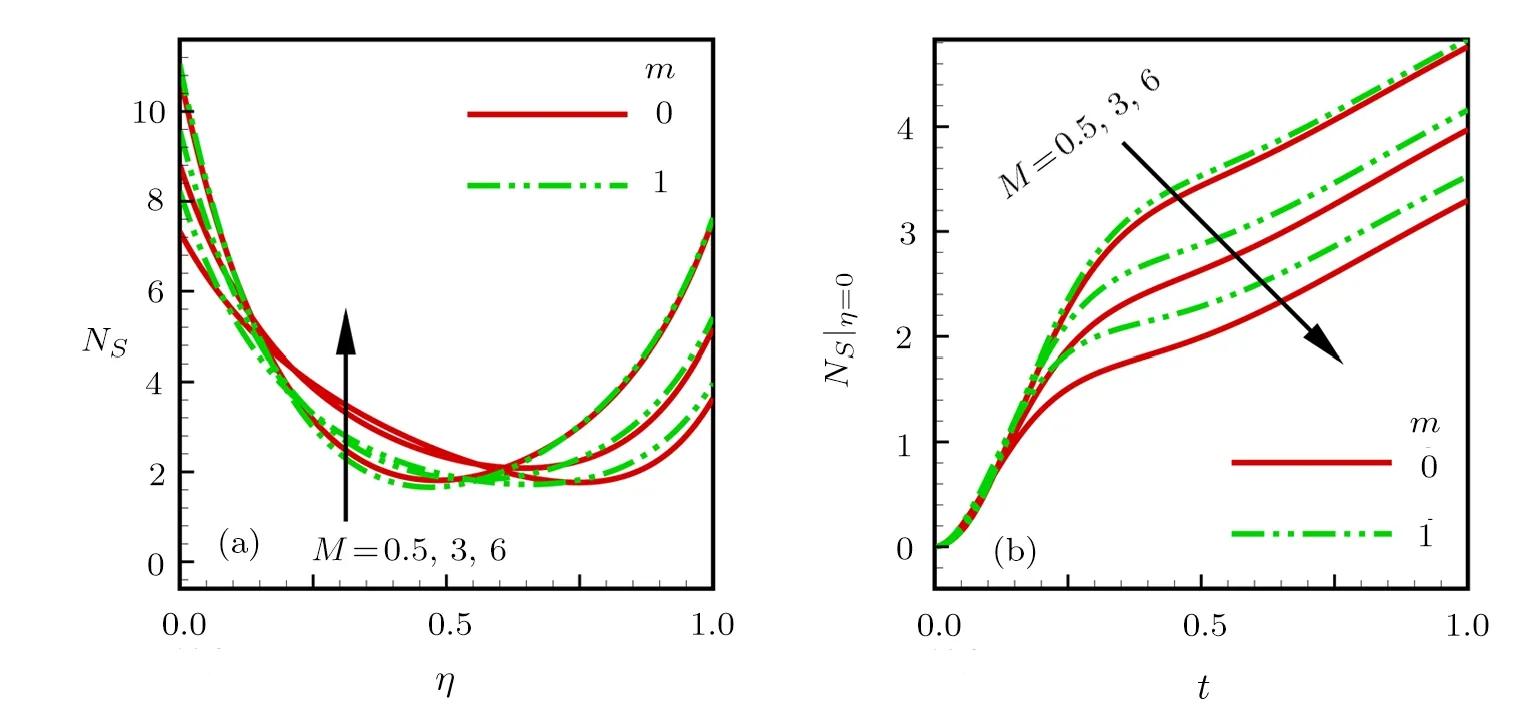
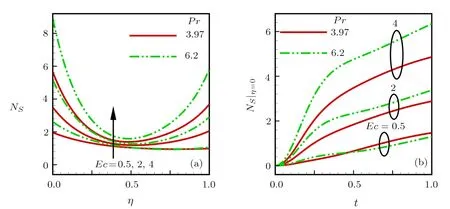
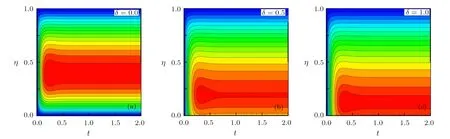
Consider the unsteady flow of an incompressible,electrically and thermally conducting viscous Newtonian fluid through a microchannel with two rotating permeable walls at y=0 and y=L under the action of an externally imposed transverse magnetic field B0taken into account Hall current.Initially at τ≤0,the fluid temperature is maintained at T0and no flow occurs.When τ>0,the flow occurs and both fluid and channel rotate simultaneously with a monotonous angular velocity ? about y-axis under the combined actions of uniform pressure gradient applied along x-direction and the suction/injection at the channel walls(See Fig.1).The channel lower wall is subjected to slip condition and maintained at temperature T0while the upper wall is kept at temperature T1such that T0 Fig.1 Flow pattern of entropy generation in two rotating permeable walls. Bearing in mind the assumptions above,the governing equations of momentum and energy balance are given as[1?4] where u,w,T,σ,ρ,m= ωeτe,ωe,τe,k,cp,Eg,V,andμare respectively,the fluid velocity in x-direction,fluid velocity in z-direction, fluid temperature, fluid electrical conductivity, fluid density,Hall current parameter,cyclotron frequency,electron collision time,thermal conductivity coefficient,specific heat at constant pressure,the volumetric entropy generation rate,the injection/suction velocity and the fluid dynamic viscosity. The initial and boundary conditions for the fluid velocities and temperature are given as where C is the slip length parameter. Introducing the dimensionless variables and parameters as follows: Substituting Eq.(6),the governing equations and conditions(Eqs.(1)–(5))can be written as where Pr is the Prandtl number,R0signifies rotation parameter,Re signifies suction Reynolds number,Ec signifies Eckert number,δ is the slip parameter,M signifies magnetic field parameter,γ is the temperature difference parameter and A represents the pressure gradient parameter.Other quantity of interest is the Bejan number(Be),which is given as with initial and boundary conditions as It is noteworthy that N1depicts the thermodynamic irreversibility due to heat transfer while N2represents the combined effects of fluid friction and magnetic field irreversibility.When Be=0.5 both N1and N2contribute equally to the entropy production in the flow field. Finite Difference Method(FDM)serves as the basis for the numerical schemes(see Le Veque[23]).To achieve the time-dependent PDE numerical solution,both the implicit and explicit methods are widely used these days.In the current analysis,the dimensionless nonlinear second order parabolic partial differential equations i.e.,Eqs.(7)–(10)subject to initial and boundary conditions in Eq.(11)have been solved with the help of an explicit Finite Difference Scheme.The given system of PDEs is well-posed,which means that a solution exists if we restrict various embedding parameters such as Re,t,R0,δ,M,Ec,Pr,and γ to some fixed values.To obtain the PDE solutions for velocities U,W and temperature θ,we restrict the pressure gradient parameter A=1 throughout the analysis.The two infinite rotating permeable walls have been surrounded by the flow in x and y directions while the secondary flow has been taken along the z-axis.To obtain the difference equations,the region of the flow is divided into mesh of finite lines.Since the flow pattern is not varying in the x-direction so it is assumed insignificant as compared to a flow in the y-direction.The space under investigation is of finite dimension and the explicit difference equations are discretized as follows: Substituting Eq.(14)into Eqs.(7)–(13),the following explicit finite difference equations have been obtained with initial and boundary conditions take the following form The Bejan number have been presented in terms of difference equations as: It has been seen,through numerical experimentation,that as the time steps increase,a stable implicit Finite difference scheme does not always reduce CPU time and the computations do not always remain stable.As the time step increases,there is an increase in CPU time and even unstable computations and this results in issues with convergence of the problem.The finite difference scheme is standard because its relaxed stability constraints can result in better computational efficiency.The stability of the simultaneous system of PDEs for a similar type of problem was presented by Callahan and Marner.[24]In the current analysis,both the small time and large time solutions have been obtained,which converge well for the selected small values of the parameters and then all the results have been shown graphically. The problem of two-dimensional laminar flow of an incompressible fluid between two rotating permeable walls is studied.The influence of pertinent parameters on dimensionless velocities,temperature,skin friction,Nusselt number and entropy generation rate are investigated.Figures 2(a)and 2(b)depict the effects of suction Reynolds number on the dimensionless primary and secondary velocity of the fluid between lower and upper walls respectively.In the transient state,the primary velocity at the lower wall increases with increasing time as illustrated in Fig.2(a).This velocity further increases about the lower wall and then starts decreasing until zero at the upper wall.For small time,the primary velocity has no considerable effect for lesser suction Reynolds number.As the suction Reynolds number and time increases,the difference in primary velocity increases.The secondary velocity shows the same behavior in Fig.2(b).The trend of dimensionless temperature is explained in Fig.2(c)for increasing time and suction Reynolds number.For smaller time and smaller suction Reynolds number,the dimensionless temperature remains uniform and then increases with time and suction Reynolds number. The effects of rotation and slip parameters on the dimensionless primary and secondary velocities are demonstrated in Figs.3(a)and 3(b)respectively.In the absence of slip,both primary and secondary velocities are zero at the lower wall.As the slip parameter increases,the primary velocity increases at the lower wall(Fig.3(a)),whereas the secondary velocity remains zero at the lower wall(Fig.3(b)).The maximum primary velocity depends upon the rotation.In the absence of rotation,this maximum velocity is largest and decreases with increasing rotation.Both the dimensionless primary and secondary velocities satisfy the boundary conditions.It is significant to note that the dimensionless secondary velocity is lowest in the absence of rotation and increases with rotation. Fig.2 Effects of increasing time and Reynolds number on dimensionless(a)primary velocity,(b)secondary velocity and(c)temperature in transient state. Fig.3 Effects of rotation and slip parameters on dimensionless(a)primary velocity and(b)secondary velocity(transient state). Fig.4 Effects of rotational and slip parameters on the dimensionless entropy generation rate for(a)steady state and(b)transient state. The variation in the rate of overall dimensionless entropy generation with rotational and slip parameters is shown in Fig.4(a)for the steady state and Fig.4(b)for the transient state respectively.It is clear from Fig.4(a)that the entire dimensionless entropy generation rate is highest at the lower surface and decreases up to a minimum value about the upper surface and then increases.The slip parameter tends to increase the total dimensionless entropy generation rate whereas the rotational parameter reduces this rate.In the transient state,see Fig.4(b),the behavior of the total dimensionless entropy generation rate is similar for a very short time and this time decreases with increasing the slip parameter.This trend is revealed for the lower wall.After transient state,the effects of rotational and slip parameters on the total dimensionless entropy generation rate can be observed noticeably.In the absence of slip parameter,the total dimensionless entropy generation rate decreases with reducing the rotational parameter and on contrary,the total dimensionless entropy generation rate increases with rotational parameters whenever the slip parameter increases. The effects of magnetic and Hall current parameters on the total dimensionless entropy generation rate are depicted in Fig.5(a)for the steady state and Fig.5(b)for the transient state individually.In the steady state,minimum dimensionless entropy generation rate can be observed for both the parameters.This minimum point moves towards the upper surface with increasing the magnetic and Hall current parameters.A fact can be established that the dimensionless entropy generation rate increases at the lower surface whereas decreases at the upper surface(Fig.5(a)).In the transient state(Fig.5(b)),the dimensionless entropy generation rate shows the same behavior at the lower surface for very small time.After that time,the dimensionless entropy generation rate increases at different rates.However,this increase in the dimensionless entropy generation rate decreases with the magnetic parameter but increases with the Hall current parameter.It is eminent to note that the Hall current effects on the flow are more prominent and this is due to a strong magnetic field and hence the flow becomes three-dimensional owing to the Hall current effects. Fig.5 Effects of magnetic and Hall current parameters on the dimensionless entropy generation rate for(a)steady state and(b)transient state. Fig.6 Effects of Eckert and Prandtl numbers on the dimensionless entropy generation rate for(a)steady state and(b)transient state. Fig.7 Effects of rotational and slip parameters on Bejan number for(a)steady state and(b)transient state. The Eckert number characterizes heat dissipation in thermodynamic systems.The dimensionless entropy generation rate is based on the heat transfer and fluid friction.Both of these processes dissipate heat energy that determines the Eckert number.The Prandtl number dictates heat diffusion rate.The greater the Prandtl number,the slower is the heat diffusion rate.The effect of these numbers on the dimensionless entropy generation rate is shown in Figs.6(a)and 6(b)for the steady and transient states.With both the Eckert and Prandtl numbers,the steady state dimensionless entropy generation rate increases at both the surfaces(Fig.6(a)).A minimum dimensionless entropy generation rate exists for each Eckert and Prandtl number that increases with an increase in each number.In the transient state,for a very small time,the behavior of the dimensionless entropy generation rate is same at the lower surface.After that time,the dimensionless entropy generation rate increases at different rates.This rate is influenced by both the Eckert and Prandtl numbers.The greater the Eckert or Prandtl number,the greater will be the rate of increase in the dimensionless entropy generation rate. The effects of pertinent parameters on the Bejan number are displayed in Figs.7–9 for both the steady and unsteady states.Thermodynamically,Bejan number can be defined as the ratio of dimensionless entropy generation rate due to heat transfer to the total dimensionless entropy generation rate due to heat transfer and fluid friction.Bejan number ranges from 0 to 1.It is imperative to mention that when: (i)Be→0, fluid friction dominates. (ii)Be→0.5,both fluid friction and heat transfer play the same role. (iii)Be→1,the heat transfer dominates. It is established that in Figs.7–9,the Bejan number exists between 0 and 1.In a steady state,the effects of rotational and slip parameters on Bejan number are demonstrated in Fig.7(a).It can be seen that,the entropy generation rate due to heat transfer dominates at the lower surface and this domination decreases up to upper surface where the entropy generation rate due to fluid friction dominates.The Bejan number increases with both the rotational and slip parameters(Fig.7(a)).In the transient state,rotational and slip parameters have no effect on Bejan number up to t=0.25 on the lower surface.After this time,the Bejan number increases with time and both parameters(Fig.7(b)).In the absence of magnetic and Hall current parameters,the entropy generation rate is almost the same due to fluid friction and heat transfer.However,it increases in the neighborhood of lower surface with increasing both the parameters at a lower surface under the steady state conditions.This is elucidated in Fig.8(a).Depending upon both parameters,after attaining maximum value,the Bejan number decreases up to the upper plate.This shows that at the upper surface, fluid friction irreversibility dominates.In the transient state,no effect could be found on the Bejan number for a very short time(Fig.8(b)).After that,the Bejan number increases with time uniformly at different rates depending upon the values of both parameters.Eckert number determines the relative importance of the kinetic energy of a flow whereas Prandtl number determines the relative importance of momentum diffusivity.The effects of these numbers on the Bejan umber are displayed in Figs.9(a)and 9(b)for the steady and transient states respectively.When these numbers are smaller,the entropy generation rates due to heat transfer and fluid friction are the same at the lower surface under the steady state condition(Fig.9(a)).However,as these numbers upsurge,the entropy generation rate due to heat transfer increases with the vertical distancrom the lower surface and then decreases up to the upper surface where the entropy generation rate due to fluid friction dominates.As usual,the entropy generation rate due to fluid friction dominates for a very short time and then de-creases with an increase in time.As t→∞,the entropy generation rate dominates due to heat transfer.The unsteady state streamline pro files with different increasing slip parameters are shown in Fig.10.Increase in slip parameter has enlarged the streamline pro file,which shows that the slip parameter has significant impact on the flow passage. Fig.8 Effects of magnetic and Hall current parameters on Bejan number for(a)steady state and(b)transient state. Fig.9 Effects of Eckert and Prandtl numbers on Bejan number for(a)steady state and(b)transient state. Fig.10 Streamlines pro files with variations in slip parameters. This article reports an unsteady two-dimensional laminar flow of an incompressible,electrically and thermally conducting fluid across the space separated by two infinite rotating permeable walls.The effects of entropy generation,Hall and slip effects on the two-dimensional MHD flow are considered within the current flow channel.The unsteady systems of dimensionless PDEs are solved by implementing the Finite Difference Scheme.To achieve the accurate movement of the laminar MHD flow in terms of velocity,temperature,skin friction coefficient,Nusselt and Bejan numbers,the pertinent parameters such as Re,t,R0, δ,M,Ec,Pr and γ have been fixed to some constant values.Furthermore,the three-dimensional graphical representations of the streamlines are presented,which ensure the precise movement of the flow field within the existing flow channel.It is expected that the current study would provide a platform for solving the system of nonlinear PDEs of the other unexplored and unsolved fluid flow models that are linked to the two-dimensional unsteady MHD flow in rotating fluid flow passages.It is further believed that the current study would be beneficial in the field of micromixing technology by enhancing exergetic effectiveness through device design for efficient operation and thermodynamic efficiency.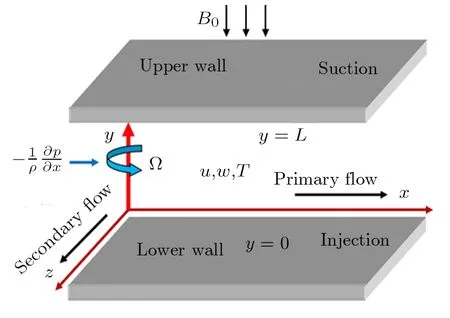
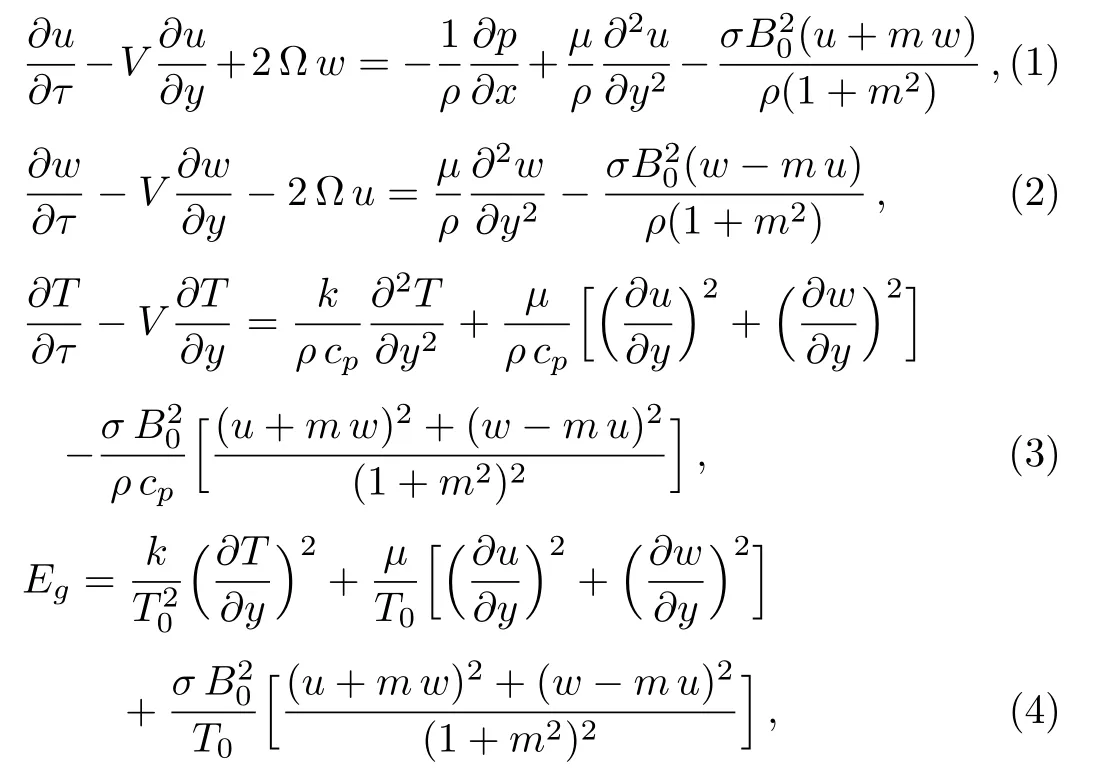

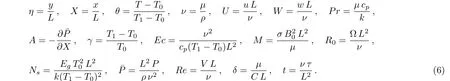
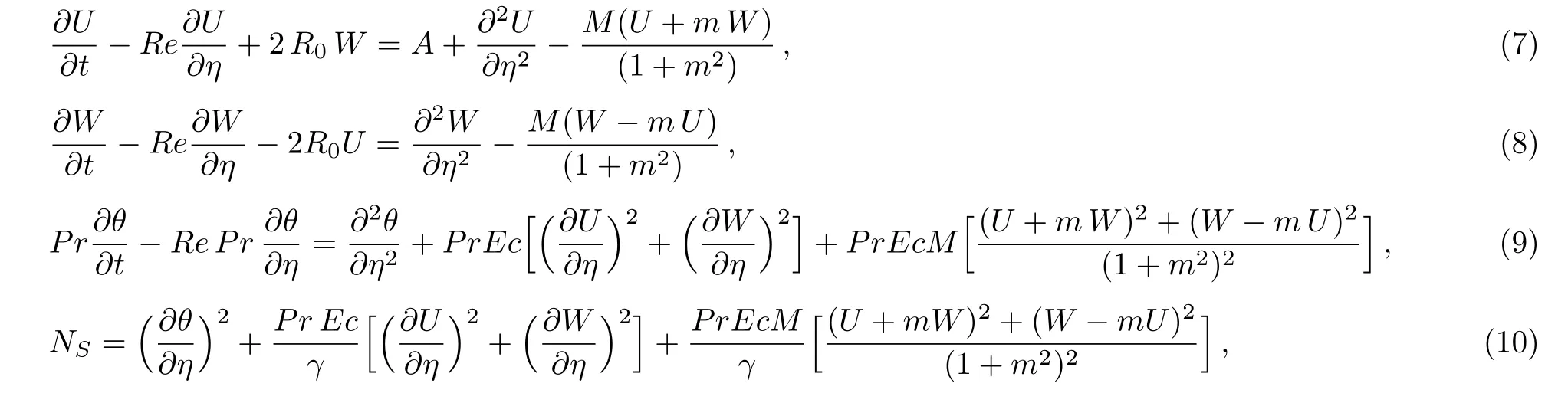


3 Finite Difference Numerical Procedure

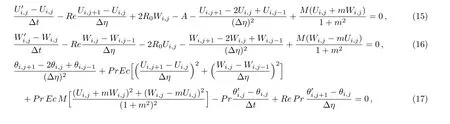

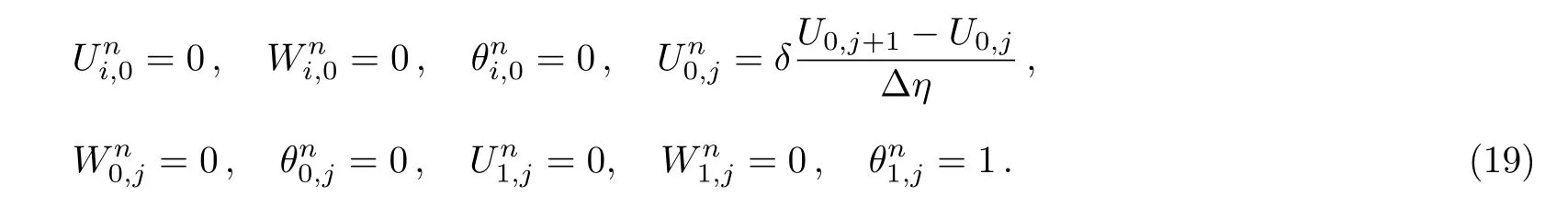
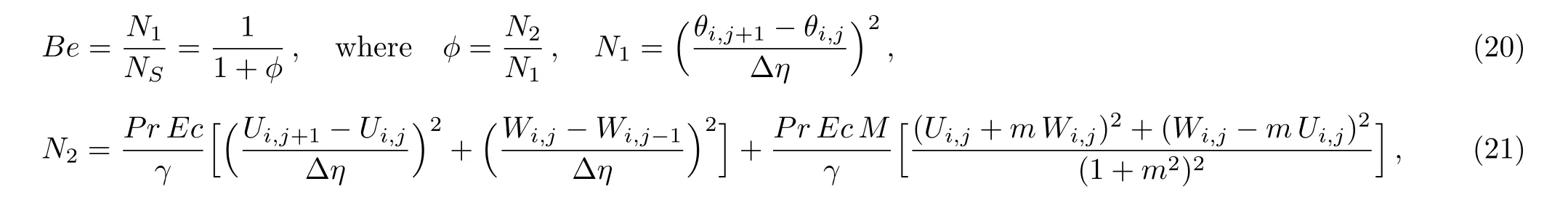
4 Results and Discussion



5 Conclusions
 Communications in Theoretical Physics2018年11期
Communications in Theoretical Physics2018年11期
- Communications in Theoretical Physics的其它文章
- Hierarchical Human Action Recognition with Self-Selection Classifiers via Skeleton Data?
- Spin Thermoelectric Effects in a Three-Terminal Double-Dot Interferometer?
- Third-Order Magnetic Susceptibility of an Ideal Fermi Gas?
- Coherent Control of the Hartman Effect through a Photonic Crystal with Four-Level Defect Layer?
- Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas?
- Relic Density of Asymmetric Dark Matter in Modified Cosmological Scenarios?
