Scattering and Bound States of the Dirac Particle for q-Parameter Hyperbolic P?schl-Teller Potential
M.C.Onyeaju, A.N.Ikot, C.A.Onate,H.P.Obong,and O.Ebomwonyi
1Theoretical Physics group,Department of Physics,University of Port Harcourt,P.M.B.5323,Choba Port Harcourt,Nigeria
2Department of Physical Sciences,Landmark University,Omu-Aran,Nigeria
3Physics Department,University of Benin,Benin City,Edo State,Nigeria
AbstractThe one-dimensional Dirac particle for equal scalar and vector asymmetric q-parameter hyperbolic P?schl-Teller potential(qHPT)is solved in terms of hypergeometric functions.The scattering and bound states are obtained by using the properties of the equation of continuity of the wave functions.We calculat in details the transmission and reflection coefficients.
Key words:dirac particles;P?schl-Teller potential,bound states,scattering states
1 Introduction
The scattering and bound states in relativistic and non-relativistic quantum mechanics with external potentials have received attention from theorist in recent years[1?3]and have assisted in the description of the behaviour of particles,atoms,and molecules in Physics.They find their applications in atomic and molecular Physics[4?17]and in condensed matter physics.[18?26]The Dirac equation covers the anti-particle scattering as well as the particle scattering.The scattering states have continuum wave functions and its energy is within the neighbourhood of E≥0 whereas the bound states with normalizable wave functions have energy E<0.For a free Dirac particle,there exist energy gaps E≤|m|(where m is the mass of the particle)that separate the positive and negative energy continuum states.The positive states correspond to the particle states and the negative energy states describe the anti-particle states.The energy gap becomes distorted on the introduction of a potential V(r)and bound states now occur between E=?m and E=m,which can be described as the band gap energy in condensed matter Physics.
The relativistic and non-relativistic symmetries have been investigated under a wide range of potentials.[27?31]The P?schl-Teller potential(PTP)in this regards has attracted the interest of many researchers in recent years owing to its applications in molecular and nuclear physics.[32?40]The relativistic solutions to the PTP have been obtained with the Duffin-Kemmer-Petiau,[1]Dirac,[32?34]Klein-Gordon,[35]and the Schr?dinger wave equation.[36?37]For instance,Jia et al.[32]obtained the analytical solutions of the Dirac equation with the generalized P?schl-Teller potential including the pseudocentrifugal term while the relativistic symmetries with the trigonometric P?schl-Teller potential plus Coulomblike tensor interaction have also been obtained by Falaye and Ikhdair.[33]The bound and scattering state of the q-hyperbolic P?schl-Teller(qHPT)has also been investigated for the Duffin-Kemmer-Petiau equation.[1]The scattering and bound states of a spinless Klein-Gordon equation with the generalized PTP has been studied[35]and the author calculated the eigenvalues,normalized wave functions,and the scattering phase shift respectively.In Ref.[34]the spin symmetry for the Dirac equation with modified qHPT in D dimensions were also solved and the relativistic energy spectrum was obtained by using the Nikiforov-Uvarov method.Also in Ref.[36]the bound state solutions of the Schr?inger wave equation with the generalized P?schl-Teller potential in D spatial dimension was obtained.The P?schl-Teller potential is a typical diatomic molecular potential that has related applications in relativistic and nonrelativistic cases for real diatomic molecules.[37?38]For instance,Jia et al.[37]used the Improved P?schl-Teller potential energy model in fitting the experimental RKR potential curves over a large range of internuclear distances for six molecules and was found to fit better than the Morse potential.Other molecular potential models of interest that have been improved upon in this regard include the Tietz,[39]Manning-Rosen,[40?41]and the Rosen-Morse.[42]the Dirac equation has been used to study the deformation of nuclei,[38]which plays a major role in understanding the deformation potentials in quantum dots(QDs).[38?40]A study made by some authors have shown that in the absence of mass term,the Dirac equation can be used to obtain the bound states of confined graphene QDs.[18?26]
Motivated by the diverse applications of the PTP model in condensed matter and molecular Physics,the scattering and bound states solution of the qHPT potential will be studied using the Dirac equation.
Accordingly,the q-parameter hyperbolic P?schl-Teller potential(qHPT)is given by[1]
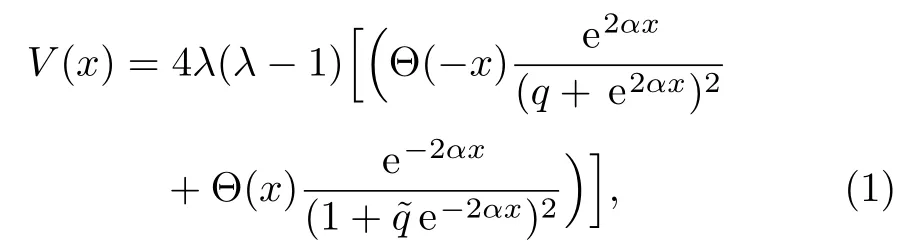
where Θ(x)is the step function,q is the deformation parameter andλ is the height of the potential,

and α is the range of the potential barrier.
The organization of this paper consists of four sections:In Sec.2,we review the basic Dirac equations with the qHPT potential and sought for the scattering states in terms of the hypergeometric function.In Sec.3 the solutions of the bound states were also calculated and finally the conclusion in Sec.4.
2 The Scattering States of Dirac Particle for q-Parameter Hyperbolic Asymmetric P?schl-Teller Potential(qHPT)
The basic theories and equations governing the Dirac particles are given in Refs.[27–34].
Let us recall that the Dirac equation with the scalar potential S(x)and vector potential V(x)in one dimensional is given by[27]

where the Dirac spinor φ(x)has the upper combination F(x)and the lower term G(x)and can be written as
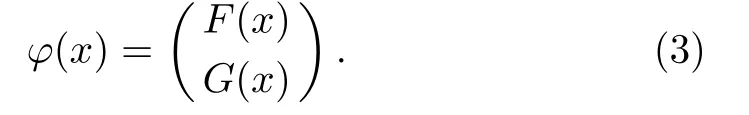
The following coupled equations are derived
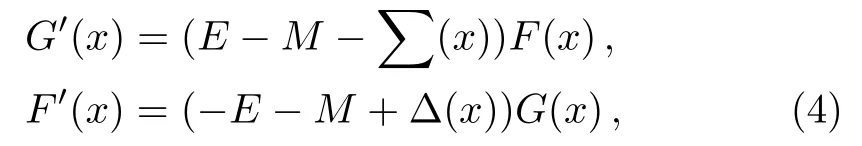
where

Eliminating one component in favour of the other yield the decoupled equations
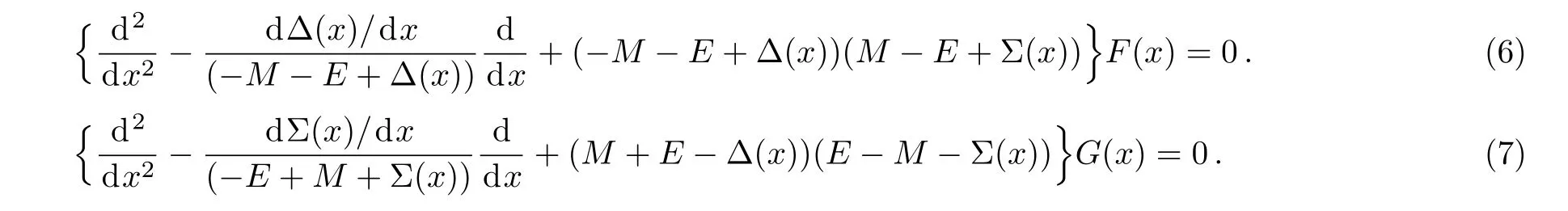
The upper and the lower component were considered here for two different wave functions φ(x).
2.1 The Case of Σ(x)=constant
First of all,let us consider the case for which Σ(x)=Cp=constant so that ?(x)has the asymmetric qHPT potential(V(x))given in Eq.(1).
In solving for the scattering states,we study the wave functions for x<0 and then the Dirac equation with the q-parameter hyperbolic P?schl-Teller Potential(qHPT)is given by inserting Eq.(1)into Eq.(7)to obtain
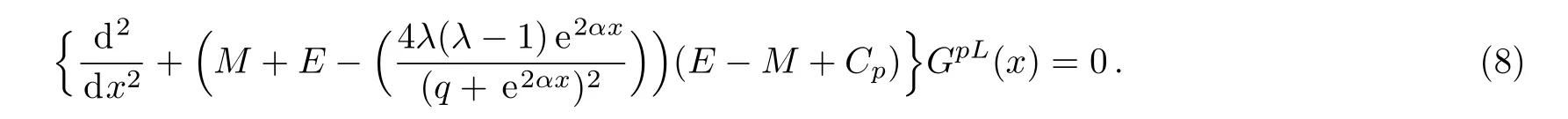

where,
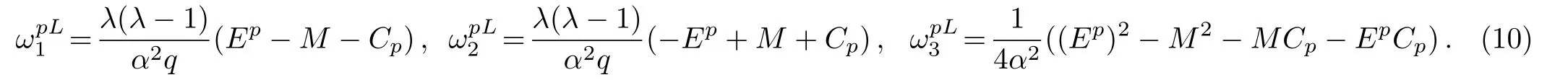
We sought for the solution at the region x>0 by insert Eq.(1)into Eq.(7)to obtain


where

2.2 Transmission and Reflection Coefficients for the Case Σ(x)=constant
Equations(9)and(12)have singularities at z=0,z=1,and z=∞,we may,therefore,define the following trial wave functions as

which turns into a hypergeometric differential equation[27]
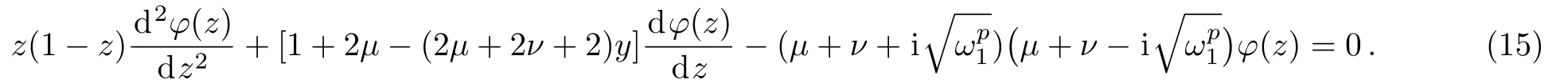
We sought for the scattering states by looking at the trial wave functions Gp(z)for the region(left)x<0.The solution to Eq.(15)is the second type of hypergeometric function[27]

with the parameters ap,bp,and cpgiven as
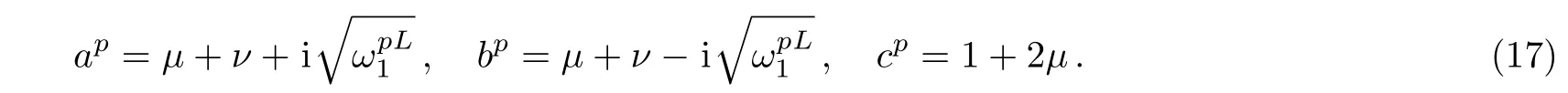
Finally,from Eqs.(14)and(16),we obtain
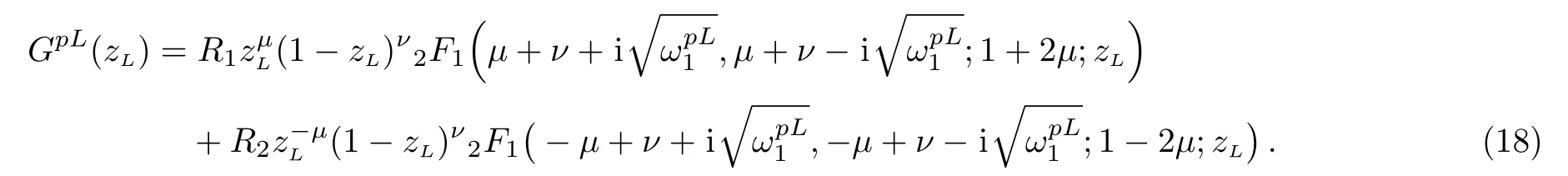
Equation(18)has the form of a hypergeometric equation and thus,by comparison,we obtain
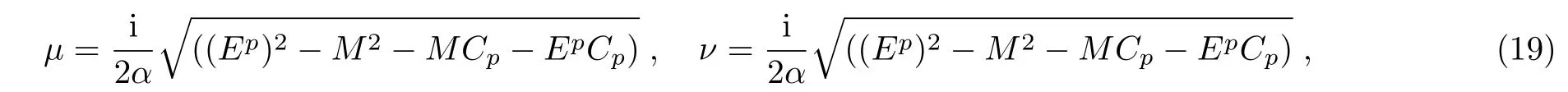
and from the upper term of Eq.(4)we have that

Now we sought for the physical interpretation of the problem under investigation so as to obtain the desired result,the solutions so far obtained must be used with appropriate boundary conditions as x→?∞and x→+∞.By applying the asymptotic behaviour of the wave function in Eq.(18)for x→?∞,zL→0,and(1?z)ν→1,we have

The right-side solution is written as

At this region we find a plane wave traveling from left to right(no reflection occurs)so that R3=0 and Eq.(22)reduces to
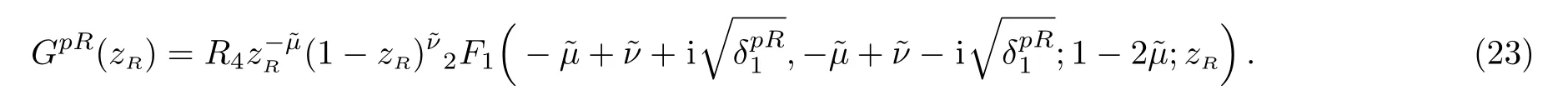
Now we consider the asymptotic behaviour of the right for which x>0 and in the limit x→∞,zR→0,and(1?zR)→1 Eq.(23)becomes

Therefore from Eqs.(21)and(24),we may write

from the upper component of Eq.(3)we have that

So that the upper component of the wave function in the infinity limit is
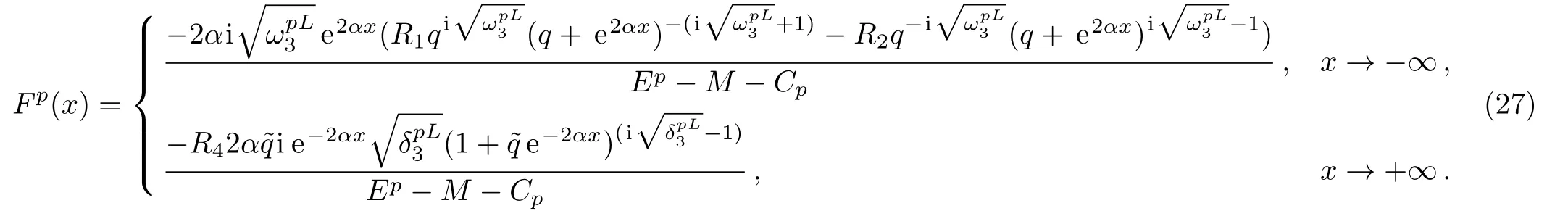
Matching the two solutions GpL(x=0)and GpR(x=0)are done by applying the continuity of the wave function and its derivatives at x=0,i.e.GpL(x=0)=GpR(x=0)and GpL′(x=0)=GpR′(x=0),which respectively give

where

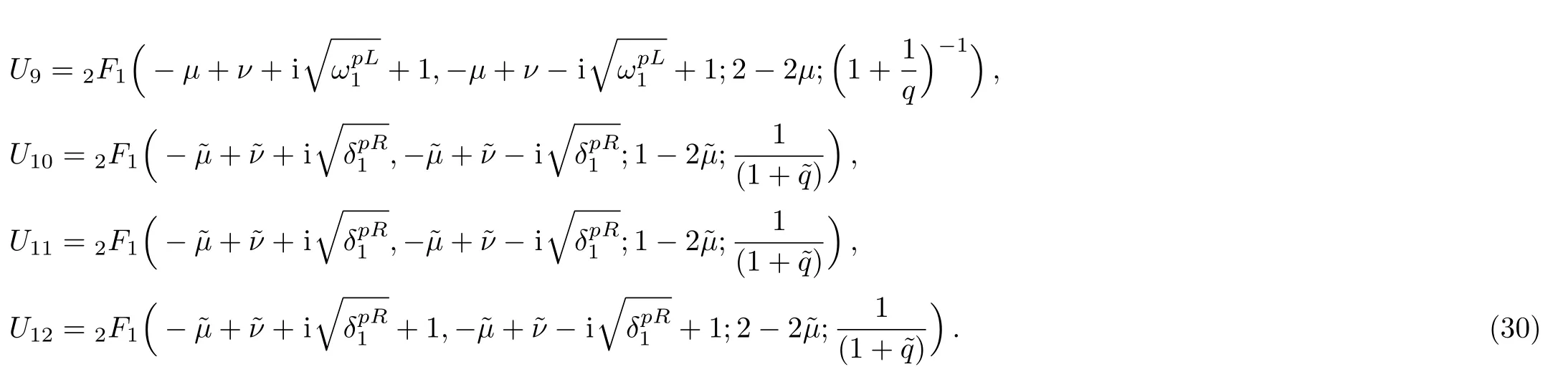
In arriving at Eq.(29)we use the formula of the hypergeometric function,i.e.
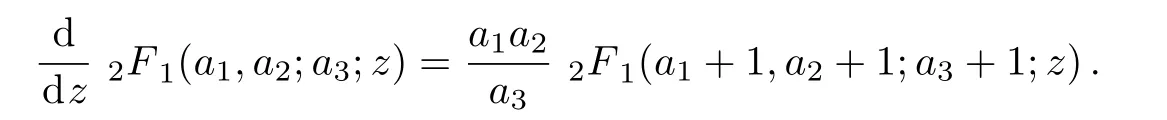
Recall that the probability current density for the Dirac equation is given by
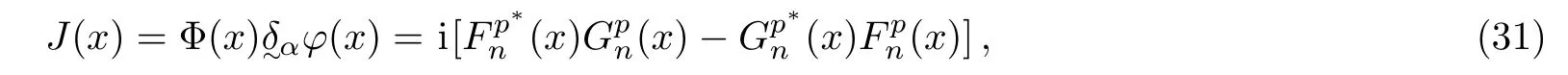
from Eqs.(31)and(33).We can compute the current density in the asymptotic regions,

where the incident,reflected and transmitted fluxes are

The continuity conditions on the current density give
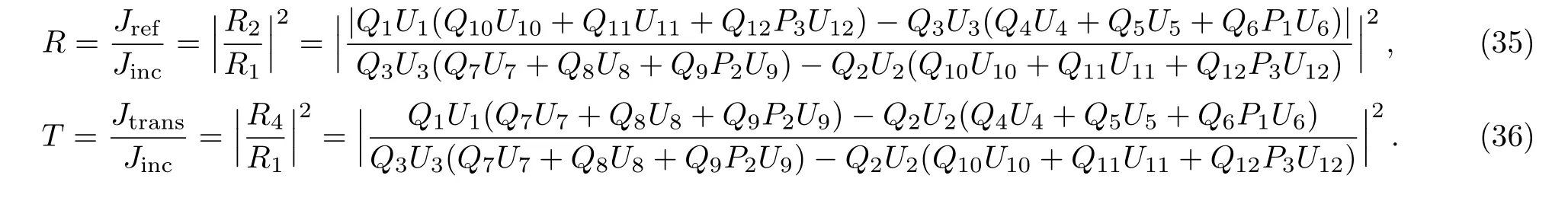
2.3 The Case of?(x)=constant
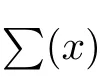
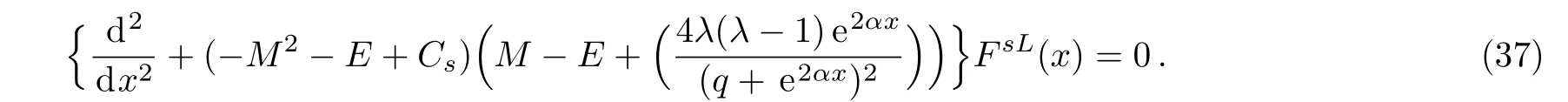
Considering the new variableand following the same steps as in Subsec.2.1,we obtain the following form of hypergeometric function that the potential V0>0 andfor x<0 region,on substituting Eq.(1)into Eq.(6)we have

where
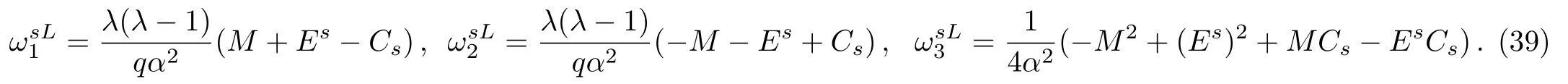

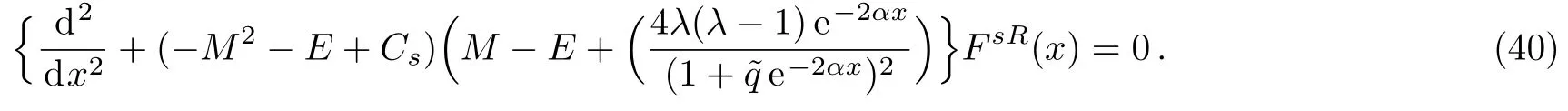
Taking the same steps in Eq.(40),the hypergeometric function takes the form
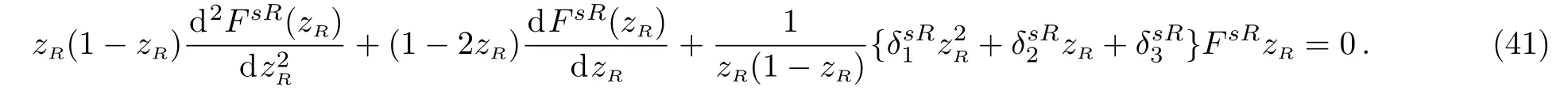
where
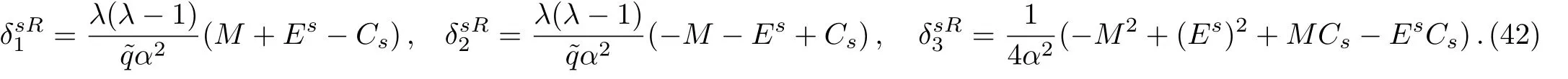
2.4 Transmission and Reflection Coefficients for the Case?(x)=constant
Again we sought for the scattering states for?(x)=constant by defining the trial wave functions as

So that Eq.(38)turns into the hypergeometric differential equation of the form[27]

whose solution in the hypergeometric function is

where a?,b?,and c? are given by,
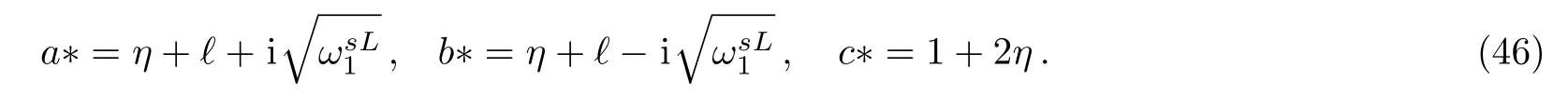
From Eqs.(43)and(45)we obtain

Equation(47)has the form of the hypergeometric equation and thus by comparison we obtain
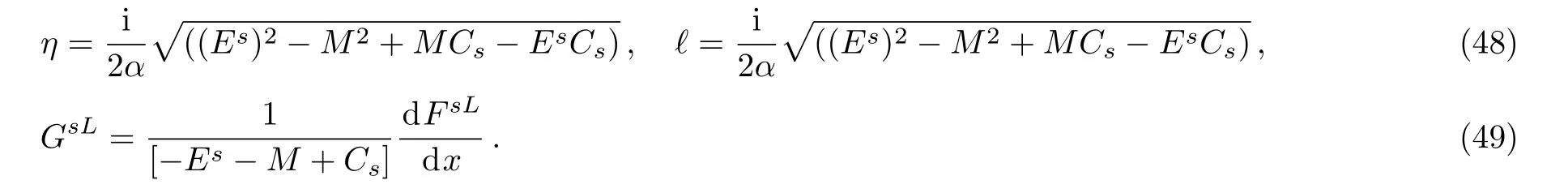
As we have done previously,we seek for the physical result of the problem under investigation and applying the asymptotic solution to Eq.(47)in the limit x→?∞,zL→0,and(1?zL)?→1,thus Eq.(48)becomes

For the right-hand side,we obtained Eq.(51)using the same steps as we did in Eq.(47).
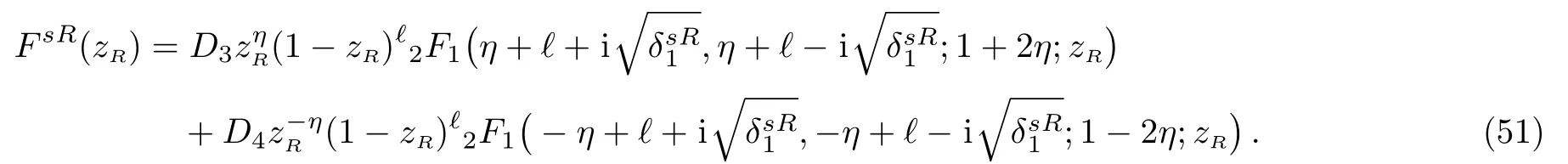
In this region no reflection occurs and so D3=0 and Eq.(51)reduces to

Finally,for x>0,in the limit x→∞,zR→0,and(1?zR)?→1 and Eq.(52)gives
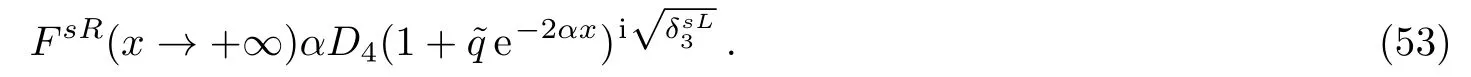
Therefore,in the two sessions,we have that,
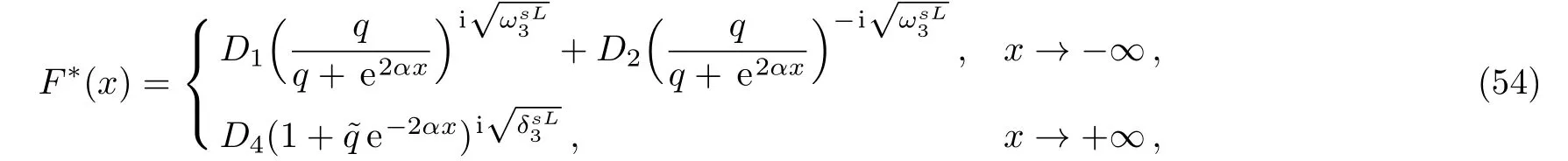
and the lower component of the wave function is

in the limit x→?∞ we have
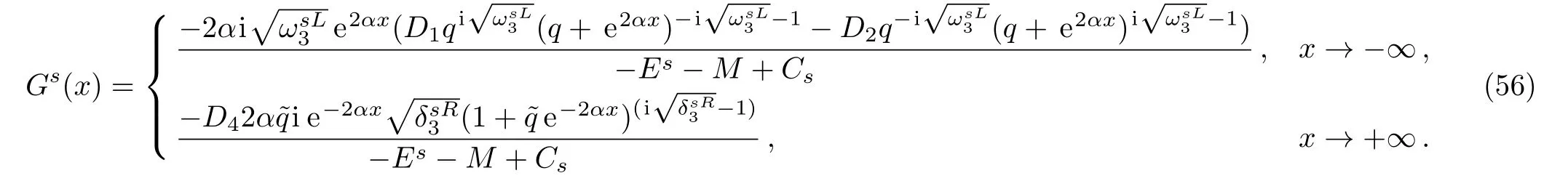
Again imposing the continuity conditions at the origin,we obtain

We now calculate the incident,reflected and transmitted fluxes

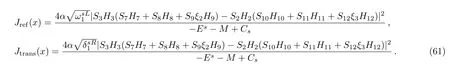
The continuity conditions on the current density is given by
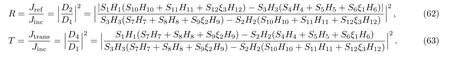
3 Bound State Solutions of the Dirac Particle for the qHPT
In order to find the bound state solution for the Dirac particle with qHPT,we map 4λ(λ ? 1)→ ?V0and the potential assume a square well form.Accordingly Eq.(1)takes the form,

where λ>1 and by so doing the solution will be in the same form as obtained in the previous Sec.2,with the exception of the definition above.
3.1 Bound State Solutions in the Negative Region(x<0)for the Case Σ(x)=constant
The bound state solutions can be calculated by changing the variable in this region as z=(1+(1/q)e2αx)?1and taking into consideration the changes in the potential so that Eq.(7)becomes
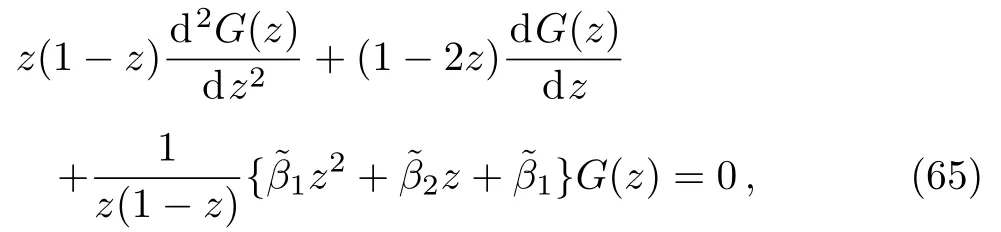
where
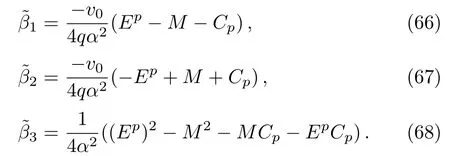
The general solution for x<0,is given as

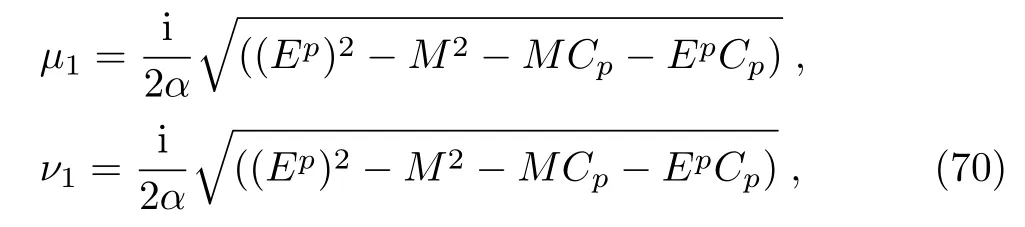
where and from the upper term in Eq.(4)we have that
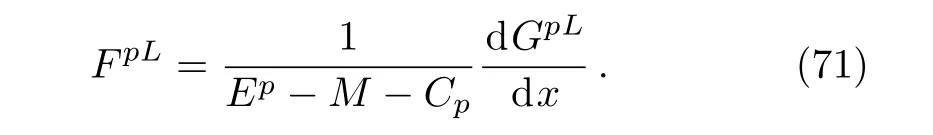
3.2 The Case of Σ(x)=constant(the Positive Region,x>0)
In the positive region,we define the variable zR=(1+and inserting Eq.(64)into Eq.(7),the wave function at this region is given byand thus following the same procedures as the case of the negative region we obtain the following

where
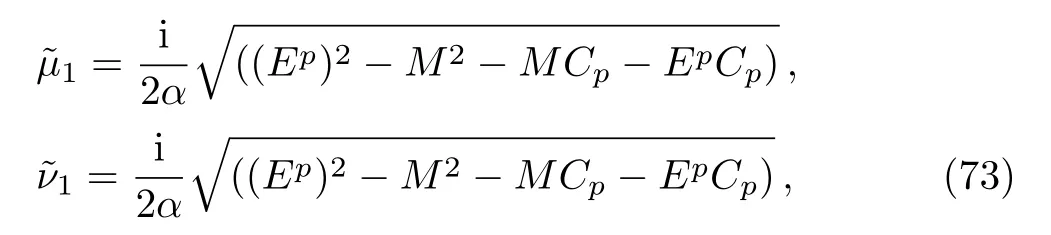
and from the upper term in Eq.(4)we have that

In order to obtain the Energy states,we set R2=R4=0 and use the condition of continuity for the wave function as,GpL(x=0)=GpR(x=0),G′pL(x=0)=G′pR(x=0),and GpR(x=0)to get

where

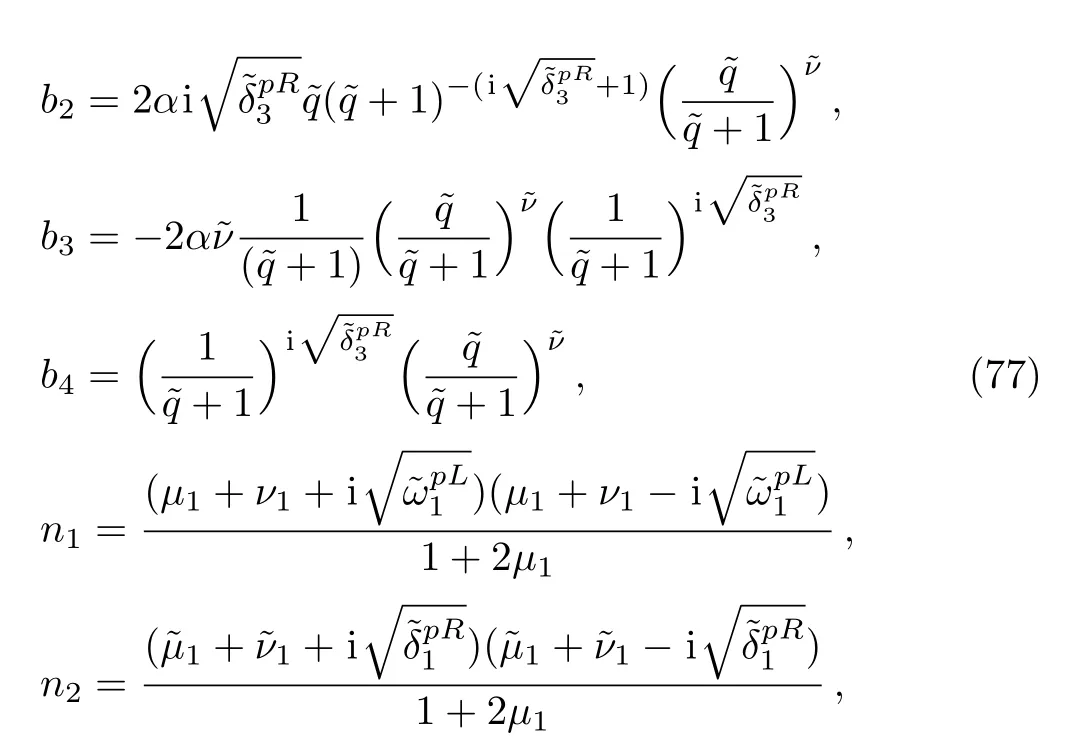
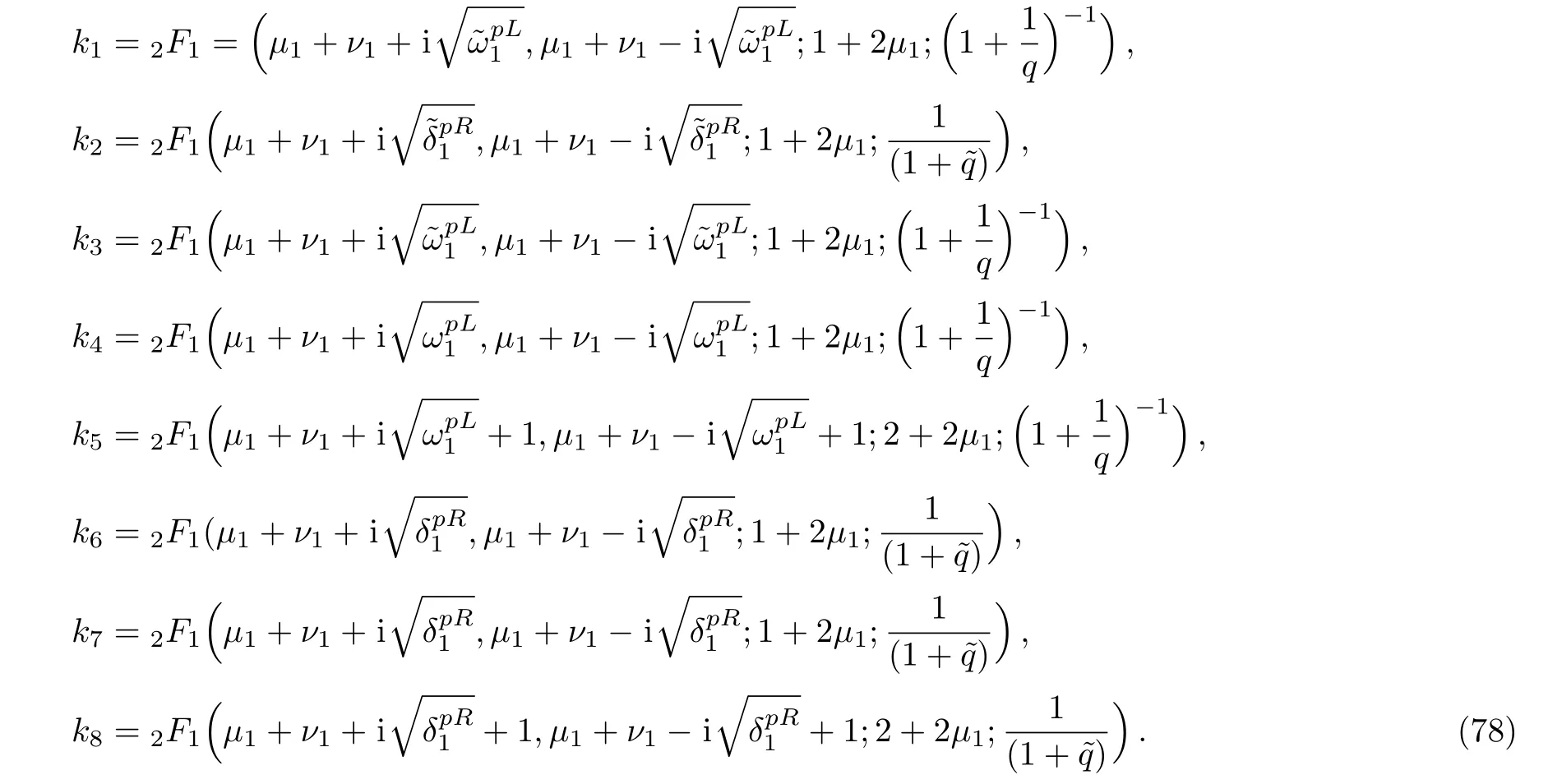
Equations(31)and(32)have a solution if and only if its determinant is zero.[41?42]This provides the solution for the energy eigenvalues as
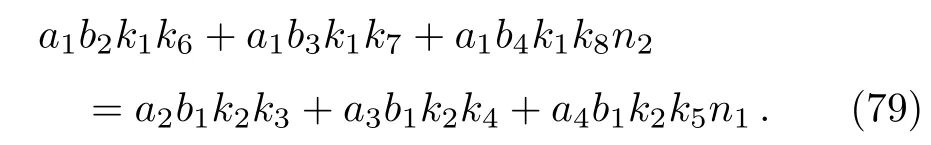
Equation(79)is a complicated transcendental energy equation and can only be solved numerically.
3.3 Bound State Solutions in the Negative Region(x<0)for the Case of?(x)=constant
In order to solve the bound state we repeat the process shown in the formal section but here we take note of the changes made in the potential.On substituting Eq.(64)into Eq.(6)and with a change in the variable z=(1+(1/q)e2αx)?1,we obtain

where
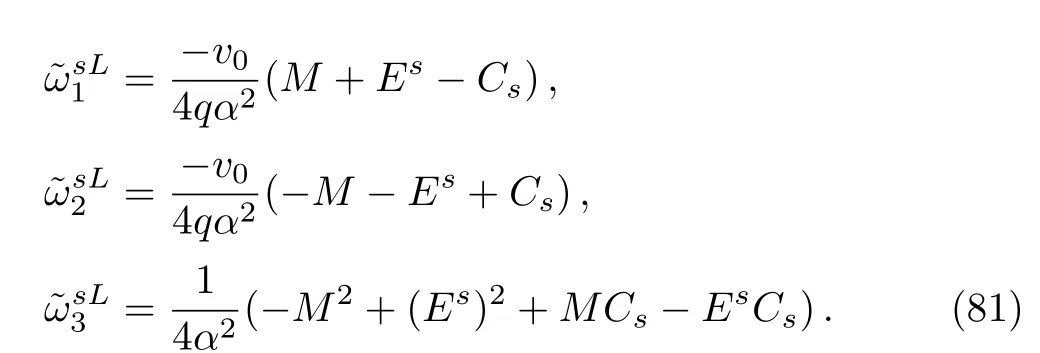
Again taking the trial wave functionφ(z)= zη1(1 ?z)?1φ(z),which turns into the hypergeometric differential equation of the form[27]

where
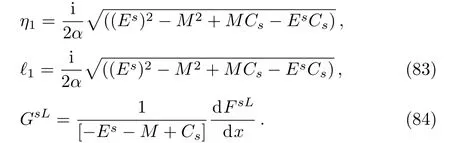
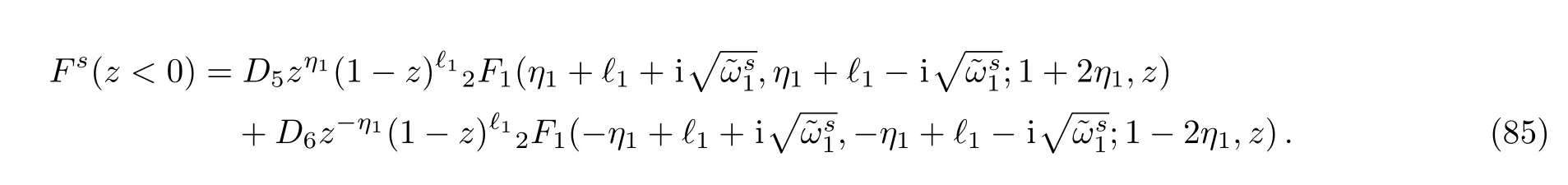
3.4 The case for x>0
On substituting by the same steps,using also the trial wave functionwe obtain Eq.(86)by defining the variable
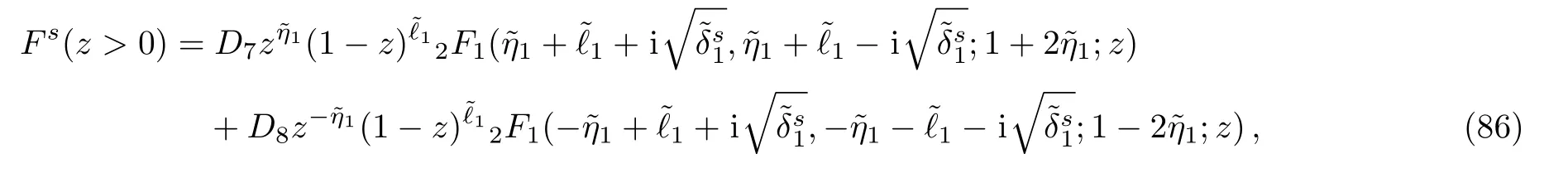
where
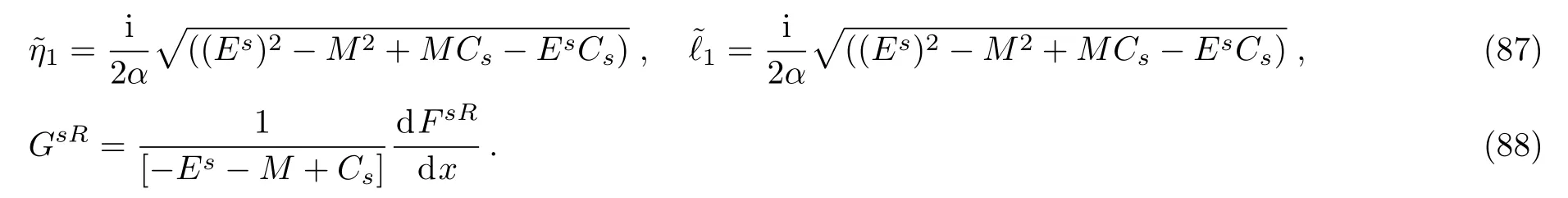
As we have done previously,we seek for the physical result for the energy eigenvalue as we set D2=D4=0 and impose the condition for the continuity of the wave function at the point FsL(x=0)=FsR(x=0),F′sL(x=0)=F′sR(x=0)to get

with

Equations(89)and(90)have a solution if and only if its determinant is zero,and this condition is used in getting the energy eigenvalue as

Equation(93)gives the energy equation,which is transcendental and can only be solved numerically.
4 Conclusion
We have solved the exact solution of a relativistic one-dimensional Dirac equation for the asymmetric qparameter hyperbolic P?schl-Teller potential and have obtained in terms of hypergeometric functions the scattering states as well as transmission and reflection coefficient us-ing the continuity conditions of the wave function and its derivatives.The bound state solution is obtained by vanishing the determinant of the coefficients of the wave function for the pHPT potential.This study can find its applications to physics especially condensed matter Physics in view of the recent development in grapheme QD materials.
Acknowledgments
It is our pleasure for us to thank the kind referee for his many useful comments and suggestions,which greatly helped us in making improvements to this paper.
 Communications in Theoretical Physics2018年11期
Communications in Theoretical Physics2018年11期
- Communications in Theoretical Physics的其它文章
- Numerical Study of Unsteady MHD Flow and Entropy Generation in a Rotating Permeable Channel with Slip and Hall Effects?
- Hierarchical Human Action Recognition with Self-Selection Classifiers via Skeleton Data?
- Spin Thermoelectric Effects in a Three-Terminal Double-Dot Interferometer?
- Third-Order Magnetic Susceptibility of an Ideal Fermi Gas?
- Coherent Control of the Hartman Effect through a Photonic Crystal with Four-Level Defect Layer?
- Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas?
