THE PICARD THEOREM ON S-METRIC SPACES?
Nihal YilmazZGRNihal TAS?
Department of Mathematics,Bal?kesir University,10145 Bal?kesir,Turkey
E-mail:nihal@balikesir.edu.tr;nihaltas@balikesir.edu.tr
Abstract Recently,the notion of an S-metric space is defined and extensively studied as a generalization of a metric space.In this paper,we define the notion of the S∞-space and prove its completeness.We obtain a new generalization of the classical“Picard Theorem”.
Key words S∞-space;completeness;Picard Theorem;initial value problem
1 Introduction
Using recent developments in metric spaces,theoretical studies can be applied in some areas such as integral equations,differential equations etc.In particular,some fixed point theorems are used to obtain solutions of integral and differential equations.For example,Krakow proved Gronwall’s lemma,Peano and Picard existence theorems in metric spaces[8].Kakde,Biradar and Hiremath used fixed point theory to solve the differential equations[7].Huang and Xu obtained the existence and uniqueness of a solution for an ordinary differential equation with a periodic boundary condition[6].Alsulami,Gülyaz,Karap?nar and Erhan improved the contractive conditions and studied fixed point theorems for a class of α-admissible contractions and obtained some applications to a boundary value problem[1].He derived the existence and uniqueness of a solution for a first-order ordinary differential equation with periodic boundary conditions[4].Farajzadeh,Kaewcharoen and Plubtieng obtained an application of fixed point theory for a nonlinear differential equation[3].
Recently,the notion of an S-metric space are introduced as a generalization of a metric space as follows.
Definition 1.1(see[11]) Let X be a nonempty set and S:X×X×X→[0,∞)be a function satisfying the following conditions for all x,y,z,a∈X,
(S1)S(x,y,z)≥0,
(S2)S(x,y,z)=0 if and only if x=y=z,
(S3)S(x,y,z)≤S(x,x,a)+S(y,y,a)+S(z,z,a).
Then S is called an S-metric on X and the pair(X,S)is called an S-metric space.
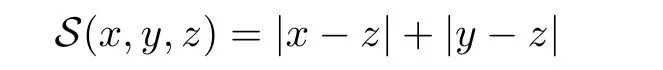
Example 1.2(see[12]) Let R be the real line.Then the function S:X×X×X→[0,∞)defined by for all x,y,z∈R is an S-metric on R.This S-metric on R is called the usual S-metric on R.
Then it is studied new fixed point theorems on S-metric spaces(see[5,9–13]for more details).For example,the following theorem was given as a generalization of the well-known Banach’s contraction principle on a complete S-metric space.
Definition 1.3(see[11])Let(X,S)be an S-metric space.A self-mapping T:X→X is called a contraction if there exists a constant L∈[0,1)such that
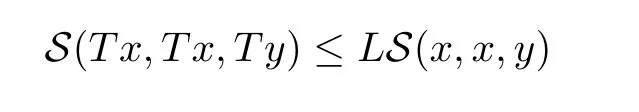
for all x,y∈X.
Theorem 1.4(see[11]) Let(X,S)be a complete S-metric space and the self-mapping T:X→X be a contraction.Then T has a unique fixed point x0∈X.Furthermore,with

for any x∈X.
In this paper,motivated by the above studies,we give an application of fixed point theory to differential equations on S-metric spaces.In Section 2,we recall some known results about S-metric spaces.In Section 3,we define the concept of the S∞-space and show its completeness.In Section 4,we prove the“Picard Theorem”on S-metric spaces.Also,we generalize the Picard Theorem using vector functions and give an example to the system of equations.In Section 5,we give an application to error analysis of nth iterations as approximation for the S-metric which is not generated by any metric given in[9].
2 Preliminaries
In this section,we recall some definitions and lemmas which are needed in the sequel.
Definition 2.1(see[11]) Let(X,S)be an S-metric space.For r>0 and x∈X,the open ball BS(x,r)and the closed ball BS[x,r]with a center x and a radius r defined as follows:
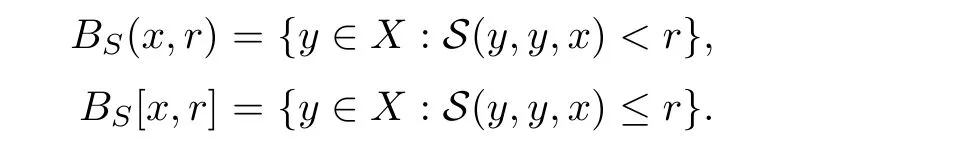
Definition 2.2(see[10]) Let(X,S)be an S-metric space and A?X be any subset.A point x∈X is a cluster point of A if
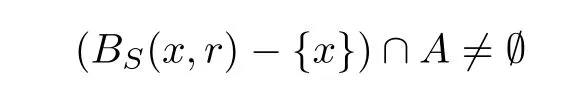
for every r>0.The set of all cluster points of A is denoted by A′S.
Definition 2.3(see[11]) Let(X,S)be an S-metric space and A?X.A subset A of X is called S-bounded if there exists r>0 such that S(x,x,y) Definition 2.4(see[11]) Let(X,S)be an S-metric space. (1)A sequence{xn}in X converges to x if and only if S(xn,xn,x)→0 as n→∞,that is,there exists n0∈ N such that for all n ≥ n0,S(xn,xn,x)< ε for each ε>0.It is denoted by (2)A sequence{xn}in X is called a Cauchy sequence if S(xn,xn,xm)→0 as n,m→∞,that is,there exists n0∈ N such that for all n,m ≥ n0,S(xn,xn,xm)< ε for each ε>0. (3)(X,S)is called complete if every Cauchy sequence is convergent. Lemma 2.5(see[11]) Let(X,S)be an S-metric space.Then we have Lemma 2.6(see[11]) Let(X,S)be an S-metric space.If xn→x and yn→y then we have In the following lemma,we see the relationship between a metric space and an S-metric space. Lemma 2.7(see[5]) Let(X,d)be a metric space.Then the following properties are satisfied: (1)Sd(x,y,z)=d(x,z)+d(y,z)for all x,y,z∈X is an S-metric on X. (2)xn→x in(X,d)if and only if xn→x in(X,Sd). (3){xn}is Cauchy in(X,d)if and only if{xn}is Cauchy in(X,Sd). (4)(X,d)is complete if and only if(X,Sd)is complete. We call the metric Sdas the S-metric generated by d.There are some examples of S-metrics which are not generated by any metric(see[5,9,13]for more details). Example 2.8(see[9]) Let X=R and consider the function S:X×X×X →[0,∞)defined by for all x,y,z∈R.Then(X,S)is an S-metric space such that the S-metric defined in(2.1)is not generated by any metric d. In this section,we define the notion of the S∞-space by using the metric S∞defined as the S-metric generated by d∞. Let F=R or F=C and C[a,b]={f|f:[a,b]→F is continuous function}.Then by Lemma 2.7(1),the function S∞:C[a,b]× C[a,b]× C[a,b]→ [0,∞)defined as for all f,g,h∈C[a,b]is an S-metric on C[a,b]and(C[a,b],S∞)is an S-metric space. Proposition 3.1 (C[a,b],S∞)is a complete S-metric space. Proof Since the S-metric S∞is generated by the metric d∞,using Lemma 2.7(4),it is deduced that(C[a,b],S∞)is a complete S-metric space. Definition 3.2 Let(X,S)be an S-metric space and Y be a nonempty subset of X.Let a function SY:Y×Y×Y→[0,∞)be defined by for all x,y,z∈Y.Then SYis called a reduced S-metric and(Y,SY)is called a sub-S-metric space of(X,S). Definition 3.3 Let(X,S)be an S-metric space and A?X.A is called closed if the set of cluster points of A is contained by A,that is,?A. Proposition 3.4 If(X,S)is a complete S-metric space and Y is a closed set in(X,S),then(Y,SY)is complete. Proof The proof follows easily by the definitions of completeness and closedness. ? Proposition 3.5 Let X be a set of all continuous functions from[a,b]to[c,d].Then(X,S∞)is a complete S-metric space. Proof Using Proposition 3.4,we only show that X is closed set in C[a,b]since X?C[a,b]and(C[a,b],S∞)is complete S-metric space.Let f∈C[a,b]be a cluster point in X.Then,there exists a sequence{fn}in X such that{fn}→f according to S∞.Hence we obtain and so for each x∈[a,b].Since c≤fn(x)≤d for each x∈[a,b]then c≤f(x)≤d.Consequently,we have f∈X. ? In this section,we give some generalizations of the well-known“Picard Theorem”on S-metric spaces. At first,we recall the definition of an initial value problem[2].Let a>0,b>0 in R and consider the set on R2.For x∈I and a function y defined on I(I is any interval),if the conditions(x,y(x))∈D and y(x0)=y0are satisfied such that y′(x)=f(x,y(x))then y is called a solution of the initial value problem where y′==f(x,y(x)). The above initial value problem is equivalent to the following integral equation on I: We consider a function y satisfying(x,y(x))∈D and for all x∈I as a solution of(4.2)on I.In equality(4.3),we can easily seen that the function y is continuous.Also,the function y is a solution of the initial value problem given in(4.1)if and only if the function y is a solution of the integral equation given in(4.2). Now we give the following generalization of the“Picard Theorem”using the S∞-space defined in the previous section.To do this,we use the S-metric defined in(2.1)which is not generated by any metric d. Theorem 4.1 Let a>0,b>0,f be a continuous function on and the following condition is satisfied for each(x,y1),(x,y2)∈D,where M>0 and the function S is the S-metric defined in(2.1)on D.Then there exists a unique function y defined on[x0?r,x0+r]such that when x ∈ [x0?r,x0+r]for some r>0,that is,there exists a unique solution ? on[x0?r,x0+r]of a first order differential equation with initial value y(x0)=y0. Proof Since the function f is continuous on D,there exists a number k>0 such that for each(x,y)∈D,that is,the function f is bounded.There exists since f is bounded and continuous on D. Assume that r=min?a,bK?and where S is the S-metric defined in(2.1).Hence(X,S∞)is a complete S-metric space by Proposition 3.5.Using the assumption of r,we see that(x,y(x))∈D for S(x,x,x0)≤r and y∈X.Now we define the following function T: Then the function y satisfies condition(4.5)if and only if Ty=y.Using the definition of r and equality(4.6)if S(x,x,x0)≤r then we have Ty∈X and T:X→X. Now we show that Tpis a contractive mapping for some integer p.We can write Suppose that x0≤x then we obtain If we repeat this argument for Ty1and Ty2we get Using the similar argument for n,we have Using Lemma 2.5,it can be easily seen that this inequality is satisfied for x≤x0.Sincethere exists an integer p such thatis a contractive mapping.Consequently,T has a unique solution. Remark 4.2 i)The proof of Theorem 4.1 can be also shown using the closed ball with 0 ii)It can be easily seen that the proof of Theorem 4.1 is valid for the usual S-metric defined in Example 1.2.Hence we can use any S-metric in Theorem 4.1 with respect to the selected region D.Theorem 4.1 will be important in the cases which are not contained in the classical Picard Theorem.Because it can be required to study on any region D and any S-metric on the selected region D. iii)In[12],it was given the relationship between an S-metric and a B-metric.Every S-metric is a B-metric with B=Therefore it is possible to obtain a new version of the Picard Theorem on B-metric spaces. Now,we give the generalized Picard Theorem in a vertical strip using the S-metric defined in(2.1). Theorem 4.3 Let I be a closed interval and f be a continuous function on If there is an M>0 such that for all(x,y1),(x,y2)∈D,then there exists a unique function y on I such that for(x0,y0)∈ D,x ∈ I,that is,there exists a unique solution ? on I of a first order differential equation with initial value y(x0)=y0. Proof By similar arguments used in the proof of Theorem 4.1,the proof follows easily.? Now we give an extension of the Picard Theorem using vector valued functions.A system of first order differential equations are defined as follows: Now we can write This is a vector of the first order equation and the Picard Theorem can be generalized in this case using the S-metric defined in(2.1). Theorem 4.4 If F is a continuous vector function on x and inequality(4.4)is satisfied on y in a region D containing x=x0,y=y0,then the ordinary differential equation with initial condition y(x0)=y0has a unique solution y(x)which depends continuously on y0. Proof The ordinary differential equation(4.7)with initial condition y(x0)=y0is equivalent to the following equation Now we define the following Picard iteration Let us consider the following region Assume that x∈(x0?r,x0+r),where r≤a and the vector function F satisfies the inequality(4.4).We complete the proof with the following steps. Step 1 We show the following inequality using the mathematical induction If n=0,we obtain where|.|denotes the norm of a vector,S is the S-metric defined in(2.1)and Suppose that inequality(4.9)is satisfied for n?1.Now we obtain converges to vector function y(x).Also we obtain Consequently,the convergence is uniform on x and the limit of uniform convergent continuous functions is continuous. Step 2 We show that the vector function y(x)is a solution.Since ynconverges uniformly to y,we assume that ynis close to y.Hence we obtain If we take limit for n→∞of then we obtain that the vector function y is a solution of the ordinary differential equation(4.8). Step 3 We show that the vector function y is a unique.Assume that u(x)is an another solution as follows: Since the vector functions y and u are continuous they are bounded on[x0?r,x0+r],that is, for all x∈[x0?r,x0+r].Hence we get and repeating this process we have as n→∞.So we obtain y(x)=u(x)on[x0?r,x0+r]. Step 4 We show that the solution vector function depends continuously on y0.Let y be a unique solution of the ordinary differential equation(4.8)with initial condition y(x0)=y0and u be a unique solution with initial condition u(x0)=y0+δ.Then the following equations are satisfied and Hence we get Since the vector functions y and u are continuous functions then we get on(x0?r,x0+r).Using inequality(4.10),we have By the mathematical induction,we obtain Hence u(x)→ y(x)as δ→ 0. Step 5 We show that all of the yn(x)remain in(y0?b,y0+b).Let r=min where For x∈(x0?r,x0+r)using the mathematical induction on n we get and so Consequently,the proof is completed. Theorem 4.5 If every component Fi(x,y)satisfies inequality(4.4)in y=that is, then the vector function F satisfies inequality(4.4)in y. Proof The following inequalities hold for any positive reel numbers a1,···,an.Hence we obtain We use our results to obtain the existence and uniqueness of a solution for a system of first order differential equations with initial conditions.We give the following example. Example 4.6 We show that the system of equations has a unique solution in some interval about x=0.To do this we can write this system as where So it can be easily seen that the function F is continuous on x everywhere.Now we consider the components of the function F: where|x|≤M1; where|v1|,|v2|≤M2.Using Theorem 4.5,we have In this section,we give an example of error analysis of nth iterations as an approximation for the S-metric defined in(2.1). Using the inequality(1.1)in Theorem 1.4,we obtain for iteration sequences.This inequality(5.1)can be used in error analysis of nth iteration as an approximation.We give the following example. Example 5.1 Using the Picard iteration,we find approximate solution of the differential equation with the initial condition y(0)= The function f(x,y)=2x?3y2satisfies the conditions of Theorem 4.1.Let Then f is defined on D and is a continuous function.Also,inequality(4.4)is satisfied.Indeed,we have where S is the S-metric defined in(2.1),f is bounded on D as|f(x,y)|≤1.Since M=4,we have r for the second iteration.Now we find y1(x).We have and so Now we see error analysis of the third and fourth iterations as follows: Consequently,the error is decreasing on n-th iterations with n≥3. We present the notion of the S∞-space and proved a new generalization of the well-known Picard Theorem on S-metric spaces.We have given an example of error analysis of n-th iterations as an approximation.As a future work,it is possible to study new generalizations of the Picard theorem on some generalized metric spaces(for example B-metric space,G-metric space etc)and to obtain various applications in different applied areas.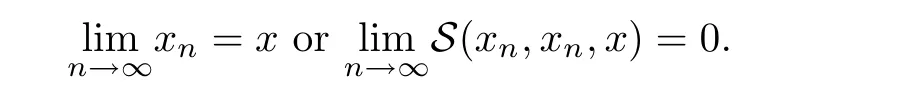
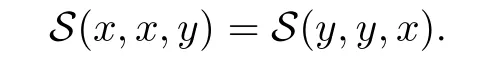
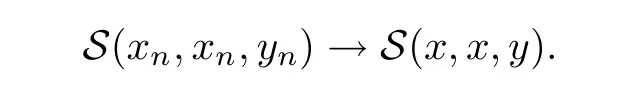
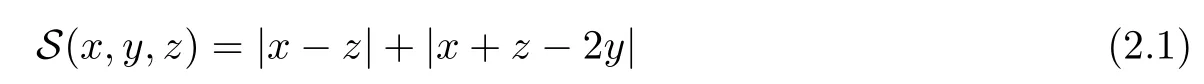
3 Definition and Completeness of the S∞-Space
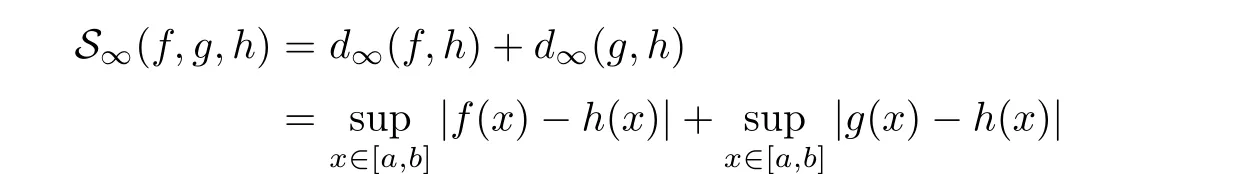
4 Some Generalizations of the Picard Theorem
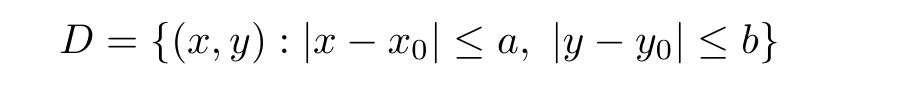




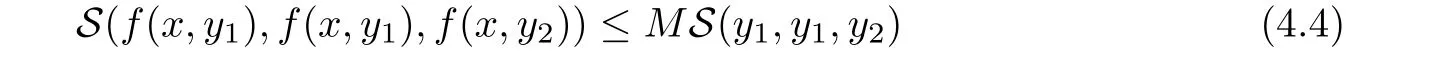
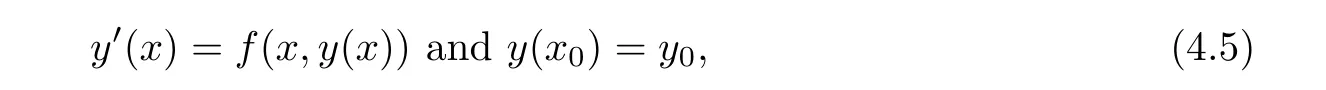
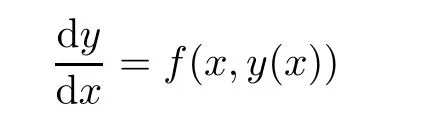
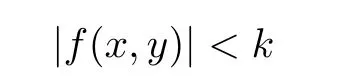
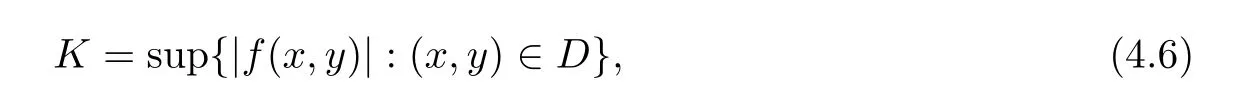
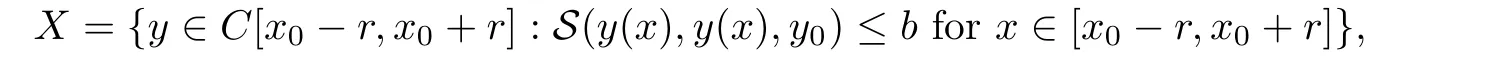
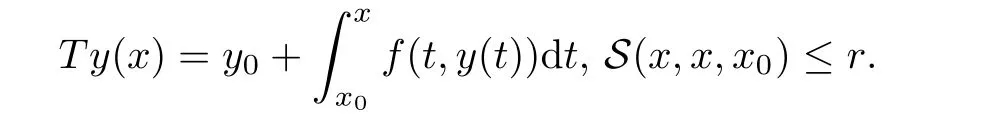
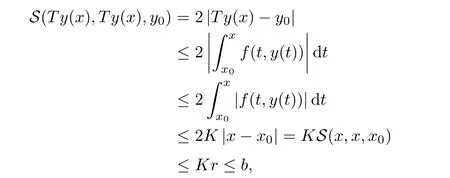
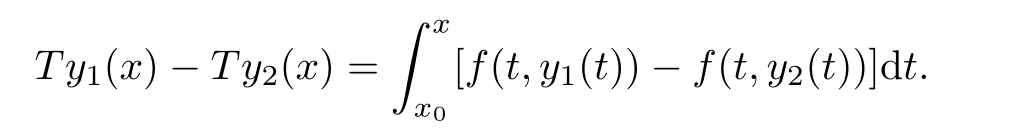
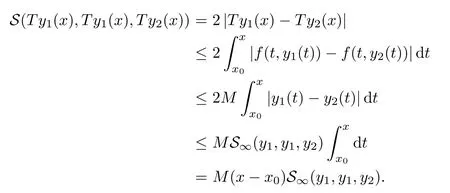
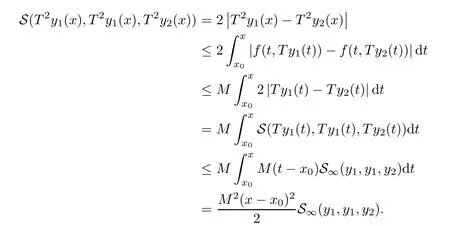
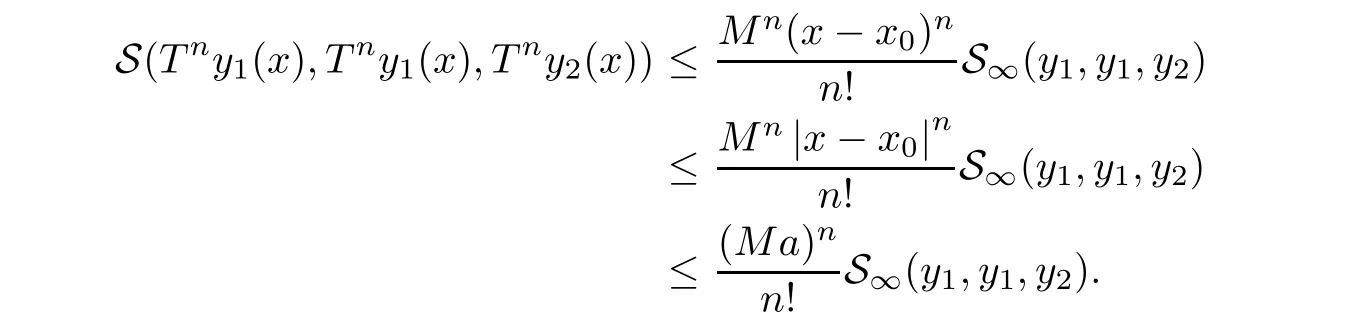
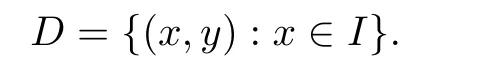
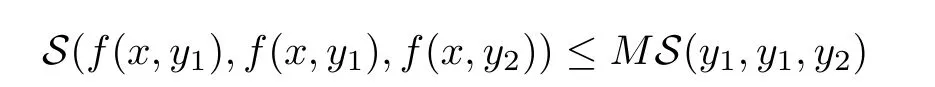
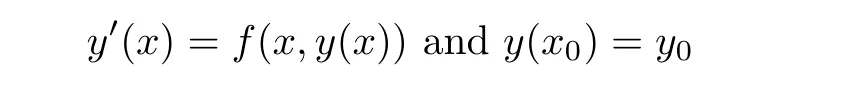
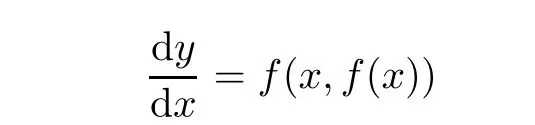
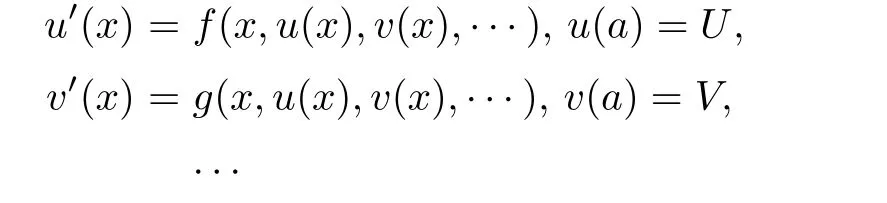
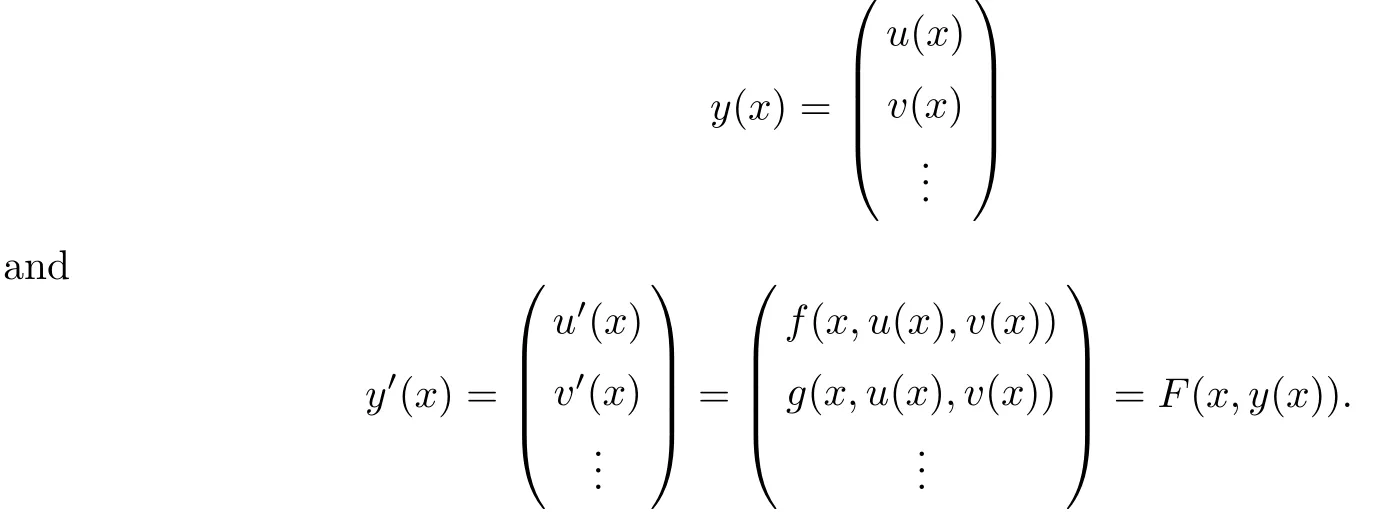

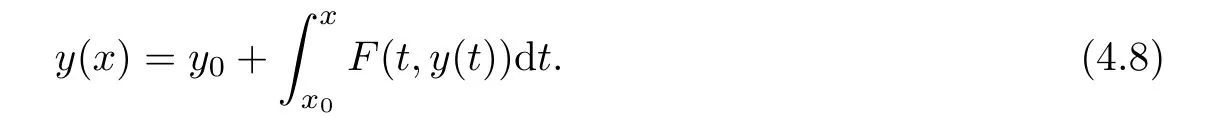
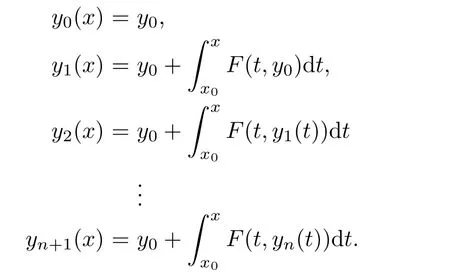
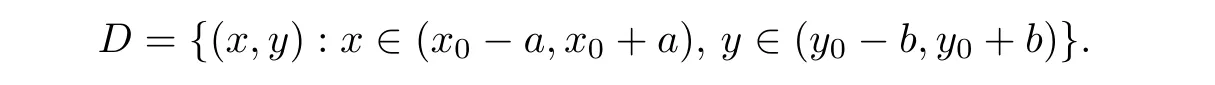
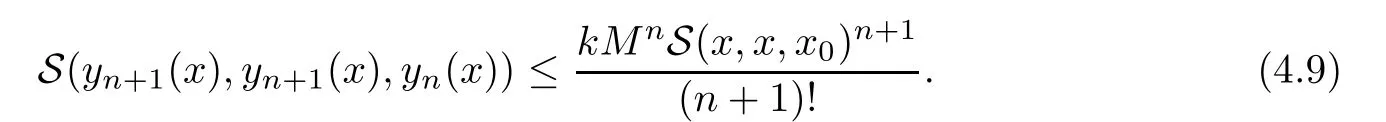
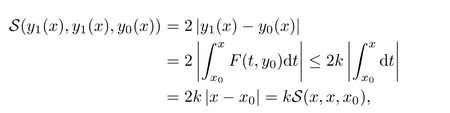
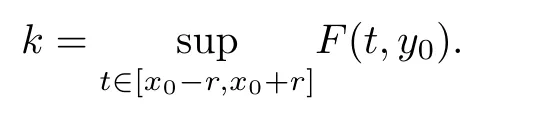
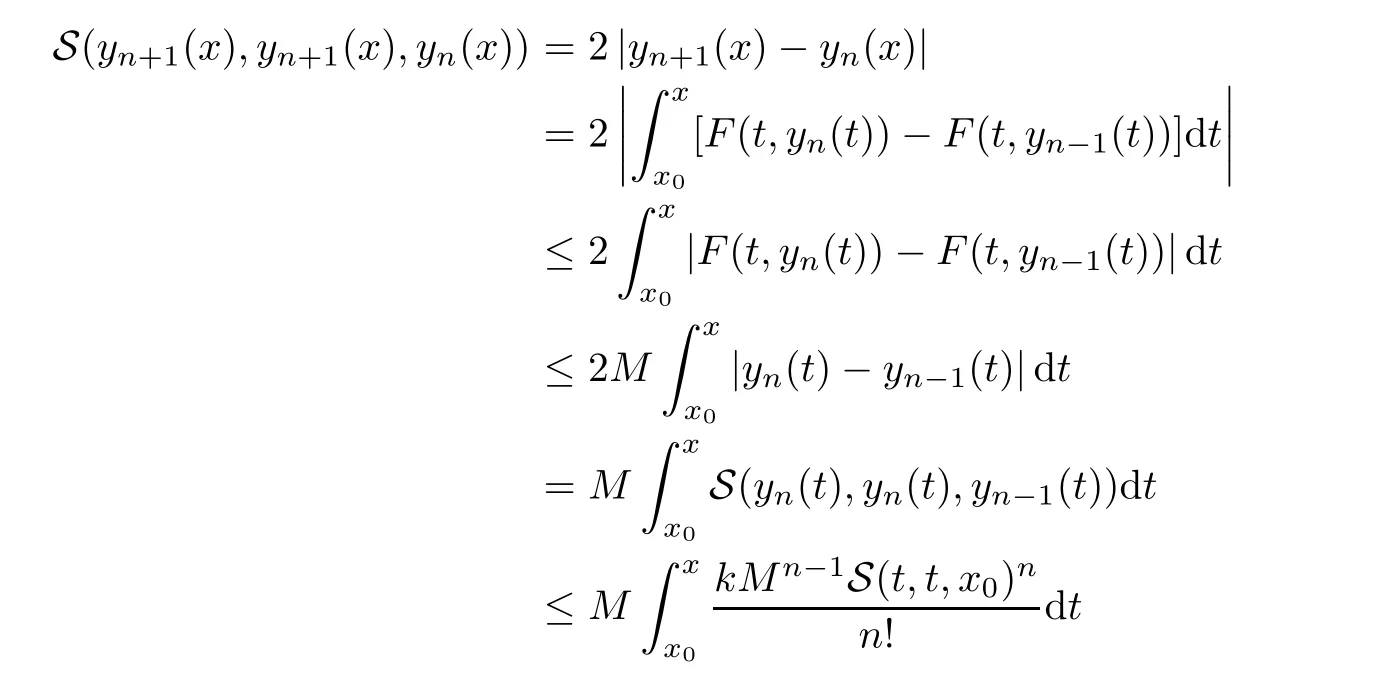
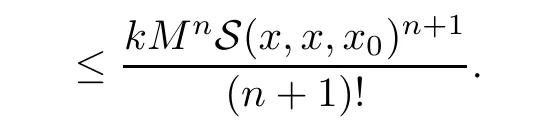
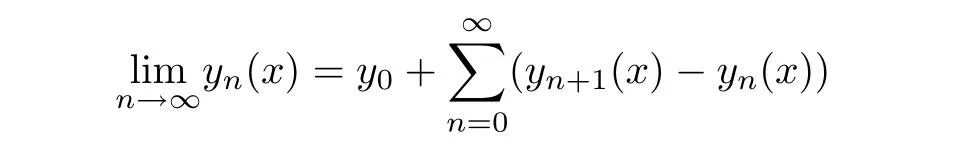
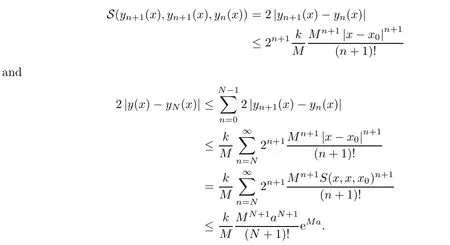
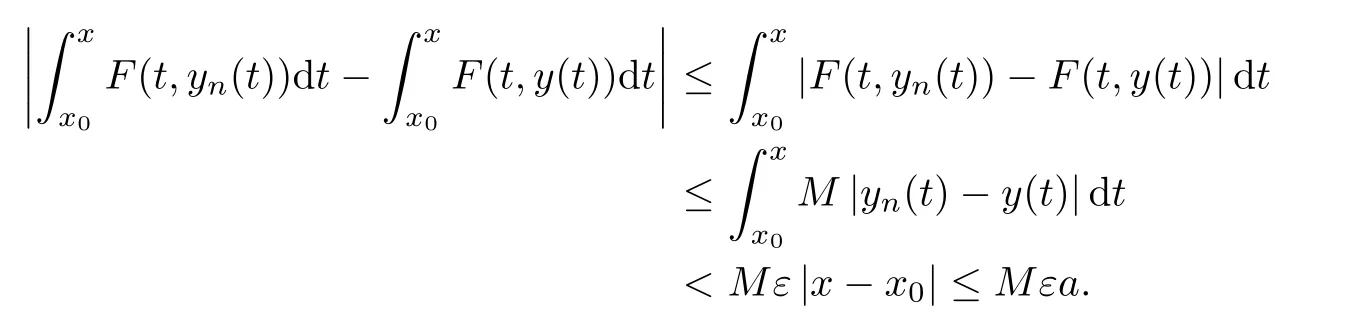
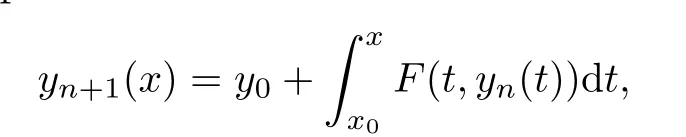
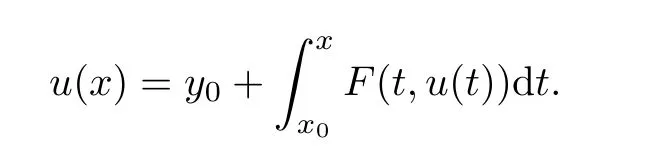
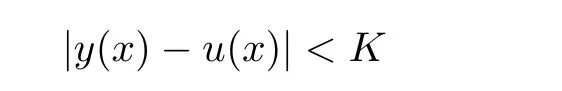
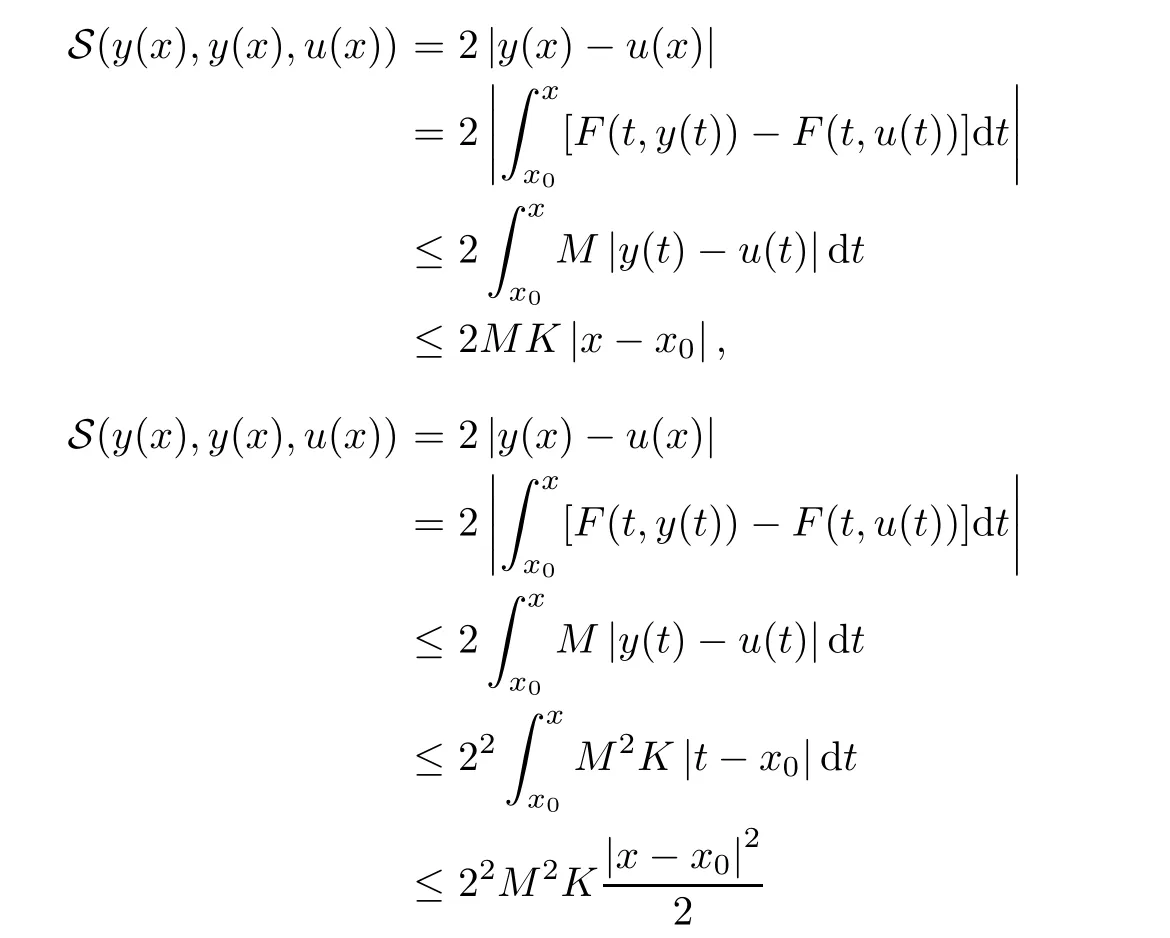
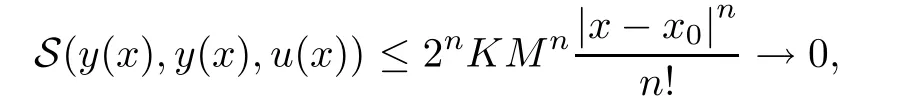
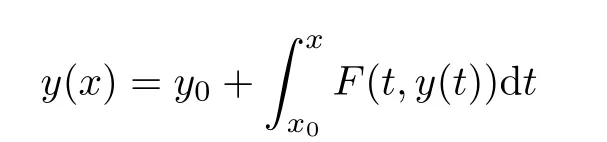
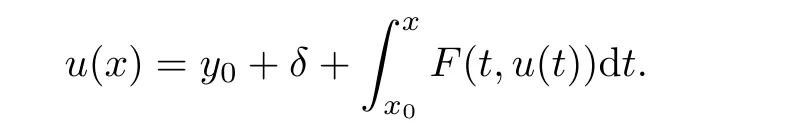
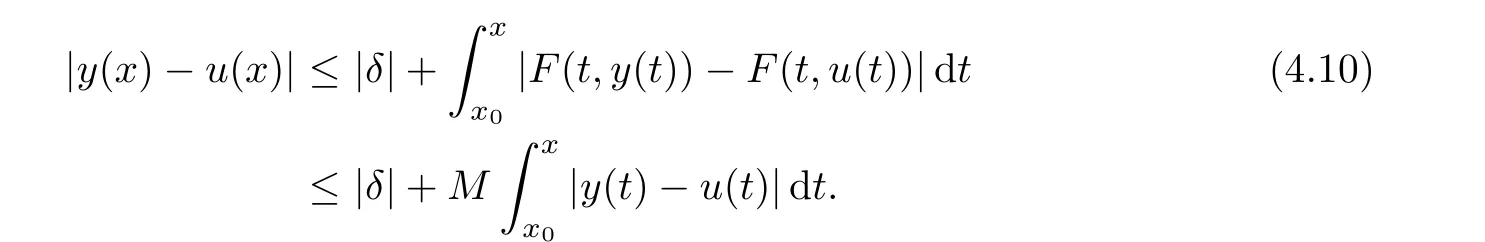
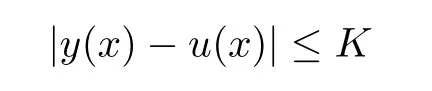
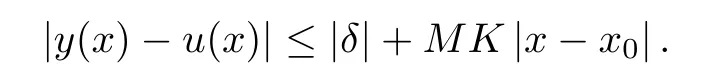
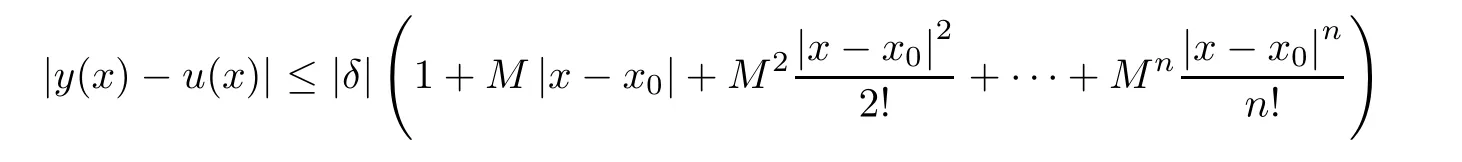
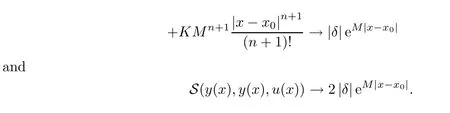
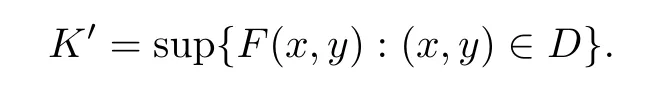
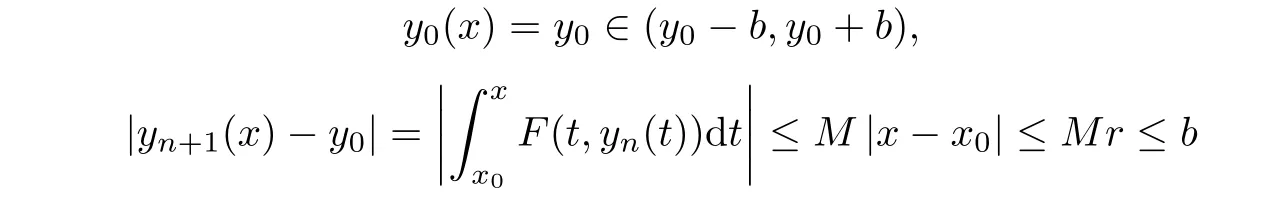
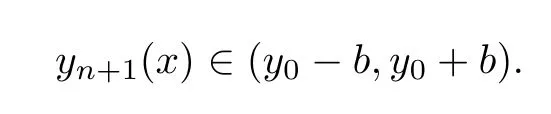
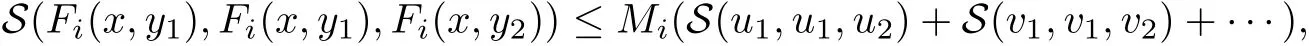
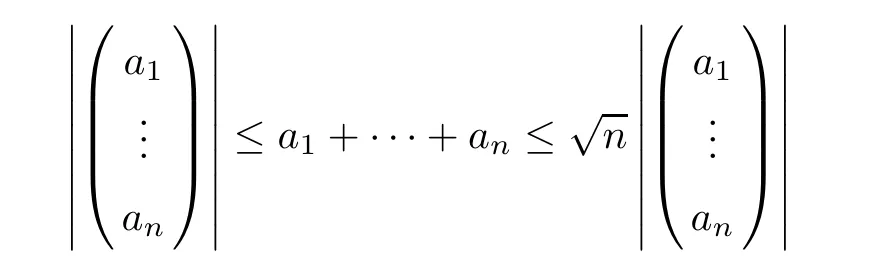
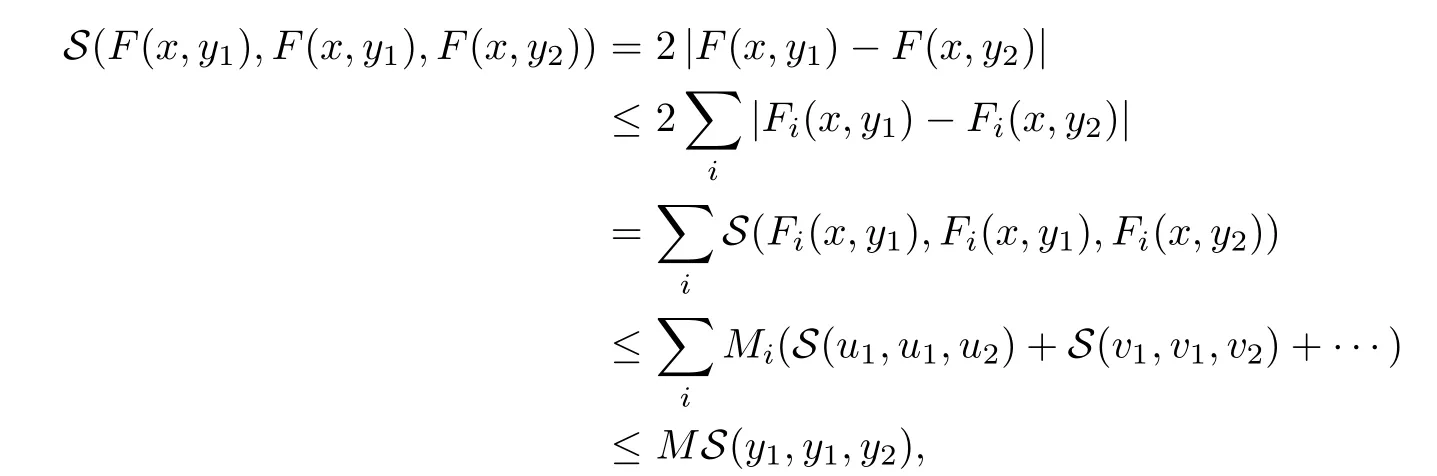
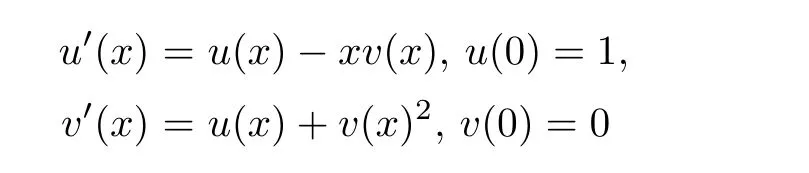
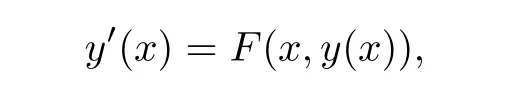
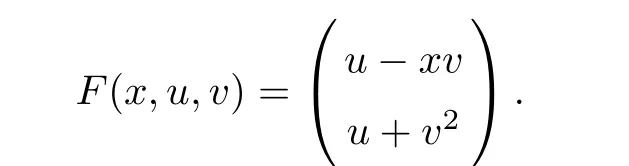
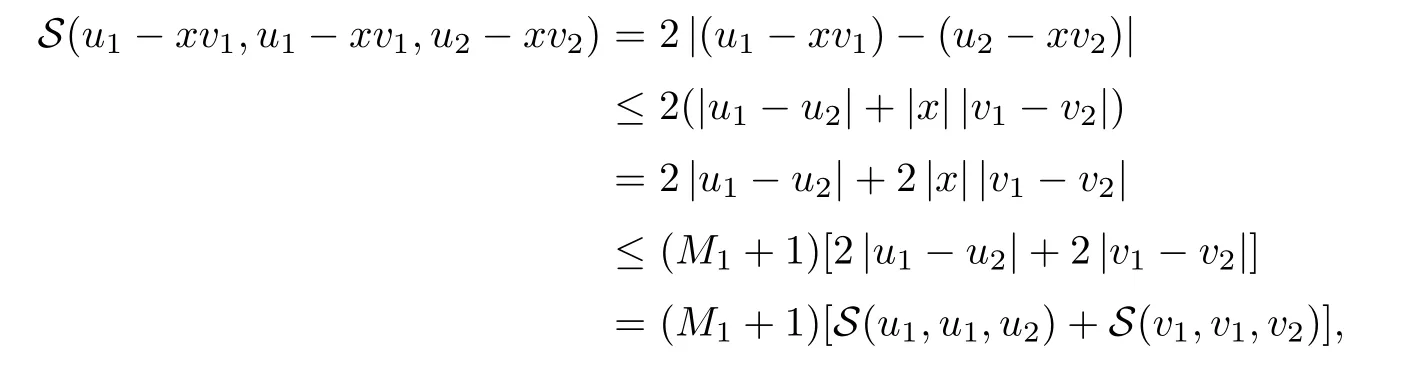
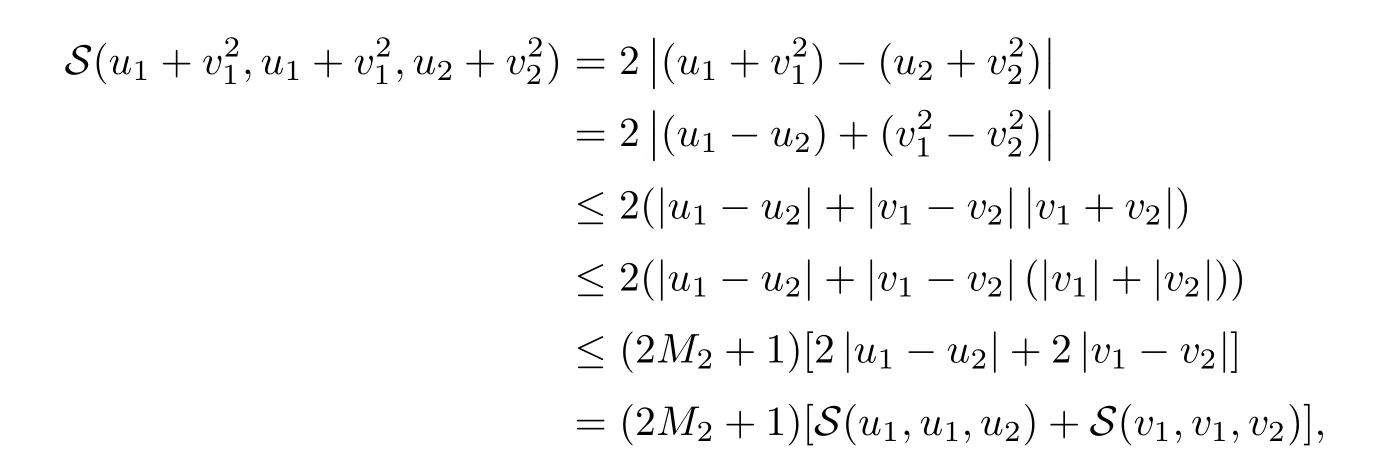
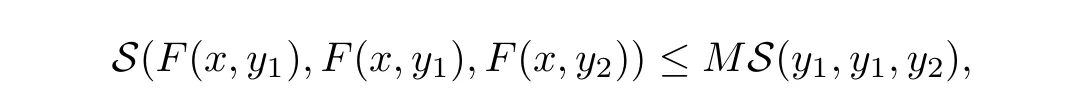
5 An Application to Approximate Solution
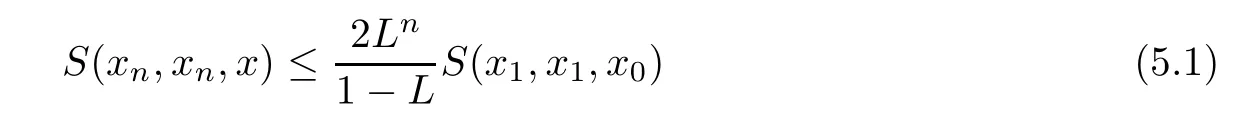
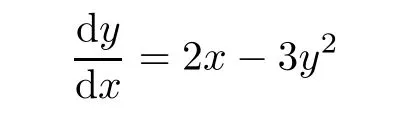
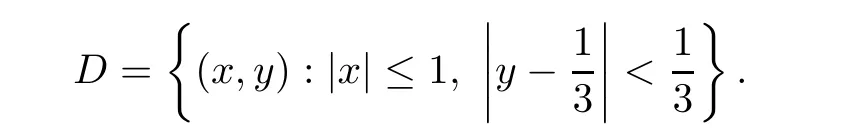
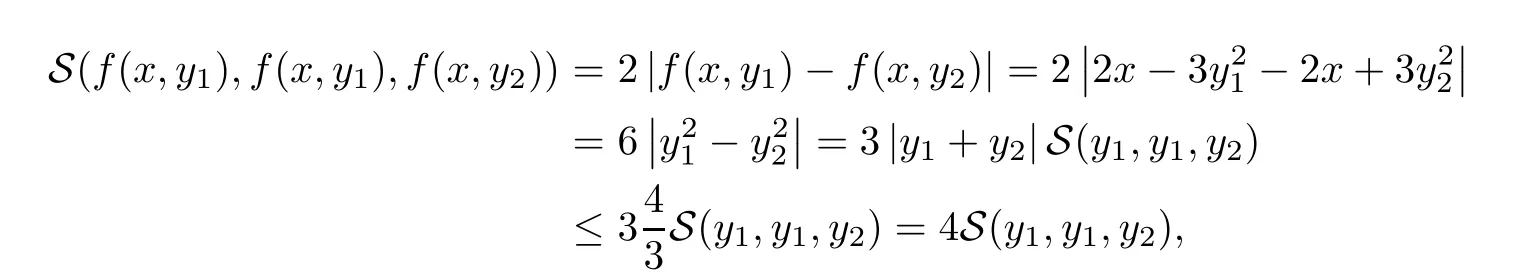
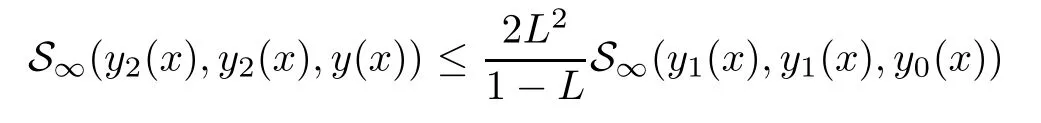
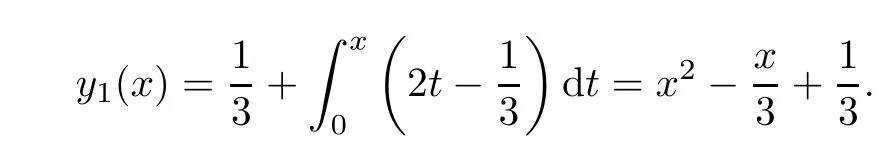
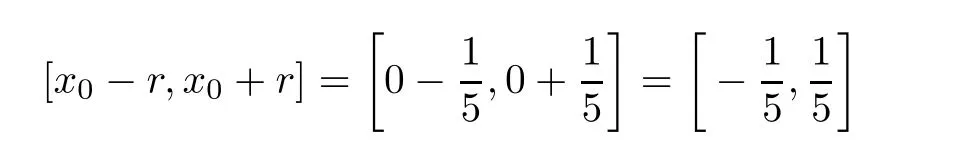
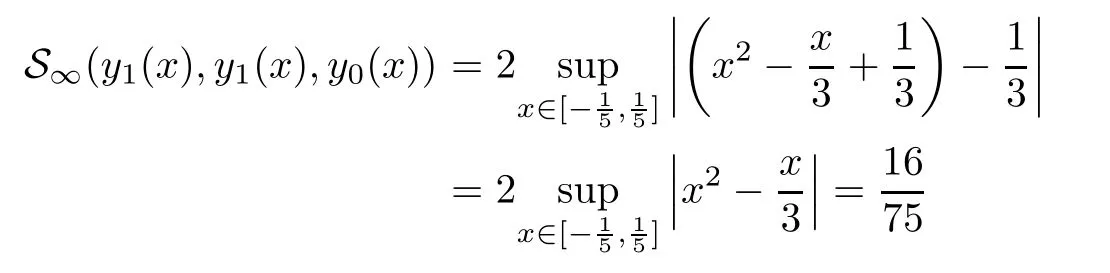
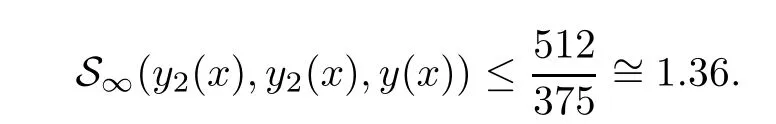
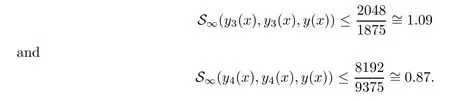
6 Conclusion and Future Work
 Acta Mathematica Scientia(English Series)2018年4期
Acta Mathematica Scientia(English Series)2018年4期
