SINGULAR LIMIT SOLUTIONS FOR 2-DIMENSIONAL ELLIPTIC SYSTEM WITH SUB-QUADRTATIC CONVECTION TERM?
Nihed TRABELSI
Higher Institute of Medicals Technologies of Tunis,University of Tunis El Manar,9 Street Dr.Zouhair Essa fi1006 Tunis,Tunisia
E-mail:nihed.trabelsi78@gmail.com
Abstract The existence of singular limit solutions are investigated by establishing a new Liouville type theorem for nonlinear elliptic system with sub-quadratic convection term and by using the nonlinear domain decomposition method.
Key words Liouville type system;singular limit solution;nonlinear domain decomposition method
1 Introduction and Statement of the Results
Although the real world seems in a muddle,many phenomena can be described by using nonlinear differential equations.A fundamental goal in the study of non-linear initial boundary value problems involving partial differential equations is to determine whether solutions to a given equation develop a singularity.Resolving the issue of blow-up is important,in part because it can have bearing on the physical relevance and validity of the underlying model.
For example,the nonlinear systems pose a lot of interesting but also challenging mathematical problems,which require people to develop new and deep theories and methods to treat them.For example,for the so-called BEC system,which has cubic nonlinearities and is weakly coupled,the least energy and the ground state have been attracting both physicists and mathematicians.With the deepening of the study on this line,some tough nuts remain uncracked.
Let ? ? R2be a regular bounded domain in R2,q ∈ [1,2).We consider the following elliptic system
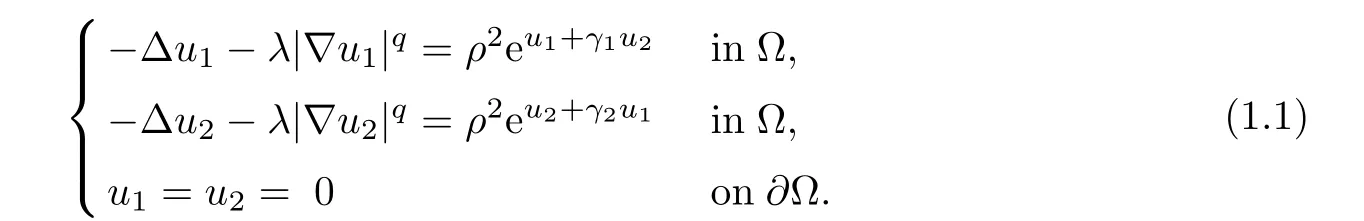
We denote by ε the smallest positive parameter satisfying
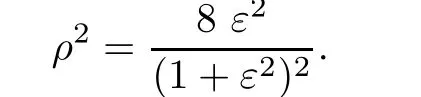
The current paper is mostly related to the papers[2,4,6,7,19].We use the same approach,namely,the nonlinear domain decomposition method,witch has already been used successfully in geometric context(constant mean curvature surfaces,constant scalar curvature metrics,extremal Kahler metrics,···).
We will ask the following question:does there exist a sequence of coupled solution(u1,ε,λ,u2,ε,λ)of previous system which converges to some nontrivial coupled function as the parameters ε,λ tends to 0.A positive answer to this question was given by Baraket and al.in[3]for q=2 under the assumption
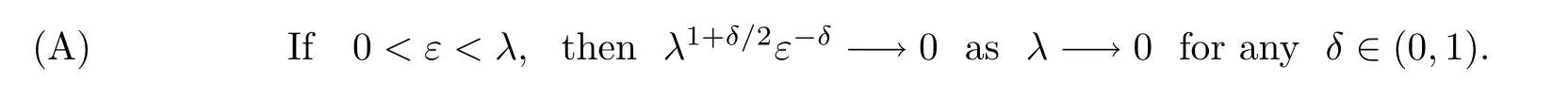
In particular,we take λ =O(ε2/3),then condition(A)is satisfied but this system
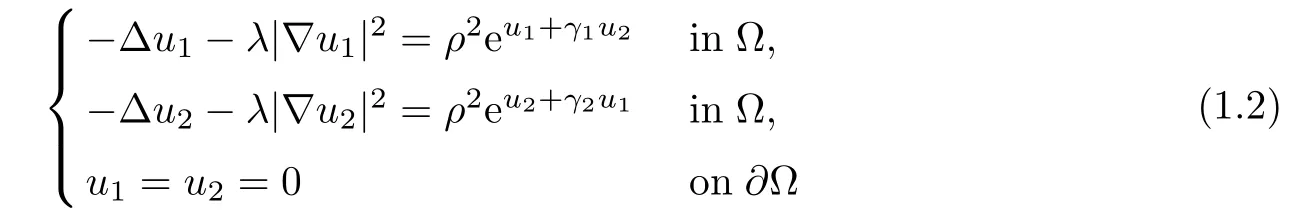
can be treated as a perturbation of the Liouville problem.Using the following transformation
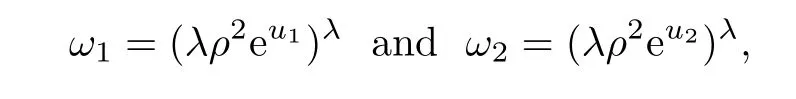
then the function(ω1,ω2)satisfies the following problem

with Qi=(λρ2)γi,i=1,2.
The Yamabe system found considerable interest in recent years as it appears in a number of physical problems,for instance in nonlinear optics.The coupled solution(ω1,ω2)denotes components of the beam in Kerr-like photorefractive media.we have self-focusing in both components of the beam.The nonlinear coupling constant Qiis the interaction between the two components of the beam.The case in which the coupling is nonlinear was studied extensively,which was motivated by applications to nonlinear optic and Bose-Einstein condensation.See for example[8–10,15,16]and references therein.
We shall therefore mainly consider the case where q∈[1,2)is a real number.We look for a sequence of coupled solutions(u1,ε,λ,u2,ε,λ)of(1.2)which converges to some nontrivial coupled function on some set as the parameters ε,λ tends to 0 without considering any condition like(A)and to see how the presence of the convection term(gradient)can have significant influence on the existence of a solution,as well as on its asymptotic behavior.
In[5]the authors were devoted the case of one equation
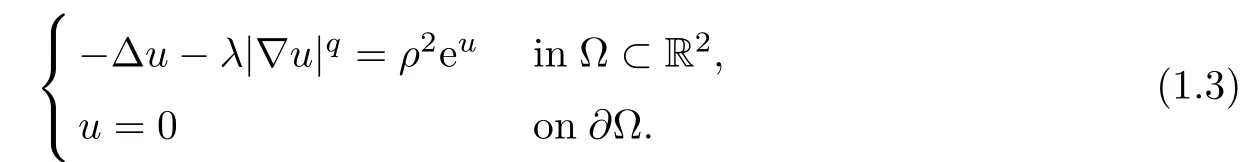
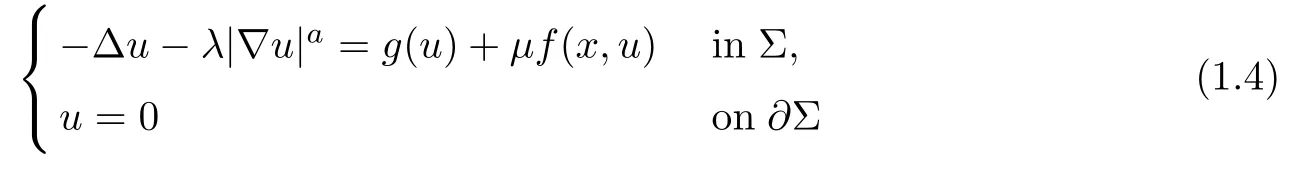
In[17],Ghergu and Radulescu studied more general problem on a domain Σ?Rn,n≥2,with 00 and some assumptions on f and g.Problems of type(1.4)arise in the study of non-Newtonian fluids,boundary layer phenomena for viscous fluids,chemical heterogeneous catalysts,as well as in the theory of heat conduction in electrically conducting materials.It also includes some simple prototype models from boundary-layer theory of viscous fluids[20].Problem(1.3)with the condition u|??=0 replaced by u|??=+∞ arises from many branches of mathematics and applied mathematics,and was discussed by many authors in many contexts,see,e.g.[1,12–14].
In this paper,we will prove the existence of some singular solution,a kind of converse for that in[21].More precisely,we prove the following result.
Theorem 1.1 Let ? be a regular bounded domain of R2and z1,···,zn∈ ? be given disjoint points.Let
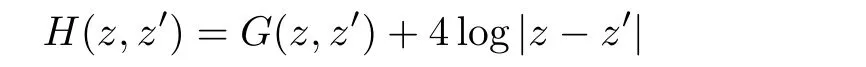
be the regular part of G,where the Green’s function G defined on ? × ? is given by

Suppose that(z1,···,zn)is a nondegenerate critical point of the function
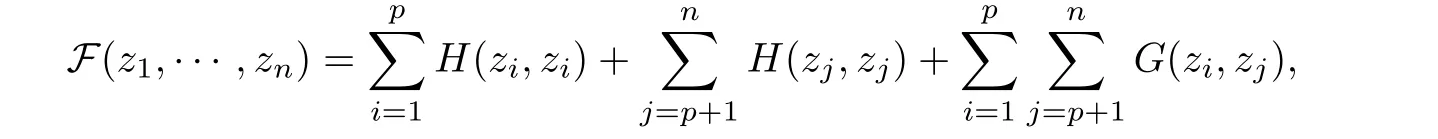
then there exist ρ0>0,λ0>0 anda family of solutions of(1.1)such that
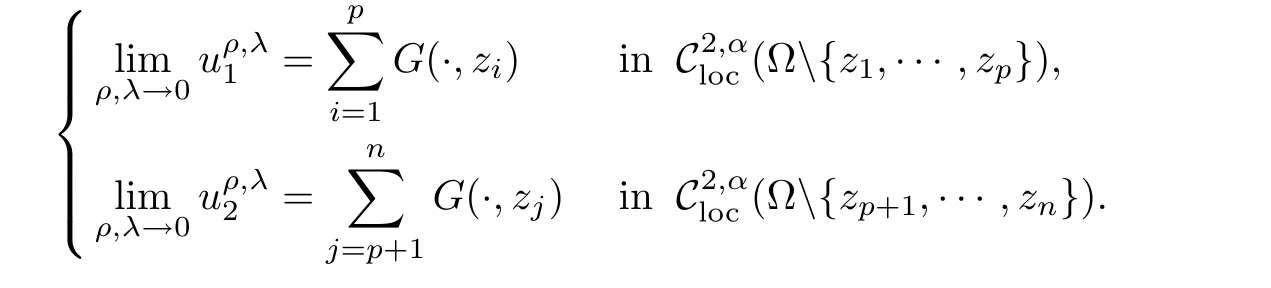
2 Proof of Theorem 1.1
Our proof is based on some refinements of arguments so we will recall some notations and results.First we construct the approximate solutions where a sharp estimate on approximate solutions is established.In the second time we solve respectively the nonlinear interior and exterior problem.Finally,we will match the nonlinear Cauchy-data solutions given to have an exactly solution defined on ?.
2.1 Construction of the Approximate Solution
We first describe the rotationally symmetric approximate solutions of
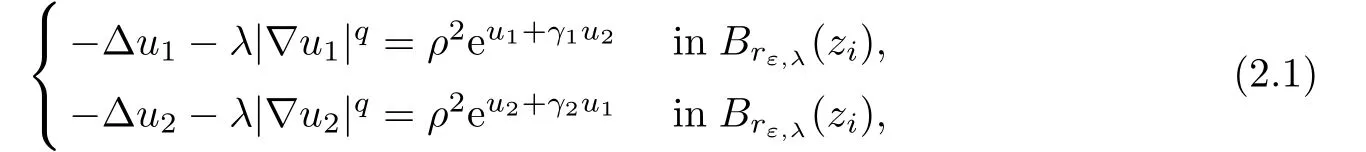
here and in the following,Br(a)denotes the ball of center a and radius r in R2.Given ε>0,let

which is a solution of
in R2.Hence for all τ>0 the function

is also solution to(2.3).
2.1.1 Linearized Operators
First we introduce some definitions and notations.
Definition 2.1 Given k ∈ N,α ∈ (0,1),μ ∈ R and|z|=r,letbe the space of functions in(R2)for which the following norm
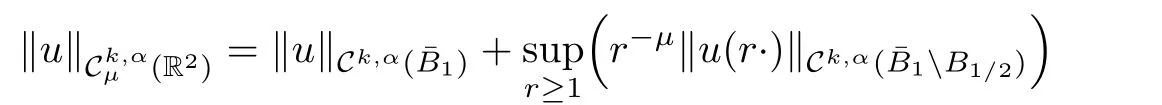
is finite.Similarly,for givenr ≥1,let(Br)be the space of function in Ck,α(Br)for which the following norm
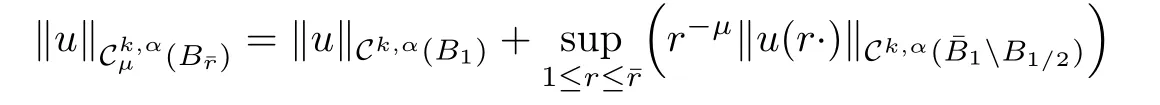
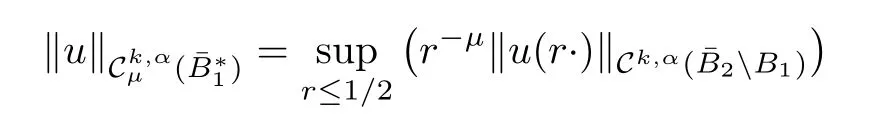
is finite.
We define the linear second order elliptic operator L by
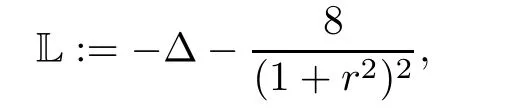
which is the linearized operator of ??u ? ρ2eu=0 about the symmetric solutions uε=1,τ=1defined by(2.4).When k ≥ 2,we letbe the subspace of functions w∈satisfying w=0 on??.
For all λ,ε,τ>0,γ1,γ2∈ (0,1),we define
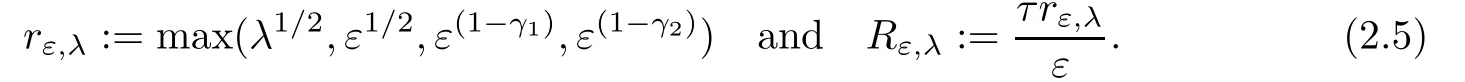
Proposition 2.2(see[7]) All bounded solutions of Lw=0 on R2are linear combination of
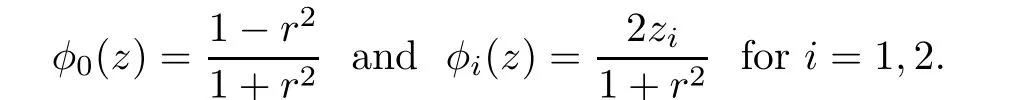
Moreover,for μ >1,μ 6∈ Z,L(R2)is surjective.
In the following,we denote by Gμto be a right inverse of L.Similarly,using the fact that any bounded harmonic function in R2is constant,we claim
Proposition 2.3 Let δ>0,δ 6∈ Z then ? is surjective fromWe denote by Kδ:a right inverse of?for δ>0,δ 6∈Z.
Finally,we consider punctured domains.For k∈{1,···,n}given∈ ? disjoint points,we defineLet r0>0 be small such thatare disjoint and included in ?.For all r ∈ (0,r0),we define
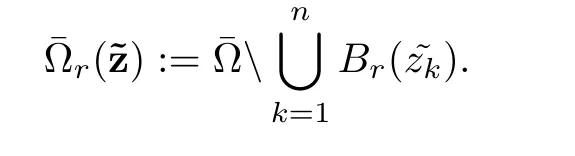
Definition 2.4 Let k ∈ R,α ∈ (0,1)and ν ∈ R,let
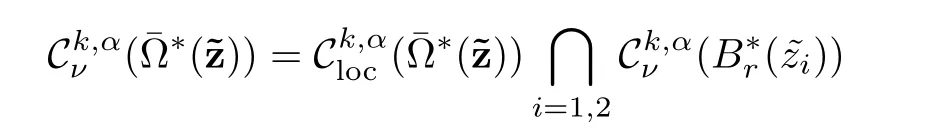
endowed the following norm
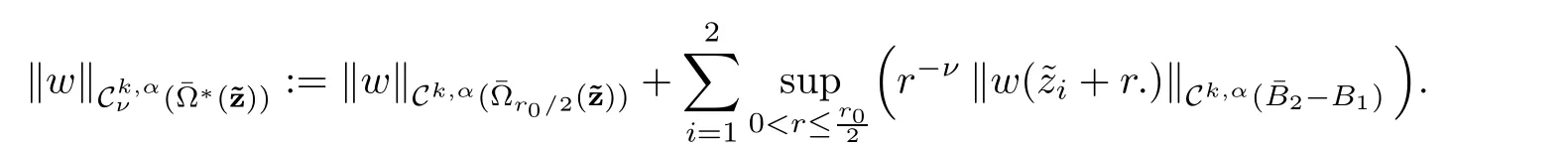
We recall the following result.
Proposition 2.5(see[11]) Let ν <0,ν 6∈ Z,then ? is surjective from
2.1.2 Ansatz and First Estimates
For all σ ≥1,we denote by ξσ:Cthe extension operator defined by
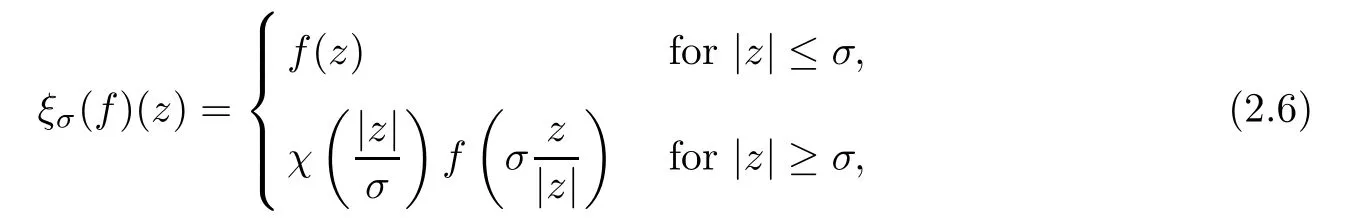
here χ is a cut-off function over R+,which is equal to 1 for t≤ 1 and equal to 0 for t≥ 2.It easy to check that there exists a constant c= c(μ)>0,independent of σ≥1,such that
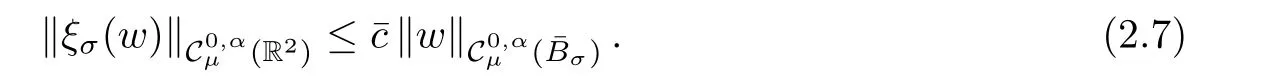
Here,we are interested in the study of system(1.1)near B(zi,rε,λ),i=1,···,p,
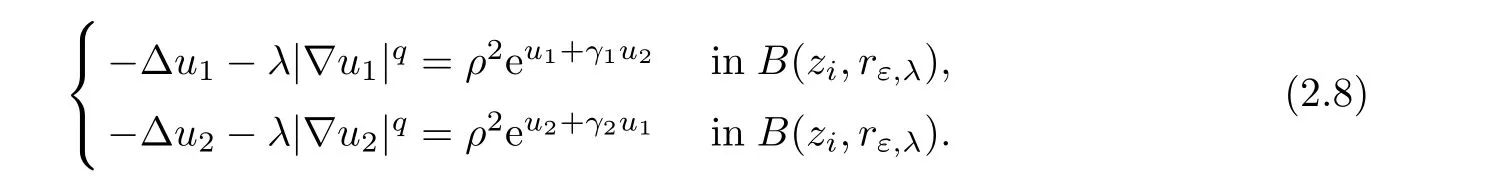
Using the transformation
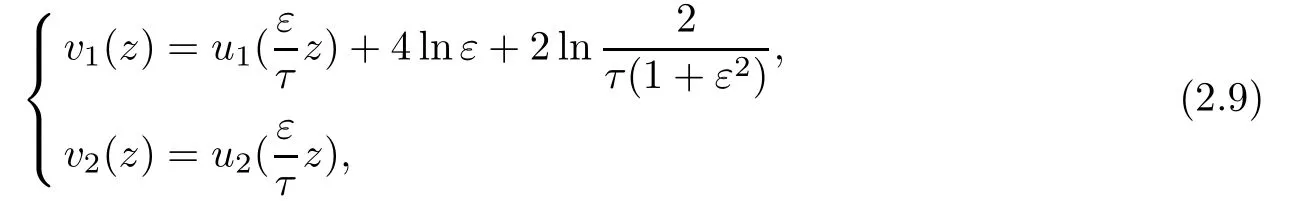
the previous system can be written as
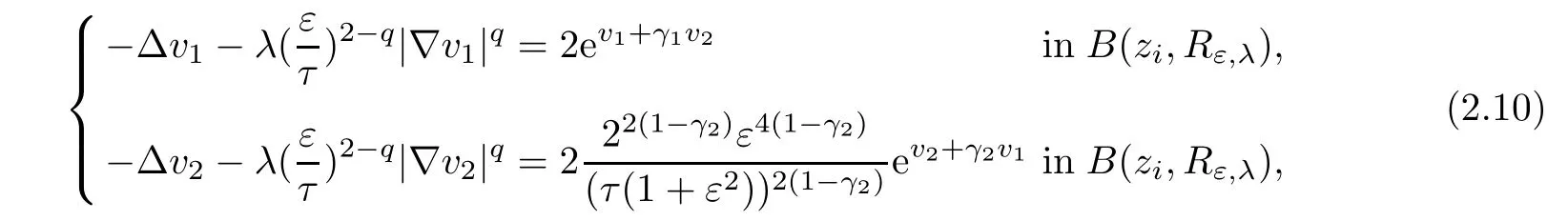
here τ>0 is a constant which will be fixed later.
We denote by u=uε=τ=1,we look for a solution of(2.10)of the form
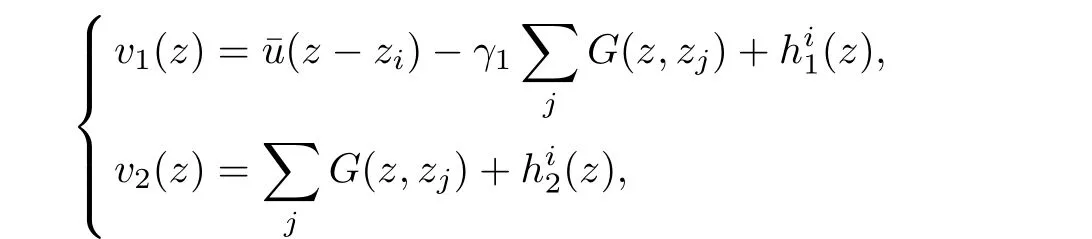
this amounts to solve the equation
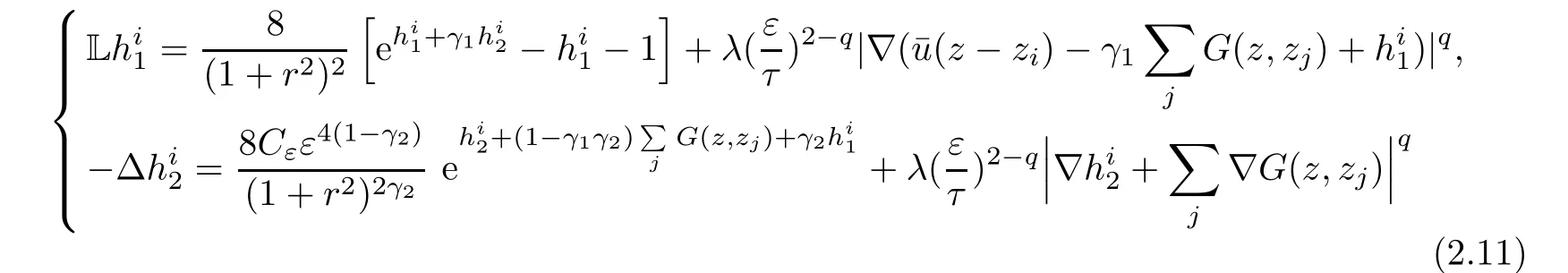
in B(zi,Rε,λ),where Cε=[τ(1+ ε2)]2(γ2?1).
For q∈ [1,2),we fixμ ∈ (1,3?q)and δ∈ (0,min{1,2(1?γ1),2(1?γ2),2?q}).To find a solution of(2.11),it is enough to find a fixed pointin a small ball ofsolutions of
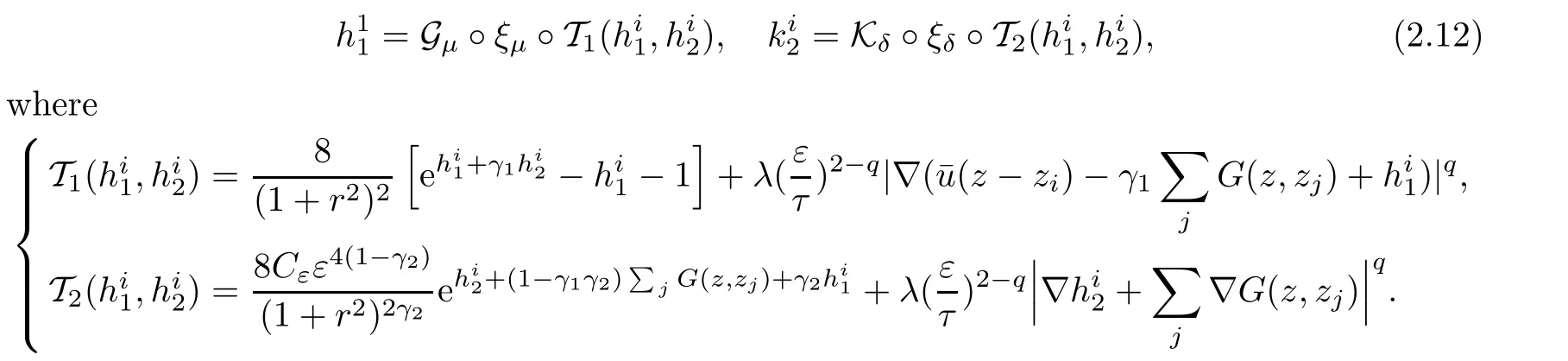
We denote by N(=Nε,τ)and M(=Mε,τ)the nonlinear operators appearing on the right hand side of equation(2.12).
Lemma 2.6 Given κ >0,there exists εκ>0 and cκ>0 such that for all ε∈ (0,εκ),μ ∈ (1,3?q)and δ∈ (0,min{1,2(1?γ1),2(1?γ2),2?q}),

Making use of Proposition 2.2 together with(2.7),forμ∈(1,3?q),we get that there exists cκsuch that

For the second estimate,we have
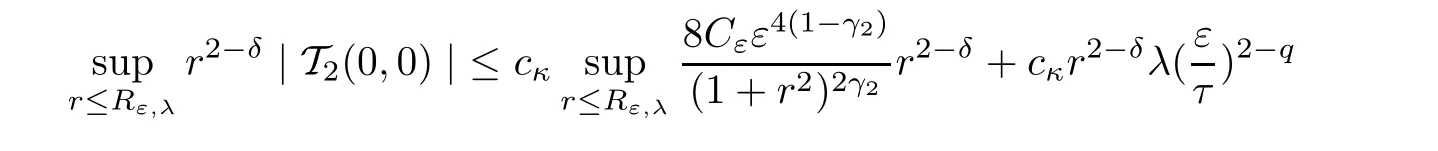

Using the same argument as above,we get
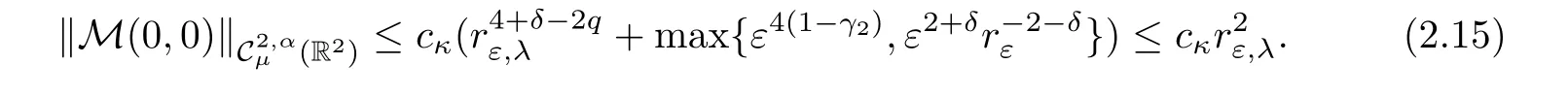
Now,we recall an important result that plays a center role in our estimates. ?
Lemma 2.7 Given x and y two real numbers,x>0,q≥ 1 and for all small η >0,there exists a positive constant Cηsuch that
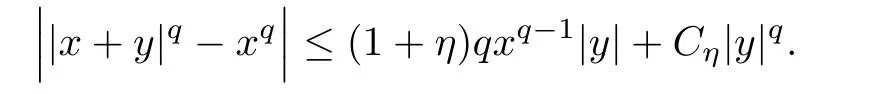
Now,to derive the third estimate,for hi,ki,i=1,2,verifying(2.28),we have
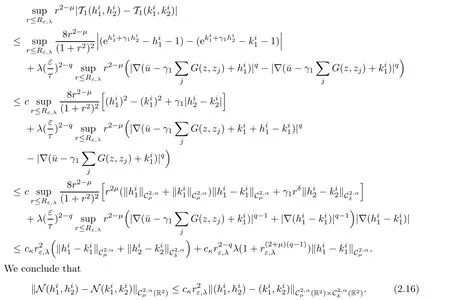
Similarly we get the estimate for
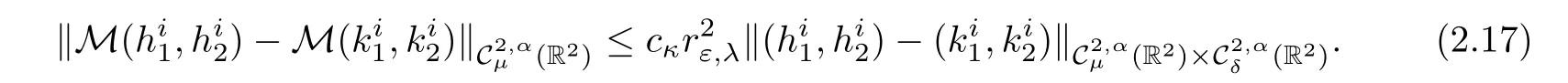
Reducing εκif necessary,we can assume thator all ε ∈ (0,εκ).Therefore(2.14),(2.15),(2.16)and(2.17)are enough to show that
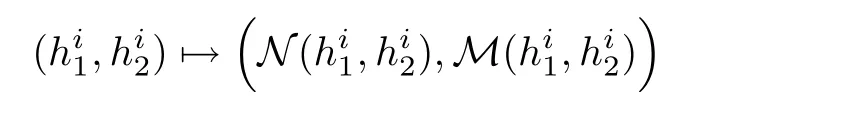
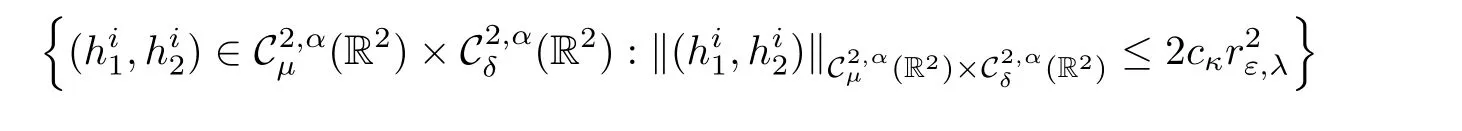
is a contraction from the ball into itself and hence a unique fixed pointexists in this set,which is a solution of(2.12).That is
Proposition 2.8 Given κ >0,there exist εκ>0 and cκ>0 such that for all ε∈ (0,εκ)for i∈ {1,···,p},there exists a uniquesolution of(2.25)such that
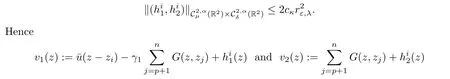
solves(2.8)in BRε,λ(zi).
Similarly,we get also
Proposition 2.9 Given κ >0,there exist εκ>0 and cκ>0 such that for any ε∈ (0,εκ),for j ∈ {p+1,···,n}there exists a uniquesolution of(2.25)verifying
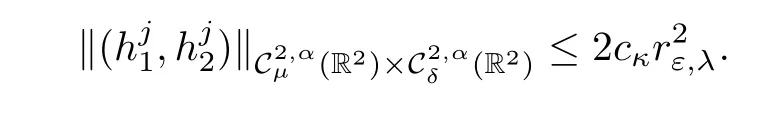
Hence
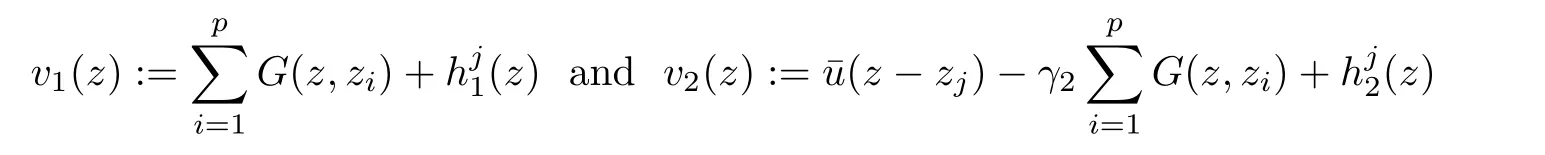
solves(2.8)in BRε,λ(zj).
2.1.3 Harmonic Extensions
Next,we will study the properties of interior and exterior harmonic extensions.Givenwe define respectivelyto be the solution of
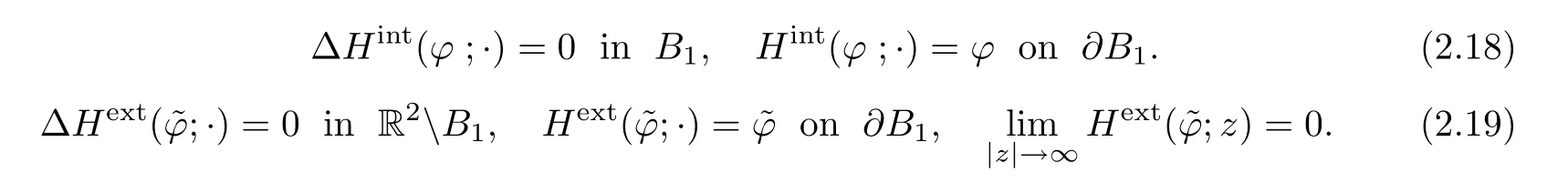
We will use also
Definition 2.10 Given k ∈ N,α ∈ (0,1)and ν ∈ R,letas the space of functions w∈for which the following norm
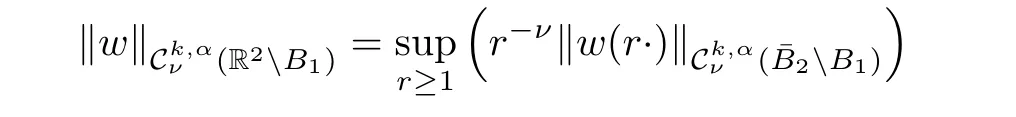
is finite.
We denote by e1(θ)=cosθ,e2(θ)=sinθ.
Lemma 2.11(see[3]) There exists c>0 such that,for any
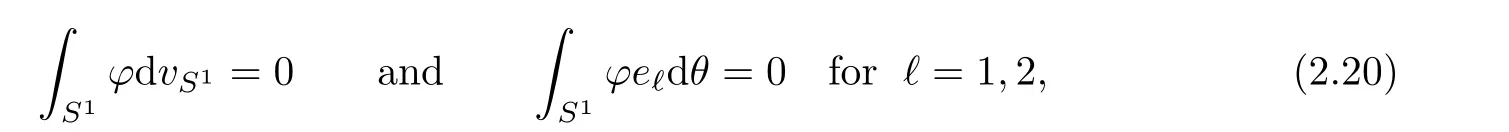
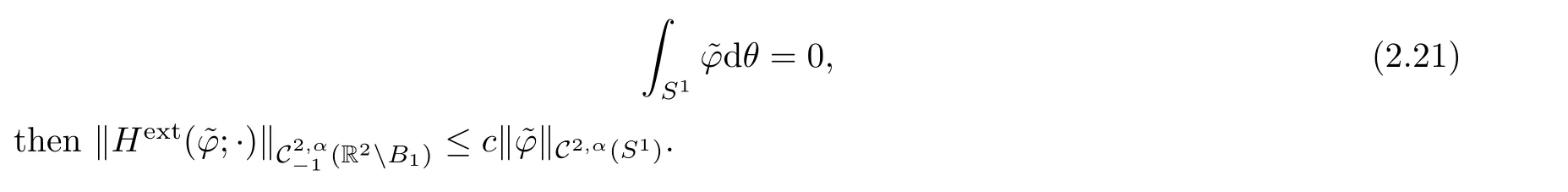
If F?L2(S1)be a subspace,we denote F⊥to be the subspace of F which are L2(S1)-orthogonal to e1,e2.We will need the following result:
Lemma 2.12(see[3]) The mapping P:C2,α(S1)⊥→ C1,α(S1)⊥defined by
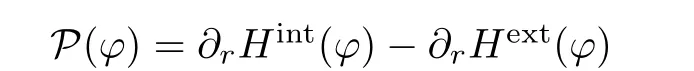
is an isomorphism.
2.2 The Nonlinear Interior Problem
Here,we are interested in the study of system(1.1)near zi.
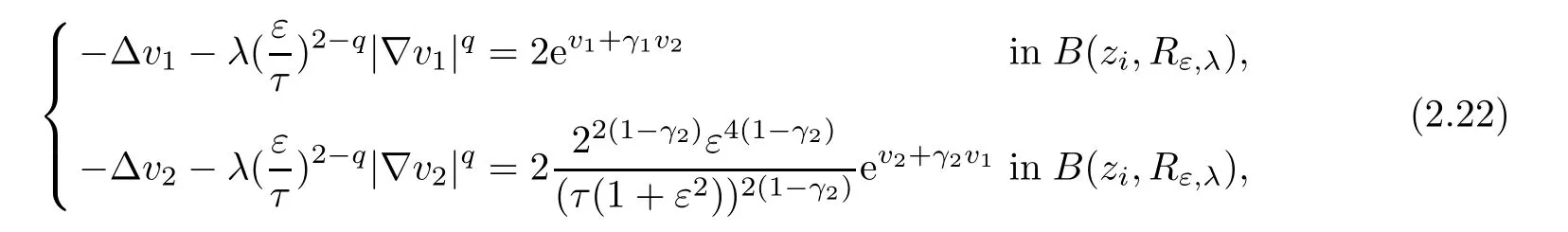
here τ>0 is a constant which will be fixed later.
Given ?1:=∈(C2,α(S1))2satisfying(2.20).We denote byu=uε=τ=1and write
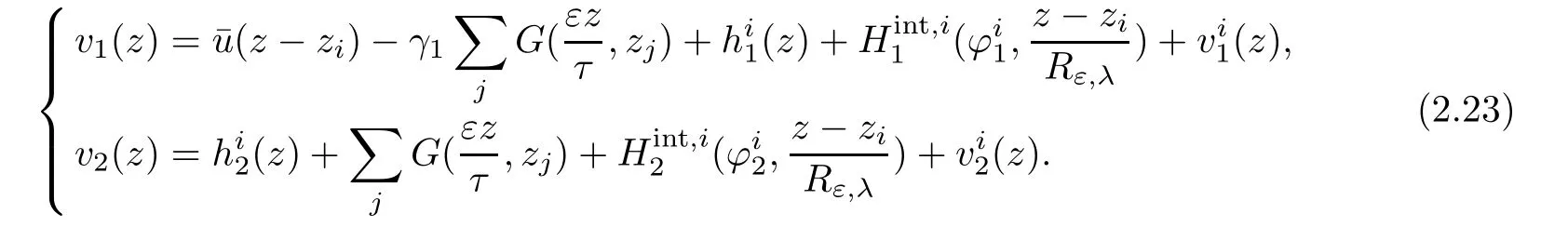
Using the fact that Hintis harmonic and the fact that 2eu=,this amounts to solve the equation
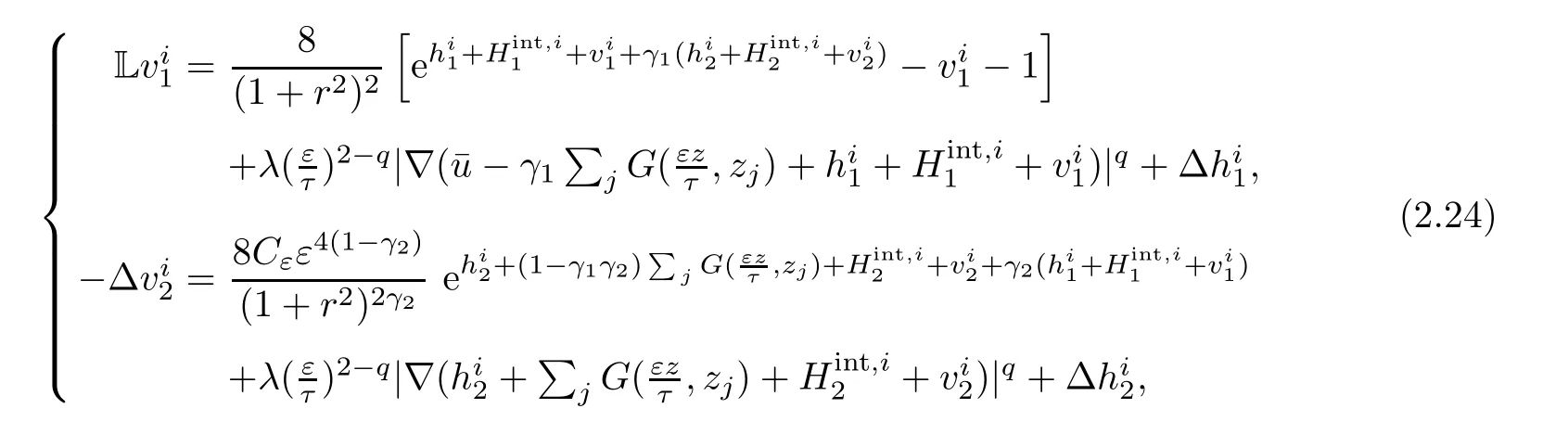
where Cε=[τ(1+ ε2)]2(γ2?1).
Fix μ ∈ (1,3?q)and δ∈ (0,min{1,2(1?γ1),2(1?γ2),2?q}).To find a solution of(2.24),it is enough to find a fixed pointin a small ball ofsolutions of
here ξσis defined in(2.6),Kδ,Gμare defined after Propositions 2.2 and 2.3,and
We denote by ?(= ?ε,τ,?1j)and Υ(= Υε,τ,?1j)the nonlinear operators appearing on the right hand side of the equation(2.25).
Given κ>0(whose value will be fixed later on),we further assume that the functionssatisfy
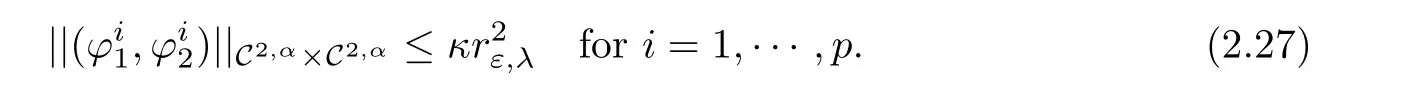
Then we have the following result
Lemma 2.13 Given κ >0,there exist εκ>0 and cκ>0 such that for all ε∈ (0,εκ),μ ∈ (1,3?q)and δ∈ (0,min{1,2(1?γ1),2(1?γ2),2?q}),
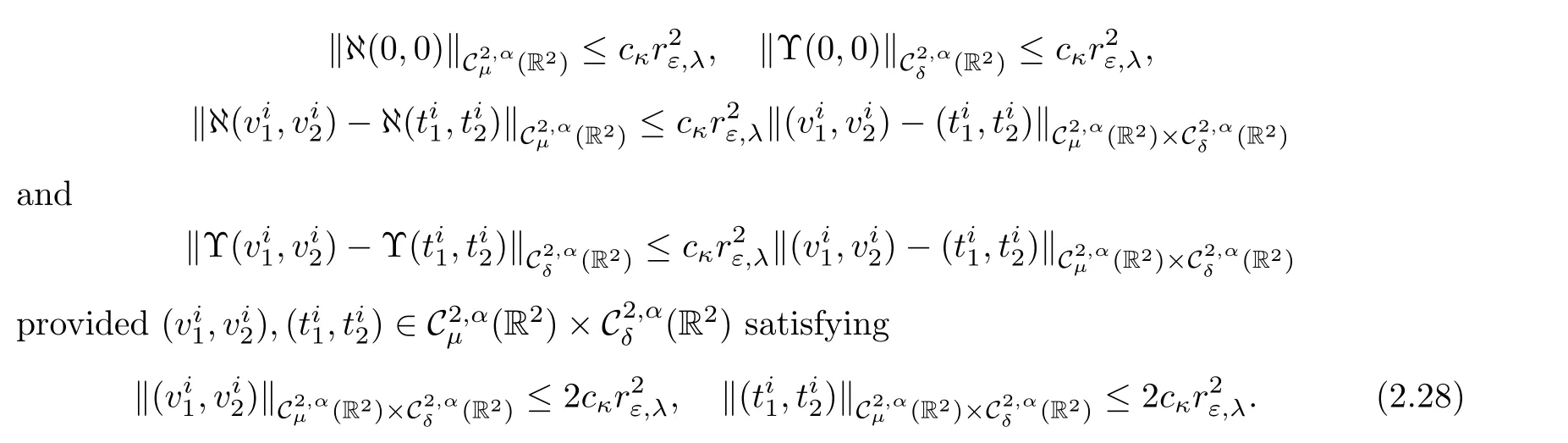
Proof The first estimate follows from Lemma 2.11 together with the assumption on the norms of ?j,we have
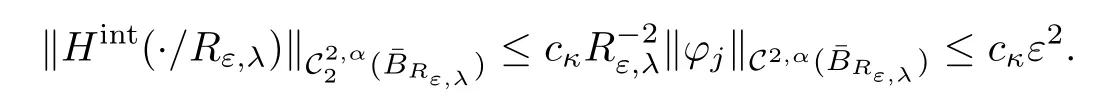
On the other hand,
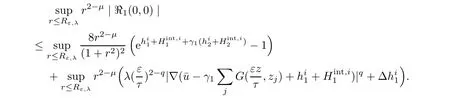
Making use of Corollary 2.2 together with(2.7),forμ∈(1,3?q),we get that there exists cκsuch that

For the second estimate,we have
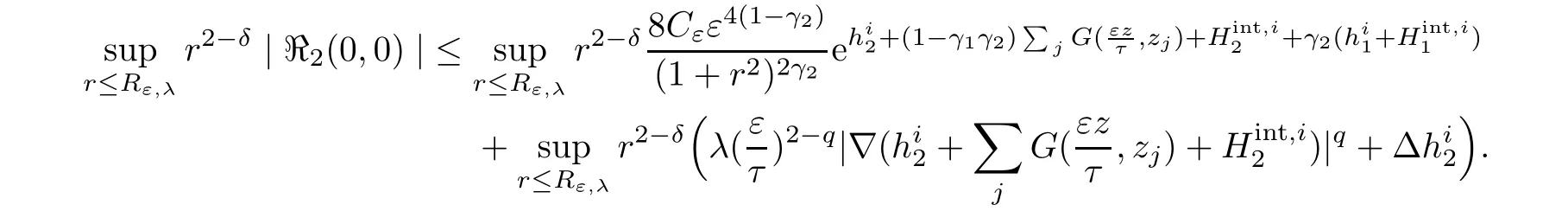
Using the same argument as above,we get

To derive the third estimate,forverifying(2.28),we have
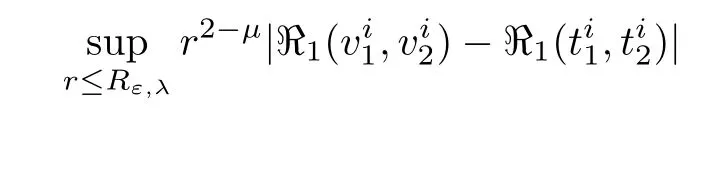
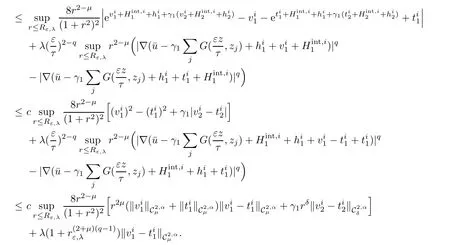
We conclude that
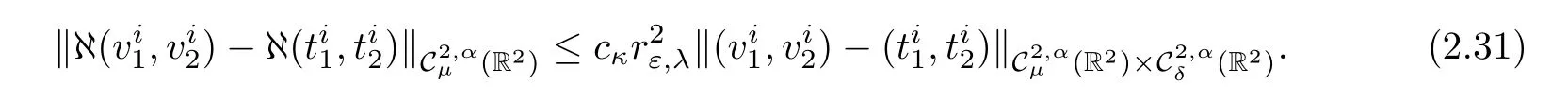
Similarly we get the estimate for

Reducing εκif necessary,we can assume thatfor all ε∈(0,εκ).Therefore(2.29),(2.30),(2.31)and(2.32)and are enough to show that for i∈ {1,···,p},
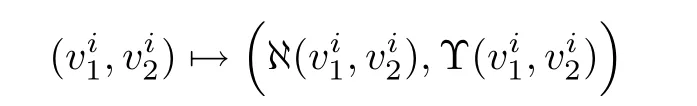
is a contraction from the ball
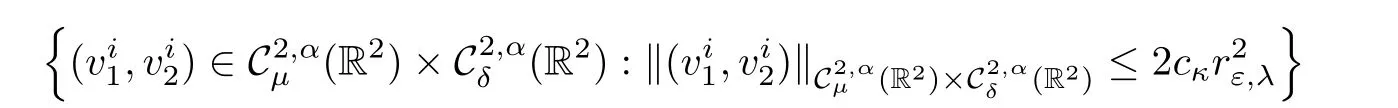
into itself and hence a unique fixed pointexists in this set,which is a solution of(2.25).That is,for i∈ {1,···,p}.
Proposition 2.14 Given κ >0,there exists εκ>0 and cκ>0 such that for all ε∈ (0,εκ)for all? (0,∞)and for a given ?isatisfying(2.20)and(2.27),there exists a unique,i∈ {1,···,p}solution of(2.25)such that
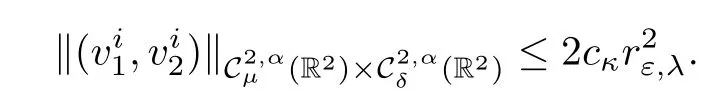
Hence
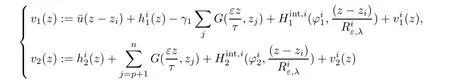
solves(2.8)in BRε,λ(zi).
Similarly,for j ∈ {p+1,···,n},we get also
Proposition 2.15Given κ>0 and τj∈[τ?j,τ+j]?(0,∞),there exist εκ>0 and cκ>0 such that for any ε∈ (0,εκ),any ?jsatisfying(2.20)and(2.27),there exists a uniquesolution of(2.25)such that
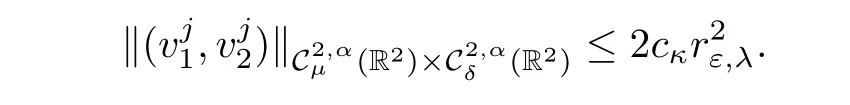
Hence
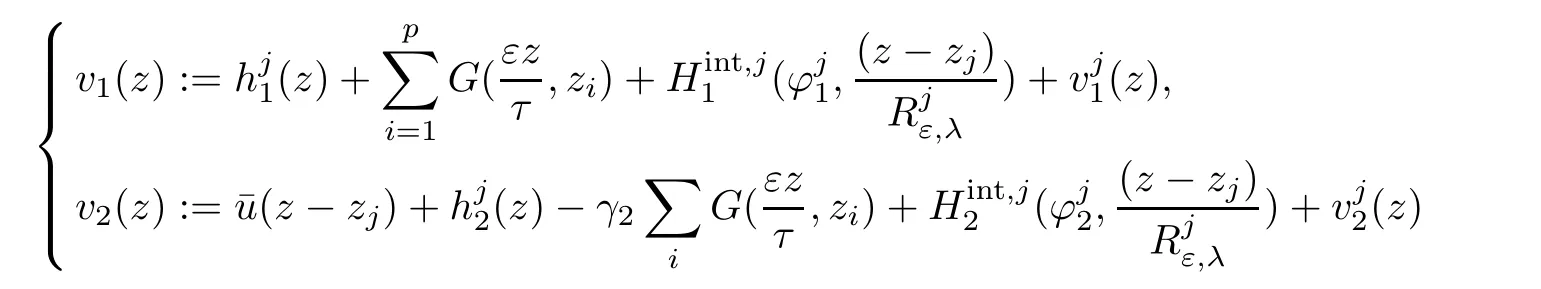
solves(2.8)in BRε,λ(zj).
Remark also that the functionsandfor i∈ {1,···,p}and j ∈ {p+1,···,n},obtained in the above Proposition,depend continuously on the parameter τ.
2.3 The Nonlinear Exterior Problem
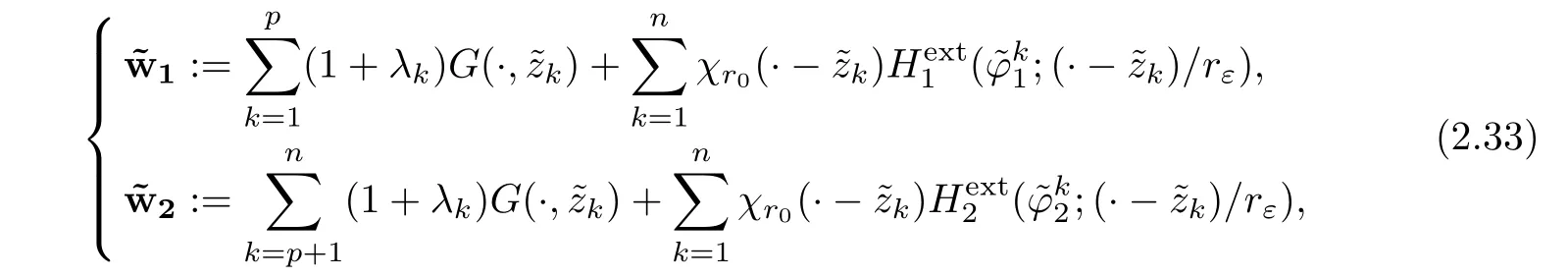
where χr0is a cut-off function identically equal to 1 in Br0/2and identically equal to 0 outside Br0.We would like to find a solution of the system
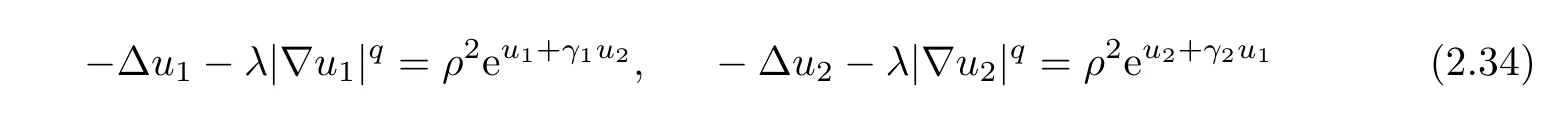
This amounts to solve in ?rε(z)
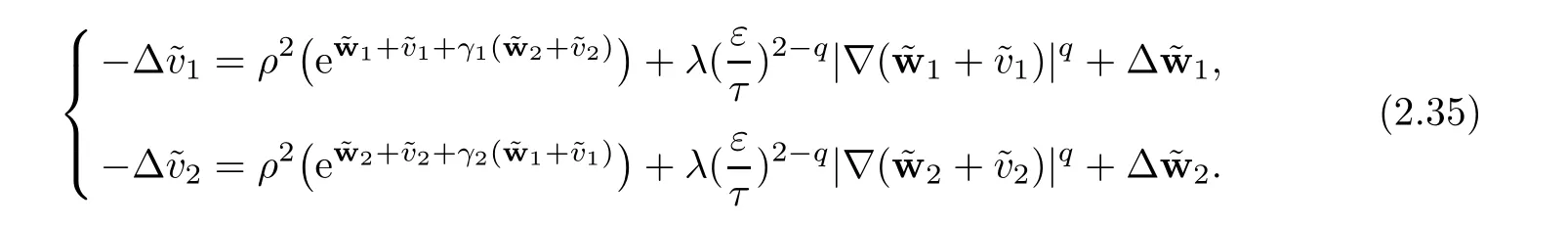
For all σ∈(0,r0/2)and all Y=(y1,y2)∈?2such that kZ?Y k≤r0/2,where Z=(zi,zj),we denote bythe extension operator defined by
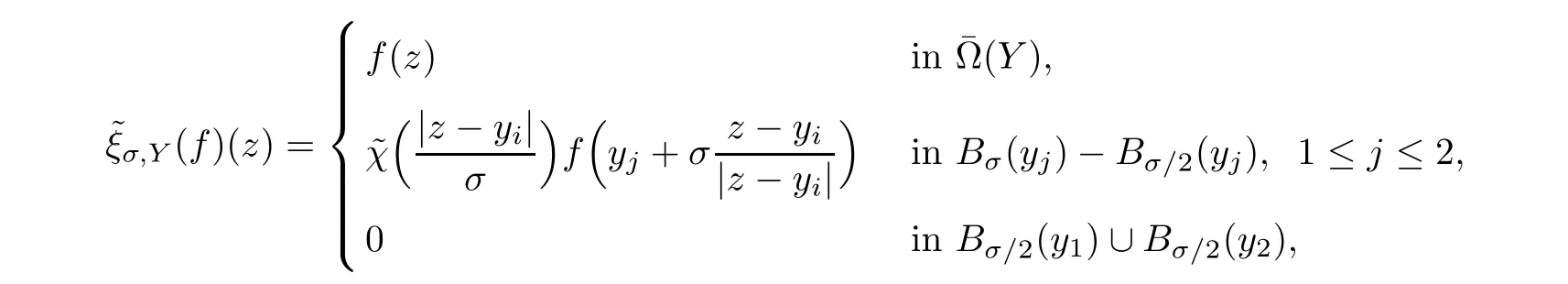
hereχ is a cut-off function over R+which is equal to 1 for t≥1 and equal to 0 for t≤1/2.Obviously,there exists a constant c= c(ν)>0 only depending on ν,such that
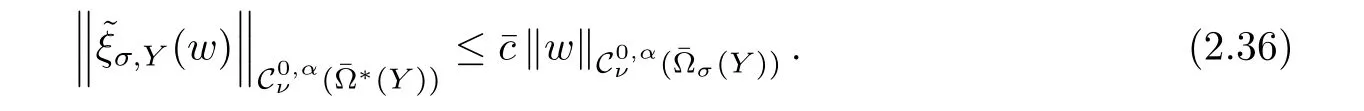
We fix ν ∈(?1,0),to solve(2.35),it is enough to findsolution of
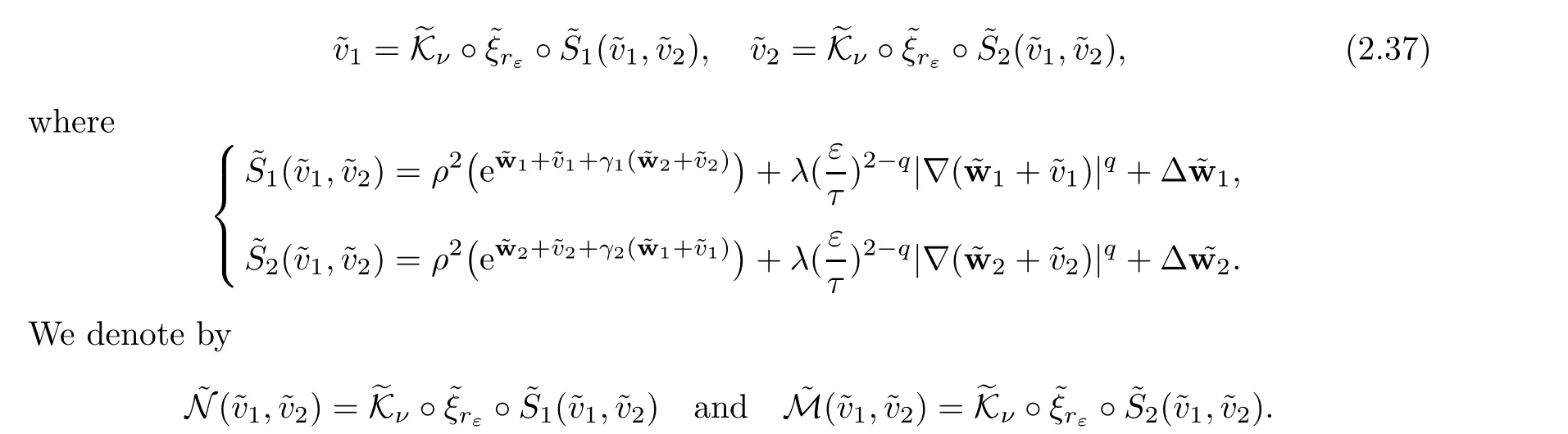
Given κ >0(whose value will be fixed later on),assume that for k ∈ {1,···,n},the functionsthe parameters λkand the pointz=(z1,···,zk)satisfy
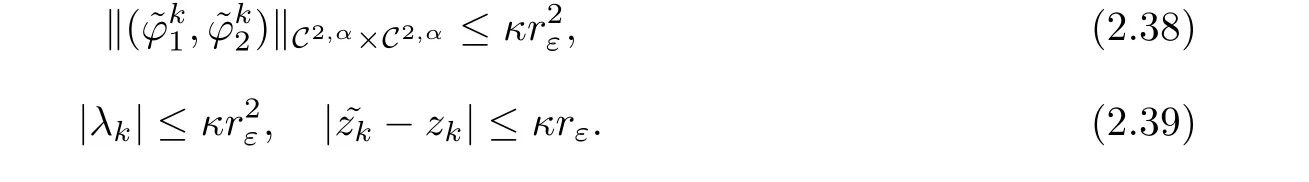
Then the following result holds
Lemma 2.16 Under the above assumptions,there exists a constant cκ>0 such that
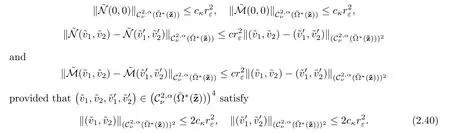
Proof As for the interior problem,the two first estimates follows from the asymptotic behavior of Hexttogether with the assumption on the norm of the boundary data?k1,?k2given by(2.38).Indeed,let cκdenote a constant depending only on κ,by Lemma 1,
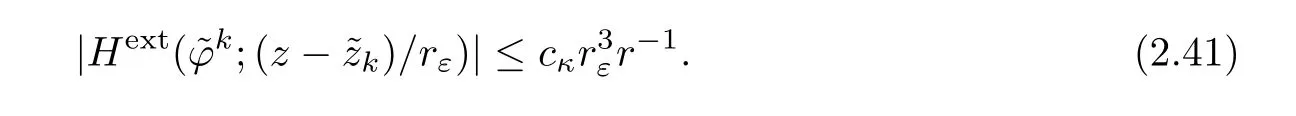
On the other hand,
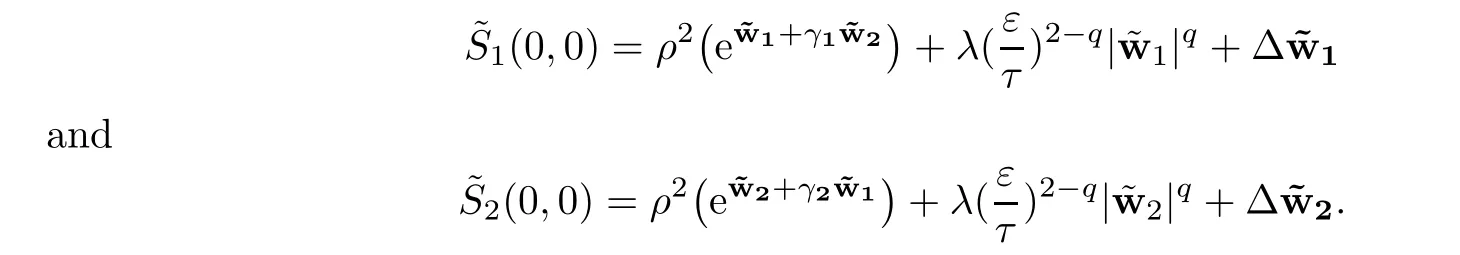
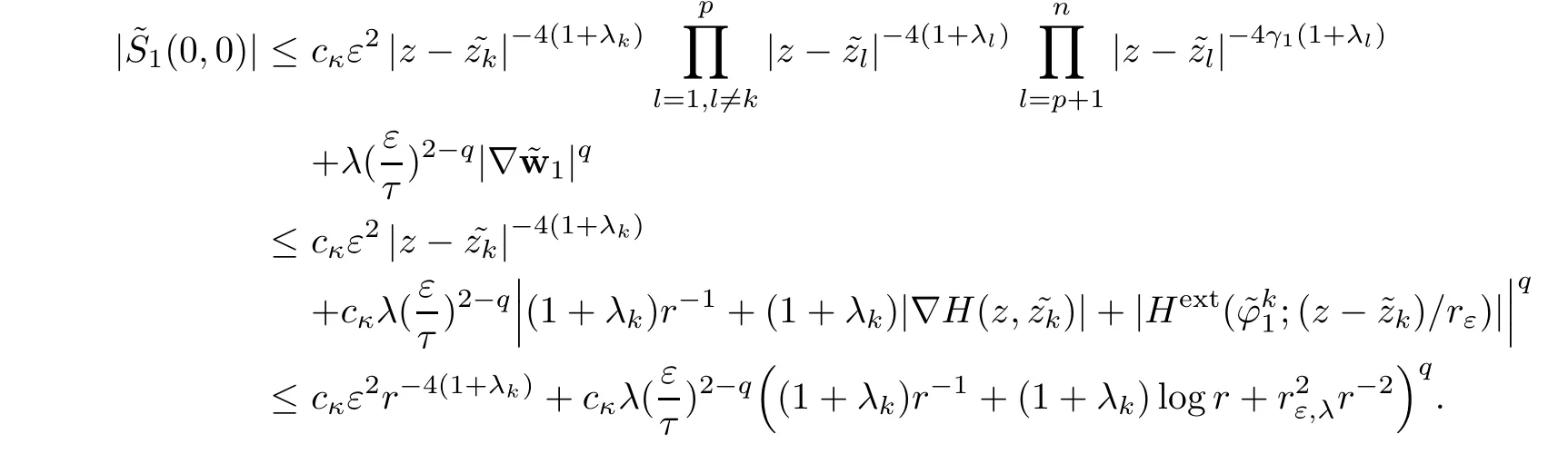
Hence for ν ∈ (?1,0)and λk,k=1,···,p small enough,we get

where[?,χr0]w= ?wχr0+w?χr0+2?w.?χr0.Hence,for ν ∈ (?1,0)and λ1small enough,we get
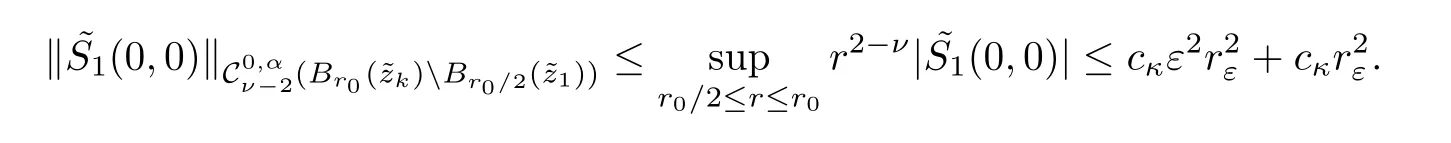
?Similarly,for k∈{p+1,···,n}we can prove that inand λ2small enough,we haveMaking use of Proposition 2.5 together with(2.36)we conclude that
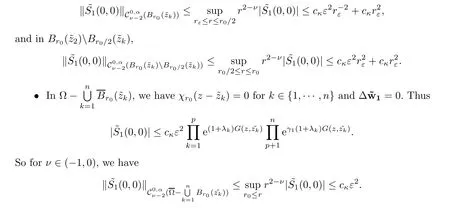
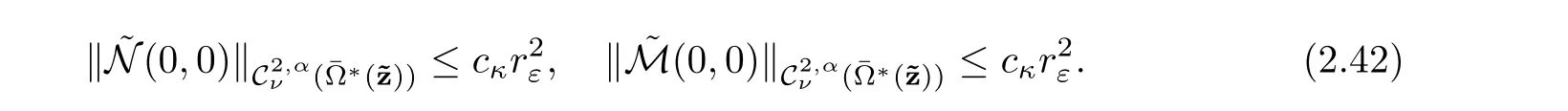
For the proof of the third estimate,letsatisfy(2.40),using Lemma 2.7,we have
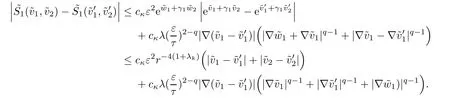
Then for λksmall enough,k ∈ {1,···,n},using estimate(2.36),there exist cκ(depending on κ)such that
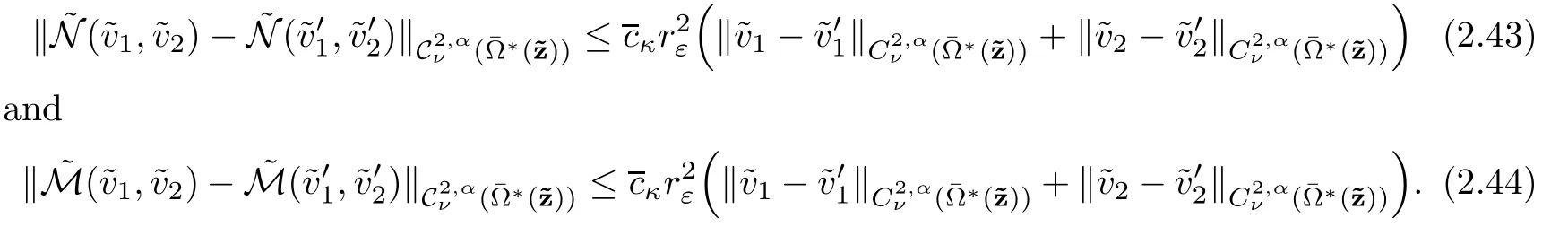
The proof is completed.
Reducing εκif necessary,we can assume thatThen,(2.43)and(2.44)are enough to show that
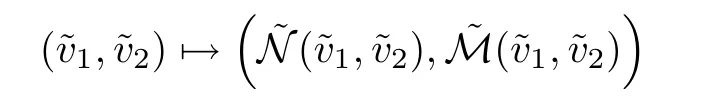
is a contraction from the ball
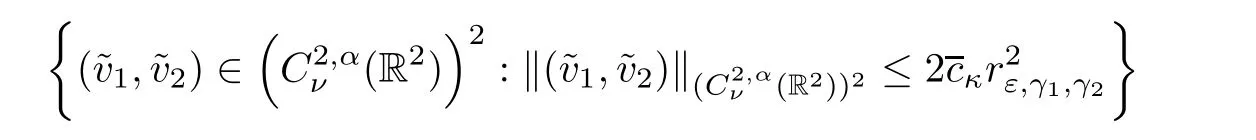
into itself.Hence there exist a unique fixed point(v1,v2)in this set,which is a solution of(2.37).We conclude then
Proposition 2.17 Given κ >0,there exists εκ>0(depending on κ)such that for any ε∈(0,εκ);λkandzksatisfying(2.39);any functionsandsatisfying(2.21)and(2.38),there exists a uniquesolution of(2.37)so that for(v1,v2)defined by
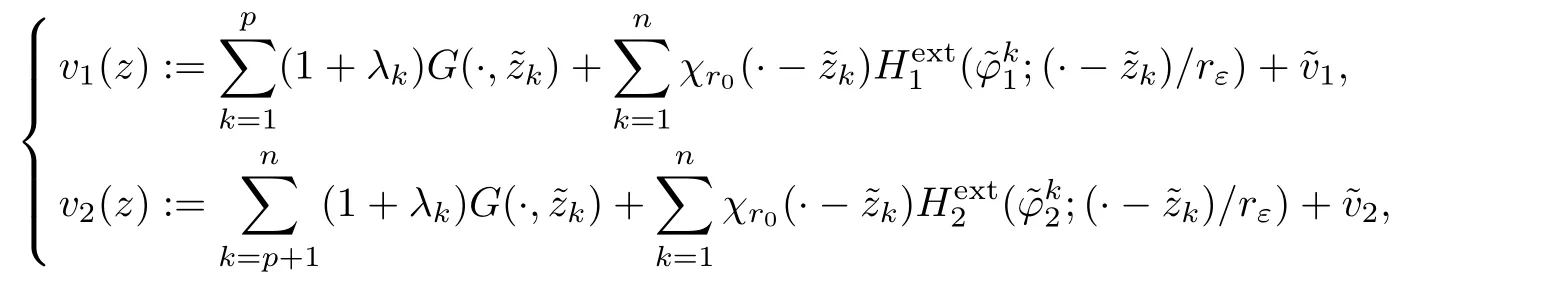
solve(2.34)in ?rε(z).In addition,we ha ve
2.4 The Nonlinear Cauchy-Data Matching
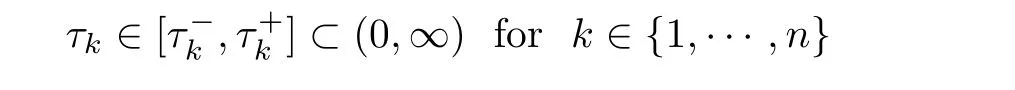
We will gather the results of previous sections.Using the previous notations,assume thatare given close to z:=(z1,···,zn).Assume also that are given(the values ofandwill be fixed later).First,we consider some set of boundary datAccording to the result of Proposition 2.15 and provided ε∈ (0,εκ),we can find,solution of
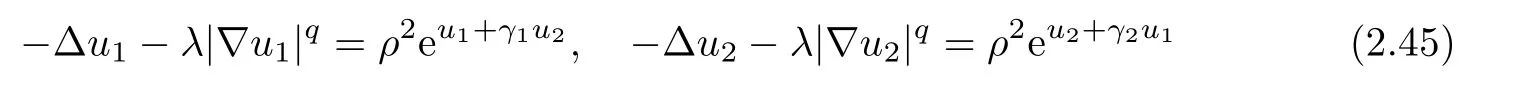
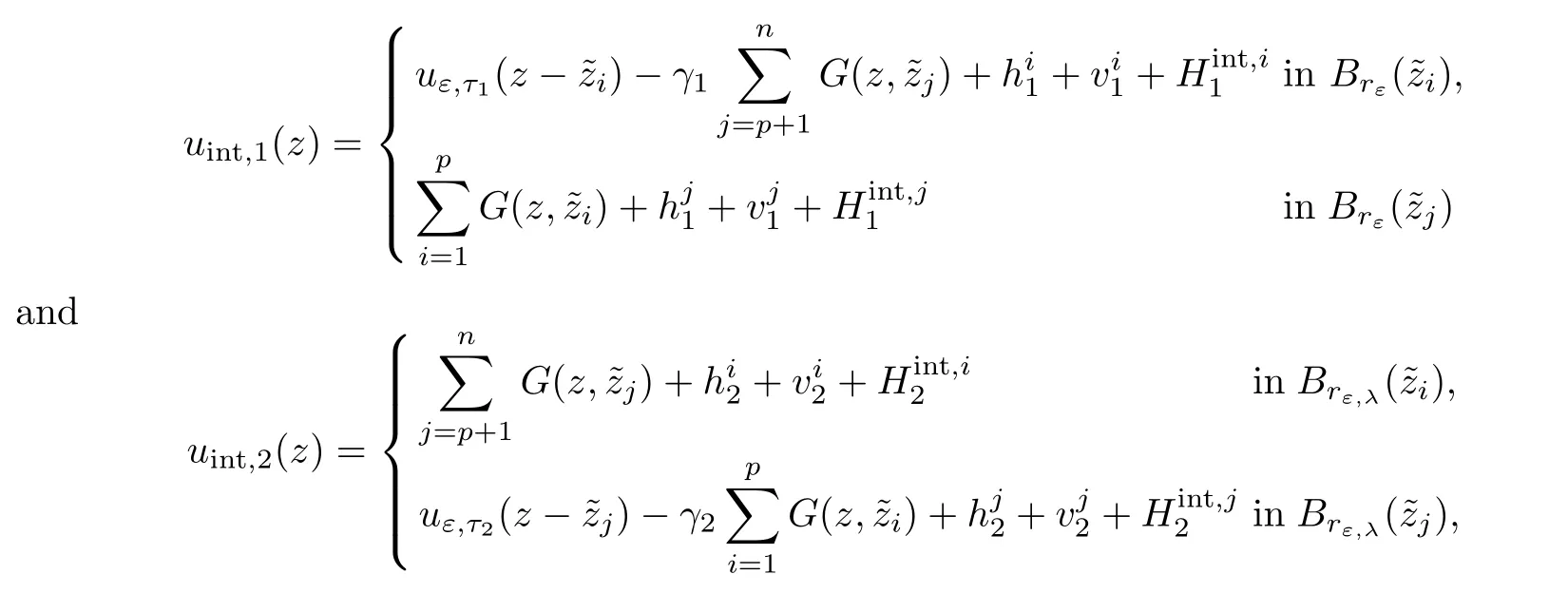
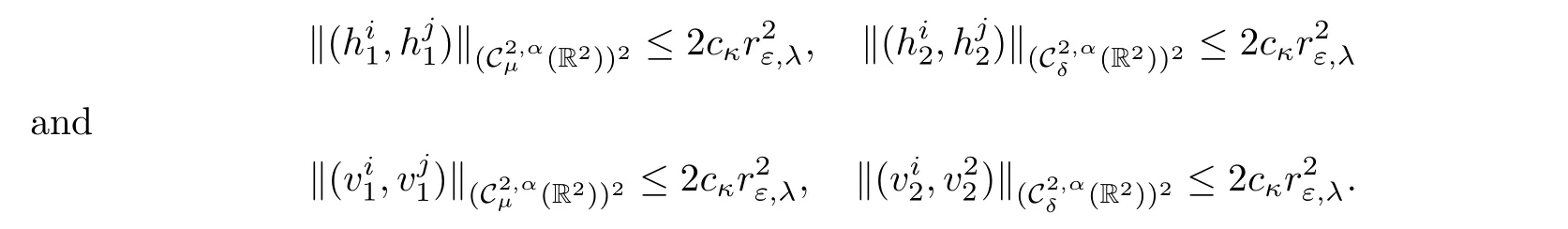
Similarly,for k∈{1,···,n},given boundary datasatisfying(2.21),λk∈R satisfying(2.39),provided ε ∈ (0,εκ),by Proposition 2.17,we find a solution uext:=which can be decomposed as
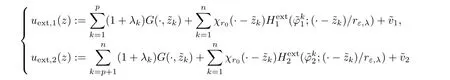
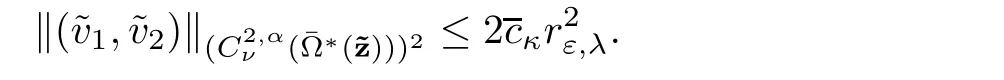
It remains to determine the parameters and the boundary data in such a way that the function equal toand equal tois a smooth function.This amounts to find the boundary data and the parameters so that for l=1,2,
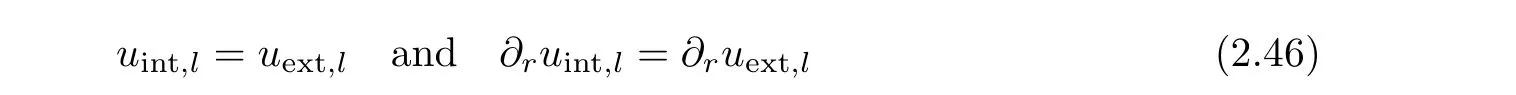
on?Brε,λ),k∈{1,···,n}.
Suppose that(2.46)is verified,this provides that for each ε small enough,uε∈ C2,α(which is obtained by patching together the functions uintand the function uext),a weak solution of our system and elliptic regularity theory implies then this solution is in fact smooth.That will complete our proof since,as ε and λ tend to 0,the sequence of solutions we obtain satisfies the required singular limit behaviors,namely,uε,λconverges to G(·,zk).
Before we proceed,the following remarks are due.First it will be convenient to observe that the function uε,τkcan be expanded as,for k ∈ {1,···,n},

? Thus,for z on ?Brε,λ(zi),i∈ {1,···,p},we have
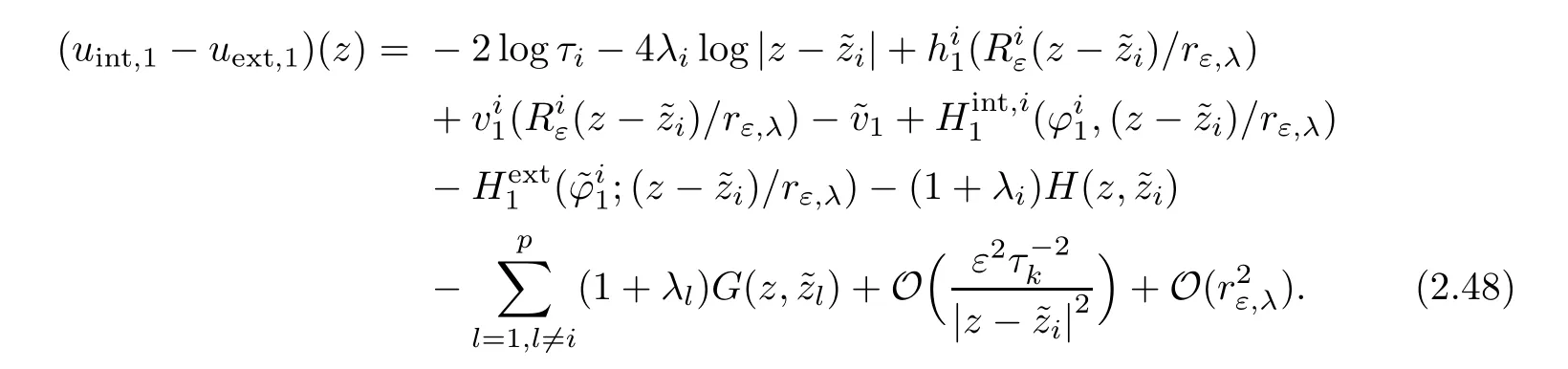
Next,even though all functions are defined on?Brε,λ(zi)in(2.46),it will be more convenient to solve on S1the following set of equations
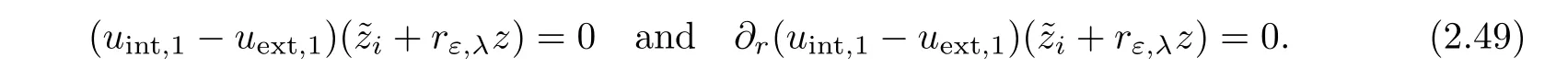
Indeed,all functions as considered as functions of z∈S1and we have simply used the change of variables y=zi+rε,λz to parameterize?Brε,λ(zi).
Since the boundary data are chosen to satisfy(2.21)or(2.20).We decompose
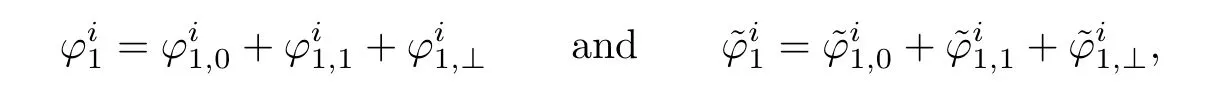
Using(2.48)and the fact that
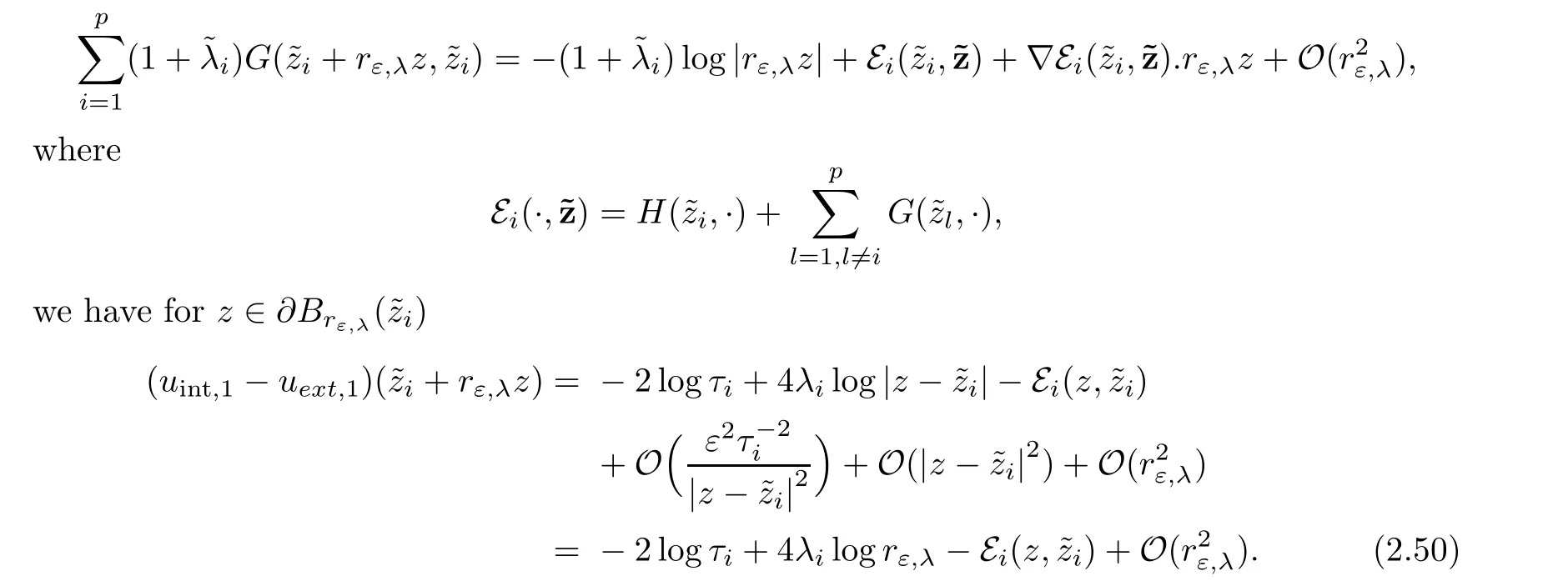
Then,the projection of the equations(2.49)over E0will yield
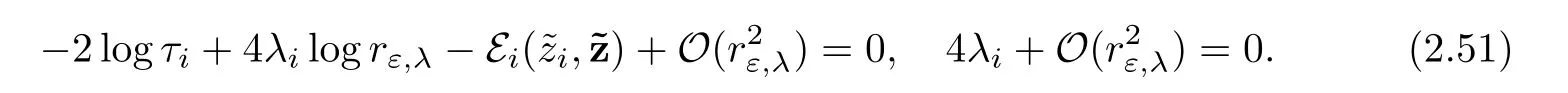
System(2.51)can be simply written as
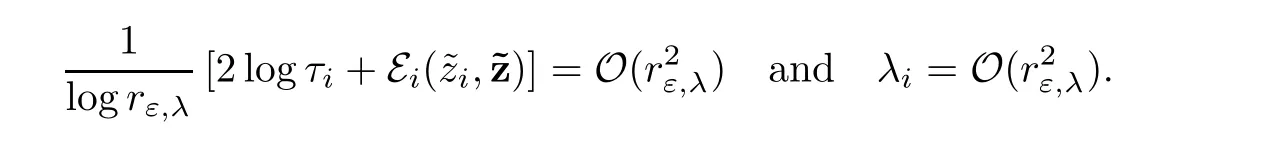
We are now in a position to defineand,i ∈ {1,···,p}.In fact,according to the above analysis,as ε and λ tend to 0,we expect thatziwill converge to zifor i∈{1,···,p}and τiwill converge tosatisfying
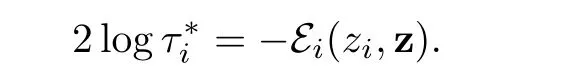
Hence it is enough to chooseandin such a way that
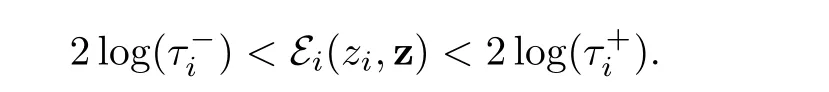
Consider now the projection of(2.49)over E1.Given a smooth function f defined in ?,we identify its gradient?f=(?x1f,?x2f)with the element of E1,
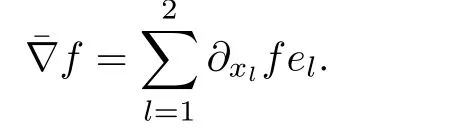
With these notations in mind,we obtain the system
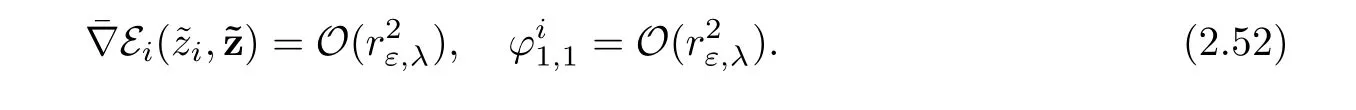
Finally,we consider the projection onto(L2(S1))⊥.This yields the system
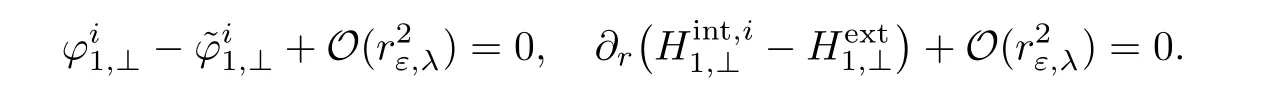
Thanks to Lemma 2.12,this last system can be rewritten as
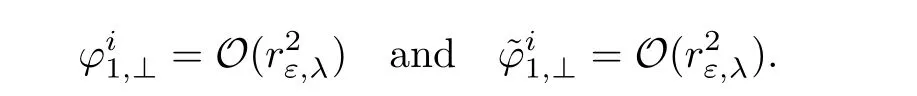
If we define,for i∈ {1,···,p},the parameters ti∈ R by
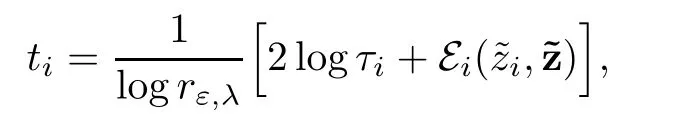
then the system we have to solve reads
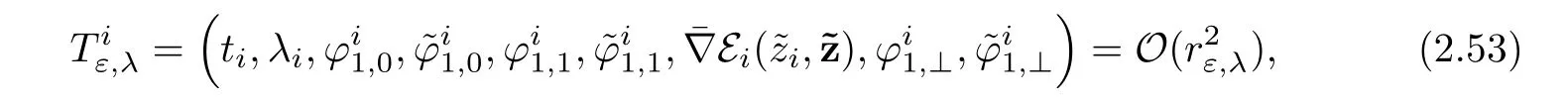
?Similarly,for j∈{p+1,···,n}when ε tends to 0,we expect thatconverges to zjand τjconverges tosatisfying
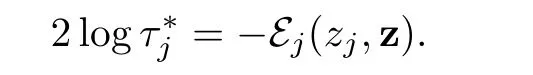
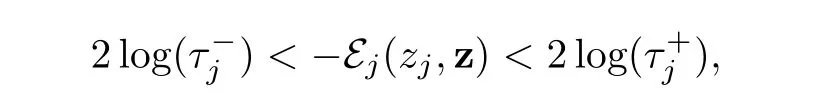
where
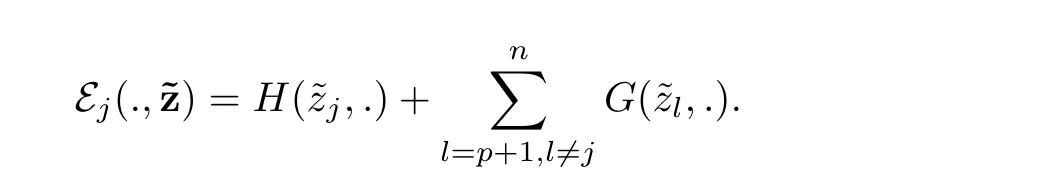
Using the decomposition E0⊕E1⊕(L2(S1))⊥,
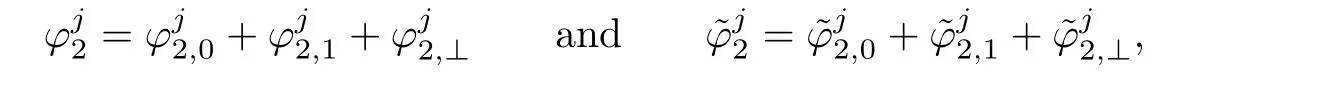
we can prove that
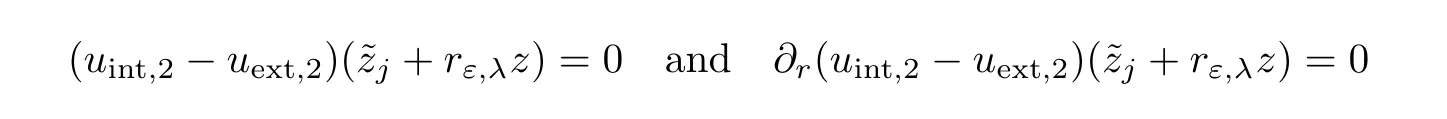
on?Brε(zj)yield to
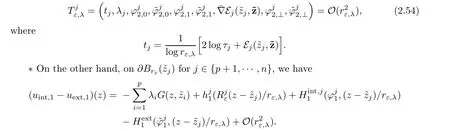
As above,we will solve on S1the following system:
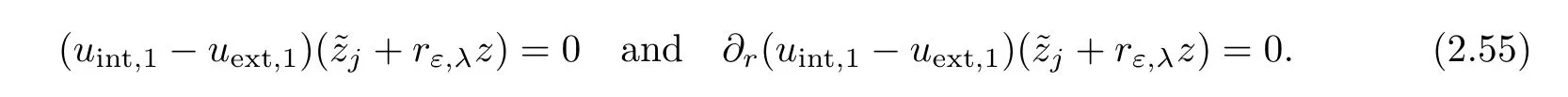
We decompose
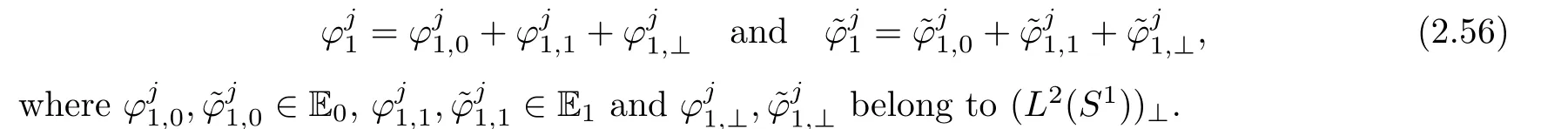
Projecting the set of equations(2.55)over E0,we get.From the L2-projection of(2.55)over E1,we obtain the equationFinally,the L2-projection onto(L2(S1))⊥yields
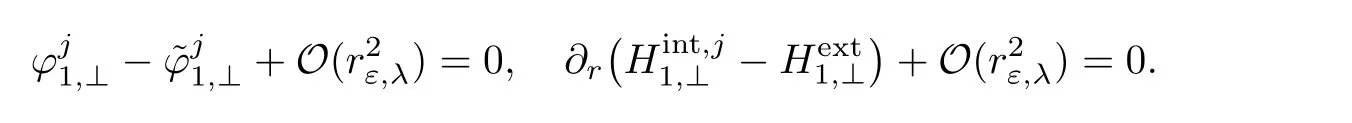
Using again Lemma 2.12,the above system can be rewritten as
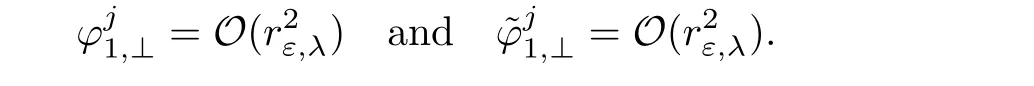
Then the system we have to solve reads
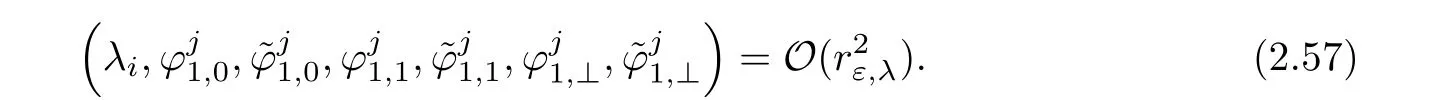
By exactly the same arguments for(2.53),we can claim a solution of equation(2.57)in the ball of radiusof the corresponding product space.
? Similarly,for i∈ {1,···,p},using the fact that
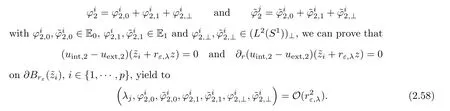
Finally,recall that x=rε,λ(z ? z),in addition the previous systems can be written as
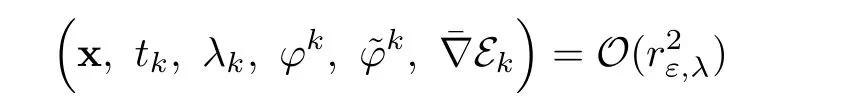
for k ∈ {1,···,n}.Combining(2.53)and(2.54),we have for i ∈ {1,···,n}and j ∈ {p+1,···,n},
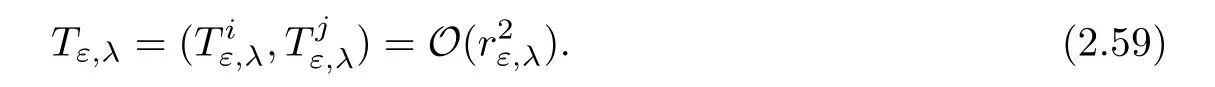
Then the nonlinear mapping which appears on the right hand side of(2.59)is continuous,compact.In addition,reducing εκif necessary,this nonlinear mapping sends the ball of radius(for the natural product norm)into itself,provided κ is fixed large enough.Applying Schauder’s fixed point Theorem in the ball of radiusin the product space where the entries live,we obtain the existence of a solution of equation(2.59).
Remark 2.18 In order to inverse problem(2.53)and(2.54),we remark that the fact that zkis a nondegenerate critical point of Ek(.,z),k ∈ {1,···,n}is equivalent to say that(z1,···,zn)is a nondegenerate critical point of the function F defined by
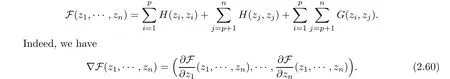
On the other hand,for i∈ {1,···,p}and j ∈ {p+1,···,n},we have
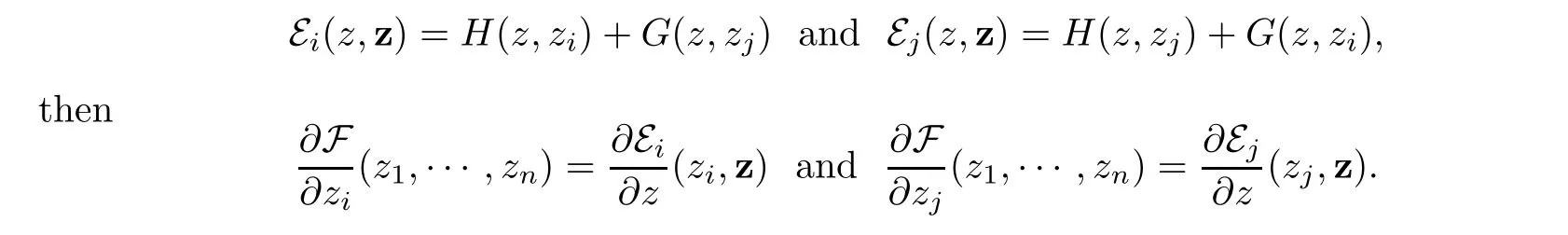
 Acta Mathematica Scientia(English Series)2018年4期
Acta Mathematica Scientia(English Series)2018年4期
- Acta Mathematica Scientia(English Series)的其它文章
- WEIGHTED COMPOSITION OPERATORS ON THE HILBERT SPACE OF DIRICHLET SERIES?
- GENERALIZED DISCRETE Q-HERMITE I POLYNOMIALS AND Q-DEFORMED OSCILLATOR?
- ON THE FINITE MELLIN TRANSFORM IN QUANTUM CALCULUS AND APPLICATION?
- PULLBACK EXPONENTIAL ATTRACTORS FOR THE NON-AUTONOMOUS MICROPOLAR FLUID FLOWS?
- OPTIMAL ERROR ESTIMATES OF A DECOUPLED SCHEME BASED ON TWO-GRID FINITE ELEMENT FOR MIXED NAVIER-STOKES/DARCY MODEL?
- PARAMETER IDENTIFICATION BY OPTIMIZATION METHOD FOR A POLLUTION PROBLEM IN POROUS MEDIA?
