ON ENTIRE SOLUTIONS OF SOME TYPE OF NONLINEAR DIFFERENCE EQUATIONS?
Huifang LIU(劉慧芳)
College of Mathematics and Information Science,Jiangxi Normal University,Nanchang 330022,China
E-mail:liuhuifang73@sina.com
Zhiqiang MAO(毛志強(qiáng))
School of Mathematics and Computer,Jiangxi Science and Technology Normal University,Nanchang 330038,China
E-mail:maozhiqiang1@sina.com
Abstract In this article,the existence of finite order entire solutions of nonlinear difference equationsare studied,where n ≥ 2 is an integer,Pd(z,f)is a difference polynomial in f of degree d(≤ n?2),p1,p2are small meromorphic functions of ez,and α1,α2are nonzero constants.Some necessary conditions are given to guarantee that the above equation has an entire solution of finite order.As its applications,we also find some type of nonlinear difference equations having no finite order entire solutions.
Key words Nevanlinna theory;difference polynomial;difference equation;entire solution
1 Introduction and Main Results
Let f be a meromorphic function in the complex plane C.It is assumed that the reader is familiar with the standard notations and basic results of Nevanlinna’s value distribution theory of meromorphic functions,such as m(r,f),N(r,f),T(r,f)etc.;see,for example,[1,2].The notation S(r,f)is defined to be any quantity satisfying S(r,f)=o(T(r,f))as r→∞,possibly outside a set E of r of finite logarithmic measure.A meromorphic function α is said to be a small function of f provided that T(r,α)=S(r,f).In general,a difference polynomial,or a differential-difference polynomial in f is defined to be a finite sum of difference products of f and its shifts f(z+cj),(cj∈C,j∈I),or of products of f,derivatives of f,and of their shifts,with small meromorphic coefficients,where I is a finite index set.
It is an important and difficult problem for complex differential equations to prove the existence of their solutions.In[3],Yang and Li pointed out that the differential equation 4f3(z)+3f′′(z)= ? sin3z has exactly three nonconstant entire solutions f1(z)=sinz,f2(z)=Furthermore,the existence of entire solutions of the more general differential equation
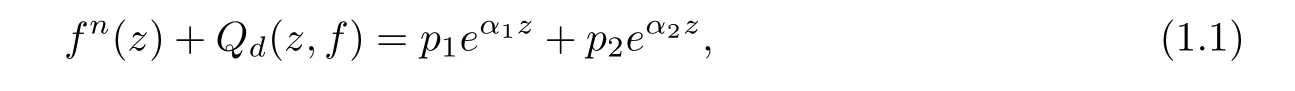
where Qd(z,f)is a differential polynomial in f of degree d,have attracted many interests(see[4–7]etc.).In[4],Li and Yang proved the following result.
Theorem A([4]) Let n≥4 be an integer and d≤n?3.If p1,p2are nonzero polynomials,and α1,α2are nonzero constants such thatis not rational,then equation(1.1)does not have any transcendental entire solutions.
When weakening the restriction on d,Li[5]proved the following result.
Theorem B([5]) Let n≥2 be an integer,d≤n?2,p1,p2be nonzero small functions of ez,and let α1,α2be real numbers.If α1<0< α2and equation(1.1)has a transcendental entire solution f,then α1+ α2=0 andwhere c1,c2are constants and
Recently,replacing the differential polynomial Qd(z,f)in equation(1.1)by a difference,or differential-difference polynomial Pd(z,f),many authors[8–10]investigated the existence of entire solutions of the difference,or differential-difference equations

where Pd(z,f)is a difference,or differential-difference polynomial in f of degree d.In[9],Zhang and Liao obtained a counterpart of Theorem A for entire solutions of finite order of equation(1.2).
Theorem C([9]) Let n≥4 be an integer,and Pd(z,f)denote an algebraic differential difference polynomial in f of degree d≤n?3.If p1,p2are two nonzero polynomials,and α1,α2are two nonzero constants with,then equation(1.2)does not have any transcendental entire solution of finite order.
It is natural to ask whether equation(1.2)has any entire solution of finite order if we weaken the restriction d≤n?3 in Theorem C.To this end,we prove the following result.
Theorem 1.1Let n≥2 be an integer,Pd(z,f)be a difference polynomial in f of degree d ≤ n ? 2 such thatbe nonzero small functions of ez,and let α1,α2be constants.Ifand equation(1.2)has an entire solution f of finite order,then α1+α2=0 andwhere γj(j=1,2)are small functions of f such that
Remark 1.1The below proof of Theorem 1.1 shows that the result of Theorem 1.1 also holds for the case Pd(z,f)being a differential-difference polynomial in f of degree d≤n?2.
Remark 1.2There exist nonlinear difference(or differential-difference)equations satisfying Theorem 1.1.For example,the difference equation

has an entire solution f(z)=eλz+e?λz.The differential-difference equation
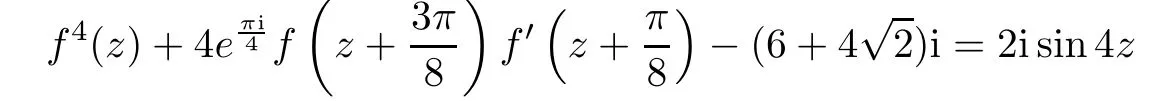
It follows from Theorem 1.1 that for the case α1+ α2=0,equation(1.2)may be have entire solutions of finite order.But in[8],Yang and Laine proved that the difference equation
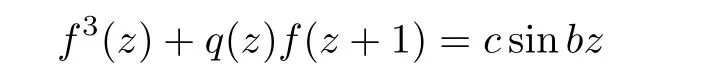
has no entire solutions of finite order,provided that q(z)is a nonconstant polynomial,where b,c are nonzero constants.In this article,we apply Theorem 1.1 to find some types of equation(1.2)having no entire solutions of finite order for the case α1+α2=0.We obtain the following results,which are supplements of Yang-Laine’s result.
Theorem 1.2Let n≥3,M(z,f)be a linear differential-difference polynomial in f,p1,p2be nonzero small functions of ez,and let λ be a nonzero constant.If q(z)is a nonzero small function of f,then the nonlinear differential-difference equation
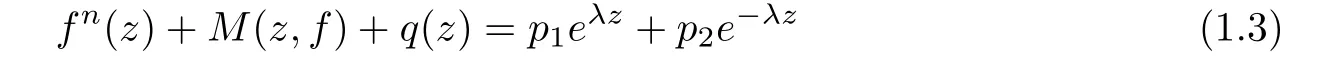
has no entire solutions of finite order.
Theorem 1.3Let a(z),b(z)be nonzero polynomials,p1,p2,λ,c be nonzero constants.If a(z)is a nonconstant polynomial,then the difference equation

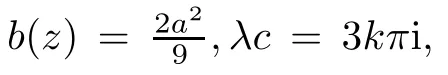
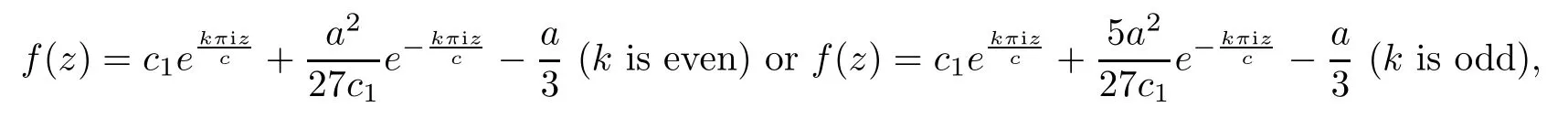
Remark 1.3For example,the difference equation
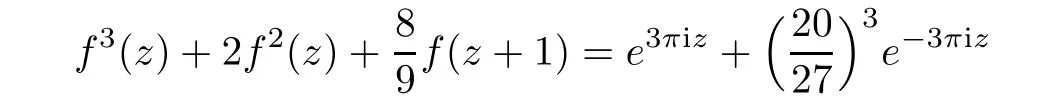
has three distinct entire solutions
2Lemmas
Lemma 2.1([11]) Let T:(0,+∞)→(0,+∞)be a non-decreasing continuous function,s>0,α<1,and let F ? R+be the set of all r such that T(r)≤ αT(r+s).If the logarithmic measure of F is in finite,then

Lemma 2.2([12]) Let f be a non-constant meromorphic function of finite order,η∈C,and δ<1.Then,

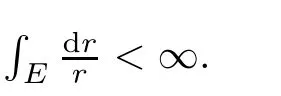
Remark 2.1By Lemmas 2.1 and 2.2,we know that for a non-constant meromorphic function f of finite order,
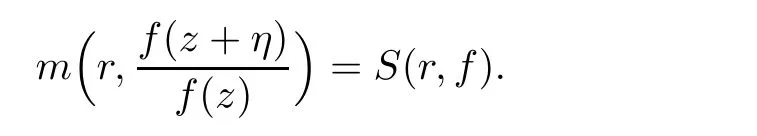
Remark 2.2Lemma 2.2 is a difference analogue of the logarithmic derivative lemma.The other version for finite-order meromorphic functions is due to Chiang and Feng[13].Recently,Halburd,Korhonen,and Tohge[14]proved that the difference analogue of the logarithmic derivative lemma also holds for meromorphic functions of hyper-order less than 1.
Lemma 2.3Let p0,p1,p2be small meromorphic functions of ez,not vanishing identically,and α1,α2be two nonzero constants,then,

ProofWithout loss of generality,we assume that p0≡1.Let

and differentiating(2.1),we obtain



If b1≡0,then by(2.3),we obtainwhich impliesthen differentiating(2.3),we obtain

Eliminating eα1zfrom(2.3)and(2.5),we obtain
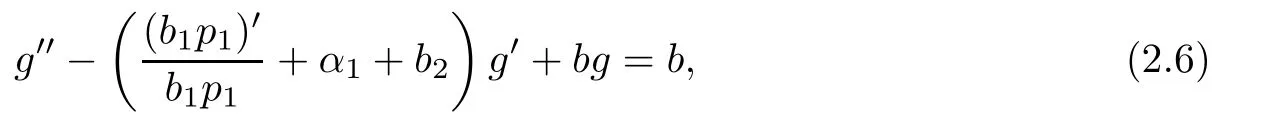
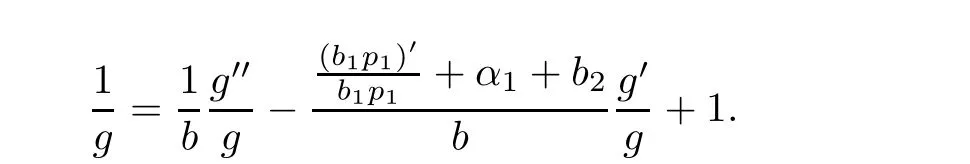

Remark 2.3Using the argument similar to that of Lemma 2.3,we also obtain

where p1,p0are small meromorphic functions of ez,not vanishing identically,α1is a constant.
Lemma 2.4Let p0,p1,p2be small meromorphic functions of ez,not vanishing identically,and α1,α2be two nonzero constants,then,

ProofWe only need to proof the case j=1.As
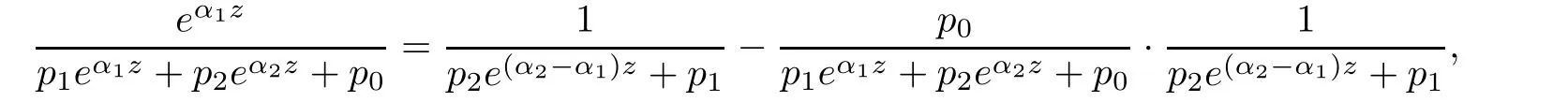
then from the above equality and Lemma 2.3,we obtain the result of Lemma 2.4.
Lemma 2.5(see[12]) Let f be a non-constant finite order meromorphic solution of fn(z)P(f)=Q(f),where P(f),Q(f)are difference polynomials in f with small meromorphic coefficients,and let δ<1.If the total degree of Q(f)as a polynomial in f and its shifts f(z+cj)(cj∈C,j∈I)is at most n,then,
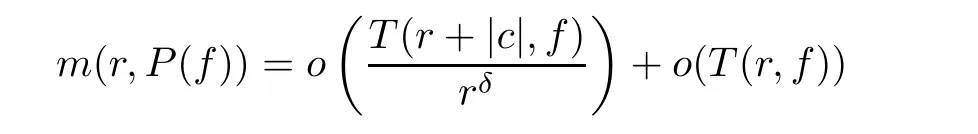
for all r outside of a possible exceptional set with finite logarithmic measure,where|c|=
Remark 2.4The result of Lemma 2.5 also holds for the case P(f),Q(f)being differential difference polynomials in f with small meromorphic coefficients.
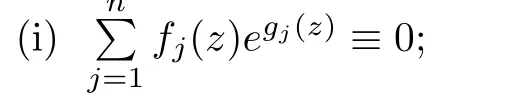
(ii)For 1≤j (iii)For 1≤ j≤ n,1≤ t E?(1,∞)is a set with finite linear measure.Then,fj(z)≡ 0,(j=1,···,n). Lemma 2.7([3]) Suppose that c is a nonzero constant,and α is a nonconstant meromorphic function.Then,the equation has no transcendental meromorphic solution f satisfying T(r,α)=S(r,f). Proof of Theorem 1.1Let Pd=Pd(z,f),and f be an entire solutions of finite order of(1.2).Differentiating(1.2)and eliminating eα1zor eα2z,we obtain and Let where I is a finite set of the index λ,tλ,lλj(λ ∈ I,j=1,···,tλ)are natural numbers,βλj(λ ∈I,j=1,···,tλ)are distinct complex numbers.Setand substituting this equality into(3.3),we obtain Differentiating(3.3)yields From Lemmas 2.1 and 2.2,and the lemma of the logarithmic derivative,we obtain m(r,cj)=S(r,f),(j=0,···,d).Hence,from(3.1),(3.4),and(3.5),we obtain On the other hand,from(1.2)and(3.4),we obtain From(3.6)and(3.7),we obtain Substituting(3.4)into(1.2),we obtain that is On the other hand,from(3.9),we obtain Then from(3.8),(3.10),(3.11)and Lemma 2.4,we obtain Setting z=reiθ,for fixed r>0,let E1={θ ∈ [0,2π):|eα2z|≥ 1},E2=[0,2π)? E1.Because for θ∈E1, we obtain While for θ∈E2,because we obtain Hence,from(3.10),(3.12),(3.13),and(3.14),we obtain Combining with(3.1)and(3.2),we obtain where and Q(z,f)is a differential-difference polynomial in f of degree n+d(≤ 2n?2)with small meromorphic coefficients.From(3.8),(3.10),(3.15),and(3.16),we obtain It follows from(3.17)that the poles of ? possibly come from the poles of p1,p2,and f.This implies that N(r,?)=S(r,f).Then,combining with(3.18),we obtain Now,we discuss the following two cases. Case 1? ≡ 0.Observe thatandcan not vanish identically simultaneously.Otherwise,from these equalitiesandwe getthat is,β ≡ 0.This is absurd.So,without loss of generality,we assume thatThis implies that where c is a nonzero constant.Substitutingand(3.20)into(3.1),we obtain Case 2Let then from(3.8),(3.17),(3.19)and(3.22),we obtain From(3.22),we obtain Differentiating the first equality of(3.24),we obtain Substituting(3.25)into the second equality of(3.24),we obtain where From(3.8),(3.22),(3.23),and(3.27),we obtain Then combining with(3.17),(3.19),(3.24),and(3.29),we obtain This is absurd.So,we have A1≡0.From this and(3.26),we obtain A2≡0.Then combining with(3.27),we obtain where c1,c2are nonzero constants.Hence,from(1.2),(3.24),and(3.30),we obtainwhere γj(j=1,2)are small meromorphic functions such thatOn the other hand,from(3.8),(3.17),(3.19),and(3.30),we obtain This implies that α1+ α2=0.Theorem 1.1 is thus proved. ? Proof of Theorem 1.2Suppose that f is an entire solution of finite order of equation(1.3),from Theorem 1.1,it follows that where γ1,γ2are small meromorphic function of f such thatSubstituting(3.31)into(1.3),we obtain Proof of Theorem 1.3Suppose that f is an entire solution of finite order of equation(1.4).Letand substituting this equality into(1.4),we obtain From Theorem 1.2 and(3.33),we obtainand and Then combining with(3.35)and(3.36),we obtain where c1,c2are constants.Substituting(3.40)into(3.34),we obtain From(3.41)and Lemma 2.6,we obtain Hence, If a(z)is a nonconstant polynomial,then(3.42)can not hold.So,equation(1.4)has no entire solution of finite order. If a(z)=a is a constant,then by(3.42),we obtainthat isand when k is even,we havewhen k is odd,we havehenceThen,combining withand(3.40),we obtain f which has the form defined as Theorem 1.3.Theorem 1.3 is thus proved. ?
3 Proofs of Results


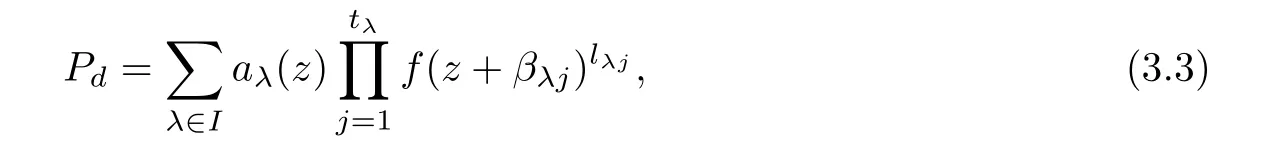
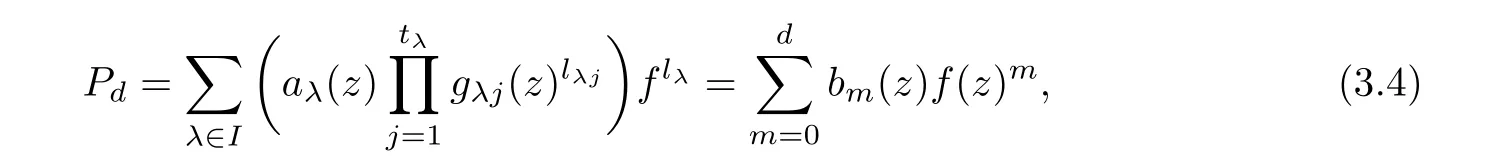
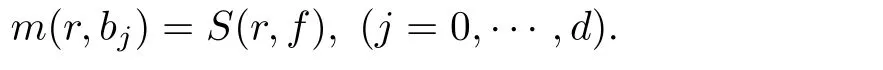
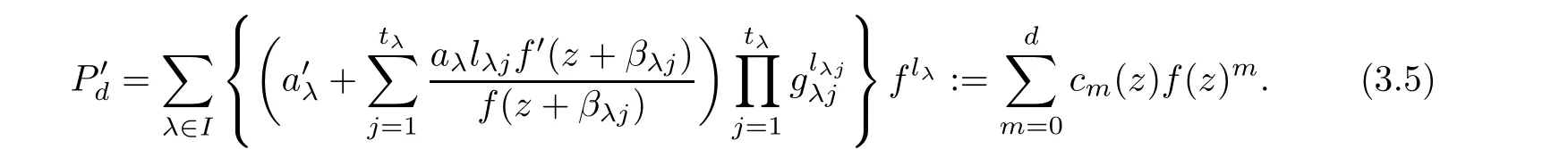
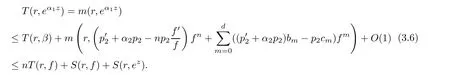
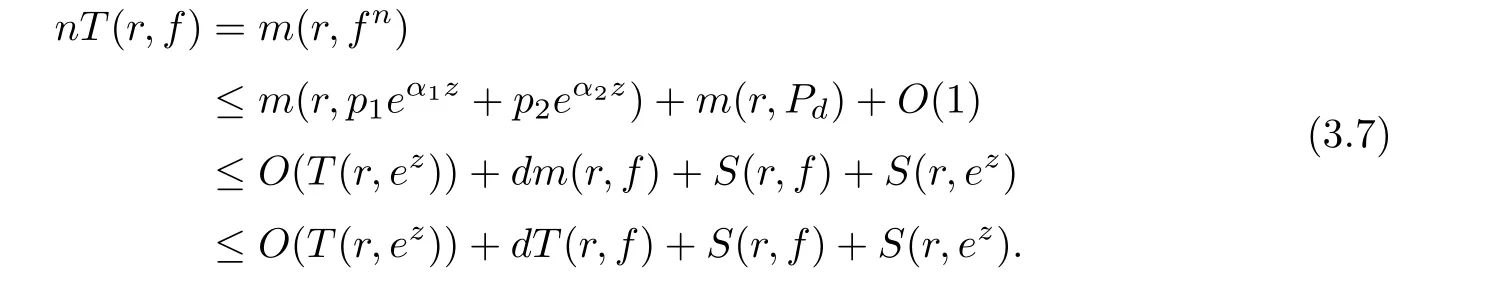
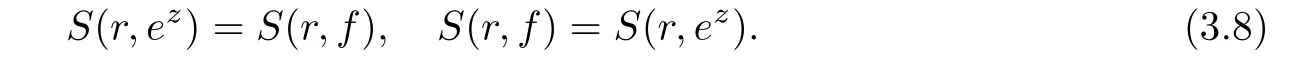
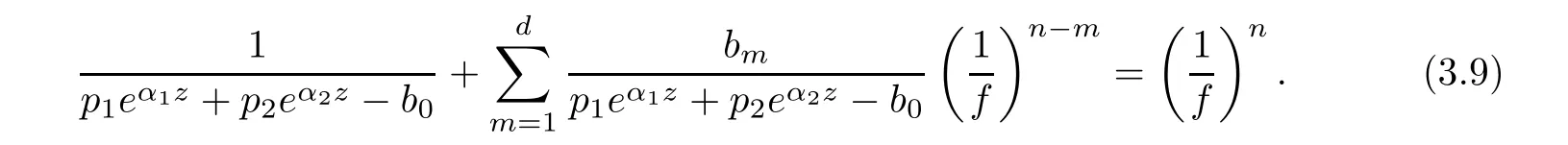


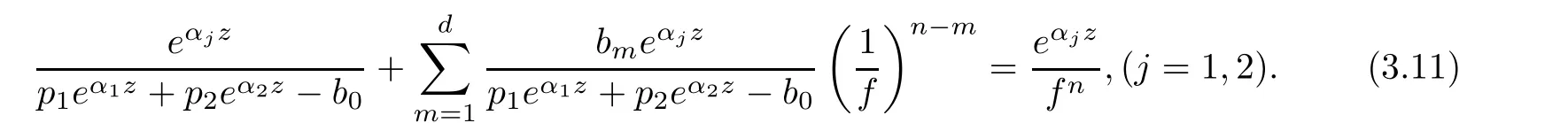

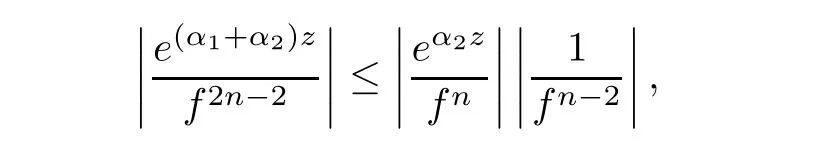
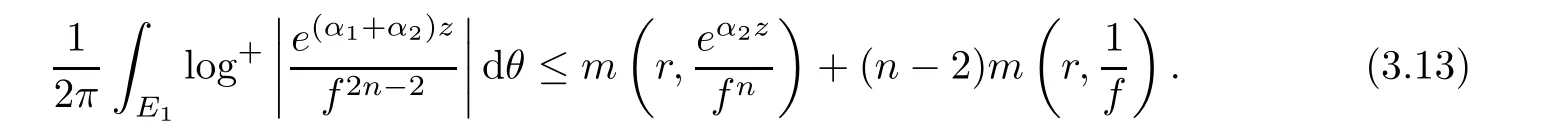
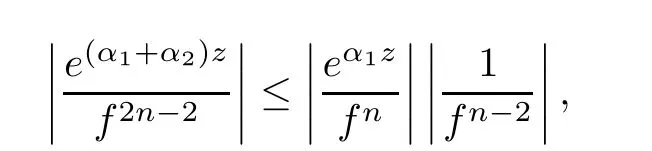
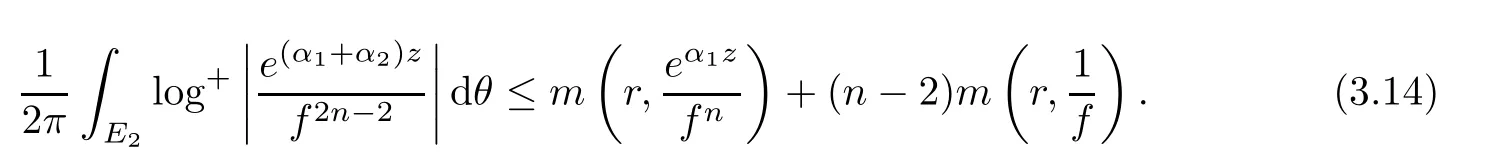
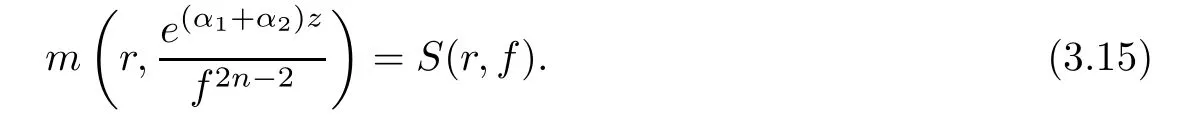
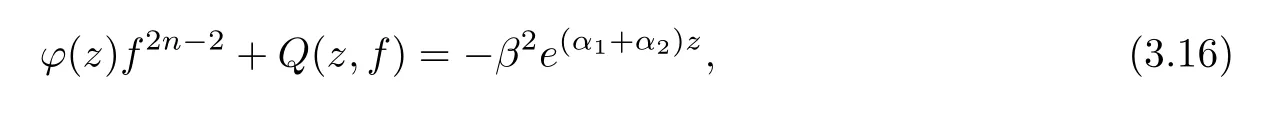
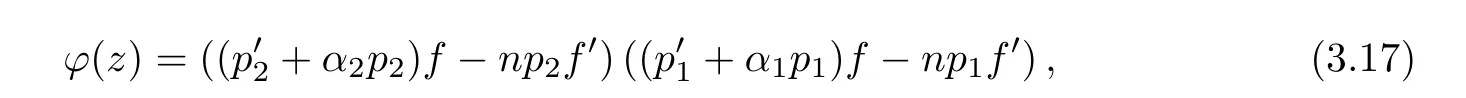
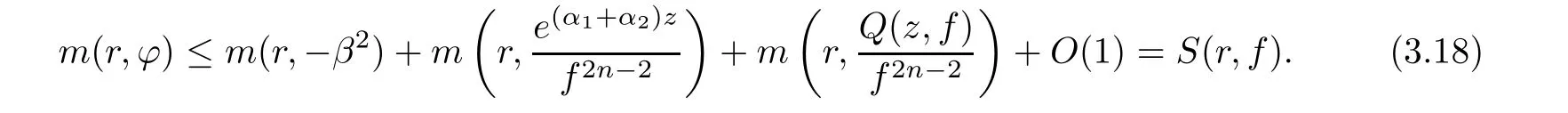



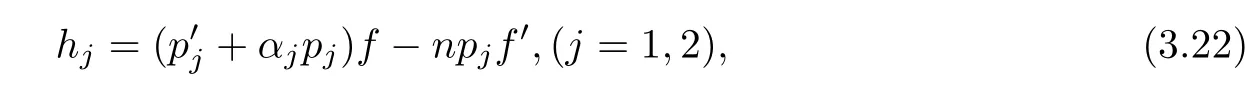
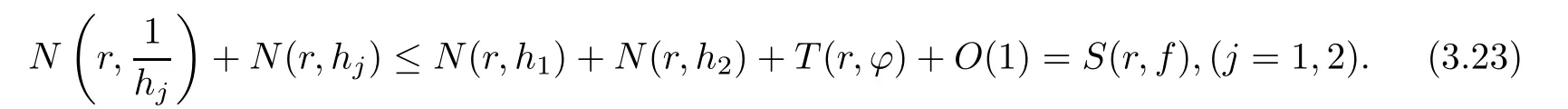



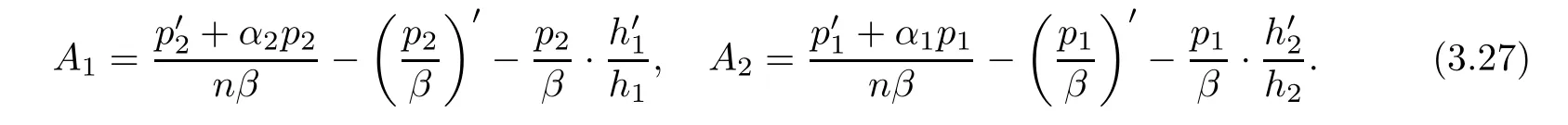
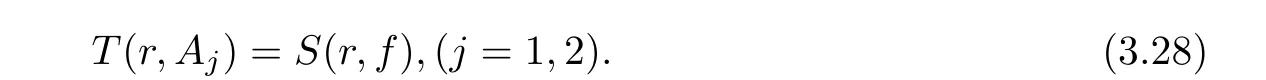
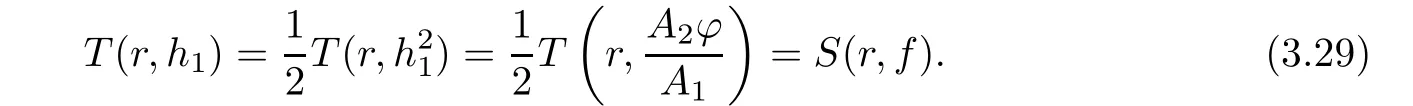
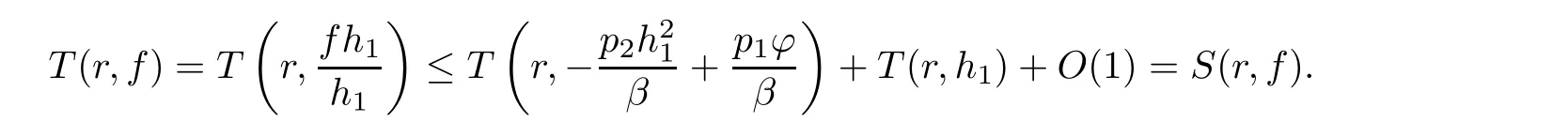

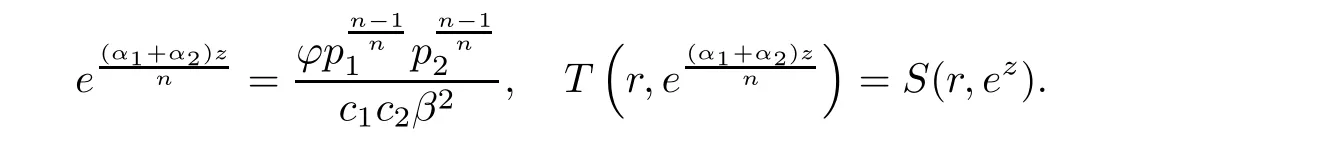

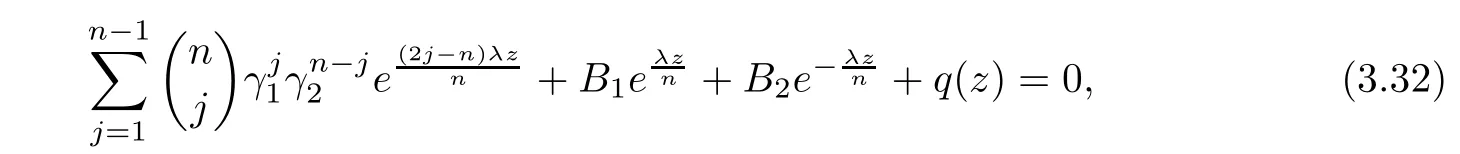

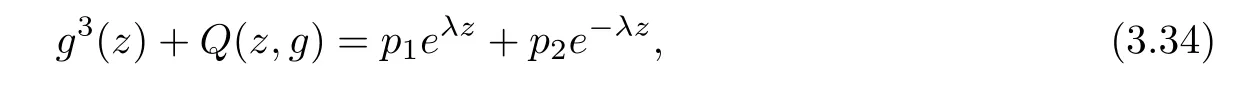
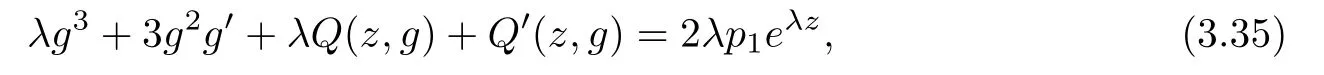
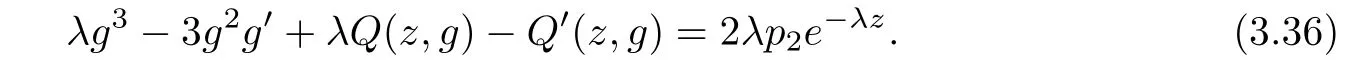
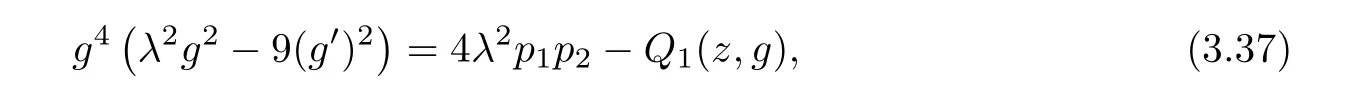
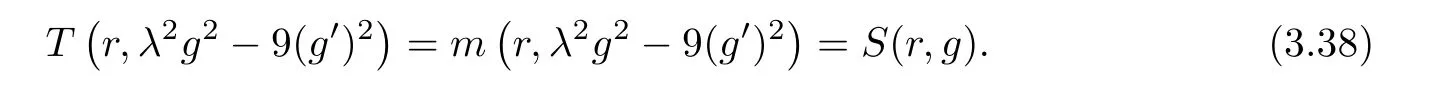



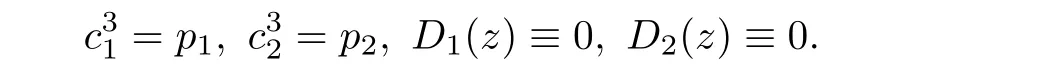
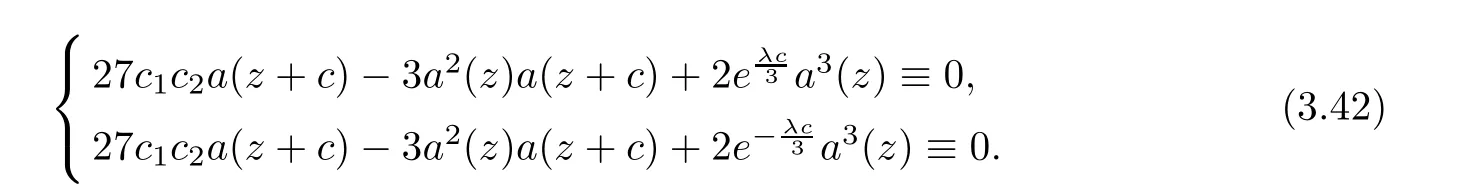
 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
