基于Melnikov方法的單自由度干摩擦振子的混沌分析*

秦瑯 謝建華

(西南交通大學(xué)力學(xué)與工程學(xué)院, 成都 610031)

引言

工程與實際生產(chǎn)問題中干摩擦因素是廣泛存在的,如制動系統(tǒng)和機床切削系統(tǒng)的干摩擦.干摩擦具有非線性效應(yīng),使得系統(tǒng)可能產(chǎn)生復(fù)雜的動力學(xué)行為,可能產(chǎn)生自激振動,多周期現(xiàn)象,甚至?xí)霈F(xiàn)混沌現(xiàn)象.Hetzler等[1]基于Stribeck干摩擦模型研究了單自由度與兩自由度干摩擦系統(tǒng)的穩(wěn)定性與Hopf分岔.Guo和Xie[2]研究了單自由度干摩擦受迫系統(tǒng)共振時的NS分岔.Van de Vrande和De Kraker[3]研究了干摩擦引起的粘滑振動現(xiàn)象.Melnikov方法是研究在弱周期力激勵下近Hamilton系統(tǒng)中的混沌運動的較為有效的解析方法[4,5].一些工程實際問題,可以將其簡化為帶有弱周期擾動項的具有同宿軌道或者異宿軌道的二階常微分方程.通過建立Poincaré映射,就可以采用Melnikov方法進行解析計算.許多學(xué)者采用Melnikov方法解決一些具有實際工程背景問題,取得了很好的結(jié)果.Wu和Mccue[6]利用擴展的Melnikov方法分析單自由度船舶模型的搖擺運動,研究了不同波浪模型對船舶搖擺運動的影響.韓寧,曹慶杰[7]基于Melnikov函數(shù)研究了柱面系統(tǒng)的混沌動力學(xué)行為.賀尚宏[8]將Melnikov方法應(yīng)用于確定多參數(shù)機械系統(tǒng)的混沌邊緣中.文獻[9,10]以兩邊受約束倒置的單擺為模型,應(yīng)用擴展的Melnikov方法研究了其動力學(xué)行為.文獻[11,12]研究了單自由非線性的傳送帶系統(tǒng),即系統(tǒng)的彈簧為非線性的.分析了傳送帶速度與摩擦力振幅改變對于系統(tǒng)的動力學(xué)行為的影響.本文的研究模型與其相似,但是采用線性彈簧,構(gòu)造出幾何非線性系統(tǒng),籍此分析系統(tǒng)相應(yīng)的動力學(xué)行為,并應(yīng)用Melnikov方法給出了系統(tǒng)的混沌解析預(yù)測得到出現(xiàn)馬蹄型混沌運動的條件,并將Melnikov解析結(jié)果同數(shù)值結(jié)果進行比對,相互印證,說明了Melnikov解析結(jié)果的有效性.

1 力學(xué)模型與運動方程

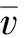
FT=-2Tsinθ

=(-2T0/l)x+(T0-kl)x3/l3+o(x3)

(1)

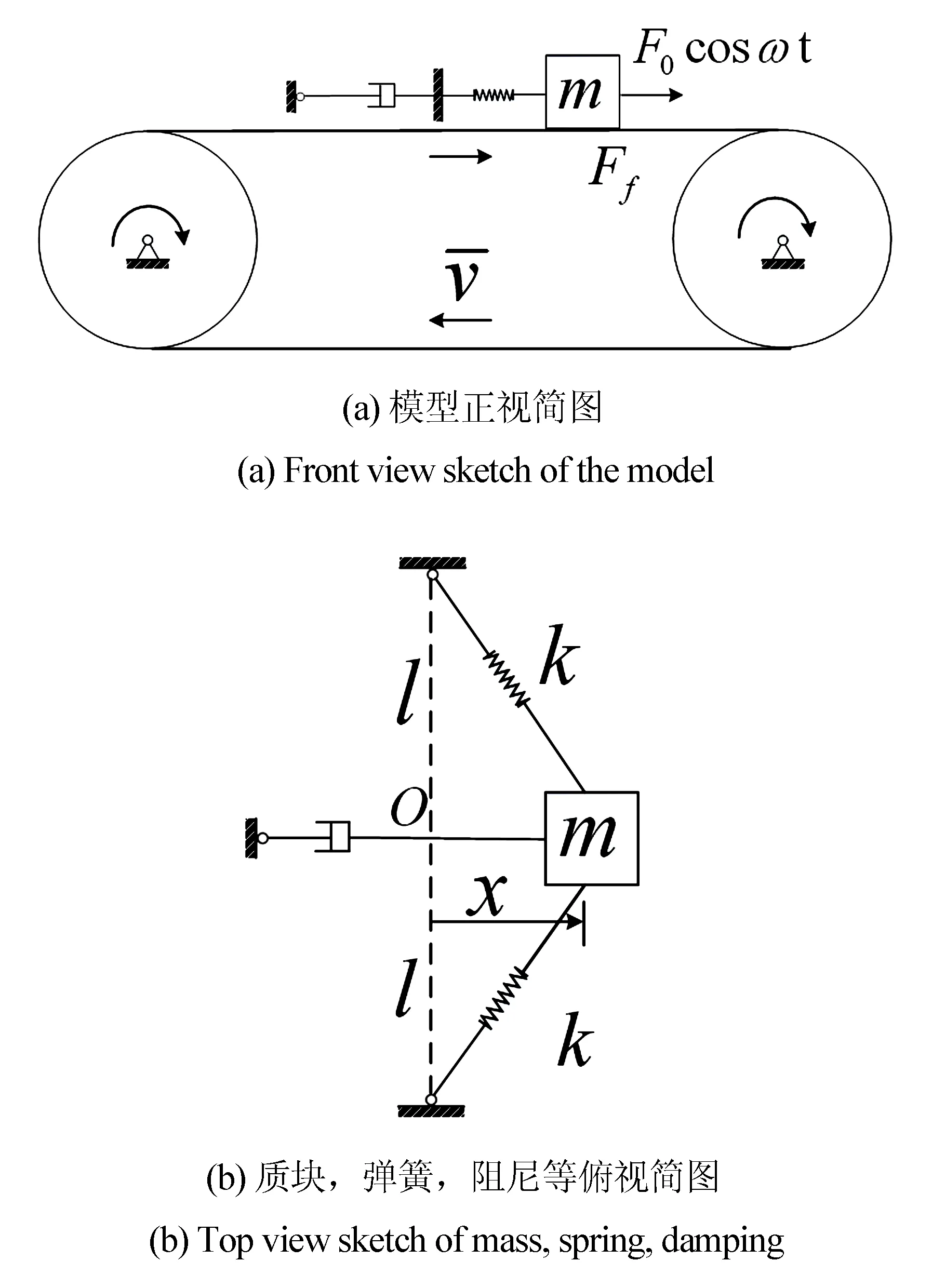
圖1 力學(xué)模型圖Fig.1 Mechanical model

質(zhì)塊的運動微分方程為：

(2)

其中a=-2T0/ml,b=(kl-T0)/ml3,F0=εmγ,c=εmα,f0=εmβ,ε為小參數(shù),假定系統(tǒng)參數(shù)a,b,α,β,γ,ω均為正值,略去o(x3)項,進一步將系統(tǒng)(2)化為微分方程組的形式：

(3)

當(dāng)ε=0時,未擾系統(tǒng):

(4)

為Hamilton系統(tǒng).未擾系統(tǒng)(4)Hamilton量為:

(5)

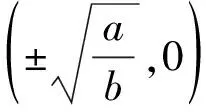
q0(t) =(x0(t),v0(t))

(6)

2 Melnikov方法分析

系統(tǒng)(3)的Melnikov積分為:

(7)

v0(t-t0)(α·v0(t-t0)+

(8)

令τ=t-t0,則有:

(9)

(10)

(11)

對于積分I2可以首先得出:

(12)

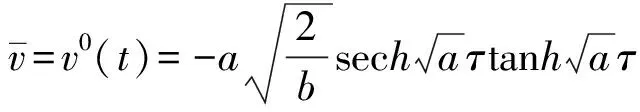
sech2x+tanh2x=1

可得:

(13)

最后得出:

(14)

由此可得,Melnikov積分:

(15)

將式(15)中的α,β,γ分別用εα,εβ,εγ替換,得到M(t0)具有簡單零點的條件:

(16)

3 數(shù)值模擬

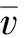
由分岔圖,相圖可以看出,隨著外激勵εγ的變化,系統(tǒng)表現(xiàn)出復(fù)雜的動力學(xué)行為.當(dāng)εγ=0.53時,位于Melnikov函數(shù)閾值曲線下側(cè),系統(tǒng)處于周期一運動.隨著εγ的不斷增加,系統(tǒng)進入了周期倍化階段.當(dāng)εγ=0.61,εγ=0.625,εγ=0.64時,均位于Melnikov函數(shù)閾值曲線上側(cè).當(dāng)εγ=0.61時,系統(tǒng)處于周期二運動,見圖4(b) .當(dāng)εγ=0.625時,系統(tǒng)做周期四運動,見圖4(c).隨著εγ進一步增大系統(tǒng)最終步入混沌運動狀態(tài),當(dāng)εγ=0.64時,系統(tǒng)處于混沌運動狀態(tài),見圖4(d).圖5(b)表明εγ=0.64時,系統(tǒng)的最大Lyapunov指數(shù)大于零,證實了系統(tǒng)處于混沌狀態(tài),這符合Melnikov函數(shù)閾值曲線結(jié)果.數(shù)值結(jié)果與解析結(jié)果相符.

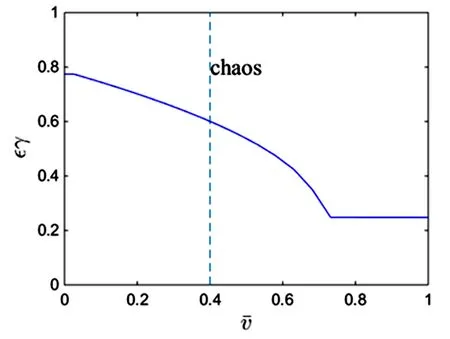
圖2 Melnikov函數(shù)閾值曲線Fig.2 Criteria curve of Melnikov function

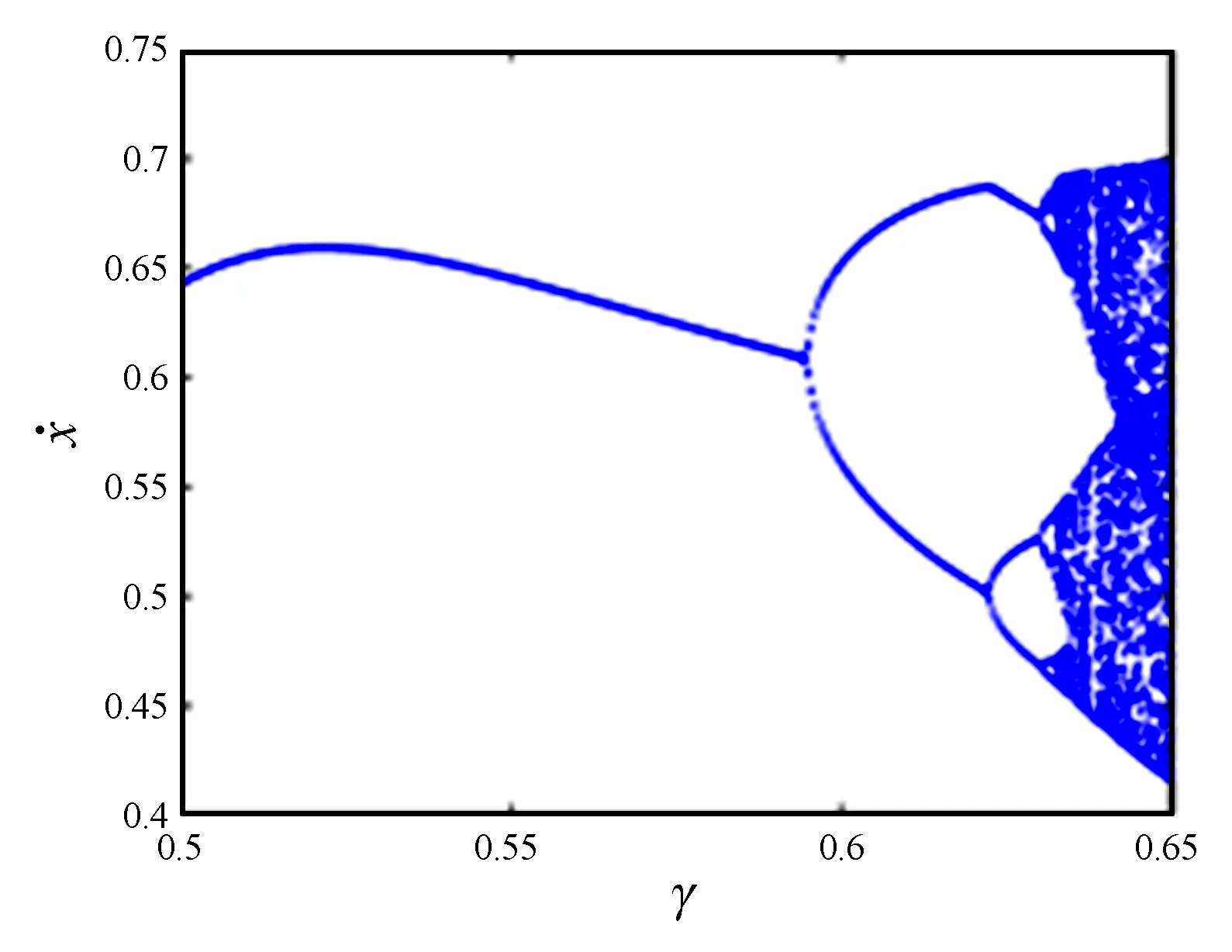
圖3 分岔圖Fig.3 Bifurcation diagram

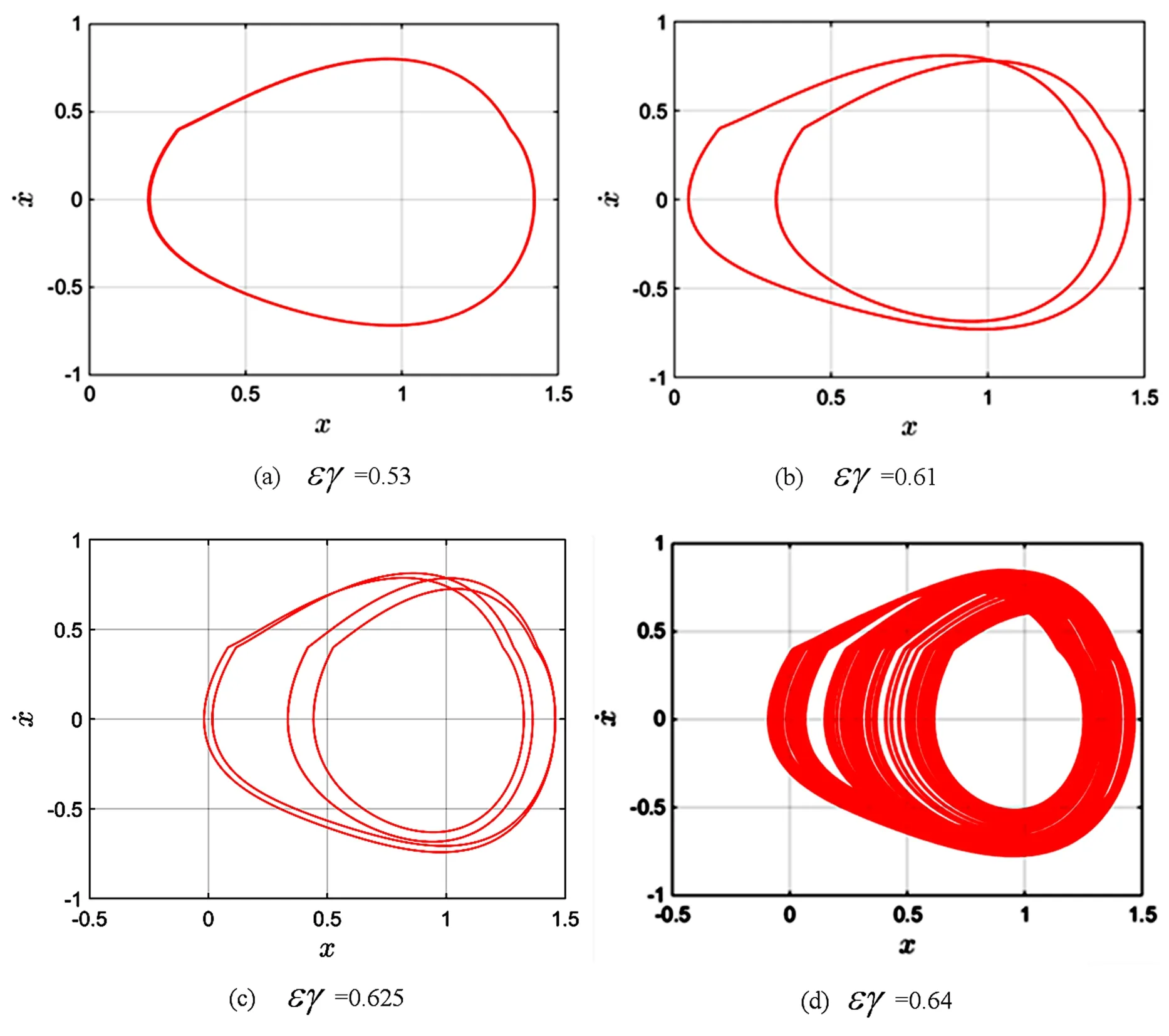
圖4 εγ變化時系統(tǒng)相圖Fig.4 System phase diagrams when εγ changes

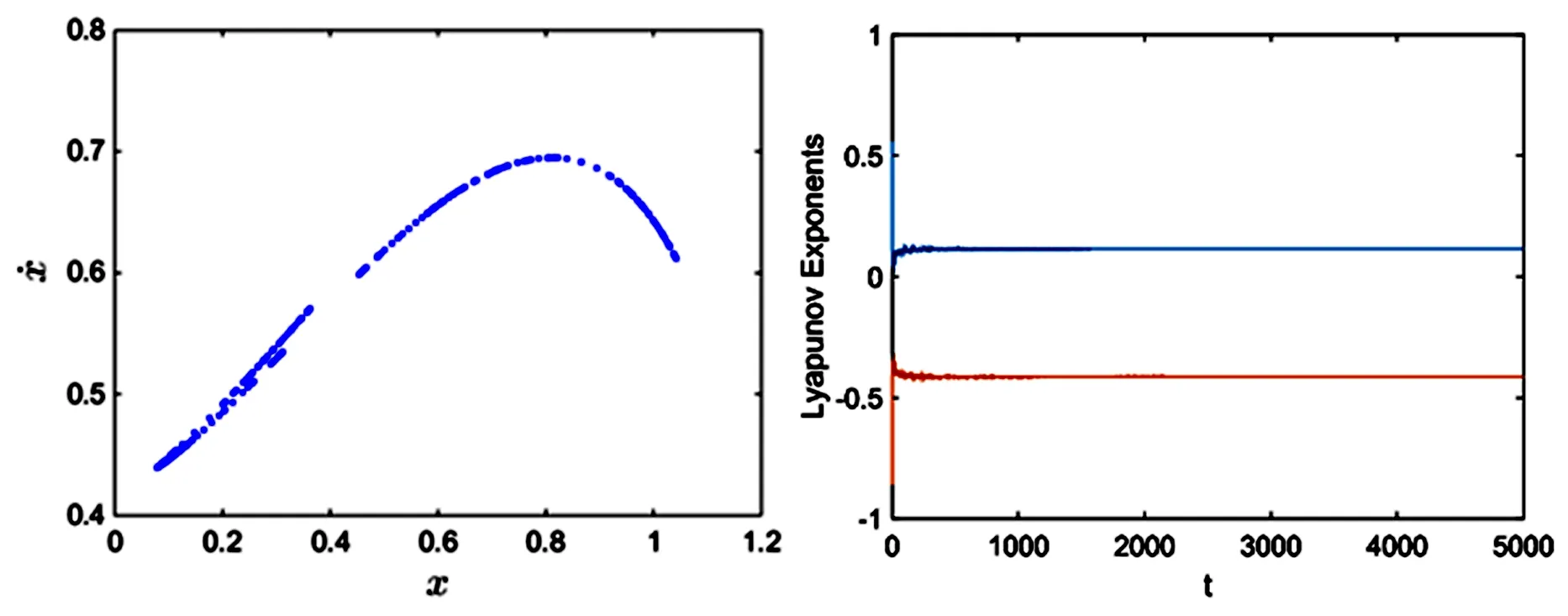
圖5 εγ=0.64系統(tǒng)Poincaré截面圖(a), Lyapunov指數(shù)(b)Fig.5 (a) Poincare cross section, and (b) Lyapunov exponent, when εγ=0.64

4 結(jié)語

Melnikov方法是判斷系統(tǒng)是否具有馬蹄型混沌的有效的解析方法,本文運用Melnikov方法對一個單自由度干摩擦振子進行分析,得出了系統(tǒng)產(chǎn)生馬蹄型混沌的條件.通過相圖,Poincaré截面圖和分岔圖等手段,證明了數(shù)值結(jié)果與通過Melnikov方法得到的解析結(jié)果相符.研究表明在一定參數(shù)條件下隨著外激勵的幅值逐漸增加,系統(tǒng)由周期運動經(jīng)歷周期倍化過程逐漸步入混沌運動.

1Hetzler H, Schwarzer D, Seemann W. Analytical investigation of steady-state stability and Hopf-bifurcations occurring in sliding friction oscillators with application to low-frequency disc brake noise.CommunicationsinNonlinearScience&NumericalSimulation, 2007,12(1):83～99

2Guo Y, Xie J H. Neimark-Sacker (N-S) bifurcation of oscillator with dry friction in 1∶4 strong resonance.AppliedMathematicsandMechanics, 2013,34(1):27～36

3Vrande B L V D, Campen D H V, Kraker A Dl. An approximate analysis of dry-friction-induced stick-slip vibrations by a smoothing procedure.NonlinearDynamics, 1999,19(2):159～171

4劉曾榮. 混沌的微擾判據(jù). 上海:上海科技教育出版社, 1994 (Liu Z R. Perturbation criterion of chaos. Shanghai:Shanghai Scientific and Technological Education Publishing House, 1994 (in Chinese))

5李繼斌,陳鳳娟. 混沌,Melnikov方法及新發(fā)展. 北京:科學(xué)出版社, 2012:125～131 (Li J B, Chen F J. Chaos, Melnikov method and new development. Beijing:Science Press, 2012:125～131 (in Chinese))

6Wu W, Mccue L. Application of the extended Melnikov′s method for single-degree-of-freedom vessel roll motion.OceanEngineering, 2008,35(17):1739～1746

7韓寧,曹慶杰. 一類典型柱面系統(tǒng)的非線性動力學(xué)分析. 全國非線性動力學(xué)和運動穩(wěn)定性學(xué)術(shù)會議. 2013 (Han N, Cao Q J. Nonlinear dynamic analysis of a typical cylindrical system. In:National Conference on nonlinear dynamics and stability of motion. 2013 (in Chinese))

8賀尚宏. Melnikov方法在確定多參數(shù)機械動力系統(tǒng)混沌邊緣中的應(yīng)用[碩士學(xué)位論文]. 成都:西南交通大學(xué), 2015 (He S H.On the application of Menikov Method to determinting edge of chaos of mechanical dynamic system with muti-parametersr[Master Thesis]. Chengdu:Southwest Jiaotong University, 2015 (in Chinese))

9Du Z, Zhang W. Melnikov method for homoclinic bifurcation in nonlinear impact oscillators.Computers&MathematicswithApplications, 2005,50(3):445～458

10 Du Z, Li Y, Shen J, et al. Impact oscillators with homoclinic orbit tangent to the wall.PhysicaDNonlinearPhenomena, 2013,245(1):19～33

11 Luo A C J, Huang J. Discontinuous dynamics of a non-linear, self-excited, friction-induced, periodically forced oscillator.NonlinearAnalysisRealWorldApplications, 2012,13(1):241～257

12 李群宏,閆玉龍,韋麗梅等. 非線性傳送帶系統(tǒng)的復(fù)雜分岔. 物理學(xué)報, 2013,62(12):120505～10 (Li Q H, Yan Y L, Wei L M, et al. Complex bifurcations in a nonlinear system of moving belt.ActaPhysicaSinica, 2013,62(12):120505～10 (in Chinese))

13 Olsson H, ?str?m K J, Wit C C D, et al. Friction models and friction compensation.EuropeanJournalofControl, 1998,4(3):5517～5522