Interaction between surface gravity wave and submerged horizontal flexible structures ＊

Sarat Chandra Mohapatra , Trilochan Sahoo , C. Guedes Soares

1. Centre for Marine Technology and Ocean Engineering (CENTEC), Instituto Superior Técnico, Universidade de Lisboa, Lisboa, Portugal

2. Department of Ocean Engineering and Naval Architecture, Indian Institute of Technology, Kharagpur, India

Introduction

With the increasing demand of multi-purpose use of coastal and offshore zones, there has been significant interest to use floating flexible breakwaters,which are light weight, cost effective and environmental friendly substitute for the conventional breakwaters[1-3]. These types of flexible floating structures are easy to carry, reusable, and rapidly deployable.For infinite water depths, these breakwaters are more economical and can be fabricated on land and easier to transport and handle. Often these structures are made of synthetic fiber, rubber or polymeric materials. The multi-mode motions of these types of flexible structures can be explored to widen the effective frequency range for wave attenuation, especially in irregular waves. Oil booms and silt curtains are practical examples of membrane structures which are used for specific purposes in sea[4].

There have been many theoretical and experimental studies with regards to the performance of vertical flexible wave barriers[5]. The major problems associated with the use of vertical flexible breakwaters are the wave loading and possible blockage of current by the structure. On the other hand, horizontal flexible barriers can reduce the wave amplitude effectively by suppressing the vertical motion of water oscillation.Although, floating flexible barriers are more suitable for deep water uses where wave energy concentration is more on the free surface, the submerged horizontal flexible structures as breakwaters do not hamper seascape and also allow the passage of ships and currents. This kind of structures can be moored despite unfavorable seabed soil conditions. These structures allow for free movement of fish and free passage of seawater and sediment transport beneath,thus friendly to the environment. Since the horizontal structures do not directly block incoming waves, the diffracted and radiated waves including various elastic modes have to be properly tuned for its use as an effective wave barrier.

Over the years, various aspects of submerged flexible plate have been studied based on different mathematical methods by many researchers. Siew and Hurley[6]analyzed the wave scattering by a submerged horizontal plate in shallow water using matched asymptotic expansion method. Yu[7]examined the reflectivity and transmissivity of the submerged horizontal plate based on analytical and semi-empirical methods. Hassan et al.[8]studied the interaction of surface gravity waves with submerged flexible plate of finite and semi-infinite length in finite water depth and suitably modified the orthogonal mode-coupling relation of Lawrie and Abrahams[9].

Further, Wu et al.[10]studied the wave reflection by a vertical wall with a submerged horizontal porous plate using eigenfunction method. Liu et al.[11]studied analytically the interaction between wave and a perforated wall breakwater with a submerged horizontal porous plate based on linear potential theory using eigenfunction expansion method. Evans and Peter[12]analyzed the interaction between gravity wave and a submerged semi-infinite porous plate by the Wiener-Hopf technique and finite porous plate by using the residue calculus technique in finite water depth based on linearized water wave theory. Liu and Li[13]provided an alternate analytical solution for water-wave motion over a offshore submerged horizontal porous breakwater based on linearized potential theory using matched-eigenfunction expansion method. Further, Liu et al.[14]studied the wave scattering by a submerged horizontal porous plate with finite thickness. Recently, Behera and Sahoo[15]studied the wave scattering by surface gravity wave in the presence of submerged horizontal flexible porous plate based on matched eigenfunction method.

On the other hand, there is an increasing interest on the study of interaction between wave and floating elastic/flexible structures. In this class of problem, the mathematical significance of wave-structure interaction problems is the existence of higher order boundary condition on the structural boundary to deal with a class of boundary value problems associated with Laplace/Helmholtz equation. Because of the presence of higher order boundary conditions, the associated boundary value problems are not Sturm-Liouville in nature[16-22]. Kohout et al.[23]studied the linear water wave propagation through multiple floating elastic plate of variable properties based on direct method. The modeling challenges associated with problems of hydroelasticity are reviewed by Korobkin et al.[24]. Different mathematical techniques have been used to deal with the problems of interaction between surface gravity wave and elastic bottom in two and three-dimension[25-26].

Recently, Mohapatra and Sahoo[27]developed the expansion formulae and orthogonal mode-coupling relations for the velocity potentials to deal with the problems of interaction between wave and a floating and submerged elastic plate system based on eigenfunction expansion method to study the effect of submerged horizontal flexible structures on the floating flexible structure in order to reduce the hydroelastic response of floating structure. Further,Mohapatra and Sahoo[28]derived the expansion formulae for interaction between oblique wave and floating and submerged flexible structures based on Green’s function technique in finite and infinite water depths. The above investigations were made keeping in mind the submerged flexible structures used as anti-motion device for floating flexible structures.

In the present study, a similar methodology to the one used by Mohapatra and Sahoo[27-28]is applied to analyze the effect of surface gravity wave motion on submerged flexible structures under the assumption of small amplitude wave theory and structural response in two-dimensions. Therefore, in the context of the present study, the wave motion characteristics in surface and submerged flexural modes are studied in finite water depth by analyzing the generalized dispersion relation which was not studied in Hassan et al.[8]and also different from those in Mohapatra and Sahoo[27]on the floating elastic plate by the present.The comparison of the expansion formulae for the velocity potentials associated with gravity wavemaker problems in the presence of submerged flexible structures obtained by the Green’s function technique and eigenfunction expansion method in finite and infinite water depths is new. The results show that the analytical solutions obtained here by these two methods are same.

The application of the derived expansion formulae are demonstrated by analyzing the solutions for interaction between surface gravity wave and submerged articulated flexible plate in water of finite depth. They are different from those in Hassan et al.[8],Williams and Meylan[29], and even if Mohapatra and Sahoo[27-28]on the floating flexible structure by the present. Further, the wave energy flux relation is discussed in the context of the problem in terms of reflection and transmission coefficients which reveal the important information for wave energy. Several numerical results on reflection and transmission coefficients related to submerged articulated flexible plate are presented in order to understand the effect of submerged flexible structures on surface gravity wave motion.

1. Mathematical formulation

The problem is considered in two-dimensional Cartesian co-ordinate system with the -xaxis being in the horizontal direction and they-axis in the vertically downward positive direction (as in Fig. 1).An infinitely extended submerged flexible plate kept horizontally aty=hin the fluid domain. The fluid occupies the region 0＜y＜h, -∞＜x＜∞ andh＜y＜H, -∞＜x＜∞ in case of finite water depth,with the submerged plate occupying the regiony=h,-∞ ＜x＜ ∞. On the other hand, the fluid occupies the region 0＜y＜h, -∞＜x＜∞ andh＜y＜∞,-∞ ＜x＜ ∞ in case of infinite water depth. It is assumed that the fluid is inviscid, incompressible and the motion irrotational and simple harmonic in time with angular frequencyω. Thus, the fluid motion is described by the velocity potential Φ(x,y,t)= where Re being the real partwith φ(x,y) is the spatial velocity potential. Further,the free surface elevation η(x,t) and submerged elastic plate deflection ζ(x,t) are of the formrespectively. The velocity potential Φ (x,y,t) satisfies the Laplace equation given by

where

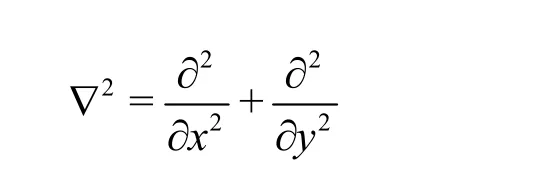
The linearized kinematic condition at the mean free surface =0yis given by

The linearized dynamic free surface boundary condition at the mean free surface =0yis given by

Combining the kinematic and dynamic boundary conditions (2) and (3), the linearized boundary condition at the mean free surface is obtained as

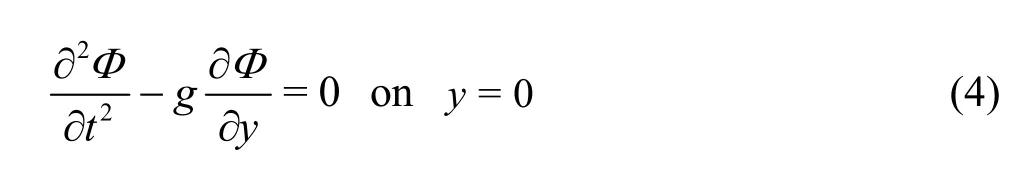
The rigid bottom boundary conditions are given by

The linearized kinematic condition on the submerged flexible plate surface =yhis given by

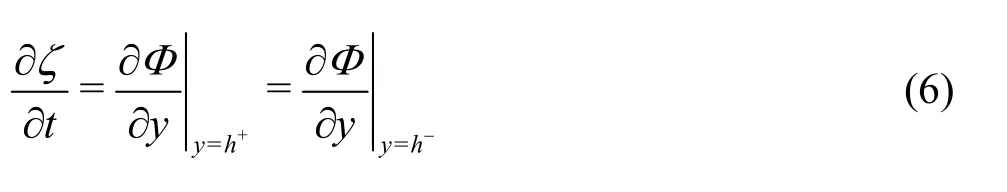
where the superscripts + and - sign denote, respectively, the values on the lower and upper sides of the plate.

The submerged plate deflection ζ under the action of compressive force satisfies[27]

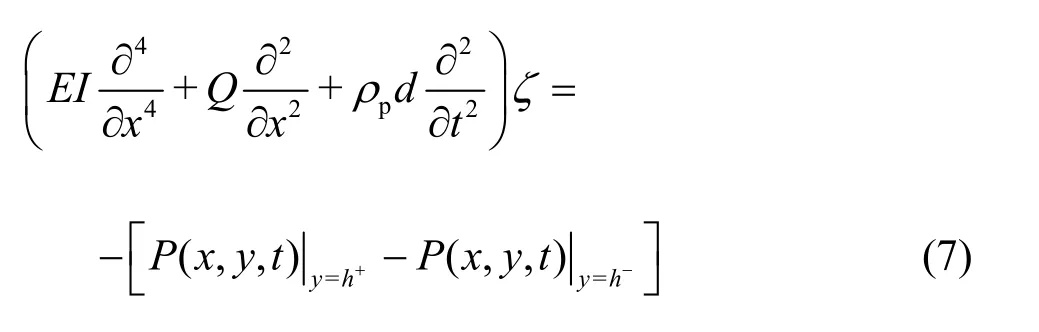
whereEIis the flexural rigidity of the elastic plate withEbeing the Young’s modulus,I=d3/[12(1-ν) ] , ν being the Poisson?s ratio of the elastic plate,dis the thickness of the elastic plate,Qis the compressive force, ρis the density of water, ρpis the density of the elastic plate, andgis the acceleration due to gravity. Further, in Eq. (7),P(x,y,t)is the linearized hydrodynamic pressure and is given by

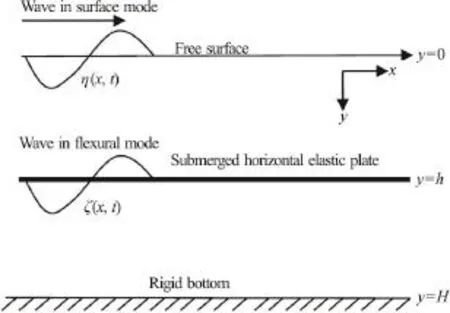
Fig. 1 Nomenclature of the problem

Thus, eliminating ζ from Eqs. (6)-(8), the condition on the submerged plate for ＜＜x-∞∞ is obtained as

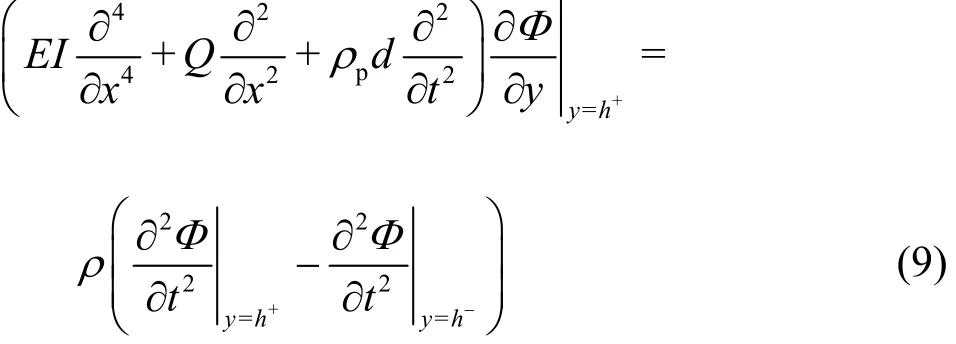
Thus, the spatial velocity potential (,)x yφsatisfies Eq. (1) along with the bottom boundary conditions as in Eqs. (5a), 5(b). The linearized free surface boundary condition in Eq. (4) yields

whereK= ω2/g. The linearized kinematic condition on the submerged flexible plate surfacey=has in Eq.(6) yields

The condition on the submerged plate for ＜＜x-∞∞ in Eq. (9) yields

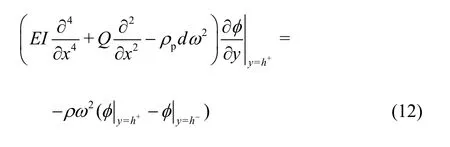
In the context of the present problem, two propagating wave modes will exist, one is due to the presence of free surface and other is because of the flexural gravity wave propagating at the interface.Thus, the far field radiation condition is assumed to be of the form

where theIpandIIpare the wave numbers of the surface gravity waves propagating at the free surface and the flexural waves propagating at the interface respectively. In Eq. (13),Fn(y)’s are the vertical eigenfunctions andAnbeing associated with the unknown wave amplitudes at far field.

Further, additional boundary conditions are to be prescribed in case of specific physical problems which will be discussed in the subsequent subsections.

2. Dispersion relation, phase, and group velocities

In this section, the behavior of a plane progressive wave is studied by analyzing the dispersion relation associated with the physical problem in specific cases. It may be noted that the details of deep water analysis are deferred here to avoid the repetition as the present study is a particular case of Mohapatra and Sahoo[27]. However, in the present section, the wave motion characteristics in surface and submerged flexural mode are studied by analyzing the phase velocity, group velocity, surface elevation, and submerged plate deflections in finite water depth.Similar approach was adopted by Mohapatra and Guedes Soares[26]for deriving the dispersion relation associated with interaction between surface gravity wave and elastic bottom in three- dimensional case.Assumingusing Eq. (1) along with the boundary conditions in Eqs. (2)-(5a) and the 1st part of Eq.(6), the velocity potential is obtained as

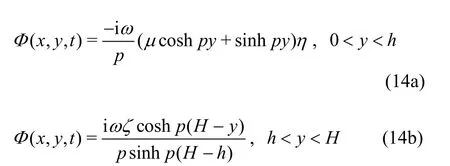
where

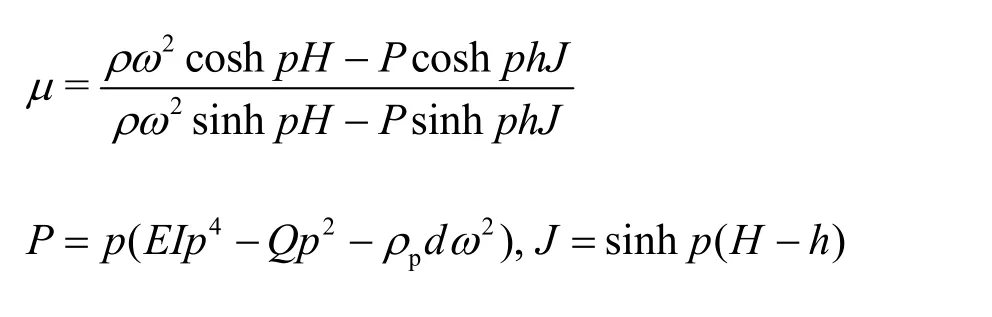
Further, the ratio of the amplitude of the surface elevation to the amplitude of plate deflection is

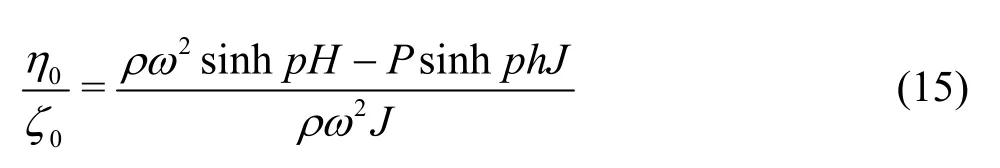
Substituting for Φ from Eq. (14) in surface boundary condition in Eq. (4), the dispersion relation is obtained as

where μ is same as in Eq. (14). The expression designated by μ contains an2ω term, so the dispersion relation is quadratic in2ω. Solving for2ω, we obtain the explicit quadratic roots

where

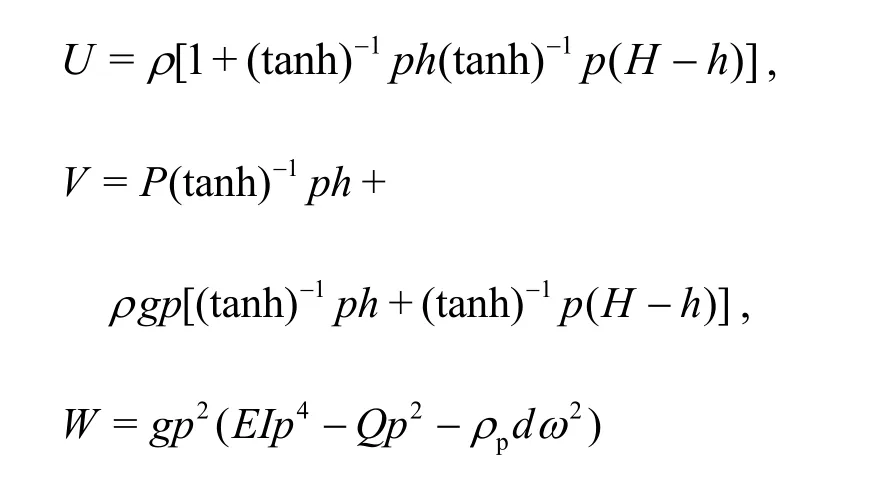
Hereafter, all computations are carried out throughout the paper by considering Poisson?s ratioν=0.3,acceleration due to gravityg=9.8m· s-2and water density ρ =1 025 kgm-3unless mentioned otherwise.It may be noted that in case of the floating elastic plate in the presence of compressive force, for computational purpose in the present paper, the value of the compressive forceQis always chosen within buckling limit as discussed in Mohapatra et al.[30]. From Eq.(17), it is obvious that there are two real positive roots,four complex roots, and infinitely many imaginary roots[27]. In Eq. (17), the subscript with + sign refers to gravity waves in surface mode and subscript with-sign refers to gravity waves in submerged flexural mode.The waves in surface mode are referred as surface gravity waves and waves in submerged flexural mode are referred as flexural gravity waves and this terminology is used throughout the paper. This is different from the case of a elastic plate floating on the water surface in which only a flexural gravity wave propagates[31]. Further, from Eq. (15) it may be noted that, if the value of η0/ζ0is real and positive then the surface and flexural gravity waves are said to be in phase and if negative then the surface and flexural gravity waves are said to be 180° out of phase.Hereafter, the term depending on ρpd/ρ is neglected assuming the term is negligible compared to the other terms. This is due to assumption that the inertia effect of the moving water layer is much larger than the inertia of the thin ice sheet[31]. In particularand neglecting the term ρpdin Eq.(17), it is clear that

which ensures that no wave will propagate at the interface and only the wave in surface mode will propagate in the presence of the submerged flexible plate irrespective of water depth. Further, forE=0 andQ= -TfwhereTfis the tensile force acting on the membrane, the dispersion relation, wave frequency in surface and membrane mode and the ratio of the amplitudes at the free surface and the submerged membrane η0/ζ0can be easily derived from Eqs.(15)-(17).

Fig. 2(a) Variations of phase and group velocities versus h / H with EI=4.7× 1011 N· m2 and Q=0.2for different values of pH in surface mode in finite water depth

Fig. 2(b) Variations of phase and group velocities versus h / H with E I=4.7× 1011 N· m2 and Q=0.2for different values of pH in submerged flexural mode in finite water depth

In Fig. 2, the variations of (a) phase velocity+cand group velocitygc+in surface mode and (b) phase velocityc-and group velocitycg-in submerged flexural mode for different values ofpHwithEI=4.7× 1011N· m2andQ=0.2versush/Hare plotted in finite water depth. From Fig. 2(a),it is observed that the phase and group velocities increase with an increase in the value of wave numberpH. However, both the phase and group velocities decrease with increase inh/H. This is due to the fact that the free surface excitation of the waves in surface mode reduces as the plate becomes away from the free surface. In Fig. 2(b), it is observed that for lower values of wave numberpH, the phase and group velocities attend maximum values forh/H=0.5. On the other hand, forh/H=0.1, both the phase and group velocities vanish which ensures that in shallow water depth and forh/H=0, both the phase and group velocities vanish but forh/H=1.0,both the phase and group velocities attend maximum.However, both the phase and group velocities increase with an increase inh/Hfor higher values of wave numberpH. The observations of phase and group velocity in surface and submerged flexural mode are similar as in Mondal and Sahoo[32]. A comparison of Figs. 2(a), 2(b) ensures that the phase and group velocities in surface mode are higher than that of submerged flexural mode. Further, in general, the group velocity is faster than the phase velocity.

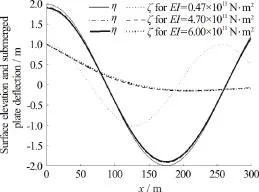
Fig. 3(a) Variations of sur face elevat ion and submerged plate deflectionversusxwithQ=0.2and wave period T =15s, for different values of flexural rigidity EIwith h / H =0.5

In Fig. 3, comparison between free surface elevation η and submerged plate deflection ζ for different (a) flexural rigidityEI(b)h/Hwith ωt=0,T=15s andQ=0.2versus water plane lengthxare plotted in finite water depth. From Fig.3(a), it is observed that for higher values of flexural rigidityEI, both surface elevation and submerged elastic plate deflection decreases. On the other hand,from Fig. 3(b), it is observed that with an increase in the value of /h Hthe free surface elevation increases. In general, from Figs. 3(a), 3(b), it may be noted that the amplitude of free surface elevation is larger compared to that of the submerged plate deflection.

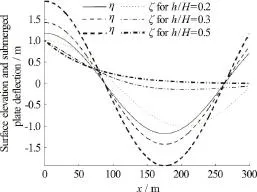
Fig. 3(b) Variations of surface elevation and submerged plate deflection versus xwith Q = 0.and wave period T =15s, for different depths of submergence of flexible plate h / Hwith E I = 4.7× 1 011 N· m2 in finite water depth

3. Expansion formulae for surface gravity wave with submerged flexible structure

This section consists of three major subsections.Using the fundamental solution, Green’s functions associated with interaction between gravity wave and submerged flexible structure are derived in both the cases of finite and infinite water depths. Using the derived Green’s functions and Green’s second identity,velocity potentials for the wavemaker problems are derived in both the cases of finite and infinite water depths. Alternate form of the Green’s functions are obtained using suitable use of the eigenfunction expansion method and a mixed type of Fourier transform associated orthogonal mode-coupling relations.The form of the orthogonal mode-coupling relations derived and used here to determine the unknown coefficients will be clear from the integral representation of the velocity potential derived based on Green’s identity in an earlier subsection.

In this subsection, the Green's functions associated with the problem of interaction between gravity wave and submerged flexible structure are derived in the two-dimensional Cartesian co-ordinate system. It may be noted that the Green’s function associated with interaction between oblique wave and floating and submerged flexible structures are derived by Mohapatra and Sahoo[27] using zeroth order modified

3.1 Green’s function for wave interaction with submerged structures

Bessel function of the second kind for reduced wave equation. Here, the Green’s functions for the problems of interaction between surface gravity wave and submerged flexible structures are derived using the fundamental solution of the source potentials for two-dimensional Laplace equation. Since the motion is simple harmonic in time with angular frequencyω,the Green's function G (x,y;α, β,t)is written aswhere (α, β)being the source point and (x,y) being any point in the fluid domain. Thus, the two-dimensional spatial Green's functionG(x,y;α, β) satisfies the twodimensional Laplace equation as in Eq. (1) except at(α, β) along with the free surface condition (10),condition on the submerged plate Eqs. (11), (12), and the bottom boundary conditions (5a), 5(b). Further,near the source point (α, β), the Green's functionG(x,y;α, β) behaves like

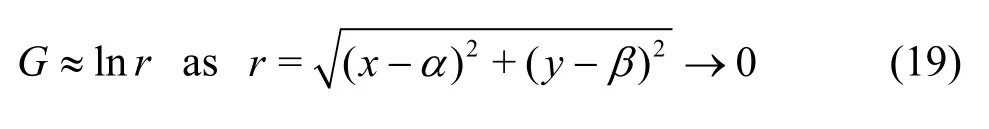
Since the submerged plate is infinitely extended along the horizontal direction, the source point(α, β) can be either in the fluid domain above/below the submerged plate boundary. In case of finite water depth,it is assumed that (α, β) is in above the submerged elastic plate, the Green’s functionG(x,y; α, β)satisfying Eq. (1) along with the boundary conditions(5a) and (19) is given by

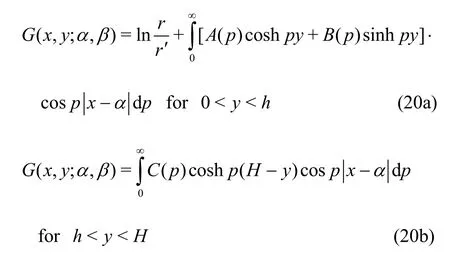
wherewithx＞0, α＜∞and 0＜β＜h. Using the free surface and submerged plate conditions (10)-(12), and the results[33-34]

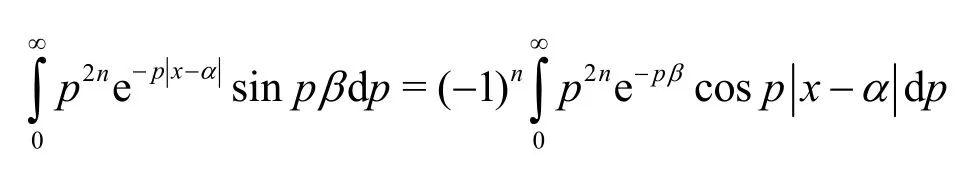
and

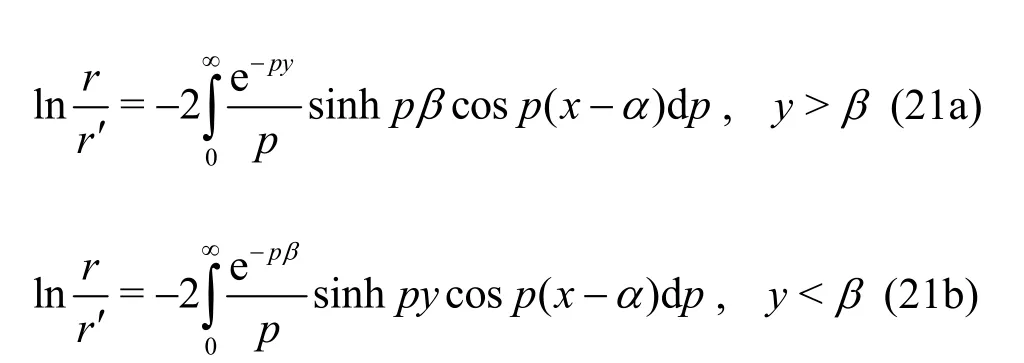
the unknown functions ()A p, ()B pand ()C pare obtained as

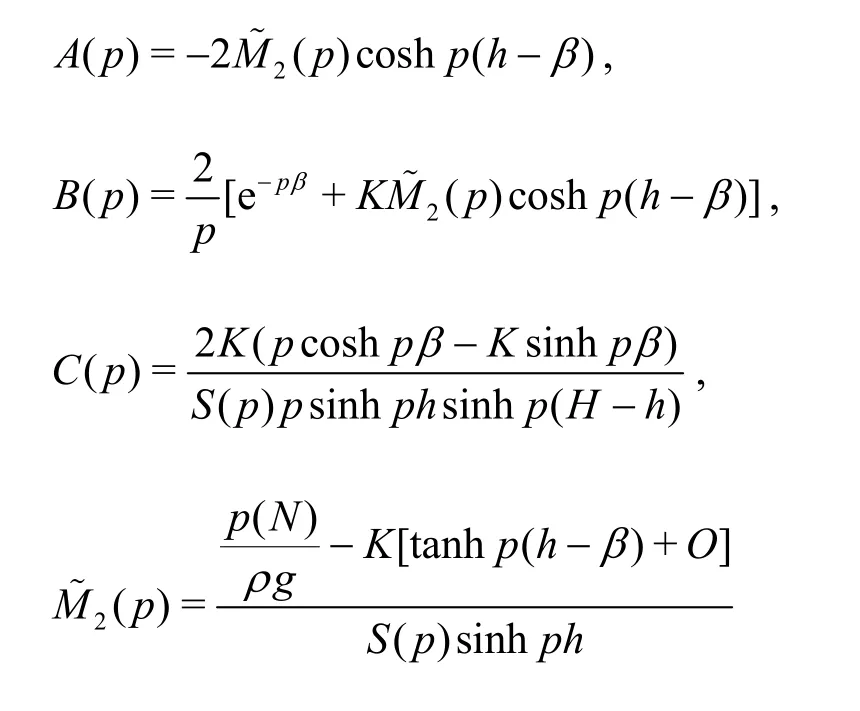
where

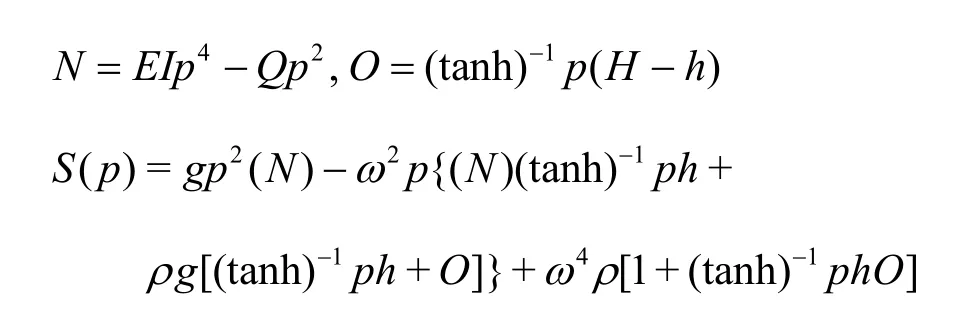
It may be noted that

is the dispersion relation associated with the gravity wave interaction with submerged elastic plate in finite water depth which is equivalent to the relation in Eq.(16).

When the source point (,)α β is in below the submerged elastic plate, the Green’s function (,;G x yα, β) satisfying Eq. (1) along with the boundary conditions (5a) and (19) is expanded as

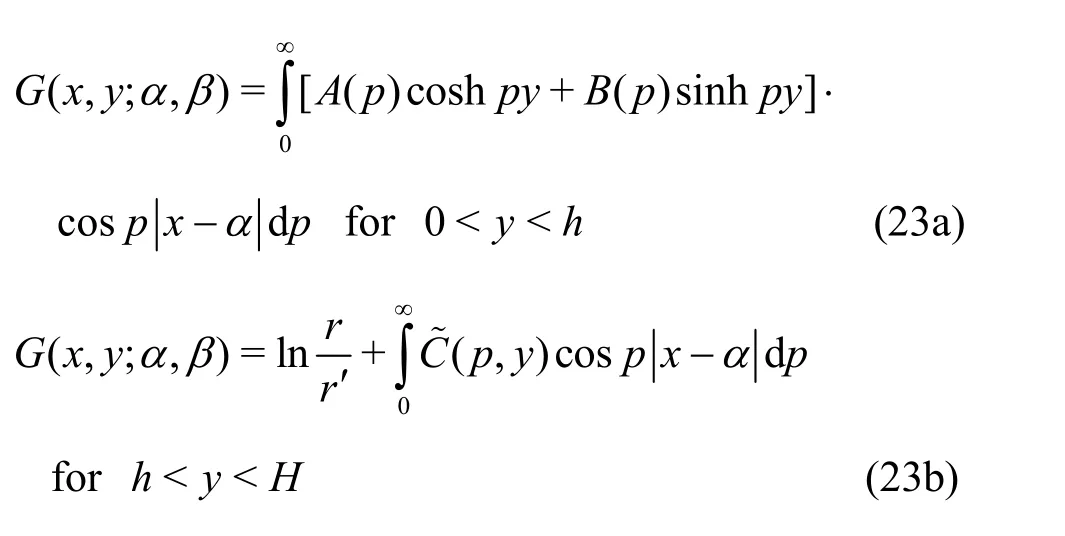
where(p,y) =C(p) coshp(H-y) +D(p) sinhp·(H-y) withx＞0, α＜∞ andh＜β＜H. The unknown functionsA(p),B(p),C(p) andD(p)in Eq. (23) are obtained as

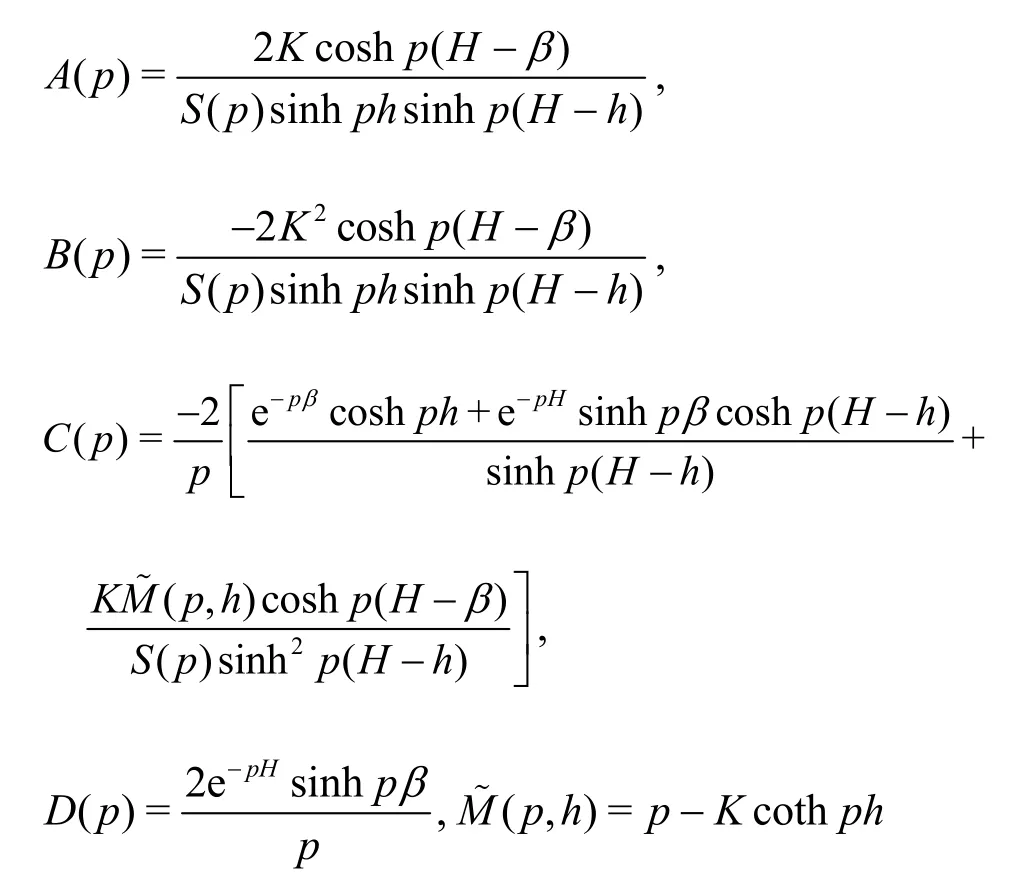
It is assumed that the dispersion relation (22) has two distinct positive real rootspn,n=I,IIpn,n=I,II, four complex rootspn,n=III,… ,VI of the forma±iband -c±idand infinite number of purely imaginary rootspn,n=1,2,…[8]. However,the roots behavior of the dispersion relation in Eq. (22)associated with the progressive waves are discussed in brief in Section 3.

Applying Cauchy residue theorem and utilizing the identity in Eq. (21), from Eqs. (20) and (23), in c tha a ste[

27o]f finite water depth, it can be easily derived

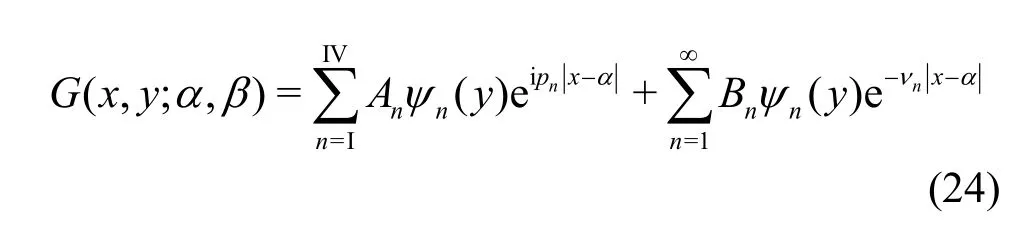
where

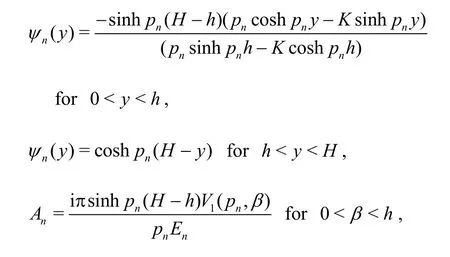
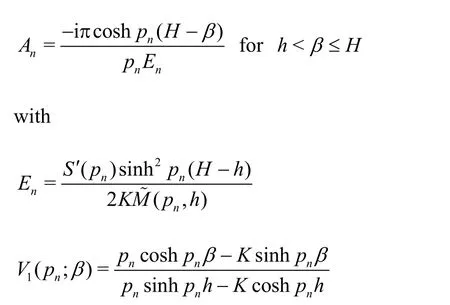
andBnin Eq.(24) can be obtained by puttingpn=iνnin the expression forAnandS′(pn) is the derivative ofS(pn) with respect topn. It may be noted that in Eq. (24), roots leading to boundedness of the Green's function are only taken in the expansion formulae. The expansion formula for the Green’s functionG(x,y;α, β) is derived based on the assumption that the dispersion relation in Eq. (22) has distinct roots.

Next, the Green’s functionG(x,y;α, β) associated with surface gravity wave interaction with submerged elastic plate is derived in case of infinite water depth. Assuming that the source point (α, β)lies above the submerged plate, the Green’s functionG(x,y;α, β) satisfying Eq. (1) along with the boundary condition (5b) is given by

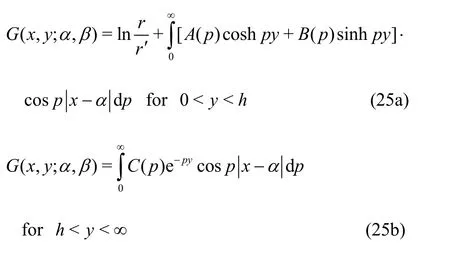
where

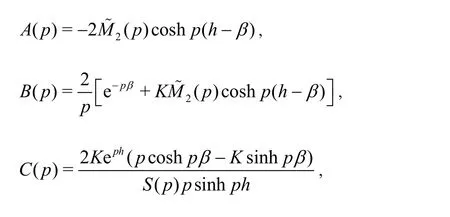
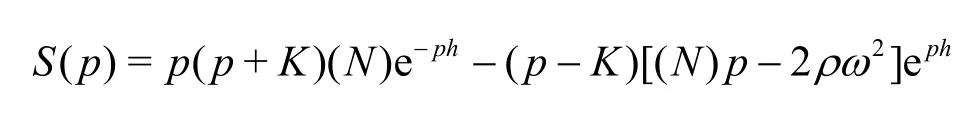
where()pbeing the same as defined in the expression ()B passociated with Eq.(27) withH→∞. In Eq. (25)

yields the dispersion relation for wave motion in the presence of infinitely extended submerged plate in infinite water depth.

On the other hand, assuming that the source point(α, β)is in below the submerged plate, the Green’s functionG(x,y;α, β) satisfying Eq. (1), along with the boundary condition (5b) is expanded as

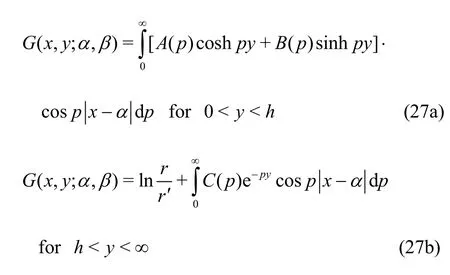
where

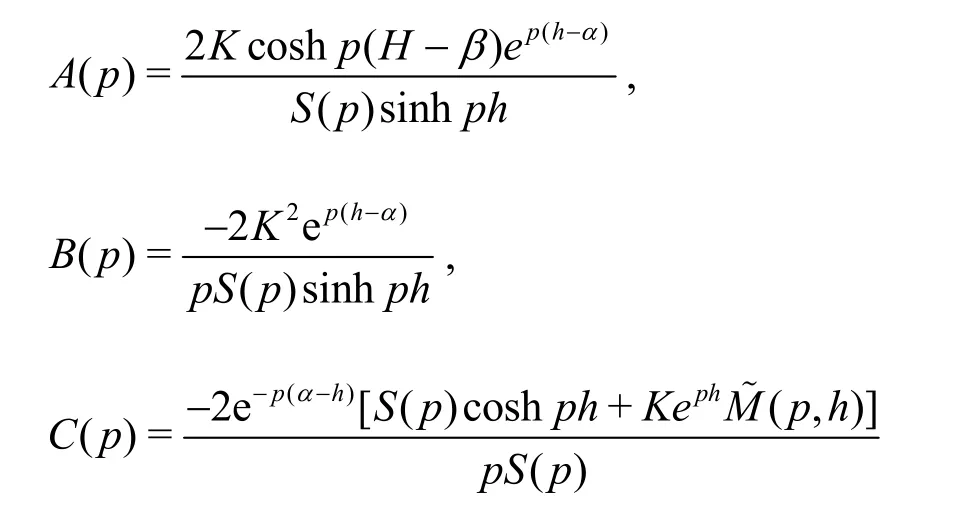
withS(p) is being same as in Eq. (26) andp,h) is same as in the expressionC(p) associated with Eq. (23).

Now, using Cauchy residue theorem of complex function theory and proceeding in a similar as in Mohapatra and Sahoo[27], the alternate form of the Green’s function associated with surface gravity wave interaction with submerged elastic plate in water of infinite depth is obtained as

where

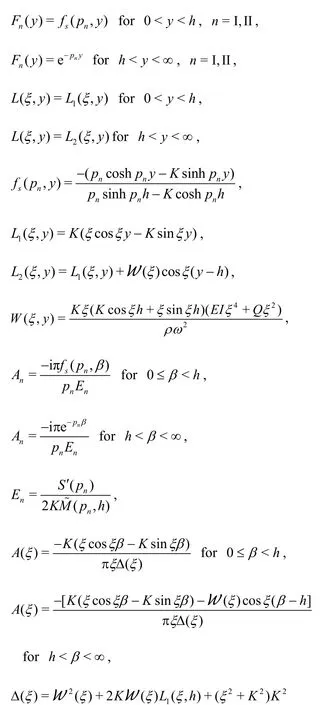
3.2 Expansion formulae based on Green’s function techniqueion

In this subsection, using the source potentialG(x,y;α, β) derived in the previous subsection and Green’s identity, the expansion formulae for the surface gravity wavemaker problem in the presence of a horizontal submerged flexible plate is derived. In this case, the spatial velocity potential (,)x yφ satisfies the Laplace equation as in Eq. (1), along with the bottom boundary conditions ((5a), (5b)), the boundary conditions on the free surface and submerged flexible plates as in Eqs. (10)-(12). In addition,assuming that a vertical wavemaker oscillates with frequency ω and amplitude ()u yabout its mean position at =x0 on the wavemaker, the velocity potential satisfies

for 0＜y＜Hin finite water depth and 0＜y＜∞in infinite water depth except aty=h. In order to derive an integral representation of the velocity potential in terms of the Green’s functionG(x,y;α, β) andu(y), set

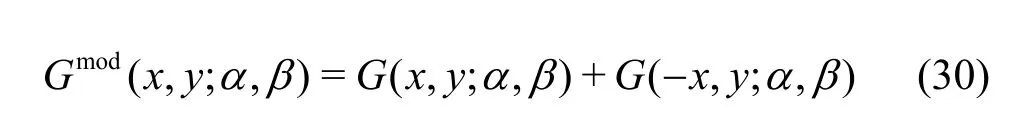
with zero normal velocity on the wavemaker, i.e.,(0,y; α, β) = 0. Further, using the conditions on the free surface and on the submerged plate, it can be derived that

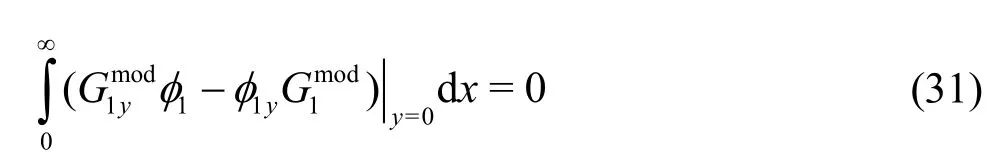
and

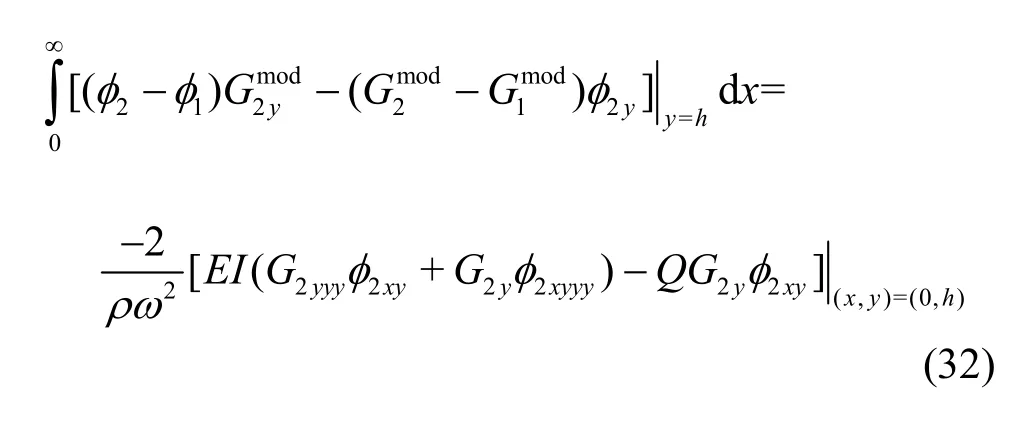
where the subscripts 1 and 2 in the velocity potentials φ and source potentialsG(x,y;α, β) refer to the fluid regions above and below the submerged plates respectively. Applying Green’s second identity to the velocity potential φ(x,y) associated with the wavemaker problem andGmod(0,y; α, β) = 0 and using Eqs. (31), (32), the velocity potential in terms of the Green’s functionGis obtained as

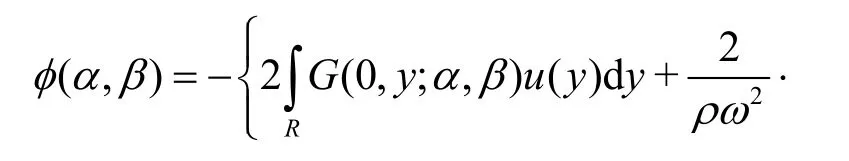
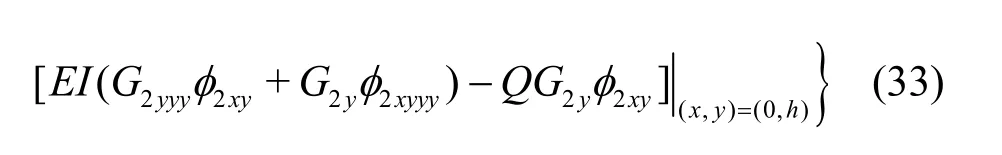
whereRis the finite interval (0, )Hin case of finite water depth and the semi-infinite interval(0,)∞ in case of infinite water depth. Next, substituting the explicit forms of the Green’s function from Eq. (24) into Eq. (33), the velocity potential (,)x yφ associated with the gravity wavemaker problem in the presence of submerged elastic plate in finite water depth is obtained as

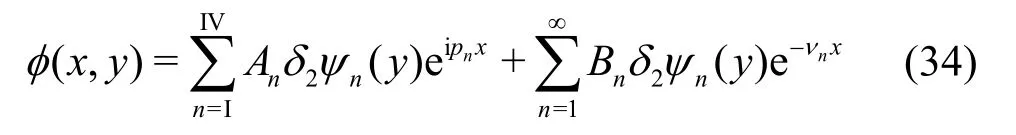
wherenA?s are given by

andBn,n=1,2,… are obtained from the expression forAnwithpn=iνn, δ2=1 for β∈ ( 0,h) ∪ (h,H),δ2=1/2 for β=0,Handu(y)is same as defined in Eq. (29). Further, the eigenfunction ψn(y)andEn?s are being same as in Eq. (24).

Proceeding in a similar manner as in case of finite depth, substituting the explicit forms of the Green's function from Eq. (28) into Eq. (33), the velocity potential in case of infinite water depth is obtained as

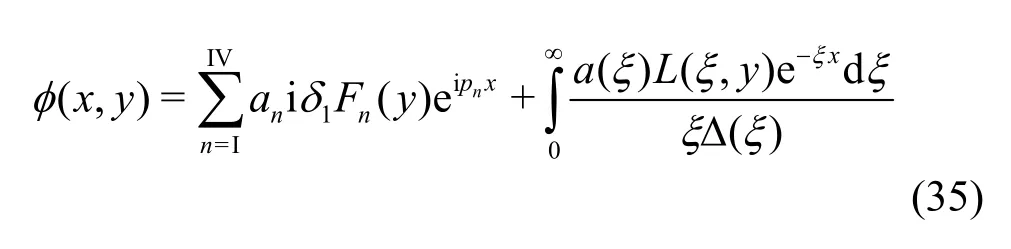
wherenaand ()aξ are given by

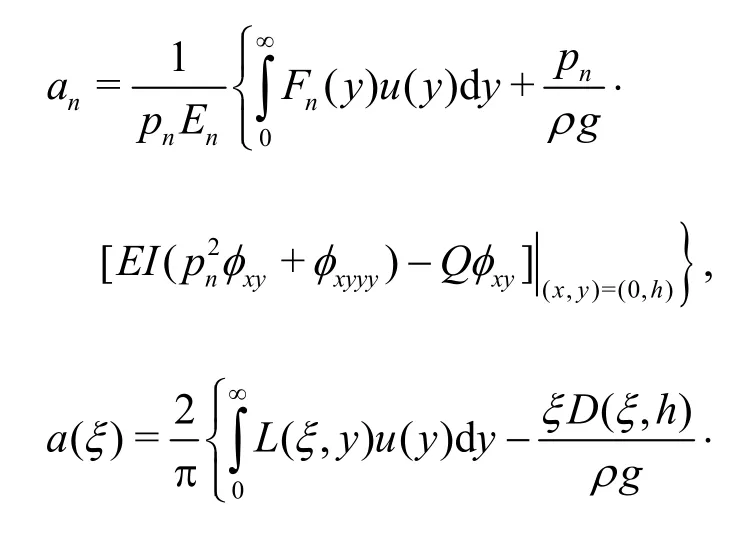
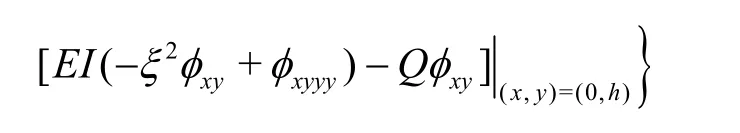
wherepn,En,Fn(y), Δ(ξ) andL(ξ,y) are being the same as defined in Eq. (28),u(y)is same as defined in Eq. (29) andD(ξ ,h) =(ξs i n ξh+Kcosξh) with δ1=1 for 0＜β＜hand δ1=1/2 for β=0. However,ananda(ξ) are expressed in terms of the two unknowns φxy( 0,0)and φxyyy(0,0)which have to be determined from appropriate edge conditions while dealing with specific physical problem.

Further, if the condition on the wavemaker, as in Eq. (29), is replaced by

thenGmodis chosen as

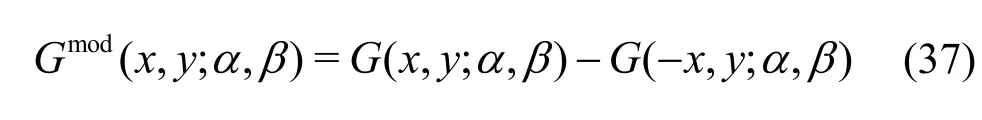
which leads toGmod(0,y; α, β) = 0 and the velocity potential in Eq. (33) will be replaced by

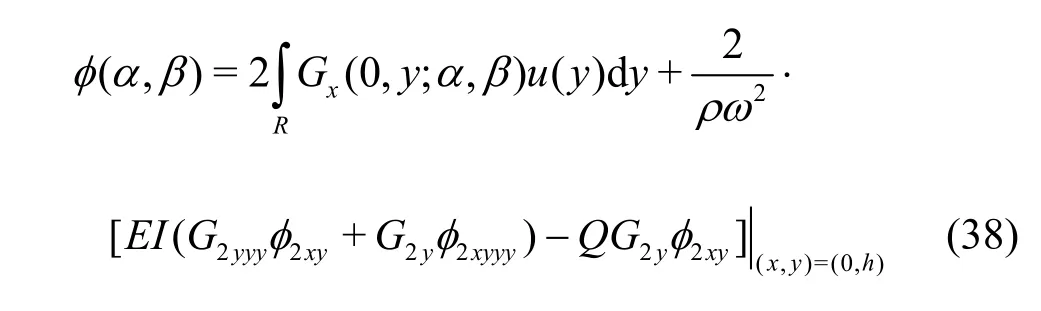
withRbeing the same as defined in Eq. (33). The velocity potential (,)x yφ in both the cases of water of finite and infinite depths can be easily obtained by proceeding in a similar manner as in previous case.

3.3 Expansion formulae based on eigenfunction expansion method

In this subsection, alternate derivation of the expansion formulae are obtained for the velocity potentials for the wavemaker problem discussed in previous subsection. The expansion formula in case of finite water depth is obtained using eigenfunction expansion method and a mixed type Fourier transform is used in case of infinite water depth. It may be noted that similar approach was used by Mohapatra and Sahoo[27]to derive the expansion formulae only for velocity potentials associated with wave interaction with floating and submerged elastic plate.

3.3.1 Case of finite water depth

The velocity potential (,)x yφ satisfying Eq. (1)along with the boundary conditions Eq. (5a) and Eqs.(10)-(12) in the case of finite depth can be expanded as

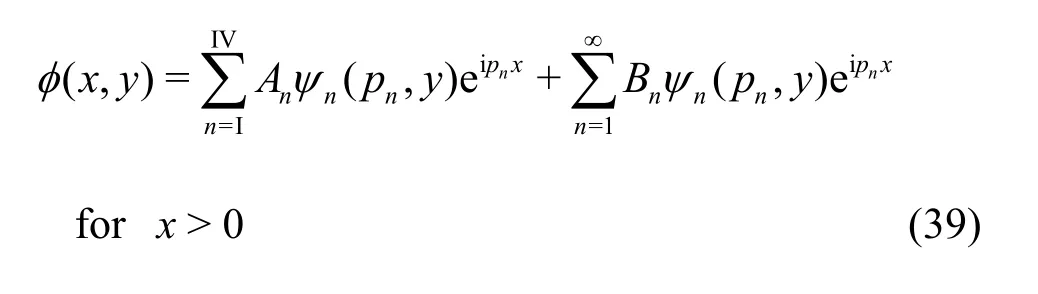
where the eigenfunction ψn?s are the same as in Eq.(24),Bn?s are unknowns to be determined. The eigenvaluespn?s satisfy the dispersion relation as in Eq.(22) withpn=iνnforn= 1,2,…. The orthogonal mode-coupling relation is given by

where

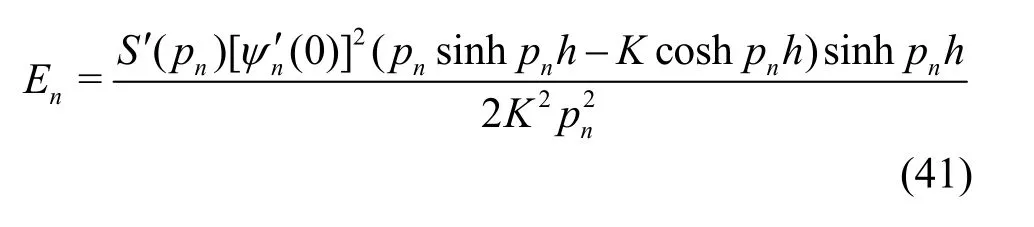
which has the alternate form in terms of′(h) as given by

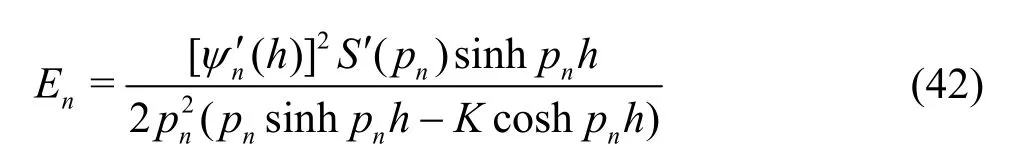
withS(pn) being the same as defined in Eq. (22) inpnand δmnis the Kronecker delta function. Using the orthogonal mode-coupling relation (40) on Eq.(39), the unknown coefficients are obtained as

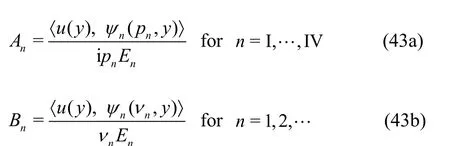
It may be noted thatnA?s in Eq. (43) are the same asnA?s in Eq. (34). This completes the deriva-tion of the expansion formula and the associated orthogonal mode-coupling relation in the case of finite water depth. It should also be noted that the orthogonal mode-coupling relation given in Eq. (40) is similar to the orthogonal mode-coupling relations used by Hassan et al.[8]in the absence of compressive force.

3.3.2 Case of infinite water depth

The velocity potential (,)x yφ satisfying Eq. (1)along with the boundary conditions Eqs. (5b), (10)-(12)in the case of infinite depth can be expanded as

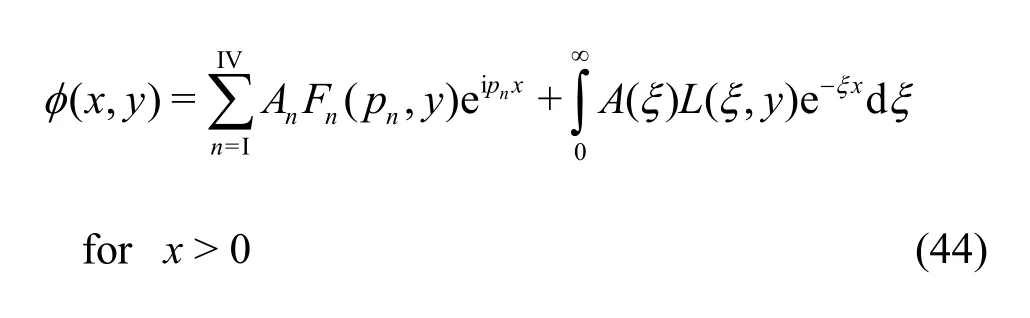
whereAn?s are unknowns,A(ξ) is the unknown function to be determined withFn(pn,y) andL(ξ,y) being the same as in Eq. (28). It can be easily derived that the eigenvaluespn?s satisfy the dispersion relation as in Eq. (26). Keeping the realistic nature of physical problems in mind, it is assumed that the dispersion relation (26) has two distinct real positive rootspIandpII, four complex rootspIII,pIV,pVandpVIare of the formsa±iband-c± id. Using a similar argument as in case of finite water depth, the boundedness criteria of the velocity potential φ(x,y) at the far field yieldsAV=AVI=0 in the expansion formula given by Eq. (44). It can be easily derived that the set of eigenfunctionsFn(pn,y) andL(ξ,y) are orthogonal with respect to the mode-coupling relation as given by

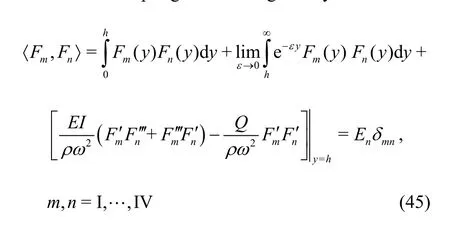
whereEnand δmnbeing the same as in Eq.(40) asH→∞. Again, it can be derived that

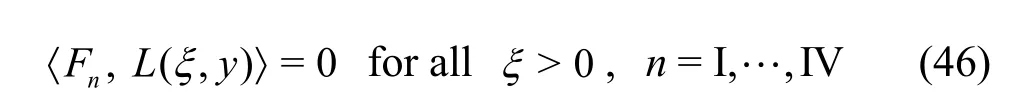
Relations (45) and (46) ensure that the eigenfunctionsFn(pn,y),n=I,… ,IV andL(ξ,y) are orthogonal with respect to the mode-coupling relation defined in Eq. (45). Using the above mentioned orthogonal mode-coupling relation (45) on Eq. (44),the coefficients associated with the expansion formulae are obtained as

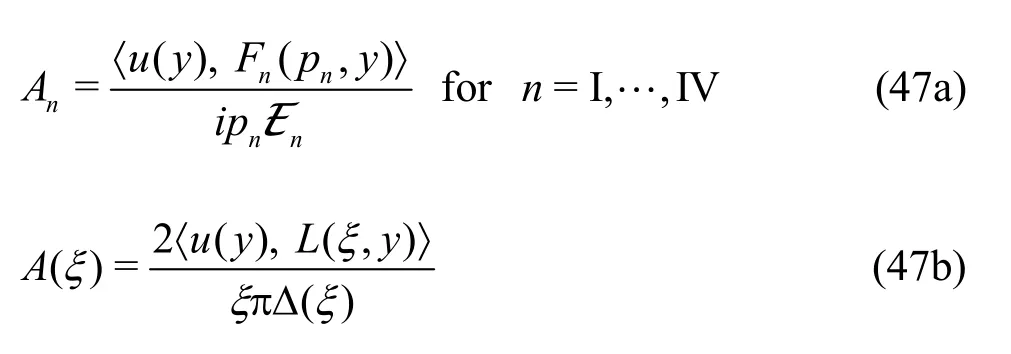
where ()ξΔ being the same as in Eq. (28) and the velocity potential φin Eq. (35) is same as in Eq.(44).

NB: It may be noted that the valuesnA?s in Eq.(43) are same as in Eq. (34) in case of finite water depth. Further, in case of infinite water depth, the velocity potential φ in Eq. (35) is same as in Eq. (44)as observed by Eq. (47).x＜∞, 0＜y＜Hin case of finite water depth except the region occupied by the articulated submerged plate as in Fig. 4. In order to obtain the velocity potential and analyze the effect of articulation on the submerged plate, the fluid domain is divided into two sub-domains, namely region 1 for ＞0xand region 2 for ＜0xin water of finite depth. The submerged plate is assumed to be infinitely large and is a combination of two semi-infinitely large plates which are kept in the planes ＞0xand ＜0xaty=h.

The spatial velocity potentials φj(x,y),j=1,2 will satisfy the Laplace equation in the fluid domain as in Eq. (1) along with the boundary conditions(10)-(12), where1(,)x yφ and2(,)x yφ correspond

4. Application of expansion formulae

In the present section, the utility of the expansion formulae are demonstrated by deriving the solutions for the velocity potentials associated with surface gravity wave interaction with articulated submerged flexible plate in the presence of compressive force in water of finite depth. The wave diffraction by submerged flexible plate in water of infinite depths will lead to the solution of certain integral equations which requires a different type of analysis and thus differed in the present study.

As a direct application of the expansion formulae,interaction of surface wave with an articulated submerged elastic plate is studied in finite water depth.The fluid characteristics remain the same as discussed in section 2. The fluid occupies the region ＜-∞to the velocity potentials in the regionsx＞ 0 andx＜ 0 respectively. In addition, at the interfacesx= 0±, the continuity of pressure and velocity yield

and

The plates are connected at =0x± and =yhby vertical linear spring with stiffness33kand flexural rotational spring with stiffness55k. Thus, the bending moment and shear force at the connected edges (0, )h± satisfy the following conditions in φ as given by[35]

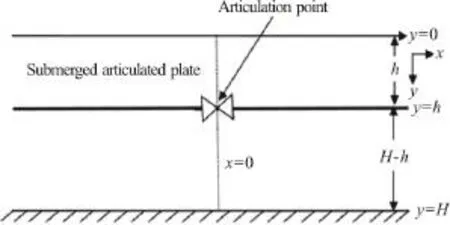
Fig. 4 Schematic diagram of articulated submerged plates

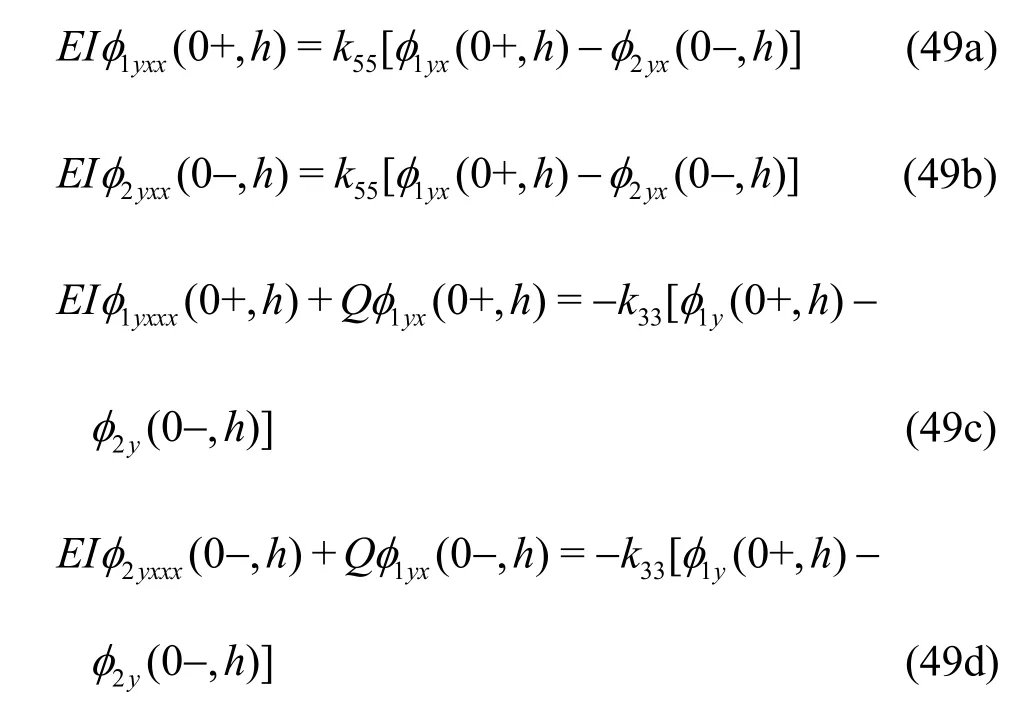
Further, the far field radiation condition is given by

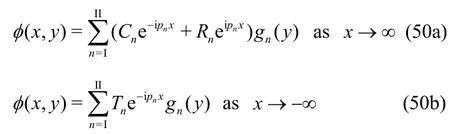
wherenC?s are the amplitude of the incident waves assumed to be known,nR?s andnT?s are the unknown constants associated with the amplitude of the reflected and transmitted waves and are to be determined. Here, subscript Iand IIrefer to the waves generated due to the gravity waves in surface and flexural mode respectively. Furthergn(y)?s are defined as:

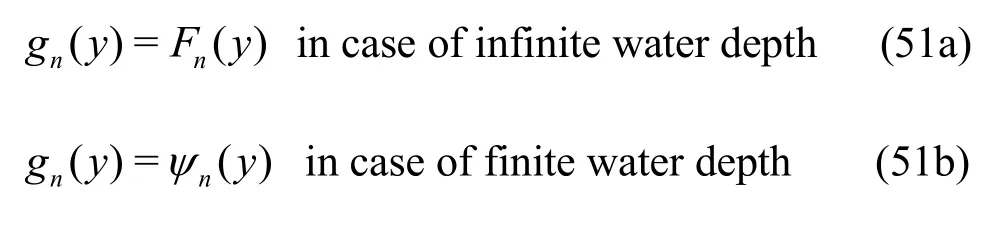
where ψn(y) andFn(y)are being the same as in Eq.(24) and Eq. (28) respectively. Exploiting the geometrical symmetry of the physical problem aboutx=0, the boundary value problem in φis split into the reduced potentials defined by[28].

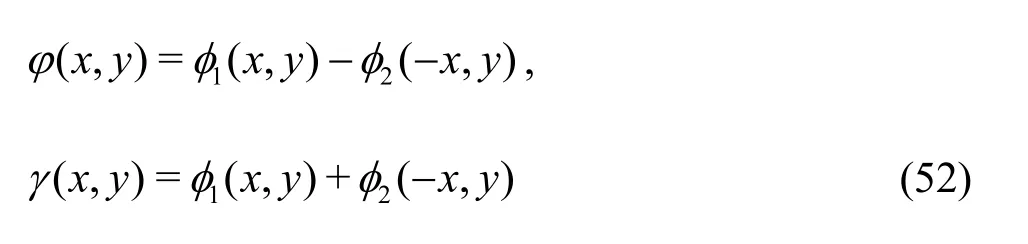
Thus, the reduced potentials φ(x,y) and γ(x,y) will satisfy the governing Eq. (1) in the region 0＜x＜∞ along with the free surface boundary condition (10) and the bottom conditions (5a) and (5b)independently in both the cases of water of finite and infinite depths. The edge conditions (49a)-(49d) for the bending moment and shear force in terms of φ(x,y) and γ(x,y) are derived as

whereAn=Rn-TnandBn=Rn+Tn. Finally, the continuity of pressure and velocity as in (48a) and(48b) yield

Thus, the boundary value problem in terms of the reduced potentials (,)x yφ and (,)x yγ are defined in a semi-infinite strip (0＜＜x∞,0＜＜yH) in water of finite depth.

In finite water depth, using the expansion formulae as in Subsection 3.3, the reduced velocity potential (,)x yφ satisfying the governing Eq. (1),the boundary conditions (5a), (10-12) is obtained as

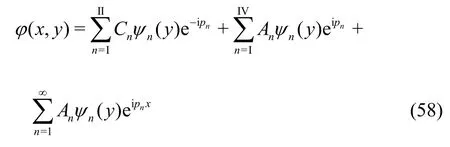
wherepn=iνnforn= 1,2,… and ψn(y)?s being the same as defined in Eq. (39). Using the edge conditions as in Eq. (54) and the orthogonal modecoupling relation as in Eq. (40), the unknown coefficientsAn?s forn= I,… , I V,1,2,… are given by

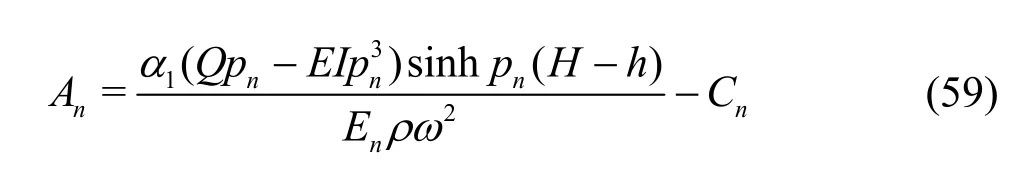
where

withnEbeing the same as defined in Eq. (41).Proceeding in the similar way, the reduced velocity potential (,)x yγ satisfying the governing Eq. (1) and the boundary conditions (5a), (10)-(12) is obtained as

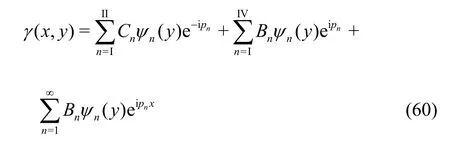
whereCnbeing the same as defined in Eq. (58).Using the edge conditions as in Eq. (53) and the orthogonal mode-coupling relation as in Eq. (40), the unknown coefficientsBn?s forn=I,… , I V are obtained as

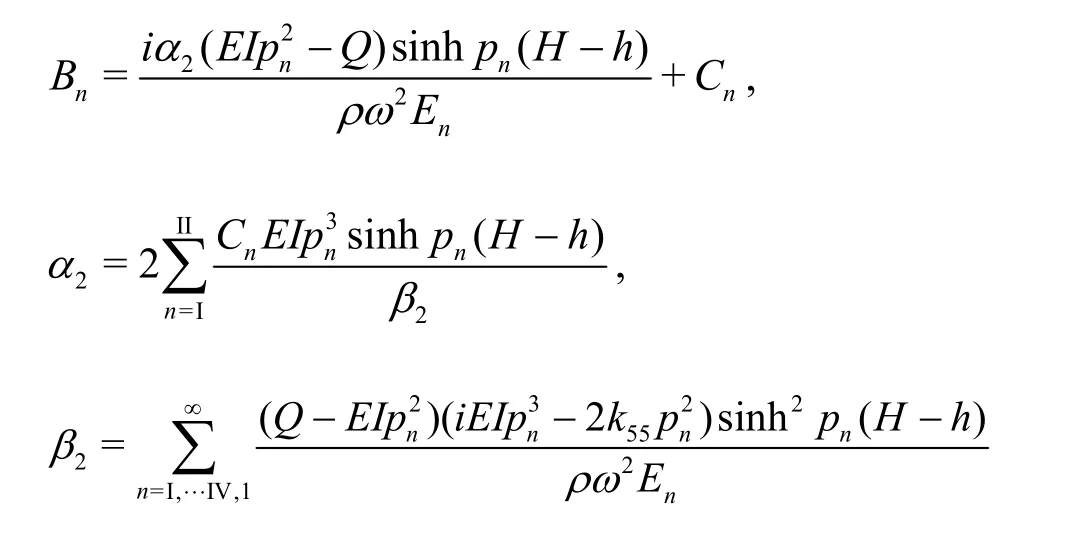
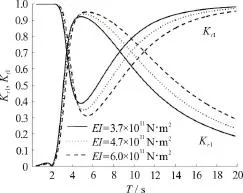
Fig. 5(a) Variations of reflection coefficients K r I and transmission coeffic ient s K t Iversus time period T for variousvaluesofflexural rigidity EI with k33=0.1× 1 011 N/m , k =0.1× 1 01 1 N· m /r ad , Q = 0.2·55, and h/ H = 0.5 in surface mode

Once the constantsAnandBnforn= I,IIare determined, then the reflection and transmission coefficients associated with the wave modes of surface and submerged articulated plate can be computed using the formulaeKrn=(An+Bn) /2CnandKtn=(A-B)/2Cforn= I,II. Using Green’s identity to the velocity potential along with its complex conjugate in the fluid domain[8], the energy relation in terms of the reflection and transmission coefficients are obtained as terms of the reflection and transmission coefficients are obtained as

whereEnforn= I,II being the same as defined in the orthogonal mode-coupling relations (40). This relation is often used to check the accuracy of the computational result. Certain numerical results are discussed next to understand the diffraction pattern.

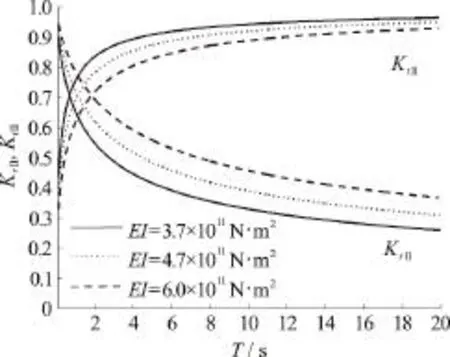
Fig. 5(b) Variations of reflection coefficients K r II and transmission coeffic ient s K tI I v ersus time period T or variousvaluesofflexuralrigidity EI with k33=0.1× 1 011N/m , k =0.1× 1 01 1 N· m /r ad , Q = 0.2·55, and h/ H = 0.5in submerged flexural mode in finite water depth

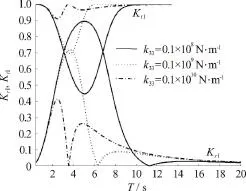
Fig. 6(a) Variations of reflection coefficients K r I and transmission coefficients K t I versus time period T for various values of k3 3 with k 55=0.1× 101 1 N· m/rad,Q=0.2, EI= 0 .47× 1 011 Nm2, and h / H =0.5 in surface mode

In Fig. 5, the reflection and transmission coefficients for different values of flexural rigidityEIwithk33= 0 .1× 1 011N/m ,k55=0.1× 1011N· m/rad ,andQ=0.2versus time periodTare plottedin (a) surface mode and (b) submerged flexural mode. From Fig. 5(a), it is observed that for smaller wave period, the effect ofEIon reflection coefficientKrIand transmission coefficientKtIis less whilst, for higher time period, the reflection coefficientKrIincreases with an increase inEI.Further, the observations of transmission coefficientKtIare opposite in nature to that of reflection coefficientKrI. However, the reflection coefficientKrIattends minimum for a particular value of time period. On the other hand, from Fig. 5(b), it observed that the reflection coefficientIIrKincreases with an increase in the value ofEIwithout attending minimum whilst, the transmission coefficientIItKpattern is opposite to that ofIIrK.

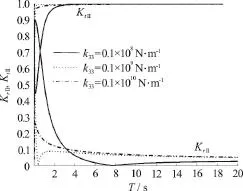
Fig. 6(b) Variations of reflection coefficients K r II and transmission coefficients K tI I versus time period T for various values of k 3 3 with k 55=0.1× 101 1 N· m/rad,Q = 0.2, E I = 0.47× 1 011 N· m2, and h/ H=0.5in submerged flexural mode in finite water depth

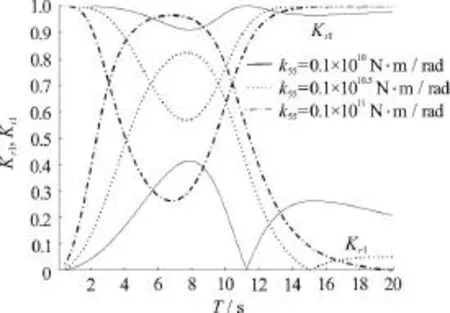
Fig. 7(a) Variations of reflection coefficients K r I and transmission coefficients K t I versus time period T for various values of k55 with k33=0.1× 1 07 N/m ,Q=0.2, EI = 0.47× 1 011 N· m2, and h/ H=0.5 in surface mode

In Fig. 6, the reflection and transmission coefficients for different values of spring stiffnessk33withk55=0.1× 1011N· m/rad ,Q=0.2andEI= 0.47× 1 011N· m2in (a) surface mode and (b)submerged flexural mode versus time periodTare plotted. From Fig. 6(a), it is observed that the reflection coefficientKrIdecreases with an increase in vertical linear spring stiffnessk33whilst, the observations in transmission coefficientKtIis oppo-site in trend to that of reflection coefficientKrI.Further, the resonating pattern for reflection coefficientKrIshifted towards origin with an increase in vertical linear spring stiffnessk33. On the other hand, from Fig. 6(b), it is observed that the variations of reflection and transmission coefficientsKrIIandKtIIfor different spring constantk33is more for smaller time period. The observations in transmission coefficientKtIIis similar to that of Fig. 6(a).

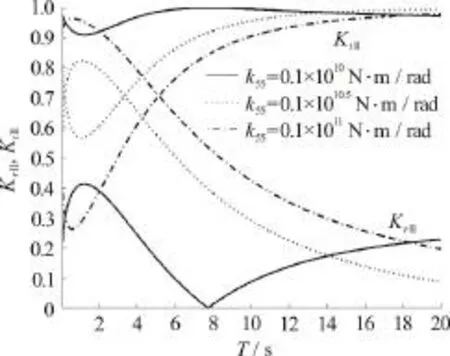
Fig. 7(b) Variations of reflection coefficients K r I and transmission coefficients K t I versus time period T for various values of k55 with k33=0.1× 1 07 N/m ,Q=0., EI = 0.47× 1 011 N· m2 and h/ H=0.5 in submerged flexural mode in finite water depth

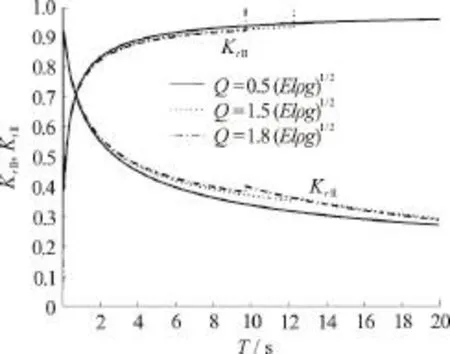
Fig. 8 Variatio ns of reflection coeffici ents K r II and transmission coeffic ien ts K tI I versu stimeperiod T for variousvaluesofcompressiveforce Q with k33=0.1× 1 011 N/m , k =0.1× 101 1 N· m/rad , EI = 0.47×55 1011 N· m2 and h/ H= 0 .5in submerged flexural mode in finite water depth

In Fig. 7, the reflection and transmission coefficients for different values of spring stiffnessk55withk33=0.1× 107N/m ,Q=0.2andEI=0.47× 1 011N· m2in (a) surface mode and (b)submerged flexural mode versus time periodTare plotted. From Fig. 7(a), the resonating patterns in reflection coefficients are observed and the reflection coefficients increases with increase ink55in surface mode. However, a reverse pattern is observed in case of transmission coefficients. On the other hand, from Fig. 7(b), the reflection coefficients increases with increase ink55and resonating pattern disappears for higher values of rotational spring stiffness in submerged flexural mode.

In Fig. 8, the reflection and transmission coefficients for different values of compressive forceQwithk33=0.1× 1 011N/m ,k55=0.1× 1011N· m/rad andEI= 0.47× 1 011N· m2versus time periodTin submerged flexural mode are plotted. From Fig. 8, it is observed that the reflection coefficient increases with an increase in compressive force. However, there is a resonating fluctuation in the reflection and more in transmission coefficients. This may be due to the fact that the presence of spring constants. It may be noted that the reflection and transmission coefficients in surface mode are deferred here because of not much variation observed.

From Figs. 5-8, it is observed that the reflection and transmission coefficients satisfy the energy relation+=1, which ensures that the accuracy of the computational numerical results.

5. Conclusions

In the present work, interaction between surface gravity waves and submerged flexible structures is analyzed based on linearized water wave theory and small structural response in both finite and infinite water depths. The wave motion characteristics in surface and submerged flexural mode are analyzed by studying the phase, group velocity, surface elevation and submerged plate deflection through generalized dispersion relation. The expansion formulae along with the corresponding orthogonal mode-coupling relations for wavemaker problems associated with interaction between surface wave and submerged flexible structures in two-dimensions are derived and compared based on Green’s function technique and eigenfunction expansion method. It is observed that the solutions obtained by the both methods are the same. The developed expansion formulae will play a significant role in obtaining realistic solution of wave-structure interaction problems in various areas of applied science in the broad area of fluid structure interaction. Application of the expansion formulae are demonstrated by deriving solutions associated with surface wave scattering by articulated submerged flexible plate in finite water depth. In addition, the long wave equations based on shallow water approximation are derived in a direct manner in Appendix A in order to compare with the shallow water results.

In numerical results, it is observed that the phase and group velocity in surface mode is higher than that of submerged flexural mode. Further, the amplitude of free surface elevation is larger compared to that of submerged flexible plate deflection due to the fact that more wave energy is concentrated near the free surface. The reflection coefficients increases with an increase in the values of rotational stiffness and flexural rigidity of the articulated plate, which may be concluded that all wave energy gets transmitted due to the fact that the articulated submerged flexible plate behaves like a continuous plate. In all these cases, it is observed that the transmission coefficient pattern is opposite to that of the reflection coefficient. The accuracy of the computed numerical results are checked with the relation which satisfies+=1.

The obtained results will be useful in developing mechanism for attenuating wave load on coastal/marine facilities used for various developmental activities that is wave energy conversion and breakwater. Furthermore, the present formulation and methodology can be easily generalized to the problems of composite breakwater with a submerged horizontal flexible structures and a lower rubble mound.

[1] Cho I. H., Kim M. H. Interaction of a horizontal flexible membrane with oblique incident waves [J].Journal of Fluid Mechanics, 1998, 367: 139-161.

[2] Cho I. H., Kim M. H. Wave deformation by a submerged circular disk [J].Applied Ocean Research, 1999, 21(5):263-280.

[3] Cho I. H., Kim M. H. Interaction of a horizontal porous flexible membrane with waves [J]. Journal of Waterway Port Coastal and Ocean Engineering, 2000, 126(5):245-253.

[4] Sawaragi T. Coastal engineering-waves, beaches, wave structures interactions [M]. Tokyo, Japan: Elsevier, 1995.

[5] Lee W. K., Lo E. Y. M. Surface-penetrating flexible membrane wave barriers of finite draft [J].Ocean Engineering, 2002, 29(14): 1781-1804.

[6] Siew P. F., Hurley D. G. Long surface waves incident on a submerged horizontal plane [J].Journal of Fluid Mechanics, 1977, 83: 141-151.

[7] Yu X. Functional performance of a submerged and essentially horizontal plate for offshore wave control: A review[J].Coastal Engineering Journal, 2002, 44(2): 127-147.

[8] Hassan U. L. M., Meylan M. H., Peter M. A. Water wave scattering by submerged elastic plates [J].Quarterly Journal of Mechanics and Applied Mathematics, 2009,62(3): 321-344.

[9] Lawrie J. B., Abraham I. D. An orthogonality relation for a class of problems with higher order boundary conditions,applications in sound-structure interaction [J].Quarterly Journal of Mechanics and Applied Mathematics, 1999,52(2):161-181.

[10] Wu J., Wan Z., Fang Y. Wave reflection by a vertical wall with a horizontal submerged porous plate [J].Ocean Engineering, 1998, 25(9): 767-779.

[11] Liu Y., Li Y. C., Teng B. Wave interaction with a perforated wall break water with a submerged horizontal porous plate [J].Ocean Engineering, 2007, 34(17): 2364-2373.

[12] Evans D. V., Peter M. A. Asymptotic reflection of linear water waves by submerged horizontal porous plate [J].Journal of Engineering Mathematics, 2011, 69(2-3):135-154.

[13] Liu Y., Li Y. C. An alternate analytical solution for waterwave motion over a submerged horizontal porous plate [J].Journal of Engineering Mathematics, 2011, 69(4):385-400.

[14] LIU Y., LI H. J., LI Y. C. A new analytical solution for wave scattering by a submerged horizontal porous plate with finite thickness [J].Ocean Engineering, 2012, 42(1):83-92.

[15] Behera H., Sahoo T. Hydroelastic analysis of gravity wave interaction with submerged horizontal flexible porous plate [J].Journal of Fluids and Structures, 2015, 54(1):643-660.

[16] Karmakar D., Sahoo T. Scattering of waves by articulated floating elastic plates in water of infinite depth [J].MarineStructures, 2005, 18(5): 451-471.

[17]Manam S. R., Bhattacharjee J., Sahoo T. Expansion formulae in wave structure interaction problems [J].Royal Society of London Proceedings Series A, 2006, 462(2065):263-287.

[18] Karmakar D., Guedes Soares C. Scattering of gravity waves by a moored finite floating elastic plate [J].Applied Ocean Research, 2012, 34(1): 135-149.

[19] Karmakar D., Guedes Soares C. Oblique scattering of gravity waves by moored floating membrane with changes in bottom topography [J].Ocean Engineering, 2012, 54:87-100.

[20] Lawrie J. B. Comments on a class of orthogonality relations relevant to fluid-structure interaction [J]. Meccanica,2012, 47(3): 783-788.

[21] Mondal R., Mohanty S. K., Sahoo T. Expansion formulae for wave structure interaction problems in three dimensions [J].IMA Journal of Applied Mathematics, 2013,78(2): 181-205.

[22] Sahoo T. Mathematical techniques for wave interaction with flexible structures, London [M], NewYork, USA:Chapman and Hall/CRC, 2012.

[23] Kohout A. L., Meylan M. H., Sakai S. et al. Linear water wave propagation through multiple floating elastic plates of variable properties [J].Journal of Fluids and Structures,2007, 23(4): 649-663.

[24] Korobkin A., Parau E. I., Broeck J. M. V. The mathematical challenges and modelling of hydroelasticity [J].Philosophical Transactions of the Royal Society A, 2011,369(1947): 2803-2812.

[25] Mohapatra S. C., Sahoo T. Surface gravity wave interaction with elastic bottom [J].Applied Ocean Research,2011, 33(1): 31-40.

[26] Mohapatra S. C., Guedes Soares C. Interaction of surface gravity wave motion with elastic bottom in threedimensions [J].Applied Ocean Research, 2016, 57:125-139.

[27] Mohapatra S. C., Sahoo T. Wave interaction with floating and submerged elastic plate system [J].Journal of Engineering Mathematics, 2014, 87(1): 47-71.

[28] Mohapatra S. C., Sahoo T. Oblique wave diffraction by a flexible floating structure in the presence of a submerged flexible structure [J].Geophysical and Astrophysical Fluid Dynamic, 2014, 108(6): 615-638.

[29] Williams T. D., Meylan M. H. The Wiener-Hopf and residue calculus solutions for a submerged semi-infinite elastic plate [J].Journal of Engineering Mathematics,2012, 75(1): 81-106.

[30] Mohapatra S. C., Ghoshal R., Sahoo T. Effect of compression on wave diffraction by a floating elastic plate [J].Journal of Fluids and Structures, 2013, 36: 124-135.

[31] Schulkes R. M. S. M., Hosking R. J., Sneyd A. D. Waves due to a steadily moving source on a floating ice plate.Part-2 [J].Journal of Fluid Mechanics, 1987, 180:297-318.

[32] Mondal R., Sahoo T. Wave structure interaction problems for two-layer fluids in three-dimensions [J].Wave Motion,2012, 49(5): 501-524.

[33] Gayen R., Mandal B. N. Motion due to fundamental singularities in finite water with an elastic solid cover [J].Fluid Dynamics Research, 2006, 38(4): 224-240.

[34] Mohapatra S. C., Sahoo T. Forced capillary-gravity wave motion of two-layer fluid in three-dimensions [J].Meccanica, 2014, 49(4): 939-960.

[35] Karmakar D., Bhattacharjee J., Sahoo T. Expansion formulae for wave structure interaction problems with applications in hydroelasticity [J].International Journal of Engineering Science, 2007, 45(10): 807-828.

Appendix A: Long wave equations based on shallow water approximation

Proceeding in a similar manner as in Mohapatra and Sahoo[27], the free surface elevationηand the submerged plate deflectionζsatisfy

Taking the double derivative of Eq. (3) with respect toxand using Eq. (A1), the linearized long-wave equation at =0yis obtained as Again, the equation of continuity for the linearized long-wave equation at =yhis given by

From Eqs. (9), (A2) and (A3), the linearized long wave equation in terms ofζis obtained as

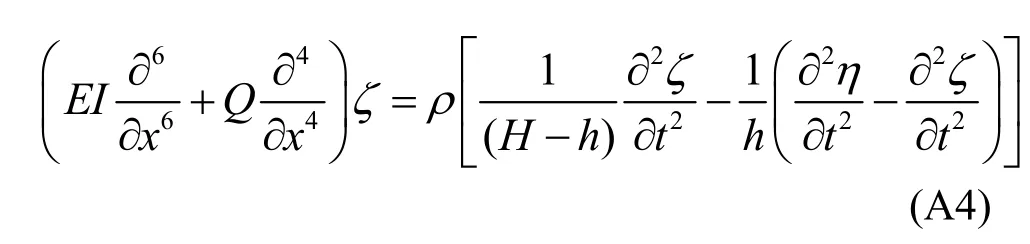
Considering the sinusoidal wavesη=Re·as discussed in Section 2, Eqs. (A2) and (A4) yields

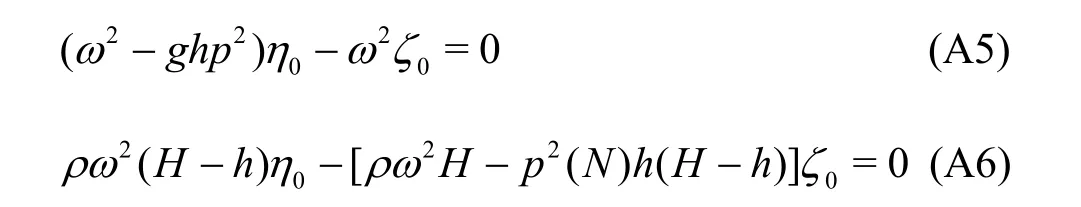
Eliminating0ηand0ζ, from Eqs. (A5) and (A6), it can be easily checked that the dispersion relation obtained here will be the same as in Eq. (16) in case of shallow water.