Broad but Brief Remarks on Paradox-driven Paraconsistency

Jc Beall

Department of Philosophy,University of Connecticut

jc.beall@uconn.edu

1 Logic

Logic,asafield,isbroadanddeep.1For a background sketch of the field of logic in general,see my essay with John P.Burgess.([14])Myfocusinthisessayisonlogicasanaccount of logical consequence.While an account of logical consequence may be given either model-theoretically(‘semantically’)or proof-theoretically(‘syntactically’)I will focus onthestandardsemanticapproach,treatinglogicalconsequenceasanentailmentrelation— a relation that(at least)‘preserves truth’over some target space of possibilities.(I choose this characterization because it is familiar,not because it holds some gods-given priority over a corresponding non-semantic characterization.)

Slightly more specifically,I will focus on logical consequence as a ‘formal’entailment relation,one where the‘form’of an argument is what matters for logical validity.

Logical validity,on this(standard)picture,applies to argument forms.Arguments are arguments in a language:an argument is a pair〈X,A〉where X is a set of sentences and A a sentence from a given language.2Sometimes the standard generalization to a set-set relation is useful.I flag some of the heuristic uses of set-set relations below.(See,e.g.,§4.1.)The form of an argument is defined via some setofexpressionsofthelanguage.Thelogicalformofasentenceisdefinedonlyinterms of the logical expressions.

Logical vocabulary,on my view,is the vocabulary of standard first-order logic(withoutidentity):thebooleanquartet(viz.,‘itistruethat…’,‘itisfalsethat…’,‘…and…’,and ‘…or….’)together with first-order quantifiers.(The material conditional is defined out of the falsity operator—that is,logical negation—and disjunction as usual:A→B is defined as?A∨B.)I have no new arguments for why this vocabulary is all there is to logicalvocabulary;butitisagoodcandidateforlogicalvocabularyinasmuchastradition has largely included it;and I henceforth treat it as the full set of logical vocabulary.

On my view,logical vocabulary is absolutely topic-neutral in the sense that it is involved ineverytrue theory — that is,every true‘complete-as-possible theory’(i.e.,complete with respect to truths about the theory’s given phenomenon),every systematic theory,everyclosedtheory.And this brings us to the role of logical consequence in our theories.

2 Logic’s role：universal closure on theories

Theories are closed under a consequence relation(which,again,I will take to be entailment relations of a certain kind).The consequence relations that close our theories are,as Tarski([35])described,closure relations or consequence operators.

There are a lot of formal entailment relations on any given natural language.([16])The role of logical consequence—logic—itself is as universal closure:it is the‘basement closure relation’involved in all consequence relations of our theories.

As theorists of a given phenomenon,we aim not only to throw into our theory various truths;we aim to ‘complete’the theory as far as possible by constructing the theory’s consequence relation — and thereby expanding the theory to contain not only the thrown-in truths(so to speak)but also all consequences of everything in the theory.In other words,the theorist has two jobs:on one hand,she must construct a set of claims thataretrueofthetargetphenomenon(or,atleast,trueaccordingtothetheorybeingconstructed),and on the other hand she must close such a set under the theory’s consequence relation?T.

Logical consequence(say,?)serves as the first-level closure relation for every theory’sT’s consequence(closure)relation?T.While each true theory’s consequence relationgoesbeyondlogicin‘validating’moreforms,no(true)theory’sconsequencerelation goes against logic by treating logically valid forms as invalid.Put another way:if logic says thatBis a consequence ofXthen so too does the theory’s consequence relation —that is,where?is logical consequence and?Ta theory’s consequence relation,ifX?Bthen alsoX?TB.

In this way logic is universal in the sense that it is involved in all of the consequence(closure)relations on our theories;and it is also in this sense that logic is topic-neutral,sinceit doesnot matterwhat the topicof theoryTmaybe,logicis involvedin its closure.

One example:logic tells us nothing at all about the consequences of knowledge claims(i.e.,claims that utilize the knowledge operatorIt is known that…)except what it tells us about all claims—namely,the logical consequence of such claims.But in our true theory of knowledge(where the knowledge operator is a key theoretical expression,defining new ‘forms’of expressions for the theory’s consequence relation),our theory’s consequence relation?Twill validate the step fromit is known that ptopitself,that is,we will have that Kp?Tpwhere K is the knowledge operator.3Of course,if the truth about knowledge is that this would-be entailment fails,then our given consequence relation had better not validate this step;but I leave the truth of that issue to epistemologists.Logic will not tell us that;we,as systematic theorists of knowledge,must construct the appropriateextralogicalconsequence relation—a relation going beyond logic.The construction of such extra-logical consequence relations do not go against logic;they build on top of it.

The foregoing gives a small sense of the target conception of logic’s role:namely,it s the universal‘basement-level’closure relation for all of our true theories,be they mathematics,biology,theory of knowledge,theology,metaphysical necessity,more obligation,or what-have-you.

3 Paraconsistent logic

Paraconsistent logic,on the foregoing account of logic and its role,takes the universal consequence relation to be ‘paraconsistent’.Here,we say that a consequence relation?is paraconsistent if and only if{A,?A}? B for some A and B,that is,iff the given form is invalid—iff the given entailment—is not sanctioned(i.e.,not valid)according to the given relation.

A paraconsistent account of logical entailment,on the view of logic and its role that I am discussing,is one according to which logic does not take a negation-inconsistent theory T(i.e.,where A ∈ T and?A ∈ T for some sentence A in T’s language)to the trivial theory LT,which is simply the set of all sentences in the language LTof theory T.In other words,when you close a negation-inconsistent theory T under logic you will not wind up with the trivial theory LTas the resulting closed theory.

What this account of logic allows are true theories that are closed under logic but are not identical to the theory’s trivial theory.

4 Subclassical logic

While there are many ways of constructing a paraconsistent account of logic,my view has always been in the direction of simple,so-called subclassical accounts.A logic is said to be subclassical iff classical logic is a proper extension of it.Let?1and?2be consequencerelations(‘logics’)definedoverthesamelanguage.Wesaythat?2properly extends?1iff for any set X of sentences(in the given language)and any sentence A(in the language)X ?1A only if X ?2A.In other words,the 2 relation properly extends the 1 relation iff X∴A is valid according to the 2 relation if it is valid according to the 1 relation.

Thinking about this‘semantically’(or model-theoretically),we can think of consequence relations as defined over various spaces of‘possibilities’(modeled by models),and these possibilities serve as candidate counterexamples.In turn,think of each possibilityasrepresentinga‘semanticstatus’thatasentencecanhavewithrespecttoTheTrue and The False.Classical logic looks at a space of possibilities that are ‘exhaustive’and‘exclusive’with respect to The True and The False in the sense that in every possibility in the space,each sentence of the language is related to exactly one of The True and The False—never Both of them,and never Neither of them.

Now,from a subclassical point of view,the possibilities in the Classical space are perfectly good possibilities that any true account of logical consequence should recognize.The problem with the Classical account is that its space of possibilities is too lim-ited.From a subclassical point of view a true account of logical consequence is one according to which logic recognizes some possibilities that go beyond the‘exhaustive and exclusive’ones;logic also recognizes either‘non-exhaustive’ones(wherein a sentence might be related to Neither the True nor the False)or‘non-exclusive’ones(where a sentence might be related to Both of the True and the False).Following an observation by Dunn([18,19])we can think of the Classical space as the usual set{t,f},where t models The True and f models The False,and in turn think of a broader(subclassical)space as?({t,f}),where now{t}models The True,{f}models The False,{t,f}models the Both status(a glut status),and finally?models the Neither status(a gap status).

4.1FDE

Let us take the full space of such possibilities to beV=?({t,f}).In turn,if we think of each atomic sentence being assigned a semantic status out ofVby a functionv:Atoms→V,so thatv(p)is the semantic value or semantic status of atomic sentencep.On this account,an atompcan be

·true only:t∈v(p)and f/∈v(p)

·false only:f∈v(p)and t/∈v(p)

·neither(gappy):t/∈v(p)and f/∈v(p)

·both(glutty):t∈v(p)and f∈v(p)

Accordingly,there are perfectly Classical possibilities(modeled byvin this context)whereby every atom is either true only or false only,but there are possibilities that go beyond these by involving glutty atoms or gappy atoms.

Extending to molecular sentences involving just the logical vocabulary involves familiar truth-in-a-model and falsity-in-a-model conditions.4For simplicity I give only boolean(propositional)connectives;extending to full first-order(without identity)is straightforward([1,2,9,18]).WhereAandBare any sentences in the language,we extend our given functions to all sentences as follows:

·Nullations:t∈v(?A)iff t∈v(A).

·Nullations:f∈v(?A)iff f∈v(A).5Nullationsareincludedhereforcompleteness(andthesymmetryofthebooleanquartet)butshallbeignored—because logically redundant—in what follows.

·Negations:t∈v(?A)iff f∈v(A).

·Negations:f∈v(?A)iff t∈v(A).

·Disjunctions:t∈v(A∨B)iff either t∈v(A)or t∈v(B).

·Disjunctions:f∈v(A∨B)iff both f∈v(A)and f∈v(B).

·Conjunctions:t∈v(A∧B)iff both t∈v(A)and t∈v(B).

·Conjunctions:f∈v(A∨B)iff either f∈v(A)or f∈v(B).What is important to emphasize is that these truth and falsity conditionsare precisely the same conditionsused in the standard classical-logic account.The difference,from an FDE perspective,is that the classical-logic account ignores the logical possibilities of ‘gaps’and ‘gluts’,and so the falsity conditions are redundant in the classical-logic picture.

So go the space of values and the truth and falsity conditions for all sentences,according to the subclassical account of logical consequence called ‘FDE’.But to get the account of logic,we need the definition of the principal relation,namely,logical consequence!And here the idea is familiar,namely,that logical consequence is‘truth preservation’(modeled as t-preservation)across all possibilities:

Definition 1(FDE Consequence) LetXbe a set of sentences,andAany sentence.ThenAis a logical consequence ofXaccording to FDE(notation:X?fdeA)iff there is no FDE modelvaccording to which t∈v(B)for allB∈Xbut t/∈v(A).

That FDE is a paraconsistent logic is clear:

A countermodel is any modelvsuch thatv(A)={t,f}and t/∈v(B).

Moreover,FDE is‘paracomplete’in the sense that

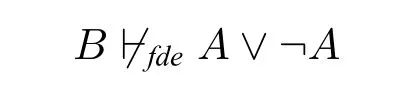
sincetherearecountermodelswhereint∈v(B)butAisagap:t/∈v(A)andf/∈v(A).6

6Toseethebeautifulsymmetry—indeed,duality—ofthegivencharacteristicmarksofparaconsistentandparacomplete accounts of logic,it is useful to generalize to multiple conclusions in a standard way to get the multiple-conclusion version FDE+([9]),where we have

But I will focus on the familiar single-conclusion case.

4.2 LP and K3

FDE([1,2,9,18])is but one of three well-known subclassical approaches to logic.LP([4,28])and K3([23])are two others—indeed,the two chief candidates for subclassical accounts of logic.The difference between FDE,on one hand,and LP and K3 on the other is only in the space of values — the space of‘logical possibilities’recognized by the account.LetVfde=?({t,f}).Then LP takes the spaceVlp=Vfde{?},reflecting a rejection of the logical possibility of gaps,while K3 takes the space to beVk3=Vfde{{t,f}},reflecting a rejection of the logical possibility of gluts.Each of LP and K3 uses Definition 1(see page 13)as a definition of consequence;it is just that the space of semantic values is different in the indicated way.

4.3 FDE,LP,and K3 as Closure

There are other subclassical logics,but the foregoing trio are the most prominent as far as my target applications go.What is important,for present purposes,is that each of the given subclassical logics is a closure relation;and so each can serve,per§2,as a candidate for logical consequence itself— as the universal‘basement-level’closure relation in all of our true theories.

Focusingonlyontheparaconsistentoptions(viz.,FDEandLP,notK3),thequestion naturally arises:why think that logic is in fact paraconsistent?

5 Glut-theoretic motivation

Why should any philosopher or logician think that logical consequence is paraconsistent in this sense?Many answers have been given([31,30]),but given the invited purpose of this essay,I will focus on my own answer—which is not incompatible with answers by others.

By my lights,the main reason to think that logic,understood as above,is paraconsistent is that some phenomena appear to be glutty — they appear to be‘gluts’of truth and falsity.A sentenceBis said to be aglutiff bothBand its negation?Bare true.A theory is said to begluttyiff it contains some gluts.And aglut-theoreticapproach to a phenomenon is one that treats the true theory of the phenomenon to be glutty theory.7Priest and Sylvan coined the term ‘dialetheism’(sometimes,‘dialethism’)for glut-theoretic approaches to various phenomena,and relatedly ‘dialetheia’(or‘dialethia’)for gluts.I prefer the simpler terminology of‘glut’(especially in contrast to the commonly used ‘gap’terminology for dual‘truth-value gap’approaches).The ‘glut’terminology predated the later neologism.([21])

By why think that there are glutty phenomena?Again,many answers have been given([31]);my own has been—and remains—paradox-driven.

6 Transparent Disquotationalism and FDE

Truth-theoretic and property-theoretic(also known as ‘naive-set-theoretic’)paradoxes have long motivated gappy approaches to logic,the idea being that such paradoxes show that some phenomena are gappy,and hence that logic itself must recognize such a possibility.My view has been—and remains—that this sort of gappy approach is well-motivated;but so too is a glutty one.

On my view([5])the truth-theoretic paradoxes are hardest for a so-called transparency view of truth.A truth predicateTr(x)in and for languageLis said to betransparentiffTr(〈A〉)andAare everywhere(non-intensional)intersubstitutable salva veritate,where〈A〉is a suitable name in L of the L sentenceA.On this view,so-called deflationists are largely right about truth itself:the predicate ‘true’,on the target usage,is entirely see-through.Why would we have such a see-through predicate?Why not just talk about the world itself using some ‘true’-freeAinstead of using ‘true’to talk aboutA?If‘true’is see-through,it all comes to the same anyway,and so there’s no need to have such a(transparent,see-through)predicate.Right?

As Quine([32]),following Leeds([25]),nicely put it,the aim of using ‘true’is alwaystotalkabouttheworlditselfbutsometimes—givenour finite,practicallimitations— we need to talk about language in order to talk about the world.And that’s what transparenttruthallowsustodo.Ifallwehadwaslogic’s(logicallyredundant)truthoperator,we could not say what we in fact say when we express generalizations like‘Everything in(infinite)theoryTis true’.To say what we say via such generalizations we use the transparent truth predicate;and that’s the predicate’s entire role and ‘reason for being’in the language.

But the trouble,as I said early on[5],is that bringing a transparent truth predicate intoourlanguagebringsaboutinevitable(andoftenunintended)sideeffects—spandrels of truth,as I have called them([6]).Perhaps the most conspicuous such side effects are sentences in which ‘true’cannot be eliminated via the so-called transparency rule(which just tells you thatTr(〈A〉)andAare everywhere(non-intensional)intersubstitutable).And perhaps the most infamous examples of such sentences are,respectively,the famous liar and truth-teller:

and

Now,these are very,very strange sentences,and depending on which account of logic is the right account we might wind up with gluts or gaps—or,if one stuck with the classical-logic story,the trivial theory.

6.1 Transparent truth and FDE

In ‘Transparent disquotationalism’([5]),I advanced the position that logic is FDE,that truth is transparent(as above),and that some liar sentences are gluts.But if one looks at logical negation,as it appears in FDE,we have no excluded middle.So,how do we wind up with the view that some liar sentences are glutty if negation does not obey excluded middle?Why not,instead,just treat liars as gaps—perhaps like the truth-teller itself?

6.2 Whither gluts?

In ‘Transparentdisquotationalism’Iadvancedtheviewthatitwasnotjust‘true’that we introduced into our language;we also introduced another negation-like connective.In particular,in our effort to ‘characterize gaps’(to truly say of a sentenceAthat neitherAnor its logical negation is true)we introduced an in-effect logical expression,present in all theories,which is(in effect)a gap-closing negation.8Note that if one uses FDE negation to say that?Aand??Ais true,one winds up with a glut,which can be true in FDE but the point was to truly characterize gaps,and so FDE negation will not do the sought-after characterization.Like FDE’s logical negation,the gap-closing negation(say,?)was fixed at{t,f},toggled{t}and{f},but— unlike FDE’s logical negation—took?to{t},that is,unlike FDE’s logical negation,ifv(A)=?thenv(?A)={t}.

Thegap-closingdevice?deliversexcluded-middlebehaviorinthesensethatevery possibility(model)is one in whichA∨?Ais true.But given the transparent truth predicate there are sentencesGequivalent to?Tr〈G〉,but,unlike the corresponding liar using logical negation,this one cannot be treated as a gap;in fact,it is forced to be a glut,whereinG∧?Gis true(and false),and so too(thereby)is the corresponding logical negationG∧?G.

Inthisearlierworkthepicturewasoneinwhichlogic(quaFDE)wassubclassical;it providedauniversalclosurerelationforourtheoriesthatallowedbothglutsandgaps;and it advanced the view that we have gluts in virtue of having a transparent truth predicate together with a gap-closing negation.

7 Spandrels of truth

DespitethesymmetryofFDEandtheattractivepictureoflogicalconsequencethatit provided,the philosophical story of transparent truth and the given gap-closing negation did not last.InSpandrels of Truth([6]),which aimed to fill out the early picture,I still advanced what has come to be called ‘simply semantic glut theory’(or,as some say,‘simplysemanticdialethism’)inthebroadercontextoftransparenttruththeory;however,the theory advanced inSpandrelsrejected FDE in favor of a more popular glut-friendly subclassical logic.

7.1 LP instead of FDE

Unlike my original position,where FDE is a more attractive account of logic,SpandrelsofTruthjoinedLPtheoristsinsayingthatLP—notFDE—islogicalconsequence.Why the switch?The answer is gestured above(§6.2)and briefly mentioned in[6,Ch.5];but it is worth saying a bit more here.

One virtue of‘precise philosophy’— or‘mathematical philosophy’— is that one aims to advance a theory.Theories,in turn,have models.And one can learn a lot about one’s theory by looking at the space of the models in which the theory is true.

FDE recognizes many ‘possibilities’,all of the ones represented by FDE models.But as one constructs one’s theory,and in turn constructs the theory’s consequence(closure)relation on top of logic(viz.,FDE),one begins to reduce the space of logical possibilities only to those that aretheoretically possible.

Transparent truth requires the transparency rule,which is modeled by requiring thatv(A)=v(Tr(〈A〉))for allAin the language of the theory.Any(FDE)model that respects this equation is a transparent model—which is one sort of fixed-point model in the familiar sense of Kripke’s‘Outline’([24]).(See[6]for further details)

Now,there are many FDE models that are transparent models in the sense above.([17,27,37,36])The question for the FDE-based transparency theory I advanced in‘Transparent Disquotationalism’—with its gap-closing negation—is whether there are transparent models,and ‘natural’ones in the sense(defined inSpandrels)that the only gluts involve ineliminable occurrences of‘true’(i.e.,occurrences of the transparent truth predicate that cannot be eliminated by repeated application of the transparency rule).

The good news:there are transparent and natural FDE models of the given theory(with transparency and the given gap-closing negation).But the good news is only good if you want to reject the existence of gaps—and thereby any genuine motivation for taking FDE to be logical consequence.The result,gestured at in[6,Ch.5],is that while there are such FDE models,they are— one and all— LP models.

To see the problem,which I did not elaborate inSpandrels,consider again the requirement on transparent models:namely,

for allAin the language of the theory.But by usual‘tricks’involving a transparent truth predicate we can form a sentenceGequivalent(in the theory)to

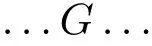
for any sentential context‘...·...’.Hence,if we have an FDE transparent model in which N is a gappy sentence(according to that model)we will have a sentenceGequivalent to

in which case,by constraints on a transparent model,we will have the equation:

But as brief calculation shows,there is no such FDE model.The only possible values ofv(G)are in?({t,f});but each one fails to satisfy the equation.Specifically,sincev(N)=?,ifGis assigned{t}thenG∨N is also{t}.(See disjunction clauses for FDE in§4.1.)IfGis assigned{t,f}thenG∨N is{t},and hence?(G∨N)is{f}.IfGis assigned?then so too isG∨N,in which case?(G∨N)is{t}.(See§6.2 for the gapclosing negation.)Finally,ifGis assigned{f}thenG∨N is?,in which case?(G∨N)is{t}.Accordingly,there is just no FDE transparent model of the theory(involving the gap-closing negation)in which we haveanygappy sentence.

Of course,every LP transparent model is an FDE transparent model.Moreover,the gap-closing device?collapses into LP’s logical negation in the absence of gaps.(The device behaves exactly as FDE’s logical negation does except for gaps;but except for gaps,which LP does not recognize,FDE’s logical negation behaves exactly as LP’s logical negation.)Hence,what the problem above—herein spelled out more explicitly than in[6,Ch.5]— shows is that if FDE is logic,and truth is transparent,then if there’s a gap-closing negation of the sort championed in ‘Transparent Disquotationalism’then the only models of the theory are LP models of the theory.Of course,every transparent LP model is(by definition)a transparent FDE model(since FDE properly subsumes LP models);but this is hardly a good reason to maintain the view that logic is in fact FDE.

FortheforegoingreasonsIrejectedtheviewthatFDEisthecorrectaccountoflogic,andproceededtojoinotherLPtheoristsinclaimingthatLPistheproperaccountoflogic.The main difference between my LP-based truth theory and that of Graham Priest’s LP-based truth theory is that the former is very,very conservative with respect to gluts(in particular,only the spandrels of truth are gluts,no other glutty account is theoretically possible),and‘true’inthetheory—unlikeinPriest’s—istransparent.Thesedifferences makeforlargerdifferences,especiallywithrespecttothespaceoftheoreticalpossibilities allowed by the given theories;but I leave this matter for a different discussion.

8 Return to balance：back to FDE

In my recent work I have returned to my roots,and have reaffirmed FDE as the right account of logic.This work is part of a larger monograph on the topic,but a sketch of some of the ideas are in my ‘There is no logical negation’([13]),which is a somewhat hyperbolictitlefor theidea thatlogical negationleaves roomfor truegappy theories,true glutty theories,and true classical theories.

There are three key ideas in the new project,which I very briefly(andbarely)sketch here.The work is also sketched in[13]and will appear in much deeper detail in a monograph(to be finished mid-2018).

Before gesturing at the three key ideas,it is worth noting the reason for returning to FDE.The reason is that,as I thought in my original work,FDE is the best of the subclassical-logic pictures if we are going to go subclassical in the first place.Yes,it is weaker than each of the main and more popular subclassical extensions(viz.,LP and K3);and for that reason most subclassical-logic theorists champion the stronger,more popular extensions.9As per§7.1,this‘strength’issue was not my motivation for rejecting FDE and climbing up to LP;however,it remains the chief reason that theorists such as Priest([29])and Field([20])and other subclassical-logic theorists reject FDE.But if we,as philosophers(and not mere technicians of logic),are to claim that the right account of logic is non-classical,and in particular that it is subclassical,then we ought to also care about the best overall philosophical account of logic.And,as I argue in[13],it is very,very difficult to see how either LP or K3 gives a better overall picture of logic(as universal closure relation)than FDE.What is strongly apparent is the asymmetry or‘imbalanced’picture of logic involved in the LP and K3 accounts.In particular,each would have it that logic—as the universal closure relation—allows gluts(gaps)but rules out gaps(gluts).But why would logic itself rule out one of the options but be perfectly happy(so to speak)with recognizing its dual?Why would logic rule out the possibility in which a sentence is gappy while being perfectly happy(so to speak)with recognizing the possibility in which it is glutty?Or vice versa?

By my lights,the imbalance of the LP and K3 accounts is a very bad mark against those accounts.It is better,in the end,to accept the beautifully symmetric FDE.On the FDE picture,the essence of logic is De Morgan interaction among dual connectives:the truth and falsity operators,the conjunction and disjunction operators,and the logical quantifiers(which I skipped in this essay,but see[15]for a user-friendly treatment).There is a lot more to say,but I leave discussion for said monograph.

9 Again,whither gluts?

But now the question arises again:whither gluts?If logic is FDE,then logic does not demand excluded middle in all of our theories.But,then,if the best—indeed,only—candidates for gluts are spandrels of truth like the liar sentence,then we are not forced by logic to treat such sentences as gluts.

In my previous work(briefly reviewed in§6.2)the question was answered via a gap-closing,extra-logical negation.But as per§7.1 there are no FDE transparent models of that approach.I have since rejected the existence of such an in-effect logical negation,present in all of our theories.And this is why the question ‘whither gluts?’is so pressing.

In ‘There is no logical negation’I advance the first paradox-driven argument for gluts in the context of an FDE account of logic.The target monograph will say more about the matter,but the argument is three-fold.

1.Naturalness:one argument for treating the liar as a glut is that,even though logic does not force the glut,the sentence ‘This sentence is not true’screams out for glutty treatment.We as theorists are constrained not just by logic’s demands;we are constrained too by a sense of naturalness.At least from a transparent-truth perspective,there is nothing unnatural about treating the twisted sentence‘This sentence is not true’as a glut— at once true and not true,where‘true’is nothing morethanasee-throughdevice.Givingthissentencesomeothersortoftreatmentis perfectly possible as far as logic goes;but,at least by my lights,from an aesthetic sense of naturalness the sentence is best treated as a glut.(On the flip side,the truth-teller sentence is most naturally treated as a gap,unlike the forced treatment it received in[6].)

2.Methodological principle:when we are engaged in systematic theorizing we are driven not just by logic but by extra-linguistic methodological precepts.One central such precept fuels our quest for negation-complete theories:we are driven not by logic but by the goal of sorting every sentence,in the language of the target theory,into The True and The False.And when we come to a sentence like the liar sentence ‘This sentence is False’our drive towards completeness motivates our treating the sentence as a glut.Logic itself does not demand such treatment;but our extra-linguistic,methodological precept towards completeness motivates such treatment.

3.Metaphysical balance:if we already recognize gappy phenomena(e.g.,vagueness,perhaps statements about the future,and other phenomena),then a natural metaphysical principle suggests that there should be a symmetry or balance in some fashion,and in particular that there should be at least some glutty phenomena.If this is so,then a natural candidate is something like the liar sentence,even if it is only ‘metaphysical’in a loose sense.

These arguments do not in any way rely on excluded middle,which is not valid in logic(viz.,FDE).But I believe that they are viable rationales for paradox-driven glut theory.

10 Non-detachment

Another key idea of the new work(to appear in said monograph)concerns the project of non-detachment.Laura Goodship([22])argued that subclassical glut theories would be both simpler and more plausible if they involved non-detachable conditionals in fundamental principles like the T-biconditionals.10Here,non-detachable conditionals are ones for which modus ponens is invalid.The material conditional is logically non-detachable in FDE and LP.She argued that the liar paradox could then naturally be treated as a glut,but also certain Curry paradoxes(e.g.,‘If I am true then everything is true’)could likewise be treated as glutty — without the absurd trivial theory following via detachment.

While I am not in full agreement with Goodship’s arguments, my recent work — and part of the monograph project — in fact follows one option that she outlines.Inparticular,I maintain that there arenouniversally detachable conditionals in the sense that there is no conditional which figures in all of our true theories and which is detachable according to all consequence(closure)relations of all such theories.The main candidates for such a conditional,on my view,would involve logical vocabulary(which is universal,present in the languages of all theories).But there is no logically detachable conditional,on my view.

All of this might seem to be radical,but I think that it is not radical and the monograph aims to make this plain.Let me briefly mention a few ways that we accomplish detachment in theories,and detachment-like effects in theorizing.Here,in this essay,I say very little;but some of the ideas are in other work([11,10,8,7,9]),and all of the ideas will be spelled out in said monograph on the topic.

10.1 Extra-linguistic ‘detachment’

One reason so many philosophers and logicians take detachment(modus ponens)to be a fundamental feature of logic’s material conditionalA→B(defined,again,as?A∨B)is that we rely on a close cousin of detachment in our theorizing.([11])In particular,while logicit self(viz.,FDE)says that material deta chment(i.e.,modusponens using the material conditional)is invalid

there is a very close cousin of detachment which a generalization of logic—namely,the multiple-conclusion relation FDE+—does validate:

The generalized relation FDE+,which is a set-set relation,says that the pair〈X,Y〉is valid iff there is no FDE model that satisfiesXbut dissatisfiesY,where an FDE modelvsatisfiesXiff t∈v(B)for allB∈X,and a modelvdissatisfiesYiff t/∈v(B)for allB∈Y.

Now,on reflection,it is clear that(material)detachment has a counterexample only in models where the antecedent ofA→Bis glutty(i.e,where both t∈v(A)and f∈v(A)).But,then,the generalized FDE+relation cannot dissatisfy{B,A∧?A}while also satisfying{A,A→B}.

How is this relevant to detachment?On my view,gluts are very few and far between;they are treated as theoretical impossibilities in virtually all of our theories(and their respective consequence relations).Accordingly,while logic tells us thatBfails to(logically)follow fromAtogether withA→B,the generalization of logic to FDE+leaves us a choice;it says thatsomethingin{B,A∧?A}is true given the joint truth ofAandA→B.Hence,whilelogicwillnotsettlethechoiceathand,we—throughextralinguistic rejection principles—settle the matter without further thought.In particular,in virtually all theories we simply reject the would-be logical possibility ofA∧?Abeing true;we reject it as a theoretical impossibility,and as such we simply acceptBwhenever we have the joint truth ofAandA∧?A.In this way,we frequently rely on a sort of detachment,even though the detachment is not one sanctioned by logic itself.

10.2 Extra-logical detachment

One might object that some of our true theoriesdohave material detachment;they have material detachment plain and simple,without any ‘extra-linguistic interference’of the sort in§10.1.Take arithmetic.The true theory of arithmetic is without gaps and without gluts.In fact,the true theory of arithmetic appears to be closed under classical logic.11Itisnotaprimetheory,wherethisisatheoryTthatcontainsadisjunctionA∨BiffeitherA∈TorB∈T.(Gdel’s limitative results,together with excluded middle being valid in arithmetic,look to directly undermine its primeness.)Moreover,this theory is one according to which material detachment is valid.How can your proposed ‘non-detachment’view be compatible with all of these appearances?

The answer is that while material detachment is in fact valid according to arithmetic’s consequence relation,it is not valid according to logic(i.e.,FDE).What is happening in this case is that the theory’s consequence(closure)relation?ais building detachment into the theory by removing some of logic’s possibilities— in particular,the glutty ones—and treating them as theoretical impossibilities(that do not count among the models of the theory).In particular,arithmetic imposes what I call ashriek rule,where ‘shriek’arises from a common abbreviation that uses the shriek symbol‘!’for contradictions,namely,‘!A’abbreviates‘A∧?A’.A shriek rule in general has the form!A?TB,whereBis some sentence in the language ofTthat entails,according to?T,all sentences in the language of the theory—and,so,Bentails the trivial theory inT.

The details of shriek rules,as I have developed them([10,8]),are not only theoryspecificbutpredicate-specific.Inparticular,ifPisa(say,forsimplicity,unary)predicate in the language of theoryT,we‘shriekP’in the theory by imposing the condition(i.e.,the shriek rule)

whereB,again,is some sentence that,according to?T,entails all sentences.12In the explicit shriek notation(the abbreviation notation),the rule isThe effect of this shriek rule on the theory’s consequence relation is that the space of FDE models is reduced to only those in which the predicatePis treated as a classical-logic predicate(i.e.,the union of its extension and antiextension is the domain of the model,and the intersection of its extension and antiextension is the emptyset).13

One can now show that for any singular termbwe have the validity of detachment forPsentences:

13Intuitively,the extension of a predicate is the set of things of which the predicate is true;the antiextension is the set of things of which the predicate is false.For more on this seeSpandrels of Truthand references therein.

Of course,one can generalize shriek rules to any arity of predicate.

In this way,a theory in which all predicates of the language are shrieked(as in arithmetic)will in fact validate material detachment.This is notlogicitself validating the detachment;but the consequence(closure)relation of the theory validates material detachment nonetheless.([10,8])

Ihavecometothinkthatalldetachmentinourtruetheoriesisachievedviashrieking.But I leave further discussion for the forthcoming monograph.

10.3 Tarskian restrictions and universalism

One third idea,salient in the forthcoming monograph,is a combination of Tarskian‘restrictivist’approaches and ‘universalist’approaches towards paradox.

I think that logic is subclassical,indeed,that logic is so-called FDE,where logic allows for both non-trivial glutty theories and non-anti-trivial gappy(prime)theories.By far the most famous motivation for subclassical logic,at least among truth theorists,is that it promises,as Woodruff puts it,

to ‘solve’the paradoxes;that is,to allow us to say that the very language we are speaking is of the sort described in our theory.([37],p.229)

And among the philosophers most famously making such a promise are Priest([28])and Sylvan(née Routley)([33]).They argued,in effect,that the promise of a ‘semantically closed’or‘semantically universal’language — one that,as Woodruff put it,‘a(chǎn)llows us to say that the very language we are speaking is of the sort described in our theory’— is achieved only via an account on which logic itself is nonclassical.14But not all theorists pursuing ‘universality’reject classical logic,as Keith Simmons famously reflects([34]),though I myself cannot help but see Simmons’view as heavily clothed in(let me say)‘Tarskian-like restrictions’.

If this is the only way to ‘solve paradoxes’— by showing that the target predicates are really in and for the very language of our theory — then a‘Tarskian response’to solving paradoxes is ruled out.After all,a ‘Tarskian response’to the quest for semantic closure is to walk away,maintaining instead that theory-specific restrictions on vocabulary are ubiquitous.15I am not saying that this was the historical Tarski’s own response;Tarski himself made infamous remarks about English being ‘semantically closed’or‘universal’.I am instead talking of the sort of approaches that are often called ‘Tarskian’—stratified or hierarchical or in any event restrictedor decidedly non-universalapproaches.

And so we sit in a field with two polar-opposite sides,apparently bare in the middle.But the apparently bare middle is only apparently bare.My own current view is a blend of the ‘universal’and ‘restricted’approaches.

In addition to holding that logic is subclassical(viz.,FDE)I also think that we have a completely unrestricted-indeed,transparent-truth predicate:the predicate is‘universal’in that it is not restricted to a particular theory’s language or a fragment thereof;it is availableifnotexplicitlypresentinallofourtruetheories.Andthefamiliarincoherencedriving paradoxes,which tend to cast doubt on such an unrestricted truth predicate,do not reach incoherence thanks to logic’s liberality with respect to gluts and gaps in our true theories.On these matters,I stand on the ‘universality’,non-restrictivist side.

But thereafter I part ways.On my view,ttruth’s unrestricted ‘nature’is special.I think that among the target(e.g.,paradox-prone)vocabulary transparent truth(like its dual falsity predicate)is unique in its lack of restrictions— unique in its‘universality’.Other(often paradox-prone)predicates that may bear a family resemblance are not unrestricted.Among these I count not only notions of entailment or consequence,as in[12],but also notions like ‘Gappy’and ‘Glutty’,and many ‘struth’predicates(stronger-than-transparent-truth predicates),and more generally vocabulary like‘paradoxical’,‘ungrounded’,‘singularity’,or whathaveyou.By my lights,Tarskian-like restrictionsapplytothesenotions;theyarerestrictedtolanguages(ortheories)inwaysthat the transparent truth predicate(similarly,falsity predicate)are not restricted.On these matters I stand on the ‘restricted’side.

This marriage of universalist and restrictivist insights is available because logic is subclassical.My current view,to be elaborated in a forthcoming monograph,is that this marriage is what is required for our best overall account of truth,logic,and strange phenomena like the paradoxes.But I leave further discussion to said monograph.

[1]A.R.Anderson and N.D.Belnap,1975,Entailment:The Logic of Relevance and Necessity,vol.1,Princeton:Princeton University Press.

[2]A.R.Anderson,N.D.Belnap and J.Dunn,1992,Entailment:The Logic of Relevance and Necessity,vol.2,Princeton:Princeton University Press.

[3]B.Armour-Garb and Jc Beall(eds.),2005,Deflationary Truth,Chicago:Open Court Press.

[4]F.G.Asenjo,1966,“A calculus of antinomies”,Notre Dame Journal of Formal Logic,7(1):103-105.

[5]Jc Beall,2005,“Transparent disquotationalism”,in Jc Beall and B.Armour-Garb(eds.),Deflationism and Paradox,pp.7-22,Oxford:Oxford University Press.

[6]Jc Beall,2009,Spandrels of Truth,Oxford:Oxford University Press.

[7]JcBeall,2012,“Truthwithoutdetachment”,presentedasaseriesoffivelecturesattheUniversity of St Andrews;it is the basis of a book project.

[8]Jc Beall,2013,“A simple approach towards recapturing consistent theories in paraconsistent settings”,Review of Symbolic Logic,6(4):755-764.

[9]Jc Beall,2013,“LP+,K3+,FDE+and their classical collapse”,Review of Symbolic Logic,6(4):742-754.

[10]JcBeall,2013,“Shrieking againstgluts:Thesolution tothe‘justtrue’problem”,Analysis,73(3):438-445.

[11]Jc Beall,2015,“Free of detachment:Logic,rationality,and gluts”,No?s,49(2):410-423.

[12]Jc Beall,2015,“Trivializing sentences and the promise of semantic completeness”,Analysis,75(4):573-584.

[13]Jc Beall,2017,“There is no logical negation:True,false,both and neither”,in P.Girarad and Z.Weber(eds.),Non-classicality:Logic,Philosophy,and Mathematics,Wellington:Australasian Journal of Logic.

[14]Jc Beall and J.P.Burgess,2017,“Logic”,in D.Pritchard(ed.),Oxford Bibliographies in Philosophy,Oxford University Press,DOI:10.1093/obo/9780195396577-0336.

[15]Jc Beall and S.A.Logan,2017,Logic:The Basics(2ed),Oxford:Routledge.

[16]Jc Beall and G.Restall,2005,Logical Pluralism,Oxford:Oxford University Press.

[17]B.Dowden,1984,“Accepting inconsistencies from the paradoxes”,Journal of Philosophical Logic,13:125-130.

[18]J.Dunn,1966,The Algebra of Intensional Logics,University of Pittsburgh,PhD.thesis.

[19]J.Dunn,1976,“Intuitive semantics for first-degree entailments and ‘coupled trees’”,Philosophical Studies,29:149-168.

[20]H.Field,2008,Saving Truth from Paradox,Oxford:Oxford University Press.

[21]K.Fine,1975,“Vagueness,truth and logic”,Synthese,30:265-300.

[22]L.Goodship,1996,“On dialetheism”,Australasian Journal of Philosophy,74:153-161.

[23]S.C.Kleene,1952,Introduction to Metamathematics,North-Holland.

[24]S.Kripke,1975,“Outline of a theory of truth”,Journal of Philosophy,72:690-716,reprinted in[26].

[25]S.Leeds,1978,“Theories of reference and truth”,Erkenntnis,13(1):111-129,reprinted in[3,pp.33-50].

[26]R.L.Martin(ed.),1984,Recent Essays on Truth and the Liar Paradox,New York:Oxford University Press.

[27]R.L.Martin and P.W.Woodruff,1975,“On representing ‘true-in-L’in L”,Philosophia,5:217-221,reprinted in[26].

[28]G.Priest,1979,“The logic of paradox”,Journal of Philosophical Logic,8:219-241.

[29]G.Priest,2006,In Contradiction,Oxford:Oxford University Press,First printed by Martinus Nijhoff in 1987.

[30]G.Priest and R.Routley,1989,“Systems of paraconsistent logic”,in G.Priest,R.Routley and J.Norman(eds.),Paraconsistent Logic:Essays on the Inconsistent,pp.151-186,Philosophia Verlag.

[31]G.Priest and R.Routley,1989,“The history of paraconsistent logic”,in G.Priest,R.Routley and J.Norman(eds.),Paraconsistent Logic:Essays on the Inconsistent,Chapter 1,Philosophia Verlag.

[32]W.V.O.Quine,1987,Quiddities,Cambridge,MA:Harvard University Press.

[33]R.Routley,1979,“Dialecticallogic,semanticsandmetamathematics”,Erkenntnis,14:301-331.

[34]K.Simmons,1993,Universality and The Liar,Cambridge University Press.

[35]A.Tarski,1956,Logic,Semantics,Metamathematics:Papersfrom1923to1938,Oxford:Clarendon Press,translated by J.H.Woodger.

[36]A.Visser,1984,“Four valued semantics and the liar”,Journal of Philosophical Logic,13:181-212.

[37]P.Woodruff,1984,“Paradox,truth,and logic”,Journal of Philosophical Logic,13:213-252.