Nonlinear dynamic analysis of cantilevered piezoelectric energy harvesters under simultaneous parametric and external excitations

Fei Fang·Guanghui Xia·Jianguo Wang

1 Introduction

Harvesting energy from ambient vibrations by using the direct piezoelectric effect has received significant attention over the last two decades[1–3].This focus is due to the need for low-power consumption devices,such as microelectro mechanical systems and sensors[4].Many review papers have summarized the literature of piezoelectric energy harvesting[5–8].The most common configuration for piezoelectric energy harvesting has been either a unimorph or a bimorph piezoelectric cantilever beam.Many researchers have focused on the mathematical modeling of this harvester.A reliable mathematical model may allow studying different aspects of energy harvesting,predicting the electrical outputs,moreover,optimizing the harvester in order to obtain the maximum electrical output for a given input.The linear models of piezoelectric energy harvesters are available in many papers.For example,Erturk and Inman[3]presented a distributed parameter electromechanical model of cantilevered piezoelectric energy harvester with the Euler–Bernoullibeam assumptions.Closed-form expressions of the voltage,current,and power outputs,as well as the mechanical response were obtained under the base excitation.Some linear models have been validated experimentally and show good agreement between theory and experiment[9–11].The study of Tang and Wang[12]presented a modified model of cantilevered piezoelectric energy harvester with tip mass offset and a dynamic magnifier by using the generalized Hamilton’s principle. The modified model was demonstrated by parametric studies.The results show that the harvesting power can be dramatically enhanced with proper selection of the design parameters of the dynamic magnifier and tip mass offset.However,these validations are very low levels of excitation and not necessarily valid in all applications.In practical application,it is likely that linear models of the energy harvester will be unable to predict accurately the resonance frequency,leading to inaccurate prediction for the performance of the harvester due to frequency shift.It is advisable to take into account the nonlinear behavior of energy harvesters in the design,particularly if the energy harvester is subjected to high levels of excitation.The paper by Daqaq et al.[13]identified the primary limitations associated with linear vibration harvesters and presented a critical review of recent research focused on the use of nonlinearity to improve the performance of vibration harvesters.

A work by Mahmoodi et al.[14–16]presented an analytical model of nonlinear vibration response for cantilevered piezoelectric beams.The Galerkin decomposition method was used to derive the equations of motion.The multiple scales method was utilized to obtain analytical solutions of the system.Also,Stanton et al.[17]studied the influence of piezoelectric material nonlinearities on the dynamic response of a geometrically linear piezoelectric energy harvester using a theoretical model and experimental validation.Work by Abdelkefi et al.[18]presented a nonlinear distributed-parameter model of cantilevered piezoelectric beam energy harvesters with tip mass under direct excitation.The presented model included geometric,inertia,and piezoelectric nonlinearities.The Galerkin decomposition method and the multiple scales method were used to determine analytical expressions of the harvester.In their study,Triplett and Quinn[19]investigated the effect of nonlinear piezoelectric coupling on avibration energy harvester,which included mechanical damping,stiffness nonlinearities,and the nonlinear piezoelectric constitutive relationship.The response of the harvesting system was approximated using Poincare–Lindstedt perturbation analysis.Work by Neiss et al.[20]provided analytical solutions of the output power and bandwidth of nonlinear energy harvester based on a lumped-parameter model of cantilevered piezoelectric beam.The results were verified by numerical simulations.The stability of the simply supported piezoelectric laminated rectangular plate under simultaneous transverse and in plane excitations was studied by Mousa et al.[21].The multiple scales method was used to achieve the second-order approximation.The work by Mahmoudi et al.[22]investigated the performance of a novel hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions.Furthermore,Friswell et al.[23]derived the electromechanical equations of nonlinear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass.The presented equations were investigated using the method of numerical simulation and experimental validation.The bistable piezoelectric inertial generators,which can produce large-amplitude motions under ambient excitations,have attracted moreattention of researchers[24–29].Thus,Karami and Inman[26]presented a unified approximation method to study the performance of linear,softly nonlinear,and bi-stable nonlinear energy harvesters.Then Stanton et al.[27]used the harmonic balance method to investigate analytically the influence of parameter variations on the intrawell and interwell oscillations of bistable piezoelectric inertial generator.A mathematical model of the multi-stable magnetic attraction energy harvester,which was composed of a bimorph cantilever beam with soft magnetic tip and two external permanent magnets,was developed based on the nonlinear Euler–Bernoulli beam theory and linear piezoelectricity[28].Based on arrays of coupled levitated magnets,Abed et al.[29]proposed a multi-modal vibration energy harvesting method.The presented differential equations of motion were solved using the harmonic balance method combined with the asymptotic numerical method.

The parametric resonance theory predicts that the vibrationenergy harvesters using parametric resonance will obtain significant performance enhancement.One of the key problems of parametric resonance is the presence of a certain initiation threshold,which must be overcome prior to reaching parametric resonance.Therefore,Daqaq et al.[30]studied the energy harvester of parametric excitation.In their approach,a lumped-parameter nonlinear model was presented to study the nonlinear dynamics of a parametrically excited cantilever-type harvester.Then Jia et al.[31–34]used a novel design and working mechanism in order to overcome the limitation of initiation threshold amplitude and reduce the shortcomings of a parametrically excited vibration energy harvester.The study by Abdelkefi et al.[35]presented a global nonlinear distributed-parameter model for a piezoelectric energy harvester under parametric excitation.Also,Bitar et al.[36]presented a discrete model for the collective dynamics of periodic nonlinear oscillators under simultaneous parametric and external excitations,which was suitable for several physical applications.The study by Chiba et al.[37]investigated the dynamic stability of a vertically standing cantilever beam under simultaneous horizontal and vertical excitations.To the best know ledge of the authors,few research has been reported for the nonlinear vibration response of a cantilevered piezoelectric beam under parametric and external excitations.In their work,Kacem et al.[38,39]and Jallouli et al.[40]investigated the benefits and applications of the nonlinear resonator simultaneously subjected to external and parametric excitations.

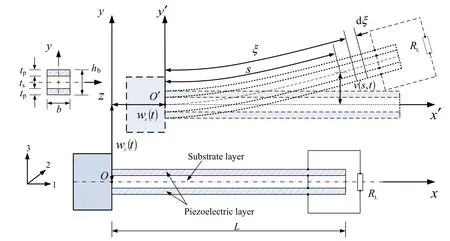
Fig.1 Configuration of the cantilevered piezoelectric beam for an energy harvester

In this paper,the nonlinear dynamics of a cantilevered piezoelectric beam is investigated under simultaneous parametric and external excitations.The beam is composed of a substrate and two piezoelectric layers and assumed as the Euler–Bernoulli model with inextensible deformation.A nonlinear distributed-parameter model of the cantilevered piezoelectric beam is developed by use of the generalized Hamilton principle.The derived model accounts for geometric nonlinearities,but neglects the material nonlinearities by assuming linear constitutive equations.The Galerkin decomposition method is employed to transform nonlinear partial differential equations of motion into a set of nonlinear ordinary differential equations in the time domain.We focus on the first mode of the beam.The harmonic balance method is used to obtain analytical solutions for the vertical displacement,output voltage,and power output amplitude.The influences of the damping,load resistance,and electromechanical coupling coefficient on the frequency–response curves are investigated.

2 Mathematical model o f energy harvester system

We consider a uniform bimorph cantilever beam with lengthLunder its base horizontal and vertical excitations as shown in Fig.1.

The beam is composed of a substrate and two piezoelectric layers.The piezoelectric layers are bounded by two in-plane electrodes of negligible thickness connected to the load resistanceRL.The beam is treated as the Euler–Bernoulli beam with lengthL,widthb,and heighthb=ts+2tp,and shearing deformation and rotatory motion are neglected.tsis the thickness of the substrate layer andtpis the thickness of each piezoelectric layer.Setting theoxyas the inertia coordinate system,the clamped end displacements of the beam arewx(t)andwy(t)in the horizontal and vertical direction,respectively.Theis the base- fixed coordinate system(moving with the base).sis the coordinate along the middle plane of the beam.u(s,t)andv(s,t)are the displacements of the beam relative to thecoordinate system.u(s,t)is in thedirection andv(s,t)in thedirection.We assume that the beam is inextensible[35]

where primeindicates the derivative with respect to the arc length,s.Using Taylor’s expansion,there are

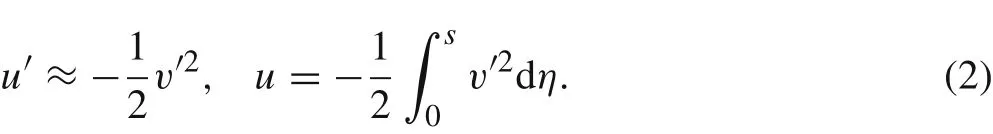
The constitutive relations of the substrate and piezoelectric layers of the beam can be expressed as

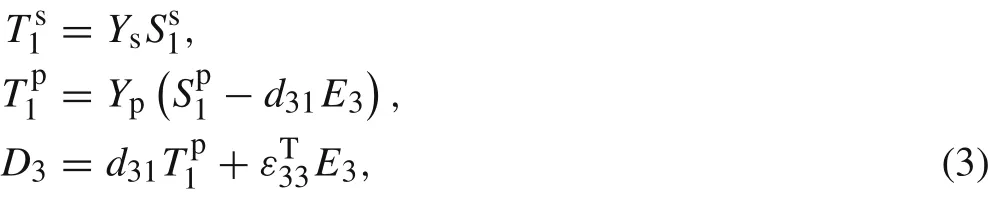
whereYis Young’s modulus,S1is the strain,T1is the stress,d31is the piezoelectric strain constant,D3is the electric displacement andis the permittivity and superscript T represents constant stress,subscript/superscript p and s stand for the piezoelectric and substrate layers,respectively;the 1 and 3 directions are coincident with thexandydirections,respectively(where 1 is the direction of axial strain and 3 is the direction of polarization).E3(t)=?V(t)/(2tp)is the electric field for series connection of piezoelectric layers.V(t)=RLdq/dtis the electric voltage.qis the electric charge.

In what follows,a nonlinear distributed parameter mathematical model of cantilevered piezoelectric vibration energy harvesting system will be derived by using the generalized Hamilton variational principle.Considering the inextensible beam condition in Eq.(1)and the Lagrange’s multiplierλ,the modified energy functional can be expressed as

Substituting Eqs.(3)and(10)into Eq.(9),the following expression is obtained

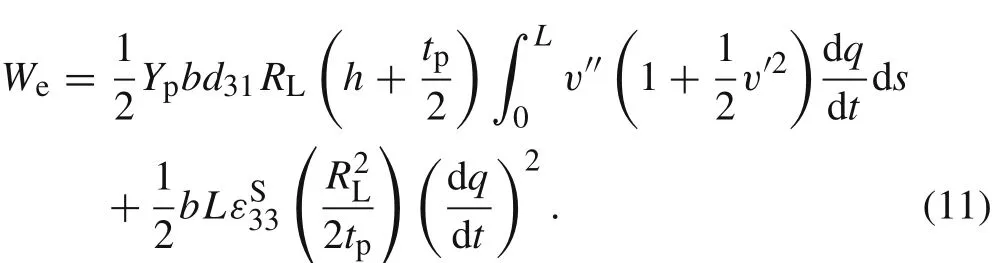
The generalized Hamilton variational principle of the electro mechanical coupling beam can be expressed as

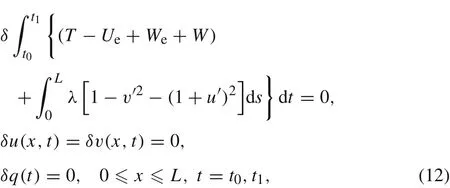
whereWis the electrically extracted work and the work done by the damping force.δWis given by

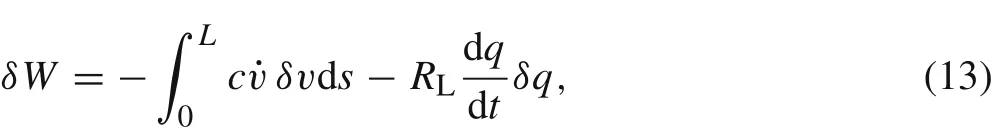
wherecis linear viscous air damping coefficient.

The variations of the kinetic energy,the potential energy,and the electrical energy can be expressed as

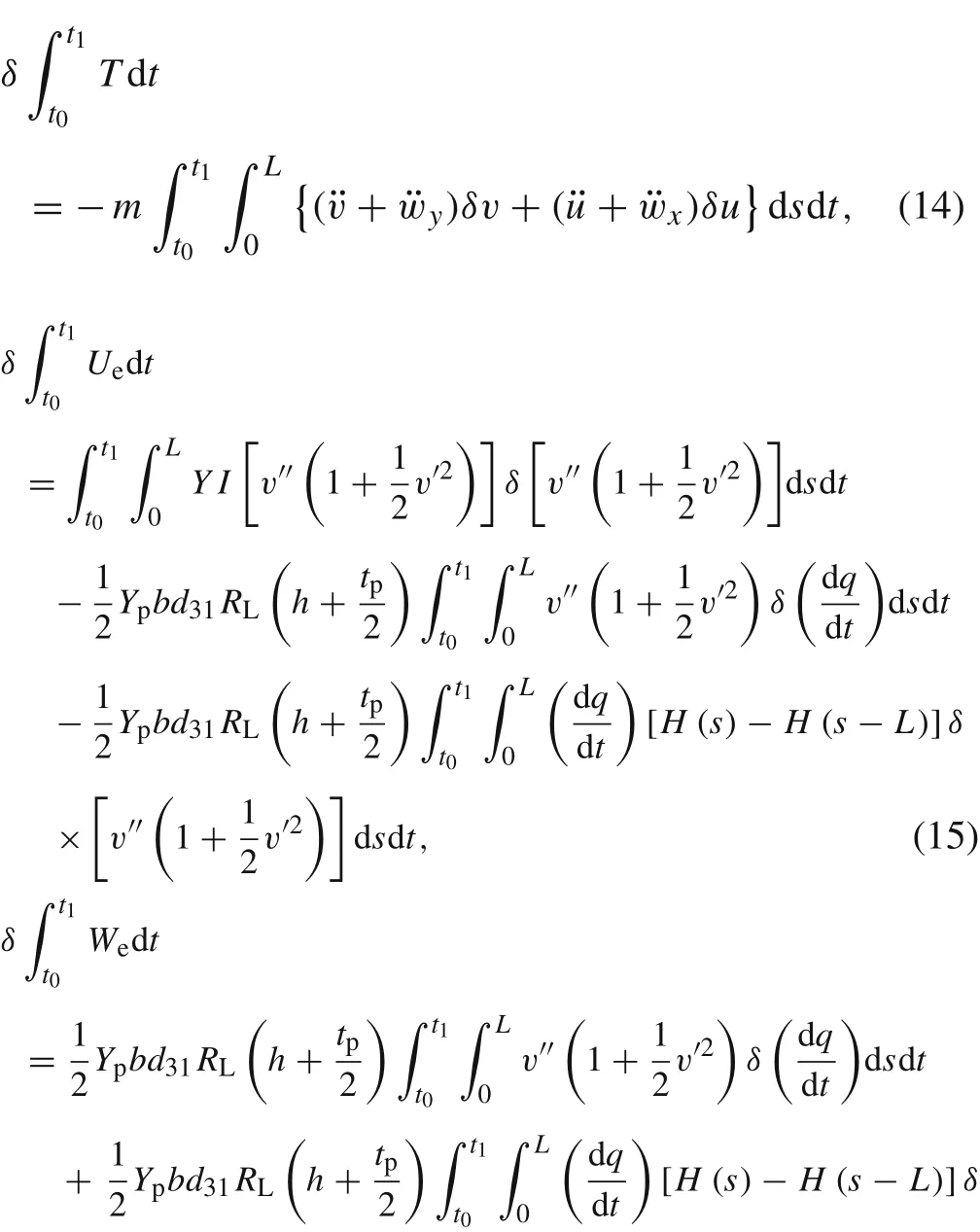
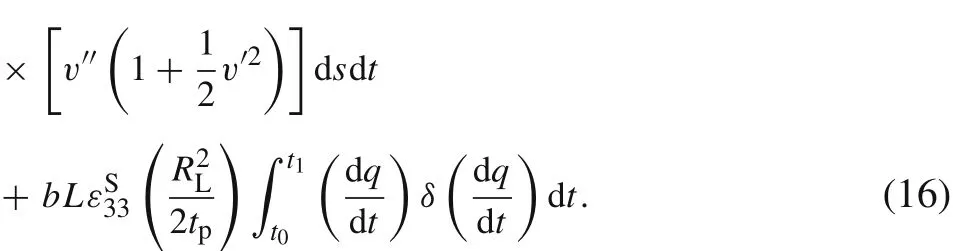
In Eqs.(15)and(16),H(s)is the Heaviside step function which is related to the Dirac delta function.They have the following relation

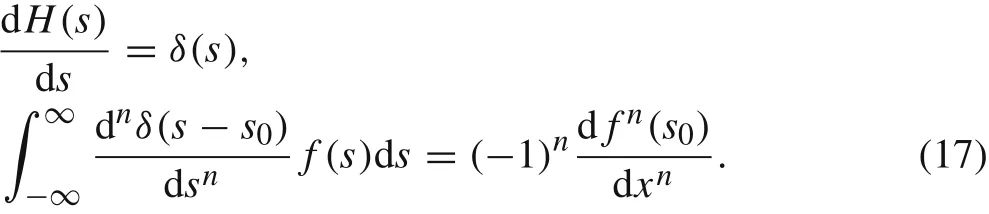
Applying Eq.(10)and the generalized Hamilton principle of Eq.(12),performing a series of variational manipulations and taking up to the cubic order ofv,the governing differential equations of motion can be obtained as follows

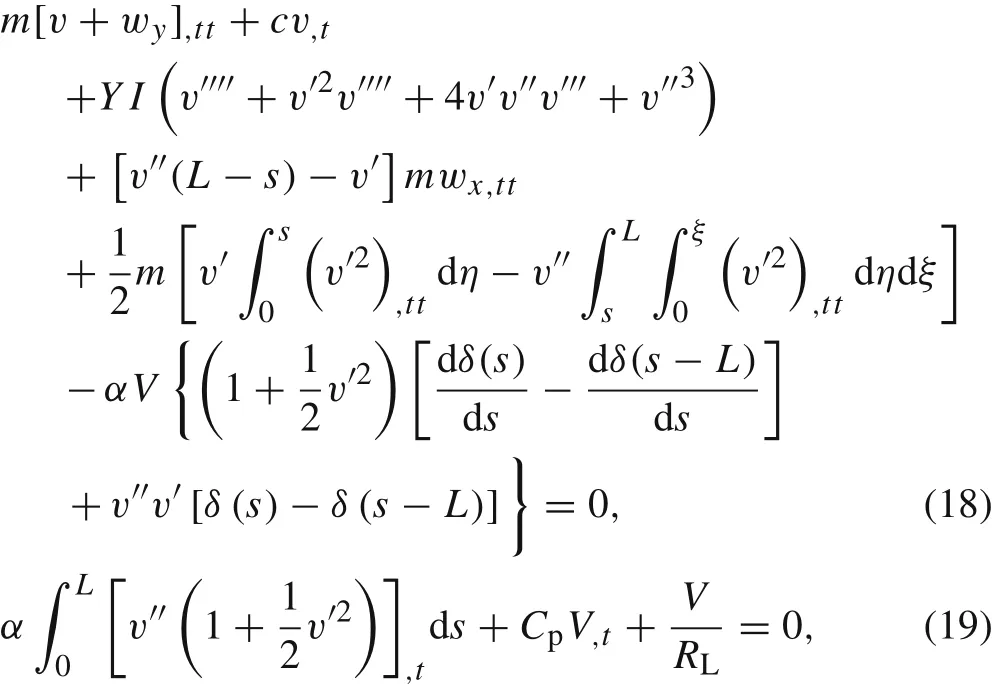
wherethe electromechanical coupling coefficient.Cpis the capacitance of the piezoelectric layers.The above equations are a mathematical model of nonlinear distributed-parameter cantilevered piezoelectric energy harvesting system under simultaneous parametric and external excitations.The horizontal external excitation is transformed into parametric excitation.By removing the nonlinear terms and the base horizontal excitation,the direct excited linear model is recovered[3].Without considering electromechanical coupling,Eq.(18)is similar to the governing equation of motion of the slender beam presented by Chiba et al.[37].

For the purpose of generality,the following dimensionless quantities are introduced into Eqs.(18)and(19)

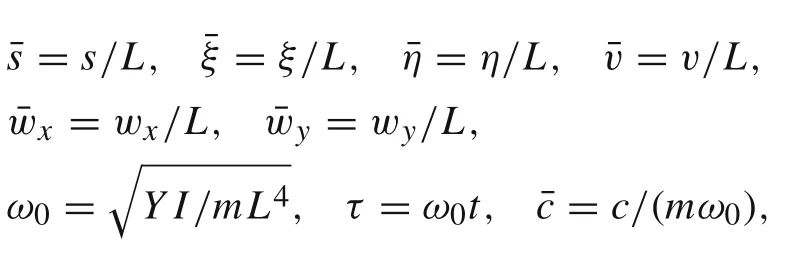
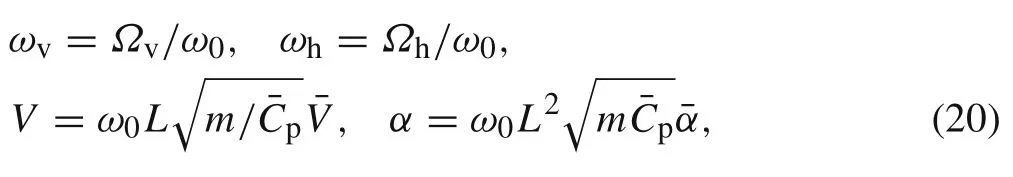
whereΩhandΩvare the horizontal and vertical excited frequencies,respectively.

Equations(18)and(19)can be represented in nondimensional form as

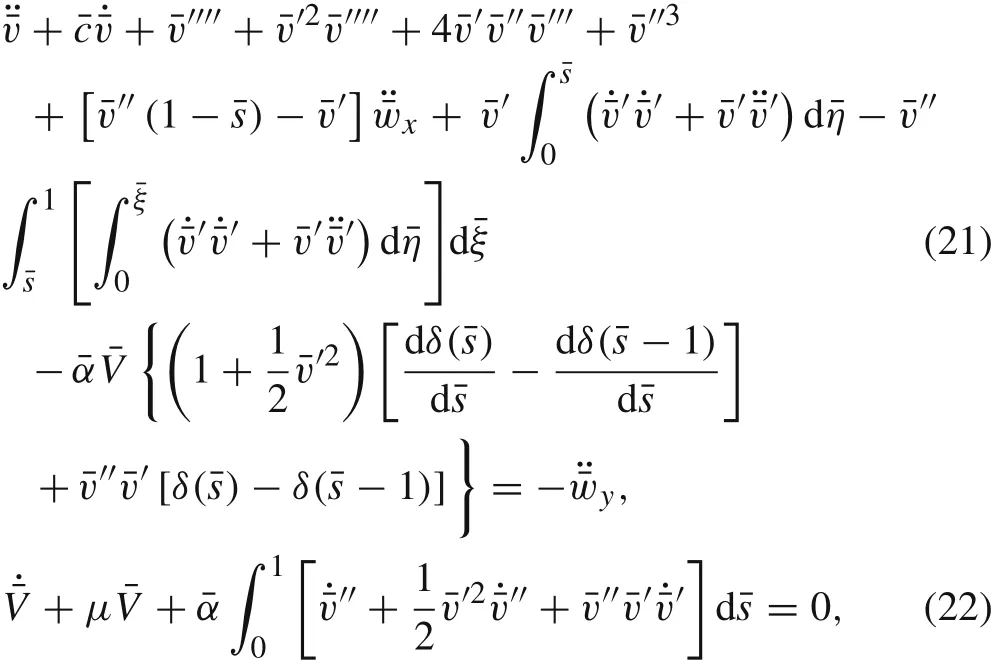
whereindicates the derivative with respect to the time variable,τ.

3 Reduced-order model

To develop a reduced-order model of cantilevered piezoelectric energy harvesting system,the modal Galerkin decomposition method is used to transform the nonlinear partial differential equations(21)and(22)into a set of coupled second order nonlinear ordinary differential equations.The transverse deflectionis decomposed into a summation ofNgeneralized displacement amplitudeand orthogonal basis functionas follows

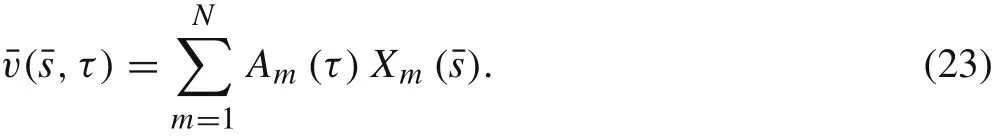
The orthogonal basis functions utilized in this analysis are the linear mode shape functions for the Euler–Bernoulli beam with fixed-free boundary conditions.The normalized mode shape function is given as follows:

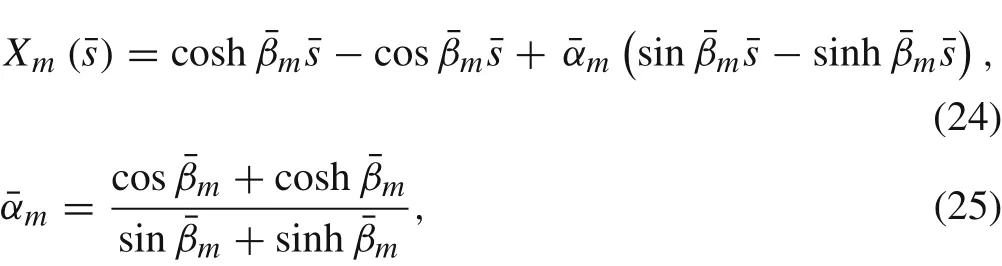
whereis themth eigenfrequency of a cantilever beam,satisfies the following frequency equation

Inserting Eq.(23)into Eqs.(21)and(22),multiplying Eq.(21)by,considering the orthogonality conditions of the mode shape functions and subsequently integrating over the length of the beam,we yield a set of nonlinear ordinary differential equations of motion(form=1,2,...,N).

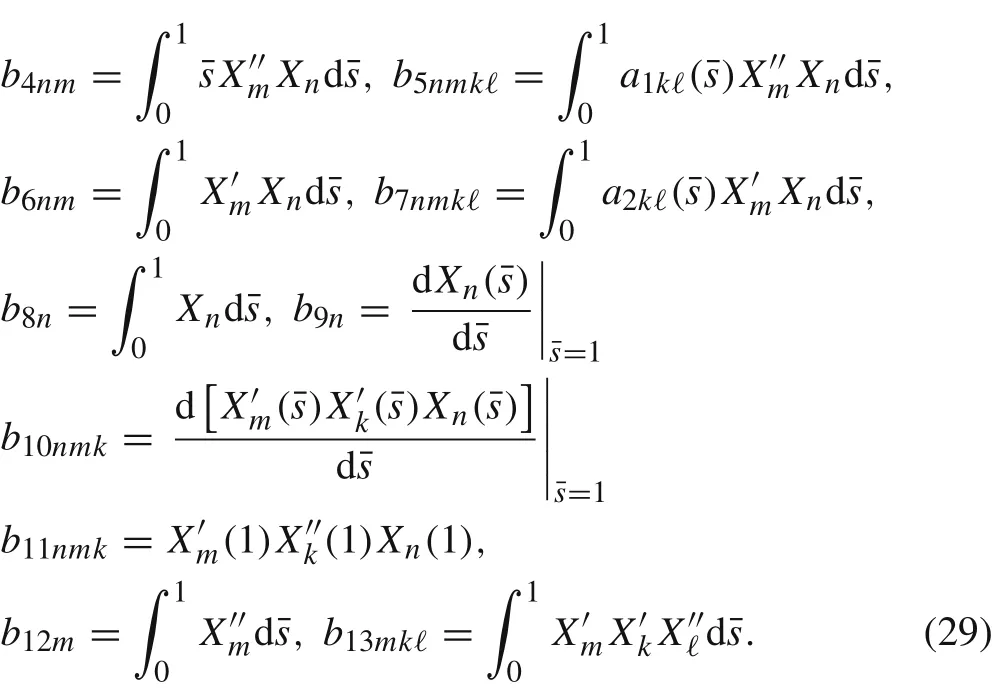
Assuming the excitation frequency is very close to thenth modal frequency,we focus on thenth vibration mode of the beam and neglect the interactions with any of the other modes.Considering only thenth term of the orthogonal basis functions andm=k=?=n,there are

The termis used to describe cubic geometric nonlinearity,represents inertia nonlinearity.are parametric and external excitations,respectively.Equation(31)is the Mathieu equation with nonlinear stiffness and inertia terms as well as with the external force term and voltage.It describes the nonlinear dynamics of cantilevered piezoelectric beams of a single mode approximation under simultaneous parametric and external excitations.Equations(31)and(32)are similar to the nonlinear lumped parameter model presented by Daqaq et al.[30].But the electromechanical coupling terms include nonlinearity,which is different from the nonlinear lumped-parameter model.

4 Harmonic balance analysis

The harmonic balance method has been extensively used to analyze periodic solutions of nonlinear differential equations.Using Fourier series,the nonlinear differential equations in the time variables are transformed into a set of nonlinear algebraic equations in the frequency variables.The number of Fourier series terms dictates the accuracy of the intended solution.The resulting algebraic equations are solved iteratively.When nonlinearities are complicated,the derivation of the algebraic system becomes very cumbersome.Works by Souayeh and Kacem[41],Kacem et al.[42],and Jallouli et al.[43]used the harmonic balance combined with the asymptotic numerical method to analyze the nonlinear problem of resonant sensors at large amplitudes.For a low level of nonlinearity,a single-term harmonic balance solution is sufficient to approximate the steady state response to harmonic excitation.Stantonet al.[27]applied the harmonic balance method to analyze the existence,stability,and influence of parameter variations of bistable piezoelectric inertial generator.

For an analytical solution of the presented problem,harmonic excitations are considered

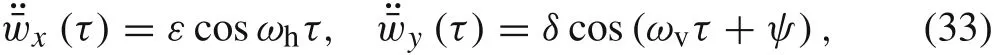
whereεandδare the non-dimensional amplitudes,respectively.

In the present analysis,assuming that the first bending mode of the beam should be the dominant mode of the system,only one mode(n=1)is retained and the other modes are neglected.A single-term harmonic balance solution is sufficient to approximate the steady state response to harmonic excitation for a low level of nonlinearity.

In what follows,the subscripts on the different variables will be omitted for the sake of simplicity.Using Eq.(33),Eqs.(31)and(32)can be rewritten as follows

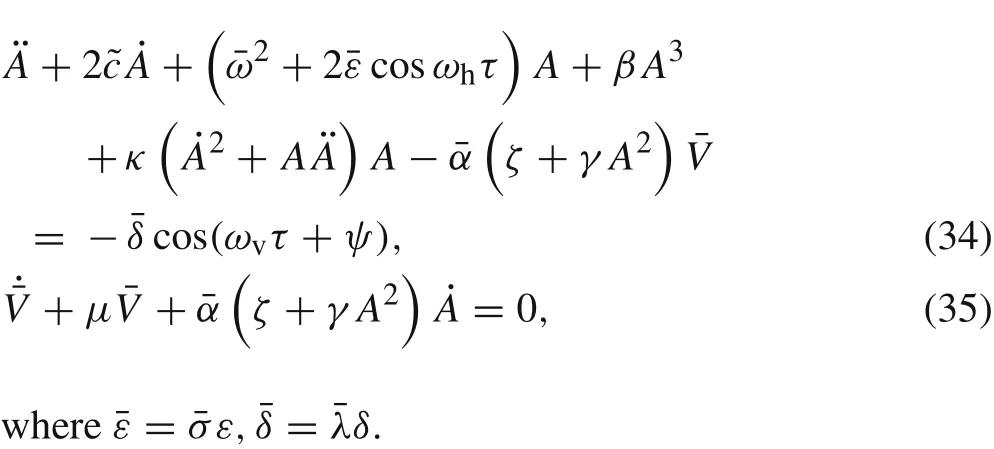
In order to achieve parametric resonance,it has been shown that the first-order(principal)parametric resonance can be attained when the parametric excited frequency is twice the natural frequency[30,31,37].Introducing the non-dimensional excitation frequencyω,ωh,andωvare presented as

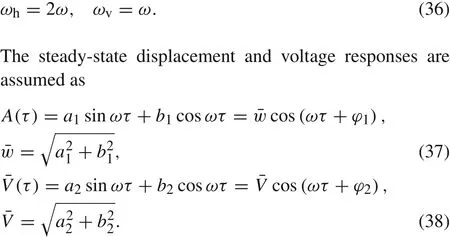
Substituting Eqs.(37)and(38)into Eqs.(34)and(35),and applying the harmonic balance method,the resulting algebraic equations can be written as

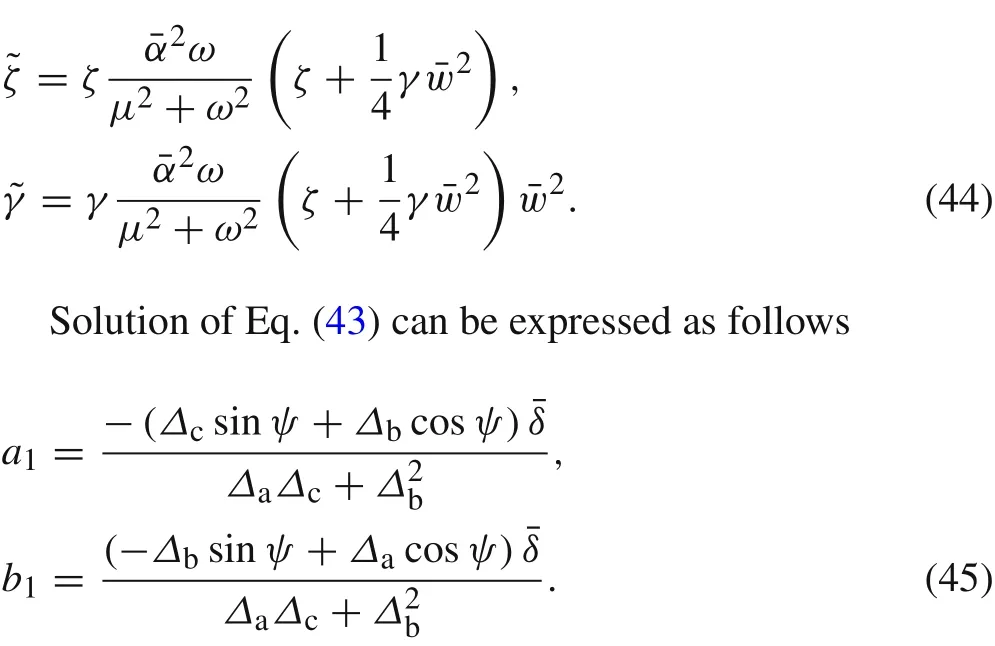
The nonlinear algebraic equation of the frequency–response curves can be expressed in terms of the displacement amplitude and excitation frequency as

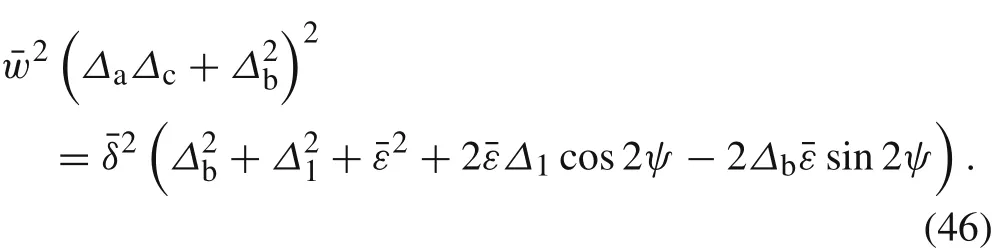
The frequency–response curves can be determined by numerically finding the positive real roots of the above equation in a range of excitation frequencies.The dimensionless response voltage can be written in terms of the mechanical amplitude as follows

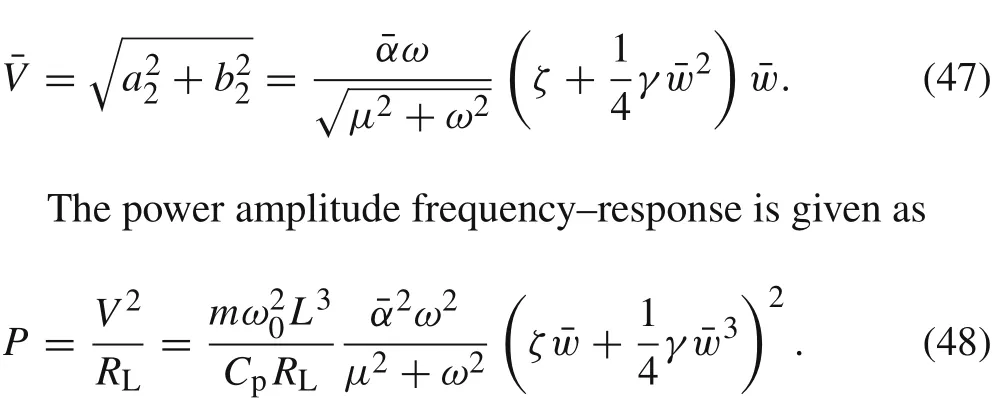
Substituting the solution of Eq.(46)into Eqs.(47)and(48),the frequency–response curve of the voltage and power amplitude can be obtained.

5 Results and discussion

In the previous section,the theoretical model and analytical method have been described for determining the harmonic solutions of the cantilevered piezoelectric energy harvesters under simultaneous parametric and external excitations.In this section,the frequency–response curves of the energy harvesting system will be given and discussed in detail.

Usingn=m=1,the influence of the model parameter variations on the performance of the energy harvester is investigated.These parameters are parametric and external excitation amplitudesεandδ,damping coefficientload resistance parameterRLand electro-mechanical coupling coefficient.The base excitations are considered as harmonic excitation.ψ=0 is assumed.In the absence of specified cases,the results presented in this paper are calculated with the geometric and material parameters given in Table 1.Using the geometric and material coefficients defined in Table 1,all parameters of Eqs.(34)and(35)are as follows

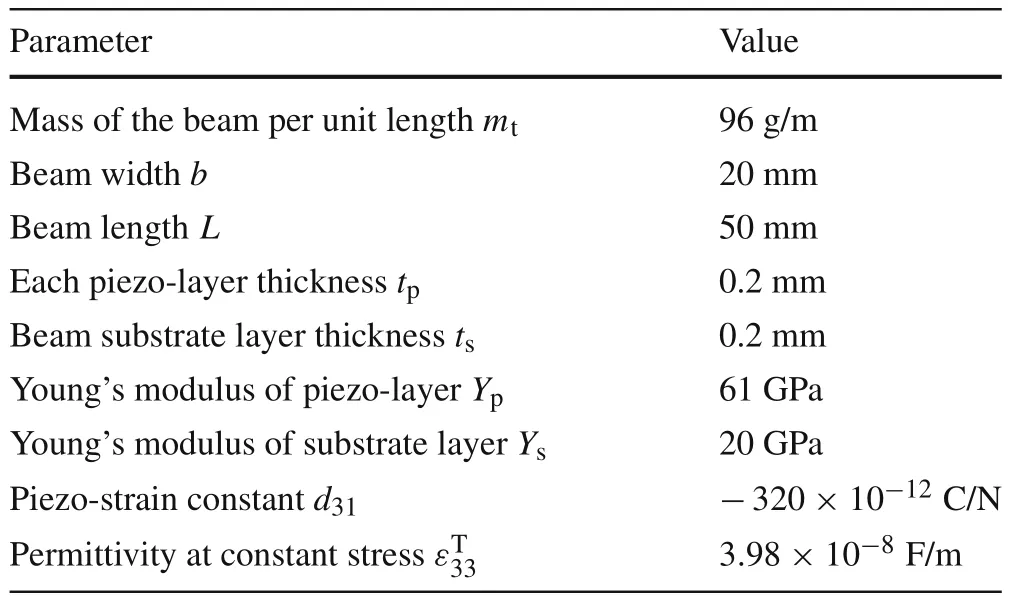
Table1 Geometric and material properties of the energy harvester

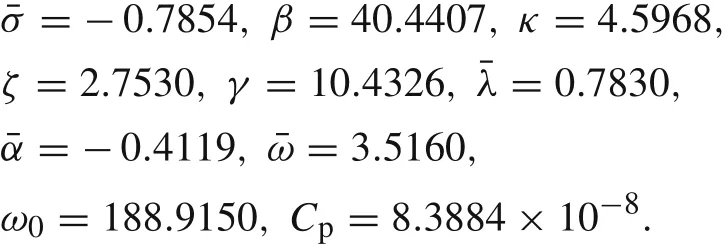
5.1 Only under parametric excitation

In this section,using the presented analytical expression,the numerical results under parametric excitation are obtained.Figure 2 gives the frequency–response curves of the deflection and output power amplitude in the case of different parametric excited amplitudeεwhenandRL=500Ω.Figure2shows that whenδ=0(only parametric excitation), electrical energy can only be harvested within a certain range of excitation frequencies where the non-trivial solutions exist. Outside of this range, only the trivial solutionexists and no electrical energy can be harvested.

Figure 2 shows the nonlinear hardening effect.The frequency–response peak curves are hysteretic and shifted to the high frequencies.The nonlinear hardening effect results in an enhancement of the bandwidth of the energy harvester.The bandwidth enhancement can be reachable when the energy harvester is excited beyond its critical amplitude[44–46].The critical electrical resistance characterizes the upper bound limit of the linear dynamic range of the harvester.

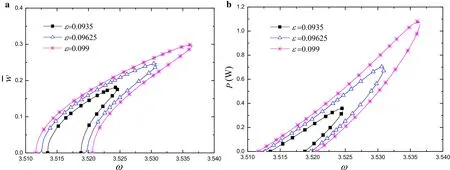
Fig.2 Frequency–response curves of the deflection and output power for different parameters ε when R L=500 Ω,δ=0,and

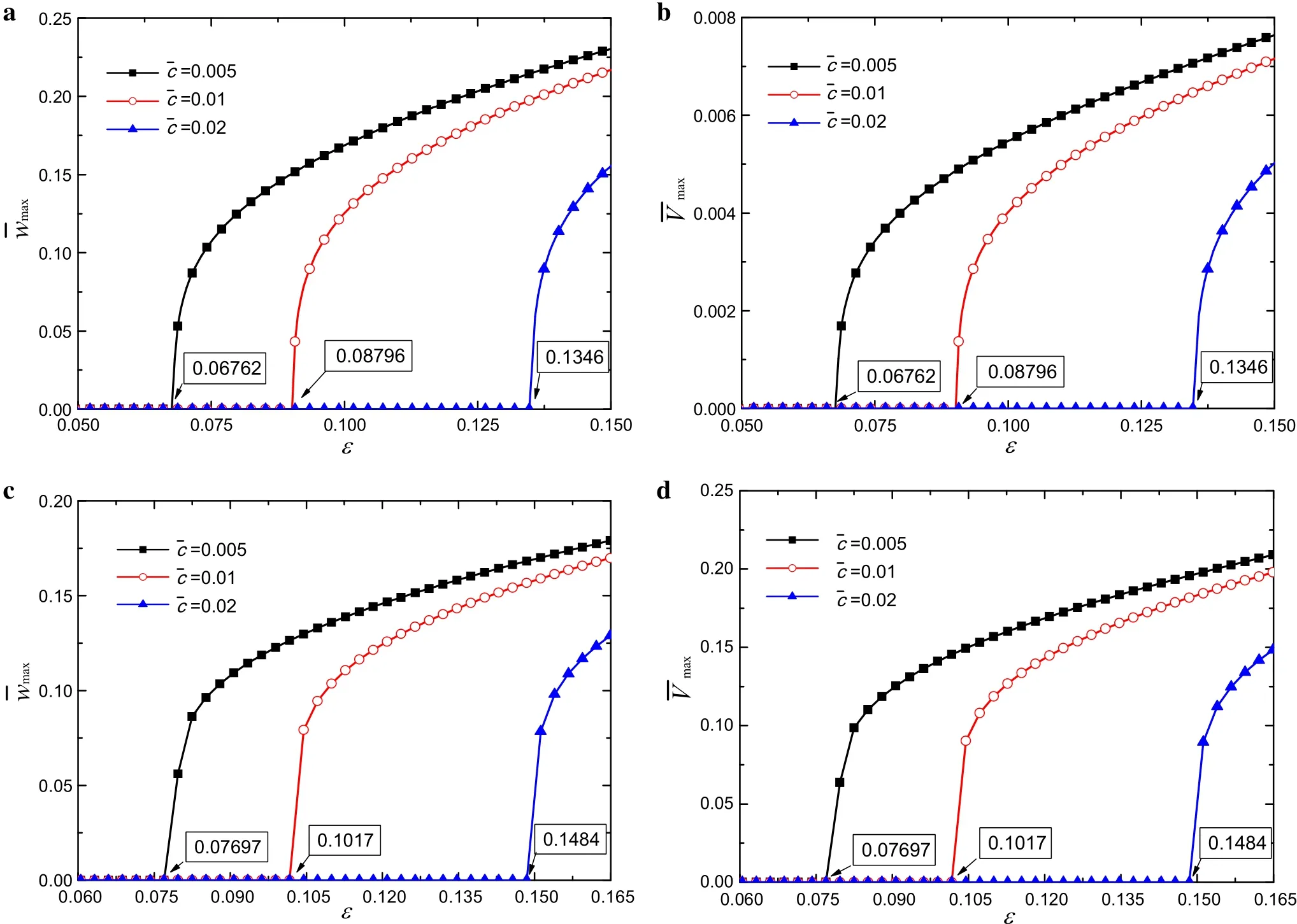
Fig.3 The steady-state resonant peak curves of the deflection and output voltage under parametric excitation at various excitation levels for different parameters and R L.a,b R L=500 Ω,and c,d R L=500 kΩ when δ=0

Figure 3 gives the steady-state resonant peak curves of the deflection and output voltage under parametric excitation at various excitation levels for different parameterswhenRL=500Ω,RL=500 kΩ,andthe dimensionless peak deflection,is the dimensionless peak voltage.Figure 3 shows that only in the case of the parametric excitation,the energy harvesting system has an initiation threshold.When the excited amplitudeεexceeds the initiation threshold,a rapid grow th of the resonant peak deflection and peak output voltage is obtained.The mechan-ical damping and load resistance have significant influence on the initiation threshold,which must be overcome prior to accessing parametric resonance.

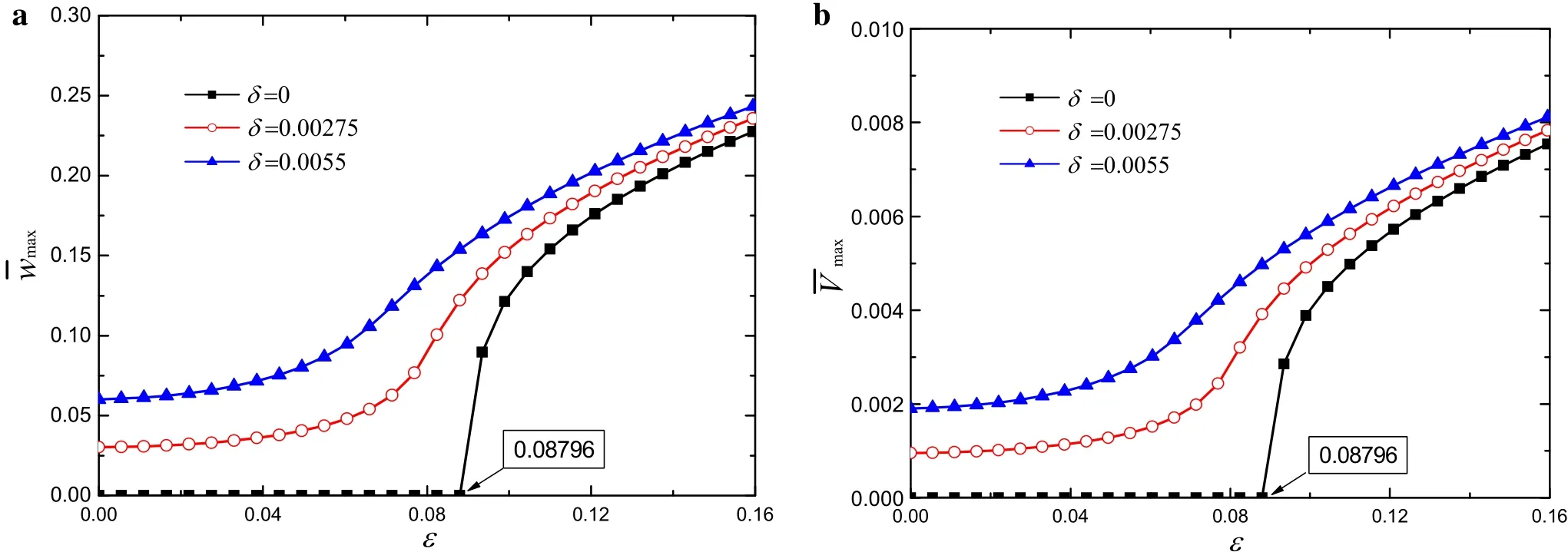
Fig.4 The steady-state resonant peak curves of the deflection and output power at various parametric excitation levels for different external excited amplitude δ when

A steep jump of the nonlinear peak response curves is observed at high parametric excited amplitudeεin Fig.3.For this behavior,a reasonable theoretical explanation can be obtained from the view of mechanics.When parametric excited amplitudeεis very small,the beam is in the state of axial deformation and the state of stable equilibrium,the beam deflection is equal to zero and no energy is harvested.When parametric excited amplitudeεreaches a certain critical value,the state of axial deformation of the beam is transformed to the bending deformation and the state of the beam buckling.The beam deflection increases rapidly and the harvested power is raised dramatically.Buckling of the beam results in significant stresses and produces large output power.However,if the beam’s buckling is not controlled,the beam will be damaged.To prevent the beam’s damage,the bending deformations of the beam must be constrained within a limited range in practical application.

Parametric resonance converges to a zero steady-state response below the initiation threshold.With excitation amplitudes increasing beyond this threshold barrier,it is able ultimately to obtain higher response amplitude.Figure3 shows that this initiation threshold is relatively larger value,whereas the ambient vibration available for energy harvester is usually very small.Accordingly,this initiation threshold must be minimized in order to use the advantages of parametric resonance in practical application.

5.2 Simultaneous parametric and external excitations

Figure 4 gives the steady-state resonant peak curves of the deflection and output power at varying parametric excitation levels for different external excited amplitudeδwhenis the dimensionless resonant peak deflection,is the dimension less resonant peak output voltage.In the case that the excited amplitudeεis below the initiation threshold,Fig.4 shows that whenδequals constant,the frequency–response curves rapidly enlarge with the parametric excited acceleration level increasing.

Figure 5 gives the frequency–response curves of the deflection and output power for different parameterεandRLwhenδ=0.22 and.Figures 4 and 5 also show that although parameterεis below the initiation threshold,the peak deflection and peak output voltage increase with the parameterεincreasing.This is because the external excitation(δ/=0)pushes the system out of axial stable equilibrium and an initial non-zero displacement is obtained.When parameterεexceeds the initiation threshold,a rapid grow th of the peak deflection and peak output voltage is obtained.

In the case of simultaneous parametric and external excitations,the external excitation pushes the system out of axial stable equilibrium,the initial non-zero deflection is obtained.Accordingly,the deflection,the harvested power and frequency bandwidth increase dramatically along with parametric excited amplitude increasing when the excited amplitudeεis below the initiation threshold.

Figure 6 gives the effect of damping coefficient on the amplitude of the steady-state deflection,output voltage.When damping coefficient is relatively small,the response curves bend to a higher frequency direction corresponding to the hardening behavior.The larger damping will weaken the effect of nonlinearity.

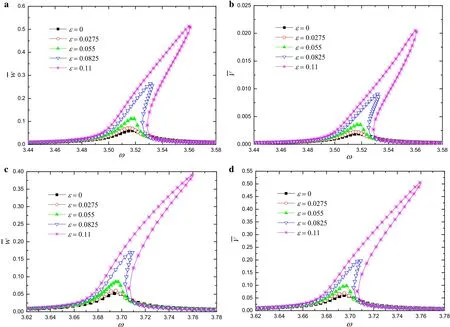
Fig.5 Frequency–response curves of the deflection and output voltage for different parameters ε and R L.a,b R L=500 Ω and c,d R L=500 kΩ when δ=0.0055 and

In what follows,we will investigate the effect of the electro-mechanical coupling coefficient change on energy harvesting performance.Electro-mechanical coupling coefficient is related to the piezoelectric strain constantd31,the width of the piezo-layer,the thickness of the piezolayer and the Young’s modulus of the piezo-layer.Different piezoelectric materials have different piezoelectric strain constants.Assuming that the piezoelectric strain constant is changed and the other parameters remain the constant,electro-mechanical coupling coefficientˉαwill be changed.

Figure 7 gives the frequency–response curves for different electro-mechanical couplingˉαwhenε=δ=0.0165,RL=500Ω,RL=500 kΩ,andˉc=0.01.The peak value of the deflection amplitudes,with increasing electro-mechanical couplingˉα,decreases because some of the harvesting energy suppresses the deformation of the beam.The peak values of the output power amplitude do not increase as one would expect.This can be explained by examining Eq.(48).For a given load resistance,the output power is affected by three major parameters which are the electromechanical coupling,the excited frequency and the deflection amplitude.If the electromechanical coupling increases and the deflection amplitude holds constant,then the output power will increase.However,Fig.7a,c clearly indicate that when the electromechanical coupling increases,the deflection amplitude reduces.Obviously,there is an optimal electromechanical coupling which makes the harvested energy maximization.This result agrees with the previous findings of Daqaq et al.[30].Figure 7 describes that the output power increases initially as electromechanical coupling increases,exhibits a maximum at an optimal electromechanical coupling and drops again beyond the optimal value.In the short-circuit resonance,Fig.7a,b shows that the shift of the resonance frequency is relatively small.In the open-circuit resonance,Fig.7c,d shows that the resonance frequency has as lightly larger shift to the right side along with the electric–mechanical couplingαˉ increasing.

Fig.6 Frequency–response curves of the deflection and output voltage for different parametersδ=ε=0.022

The effect of the load resistanceRLon the displacement and power frequency–response curves,withε=δ=0.0165 andcˉ=0.01,is shown in Fig.8.The load resistance affects the performance of the energy harvester when the base excitation,the damping and the electromechanical coupling remain constant.Figure 8a shows that the frequency–response curves have the two resonant ranges which are the open-circuit resonance and the short-circuit resonance.WhenRLis between 100 and 10 kΩ,the electrical net work approaches the short-circuit resonance.ForRLis greater than 50 kΩ,the electrical net work approaches the open-circuit resonance.The change of the load resistance is similar to the change of the damping and the frequency of the given system.The electro-mechanical coupled damping and resonance frequency can be shown as a function of the load resistance.In the case of near the short-circuit resonance,the peak of the deflection frequency–response curves decreases with the increasing load resistance.In the case near the open-circuit resonance,the peak of the deflection frequency–response curves increases with increasing load resistance.In these two cases, Fig. 8b demonstrates that the power increases initially as the load resistance increases, exhibits a maximumat an optimal load resistance and drops again beyond the optimalvalue.It can be inferred that there exists an optimal load resistance to extract maximum power for a certain set of excitation,damping and electro-mechanical parameter.

5.3 Comparison of distributed-parameter and lumped-parameter models

In this section,we study the difference between the distributed-parameter and lumped-parameter models.Equations(31)and(32)of nonlinear distributed-parameter model of cantilevered piezoelectric energy harvesting system are similar to the nonlinear lumped parameter model presented by Daqaq et al.[30].But the electromechanical coupling terms include nonlinearity,which is different from the nonlinear lumped-parameter model.The electromechanical terms of Eq.(31)are proportional to the voltage,as well as the square of the generalized displacement amplitude.The electromechanical terms of Eq.(32)are proportional to the rate of the generalized displacement amplitude and the square of the generalized displacement amplitude.γ=0 corresponds to the nonlinear lumped-parameter model[30].γ/=0 indicates the nonlinear distributed-parametric model.Figure 9 shows the effect of nonlinear electro-mechanical coupling term on the frequency–response curves.ForRL=500Ω(the short-circuit resonance),Fig.9a,b shows that for these two models,the hardening characteristics of the frequency–response curves are not changed.ForRL=500 kΩ(the open-circuit resonance),Fig.9c,d illustrates that for the nonlinear distributed-parametric model,the frequency–response curves bend to the higher frequency direction,which reflects the effect of the nonlinear electro-mechanical coupling term on the hardening behavior.Compared with the nonlinear lumped parameter model,the nonlinear distributed-parametric model reduces slightly the amplitude of the deflection and the output power of energy harvester,but enhances the frequency bandwidth of the energy harvester.

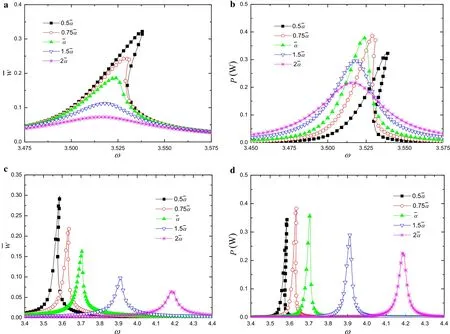
Fig.7 Frequency–response curves of the deflection and output power for different

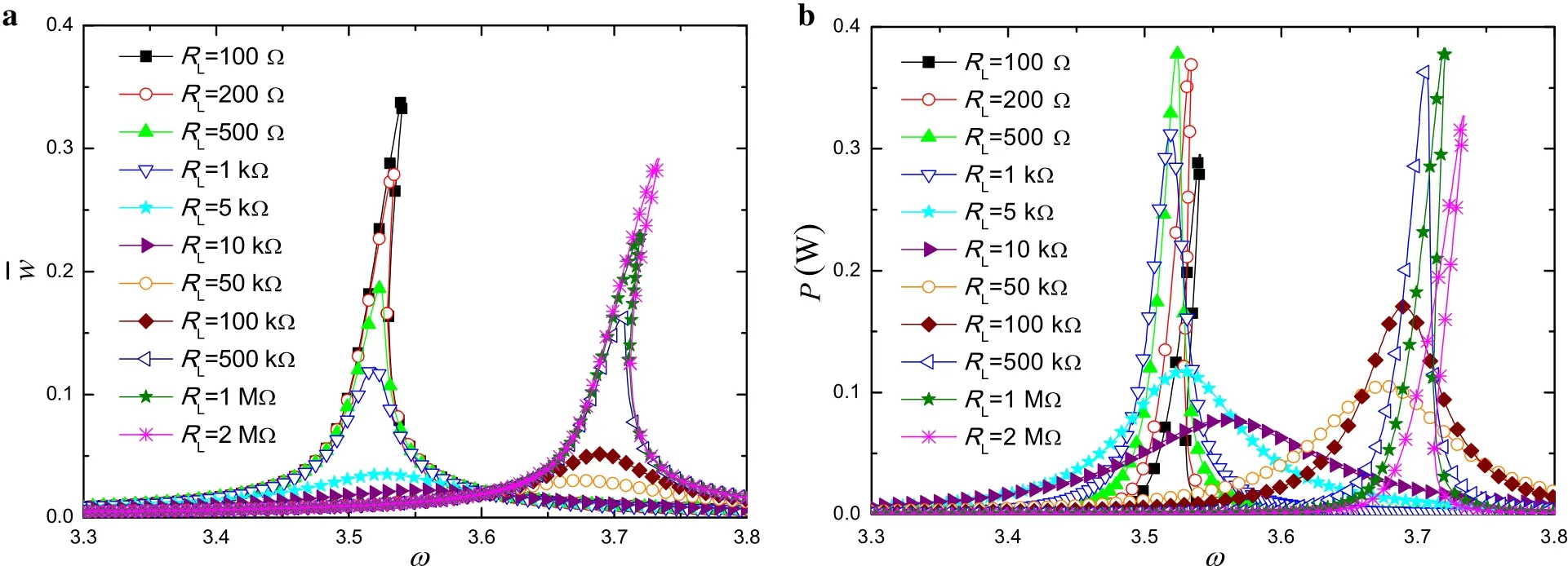
Fig.8 Frequency–response curves of the deflection and output power for different load resistance R L when

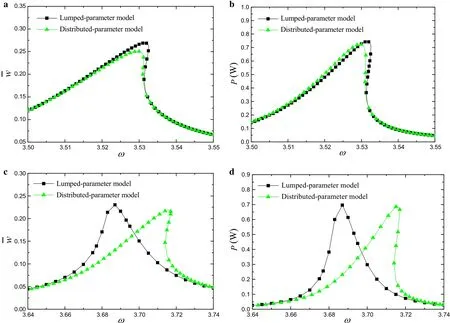
Fig.9 Comparison of frequency–response curves of the deflection and output power between distributed-parameter and lumped-parameter models for different load resistance R L.a,b R L=500 Ω and c,d R L=500 kΩ when δ=ε=0.022 andˉc=0.01

Figures 9 and 10 compare with the resonant peak curves of the deflection and output voltage between the lumped parameter model presented by Daqaq et al.[30]and the proposed distributed-parameter model.For varying excited acceleration levelε,Fig.10shows that in the short-circuit resonance(RL=500Ω),there are small differences between the resonant peak curves of two models.In the open-circuit resonance(RL= 500 kΩ),there are larger differences between the resonant peak curves of the two models.This physical phenomenon can be explained as the damping of the electro-mechanical coupling system increases with the load resistance increasing.The initiation thresholds of the two models are not changed.This phenomenon can be explained as when the energy harvester is the state of axial stable equilibrium there is no bending deformation and geometric nonlinearity.

6 Conclusions

In this study,a nonlinear distributed parameter model of piezoelectric cantilevered beam harvesters under external and parametric excitations has been developed by the generalized Hamilton principle.Analytical expressions of the frequency–response curves have been presented by use of the Galerkin method and harmonic balance method.Utilizing the resulting expressions,we have discussed the effects of the damping,load resistance,electromechanical coupling,and excitation amplitude on the frequency–response curves.We have also studied the difference between the nonlinear lumped-parameter and nonlinear distributed-parameter model for predicting the performance of the energy harvesting system.Several main conclusions are as follows:

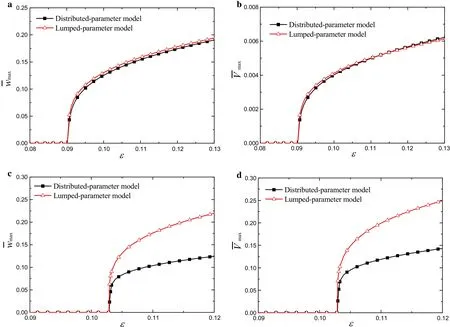
Fig.10 Comparison of resonant peak curves of the deflection and output voltage between distributed-parameter and lumped-parameter models for different load resistance R L.a,b R L=500 Ω and c,d R L=500 kΩ when δ=0 andˉc=0.01

(1)The presented nonlinear distributed parameter model,which includes the nonlinear electro-mechanical coupling term,is different from the nonlinear lumped parameter model.In the case of the short-circuit resonance,the nonlinear electromechanical coupling term does not affect the hardening characteristics of the frequency–response curves.In the case of the opencircuit resonance,the frequency–response curves bend to the higher frequency direction,which reflects the effect of the nonline are lectro-mechanical coupling term on the hardening behavior.

(2)The peak of the deflection frequency–response curves,in the case of the short-circuit resonance,decreases with the load resistance increasing.The peak of the deflection frequency–response curves,at the case of the open-circuit resonance,increases with the load resistance increasing.In these two cases,the output power increases initially as the load resistance increases,exhibiting a maximum at an optimal load resistance and dropping again beyond the optimal value.For a certain set of excitation and electro-mechanical coupling,there exists an optimal load impedance to extract maximum power.

(3)The peak of the deflection frequency–response curves decreases with the electromechanical coupling coefficient increasing.The peak of power frequency–response curves increases initially with electromechanical coupling coefficient increasing,reaches a maximum at an optimal electromechanical coupling and drops again beyond the optimal value.

(4)In the case of parametric resonance,the energy harvesting system has an initiation excitation threshold below this threshold no energy can be harvested.The mechanical damping and load resistance have significant influence on the initiation threshold.

(5)In the case of simultaneous parametric and external excitations,the external excitation pushes the system out of axial stable equilibrium,the initial non-zero deflec-tion is obtained.Accordingly,the deflection,harvested power and frequency bandwidth increase dramatically along with parametric excitation amplitudes increasing although the parametric excitation amplitude is below the initiation threshold.

AcknowledgementsThis research was supported by the National Natural Science Foundation of China(Grant 11172087).

1.Cook-Chennault,K.A.,Thambi,N.,Sastry,A.M.:Powering MEMS portable devices—a review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems.Smart Mater.Struct.17,043001(2008)

2.Anton,S.R.,Sodano,H.A.:A review of power harvesting using piezoelectric materials(2003–2006).Smart Mater.Struct.16,R1–R21(2007)

3.Erturk,A.,Inman,D.J.:A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters.ASME J.Vib.Acoust.130,041002(2008)

4.Muralt,P.:Ferroelectric thin films for micro-sensors and actuators:a review.J.Micromech.Microeng.10,136–146(2000)

5.Caliò,R.,Rongala,U.B.,Camboni,D.,et al.:Piezoelectric energy harvesting solutions.Sensors 14,4755–90(2014)

6.Beeby,S.P.,Tudor,M.J.,White,N.M.:Energy harvesting vibration sources for microsystems applications.Meas.Sci.Technol.17,R175–R195(2006)

7.Priya,S.:Advances in energy harvesting using low profile piezoelectric transducers.J.Electroceram.19,167–184(2007)

8.Sodano,H.A.,Inman,D.J.,Park,G.:A review of power harvesting from vibration using piezoelectric materials.Shock Vib.Dig.36,197–205(2004)

9.Kim,M.,Hoegen,M.,Dugundji,J.,et al.:Modeling and experimental verification of proof mass effects on vibration energy harvester performance.Smart Mater.Struct.19,045023(2010)

10.Sodano,H.A.,Park,G.,Inman,D.J.:Estimation of electric charge output for piezoelectric energy harvesting.Strain 40,49–58(2004)

11.Rafique,S.,Bonello,P.:Experimental validation of a distributed parameter piezoelectric bimorph cantilever energy harvester.Smart Mater.Struct.19,094008(2010)

12.Tang,L.P.,Wang,J.G.:Size effect of tip mass on performance of cantilevered piezoelectric energy harvester with a dynamic magnifier.Acta Mech.228,3997–4015(2017)

13.Daqaq,M.F.,Masana,R.,Erturk,A.,et al.:On the role of nonlinearities in vibratory energy harvesting:acritical review and discussion.ASME Appl.Mech.Rev.66,040801(2014)

14.Mahmoodi,S.N.,Daqaq,M.F.,Jalili,N.:On the nonlinear- flexural response of piezoelectrically driven microcantilever sensors.Sens.Actuators A Phys.153,171–179(2009)

15.Mahmoodi,S.N.,Jalili,N.:Non-linear vibrations and frequency response analysis of piezoelectrically driven microcantilevers.Int.J.Non-Linear Mech.42,577–587(2007)

16.Mahmoodi,S.N.,Jalili,N.,Ahmadian,M.:Subharmonics analysis of nonlinear flexural vibrations of piezoelectrically actuated microcantilevers.Nonlinear Dyn.59,397–409(2010)

17.Stanton,S.C.,Erturk,A.,Mann,B.P.,et al.:Nonlinear piezoelectricity in electroelastic energy harvesters:modeling and experimental identification.J.Appl.Phys.108,074903(2010)

18.Abdelkefi,A.,Nayfeh,A.H.,Hajj,M.R.:Effects of nonlinear piezoelectric coupling on energy harvesters under direct excitation.Nonlinear Dyn.67,1221–1232(2012)

19.Triplett,A.,Quinn,D.D.:The effect of non-linear piezoelectric coupling on vibration-based energy harvesting.J.Intell.Mater.Syst.Struct.20,1959–1967(2009)

20.Neiss,S.,Goldschmidtboeing,F.,Kroener,M.,et al.:Analytical model for nonlinear piezoelectric energy harvesting devices.Smart Mater.Struct.23,105031(2014)

21.Mousa,A.A.,Sayed,M.,Eldesoky,I.M.,et al.:Nonlinear stability analysis of a composite laminated piezoelectric rectangular plate with multi-parametric and external excitations.Int.J.Dyn.Control 2,494–508(2014)

22.Mahmoudi,S.,Kacem,N.,Bouhaddi,N.:Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions.Smart Mater.Struct.23,075024(2014)

23.Friswell,M.I.,Ali,S.F.,Bilgen,O.,et al.:Non-linear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass.J.Intell.Mater.Syst.Struct.23,1505–1521(2012)

24.Chen,L.Q.,Jiang,W.A.:A piezoelectric energy harvester based on internal resonance.Acta.Mech.Sin.31,223–228(2015)

25.Sun,S.,Cao,S.Q.:Analysis of chaos behaviors of abistable piezoelectric cantilever power generation system by the second-order Melnikov function.Acta Mech.Sin.33,200–207(2017)

26.Karami,M.A.,Inman,D.J.:Equivalent damping and frequency change for linear and nonlinear hybrid vibrational energy harvesting systems.J.Sound Vib.330,5583–5597(2011)

27.Stanton,S.C.,Owens,B.,Mann,B.P.:Harmonic balance analysis of the bistable piezoelectric inertial generator.J.Sound Vib.331,3617–3627(2012)

28.Kim,P.,Seok,J.:Amulti-stableenergy harvester:dynamic modeling and bifurcation analysis.J.Sound Vib.333,5525–5547(2014)

29.Abed,I.,Kacen,N.,Bouhaddi,N.,et al.:Multi-modal vibration energy harvesting approach based on nonlinear oscillator arrays under magnetic levitation.Smart Mater.Struct.25,025018(2016)

30.Daqaq,M.F.,Stabler,C.,Qaroush,Y.,et al.:Investigation of power harvesting via parametric excitations.J.Intell.Mater.Syst.Struct.20,545–557(2009)

31.Jia,Y.,Yan,J.,Soga,K.,et al.:Parametrically excited MEMS vibration energy harvesters with design approaches to overcome the initiation threshold amplitude.J.Micromech.Microeng.23,114007(2013)

32.Jia,Y.,Seshia,A.A.:An auto-parametrically excited vibration energy harvester.Sens.Actuators A 220,69–75(2014)

33.Jia,Y.,Yan,J.,Soga,K.,et al.:Parametric resonance for vibration energy harvesting with design techniques to passively reduce the initiation threshold amplitude.Smart Mater.Struct.23,065011(2014)

34.Jia,Y.,Yan,J.,Soga,K.,et al.:A parametrically excited vibration energy harvester.J.Intell.Mater.Syst.Struct.25,278–289(2014)

35.Abdelkefi,A.,Nayfeh,A.H.,Hajj,M.R.:Global nonlinear distributed-parameter model of parametrically excited piezoelectric energy harvesters.Nonlinear Dyn.67,1147–1160(2012)

36.Bitar,D.,Kacem,N.,Bouhaddi,N.,et al.:Collective dynamics of periodic nonlinear oscillators under simultaneous parametric and external excitations.Nonlinear Dyn.82,749–766(2015)

37.Chiba,M.,Shimazaki,N.,Ichinohe,K.:Dynamic stability of a slender beam under horizontal–vertical excitations.J.Sound Vib.333,1442–1472(2014)

38.Kacem,N.,Baguet,S.,Dufour,R.,et al.:Stability control of nonlinear micromechanical resonators under simultaneous primary and superharmonic resonances.Appl.Phys.Lett.98,193507(2011)

39.Kacem,N.,Baguet,S.,Duraffourg,L.,et al.:Overcoming limitations of nanomechanical resonators with simultaneous resonances.Appl.Phys.Lett.107,073105(2015)

40.Jallouli,A.,Kacem,N.,Bouhaddi,N.:Stabilization of solitons in coupled nonlinear pendulums with simultaneous external and parametric excitations.Commun.Nonlinear Sci.Numer.Simul.42,1–11(2017)

41.Souayeh,S.,Kacem,N.:Computational models for large amplitude nonlinear vibrations of electrostatically actuated carbon nanotubebased mass sensors.Sens.Actuators A Phys.208,10–20(2014)

42.Kacem,N.,Baguet,S.,Hentz,S.,et al.:Computational and quasianalytical models for non-linear vibrations of resonant MEMS and NEMS sensors.Int.J.Non-Linear Mech.46,532–542(2011)

43.Jallouli,A.,Kacem,N.,Bourbon,G.,et al.:Pull-in instability tuning in imperfect nonlinear circular microplates under electrostatic actuation.Phys.Lett.A 380,3886–3890(2016)

44.Juillard,J.,Bonnoit,A.,Avignon,E.,et al.:From MEMS to NEMS:closed-loop actuation of resonant beams beyond the critical duffing amplitude.In:Proceedings of IEEE Sensors Conference,Lecce,Italy,510–513(2008).https://doi.org/10.1109/ICSENS.2008.4716489

45.Kacem,N.,Baguet,S.,Hentz,S.,et al.:Nonlinear phenomena in nanomechanical resonators:mechanical behaviors and physical limitations.Mécan.Ind.11,521–529(2010)

46.Kacem,N.,Baguet,S.,Hentz,S.,et al.:Pull-in retarding in nonlinear nanoelectromechanical resonators under superharmonic excitation.J.Comput.Nonlinear Dyn.7,021011(2012)