Enriched reproducing kernelparticle method for fractional advection–diffusion equation

Yuping Ying·Yanping Lian·Shaoqiang Tang·Wing Kam Liu

1 Introduction

Mesh free methods are proposed as an alternative or enhancement to commonly used mesh-based numerical methods such as the finite element method,which exhibits shortcomings in handling problems with large deformations,high gradients or systems with wide range of response spectra.By the elimination of a mesh,meshfree methods avoid the difficulty of maintaining connectivity through an entire simulation where severe mesh distortion may occur.Meshfree methods have been successfully applied to problems such as metal forming[1],large deformation analysis[2–4],fracture modeling[5,6]and fragment-impact problems[7,8].Among the existing meshfree methods,the reproducing kernel particle method(RKPM)is characterized by its capability in regard to multi-resolution analysis[9,10].Multi-resolution analysis makes use of a window function which can be translated and dilated simultaneously.By this operation,a desired and width-selected portion of the spectrum of a signal can be isolated or focused on.In addition to large deformation problems,RKPM has been used in structural acoustics,computational fluid dynamics and micro-mechanics[11–14],among many other fields.In this paper,RKPM is enriched and extended to study a nonlocal problem modeled by a fractional differential equation(FDE).

Fractional calculus is concerned with integrals and derivatives of fractional or non-integer order[15].In recent years,FDEs based on fractional calculus have attracted increasing attention due to their success in modeling time-history related and space-correlated problems[16].For instance,several kinds of physical phenomena,such as transfer of particles in porous media,turbulent flow,optical lattices,are found to be well described by FDEs[17–22].Differential equations of fractional order are more complicated for mathematical analysis than those of integer order.The fractional operators are nonlocal and contain weakly singular convolution kernels,which leads to non-smoothness or low regularity of the solutions to FDEs[23].Accordingly,the applicable numerical methods are also more challenging[24].

Many numerical methods have been proposed for solving FDEs[25,26].However,they are mainly based on the assumption of smoothness and high regularity of the solutions.Recently,Ding et al.[27]proposed a high-order finite difference scheme for the Riesz fractional derivative.We[28]proposed a high-order central difference scheme for the Caputo fractional derivative and used it to solve a fractional advection–diffusion equation(FADE)with fractional derivatives in space.Both need high regularity of the solutions to guarantee numerical accuracy.FDEs were solved with the Galerkin finite element method by Ervin et al.[29–31],who also analyzed the existence and uniqueness of the numerical solution.It is noted that the accuracy and stability of the traditionally well developed finite element method may be challenged by small fractional order of the concerned spatial derivative.The Galkerin finite element method was used by Lian et al.[32]to solve an FADE and to prove that spurious oscillations may occur at the ending points and on the boundaries,where the exact solution has singularity in its first-order derivative.

In order to resolve the singularity and non-smoothness of the solutions to FDEs,several numerical approaches have been proposed.An FADE was solved using a Petrov–Galerkin finite element method by Lian et al.[32];the method utilized an upwind property,which suppressed numerical oscillations near the boundaries.The integer-order shape function in the Galerkin finite element method,in the work of Luan et al.[33],was replaced by one of fractional order,which is identical to the order of the solved FDE.A series of spectral collocation methods was developed by Karniadakis et al.to solve FDEs with non-smooth solutions.They studied several kinds of Sturm–Liouville problems,obtained the eigen-solutions in the form of Jacobi polynomials and proved orthogonality of the eigen-solutions[34].Then they used the eigen-solutions as basis of spectral methods to solve fractional ordinary differential equations,fractional partial differential equations and FDEs with variable fractional order[35–37].

Mesh free methods are famous for not only their high accuracy in large deformation problems but also for the convenience they provide for adding base functions for specific problems,like the simulation of crack tip fields with low regularity[38].In this paper,we generalize the polynomial reproducing property of RKPM to power functions of noninteger orders,and apply the enriched RKPM to solve an FADE.An RKPM withnth-order monomial basis exhibitsnth-order consistent property[39].In other words,anynthorder polynomials can be exactly reproduced by the RKPM interpolation.When RKPM is utilized to solve an FADE,it should be noted that the fractional power property of the solution can not be resolved.Instead,numerical oscillations occur.To ensure the reproducing condition for the fractional power functions,the monomial bases are enriched by related power functions of fractional order.For convenience,the enriched RKPM is formulated on a moving least-square approach.Compared with the enriched finite element method by Luan et al.[33],the enriched RKPM provides more freedom to add bases and is easier to operate.

The rest of this paper is organized as follows.In Sect.2,analytical solution of an FADE is discussed.In Sect.3,the enriched RKPM interpolation formula is derived and its completeness property is proved.Then we discuss the error caused by the non-reproduced part of the solution to the FADE.In Sect.4,a Galerkin procedure for the FADE is formulated with the shape functions constructed by the enriched basis.In Sect.5,several numerical examples are presented to illustrate the effectiveness of the proposed method.

2 Problem statement

We consider the following FADE in one space dimension

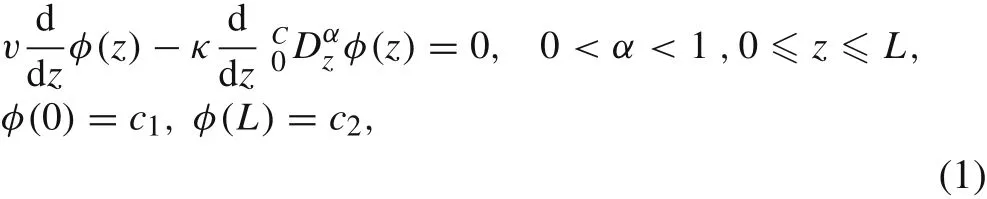
wherev≥ 0 is the advection speed,κ＞0 is the diffusion coefficient,φrepresents the solution concentration,Lis the right boundary of the computing domain.The Caputo fractional derivative in Eq.(1)is defined as

By re-scalingx=z/S,x0=L/S,whereS/=0 is the scaling length,the following non-dimensional problem is obtained

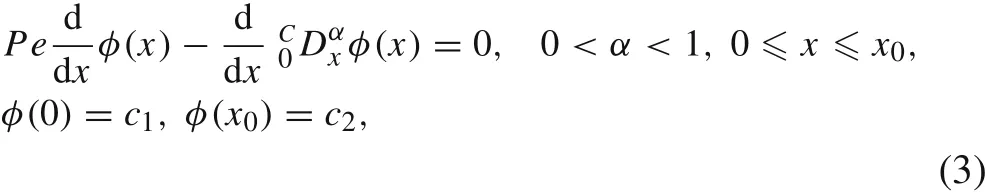
with the dimensionless parameterPe=vSα/κ,which characterizes the relative strengths of the advection term and the diffusion term.Whenα=1 is taken,it reduces to the conventional Peclet numberPe=vS/κfor advection–diffusion equation of integer order.

WhenPe＞0,it can be checked that Eq.(3)is solved by

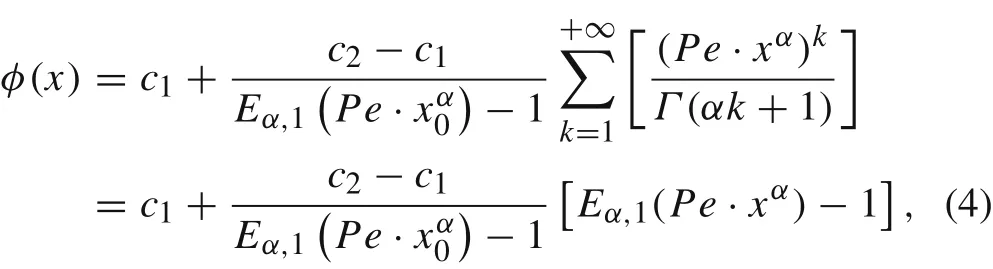
3 Enriched RKPM interpolant

RKPM constructs a series of shape functions and solves partial differential equations by the Galerkin procedure.Based on an integer order basis,regular RKPM shape functions can reproduce polynomials exactly,which leads to a globally conforming interpolation field of the desired order.As for the FADE Eq.(1),however,RKPM cannot reproduce the fractional power functions in the solution.Then numerical oscillations may occur.RKPM is enriched in this section to resolve the fractional power functions.

3.1 Moving least-square reproducing formula with terms

To include functions that appear in the asymptotic field near 0,fractional order monomials are used to enrich the basis of traditional RKPM,which makes the formulation slightly different from that proposed by Liu in Ref.[39].The enriched basis reads

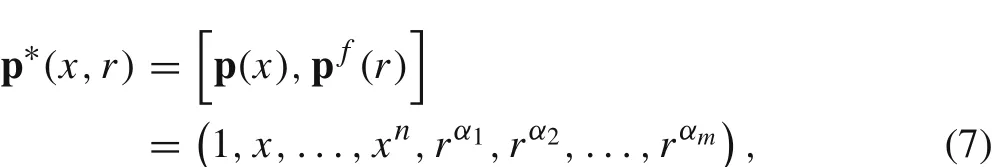
where p(x)=(1,x,...,xn)is the traditional basis of integer order with the highest order ofn,ris a global coordinate representing the distance to 0,pf(r)=(rα1,rα2,...,rαm)is the additional terms withmthe number of terms.Then a local approximation functionφl(x,ˉx)toφ(x)atˉxis constructed as

Considering a process of moving the local approximation through the whole domain,we obtain a global approximationφg(x)by takingˉx→xin Eq.(12)

After choosing a suitable particle distribution,we apply the rectangle quadrature rule to both Eqs.(13)and(14).A discrete approximation functionφh(x)then follows

Fig.1 Comparison of shape functions.The left and right figures depict shape functions constructed based on traditional basis and the proposed enriched basis,respectively

where NP is the number of particles,xI,I=1,2,...,NP denotes the position of each particle,ΔVIis the corresponding integration weighting of each particle,and

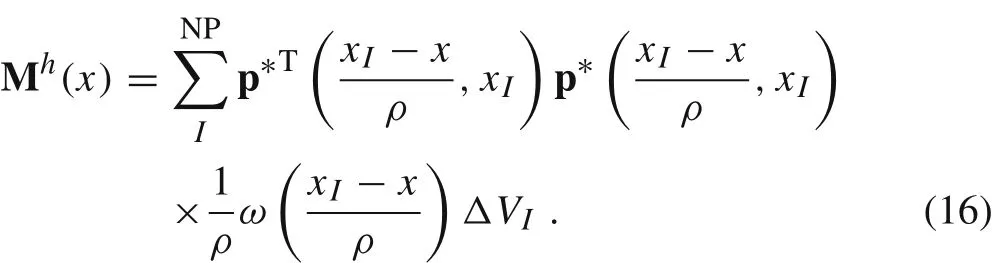
The discrete formula(15)can be recast to a shape function expansion,which is especially convenient in the Galerkin procedure.That is,

In Fig.1,shape functions constructed based on the traditional basis of integer order and the enriched basis are compared.For simplicity,we take particles on[0,1]with uniform spacingΔx=0.1.The left sub figure of Fig.1 depicts the shape functions when pT(x,r)=(1,x),h=0.1,ρ=1.The right sub figure depicts the shape functions constructed based on the enriched basis pT(x,r)=(1,x,r0.3)withh=0.1,ρ=1.5.It can be noted that the shape functions have infinite derivatives atx=0 if 0 is in their supports.

3.2 Completeness of interpolants

To meet the convergence requirement,Liu et al.[39]proved ann-consistency structure for RKPM.Here,a similar consistency structure is proved for the enriched RKPM.

The enriched RKPM with basis Eq.(7)can reproduce any functionf(x)=f1(x)+f2(x)exactly by using the sampling values,wheref1(x)are polynomials,andcjare constants.That is,

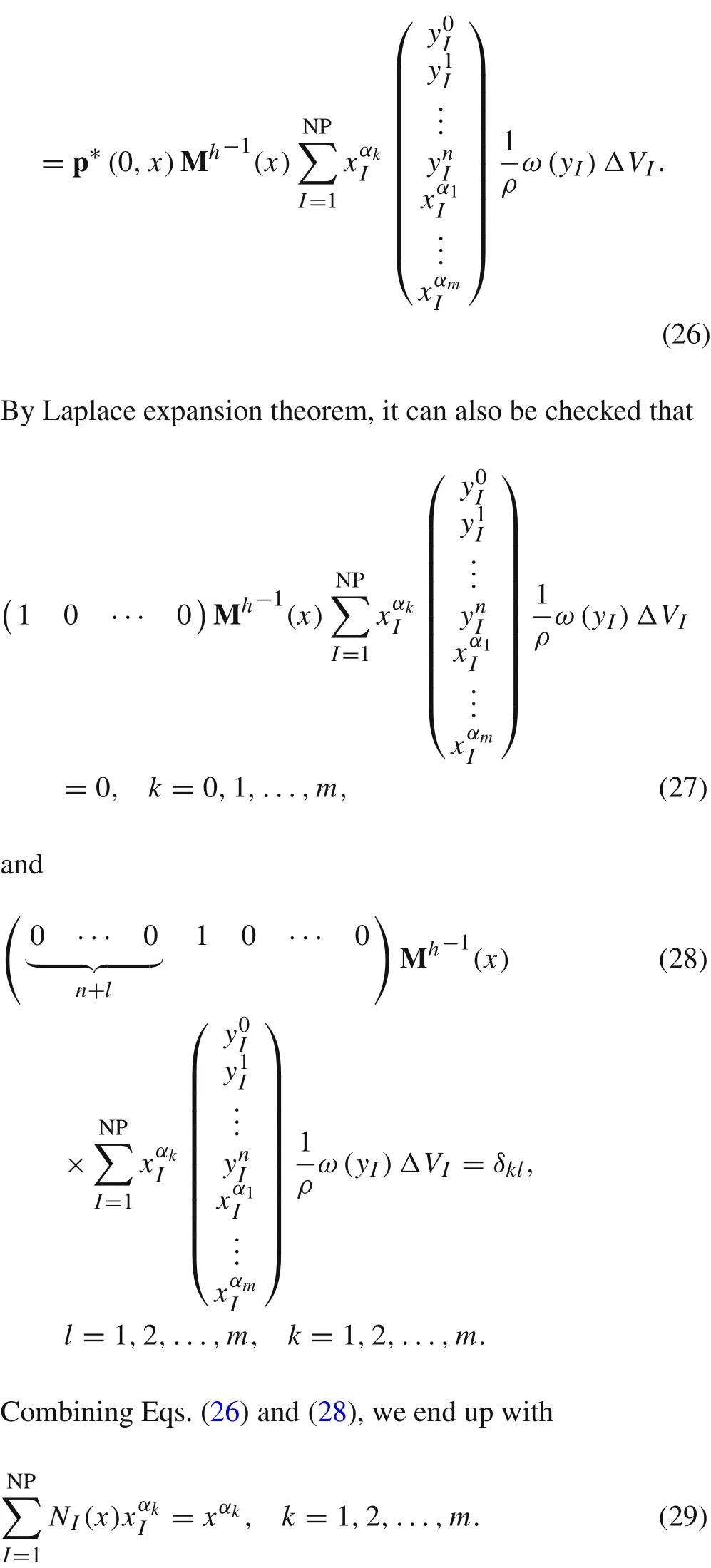
3.3 Approximation error for the enriched RKPM interpolant to FADE solution

Monomials of fractional order can be exactly reproduced by the shape functions constructed based on the enriched basis Eq.(7).However,since Eq.(4)is a series of fractional monomials,fractional-order terms remain which can not be reproduced.The orders of these dropped terms may be less than 1 and lead to singular derivatives atx=0.The non-reproduced singular field will cause oscillation of the numerical solution to Eq.(3).

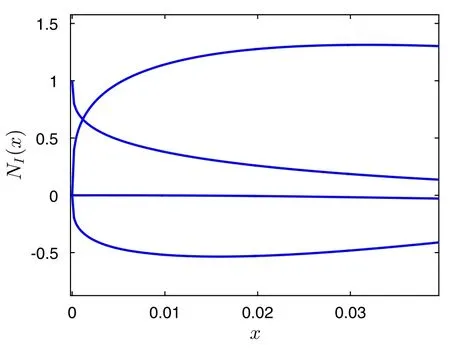
Fig.2 Zoom in near the left boundary of the right figure in Fig.1

In this section,we discuss a function reproducing error of the enriched RKPM to Eq.(4),which is defined as the nonreproduced part of Eq.(4)by the enriched shape functions(Fig.2).

By choosing the rescaling parameterS=L,we obtain

WhenPe=0,Eq.(3)reduces to a fractional pure diffusion equation,which is solved by Eq.(6).According to the reproducing property Eq.(19),Eq.(6)can be exactly reproduced by utilizing an enriched basis p?T(x,r)=(1,rα).

WhenPe＞0,we rew rite Eq.(4)as

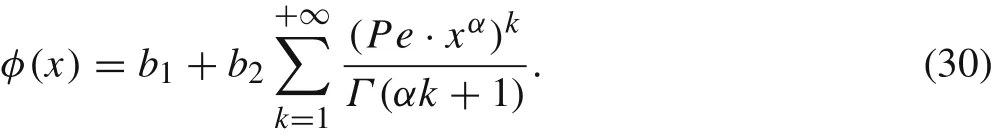
It is obvious that Eq.(30)cannot be exactly reproduced by a basis enriched with a finite number of terms of fractional power.Moreenriched terms in the basis lead to more accurate approximation.However,more terms also make the moment matrix more ill-conditioned.Considering this trade off,we suggest using the leading fractional term.That is,

whereφr(x)can be reproduced by the enriched basis Eq.(31)andφe(x)is the function reproducing error.Their expressions are

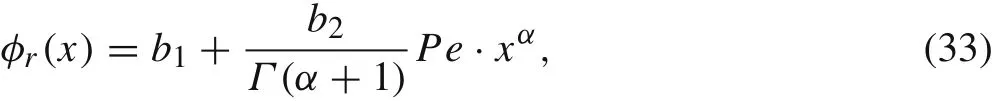
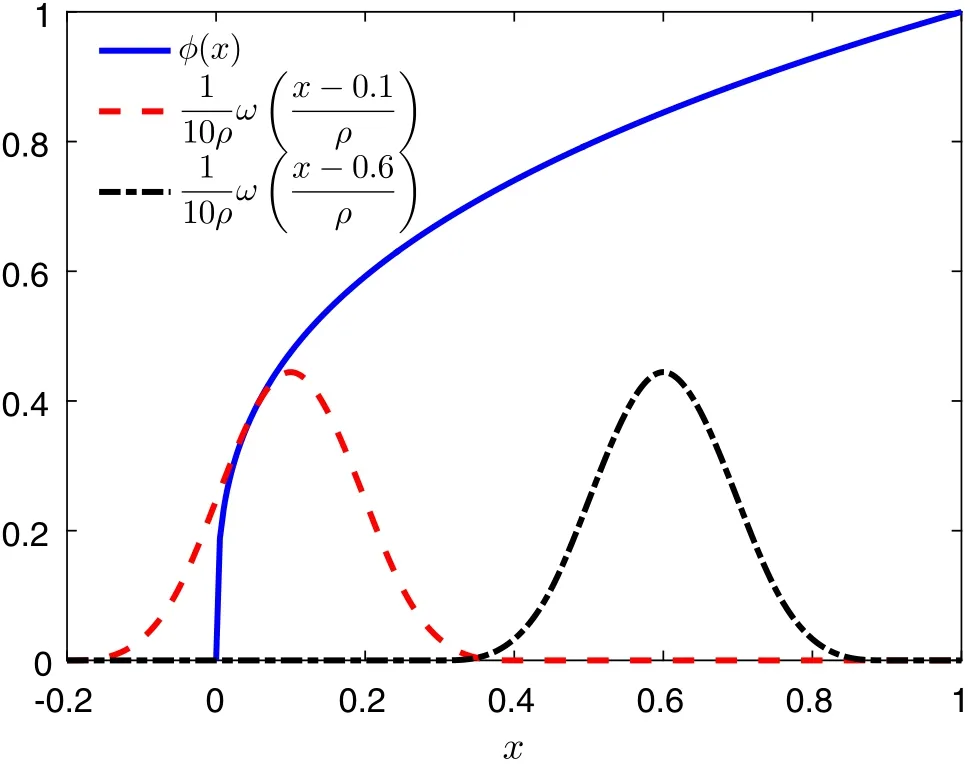
Fig.3 The solid line denotes the exact solution of Eq.(3)when α=0.3,Pe=0.1,c1=0,c2=1.The dashed line and dash-dotted line show the supporting domain of the shape functions at x=0.1,0.6,respectively

According to Eq.(18),enriched shape functions and their window functions are compactly supported in the same domain.In Fig.3,the solid line denotes the exact solution whenα=0.3,Pe=0.1,c1=0,c2=1.The dashed line and the dash-dotted line denote the window functions atx=0.1,0.6,respectively,withh=0.1 and a dilation parameterρ=1.5.The curves of the window functions show the support of the shape functions.It can be observed that the support of the shape function atx=0.1 includesx=0,so that all the area covered by this domain is associated with the function reproducing error.In contrast,the shape function atx=0.6 is free from function reproducing error becausex=0 is out of its support.

Based on the above analysis,the region where the function reproducing error should be considered is the union of all the support of the shape functions affected by the boundary.With the window function Eq.(11),the region is the intervalx∈ [0,4ρh].

We compare the function reproducing errorφe(x)and the leading term ofφr(x)in[0,4ρh]and obtain

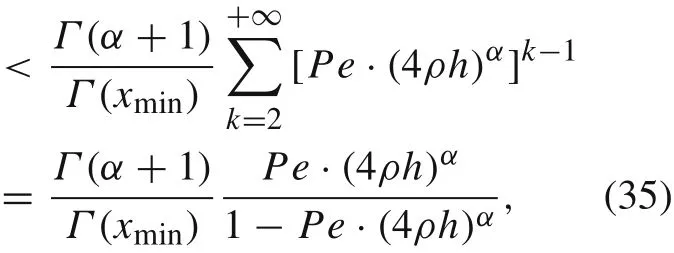
wherePe(4ρh)α＜1 is assumed,Γ(xmin)is the minimum value of the gamma function on the positive real axis and takes a value between 0.8 and 0.9.WhenPe(4ρh)αis small enough,fractional diffusion dominates in Eq.(3).It is also observed from Eq.(35)thatφe(x)can be ignored inφ(x),so the solution to Eq.(3)is well approximated by the enriched shape functions.WhenPe(4ρh)αis large,e.g.Pe(4ρh)α=0.5,the advection effect in Eq.(3)cannot be ignored.In this case,the function reproducing errorφe(x)is not negligible inφ(x)and represents itself in the form of an oscillatory numerical solution.

For a fixedPe,choosing smallerρ,hyields better approximation results.However,it should be noted that the mesh refinement is not efficient whenαis small.For example,whenα=0.1,a refinement of 1010times just makesPe(4ρh)α10 times smaller.

4 A Galerkin procedure for the fractional advection–diffusion equation

In this section,a Galerkin method is formulated based on the enriched RKPM interpol ant to solve the fractional advection–diffusion equation Eq.(3).

4.1 Discretization of equation

Taking a re-scaling parameterS=L,we rewrite equation Eq.(3)as

An appropriate particle distribution is denoted asxI,I=1,2,...,NP,where NP is the number of particles andx1=0,xNP=1.We substitute the interpolation formula(17)into Eq.(36)as a trial function and take Eq.(18)as test functions.Then the following strong form of Eq.(36)is obtained

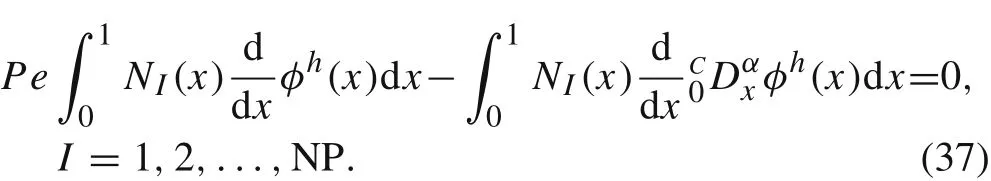
We apply integration by parts to Eq.(37)and obtain its weak form

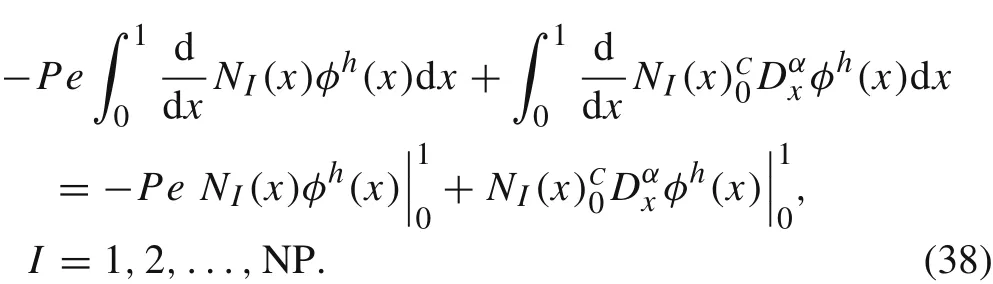
A suitable dilation parameterρcan be chosen in specific cases to make the shape functions Eq.(18)perform strict interpolation on the boundaries.That isNI(x1)=δ1IandNI(xNP)=δI,NP,which is depicted in Fig.2.Then were cast Eq.(38)into matrix form as

where K is a(NP?2)×(NP?2)matrix,u=(φ2,φ3,...,φNP?1)and f is a column vector with(NP?2)entries.More precisely,the entries of K and f are

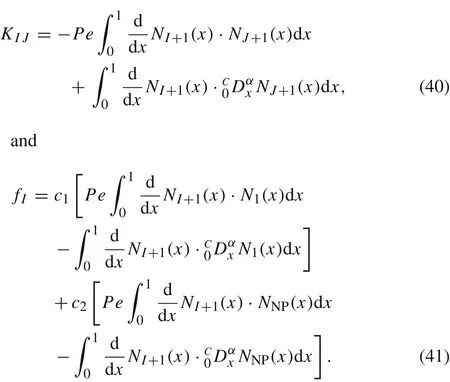
4.2 Fractional derivative of shape functions and Gauss–Jacobi quadrature

In Eqs.(40)and(41),fractional derivatives of the enriched shape functions Eq.(18)are carried out numerically.

For precision of the numerical integration,the shape functions are decomposed as

whereIt can be observed thatis singular atξ=1 whenis singular atξ= ?1 whenhas singular derivatives atξ= ?1 whena=0.Gauss–Jacobi quadrature can deal with the above situations(see “Appendix A”).

Figure 4 depicts fractional derivatives of the enriched shape functionsNI(x)in Fig.1,which are obtained by the 30th-order Gauss–Jacobi quadrature applied to Eq.(54)whenα=0.3.The left figure of Fig.4 shows the derivatives corresponding toxI=0,0.1,0.2 and the right figure shows the cases forxI=0.3,0.7,1.It is noted that fractional derivatives ofNI(x)are no longer compactly supported.They take non-vanishing values on the right side of the supporting domains ofNI(x),which makes Kloseits compact property.

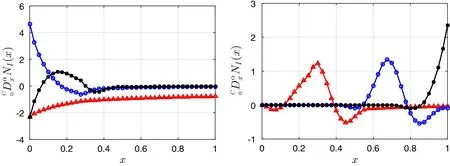
Fig.4computed by Gauss–Jacobi quadrature

Via the variable transformation and Gauss–Jacobi quadrature above,Eqs.(40)and(41)can also be carried out for K and f.For numerical efficiency,the integrations are also suggested to be computed on the supporting domain of the integrants.

5 Numerical examples

Since the solution of a fractional diffusion–advection equation has a singular derivative on the boundary,numerical solutions of traditional meshfree methods based on basis of integer order,like RKPM,may give rise to oscillations near the boundary.In this section,several examples are given to illustrate the problem of RKPM and the effectiveness of the proposed enriched RKPM in suppressing the oscillations.For steady state problems,RKPM and the enriched RKPM are compared in a fractional pure diffusion equation and a fractional advection–diffusion equation.Moreover,the results of the two methods for a time-dependent fractional advection–diffusion equation are presented.

5.1 Steady state fractional pure diffusion equation

A fractional pure diffusion equation is considered as follows

whereis fractional integration of the forcing term andccan be determined by the boundary conditions.

5.1.1 Pure fractional diffusion with out a forcing term

Whenf(x)=0andα=0.3,Eq.(56)reduces to a fractional power function

RKPM and the enriched RKPM are applied to solve the case with a uniform spacingh=0.2 and the window function Eq.(11).The shape functions of RKPM and the enriched RKPM are constructed based on(1,x)and(1,x,r0.3),respectively.RKPM takesρ=1 and the enriched RKPM takesρ=1.5.Both methods use Gauss–Jacobi quadrature of 30th order.

Figure 5 presents the results of RKPM and the enriched RKPM whenα=0.1,0.3,0.7 from the left figure to the right one.For RKPM,spurious oscillation is observed,with the worst situation happening near the left boundary.As for the enriched RKPM,due to the vanishing function reproducing error,the numerical results agree very well with the analytical solution in all cases.

5.1.2 Pure fractional diffusion with a forcing term

We consider a non-zero forcing termf(x)=xand setα=0.3.The exact solution of Eq.(55)then becomes

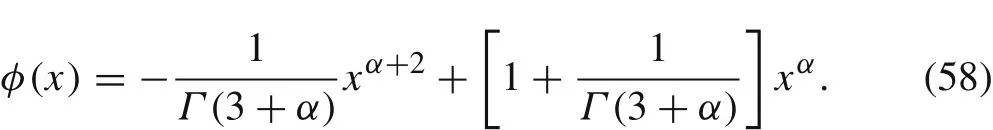
A ll discretization parameters adopt the same values as in the previous section.

Figure 6 compares the results whenα=0.2(left figure)andα=0.7(right figure).The results of the enriched RKPM are in good agreement with the exact solutions,whereas RKPM still presents spurious oscillations.

Fig.5 Numerical results for steady state fractional pure diffusion equation,f(x)=0

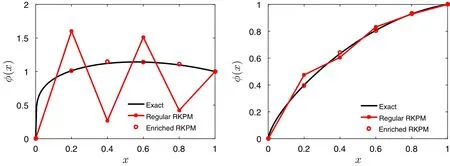
Fig.6 Numerical results for steady state fractional pure diffusion equation,f(x)=x

Fig.7 Numerical results for steady state fractional advection–diffusion equation,f(x)=0,Pe=0.03

5.2 Steady state fractional advection–diffusion equation

The following steady state fractional advection–diffusion example is considered

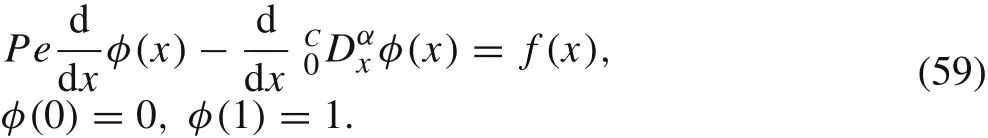
The exact solution is given by

whereis the Mittag-Leffler function,cis a constant determined by the boundary conditions and?denotes convolutionξ)g(ξ)dξ.

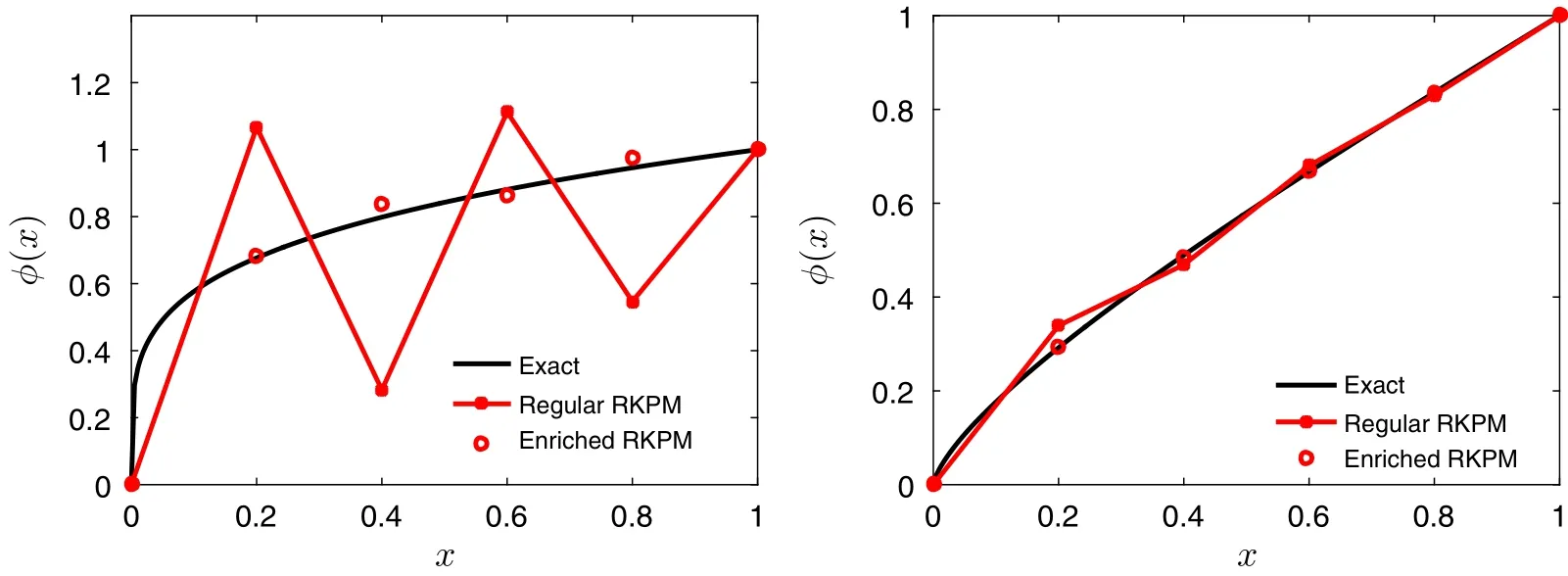
Fig.8 Numerical results for steady state fractional advection–diffusion equation,f(x)=0,Pe=0.2

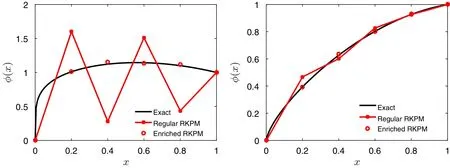
Fig.9 Numerical results for steady state fractional advection–diffusion equation,f(x)=x,Pe=0.03

We apply RKPM and the enriched RKPM to solve Eq.(59)and set the same numerical parameters as those for Eq.(55).Figure 7 depicts the results whenf(x)=0 andPe=0.03.The two sub- figures correspond toα=0.2(left)andα=0.7(right),respectively.Spurious oscillations of RKPM are observed in both cases,while the results of the enriched RKPM show good agreement with the exact solutions.For the enriched RKPM,it is easy to computePe(4ρh)α=0.03?(4?1.5?0.1)0.2≈0.027 andwhich indicate a small function reproducing error and a good approximation of the enriched RKPM to the exact solutions.

Figure 8 presents the results forf(x)=0 andPe=0.2.The parameterPeis chosen in such a way that the function reproducing error cannot be ignored.For the case ofα=0.2 in the leftsub- figure,the enriched RKPM starts to show some oscillations near the exact solution.Whenα=0.7,the function reproducing error does not cause spurious oscillations for the enriched RKPM,as shown in the right sub- figure.

For a non-vanishing forcing term,we setf(x)=x,Pe=0.03.As shown in Fig.9,the enriched RKPM gives numerical solutions in good agreement with the exact solutions whenα=0.2(left)andα=0.7(right),whereas the result from RKPM still contains spurious oscillations.

5.3 Time-dependent fractional advection–diffusion equation

The time-dependent example for fractional advection–diffusion equations is given in the physical domainz∈[0,1]as

Fig.10 Numerical results for time-dependent fractional advection–diffusion equation

In this example,we setα=0.1,u=0.01,κ=1.A uniform spacingΔz=0.01 is chosen.RKPM takes the basis(1,z)and the enriched RKPM uses(1,z,r0.1).The window function is supported on a domain with ratio of 2h=2Δz=0.02.The dilation parameter is set asρ=1 for RKPM andρ=1.5 for the enriched RKPM.After spatial discretization,we integrate the equation by the Crank–Nicolson method in time with a time-step sizeΔt=0.001.Figure 10 compares the numerical results for RKPM and the enriched RKPM att=0,0.167,0.334,0.5(top left,top right,bottom left,bottom right).It is observed that spurious oscillations are not present in the results from the enriched RKPM.For the results from RKPM,severe oscillations occur when the profile reaches the left boundary.

6 Conclusion

The reproducing kernel particle method is enriched to solve a fractional advection–diffusion equation.The method expands the integer-order basis of regular RKPM to include power functions of fractional orders.In this way,an enriched RKPM interpolation formula is obtained and proven to be able to exactly reproduce the involved fractional power functions.A FADE is solved by the enriched RKPM method.One enriched term is applied and its order is identical to that of the FADE.Numerical examples show the significant accuracy improvement by the basis enrichment.

It should be noted that Gauss–Jacobi quadrature is used for the computation of fractional derivative of shape functions and entries of the stiffness matrix,which causes heavy computational load.According to the analysis in Sect.3.3,the enrichment is only necessary near the boundary.A combination of the enriched RKPM with other approaches such as finite element method or RKPM can improve computational efficiency.We will report further results along this line in a future publication.

AcknowledgementsThe project was supported partly by the National Natural Science Foundation of China(Grant11521202).Ying is grateful for the support from the Chinese Scholarship Council.Lian and Liu are partially support by an Army Research Office(Grant W 911NF-15-1-0569).

Appendix A.Gauss–Jacobi quadrature

Gauss–Jacobi quadrature can be used to approximate integrals in the form

wheref(x)is a smooth function on[?1,1],α,β＞?1.More precisely,

wherexi,i=1,2,...,nare the roots of the Jacobi polynomial of degreen.The weightsλiare given by

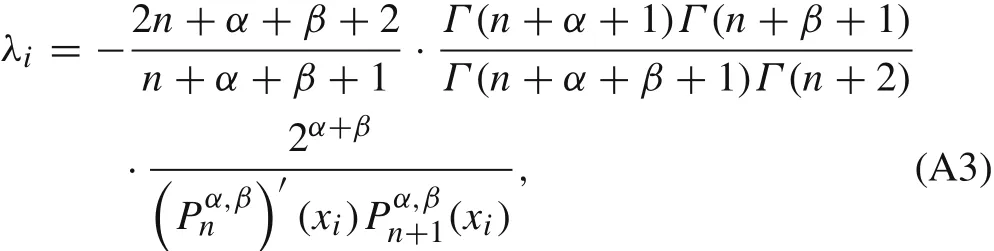
whereis the Jacobi polynomial of degreenanddenotes first order derivative.Whenα=β=0,Eq.(A2)reduces to Gauss quadrature.

1.Chen,J.S.,Pan,C.,Roque,C.M.O.L.,et al.:A Lagrangian reproducing kernel particle method for metal forming analysis.Comput.Mech.22,289–307(1998)

2.Chen,J.S.,Pan,C.,Wu,C.,et al.:Reproducing kernel particle methods for large deformation analysis of non-linear structures.Comput.Methods Appl.Mech.139,195–227(1996)

3.Chen,J.S.,Pan,C.,Wu,C.:Large deformation analysis of rubber based ona reproducing kernel particle method.Comput.Mech.19,211–227(1997)

4.Lian,Y.,Zhang,X.,Liu,Y.:An adaptive finite element material point method and its application in extreme deformation problems.Comput.Methods Appl.Mech.241,275–285(2012)

5.Belytschko,T.,Lu,Y.,Gu,L.:Crack propagation by element-free Galerkin methods.Eng.Fract.Mech.51,295–315(1995)

6.Belytschko,T.,Tabbara,M.:Dynamic fracture using element-free Galerkin methods.Int.J.Numer.Mech.Eng.39,923–938(1996)

7.Guan,P.C.,Chi,S.W.,Chen,J.S.,et al.:Semi-Lagrangian reproducing kernel particle method for fragment-impact problems.Int.J.Impact Eng.38,1033–1047(2011)

8.Chi,S.,Lee,C.,Chen,J.S.,et al.:A level set enhanced natural kernel contact algorithm for impact and penetration modeling.Int.J.Numer.Mech.Eng.102,839–866(2015)

9.Liu,W.K.,Chen,Y.:Wavelet and multiple scale reproducing kernel methods.Int.J.Numer.Methods Fluids 21,901–931(1995)

10.Li,S.,Liu,W.K.:Moving least-square reproducing kernel method part II:Fourier analysis.Comput.Methods Appl.Mech.139,159–193(1996)

11.Liu,W.K.,Jun,S.,Li,S.,et al.:Reproducing kernel particle methods for structural dynamics.Int.J.Numer.Mech.Eng.38,1655–1679(1995)

12.Liu,W.K.,Jun,S.,Zhang,Y.:Reproducing kernel particle methods.Int.J.Numer.Methods Fluids 20,1081–1106(1995)

13.Liu,W.K.,Chen,Y.,Jun,S.,et al.:Overview and applications of the reproducing kernel particle methods.Arch.Comput.Methods Eng.3,3–80(1996)

14.Bessa,M.A.,Foster,J.T.,Belytschko,T.,et al.:A meshfree unification:reproducing kernel peridynamics.Comput.Mech.53,1251–1264(2014)

15.Carpinteri,A.,Mainardi,F.:Fractals and Fractional Calculus in Continuum Mechanics.Springer,Vienna(1997)

16.Metzler,R.,Klafter,J.:The random walk’s guide to anomalous diffusion:a fractional dynamics approach.Phys.Rep.339,1–77(2000)

17.Benson,D.A.,Wheatcraft,S.W.,Meerschaert,M.M.:Application of a fractional advection–dispersion equation.Water Resour.Res.36,1403–1412(2000)

18.Chen,W.,Sun,H.,Zhang,X.,et al.:Anomalous diffusion modeling by fractal and fractional derivatives.Comput.Math.Appl.59,1754–1758(2010)

19.West,B.J.:Colloquium:fractional calculus view of complexity:a tutorial.Rev.Mod.Phys.86,1169(2014)

20.Chen,W.,Liang,Y.,Hu,S.:Fractional derivative anomalous diffusion equation modeling prime number distribution.Fract.Calc.Appl.Anal.18,789–798(2015)

21.Lei,D.,Liang,Y.,Xiao,R.:A fractional model with parallel fractional Maxwell elements for amorphous thermoplastics.Physica A 450,465–475(2018)

22.Xiao,R.,Sun,H.,Chen,W.:A finite deformation fractional viscoplastic model for the glass transition behavior of amorphous polymers.Int.J.Nonlinear Mech.93,7–14(2017)

23.Podlubny,I.:Fractional Differential Equations:An Introduction to Fractional Derivatives,Fractional Differential Equations,to Methods of Their Solution and Some of Their Applications.Academic press,New York(1998)

24.Li,C.,Zeng,F.:Numerical Methods for Fractional Calculus.CRC Press,Boca Raton(2015)

25.Chen,W.,Ye,L.,Sun,H.:Fractional diffusion equations by the Kansa method.Comput.Math.Appl.59,1614–1620(2010)

26.Pang,G.,Chen,W.,Sze,K.Y.:A comparative study of finite element and finite difference methods for two-dimensional space fractional advection–dispersion equation.Adv.Appl.Math.Mech.8,166–186(2016)

27.Ding,H.,Li,C.,Chen,Y.:High-order algorithms for Riesz derivative and their applications(II).J.Comput.Phys.293,218–237(2015)

28.Ying,Y.,Lian,Y.,Tang,S.,et al.:High-order central difference scheme for Caputo fractional derivative.Comput.Methods Appl.Mech.317,42–54(2017)

29.Ervin,V.J.,Roop,J.P.:Variational solution of fractional advection dispersion equations on bounded domains in Rd.Numer.Methods Parial Differ.Equ.23,256–281(2007)

30.Fix,G.J.,Roof,J.P.:Least squares finite-element solution of a fractional order two-point boundary value problem.Comput.Math.Appl.48,1017–1033(2004)

31.Ervin,V.J.,Roop,J.P.:Variational formulation for the stationary fractional advection dispersion equation.Numer.Methods Partial Differ.Equ.22,558–576(2006)

32.Lian,Y.,Ying,Y.,Tang,S.,et al.:A Petrov–Galerkin finite element method for the fractional advection–diffusion equation.Comput.Methods Appl.Mech.309,388–410(2016)

33.Luan,S.,Lian,Y.,Ying,Y.,et al.:An enriched finite element method to fractional advection–diffusion equation.Comput.Mech.60,181–201(2017)

34.Zayernouri,M.,Karniadakis,G.E.:Fractional Sturm–Liouville eigen-problems:theory and numerical approximation.J.Comput.Phys.252,495–517(2013)

35.Zayernouri,M.,Karniadakis,G.E.:Exponentially accurate spectral and spectral element methods for fractional ODEs.J.Comput.Phys.257,460–480(2014)

36.Zayernouri,M.,Karniadakis,G.E.:Fractional spectral collocation methods for linear and nonlinear variable order FPDEs.J.Comput.Phys.293,312–338(2015)

37.Kharazmi,E.,Zayernouri,M.,Karniadakis,G.E.:Petrov–Galerkin and spectral collocation methods for distributed order differential equations.SIAM J.Sci.Comput.39,A1003–A1037(2017)

38.Fleming,M.,Chu,Y.A.,Moran,B.,et al.:Enriched element-free Galerkin methods for crack tip fields.Int.J.Numer.Mech.Eng.40,1483–1504(1997)

39.Liu,W.K.,Li,S.,Belytschko,T.:Moving least-square reproducing kernel methods(I):methodology and convergence.Comput.Methods Appl.Mech.143,113–154(1997)