A prediction model for the effective thermal conductivity of nanofluids considering agglomeration and the radial distribution function of nanoparticles

Z.M.Zheng·B.Wang

1 Introduction

The intrinsically low thermal conductivity of conventional heat transfer fluids is one of the major limitations on development of high-efficiency cooling devices in industrial fields.To achieve development objectives,these fluids must be replaced or their thermal properties improved.On the other hand,it is well known that solid particles exhibit better thermal conductivity compared with conventional heat transfer fluids.However,addition of micro-or millisize solid particles to base fluids,which will enhance the thermal conductivity,also results in anomalous,high flow resistance and severe pipe wear.These negative side-effects have been obstacles to their feasible applications.In 1995,a breakthrough study on enhancing the thermal conductivity of conventional heat transfer fluids was carried out by Choi and Eastman[1],who put forward the concept of,viz.a suspension of nanoparticles dispersed in a conventional fluid,and firstly synthesized A l2O3–water nanofluid.Intriguingly,he found that addition of nanoparticles to conventional fluids resulted in anomalously enhanced thermal conductivity.In recent years,many experimental investigations have also been performed on thermal conductivity enhancement of nanofluids[2–8].For example,Lee et al.[2]measured the thermal conductivity of several kinds of nanofluids,revealing enhancements of about 12.1%for 3.4vol.%CuO–water nanofluid and 9.3%for 4.0vol.%A l2O3–water nanofluid.They also found that the nanoparticles in these systems were agglomerated(Fig.1a,b),since they did not use an electrostatic repulsion technique during the preparation of nanofluids.Kole and Dey[8]studied the effects of volume fraction and temperature on the enhancement of the thermal conductivity of gear-oil-based nanofluid.Data from transmission electron microscopy(TEM)(Fig.1c)and dynamic light scattering(DLS)measurements confirmed the presence of agglomerated nanoparticles in their prepared nanofluids.Moreover,the thermal conductivity enhancement was about 10.4%for 2.5vol.%CuO loading at 30°C.Intriguingly,the results of Eastman et al.[3]showed that,for a nanofluid consisting of ethylene glycol(EG)and only 0.3vol.%Cu nanoparticles,the thermal conductivity was measured to be increased by 40%,while very little agglomeration of Cu particles was observed by TEM(Fig.1d).

Fig.1 TEM images of different nanofluids.a Al2O3–water(from Lee et al.[2]).b CuO–water(from Lee et al.[2]).c CuO–gear oil(from Kole and Dey[8]).d Cu–EG(from Eastman et al.[3])

These amazing experimental results motivated researchers to study the heat conduction mechanisms behind the effective thermal conductivity of nanofluids theoretically.Most existing models are based on effective medium theory,in which the size,shape,and volume fraction of particles are typically incorporated as variables,and the interfacial nanolayer at solid–liquid interfaces is also taken into account[9–14].For instance,Lu and Song[9]developed a theoretical model to second order in volume fractionφto predict the effective thermal conductivity of composites with coated or bonded spherical inclusions.Yu and Choi [10,11] believed that the severalnanometer-thick interfacial nanolayer at solid–liquid interfaces played an important role in the effective thermal conductivity of nanofluids, proposing two novel models based on the Maxwell model and Hamilton and Crosser model, respectively.Xue and Xu[12] also modified Bruggeman’s model for the effective thermal conductivity of nanofluids by taking the interfacial layer effect into account.However, like the predictions of classical models (some of which are listed in Table1)applied for computing the effective thermal conductivity of mixtures including millimeter-size or micrometer-size solid particles,the predictions of their models were lower than experimental results for the thermal conductivity of nanofluids.The weakness of these modified classical models for the thermal conductivity of nanofluids indicates that some mechanisms may have been missed.

Since nanoparticles have high surface energy,they easily agglomerate together when added to a base fluid,as shown in some experimental results[2,4–8].Moreover,adjacent particles in agglomerates create percolation paths with lower thermal resistance,which may have a major effect on the effective thermal conductivity[15,16].To estimate the contribution of this agglomeration effect to the thermal conductivity enhancement of nanofluids,several prediction models have been proposed.Based on the effective thermal medium approximation and fractal theory,Wang et al.[17]developed a fractal model for nanofluids to take the agglomerates and their radial distribution into account.Their predictions for the effective thermal conductivity of CuO nanofluids fit successfully with their experimental data forφ＜5%.However,this model could not match a wide range of experimental results and not be able to predict the nonlinear behavior of the effective thermal conductivity of nanofluids.Prasher et al.[18]used a three-level homogenization method,validated by Monte Carlo simulations of heat conduction in fractal aggregates,to investigate the role of agglomeration in the enhancement of the purely conductive phenomenon in nanofluids.Their prediction results showed that the conductivity enhancement strongly depended on the fractal dimension of the agglomerates and their radius of gyration.Feng et al.[19]considered the nanolayer and agglomeration effects of particles and proposed a theoretical model for the thermal conductivity of nanofluids based on a two-dimensional(2D)lattice model,assuming that the formation of agglomerates followed the simple packing principle.Zhou and Wu[20]proposed a theoretical model to predict the thermal conductivity of nanofluids,in which the influence of nanoparticle clusters was considered,by introducing particle size distribution,with an assumption that particles in clusters aggregated with each other closely.Xiao et al.[21]took into account heat convection between nanoparticles and liquids due to Brownian motion of nanoparticles in nanofluids.Their expression for the thermal conductivity of nanofluids was developed based on fractal geometry theory.However,therandom distribution and disorder effect of nanoparticles to structure formation in nanofluids contribute to heat conduction.Therefore,these effects should be considered in the prediction model for effective thermal conductivity of nanofluids,by introducing the radial distribution function of nanoparticles[9,22–24].

Against this background,we propose herein a model for predicting the effective thermal conductivity of nanofluids.The development of the model proceeds as follows:The nanofluid system is first divided into several parts,each of which contains agglomerates at a specific level with a nanolayer and the surrounding base fluid;We treat each agglomerate and its surrounded nanolayer as an equilibrium agglomerate with equilibrium nanolayer.To describe the effect of the presence of agglomerates on the effective thermal conductivity in each equilibrium part,a radial distribution function is introduced.Thus,the effective thermal conductivity of the whole system can be evaluated by combining each part.In this way,the agglomeration effect and the radial distribution function of the nanoparticles are taken into account.Finally,the predictions of the present model for several sets of nanofluids are also compared with experimental results,as well as with other theoretical models.

2 Models of effective thermal conductivity

2.1 Earlier models

Many classical models have been developed to calculate the effective thermal conductivity of solid–liquid suspensions.However,these classical models apply to dilute suspensions containing milli-or microparticles.To extend them to predict the effective thermal conductivity of nanofluids,various researchers have proposed modified models derived from classical models.Some of these are listed in Table 1.

2.1.1 Present model

The TEM images in Fig.1a–c show nanoparticle agglomerates of different sizes.This random distribution of multisize agglomerates(or multilevel agglomerates)makes a great contribution to the enhancement of the heat conduction in nanofluids.Therefore,we introduce an equivalent agglomeration method[28]to take the agglomeration effect into account in the thermal conductivity calculation.A schematic of the method is shown in Fig.2.The main idea is that the multilevel agglomerates consist of two parts:pure solid-phase particle material and liquid phase bounded in pores.For anith-level agglomerate, the contained solid-phase particles areregarded as an equivalent solid particle with the same volume,while the liquid phase,including the liquid in the gaps and the nanolayer on the surface of the agglomerate,is considered as an equivalent interfacial nanolayer on the surface of the equivalent solid particle.The equivalent nanolayer thicknesstisatisfies the equation:are the radius of the equivalent agglomeration particleiand equivalent solid particlei,respectively.Moreover,each primary single particle with its interfacial nanolayer is treated as a zero-level agglomerate for convenience,thusrepresents the radius of such a single solid particle.

Since the random distribution of each level of agglomeratesmakes a different partial contribution to the enhancement of the heat conduction in the nanofluid,the agglomeration ratioλiof theith-level agglomerates is introduced to weigh their contribution to the total thermal conductivity enhancement.The agglomeration ratioλican be calculated asandNare the number of agglomeratesiand the total number of particles(single particles and agglomerates),which can both be measured approximately from TEM images.Moreover,λishould satisfy

To calculate the effective thermal conductivity,we assume that the contribution of each level of agglomerates to the effective thermal conductivity of the nanofluid complies with the principle of linear weighted superposition.Thus,we defineas the effective thermal conductivity of a nanofluid in the presence of onlyith-level agglomerates,which can be expressed as[9]

Table 1 Earlier theoretical models of effective thermal conductivity of solid–liquid suspensions or nanofluids

Fig.2 Scheme of equivalent agglomeration method[28]

In Eq.(1),is the effective volume fraction of agglomerateiwith its combined nanolayer.The second term on the right-hand side, first obtained by Maxwell,accounts for the presence of rigid spheres without interactions;the third term is a correlation to the first-order coefficient due to the mutual impenetrability of the spheres.The fourth term takes into account the thermal interactions(i.e.,how the temperature field around the first spherical particle is affected by the presence of the second),as well as the structural distribution of pairs of particles(i.e.,how the presence of one particles affects the location of the other),where the coefficientM?can be expressed as

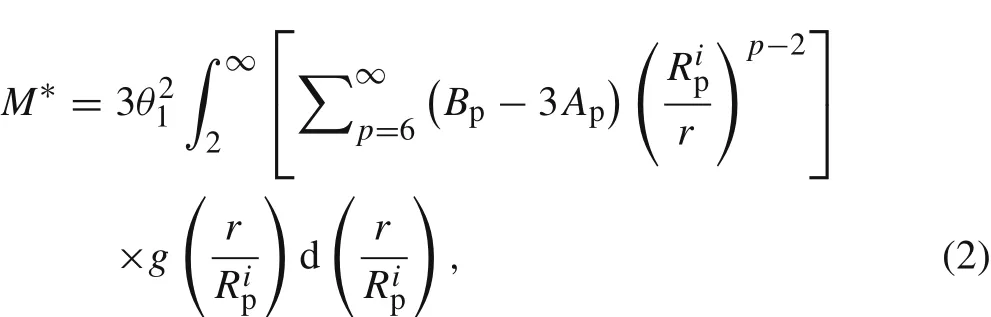
In Eqs.(2)–(5),φandare the volume fraction of all particles without their nanolayers and the effective volume fraction of agglomerateiwith its combined nanolayer,respectively;ApandBpare the coefficients of each term in the summation,which are expressed in detail in Ref.[22];ris the distance between the center of each pair of particles in the system;θ1is the dimensionless polarizability,characterizing the interfacial nanolayer effect;βxyis a convenient measure of the disparity betweenkxandky[22,24];kxandkyrefer tokp,kf,andkl,which are the thermal conductivity of solid-phase particle,base fluid,and interfacial nanolayer,respectively.is a radial distribution function to describe the structure of suspensions of identical rigid spherical particles within a liquid, first proposed by Jeffrey[22].Employing the simplified statistics of a homogeneous structure,he assumed that the radial distribution function should satisfy the conditions of low-density limits and temperature continuity at liquid–solid interfaces,taking the following form:(whereHis a step function).However,a step function cannot represent the structure of an equilibrium rigid sphere fluid at any finite density.Thus,an alternative radial distribution function is introduced in the present model,and can be accurately evaluated using the procedure proposed by Verlet and Weis[29].

It is worth mentioning that the thermal conductivity of the interfacial nanolayerklshould be a nonlinear function ofδ(ranging from 0 toδi).If not,it would tend to an infinite value as the nanolayer became ultrathin[30,31](t→0).Moreover,it decreases fromkptokfasδchanges from 0 toδi,because the interfacial nanolayer represents an intermediate state between the bulk solid and liquid phase.Following the analysis above,the thermal conductivity of nanolayerklshould become[28,32,33]

whereis related to the ratio

We then use the integral average of Eq.(6)to calculate the effective thermal conductivity of nanolayerkl,with the form

Now,the effective thermal conductivity of the nanofluid,considering the agglomeration effect,can be expressed as

and the effective thermal conductivity of the nanofluid can be predicted by substituting Eqs.(1)–(5)and Eq.(7)into Eq.(8).According to experimental studies[2,8],we posit that there exists one level of agglomeration in a dilute suspension,for simplicity,thus Eq.(8)becomes

For the computation using just one-level agglomeration,the radius of the equivalent solid particlecan be replaced by the radius of the first-level agglomerate,sincecan be measured by TEM and the volume of liquid gaps in a one-level agglomerate are small compared with the solid phase particles.Also,the agglomeration ratio of the one-level agglomerateλ1can also be estimated by TEM.

Through its consideration of the structural distribution of pairs of particles,the accuracy of our model is up to orderφ2.Moreover,the present model can also be used to predict the effective thermal conductivity of nanofluids without agglomerates.For such cases,one lets the agglomeration ratioλ1be zero,then Eq.(9)degenerates to the model of Lu and Song with an exponential distribution of thermal conductivity in the nanolayer.

3 Results and discussion

The present model was validated by comparing its prediction results with several sets of experimental data,as well as results calculated using other theoretical models for nanofluids.A linear distribution and a constant value of thermal conductivity in the nanolayer are employed in the calculations using the models of Lu and Song and of Yu and Choi,respectively.

Table 2 presents the values of the parametersλi,δi,andti(i=0,1)used in our model according to the experimental data from Lee et al.[2],Kole and Dey[8],and Eastman et al.[4].The agglomeration ratio of the one-level agglomerateλ1was taken as 19%,14%,26%,0%for A l2O3–water,CuO–water,CuO-gear oil,and Cu–EG,respectively.

The predictions of the present model for the A l2O3–water nanofluid are in good agreement with the experimental datafor the Al2O3–water nanofluid synthesized by Lee et al.[2],as shown in Fig.3.The average equivalent radius of one level agglomerates used in the present calculation is about≈70nm based on the scale bar in the TEM images(Fig.1a),and the nanolayer thickness of the original particle and equivalent agglomeration particle aret0=0.96nm andt1=7.00nm,respectively.The value oft0is close to the results of molecular dynamics(MD)simulation(≈1nm)carried out by Xue et al.[34]and direct observations using the X-ray reflection technique,suggesting that the nanolayer thickness should be several times the water molecule diameter[35].Meanwhile,the calculation results of Maxwell model,Lu and Song model witht0=1nm and Yu an Choi model witht0=1nm,show higher deviations from experimental data.Comparison between the predictions of the present model and those obtained using the model of Lu and Song indicates that the agglomerates of nanoparticles would make a negative contribution to the effective thermal conductivity of nanofluids.

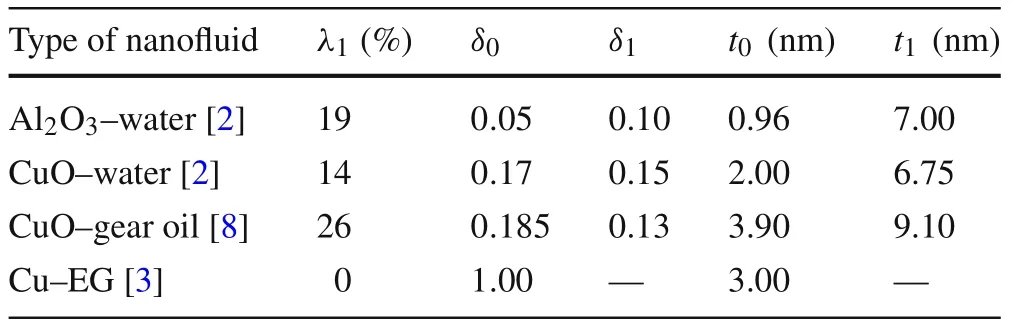
Table 2 Values of parameters used in our model

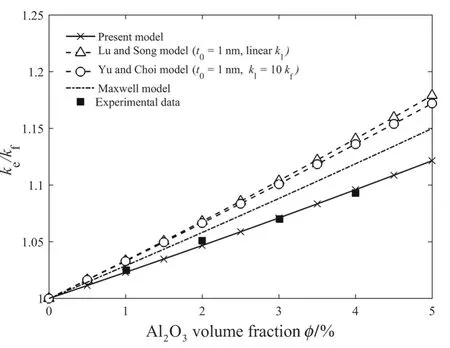
Fig.3 Thermal conductivity variation for Al2O3–water nanofluid[2]

For the CuO–water nanofluid,the predictions of the present and other models are shown in Fig.4,in comparison with the experimental data obtained by Lee et al.The values of the nanolayer thickness used in the present calculations are chosen ast0=2.00 nm andt1=6.75nm,while the average equivalent radius of one-level agglomerates was≈45nm,based on the scale bar in the TEM image(Fig.1b).Meanwhile,the same value oft0is adopted for the predictions using the model of Lu and Song,with a linear distribution ofkl,as well as the predictions obtained using the model of Yu and Choi,with a constantkl=50kf.As expected,good agreement is found between the predictions of the present model and the experimental data.

Fig.4 Thermal conductivity variation for CuO–water nanofluid[2]

Fig.5 Thermal conductivity variation for CuO–gear oil nanofluid[8]

The predictions for the CuO–gear oil nanofluid are illustrated in Fig.5,using values for the nanolayer thickness oft0=3.90 nm andt1=9.10nm,and the average equivalent radius of one-level agglomerates is≈70 nm based on the scale bar in the TEM image(Fig.1c).By considering the agglomeration effect to reach order up toφ2,the present predictions show better agreement with experimental data[4]compared with the other models.In addition,Figs.4 and 5 reveal that the nanolayer thickness of CuO nanoparticles in water is much thinner than that in gear oil,indicating that the nanolayer thickness depends on the type of base fluid,as also reported in several previous investigations[30,36,37].

Fig.6 Thermal conductivity variation for Cu–EG nanofluid[3]

In the case of the Cu–EG nanofluid,the predictions of the present model are shown in Fig.6,in comparison with the results of other models and experimental data[3].The method used by Eastman et al.to synthesize their nanofluid resulted in little or no agglomerates,as shown in the TEM image(Fig.1d).Therefore,we chose an agglomeration ratio for one-level agglomerates ofλ1=0%in our calculations.The good consistency between the effective thermal conductivity predictions and the experimental data and the results of other models results from the contribution of orderφ2and the nonlinear distribution of thermal conductivitykl.In addition,this also indicates that the chosen values ofδipresented in Table 2 are reasonable.Another impressive finding is that the ratioδibecomes relatively large ifis small enough,both with and without agglomerates.

4 Conclusions

We present a prediction model for the effective thermal conductivity of nanofluids,using the equivalent agglomeration method to consider the agglomeration effect.With the help of the radial distribution function of the nanoparticles in the nanofluid,the present model is up to orderφ2in the volume fraction,comparable to most other theoretical models.The highly consistent predictions of the present method indicate that its application for predicting the thermal conductivity of nanofluids,with or without agglomerates,is more appropriate than other models,based on comparisons with experimental datasets.However,validation of the chosen values,including the agglomeration ratio and nanolayer thickness,must be further investigated.Moreover,other mechanisms for thermal conductivity enhancement,e.g.,based on temperature,pH value,and even viscosity,might also be considered in future studies.

AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grants 11472313,11232015,and 11572355)and the Guangdong Province Research Fund for Applied Research.

1.Choi,S.U.S.,Eastman,J.A.:Enhancing Thermal Conductivity of Fluids with Nanoparticles.In:International mechanical engineering congress and exhibition,San Francisco,Nov.12–17(1995)

2.Lee,S.,Choi,S.U.S.,Li,S.,et al.:Measuring thermal conductivity of fluids containing oxide nanoparticles.ASME J.Heat Transf.121,280–9(1999)

3.Eastman,J.A.,Choi,S.U.S.,Li,S.,et al.:Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles.Appl.Phys.Lett.78,718–720(2001)

4.Das,S.K.,Putra,N.,Thiesen,P.,et al.:Temperature dependence of thermal conductivity enhancement for nanofluids.ASME J.Heat Transf.125,567–574(2003)

5.Kang,H.U.,Kim,S.H.,Oh,J.M.:Estimation of thermal conductivity of nanofluid using experimental effective particle volume.Exp.Heat Transf.19,181–191(2006)

6.Karthikeyan,N.R.,Philip,J.,Raj,B.:Effect of clustering on the thermal conductivity of nanofluids.Mater.Chem.Phys.109,50–55(2008)

7.Mintsa,H.A.,Roy,G.,Nguyen,C.T.,et al.:New temperature dependent thermal conductivity data for water-based nanofluids.Int.J.Therm.Sci.48,363–371(2009)

8.Kole,M.,Dey,T.K.:Enhanced thermophysical properties of copper nanoparticles dispersed in gear oil.Appl.Therm.Eng.56,45–53(2013)

9.Lu,S.Y.,Song,J.L.:Effective conductivity of composites with spherical inclusions:effect of coating and detachment.J.Appl.Phys.79,609–618(1996)

10.Yu,W.,Choi,S.U.S.:The role of interfacial layers in the enhanced thermal conductivity of nanofluids:a renovated Maxwell model.J.Nano.Res.5,167–171(2003)

11.Yu,W.,Choi,S.U.S.:The role of interfacial layers in the enhanced thermal conductivity of nanofluids:a renovated Hamilton–Crosser model.J.Nano.Res.6,355–361(2014)

12.Xue,Q.,Xu,W.M.:A model of thermal conductivity of nanofluids with interfacial shells.Mater.Chem.Phys.90,298–301(2005)

13.Rizvi,I.H.,Jain,A.,Ghosh,S.K.,et al.:Mathematical modelling of thermal conductivity for nanofluid considering interfacial nanolayer.Heat Mass Transf.49,595–600(2013)

14.Jiang,H.,Xu,Q.,Huang,C.,et al.:The role of interfacial nanolayer in the enhanced thermal conductivity of carbon nanotube-based nanofluids.Appl.Phys.A 118,197–205(2015)

15.Buongiorno,J.:Convective transport in nanofluids.J.Heat Transf.128,240–250(2006)

16.Keblinski,P.,Prasher,R.,Eapen,J.:Thermal conductance of nanofluids:Is the controversy over?J.Nano.Res.10,1089–1097(2008)

17.Wang,B.X.,Zhou,L.P.,Peng,X.F.:A fractal model for predicting the effective thermal conductivity of liquid with suspension of nanoparticles.Int.J.Heat Mass Transf.46,2665–2672(2003)

18.Prasher,R.,Evans,W.,Meakin,P.,et al.:Effect of aggregation on thermal conduction in colloidal nanofluids.Appl.Phys.Lett.89,143119(2006)

19.Feng,Y.,Yu,B.,Xu,P.,et al.:The effective thermal conductivity of nanofluids based on the nanolayer and the aggregation of nanoparticles.J.Phys.D:Appl.Phys.40,3164(2007)

20.Zhou,D.,Wu,H.:A thermal conductivity model of nanofluids based on particle size distribution analysis.Appl.Phys.Lett.105,083117(2014)

21.Xiao,B.,Yang,Y.,Chen,L.:Developing a novel form of thermal conductivity of nanofluids with Brownian motion effect by means of fractal geometry.Powder Technol.239,409–414(2013)

22.Jeffrey,D.J.:Conduction through a random suspension of spheres.Proc.R.Soc.Lond.A:Math.Phys.Eng.Sci.335,355–367(1973)

23.Chiew,Y.C.,Glandt,E.D.:The effect of structure on the conductivity of a dispersion.J.Colloid Interface Sci.94,90–104(1983)

24.Chiew,Y.C.,Glandt,E.D.:Effective conductivity of dispersions:the effect of resistance at the particle surfaces.Chem.Eng.Sci.42,2677–2685(1987)

25.Maxwell,J.C.:Electricity and Magnetism.Clarendon Press,Oxford(1873)

26.Hamilton,R.L.,Crosser,O.K.:Thermal conductivity of heterogeneous two-component systems.Ind.Eng.Chem.Fund.1,187–191(1962)

27.Murshed,S.M.S.,Leong,K.C.,Yang,C.:Investigations of thermal conductivity and viscosity of nanofluids.Int.J.Therm.Sci.47,560–568(2008)

28.Sui,J.,Zheng,L.C.,Zhang,X.X.,et al.:A novel equivalent agglomeration model for heat conduction enhancement in nanofluids.Sci.Rep.6,19560(2016)

29.Verlet,L.,Weis,J.J.:Equilibrium theory of simple liquids.Phys.Rev.A 5,939–952(1972)

30.Liang,Z.,Tsai,H.L.:Thermal conductivity of interfacial layers in nanofluids.Phys.Rev.E 83,041602(2011)

31.Tso,C.Y.,Fu,S.C.,Chao,C.Y.:A semi-analytical model for the thermal conductivity of nanofluids and determination of the nanolayer thickness.Int.J.Heat Mass Transf.70,202–214(2014)

32.Xie,H.,Fujii,M.,Zhang,X.:Effect of interfacial nanolayer on the effective thermal conductivity of nanoparticle- fluid mixture.Int.J.Heat Mass Transf.48,2926–2932(2005)

33.Sohrabi,N.,Masoum i,N.,Behzadmehr,A.,et al.:A simple analytical model for calculating the effective thermal conductivity of nanofluids.Heat Transf.Asian Res.39,141–150(2010)

34.Xue,L.,Keblinski,P.,Phillpot,S.R.,et al.:Effect of liquid layering at the liquid–solid interface on thermal transport.Int.J.Heat Mass Transf.47,4277–4284(2004)

35.Yu,C.J.,Richter,A.G.,Datta,A.,et al.:Molecular layering in a liquid on a solid substrate:an X-ray reflectivity study.Phys.B:Cond.Mater.283,27–31(2000)

36.Xue,Q.Z.:Model for effective thermal conductivity of nanofluids.Phys.Lett.A 307,313–317(2003)

37.Firlar,E.,??nar,S.,Kashyap,S.,et al.:Direct visualization of the hydration layer on alum in a nanoparticles with the fluid cell STEM in situ.Sci.Rep.5,9830(2015)