The dimension split element-free Galerkin method for three-dimensional potential problems

Z.J.Meng·H.Cheng·L.D.Ma·Y.M.Cheng

?The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag GmbH Germany,part of Springer Nature2018

1 Introduction

The meshless method is an effective tool to solve boundary value problems of partial differential equations in addition to the finite difference method(FDM), finite element method(FEM),and boundary element method(BEM).The main difference between these conventional numerical methods and meshless method is the different approaches to obtain the shape functions.However,once the shape function has been formed,they use the same procedure to obtain the equation system to get the numerical solution of a problem.FDM,FEM,and BEM rely on meshes,then remeshing must be used to solve some complicated problems,such as extremely large deformations and crack grow th problems.The meshless method only needs nodes or particles,and it can solve many complicated physical and engineering problems that cannot be solved well with conventional computational methods[1,2].

The potential problem is an important physical and engineering problem,whose governing equations are commonly Laplace’s equations or Poisson’s equations.The popular numerical methods solving potential problems include FEM,FDM, BEM, and meshless methods [3–7]. The meshless method is actually amore effective numerical method to solve partial differential equations that govern various physical and engineering phenomena than traditional methods.

In recent years,several meshless methods,such as boundary node method[8–10],element-free Galerkin method[11–18],boundary element-free method[19,20],and meshless local Petro-Galerkin method coupled with FEM[21],were developed to solve potential problems.The improved element-free Galerkin(IEFG)method is an effective mesh-less method to solve three-dimensional potential problems,because in the IEFG method,the improved moving least squares(IMLS)approximation,in which the orthogonal function system is selected as the basis function,is used to obtain the shape function[12,22].The algebraic equations system in the IMLS approximation is well-conditioned,and it can be solved without deriving the inverse matrix. There are fewer coefficients in the IMLS approximation than the ones in the moving least-squares(MLS)approximation,which is the basis of the EFG method,then the computational efficiency of the IEFG method is greater than the EFG method.Using the IEFG method,the three-dimensional potential problem was effectively solved[12].Furthermore,the IEFG method can also be successfully applied to other science and engineering problems.In their work,Zhang et al.[23]employed the IEFG method for two-dimensional elasticity problems,2D fracture problems[24],three-dimensional wave equation[25],and two-dimensional elastodynamics problems[26].

The dimension split method(DSM)was proposed by Li and Huang[27].The essential features of the DSM are that the three-dimensional domain is partitioned by several two dimensional surfaces into several sub-domains.They used optimal control to deal with the stream-function equations of compressible turbomachinery flows and their finite element approximation[27].They also applied the DSM for the 3D compressible Navier–Stokes equations in turbomachine[28],the three dimensional rotating Navier–Stokes equations[29],the incompressible Navier–Stokes equations in three dimensions[30],and the linearly elastic shell[31].Additionally,Hansen and Ostermann[32]presented the DSM for evolution and quasilinear parabolic equations[33].The dimension split method is actually an efficient and convenient numerical method to solve various problems[34–37].The work of Cheng et al.[38,39]introduced the DSM into the improved complex variable element-free Galerkin method for solving three-dimensional potential and wave propagation problems.It is obvious that the DSM is different from the traditional domain decomposition method because only two-dimensional problems are solved in each sub-domain without solving a three-dimensional problem,then the computational efficiency is improved greatly.

Three-dimensional potential problems are effectively solved with the dimension split element-free Galerkin method.For these two-dimensional problems,the IMLS approximation is applied to construct the shape function.The Galerkin weak form is applied to obtain a discretized system equation,and the penalty method is employed to impose the essential boundary condition.The finite difference method is selected in the splitting direction.Finally,several numerical examples are solved using the dimension split element-free Galerkin(DSEFG)method.These numerical examples test and verify DSEFG theoretical result.The convergence study and error analysis of the DSEFG method are presented.The numerical examples show that the DSEFG method has greater computational precision and computational efficiency than the IEFG method.

2 The basic equations of three-dimensional potential p rob lem s with dimension split scheme

Consider the following three-dimensional potential problem

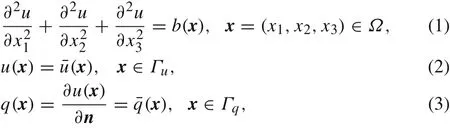
whereu(x)is an unknown function,b(x)is a known function.In the general case,there exist mixed boundary conditions on the boundaryΓof the domainΩ.Γuis one part of the boundaryΓwith known potential function,andΓqis the remaining boundary with known normal derivativeNotice that,andnis the unit outward normal to the boundaryΓ.

When using the DSEFG method to solve potential problems,we can choose the splitting direction according to the control equations and boundary conditions,which results in that the process of calculating and programming are easy to achieve.

In this paper,we assume that the problem domainΩis split intoLlayers along the directionx3,and the distance between adjacent layers isΔx3.Then we haveL+1 two dimensional sub-domainsΩ(k),k=0,1,...,L,and

The corresponding boundary conditions are

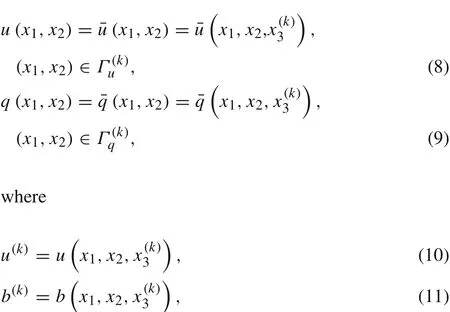
u(x1,x2)is the field potential in the sub-domainΩ(k),is the given potential on essential boundaryis the given gradient on natural boundary

Then we can solve Eqs.(7)–(9)in the sub-domainby using the IEFG method,and in the directionx3finite difference method is used to obtain the solution of the original problem,i.e.Eqs.(1)–(3).This is the idea of the DSEFG method for three-dimensional potential problems.

The equivalent functional of Eqs.(7)–(9)is

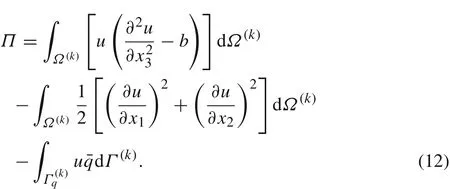
The shape function of the IMLS approximation does not satisfy the property of the Kronecker delta function;therefore,the essential boundary cannot be directly imposed to Eq.(12).In this paper,the penalty method is used to impose the essential boundary conditions.The modified functional can then be expressed as

the equivalent integral weak form can be obtained as

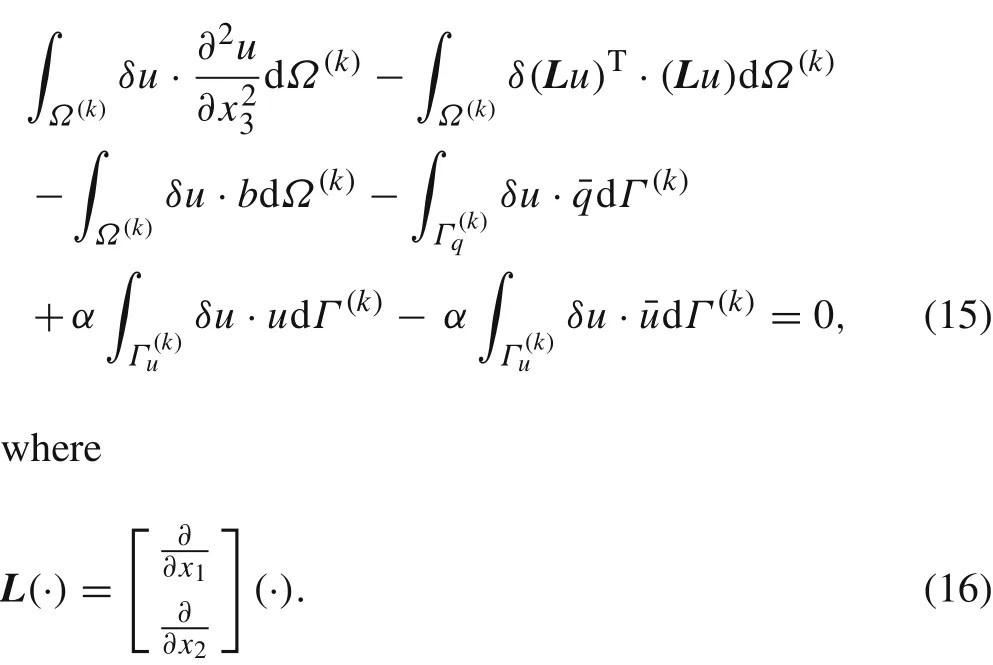
3 The dimension split elem en t-free Galerkin method for three-dimensional potential problems

3.1 Improved moving least-squares approximation

Mnodesare distributed in a two dimensional sub-domainTheu(x)at nodeis represented as

whereis the basis functionis a vector of basis functions that consist mostly of monomials of the lowest order to ensure minimum completeness,mis the number of terms of the monomials,andais a vector of coefficients.For the two-dimensional sub-domain,in this paper the basis function is chosen as the linear basis,i.e.

Define a functional

In the IMLS approximation,a weighted orthogonal polynomial set(p1,p2,...,pm)is selected as the basis functions,which results in

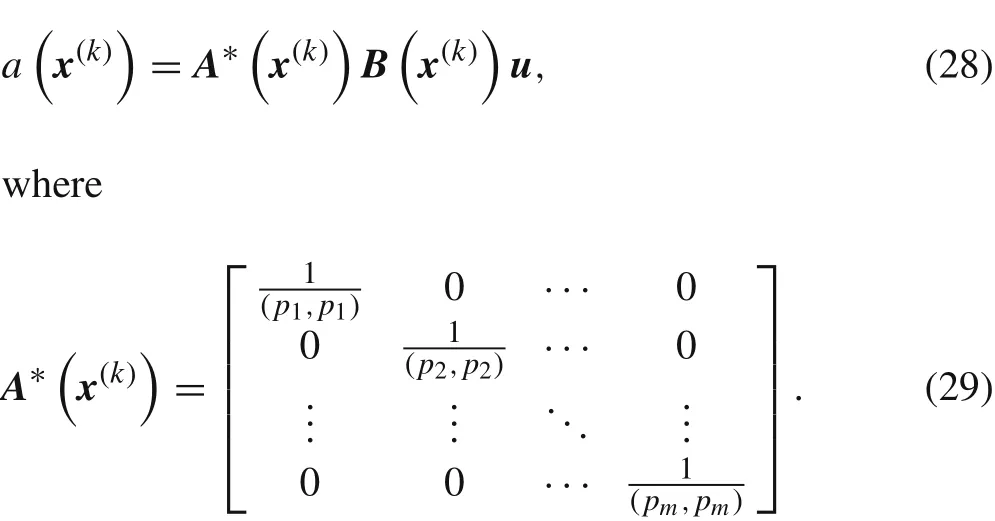
Substituting Eq.(28)into Eq.(18),we can obtain

is the size of the domain of influence of the nodexI,dmax·cI,dmaxis a scaling parameter,andcIis the distance betweenxIand the nearest node from it.

3.2 The dimension split element-free Galerkin method for three-dimensional potential problems

To obtain the solution of the original problem,i.e.Eqs.(1)–(3),the Galerkin weak form of the three-dimensional potential problem is used to get the final discretized equations.

From Eq.(30),we have

In order to obtain the discrete equations,we discuss each integration term of Eq.(42)as follows.

The first integration term of Eq.(42)is

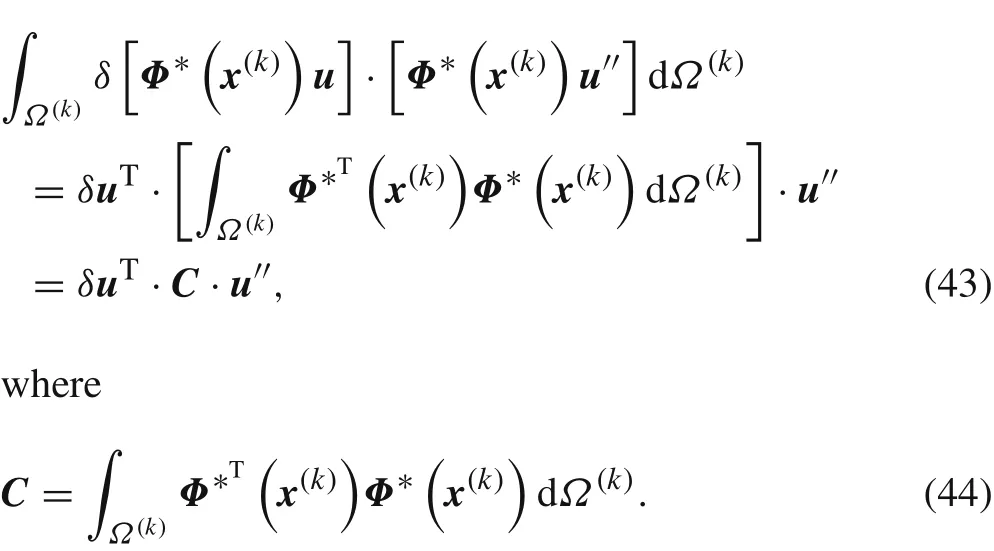
The second integration term of Eq.(42)is

The sixth integration term of Eq.(42)is

Then,Eq.(56)can be written as

Equation(69)can be simplified as

4 Example problems

Four example problems are selected to demonstrate the effectiveness and advantages of the DSEFG method presented in this paper.The convergence of the DSEFG method is discussed by analyzing the final potential function values under different nodes distribution and different scaling factors.The numerical results of these examples are compared with analytical solutions and the ones of the IEFG method.

In this section,Gaussian quadrature scheme with 4×4 points is used for numerical integrations on each cell of the background mesh.The cubic spline function is used as the weight function,and the linear basis function is selected.

4.1 Lap lace’s equation with Dirichlet boundary conditions on a cube

As the first example,we consider Laplace’s equation

Depending on the boundary conditions,the domainΩis divided intoLequal parts alongx1direction.Uniform node distribution is used in the planeOx2x3.That is,the domainΩcan be represented

Fig.1 Results obtained by the DSEFG method with different node distributions

Fig.2 Results obtained by the DSEFG method with different d max

Results obtained with the DSEFG method with different node distributions and differentdmaxalong the directionx1are shown in Figs.1 and 2.

The convergence of the DSEFG method with different node distributions and differentdmaxalong the directionx1are shown in Figs.3and 4.In Fig.3,the domainΩis divided intoLequal parts in directionx1,and the node distribution in the planeOx2x3is 10×10,that is,the node distribution in the problem domainΩis(L+1)× 10 × 10.

From Figs.1–4,we can observe that the DSEFG method has greater computational precision under the node distribution 19×10×10 whendmax=1.3.

The relationship between the relative error norm and the CPU time of the DSEFG and IEFG methods under different node distributions and differentdmaxare shown in Tables 1 and 2.

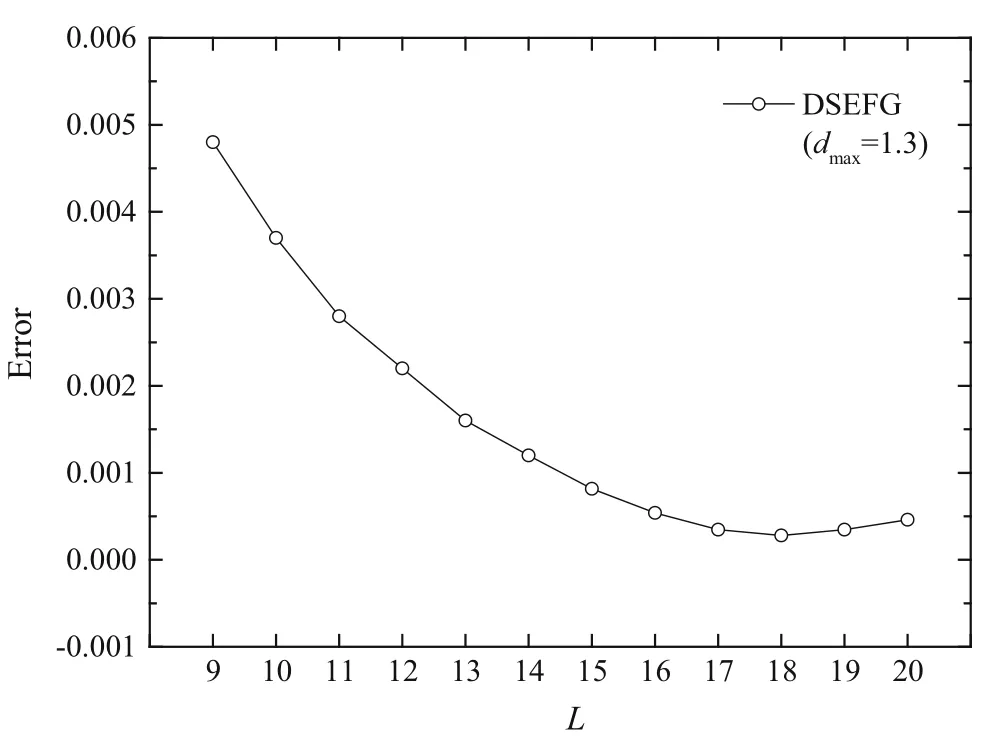
Fig.3 The convergence of the DSEFG method with different node distributions.

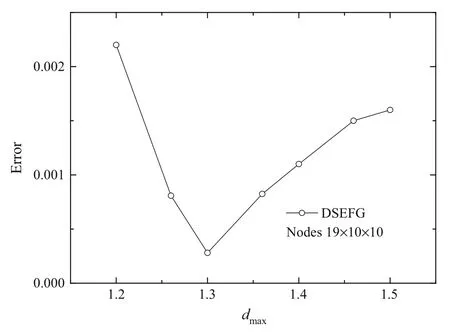
Fig.4 The convergence of the DSEFG method with different d max

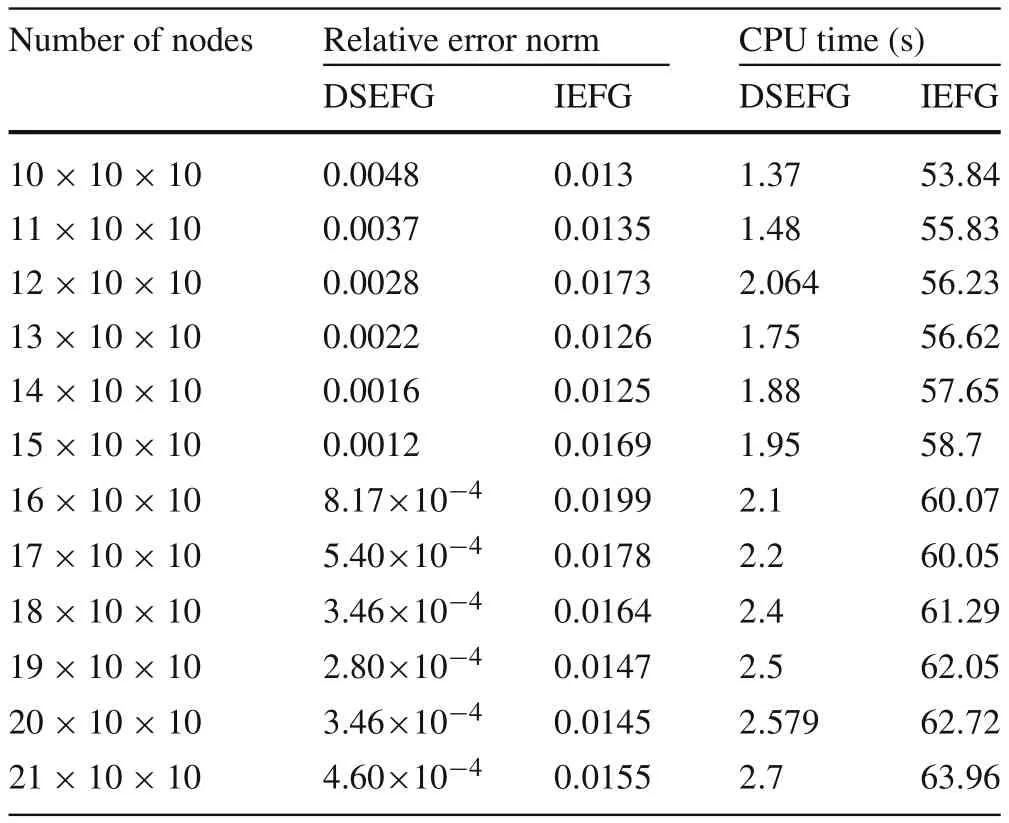
Table1 The relative error norm and CPU time of the DSEFG and IEFG methods under different node distributions

Table2 The relative error norm and CPU time of the DSEFG and IEFG methods under different d max

Fig.5 The results of the DSEFG and IEFG methods along the direction x1

From Tables 1 and 2,we can see that the DSEFG method has higher accuracy and computational efficiency than the IEFG method under the same node distribution anddmax.

Figures5–7show the numerical solutions obtained by both the IEFG method and DSEFG method along the three axes with the node distribution 19×10×10 anddmax=1.3.We can observe that the result of the DSEFG method and the IEFG method are in agreement with the analytical solution,and the DSEFG method has greater computational precision and efficiency than the IEFG method.

4.2 Poisson’s equation with Dirichlet boundary conditions

As a second example,we solve a three-dimensional Poisson’s equation

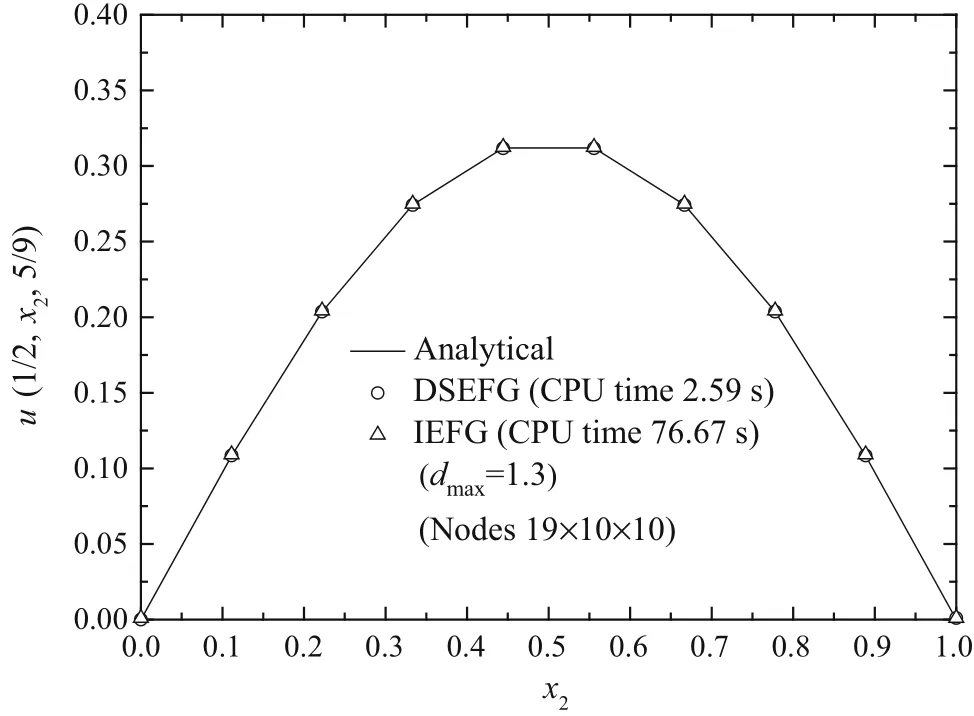
Fig.6 The results of the DSEFG and IEFG methods along the direction x2

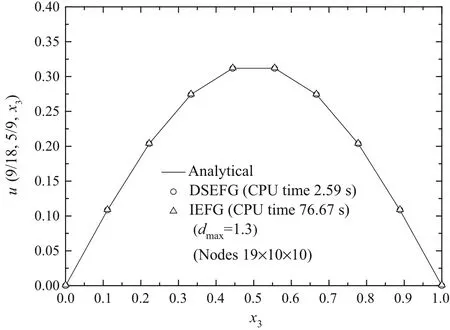
Fig.7 The results of the DSEFG and IEFG methods along the directionx3

Using the IEFG method to solve this problem,9×21×17 regular nodes are distributed in the problem domainΩanddmax=1.22.The relative error is 0.0025 and CPU time is 68.3s.

Then using the DSEFG method to solve this problem,and three cases in which different splitting direction is selected are discussed.

(1)The splitting direction isx1.For the first case,the problem domainΩis divided into 8 planes equally along the directionx1.And on each planeOx2x3,21×17 nodes are regularly chosen.It means that the integral node distribution is 9×21×17.Anddmax=2.1,α=3.0×103.Then the relative error is 0.0091 and the CPU time is 7.06s.

(2)The splitting direction isx2.For the second case,the problem domainΩis divided into20planes equally along the directionx2.And on each planeOx1x3,9×17 nodes are regularly chosen.This means that the integral node distribution is also9×21×17anddmax=1.7,α=3.0×103.Then the relative error is 0.0016 and the CPU time is 5.24s.

(3)The splitting direction isx3.For the third case,the problem domainΩis divided into 16 planes equally along the directionx3.On each planeOx1x2,9×21 nodes are regularly chosen.This means that the integral node distribution is also 9×21×17.Anddmax=1.13,α=3.0×103.Then the relative error is 0.0013 and the CPU time is 4.55s.

From the discussion above,we can see that splitting direction will influence the computational accuracy.Thus,we should select the apposite splitting direction according to the control equations and boundary conditions.

In this paper,we choosex3as the splitting direction and the better result can be obtained.Figures 8–10 show the numerical solutions obtained with the IEFG method and the DSEFG method along the three axes under the same node distribution 9×21×17.From these figures,we can observe that the numerical results obtained with the IEFG method and the DSEFG method are in agreement with the analytical ones.The CPU time of the DSEFG is less than the one for the IEFG method.

4.3 Lap lace’s equation with Neumann boundary conditions on a cube

As a third example,we study Laplace’s equation

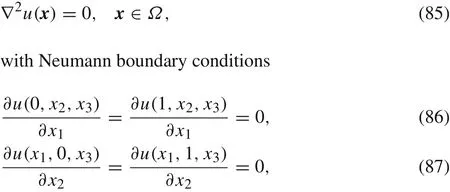
Fig.8 The results of the DSEFG and IEFG methods along the direction x1

Fig.9 The results of the DSEFG and IEFG methods along the direction x2

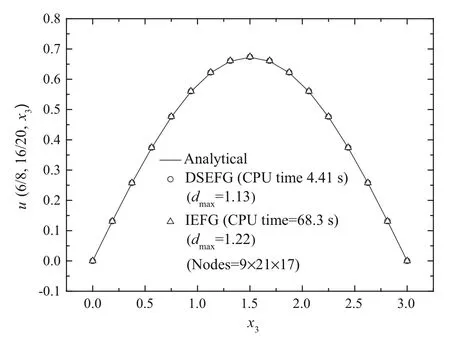
Fig.10 The results of the DSEFG and IEFG methods along the direction x3

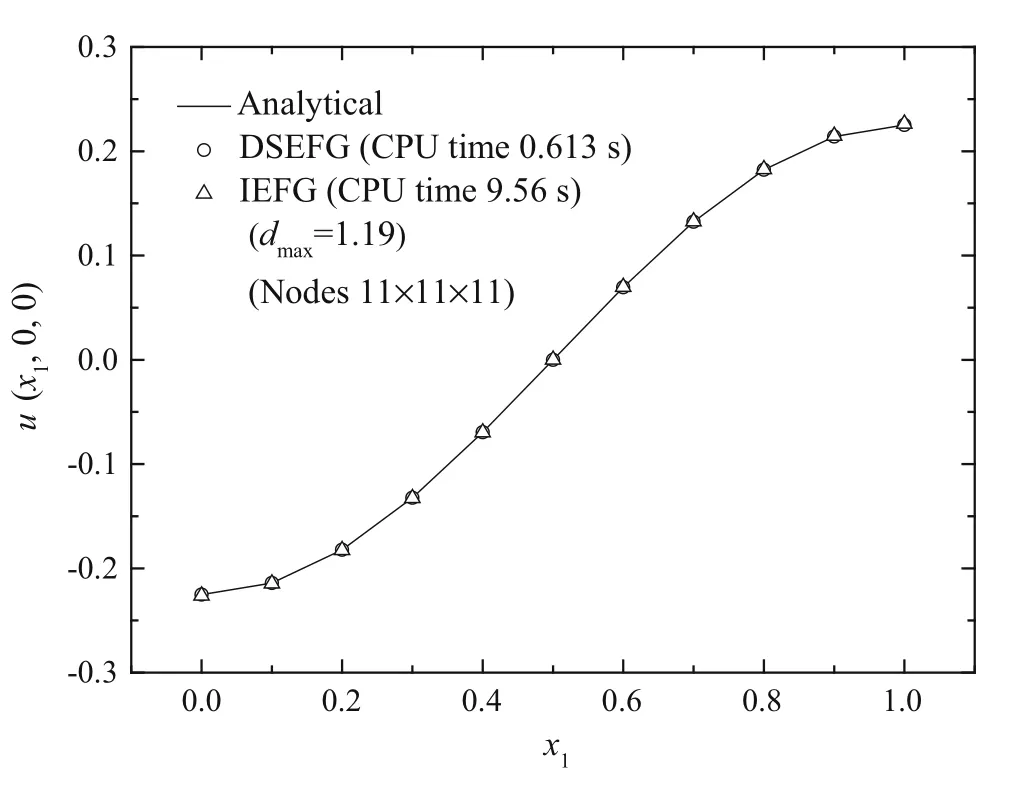
Fig.11 The results of the DSEFG and IEFG methods along the direction x1

For this example,we selectx3as the splitting direction and the uniform node distribution is also adopted.Figures 11–13 show the numerical results obtained with the IEFG method and the DSEFG method along the three axes under the node distribution 11×11×11 anddmax=1.19.For the IEFG method,the error is 0.0072,and the CPU time is 9.56s.For the DSEFG method,the error is 0.0043,and the CPU time is 0.613s.Comparing both methods,the computation accuracy and computation speed of the DSEFG method is higher than IEFG method.

4.4 Lap lace’s equation with Dirichlet boundary conditions on a half-torus cylinder

As a fourth example,we study Laplace’s equation

Fig.12 The results of the DSEFG and IEFG methods along the direction x2

Fig.13 The results of the DSEFG and IEFG methods along the direction x3

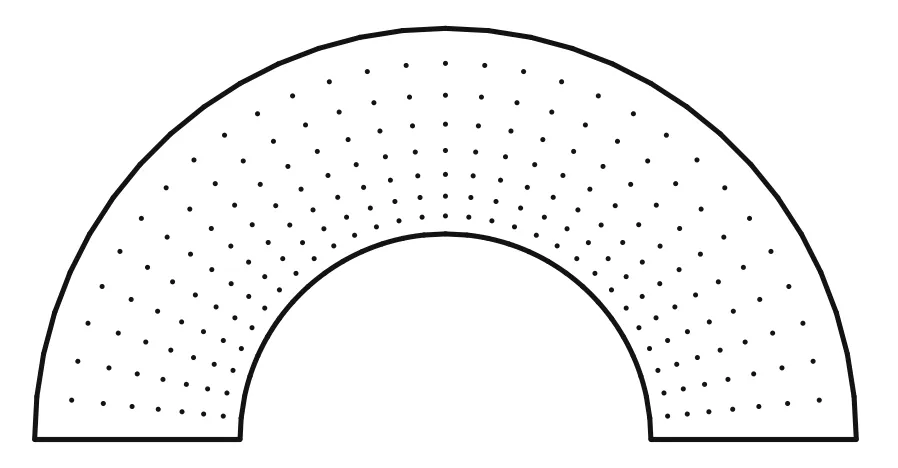
Fig.14 Node distribution in two-dimensional sub-domain of a halftorus

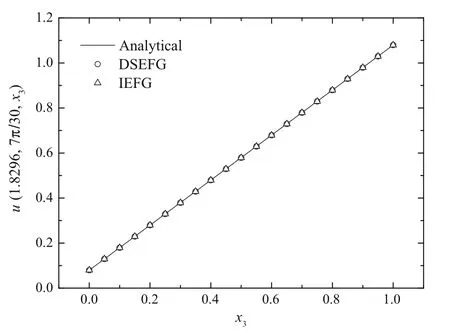
Fig.15 The results of the DSEFG and IEFG methods along the direction x3

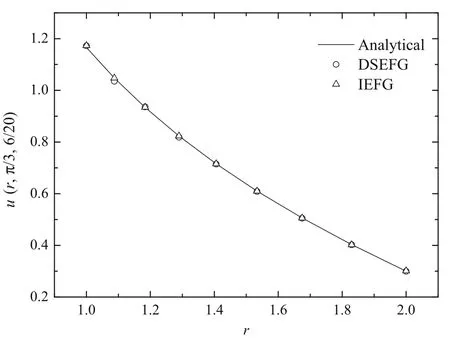
Fig.16 The results of the DSEFG and IEFG methods along the radial direction r

For this example,the problem domain is divided into 20 equal parts along thex3direction.9×31nodes are distributed on a half-torus domain of two-dimensional problem.Nine nodes are laid along the radial directionrin a 1.1 proportion and 31 nodes are uniform ly laid along the angle axisθas shown in Fig.14.It means that the integral node distribution is 9×31×21,anddmax=1.2,α=1.0×104.

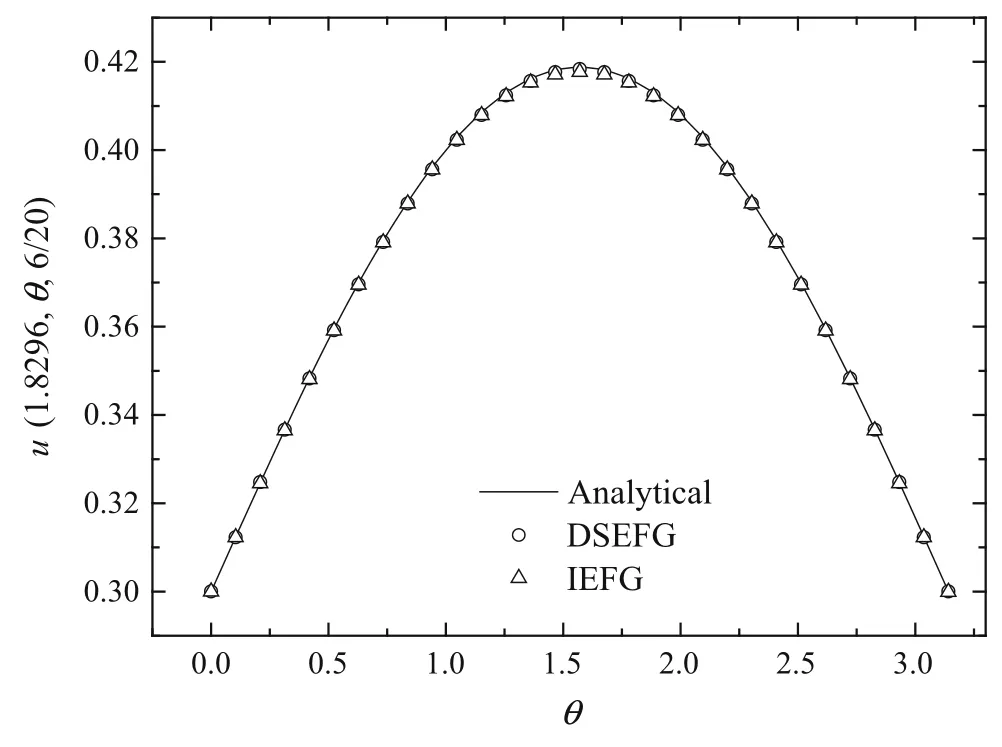
Fig.17 The results of the DSEFG and IEFG methods along the angle axis θ

Figures 15–17 show the results obtained using the IEFG method and the DSEFG method.It can be found that the results of two methods are in agreement with the analytical solution.Under similar precision,the CPU time of the IEFG method is 224.57s,and the one for the DSEFG method is 3.74s.Then the DSEFG method has greater computational efficiency than the IEFG method.

5 Conclusions

This paper presents a new fast meshless method to solve the three-dimensional potential problems.The main idea of the DSEFG method is that a three-dimensional problem can be transformed into a series of two-dimensional problems.We only need to solve a two-dimensional problem in each subdomain.For two-dimensional problems,the IEFG method is applied,which uses an orthogonal function system with a weight function as the basis functions.It is efficient to avoid an ill-conditioned system of equations.Then,the finite difference method is selected for the splitting direction.From numerical results obtained by the DSEFG method,together with comparisons with analytical solutions and the ones for the IEFG method,we can observe that DSEFG method is efficient to solve three-dimensional potential problems and generally has greater computational precision and higher computation speed than the IEFG method.

AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grants11571223,51404160)and Shanxi Province Science Foundation for Youths(Grant 2014021025-1).

1.Belytschko,T.,Krongauz,Y.,Organ,D.,et al.:Meshless methods:an overview and recent developments.Comput.Methods Appl.Mech.Eng.139,3–47(1996)

2.Dolbow,J.,Belytschko,T.:An introduction to programming the meshless element free Galerkin method.Arch.Comput.Methods Eng.5,207–241(1998)

3.Canelas,A.,Laurain,A.,Novotny,A.A.:A new reconstruction method for the inverse potential problem.J.Comput.Phys.268,417–431(2014)

4.Sun,L.L.,Chen,W.,Zhang,C.Z.:A new formulation of regularized meshless method applied to interior and exterior anisotropic potential problems.Appl.Math.Model.37,7452–7464(2013)

5.Khaji,N.,Javaran,S.H.:New complex Fourier shape functions for the analysis of two-dimensional potential problems using boundary element method.Eng.Anal.Bound.Elem.37,260–272(2013)

6.Gong,Y.P.,Dong,C.Y.,Qin,X.C.:An isogeometric boundary element method for three dimensional potential problems.J.Comput.Appl.Math.313,454–468(2017)

7.Sun,F.L.,Zhang,Y.M.,Young,D.L.,et al.:A new boundary meshfree method for potential problems.Adv.Eng.Softw.100,32–42(2016)

8.Mukherjee,Y.X.,Mukherjee,S.:The boundary node method for potential problems.Int.J.Numer.Methods Eng.40,797–815(1997)

9.Chati,M.K.,Mukherjee,S.:The boundary node method for three dimensional problems in potential theory.Int.J.Numer.Methods Eng.47,1523–1547(2000)

10.Zhang,Y.M.,Sun,F.L.,Young,D.L.,et al.:Average source boundary node method for potential problems.Eng.Anal.Bound.Elem.70,114–125(2016)

11.Li,X.L.:Error estimates for the moving least-square approximation and the element-free Galerkin method in n-dimensional spaces.Appl.Numer.Math.99,77–97(2016)

12.Lu,Y.Y.,Belytschko,T.,Gu,L.:A new implementation of the element free Galerkin method.Comput.Methods Appl.Mech.Eng.113,397–414(1994)

13.Li,X.L.,Zhang,S.G.,Wang,Y.,et al.:Analysis and application of the element-free Galerkin method for nonlinear Sine-Gordon and generalized Sinh-Gordon equations.Comput.Math.Appl.71,1655–1678(2016)

14.Vahid,S.:Topology optimization using bi-directional evolutionary structural optimization based on the element-free Galerkin method.Eng.Optim.48,380–396(2016)

15.Dehghan,M.,Abbaszadeh,M.,Mohebbi,A.:The use of interpolating element-free Galerkin technique for solving 2D generalized Benjam in–Bona–Mahony–Burgers and regularized longwave equations on non-rectangular domains with error estimate.J.Comput.Appl.Math.286,211–231(2015)

16.Joldes,G.R.,Wittek,A.,Miller,K.:Adaptive numerical integration in element-free Galerkin methods for elliptic boundary value problems.Eng.Anal.Bound.Elem.51,52–63(2015)

17.Chen,L.,Liu,C.,Ma,H.P.,et al.:An interpolating local Petrov–Galerkin method for potential problems.Int.J.Appl.Mech.6,1450009(2014)

18.Deng,Y.J.,Liu,C.,Peng,M.J.,et al.:The interpolating complex variable element-free Galerkin method for temperature field problems.Int.J.Appl.Mech.7,1550017(2015)

19.Peng,M.J.,Cheng,Y.M.:A boundary element-free method(BEFM)for two-dimensional potential problems.Eng.Anal.Bound.Elem.33,77–82(2009)

20.Lian,H.,Kerfriden,P.,Bordas,S.:Implementation of regularized isogeometric boundary element methods for gradient-based shape optimization in two-dimensional linear elasticity.Int.J.Numer.Methods Eng.106,972–1017(2016)

21.Chen,T.,Raju,I.S.:A coupled finite element and meshless local Petrov–Galerkin method for two-dimensional potential problems.Comput.Methods Appl.Mech.Eng.192,4533–4550(2003)

22.Cheng,Y.M.,Chen,M.J.:A boundary element-free method for linear elasticity.Acta.Mech.Sin.19,181–186(2003)

23.Zhang,Z.,Liew,K.M.,Cheng,Y.M.:Coupling of the improved element-free Galerkin and boundary element methods for two-dimensional elasticity problems.Eng.Anal.Bound.Elem.32,100–107(2008)

24.Zhang,Z.,Liew,K.M.,Cheng,Y.M.,et al.:Analyzing 2D fracture problems with the improved element-free Galerkin method.Eng.Anal.Bound.Elem.32,241–250(2008)

25.Zhang,Z.,Li,D.M.,Cheng,Y.M.,et al.:The improved element free Galerkin method for three-dimensional wave equation.Acta Mech.Sin.28,808–818(2012)

26.Zhang,Z.,Hao,S.Y.,Liew,K.M.,et al.:The improve delement-free Galerkin method for two-dimensional elastodynamics problems.Eng.Anal.Bound.Elem.37,1576–1584(2013)

27.Li,K.T.,Huang,A.X.:Mathematical aspect of the stream-function equations of compressible turbomachinery flows and their finite element approximation using optimal control.Comput.Methods Appl.Mech.Eng.41,175–194(1983)

28.Li,K.T.,Huang,A.X.,Zhang,W.L.:A dimension split method for the 3-D compressible Navier–Stokes equations in turbomachine.Commun.Numer.Methods Eng.18,1–14(2002)

29.Li,K.T.,Yu,J.P.,Shi,F.,et al.:Dimension splitting method for the three dimensional rotating Navier–Stokes equations.Acta Math.Appl.Sinica 28,417–442(2012)

30.Chen,H.,Li,K.T.,Wang,S.:A dimension split method for the incompressible Navier–Stokes equations in three dimensions.Int.J.Numer.Methods Fluids 73,409–435(2013)

31.Li,K.T.,Shen,X.Q.:A dimensional splitting method for the linearly elastic shell.Int.J.Comput.Math.84,807–824(2007)

32.Hansen,E.,Ostermann,A.:Dimension splitting for evolution equations.Numer.Math.108,557–570(2008)

33.Hansen,E.,Ostermann,A.:Dimension splitting for quasilinear parabolic equations.IMA J.Numer.Anal.30,857–869(2010)

34.Hou,R.Y.,Wei,H.B.:Dimension splitting algorithm for a three dimensional elliptic equation.Int.J.Comput.Math.89,112–127(2012)

35.ter Maten,E.J.W.:Splitting methods for fourth order parabolic partial differential equations.Computing 37,335–350(1986)

36.Bragin,M.D.,Rogov,B.V.:On exact dimensional splitting for a multidimensional scalar quasilinear Hyperbolic conservation law.Dokl.Math.94,382–386(2016)

37.D’souza,R.M.,Margolus,N.H.,Smith,M.A.:Dimension-splitting for simplifying diffusion in lattice-gas models.J.Stat.Phys.107,401–422(2002)

38.Cheng,H.,Peng,M.J.,Cheng,Y.M.:The hybrid improved complex variable element-free Galerkin method for three-dimensional potential problems.Eng.Anal.Bound.Elem.84,52–62(2017)

39.Cheng,H.,Peng,M.J.,Cheng,Y.M.:A fast complex variable element-free Galerkin method for three-dimensional wave propagation problems.Int.J.Appl.Mech.9,1750090(2017)