Density enhancement mechanism of upwind schemes for low Mach number flows

Bo-Xi Lin·Chao Yan·Shu-Sheng Chen

1 Introduction

When with low-speed flow configurations[1–4],numerical schemes developed for compressible flows suffer because the non-physical behavior deteriorates the solution accuracy and because there is a large disparity between the speed of fluid and acoustic wave.There is also a stiffness problem leading to slow calculation.Low-speed preconditioning techniques have been developed to overcome issue of compressible flow solvers in the in compressible limit[5,6].Later,the non-physical behavior was demonstrated by asymptotic analysis by Guillard and Viozat in Ref.[7].As pointed out in the asymptotic analysis,discrete equations of the shock capturing schemes lead to pressure fieldPfluctuation withbut the true physical pressure should scale as,whereMis the local Mach number,xandtdenote space and time.During recent years,some new attempts to improve the accuracy of conservative schemes in the low-speed limit have been proposed,which focus on dissipation characteristics of flux functions and are different from the previous preconditioning idea.Among the conservative schemes,the Roe scheme[8]is a widely used method for solving compressible flows due to its high resolution for discontinuities and contact shear waves.Many Roe-type schemes with low Mach improvement have been proposed for all speed flows[9].The work of Li and Gu[10]investigated the joint mechanism of many improved schemes,which include all-speed Roe(A-Roe)[11,12],Thornber-Drikakis-Roe(TD-Roe)by Thornber and Drikakis[13],LMRoe by Rieper[14],Fillion-Roe(F-Roe)by Fillion et al.[15].To construct satisfactory schemes showing the correct asymptotic behavior,Li and Gu[10]found three rules for low speeds through asymptotic theoretical analysis.Based on these disciplines,improvements for low speeds have been applied to schemes include Harten,Lax,and van Leer(HLL)[10,16],Roe[17],Toro-Vázquez flux splitting[18].Another group of popular upwind methods are AUSM-family schemes[19,20],and their low Mach number modification[21,22]based on a careful design of dissipation also have been proposed.Besides the accuracy problem,some authors[23,24]also investigated preconditioned implicit time integration methods for efficient calculation of low-speed flows.

However,the proposed schemes only concern the nonphysical behavior of pressure and the checkerboard problem(i.e.correction of pressure and velocity fields),without concerning the correct asymptotic behavior of density field,which is also important as all-speed schemes are mostly applied to density variable flows(low Mach flows[25,26])or compressible field with low-speed zones(mixed compressible incompressible flows[27]).In the low Mach number speeds,the pressure field gradually decouples with density as the Mach number decreasing to zero,so the asymptotic density variations of these schemes must also be considered in addition to pressure problems.

The rules for low speed flows developed by Li et al.only concern terms in momentum and continuity equations.In the original T-D-Roe[13]and F-Roe[15]schemes,the energy equation is untouched,while Li and Gu[10]add fixed terms to the energy equation for uniformity,which is just like the form of the momentum equation,and concluded that the modification has little effect on the energy equation.However,it has been found that the correction terms in the energy equation are related closely to the density fluctuation of the flow field in our numerical experiments.These things motivate us to understand the mechanism of density fluctuation with the correction terms in the energy equation and then to find the rules to improve the schemes that have not considered density effects,such as the recently proposed TV-MAS[18].

The outline of this paper is as follows.Section 2 presents the governing equations.Section3briefly reviews the Roe,TD-Roe,F-Roe schemes and the recently proposed TV-MAS method.Their density enhanced versions are also discussed in this section.Section4 discusses the density fix mechanism with energy equation underlying these schemes and conducts an asymptotic analysis to demonstrate it.The resulting rules of the density fix mechanism are applied to the TV-MAS scheme.Section5 presents the numerical experiments to support the theoretical analysis and prediction.Finally,Sect.6 closes the paper with some conclusions.

2 Governing equations

Firstly,the compressible Euler equations in2D can be written as the following form

where the specific heat ratioγ=1.4.

The finite volume discretization of Eq.(1)can be written as

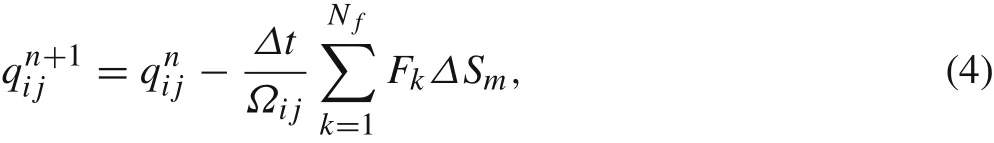
whereΩijis the 2D finite volume,ΔSmis the edge length,Nfis the total number of edges composing the finite cell,Fkis the flux function at the edge normal.

3 Review of the schemes

3.1 The original Roe scheme

The original Roe–Pike[8]scheme can be expressed in the following form

3.2 The F-Roe scheme

Fillion et al.[15]propose a low Mach Roe scheme by adding a pressure correction to the momentum flux as follows

This F-Roe scheme is further investigated by Qu et al.[28,29]in supersonic heating problems and Reynolds averaged Navier Stokes(RANS)simulations.There are no energy fix terms in the original F-Roe scheme,and this would result in incorrect density fluctuation which will be shown in asymptotic and numerical experiment.The density correction term is added to energy equation as follows and the scheme is called F-Roe2:

3.3 The T-D-Roe scheme

In order to improve the Roe scheme,Thornber and Drikakis[13]modified the right eigenvector as follows

In Eq.(16),the acoustic terms in RT?D?Roe2(4,1)and RT?D?Roe2(4,4)are also scaled byf(M),while in the original T-D-Roe they are the same as Roe scheme.

Through mathematical transformation,the T-D-Roe2 can be written as the form of F-Roe2 as follows

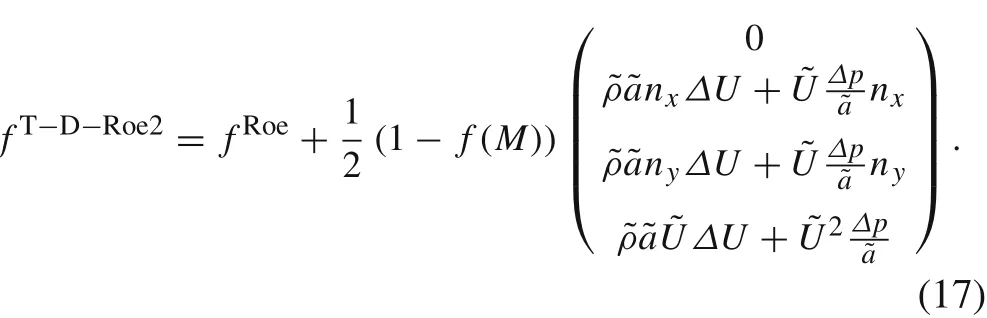
As we can see from Eq.(17),the T-D-Roe2has avery similar form of F-Roe2 in Eq.(12),which implies that they may have similar performance at low speeds.

3.4 The TV-MAS scheme

Based on the idea that velocity and pressure should be separately treated owing to the different physics between the convective and acoustic waves,new flux vector splitting(FVS)schemes have been developed.These methods rely on some forms of splitting procedures.Up to now,there mainly exist procedures of Liou-Steffen[19],Zha-Bigen[30],and Toro-Vázquez[31]to split the Euler equations into theadvection systemandpressure system.Further discussions and developments for these methods can be found in Refs.[18,32–34].The main differences between those splitting procedures lie in the energy equation of theconvective system:Liou-Steffen’s total enthalpy,Zha-Bigen’s total energy,and Toro-Vázquez’s kinetic energy respectively.

The TV-MAS scheme proposed by Sun et al.[18]based on Toro-Vázquez’s splitting is reviewed here,and the TVMAShasbeen claimed as an all-speed scheme in the original paper.In the Toro-Vázquez’s splitting,advection systemhas no pressure terms,and it only appears inpressure system,moreover,this splitting allows direct use of Godunov-type methods to the separated system.These characteristics make the splitting procedures attractive.

Following Toro-Vázquez’s splitting,the flux vector of Eq.(1)is split into theadvectionsystemandpressure system:

Thepressure systemis dealt with using an HLL-type[35]Riemann solver,and then the authors follow an isoentropy transformation in AUFS scheme[36],and the resulting pressure dissipation vector is written as

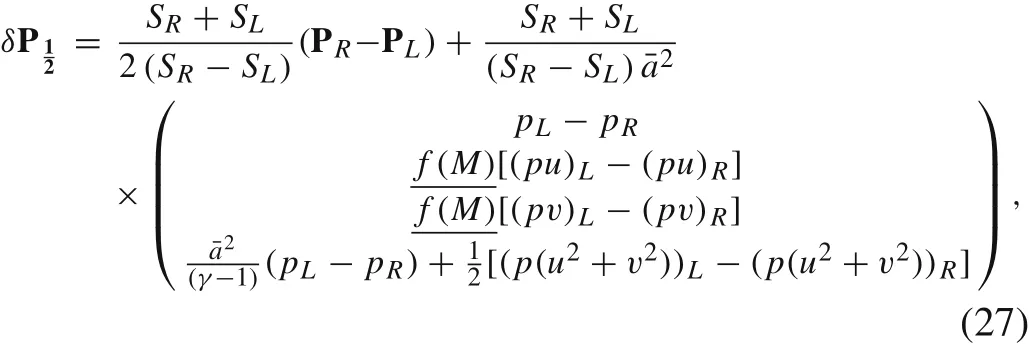
whereAs we can see,the TV-MAS scheme has applied the rules proposed by Li and Gu[10]to pressure dissipation terms,which modifies the pressure-difference terms in momentum equations by the factorf(M),but apparently the energy equation is neglected by the original authors.

4 Asymptotic analysis

Under the adiabatic compression condition,pressure and density are related to each other as=const[37],so the density field would have the same fluctuation pattern as the pressure.To find the mechanism for how the correction term in the energy equation influences density fluctuation,an asymptotic analysis,which has been widely used in Refs.[7,10,11,14],is performed.Previous asymptotic analysis of continuous Euler equation has found that pressure field fluctuates with the square of Mach number,and the asymptotic analysis of the discrete equations with Roe scheme has revealed the terms related to the pressure fluctuation.This time we will find the density related terms in the discrete equations.

Following Ref.[7],the parametersρ?,u?,anda?are used to normalize the compressible Euler equations,which are defined asand the acoustic speedρi(x),ui(x),andpi(x)are the initial values of the discrete domain.The normalized variables are listed in the following form

HereM?is the reference Mach number andδ?is the characteristic mesh element size.Then all normalized variables are asymptotically expanded into powers of the reference Mach numberM?

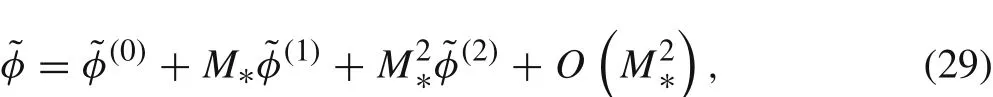
Table 1 Symbols in asympototics

whererepresents all the physical variablesrespectively.In the following sections,we will drop the tildeconvenience and all the symbols used in analysis are presented in Table 1.

Inserting the asymptotic expansion Eq.(29)into the FRoe scheme,we collect terms with the same power ofM?.In Ref.[14],Rieper has analyzed the terms with the order,and has found the mechanisms to get the correct pressure field.This correction also fixes the Mach contours of the flows.However,the pressure has a limited influence on density in low Mach number.So further analysis must be conducted upon the asymptotic expansion of pressure to find the density enhance mechanism.We gather the terms with orderin continuity and energy equations as follows continuity equation:

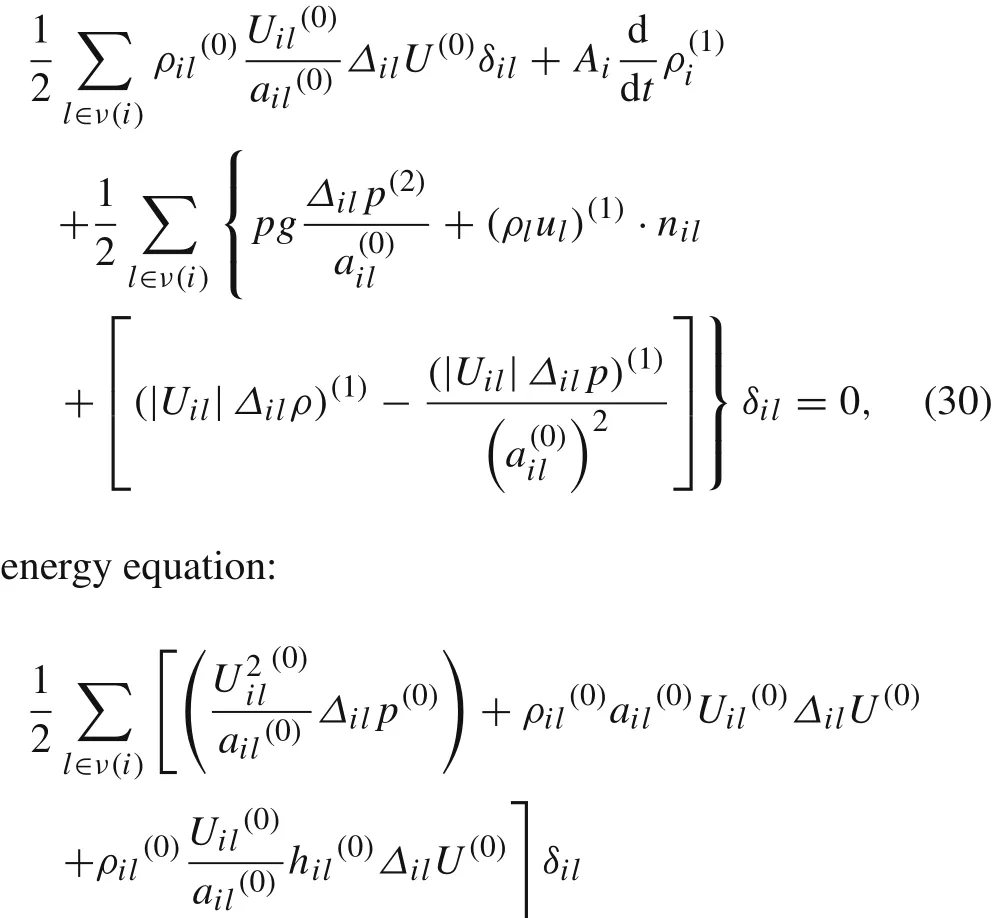
Note that for a simple entropy conservative shear flow with constant density and pressure,Ronly has the transport term forρ(1).An excessive damping of theρ(1)origins from the underline term in Eq.(35).In the F-Roe2 and TD-Roe2 schemes,this term is lifted with thef(M)function(ΔilU(0)→ 0),and reduces the artificial viscosity to the correct level.This density correction effects will be shown in the following numerical experiments.

That is to say, fix terms also should be applied to the energy equation to get the right density fluctuation,based on the pressure fix added to momentum equations.The nonphysical phenomenon of upwind schemes at low speed can be cured following the rules of Li and Gu[10],and now we have shown that extra fix terms in the energy equation needed to be considered based on a similar form of momentum correction.According to this theory,we propose the TV-MAS2 scheme,which fixes the energy equation with thef(M)function upon the original TV-MAS scheme.In order to get the correct density fluctuation,the energy equation inis modified as the way in momentum equations,resulting the following TV-MAS2 scheme

5 Numerical results

5.1 Greshovortex

In their work,Gresho and Chan[38,39]proposed a time independent solid body rotating vortex flow.In this unsteady moving flow,the vortex can be transported without distortion by the background flow.We choose a computation domain of[0,1]×[0,1],and periodic conditions are applied on the horizontal direction,while characteristic conditions are on the vertical edges.The domain is first initialized with a uniform background flow of densityρ0,pressureP0,and given MachM0as follows

A perturbed initial condition permitting different Mach numbers is proposed in Ref.[14].At the timet=0 of the perturbed flow,a vortex is located at(x0,y0)=(0.5,0.5)with the radiusR=0.4.At the positionr=R,the vortex tangential velocity decreases to zero.This perturbed vortex is added to the background flow as follows

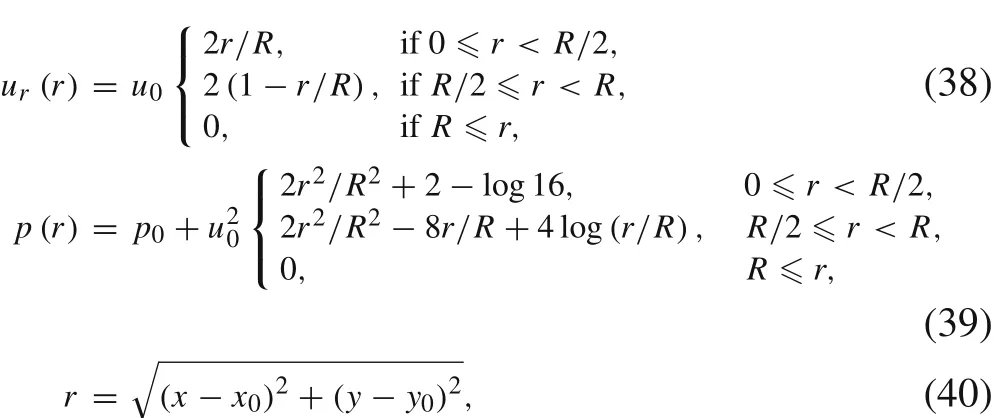
where theur(r)denotes the radial velocity and we obtain the Cartesian components by

The original incompressible test case is extended to a weakly compressible one by introducing the adiabatic compressionp=ργ,which makes the initial density field have a similar form to pressure fluctuations

We use a Cartesian grid of[120×120],and all simulations are run until one domain passage is reached.The strong stability preserving a three-stage third-order Runge-Kutta(SSP-RK3)[40]scheme is used for temporal discretization.

In Ref.[9],the evolution of a normalized pressure field∈[0,1]is used to characterize the accuracy of the computations in incompressible limit.The normalized pressure fieldis expressed as

In the Gresho vortex test case,the normalized pressure and density field should be unchanged during transportation independent of initial Mach number.Thus,we use this to evaluate the quality of different schemes in the simulation of Gresho vortex.

Figure 1 shows the normalized pressure fluctuation field of the Gresho vortex forMa=0.1.Figure 2 shows the corresponding normalized density fluctuation field.As we can see,the original Roe scheme holds the initial maximumPfof 50%–60%after one domain passage due to the strong dissipation;on the contrary,all others plotted in the figures have preserved the original maximumPf.All the improved schemes(T-D-Roe,F-Roe,TV-MAS,T-D-Roe2,F-Roe2,TV-MAS2)have achieved the same contour onPfas F-Roe,thus not all of them are plotted in the figure.However,the difference lies in the density field.Schemes in the group with no energy correction(T-D-Roe,F-Roe,TV-MAS)show excessive dissipation to density fluctuation.The original Roe preserves30%of the maximumρfafter one domain passage,while F-Roeis40%,TV-MAS is20%.The schemes with energy fix terms(T-D-Roe2,F-Roe2,TV-MAS2)have almost constant density fluctuation as the initial field.This shows the importance of the energy equation fix to get the correct density field in low Mach speeds.

Fig.1 Normalized pressure field for simulations of a Gresho vortex.a Initial pressure field.b Roe scheme for M a0=0.1.c F-Roe scheme for Ma0=0.1.d F-Roe2 scheme for Ma0=0.1.e TV-MAS scheme for Ma0=0.1.f TV-MAS2 scheme for Ma0=0.1

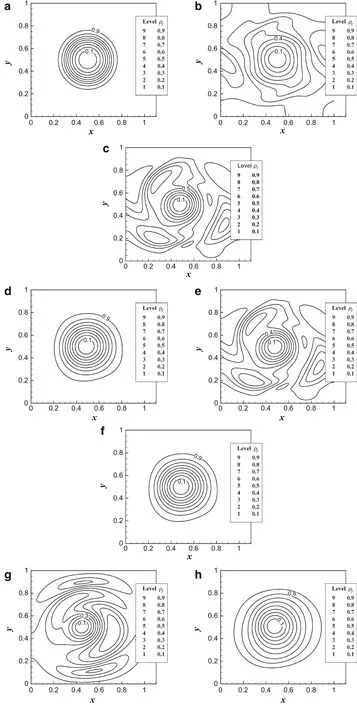
Fig.2 Normalized density field for simulations of a Gresho vortex.a Initial density filed.b Roe scheme for Ma0=0.1.c F-Roe scheme for Ma0=0.1.d F-Roe2 scheme for Ma0=0.1.e T-D-Roe scheme for M a0=0.1.f T-D-Roe2 scheme for M a0=0.1.g TV-MAS scheme for Ma0=0.1.h TV-MAS2 scheme for Ma0=0.1

Fig.3 Vorticity contours of double shear-layer by F-Roe2 schemes at Mach 0.01.a t=0.b t=4.0.c t=8.0

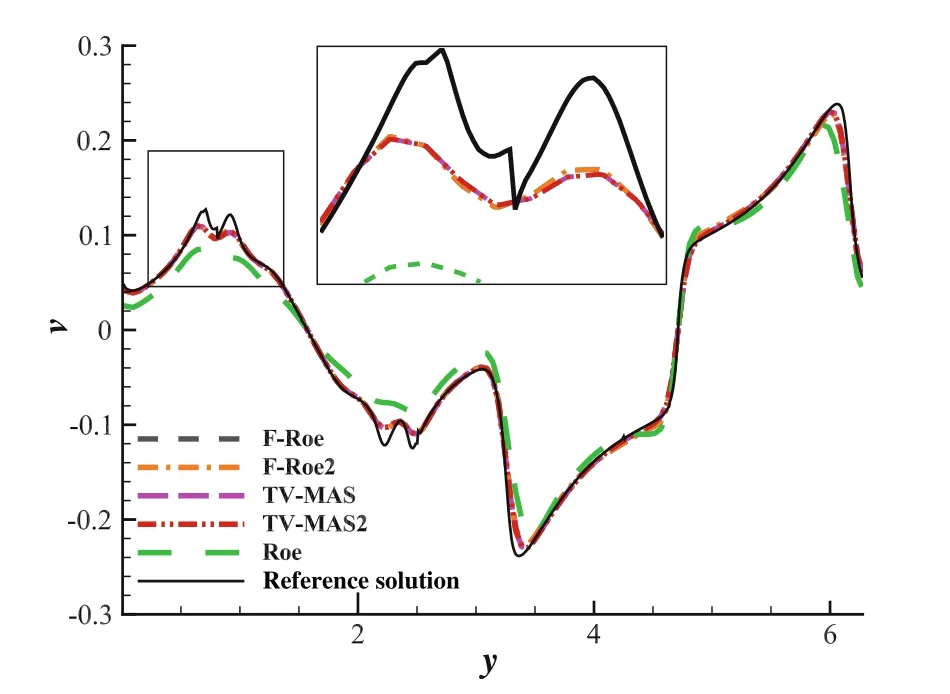
Fig.4 Velocity v profiles along x=π at t=8.0 of double shear layer cases

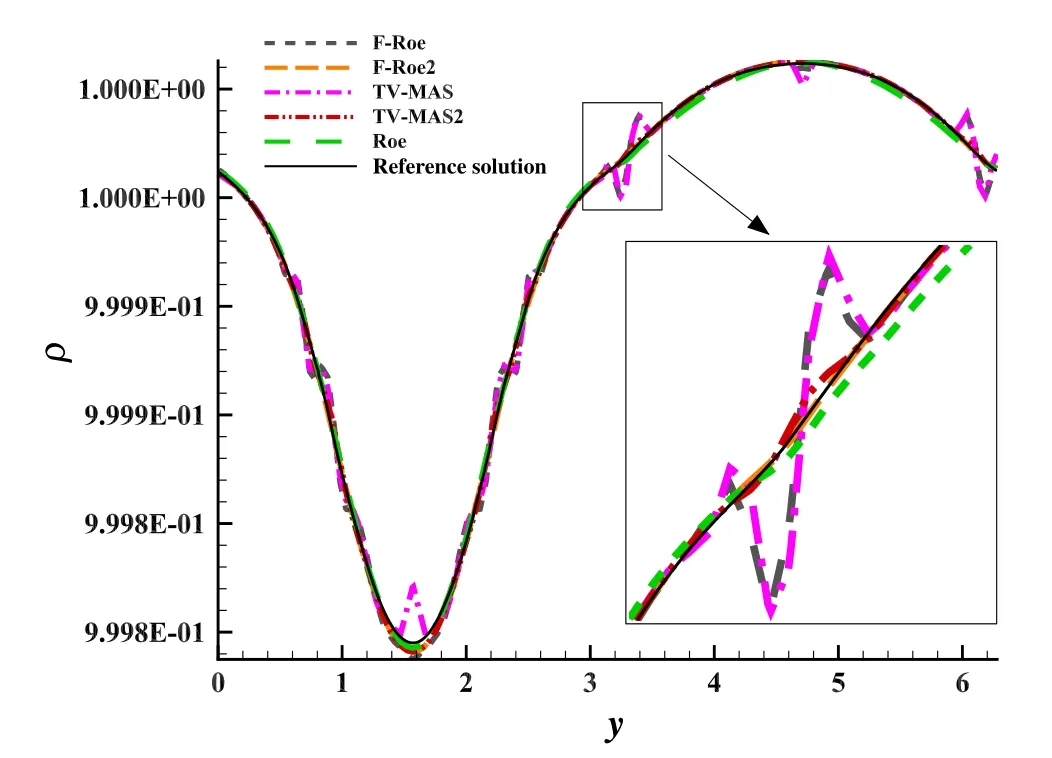
Fig.5 Density profiles along x=π at t=8.0 of double shear layer cases

The T-D-Roe series have similar formulas and numerical results as corresponding schemes in F-Roe series,and that is verified in the following numerical examples.So in some sections,only the F-Roe results are listed in the discussion.

5.2 Double shear-layer

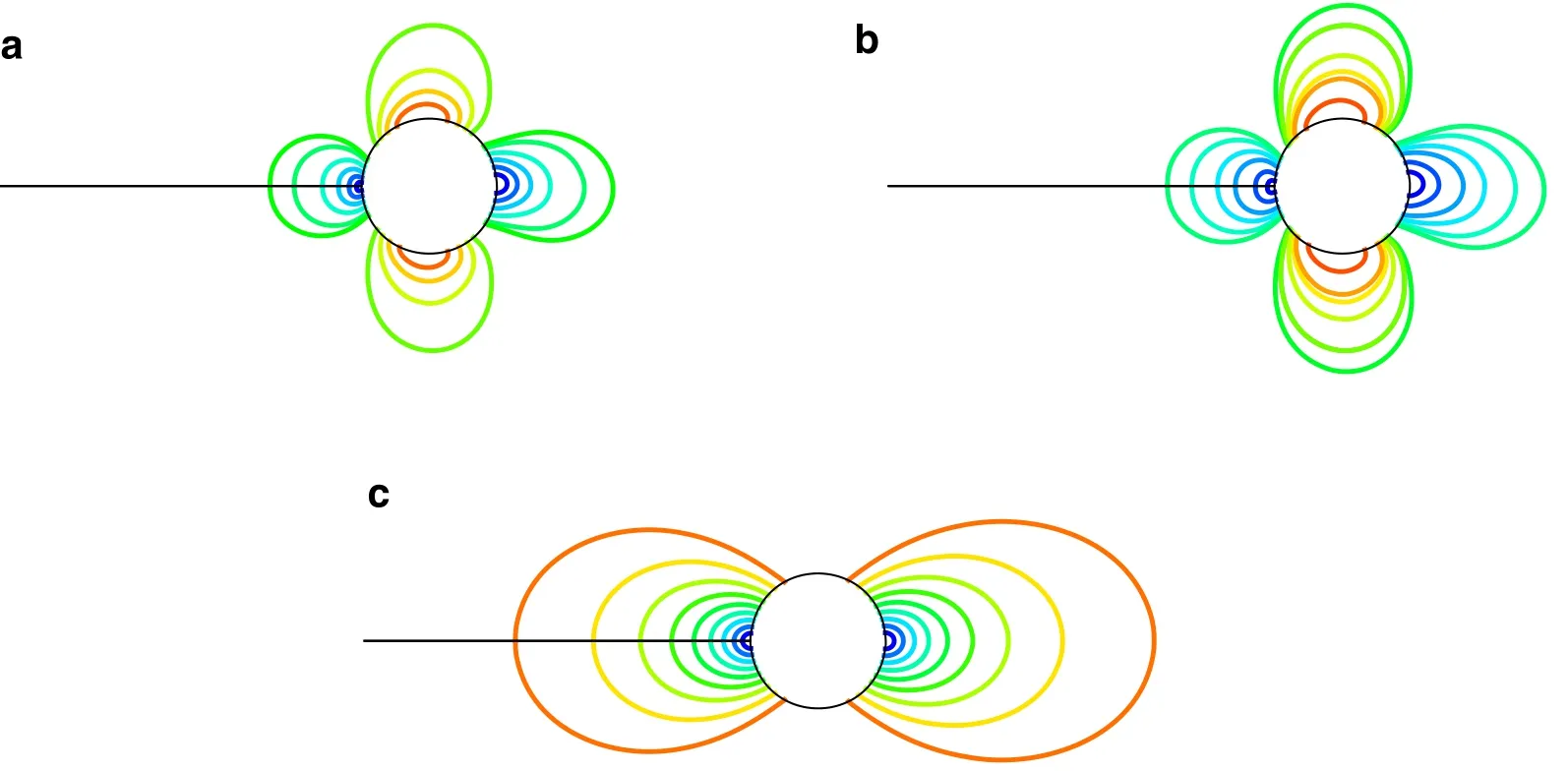
Fig.6 Mach contours for simulations of flow around inviscid cylinder at Mach 0.001.a TV-MAS scheme.b TV-MAS2 scheme.c Roe scheme

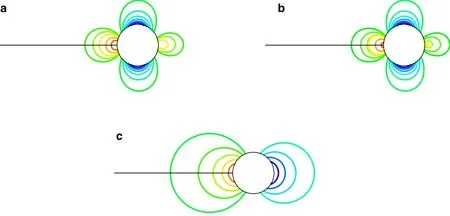
Fig.7 Pressure contours for simulations of flow around inviscid cylinder at Mach 0.001.a TV-MAS scheme.b TV-MAS2 scheme.c Roe scheme

The “double shear-layer”problem is a typical 2D unsteady inviscid flow.We mostly follow the setup of Ishiko et al.[41]and Kitamura and Hashimoto[42],which makes this problem a weakly compressible flow.Initially,two shear layers are generated by fluids with opposite velocity(Fig.3a),then as time progresses,the initial layers will gradually roll up and develop a strong vortical flow structure (Fig.3b,c)[42].This vortical structure developed by shear-layer is very different to Gresho’s vortex flow,which possesses a consistent pattern.Thus,we conduct it to highlight further the characteristics of density correction.

The initial conditions for velocity components are

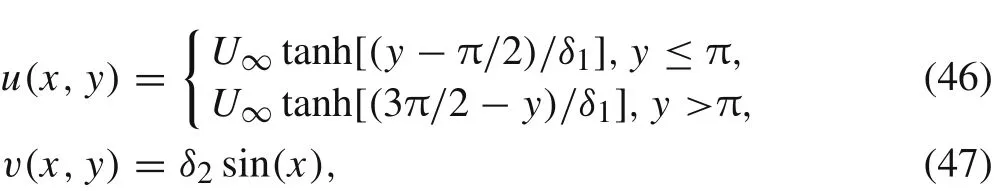
whereU∞=1.0,δ1= π/15,δ2=0.05.The density is set to beρ=1.0 and the pressure is chosen to satisfy a Mach number ofM∞=0.01 with.The computational domain is [0,2π]×[0,2π]and consists of 1282grid cells.A periodic boundary condition is adopted at all directions of the computational domain.The simulations are run up tot=8.0with the SSP-RK3 time scheme at a time step ofδt=5.0 × 10?5.The reference solution is achieved with Roe scheme at a very fine grid of 5122cells.“At this level of resolution,the flux functions have no influence on the results”[42].

The differences of all simulated schemes are compared in Fig.4,in which velocityvprofiles are listed alongx=π slice.In Fig.5,the density profiles alongx=π are plotted.As we can see from Fig.4,all the low-Mach enhanced schemes get a more precise velocityvprofile than the original Roe,and there are marginal differences among themselfs.This proves that the momentum fix can recover the velocity and pressure profile at low Mach limit.However,in Fig.5,the density profile is very different.The F-Roe and TV-MAS have density jump glitches at the position of strong shear effect,while the fixed F-Roe2 and TV-MAS2 can recover correct density profile compared to the reference solution.

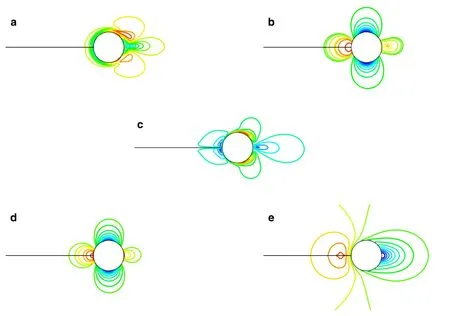
Fig.8 Density contours for simulations of flow around inviscid cylinder at M a=0.001.a F-Roe scheme.b F-Roe2 scheme.c TV-MAS scheme.d TV-MAS2 scheme.e Roe scheme

Fig.9 Convergence comparison of NACA0012 test case at Ma=0.01

5.3 Inviscid cylinder

The Euler flow over a two-dimensional cylinder is a typical low speed flow of blunt body.In this case,the size of the computational domain isΩ=[r0,r1] × [φ0,φ1],which is[0.5,20]× [0,2π]in details,wherer0is the radius of a cylinder surface andr1is the radius of exterior boundary.The adopted mesh is O-type and contains 301(cuicumference)×401(radius)grid points.The in flow Mach numbers??0.001 with initial conditions ofρ=1.0,The far field condition is used at the outer boundary,and the slip wall condition is applied at the cylinder wall.

Figure 6 shows the Mach contours of the TV-MAS,TVMAS2,and Roe schemes,while Fig.7 shows the pressure contours.As we can see,in this condition,the TV-MAS and TV-MAS2 get the physical Mach and pressure field,while the original Roe scheme gets nonphysical contours.The TD-Roe and F-Roe series have the same Mach and pressure results,so are not plotted here.In Refs.[10,18],it has been shown that the Mach and pressure fields can be solved by the momentum corrections together,so only the pressure fields are used for comparison in the following.Figure 8 shows the density contours of the F-Roe,F-Roe2,TV-MAS,TVMAS2,and Roe schemes.The Roe,F-Roe,and TV-MAS get diffusive density field,while the TV-MAS2 and F-Roe2 can recover the correct density field.It also can be noticed that the F-Roe and TV-MAS get more diffusive density field than original Roe scheme.

5.4 Inviscid NACA0012 airfoil

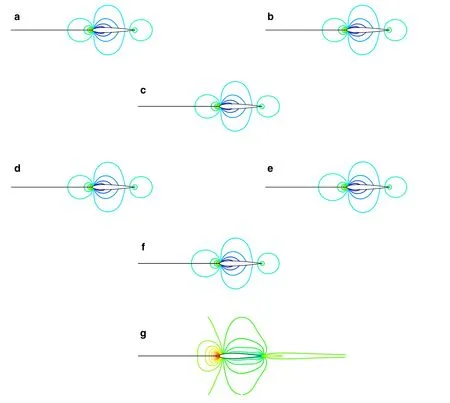
Fig.10 Pressure contours for simulations of inviscid flow around NACA0012 at Ma=0.01.a F-Roe scheme.b F-Roe2 scheme.c T-D-Roe scheme.d T-D-Roe2 scheme.e TV-MAS scheme.f TV-MAS2 scheme.g Roe scheme

The inviscid flow over NACA0012 airfoil is a typical test case at the low-speed condition.An O-type mesh that contains points of 241(airfoil)×121(normal)is used for the following computations.The discretization domain extends 19 chord lengths from the airfoil wall,the far field condition is used at the exterior boundary and the slip wall condition is applied to the airfoil surface.The flow results with several in flow Mach numbersMinf=0.1,0.01,0.001 at a zerodegree angle of attack are investigated to assess the density fix effects.In addition,the flow simulations are conducted by the implicit LU-SGS approach[43]withCFL=5 for over 100,000-time iterations,which achieve at least five orders of the density residual reduction(L2?norm).Though the preconditioned implicit LU-SGS[23]is a better choice,we still use LU-SGS since we mainly focus on the flux functions.

Figure 9 shows the convergence history of in flow Mach number 0.01 by different schemes.The T-D-Roe serial schemes perform similarly to F-Roe and are not shown in the figure for clarity.We can see clearly in the convergence history that schemes without the energy correction stall after five orders of residual reduction.The schemes with corresponding corrections can continue with the residual drop.

The results of pressure profiles with in flow Mach 0.01 are plotted in Fig.10,and density fields of the solutions are presented in Fig.11.It is important to note that although T-D-Roe,F-Roe,and TV-MAS schemes can obtain accurate pressure flow fields at low speeds,but fail in density fluctuation fields.The schemes with corrections in energy equation can get the accurate density field corresponding to the pressure field.However,in Fig.11f,the density field of TV-MAS2 seems more diffusive than F-Roe2and T-D-Roe2,especially in the wake region.This may owe to the inherent dissipation characteristic of HLL Riemann solver solving the pressure system,which is more diffusive than the Roe Riemann solver in nature.

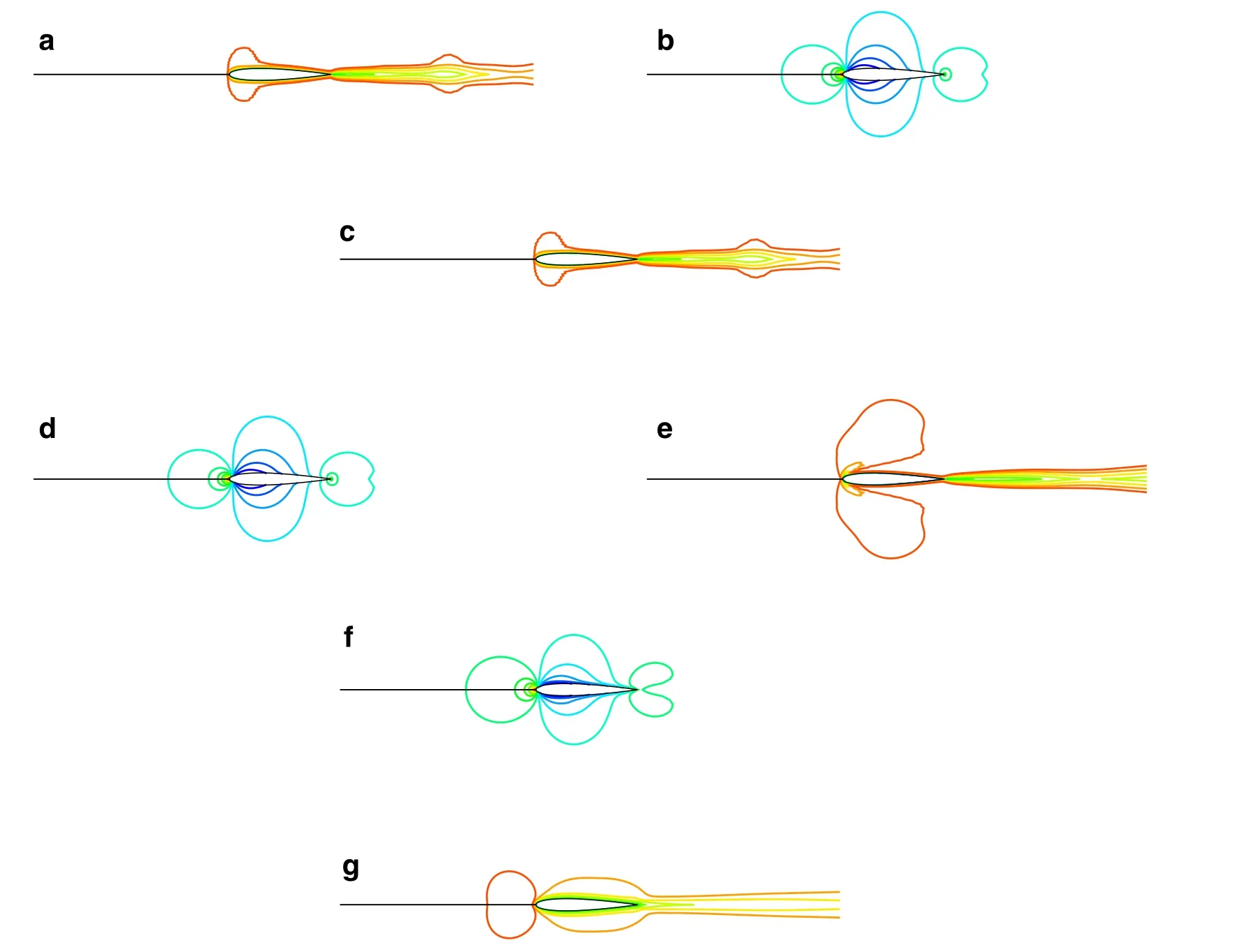
Fig.11 Density contours for simulations of inviscid flow around NACA0012at M a=0.01.a F-Roescheme.b F-Roe2 scheme.c T-D-Roescheme.d T-D-Roe2 scheme.e TV-MAS scheme.f TV-MAS2 scheme.g Roe scheme

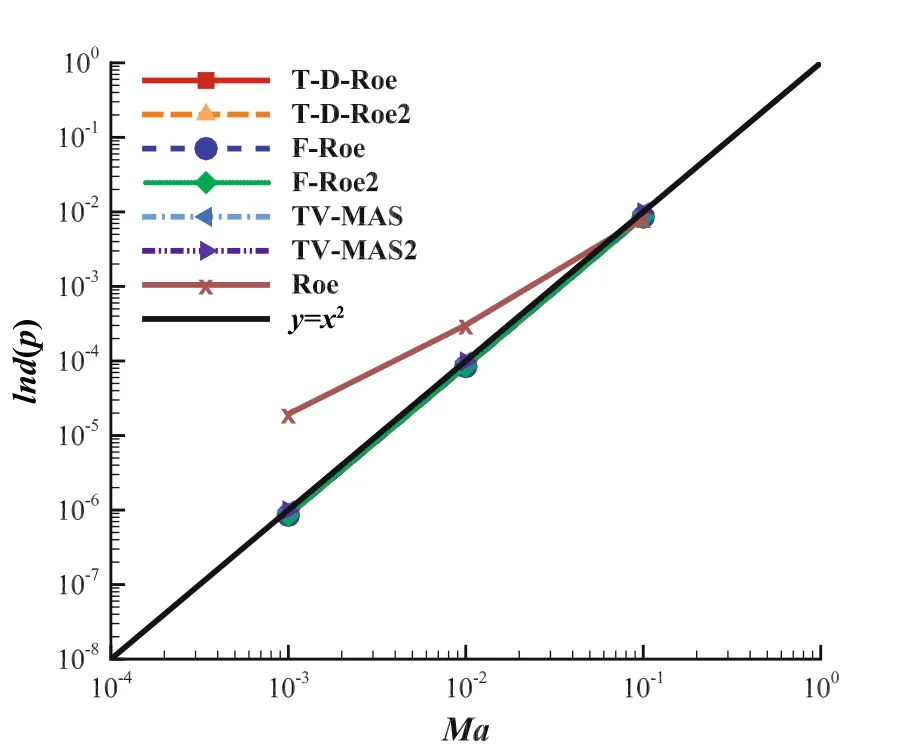
Fig.12 Comparison of pressure fluctuations computed by different schemes versus in flow Mach number

Following Ref.[17],we define two fluctuation coefficients as follows

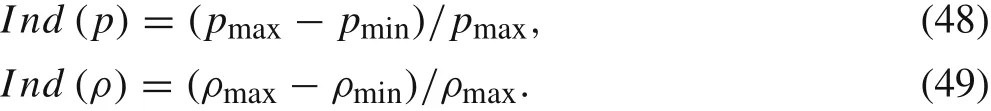
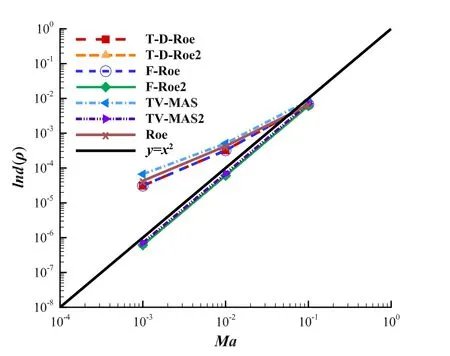
Fig.13 Comparison of density fluctuations computed by different schemes versus in flow Mach number

Figure 12 shows pressure fluctuationsInd(p)versus in flow Mach number for inviscid flows over NACA0012 airfoils.Figure 13 shows corresponding density fluctuationsInd(ρ).From these figures,we can draw the conclusions as follows:

(1)T-D-Roe,F-Roe,and TV-MAS schemes are perfectly consistent with the theoretical asymptotic analysis that the pressure fluctuations scale with the square of the Mach number[7],but fails with the theoretical prediction of density fluctuation.

(2)T-D-Roe2,F-Roe2,and TV-MAS2 schemes are able to obtain the correct scaling of both pressure and density fluctuations.Thus,they can simulate low Mach number flows more concisely.

6 Conclusion

In this work,we have presented a comprehensive study of the enhancement to a low-speed density fluctuation accuracy problem.The asymptotic analysis has shown the relation of density fluctuation with terms of?ρ?a?UΔUin energy equation at low Mach number limit of Roe-type schemes.Applying fix terms in momentum and energy equations at the same time not only can get the expected pressure fluctuations scales of square Mach number and the physical velocity fields,but also can correct the density field into the correct square Mach number scale.An improved TV-MAS scheme,i.e.TVMAS2,is proposed based on these study.Unsteady Gresho vortex flow,double shear-layer,low Mach number flows over an inviscid cylinder and the NACA0012 airfoil show that energy enhancement terms effectively obtain the expected square of Mach number scaling of density fluctuations,which is in good agreement with corresponding asymptotic analysis.In summary,the energy correction is recommended for low-speed enhancement of upwind schemes when using compressible flow solvers.

AcknowledgementsThe authors would like to acknowledge the support for this work provided by the National Natural Science Foundation of China(Grant11402016),and all the authors are grateful to the anonymous reviewers for their constructive comments.

1.Zheng,X.,Zhou,S.,Hou,A.,et al.:Separation control using synthetic vortex generator jets in axial compressor cascade. Acta Mech.Sin.22,521–527(2006)

2.Xu,G.,Jiang,X.,Liu,G.:Delayed detached eddy simulations of fighter aircraft at high angle of attack.Acta Mech.Sin.32,588–603(2016)

3.Zheng,W.,Yan,C.,Liu,H.,et al.:Comparative assessment of SAS and DES turbulence modeling for massively separated flows.Acta Mech.Sin.32,12–21(2016)

4.Fang,J.,Lu,L.-P.,Shao,L.:Heat transport mechanisms of low Mach number turbulent channel flow with spanwise wall oscillation.Acta Mech.Sin.26,391–399(2010)

5.Turkel,E.:Preconditioning techniques in computational fluid dynamics.Annu.Rev.Fluid Mech.31,385–416(1999)

6.Weiss,J.,Smith,W.:Preconditioning applied to variable and constant density flows.AIAA J.33,2050–2057(1995)

7.Guillard,H.,Viozat,C.:On the behaviour of upwind schemes in the low Mach number limit.Comput.Fluids 28,63–86(1999)

8.Roe,P.L.,Pike,J.:Efficient construction and utilisation of approximate Riemann solutions.In:Computing Methods in Applied Sciences and Engineering,VI,North Holland,499–518(1984)

9.Boniface,J.-C.:Rescaling of the Roe scheme in low Mach-number flow regions.J.Comput.Phys.328,177–199(2017)

10.Li,X.-S.,Gu,C.-W.:Mechanism of Roe-type schemes for all-speed flows and its application.Comput.Fluids 86,56–70(2013)

11.Li,X.,Gu,C.:An all-speed Roe-type scheme and its asymptotic analysis of low Mach number behaviour.J.Comput.Phys.227,5144–5159(2008)

12.Li,X.-S.,Gu,C.-W.,Xu,J.-Z.:Development of Roe-type scheme for all-speed flows based on preconditioning method.Comput.Fluids 38,810–817(2009)

13.Thornber,B.J.R.,Drikakis,D.:Numerical dissipation of upwind schemes in low Mach flow.Int.J.Numer.Methods Fluids56,1535–1541(2008)

14.Rieper,F.:A low-Mach number fix for Roe’s approximate Riemann solver.J.Comput.Phys.230,5263–5287(2011)

15.Fillion,P.,Chanoine,A.,Dellacherie,S.,et al.:FLICA-OVAP:a new platform for core thermalhydraulic studies.Nucl.Eng.Des.241,4348–4358(2011)

16.Li,X.-S.:Uniform algorithm for all-speed shock-capturing schemes.Int.J.Comput.Fluid Dyn.28,329–338(2014)

17.Qu,F.,Yan,C.,Sun,D.,et al.:A new Roe-type scheme for all speeds.Comput.Fluids 121,11–25(2015)

18.Sun,D.,Yan,C.,Qu,F.,et al.:A robust flux splitting method with low dissipation for all-speed flows.Int.J.Numer.Methods Fluids 84,3–18(2016)

19.Liou,M.-S.,Steffen,C.J.:A new flux splitting scheme.J.Comput.Phys.107,23–39(1993)

20.Liou,M.S.:A sequel to{AUSM:AUSM}+.J.Computat.Phys.129,364–382(1996)

21.Liou,M.:A sequel to AUSM,part II:AUSM+-up for all speeds.J.Comput.Phys.214,137–170(2006)

22.Shima,E.,Kitamura,K.:Parameter-free simple low-dissipation AUSM-family scheme for all speeds.AIAA J.49,1693–1709(2011)

23.Kitamura,K.,Shima,E.,Fujimoto,K.,et al.:Performance of low dissipation euler fluxes and preconditioned LU-SGS at low speeds.Commun.Comput.Phys.10,90–119(2011)

24.Shima,E.,Kitamura,K.:New approaches for computation of low Mach number flows.Comput.Fluids 85,143–152(2013)

25.Yao,S.B.,Sun,Z.X.,Guo,D.L.,et al.:Numerical study on wake characteristics of high-speed trains.Acta Mech.Sin.29,811–822(2013)

26.Guo,D.,Shang,K.,Zhang,Y.,et al.:Influences of affiliated components and train length on the train wind.Acta Mech.Sin.32,191–205(2016)

27.Xiao,Z.,Fu,S.:Studies of the unsteady supersonic base flows around three after bodies.Acta Mech.Sin.25,471–479(2009)

28.Qu,F.,Yan,C.,Sun,D.:Investigation into the influences of the low speed’s accuracy on the hypersonic heating computations.Int.Commun.Heat Mass Transf.70,53–58(2016)

29.Qu,F.,Sun,D.,Shi,Y.,et al.:Investigation into the influences of the low speeds’accuracy on RANS simulations.In:21st AIAA International Space Planes and Hypersonics Technologies Conference,Xiamen,China,1–14(2017)

30.Zha,G.,Bilgen,E.:Numerical solutions of Euler equations by using a new flux vector splitting scheme.Int.J.Numer.Methods Fluids 17,115–144(1993)

31.Toro,E.F.,Vazquez-Cendon,M.E.:Flux splitting schemes for the Euler equations.Comput.Fluids 70,1–12(2012)

32.Qu,F.,Yan,C.,Yu,J.,et al.:A new flux splitting scheme for the Euler equations.Comput.Fluids 102,203–214(2014)

33.Kapen,P.T.,Tchuen,G.:An extension of the TV-HLL scheme for multi-dimensional compressible flows.Int.J.Comput.Fluid Dyn.29,303–312(2015)

34.Xie,W.,Li,H.,Tian,Z.,et al.:A low diffusion flux splitting method for inviscid compressible flows.Comput.Fluids112,83–93(2015)

35.Toro,E.F.:Riemann Solvers and Numerical Methods for Fluid Dynam ics.Springer,Berlin(1997)

36.Sun,M.,Takayama,K.:An artificially upstream flux vector splitting scheme for the Eulerequations.J.Comput.Phys.189,305–329(2003)

37.Tong,B.G.,Kong,X.Y.,Deng,G.H.:Gas Dynamics,2nd edn.Higher Education Press,Beijing (2012).(in Chinese)

38.Gresho,P.M.:On the theory of semi-implicit projection methods for viscous incompressible flow and its implementation via a finite element method that also introduces a nearly consistent mass matrix.Part 1:theory.Int.J.Numer.Methods Fluids 11,620–687(1990)

39.Gresho,P.M.,Chan,S.T.:On the theory of semi-implicit projection methods for viscous incompressible flow and its implementation via a finite element method that also introduces a nearly consistent mass matrix.Part2:implementation.Int.J.Numer.Methods Fluids 11,621–659(1990)

40.Gottlieb,S.:On high order strong stability preserving Runge–Kutta and multi step time discretizations.J.Sci.Comput.25,105–128(2005)

41.Ishiko,K.,Ohnishi,N.,Sawada,K.:Implicit LES for Two-Dimensional Turbulence Using Shock Capturing Monotone Scheme.In:44th AIAA Aerospace Sciences Meeting and Exhibit,Reno,Nevada,1–12(2006)

42.Kitamura,K.,Hashimoto,A.:Reduced dissipation AUSM-family fluxes:HR-SLAU2 and HR-AUSM+-up for high resolution unsteady flow simulations.Comput.Fluids 126,41–57(2016)

43.Yoon,S.,Jamesont,A.:Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations.AIAA J.26,1025–1026(1988)