Instability waves and low-frequency noise radiation in the subsonic chevron jet

Lingke Ran·Chuangchao Ye·Zhenhua Wan·Haihua Yang·Dejun Sun

1 Introduction

Jet mixing noise is a dominant source of commercial aircraft,the reduction of which can be realized by machining serrations or chevrons into the nozzle lip,resulting in a serrated jet flow.Although the effects of chevrons on jet mixing and noise radiation have been extensively studied,e.g.Refs.[1,2],the influence of chevron parameters and the reduction mechanisms of dominant low-frequency noise at shallow polar angles are still poorly understood,which imposes serious problems on design and optimization of parameters of a chevron nozzle.The main evaluation methods,i.e.the large eddy simulation(LES)and experiments,are expensive in both time and cost.Currently,the design of the chevron nozzle primarily relies on trial and error,which needs faster and more effective evaluation methods for noise radiation.

In the round jet,the dominant low-frequency noise at shallow polar angles is believed to be generated by large-scale coherent structures,which can even be modeled with spatially developing instability waves[3].Through parabolized stability equations(PSE)[4–6]or linearized Euler equation(LEE)[7],the connections among the linear instability waves inside the potential core,near- field hydrodynamic fluctuations,and far- field noise can be constructed in the linear regime.Although the far- field noise calculated with the linear instability wavepackets is not as accurate as LES in subsonic jets,this approach can still capture some noise emission properties.Hence,this approach seems be well suited to quickly evaluate the noise radiation.Recently,this kind of modeling has been attempted to analyze the noise generation mechanisms of the chevron jet.

The temporal stability of chevron jets was firstly analyzed by Gudmundsson and Colonius[8],who found that the chevron jet contains more unstable modes,and the grow th rate of the most unstable mode is lower than that of the round jet based on their base flows.In their subsequent studies[9],spatial instability waves were analyzed,and they found that the peak grow th rates shift to lower frequencies in the chevron jet.Very recently,Uzun et al.[10]and Sinha et al.[11,12]further analyzed the spatial stability of chevron jets at the low frequency and investigated the influence of the chevron parameters.Additionally,Sinha et al.[13]studied the instability waves in the downstream region and found a good match between the instability waves and the hydrodynamic fluctuations in the near field.Therefore,there is no doubt that instability waves play an important role in flow mixing and noise radiation in the chevron jet.

It has long been suspected that noise reduction at low frequencies in the chevron jet is attributed to lower grow th rates of instability waves.But because PSE are not suited to capture the noise emission in the far field,direct connections between the noise emission efficiency and the instability waves have not yet been presented.Also,we note that the growth rates of instability waves in chevron jets are higher than those of round jets in the vicinity of the nozzle in many cases.Moreover,Jeun et al.[14]in their work addressed that the grow th rate of instability wave is not equivalent to the acoustic emission efficiency.Hence,the instability wave,and particularly its efficiency of acoustic emission in the chevron jet,require further investigation.In this paper,in order to have a better understanding of instability waves in the chevron jet,we perform spatial stability analysis at different streamwise locations,and the changes of the unstable modes with respect to streamwise location are examined in detail and are also compared to the round counterpart.For the purpose of evaluating acoustic efficiency of instability waves,LEE is particularly utilized to obtain the linear wave packet in the hydrodynamic region and the beam pattern in the far field.Noise emission efficiency is compared between chevron and round jets.

The rest of the paper is organized as follows.A detailed description of numerical procedures is presented in Sect.2.In Sect.3.1,the instability modes in chevron jets are discussed.In Sect.3.2,the spatial development of instability waves at different streamwise locations is discussed.Also,the comparisons of the eigenvalues between the round and chevron jets are presented.In Sect.3.3,the acoustic efficiency of the instability waves is investigated by LEE.Finally,some conclusions are summarized in Sect.4.

2 Numerical procedures

This section provides the details of the baseflows and the numerical schemes employed in linear stability theory(LST)and LEE.

2.1 Description of the baseflow

For calculations of LST and LEE,the baseflow is required as the input.Here,two jets ejected from nozzles designated SMC000(round nozzle)and SMC001(chevron nozzle)[1]are considered in stability analysis,which has been investigated by experiments[1],Reynolds-averaged Navier–Stokes(RANS)simulations[15],and large eddy simulations[16,17].The jets are operated at identical conditions with Mach numberM a=U j/a∞=0.9,Reynolds numberR e=ρj U j D j/μj=1.35×106,wherea∞,U j,D j,μjare far-field speed of sound,jet exit velocity,diameter,and viscosity,respectively.The non-dimensional in flow total conditionsP0,T0and far-field parametersp∞,T∞based on jet exit pressurep jand temperatureT jare summarized in Table 1.The SST model[18]was selected for RANS simulations.Two grids with different resolution were used to test the grid convergence.The first grid contains about six million grid cells,while the other contains about eight million cells.An in-house,second-order-accurate,finite-volume structured-grid solver in generalized coordinates is employed in RANS simulations,where the spatial derivatives are discretized by Roe scheme and time integrations are advanced by an implicit approximate-factorization.

Figure 1 presents the centerline axial velocity profiles of SMC001,and the iso-contours ofˉu zatz=r0are depicted in the small figure.The two grids give similar profiles implying that current grid resolution is sufficient.Compared with LES and experimental data,the present simulation shows a longer potential core length and faster decay rate beyond the poten-tial core.Similar deviations are also found in round jet case SMC000.Such discrepancy seems to be common in jet simulations by RANS[19,20]because the RANS model cannot simulate the vortex stretching term well[21].Nevertheless,the present results match well with RANS solutions of Engel et al.[15].Also,the profiles of axial velocities with respect tozat the lip-line match well with those of Sinha et al.[13]and Bridges and Brown[1],as illustrated in Fig.2.As the rapid grow th of instability waves occur primarily inside the potential core,the current RANS results are still reliable for the rest of the stability analysis.

Table 1 The flow conditions of the round and chevron jet

Fig.1 Mean axial velocity along the centerline.Dotdashed line denotes line 1st mesh,solid line denotes 2nd mesh,open circle from Bridges and Brown[1],filled square from Engel et al.[15],filled triangle from Xia et al.[16].The small figure shows the iso-contours ofˉu z at z=r0

Fig.2 Mean axial velocityalong the tip-line and valley line.Solid line denotes tip line,dashed line denotes valley line, filled diamond from Sinha et al.[13],open circle from Bridges and Brown[1]

2.2 Linear stability analysis

For linear stability analysis,the compressible Navier–Stokes(N–S)equations in cylinder coordinates(z,r,θ)are linearized for a quasi-parallel mean flow described by

Then the linearized N–S equations become:

where the operator L and K are the functions of base flowˉq,parametersRe,Ma,and Prandtl numberPr.

Different from the round jet,the chevron jet is inhomogeneous in the azimuthal direction.Without invoking any simplifying assumptions,an extremely large matrix must be solved after discretizing the radial and azimuthal direction.A simplified method was proposed in Refs.[9,13],and here we briefly introduce this method.In the current chevron configuration,the chevron jet is periodic in the azimuthal direction,thus the energy is lumarized in azimuthal wave numbers that are integral multiples of the chevron count(C).The base flow variables and the operators can thus be expanded as

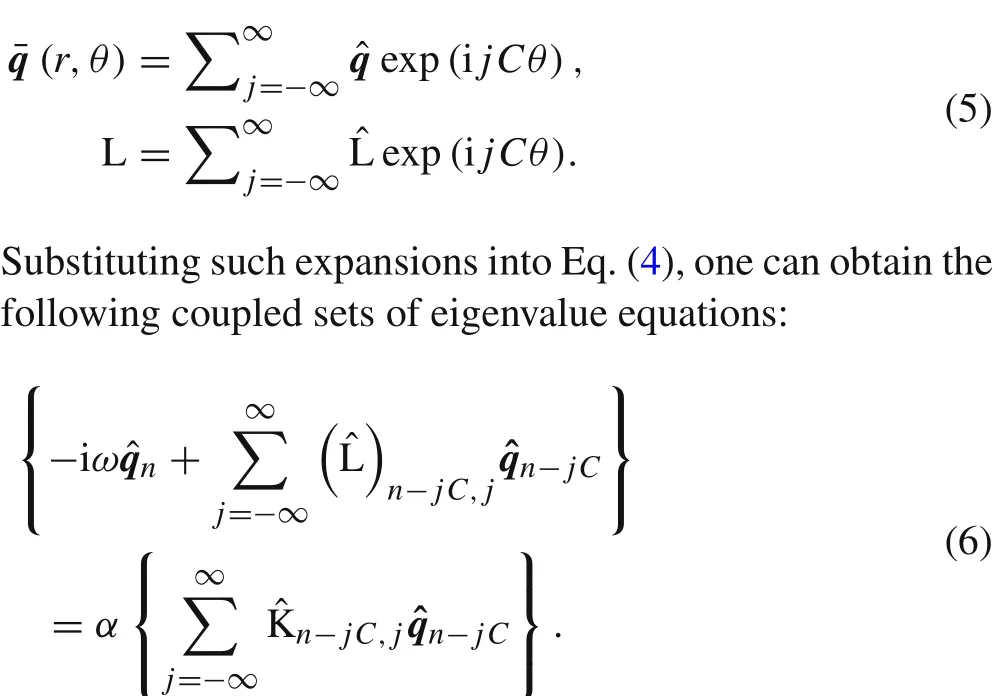
The coupling relation is based onn=M+lC,l∈ [?∞,∞],whereMdenotes the lowest azimuthal mode appearing in one coupling set and also denotes the coupling set.

The coupling equation(6)indicates that to solve the eigenfunction,one must also solve the eigenfunctionwithl∈[?∞,∞].Because of the limitation of the computation ability and the mesh resolution,the coupling equation number and the expansion order in Eq.(5)must be truncated.After testing for convergence,the base flow expansion order is truncated toJ=3,while the eigenfunction coupling number is truncated toN=5.

In the radial direction,boundary conditions are required.At the centerline(r=0),boundary conditions adopted in Ref.[22]are applied to each azimuthal wavenumber.In the far- field(e.g.rmax=10),the fluctuations should decay to 0.For the coupling set,2-D eigenfunction is recovered by:

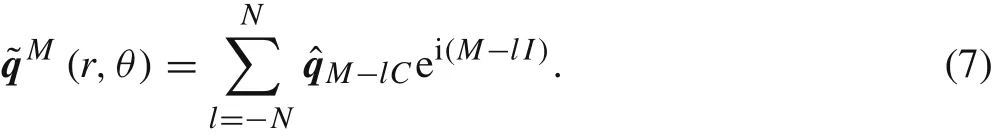
2.3 Linearized Euler equations

Since the Reynolds number of the examined jet flows is high,viscosity does not play a key role in instability wave development.Linearized Euler equations are used to examine the downstream development of the instability modes obtained by linear stability analysis.

2.3.1 Numerical method

The LEE in generalized coordinates are solved using a finite-difference solver,in which spatial derivatives are approximated with a seven-point,fourth-order dispersion relation preserving(DRP)scheme[23].A four-stage optimized explicit Runge–Kutta scheme[24]is used to advance the time solution.A seven-point Padé filter with the free parameterαf=0.40[25]is performed every two time steps at the computational coordinates to eliminate the parasite waves.The radiation and out flow non-reflecting boundary conditions[26,27]are used at the in flow,far- field,and outflow boundary,respectively.An additional buffer zone with a damping term[28,29]?σ(z)(q?qt)is added to the right hand side of LEE to further reduce unphysical reflection at the out flow boundary and to introduce linear instability waves at the in flow.The base flow in the in flow buffer zone is set to be parallel to avoid introducing unphysical pressure waves,and the target solutions are updated at each time step withThe target solutions in out flow buffer zone are set to zero.In this study,as the frequency of fluctuations is constant,Fourier transformation is performed upon instantaneous flow variables when the transient effects become negligible.

2.3.2 Validation

To validate the LEE solver,axial velocity fluctuations for a round jet withMa=0.83 at the Strouhal numbers(St)0.5 are compared with the PSE result[30].The linear solutions have a free amplitude,which can be adjusted using the inlet amplitude.The LEE solutions and PSE solutions are both normalized by their solutions at inlet(z=0).Figure 3a presents the comparison of the fluctuation profiles along the centerline.The magnitude of fluctuation energy has been amplified of two orders between the jet inlet andz≈6r0.Remarkably,in this region,LEE,LST,and PSE results are in good agreement.However,discrepancies between PSE and LEE occur in the downstream region beyond the end of the potential core,which is attributed to truncation errors in linearized PSE because of a strong non-parallel effect.Figure 3b shows the comparison of the radial profile of axial velocity fluctuation at the streamwise location ofz=4r0.The LEE results also agree well with those of PSE,illustrating that the present LEE solver is accurate and robust for calculating the spatial evolution of instability waves in the hydrodynamic region.

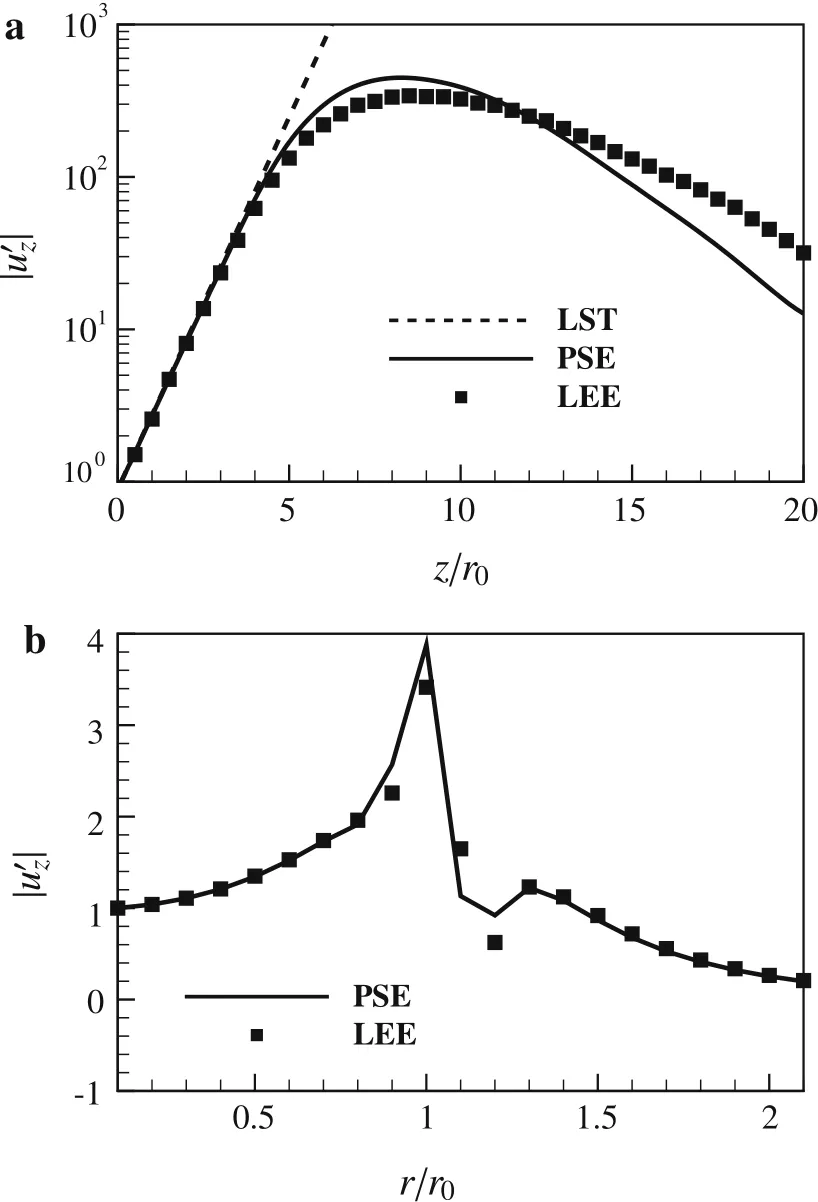
Fig.3 Comparison of axial velocity fluctuationsbetween LEE and PSE.a Axial profiles on the centerline.b Radial profiles at the location of z=4.0r0

3 Results and discussion

In previous studies,it is known that the low-frequency noise at shallow polar angles is mainly contributed by the axisymmetric Fourier mode[31,32]and mainly produced by the axisymmetric coherent structures in the hydrodynamic region[33].Therefore,we focus on studying the instability waves associated with the axisymmetric mode.The spatial structures and their evolution atM=0 azimuthal mode will be elucidated in the following section.

3.1 Multiple instability modes of the chevron jet

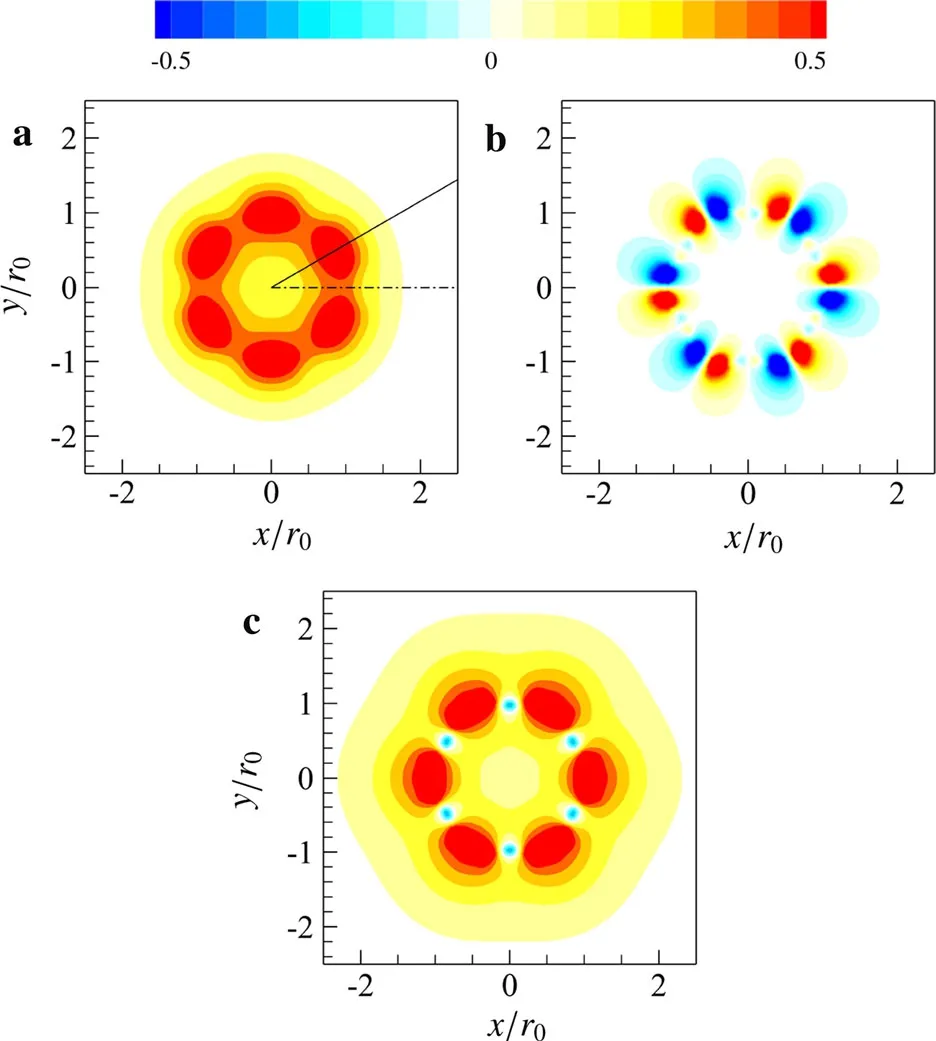
Fig.4 Real part of eigenfunctions of pressure at z=0.5r0,St=0.5,M=0 in the chevron jet.a The first mode.b The second mode.c The third mode.The amplitudes are normalized by their maximum value.Solid line denotes tip-plane,dot dashed line denotes valley-plane

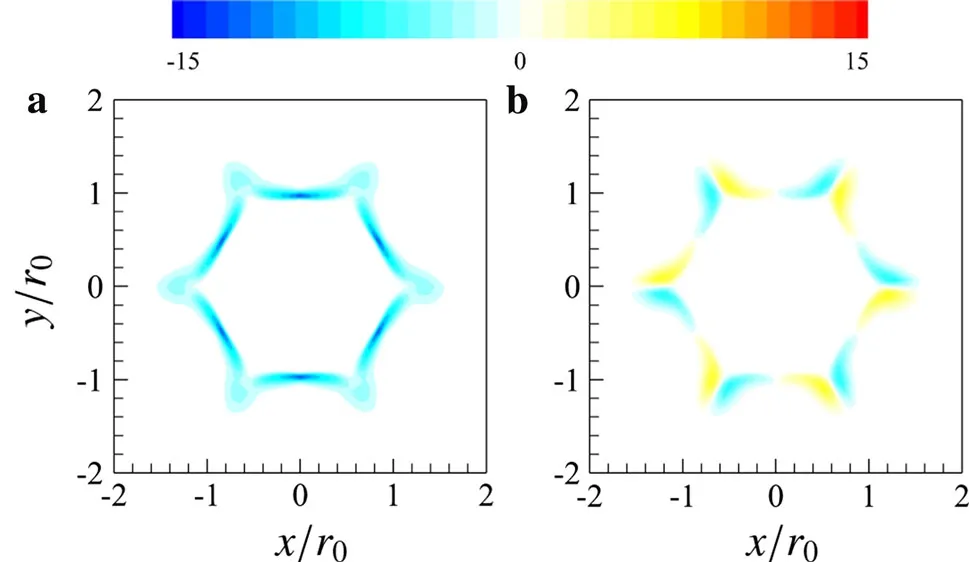
Fig.5 Radial and azimuthal derivatives of axial velocities of base flow in the chevron jet at

Here,we first perform linear stability analysis for present chevron base flow in the vicinity of inlet(z=0.5r0),and find multiple unstable modes at different frequencies,which are also identified at a frequency ofSt=0.35 in Refs.[9,10].For simplicity,we only take the frequencySt=0.5 as an example,in which three types of most unstable modes are found atz=0.5r0,and the real parts of eigenfunctions of pressure are plotted in Fig.4.It is clear that all eigenfunctions present a sixfold periodicity,which is consistent with the sixfold periodicity of the mean flow.It is observed that all peaks of eigenfunction amplitude locate in the shear layer region,suggesting that these instability modes are associated with the shear effects.Nevertheless,unlike the round jet,there are two kinds of shear effect,i.e.the radial shear and azimuthal shear effect,in the chevron jet.To further illustrate this point,we plot the radial and azimuthal derivatives of axial velocities of base flow in Fig.5 for comparison.

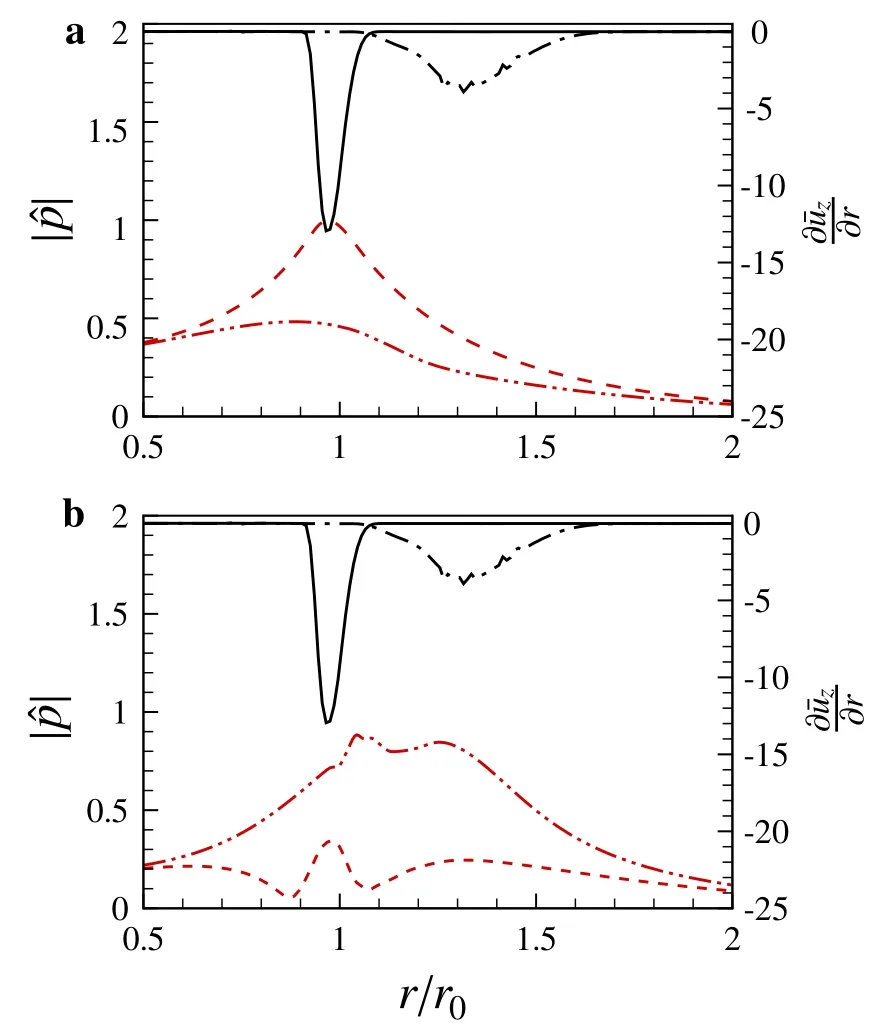
Fig.6 Radial variation of eigenfunction amplitude and radial shear.a The first mode.b The third mode.Solid line at tip plane,dot dashed line? atvalley-plane,dashed lineat tip-plane,two-dotdashed lineat valley-plane

Comparing Figs.4a and 5a,one can see that the peak locations of the eigenfunction amplitudes for the first mode in general match with the locations of peak values ofimplying that the first mode should be correlated with the radial shear effect.Comparing Figs.4b and 5b,the same matching is also observed between the eigenfunction of the second mode and,which suggests that the second mode is mainly associated with the azimuthal shear effect.However,the eigenfunction of the third mode seems to be much more complicated.The peaks of pressure amplitudeappear around the valley plane,but its variation disagrees with the change of azimuthal shearθ.To identify which effect is corresponding to the third mode,the radial and azimuthal variations of the eigenfunction amplitude ofradial shearand azimuthal shearare further plotted in Figs.6 and 7.

In the chevron jet,two azimuthal locations,known as the tip-plane and valley-plane, are of special concern when investigatingthe radial shear effect. The former corresponds to thelocation of maximum radial shear, but minimum azimuthalshear,while the latter is just reversed. Figure 6 shows the pressure amplitude and radial shear as functions ofrat tip-plane and valley-plane for the first and third mode.The eigenfunctions are normalized by their global maximum value.For the first mode,the peak of pressure amplitudeoccurs at tipplane nearr≈r0,and also the radial position of the peak is in accordance with the maximum radial shear of base flow.However,for the third mode,the peak amplitude ofat the tip-plane is decreased significantly although its radial position still matches with that ofwhich is over whelmed by the value ofat the valley-plane.It is worth mentioning that there is a plateau ofwith two peaks in the regionr∈[1,1.3]r0at the valley plane,and one of the peaks corresponds to maximumat the valley-plane.The above results suggest that the third mode is also influenced by,but not determined by,the radial shear effect.

Fig.7 Azimuthal variation of eigenfunction amplitudeand azimuthal sheara The second mode.b The third mode;soliddashed line

In addition,Fig.7 presents the azimuthal variation of amplitude ofand the azimuthal shear1.17r0for the second and third mode,where the azimuthal shear reaches its maximum.For the second mode,it is noted that the variation ofconsists with the variationThis consolidates that the second mode is primarily determined by azimuthal shear effect.As illustrated in Fig.7b,although the variation of amplitude of the third mode generally coincides with the azimuthal shear,it is noted that the amplitude of pressure fluctuation depends on more than the azimuthal shear.Significant deviations are observed around the valley-plane.In other words,from Figs.6 and 7,we speculate that the third mode should be determined by integrated effect of both radial and azimuthal shear.

3.2 Spatial evolution of instability waves

Fig.8 The grow th rates for the chevron jet SMC001 and round jet SMC000.Solid line denotes,the first mode,dashed line denotes the second mode,dotdashed line denotes,the third mode,Dotted line denotes the unstable mode of SMC000.a z=0.5r0.b z=r0.c z=2r0.d z=3r0

Previously,we have identified that there are more unstable modes in the chevron jet.However,the phase speeds of current instability waves are all subsonic,which means that they cannot radiate noise directly.The only way for them to produce noise is to generate spatial pressure wavepackets.From Fig.2,one can see that the base flow spreads rapidly in the radial direction,which greatly alters the development of instability waves.In this section,we are devoted to investigate the spatial development of these instability waves at pertinent frequencies for dominant noise radiation.As addressed in Refs.[3,16,31],the noise radiation of round and chevron jets at shallow polar angles is all dominated by low-frequency components,and thus we here plot the grow th rates of instability waves in the chevron jet SMC001 in the frequency range ofSt=ωDj/Uj=0.2?0.7 at four different streamwise locationsz/r0=0.5,1.0,2.0,3.0.Meanwhile,the grow th rates of round jet SMC000 at the same locations and frequencies are also presented for comparison.

Close to the nozzle atz=0.5r0in Fig.8a,in the current frequency range,the grow th rates(?αi)of the first and third modes of the chevron jet and the most unstable mode of round jet increase with frequency.Clearly,the most amplified frequencies for the first and third mode of the chevron jet are over the present frequency range.It is note worthy that the first mode of the chevron jet has higher growth rates than that of the round jet at all frequencies.Another important finding is that the most unstable mode has a transition betweenSt=0.3?0.4 in the chevron jet.At low frequencies,i.e.St=0.2,0.3,the second mode is the most unstable mode,while at higher frequencies,i.e.St=0.4?0.7,the grow th rates of the second mode are overwhelmed by the first mode.This type of mode transition is also found at downstream locations untilz=2r0.As aforementioned,we have shown that the first and second mode in the chevron jet mainly result from the radial and azimuthal shear effects,respectively.The mode transition demonstrates that the radial shear of base-flow prefers to induce the relatively high frequency instability waves,while the azimuthal shear tends to amplify the low frequency instability waves.

Compared with Fig.8a,the grow th rate of the first mode is decreased greatly due to radial spreading atz=r0.The grow th rates of the first mode are now close to that of the round jet at all frequencies as illustrated in Fig.8b.At this location,the most unstable frequency of the second and third mode of the chevron jet isSt=0.3,0.5,respectively.However,atz=2r0,the most unstable frequencies of the three modes of the chevron jet areSt=0.4,0.2,0.2,as shown in Fig.8c.Basically,aszincreases,the most unstable frequency of all unstable modes decreases in the chevron jet,which is similar to the round jet[6].The decrease of the most unstable frequencies implies that the high frequency modes are mainly amplified near the nozzle in the linear regime,but the low frequency modes will dominate the development of instability waves in a wider downstream region in both the round and chevron jets.Atz=3.0r0in Fig.8d,we are even unable to find unstable modes in the frequency range ofSt=0.4?0.7 in the chevron jet.The first and second modes vanish,thus the third mode becomes the most unstable one atSt=0.2,0.3.Aszfurther increases,we also only find the third mode in the chevron jet,since the inhomogeneity of the base flow in the azimuthal direction also decreases withzrapidly.It is well known that the dominant noise is mainly generated near the end of the potential core in the turbulent jets[3];however,the first and second modes can only be found near the nozzle,which means that they have little direct influence on noise generation.Nevertheless,the grow th rates of the two modes are quite high,so they undoubtedly play important roles in enhancing flow mixing near the nozzle in the chevron jet.

As demonstrated in Fig.8,there would be no high frequency unstable modes asz?3r0.In Fig.9,we further plot the phase speeds(cp=ω/αr)and grow th rates of the most unstable mode in the low frequency range ofSt=0.2?0.4 to show the development of instability waves in a global view.In Fig.9a,b,it is shown that the phase speeds of SMC001 are much lower than those of SMC000 atSt=0.2 and 0.3 asz?2r0,when the most unstable mode of SMC001 is the second mode.From Fig.9,the maximum grow th rates clearly indicate that the low-frequency perturbations(St=0.2?0.4)near the nozzle are more likely amplified in the chevron jet than in the round jet,whereas the reverse is true asz?3r0.Furthermore,it is worth noting that only the low-frequency third mode is unstable asz?3r0,implying that this mode is most likely related with acoustic emission.

3.3 Acoustic efficiency of linear wavepackets

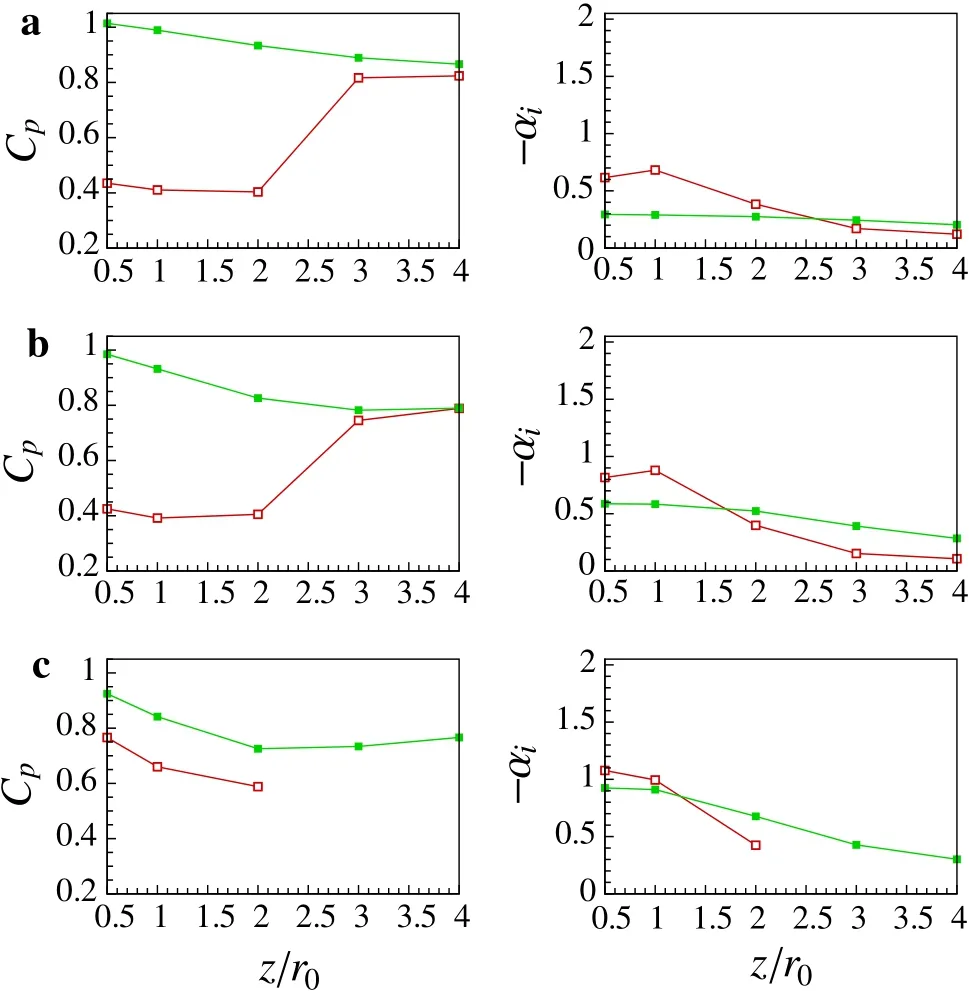
Fig.9 Comparison of the phase speed and grow th rate of the most unstable mode as functions of z between SMC000(solid square)and SMC001(hollow square)at different frequencies.a St=0.2.b St=0.3.c St=0.4

In Sect.3.2,we have identified that the grow th rates and phase speeds of the chevron jet are both lower than that of the round jet asz?2r0.It has been argued that the higher grow th rate and closer to sonic of phase speed,the higher acoustic radiation efficiency of wavepackets[8,10].This has been suggested as one reason of the low-frequency noise reduction in chevron jets.Because of strong azimuthal,inhomogeneous,and non-parallel effect of base flow in the chevron jet,we will employ LEE rather than PSE to verify this argument and to check the global effect of linear wavepacket in the chevron jet on noise radiation.

Since chevron jets mainly reduce low-frequency noise at shallow polarangles[16,17,31],we currently select an instability wave atSt=0.3 as a typical example to investigate the spatial development and acoustic efficiency. As discussed before, although the chevron jet has multiple unstable modes,only the third mode is unstable asz?3.0 and related to acoustic emission.Here,we only consider the third mode as the in flow forcing implemented in the buffer zone during LEE simulations.The instability waves are introduced in the in flow buffer zone with the same method elucidated in Sect.2.3,where the round and chevron jet have the same small forcing amplitude of 10?3.The identical configurations are applied to the round jet case SMC000.A cubic computational domain is used in present simulations.The computational domain size,grid numbers,and mesh sizes are all summarized in Table 2.Fourier transformation is performed upon instantaneous flow variables after the pressure fluctuations are full of the entire computational domain.The following discussions are all based on the Fourier transformed data.

Table 2 The mesh grid and computational domain in LEE simulation

Fig.10 Beam patterns of pressure fluctuations at St=0.3 of the round and chevron jets at the central plane of x=0 computed by LEE.a SMC000.b SMC001

Figure 10 presents the beam patterns of pressure fluctuations obtained by LEE for the round and chevron jets.The grow th and decay for the pressure wavepackets have been clearly demonstrated.Moreover,it is found that the noise is produced from the region near the end of the potential core,and mainly radiates towards shallow polar angles,which are in agreement with experimental and LES results[2,16].In general,the beam patterns produced by the wavepackets in two jets show no qualitative difference.However,if examining the wavepackets in the hydrodynamic region carefully,we can find that the wavepackets in chevron jets saturate a bit earlier and decay faster,and thus emit less noise.Moreover,Fig.11 plots the normalized pressure as a function ofznear the shear layer atr=r0,where the pressure wavepackets are compared for the two jets.It is clearly shown that the peak amplitude of the round jet is three times as large as that of the chevron jet.Additionally,we observe that the pressure amplitudes keep growing beforez?10r0in both jets,in agreement with LST analysis that the low-frequency mode is unstable over a wider region and dominate the developing of instability waves.

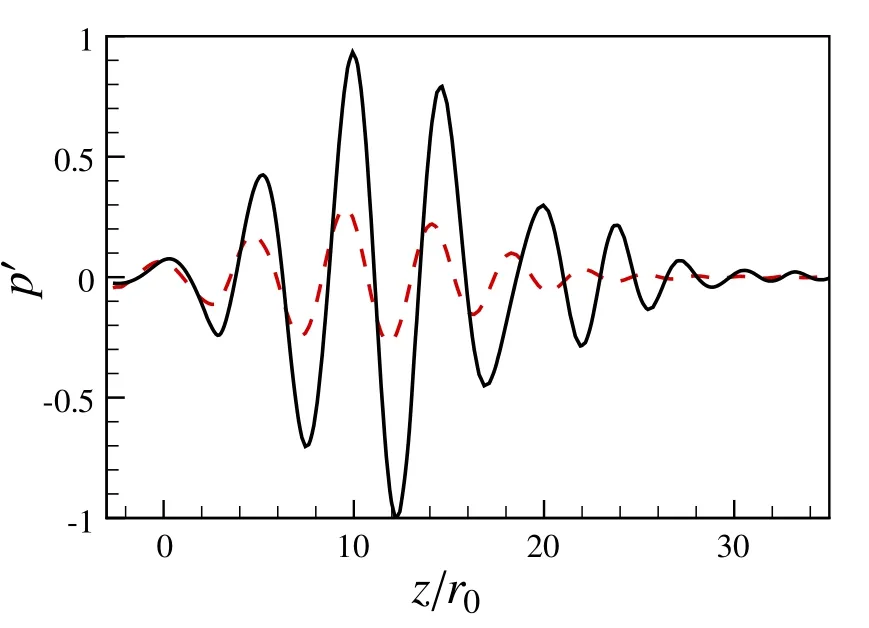
Fig.11 The profiles of normalized pressure as a function of z at the radial position of r=r0,solid line denotes SMC000,dashed line denotes SMC001

In the present case,only the linear wavepacket is considered,and therefore,the base flow can be regarded as an amplifier,which amplifies the fluctuations at in flow and emit far- field noise as output.In order to quantify the acoustic emission of wavepackets,the acoustic efficiency is defined as the ratio of output energy of acoustics and input energy of fluctuations,i.e.

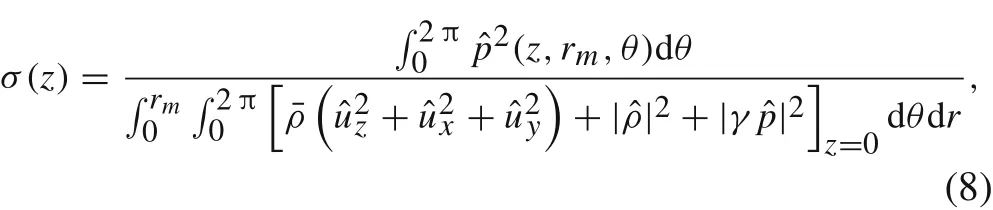
whererm=15 is a selected radial location for measuring far- field noise.

Figure 12 indicates the acoustic efficiency factorσas a function ofz.Apparently,the acoustic emission factor in the chevron jet is one order smaller than that in the round jet.In the linear regime,this point means that if we perturb the flow at inlet with the same energy,the chevron jet will emit much lower noise than the round jet.Here,we should also mention that only the noise radiation in the linear regime is studied with out consideration of nonlinearity or intermittency effect,which is also important in noise generation[3,6].In other words,LEE has been proven to be a robust tool for evaluating the linear wavepackets in the hydrodynamic region and far field noise simultaneously in a convenient way.

4 Conclusions

In this paper,instability waves and the acoustic efficiency of the unstable wavepackets are investigated in the chevron jet,which are compared to those of round jet.The RANS is utilized to obtain the base flow produced by the round and six-chevron nozzles. Spatial stability analysis is performed atdifferent frequencies and streamwise locations, and then LEE is employed to evaluate the wavepacket in the hydrodynamic region and acoustic efficiency.

By performing spatial linear stability analysis,it is observed that there are multiple unstable modes in the chevron jet,while just one unstable mode can be found in the round jet.In the chevron jet,due to the strong azimuthal inhomogeneous of the baseflow,three types of unstable modes are identified in the vicinity of the nozzle,which are closely related with the radial shear effect,azimuthal shear effect,and integrated effect of both,respectively.Near the nozzle,the azimuthal shear effect related modes are more unstable than radial shear effect related modes at low frequencies,while the latter have much more higher grow th rates at high frequencies.By investigating the eigenspectra at different streamwise locations,it is found that the high frequency modes grow much faster than low-frequency modes near the nozzle,while the latter dominates the development of instability waves in the downstream region in both the round and chevron jet because high frequency modes are stabilized quickly as the increase ofz.In general,the most unstable frequency of all chevron modes and round modes in both jets will decrease.Moreover,we find that the first and second unstable modes in the chevron jet can only be identified near the nozzle(z＜3r0),which means that they would mainly be responsible for faster radial spreadings and have less influence on noise generation.Far away from the nozzle,only the low-frequency third mode is unstable in the chevron jet,the grow th rate of which is reduced compared to the round jet.

For a dominant low frequencySt=0.3,linearized Euler equations rather than PSE are solved to obtain the wavepacket in the hydrodynamic region, as well as beam patterns of pressure in the two jets.The comparison of the acoustic emission efficiencyσ(z)demonstrates that the chevron jet has reduced an order of magnitude of the acoustic efficiency in the linear regime.The present results prove that in combination of LST analysis and LEE based on RANS base flows,one can evaluate the acoustic efficiency and beam patterns conveniently at dominant low-frequencies in the linear regime for turbulent jets even with complex geometry at high Reynolds numbers,which will be helpful for quicke valuation of acoustic efficiency when designing the chevron nozzle.It is also important to point out that an efficient evaluation method for noise radiation including nonlinearity and some other turbulent effects is still desired,which is a work in progress.

AcknowledgementsThis work was supported by the National Natural Science Foundation of China(Grants 11232011,11402262,11572314,and 11621202),the Fundamental Research Funds for the Central Universities,and the China Postdoctoral Science Foundation(Grant 2017M 610823).

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecomm ons.org/licenses/by/4.0/),which permits unrestricted use,distribution,and reproduction in any medium,provided you give appropriate credit to the original author(s)and the source,provide a link to the Creative Commons license,and indicate if changes were made.

1.Bridges,J.,Brown,C.:Parametric testing of chevrons on single flow hot jets.AIAA Paper,2004–2824(2004)

2.Callender,B.,Gutmark,E.J.,Martens,S.:Far- field acoustic investigation into chevron nozzle mechanisms and trends.AIAA J.43,87–95(2005)

3.Jordan,P.,Colonius,T.:Wavepackets and turbulent jetnoise.Annu.Rev.Fluid Mech.45,173–195(2013)

4.Sinha,A.,Rodr?guez,D.,Brs,G.A.,et al.:Wavepacket models for supersonic jet noise.J.Fluid Mech.742,71–95(2014)

5.Colonius,T.,Samanta,A.,Gudmundsson,K.:Parabolized stability equation models of large-scale jet mixing noise.Procedia Eng.6,64–73(2010)

6.Wan,Z.H.,Yang,H.H.,Zhang,X.C.,et al.:Instability waves and aerodynamic noise in a subsonic transitional turbulent jet.Eur.J.Mech.B Fluids 57,192–203(2016)

7.Baqui,Y.B.,Agarwal,A.,Cavalieri,A.V.G.,et al.:A coherence matched linear source mechanism for subsonic jet noise.J.Fluid Mech.776,235–267(2015)

8.Gudmundsson,K.,Colonius,T.:Linear stability analysis of chevron jet profiles.In:APS Division of Fluid Dynamics Meeting,Salt Lake City,Utah,497–504(2007)

9.Gudmundsson,K.,Colonius,T.:Spatial stability analysis of chevron jet profiles.In:13th AIAA/CEAS Aeroacoustics Conference(28th AIAA Aeroacoustics Conference),Reston,Virigina,1–14(2007)

10.Uzun,A.,Alvi,F.S.,Colonius,T.,et al.:Spatial stability analysis of subsonic jets modified for low-frequency noise reduction.AIAA J.53,2335–2358(2015)

Fig.12 The profiles of relative pressure amplitude σ(z)as a function of z ata radial position of r=15r0,solid linedenotes SMC000,dashed line denotes SMC001

11.Sinha,A.,Colonius,T.:Linear stability implications of mean flow variations in turbulent jets issuing from serrated nozzles.In:21st AIAA/CEAS Aeroacoustics Conference,Reston,Virginia,1–11(2015)

12.Sinha,A.,Rajagopalan,A.,Singla,S.:Linear stability implications of chevron geometry modifications for turbulent jets.In:22nd AIAA/CEAS Aeroacoustics Conference,Reston,Virginia,1–10(2016)

13.Sinha,A.,Gudmundsson,K.,Xia,H.,et al.:Parabolized stability analysis of jets from serrated nozzles.J.Fluid Mech.789,36–63(2016)

14.Jeun,J.,Nichols,J.W.,Jovanovic,M.R.:Input-output analysis of high-speed axisymmetric isothermal jet noise.Phys.Fluids 28,564–587(2016)

15.Engel,R.C.,Silva,C.R.I.,et al.:Application of RANS-based method to predict acoustic noise of chevron nozzles.Appl.Acoust.79,153–163(2014)

16.Xia,H.,Tucker,P.G.,Eastwood,S.:Large-eddy simulations of chevron jet flows with noise predictions.Int.J.Heat Fluid Flow 30,1067–1079(2009)

17.Xia,H.:Turbulent jet characteristics for axisymmetric and serrated nozzles.Comput.Fluids 110,189–197(2015)

18.Menter,F.,Rumsey,C.:Assessment of two-equation turbulence models for transonic flows.AIAA Paper,94–2343(1994)

19.Birch,S.,Lyubimov,D.,Maslov,V.,et al.:ARANS based jet noise prediction procedure.In:13th AIAA/CEAS Aeroacoustics Conference(28th AIAA Aeroacoustics Conference),Reston,Virigina,1–15(2007)

20.Engblom,W.,Khavaran,A.,Bridges,J.:Numerical prediction of chevron nozzle noise reduction using wind-MGBK methodology.In:10th AIAA/CEAS Aeroacoustics Conference,Reston,Virigina,1–19(2004)

21.Tam,C.K.,Ganesan,A.:Modified kappa-epsilon turbulence model for calculating hot jet mean flows and noise.AIAA J.42,26–34(2004)

22.Batchelor,G.K.,Gill,A.E.:Analysis of the stability of axisymmetric jets.J.Fluid Mech.14,529–551(1962)

23.Tam,C.K.W.,Webb,J.C.:Dispersion-relation-preserving finite difference schemes for computational acoustics.J.Comput.Phys.107,262–281(1993)

24.Hu,F.Q.,Hussaini,M.Y.,Manthey,J.L.:Low-dissipation and low dispersion Runge–Kutta schemes for computational acoustics.J.Comput.Phys.124,177–191(1996)

25.Gaitonde,D.V.,Visbal,M.R.:High-order schemes for navierstokes equations:algorithm and implementation into FDL3DI.Technical report,DTIC Document,Air Force Research Laboratary W right-Patterson AFB(Ohio)(1998)

26.Bogey,C.,Bailly,C.:Three-dimensional non reflective boundary conditions for acoustic simulations:far- field formulation and validation test cases.Acta Acust.88,463–471(2002)

27.Tam,C.K.W.:Computational aeroacoustics—issues and methods.AIAA J.33,1788–1796(1995)

28.Wan,Z.H.,Zhou,L.,Yang,H.-H.,et al.:Large eddy simulation of flow development and noise generation of free and swirling jets.Phys.Fluids 25,564–587(2013)

29.Bodony,D.J.,Jambunathan,R.:On the linearity of the quieting of high speed mixing layers by heating.AIAA Paper,2012–2119(2013)

30.Yang,H.,Zhang,X.,Ran,L.,et al.:Coherent structures and wavepackets in subsonic transitional turbulent jets.Acta Mech.Sin.33,10–19(2017)

31.Ran,L.K.,Yang,H.H.,Zhang,X.C.,et al.:Investigation of flow development and noise generation of free and chevron jet.Appl.Math.Mech.37,1225–1271(2016)

32.Cavalieri,A.V.G.,Daviller,G.,Com te,P.,et al.:Using large eddy simulation to explore sound-source mechanisms in jets.J.Sound Vib.330,4098–4113(2011)

33.Cavalieri,A.V.G.,Rodr?guez,D.,Jordan,P.,et al.:Wavepackets in the velocity field of turbulent jets.J.Fluid Mech.730,559–592(2013)