A NOTE ON MALMQUIST-YOSIDA TYPE THEOREM OF HIGHER ORDER ALGEBRAIC DIFFERENTIAL EQUATIONS?
Jianjun ZHANG(張建軍)
Mathematics and Information Technology School,Jiangsu Second Normal University,Nanjing 210013,China
E-mail:zhangjianjun1982@163.com
Liangwen LIAO(廖良文)
Department of Mathematics,Nanjing University,Nanjing 210093,China
E-mail:maliao@nju.edu.cn
1 Introduction and Main Results
Let f(z)be a function meromorphic in the complex plane C.We assume that the reader is familiar with the standard notations and results in Nevanlinna’s value distribution theory of meromorphic functions such as the characteristic function T(r,f),proximity function m(r,f),counting function N(r,f),the first and second main theorems etc.;see,for example,[1,4,9].The notation S(r,f)denotes any quantity that satisfies the condition:S(r,f)=o(T(r,f))as r→∞possibly outside an exceptional set of r of finite linear measure.
In general,a nonlinear algebraic differential equation is of the form

where P is a polynomial in f and its derivatives with meromorphic coefficients.One can rewrite equation(1.1)as
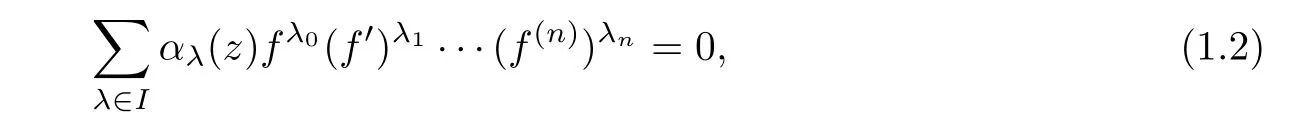
where I is a finite set of multi-indices(λ0,λ1,···,λn)= λ and αλ(z)is a meromorphic function.We define a differential monomial in f as
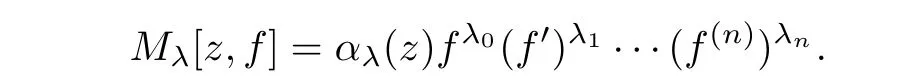
The degree γMλand the weight ΓMλof Mλare defined by
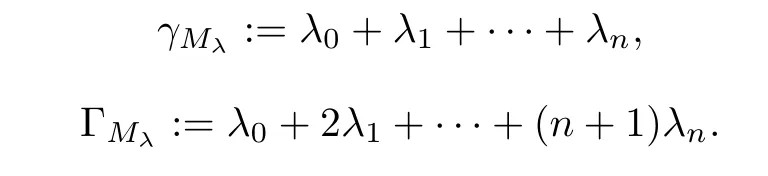
Thus,the left hand side of equation(1.2)can be expressed as a finite sum of differential monomials,which will be called a differential polynomial in f,that is,
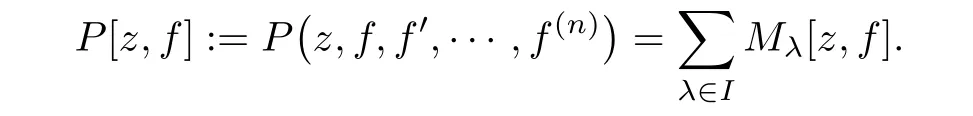
The degree γPand the weight ΓPof P are defined by
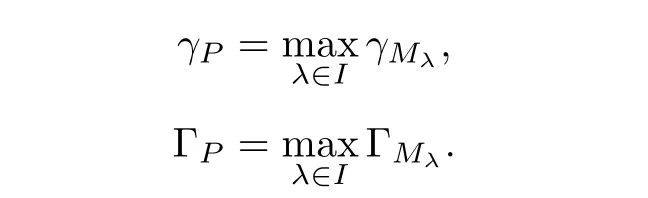
We say that a meromorphic solution f of equation(1.2)is admissible if T(r,αλ(z))=S(r,f)holds for all λ∈I.
For the first-order algebraic differential equations,Malmquist[10]proved the following famous theorem in 1913.
Theorem 1.1Let R(z,f)be birational function.If a differential equation of the form
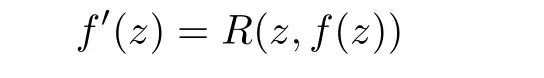
admits a transcendental meromorphic solution,then the equation can be reduced into a Riccati differential equation
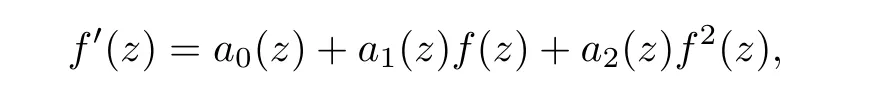
where ai(z)(i=0,1,2)are rational functions.
The proof of Theorem 1.1 was independent of the Nevanlinna theory at the outset.In 1933,Yosida[14]proved the Malmquist’s theorem using the Nevanlinna theory.In 1970s,Laine[8],Yang[13],and Hille[7]gave a generalization of Theorem 1.1 with the coefficients of R(z,f)being meromorphic functions.Steinmetz[12]extended Malmquist’s theorem to the following result.
Theorem 1.2Let R(z,f)be birational function.If the following differential equation
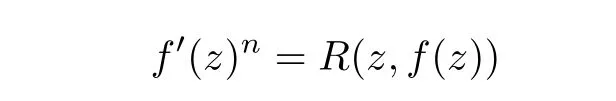
admits a transcendental meromorphic solution,then the differential equation can be reduced into
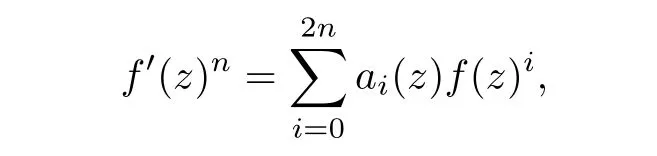
where ai(z)(i=0,1,···,2n)are rational functions and at least one of them does not vanish.
Theorem 1.2 was finally extended to the case of R(z,f)rational with meromorphic coefficients by Rieth[11]and He-Laine[5].In 1980,Gackstatter and Laine[2]gave a generalized result of Theorem 1.1 and Theorem 1.2.
Theorem 1.3If the algebraic differential equation
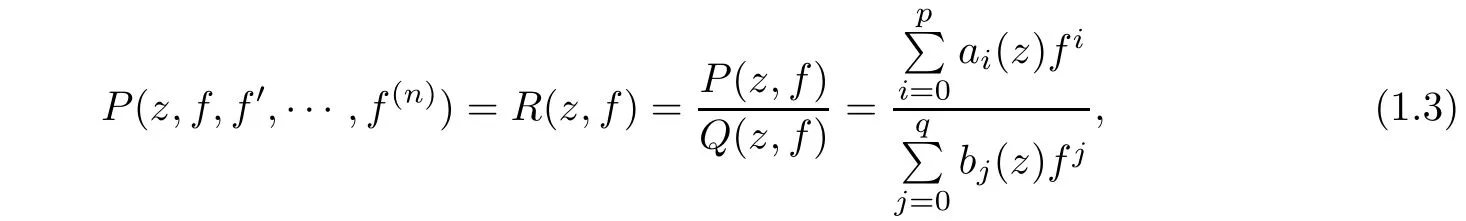
where P(z,f,f′···,f(n))is a differential polynomial in f with meromorphic coefficients and ai(z)(i=0,1,···,p)and bj(z)(j=0,1,···,q)are meromorphic functions,possesses an admissible meromorphic solution,then R(z,f)is reduced to a polynomial in f of degree≤ΓP.
The proof of Theorem 1.3 given by Gackstatter and Laine[2]strongly relies on Valiron deficient values.Steinmetz[12]constructed a number of auxiliary functions in his proof on Theorem 1.3.In this article,we will give a more simple proof of Theorem 1.3.From our proof and the fact that the counting function N(r,f)of entire function vanishes identically.We can obtain the following result easily.
Corollary 1.4If the algebraic differential equation
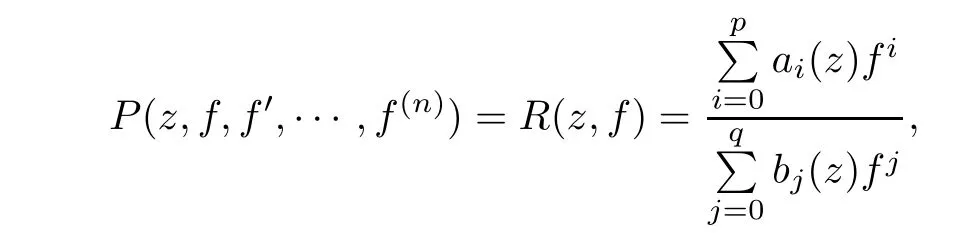
where P(z,f,f′···,f(n))is a differential polynomial in f with meromorphic coefficients and ai(z)(i=0,1,···,p)and bj(z)(j=0,1,···,q)are meromorphic functions,possesses an admissible entire solution,then R(z,f)is reduced to a polynomial in f of degree≤ γP.
The following two examples show that the estimations in Theorem 1.3 and Corollary 1.4 are sharp.
Example 1.5It is easy to check that f(z)=tanz solves the following differential equation
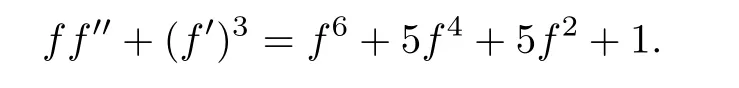
Example 1.6It is easy to check that f(z)=zezsolves the following differential equation
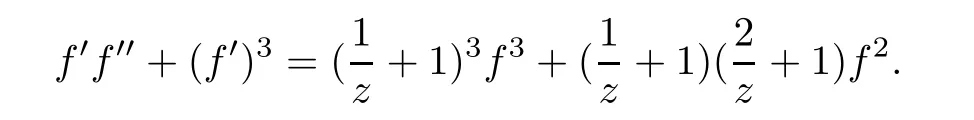
In Example 1.5,we have ΓP=6 and in Example 1.6,we have γP=3.
2 Some Lemmas
The following lemmas will be needed in the proof of our result.
Lemma 2.1(see[9]) Let f(z)be a meromorphic function.Then,for all irreducible rational functions in f,we have
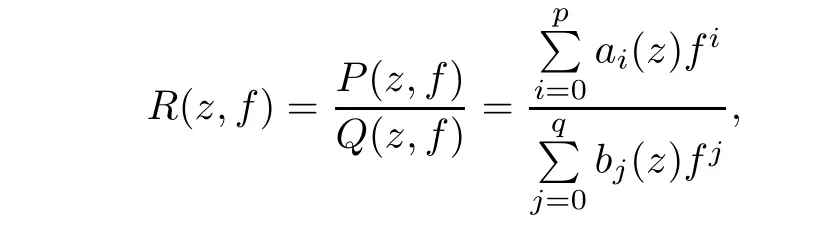
such that the meromorphic coefficients ai(z),bj(z)satisfy
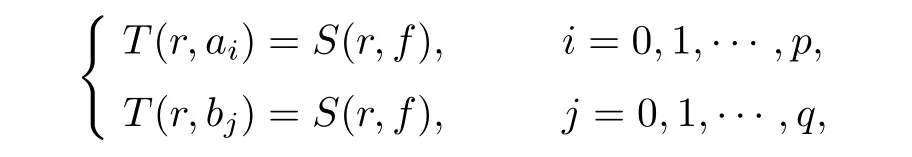
we have
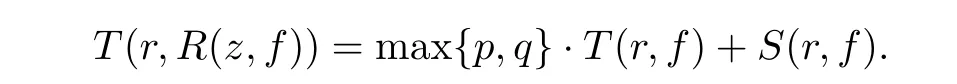
Lemma 2.2(see[6,9]) Let f(z)be a transcendental meromorphic solution of
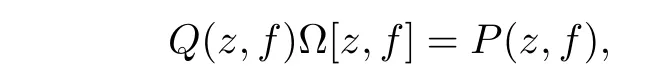
where
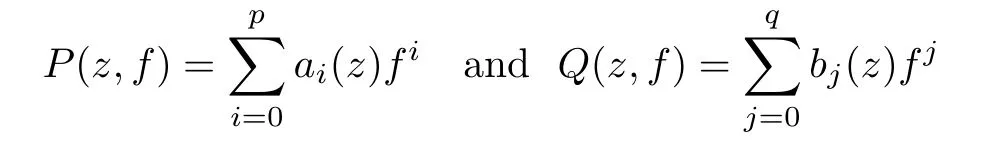
are polynomials in f with meromorphic coefficients such that
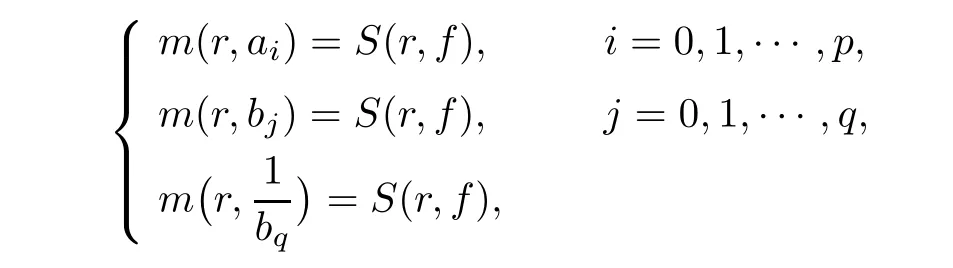
and ?[z,f]is a polynomial in f and its derivatives with meromorphic coefficients αλ,λ ∈ I,such that
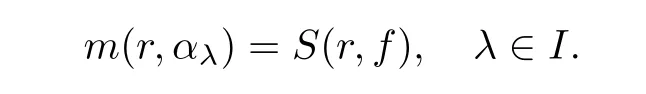
If p≤q,then
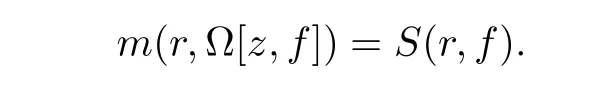
From the proof of Lemma 3.1 in[3],we have the following result.
Lemma 2.3Let f be a meromorphic function with N(r,f)/=S(r,f)(counting multiplicities)and let the coefficients ai(i=1,2,···,n)of R(z,f)be small meromorphic functions with respect to f.Let
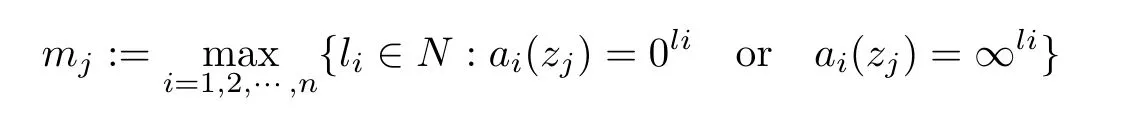
be the maximal order of zeros and poles of the functions aiat zj,where ai(zj)=0limeans that zjis a zero of ai(z)with multiplicity li,ai(zj)=∞limeans that zjis a pole of ai(z)with multiplicity li.Then,for any ε> 0,the counting function of points zjsuch that
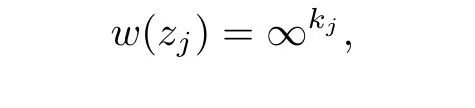
where mj≥ εkj,is at most S(r,f).
3 A New Proof of Theorem 1.3
ProofWe assume that f(z)is an admissible meromorphic solution of equation(1.3).Define
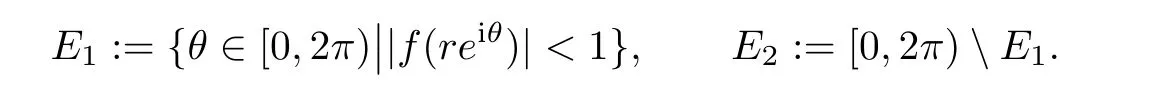
We may consider the proximity function m(r,P[z,f])in two parts:
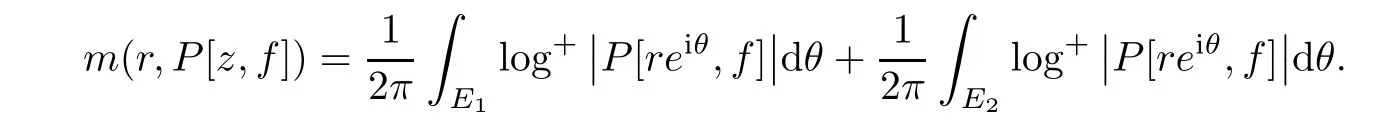
If z∈E1,then we have
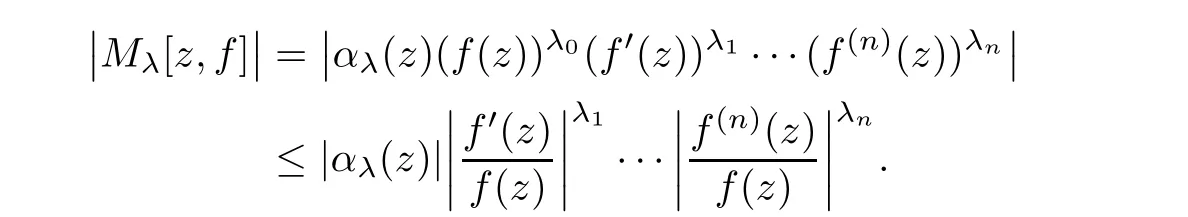
Therefore,by the logarithmic derivative Lemma,we obtain
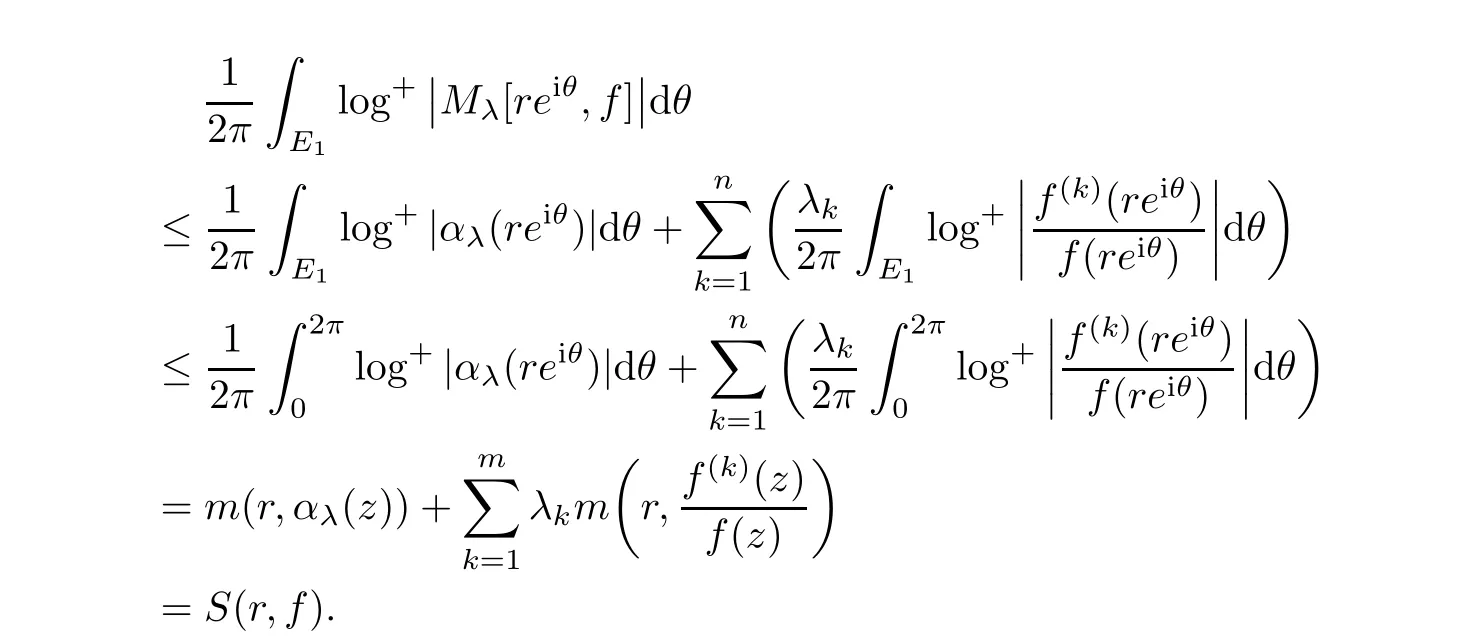
Hence,
If z ∈ E2,as λ0+ λ1+ ···+ λn≤ γPfor any all λ =(λ0,λ1,···,λn)∈ I,we have
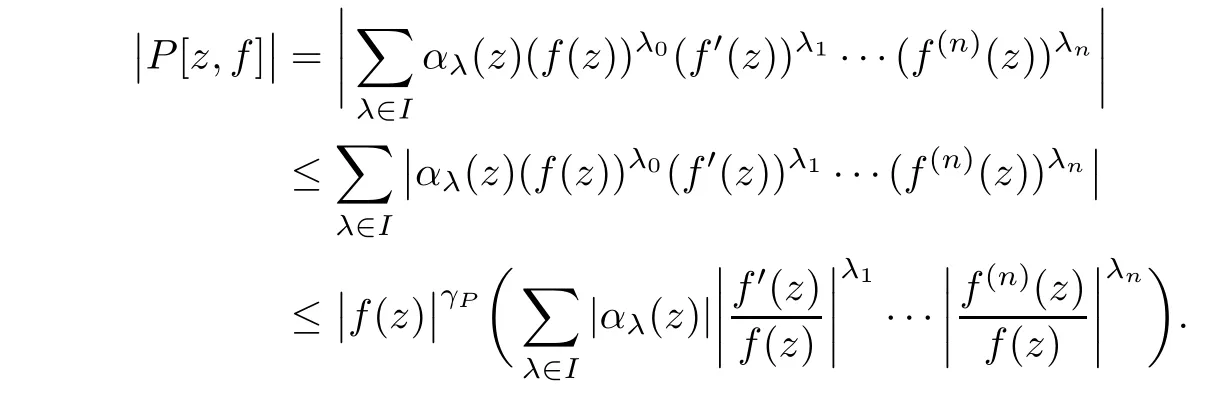
Thus,for some constant K>0,we have
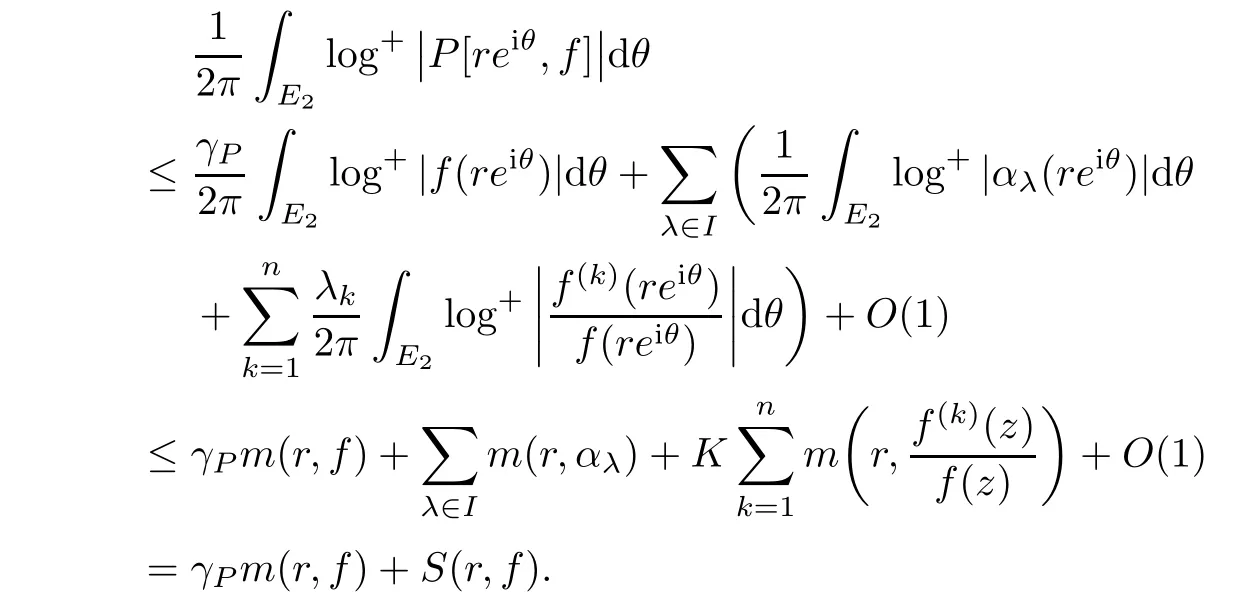
Combining(3.1)and the above inequality,we obtain
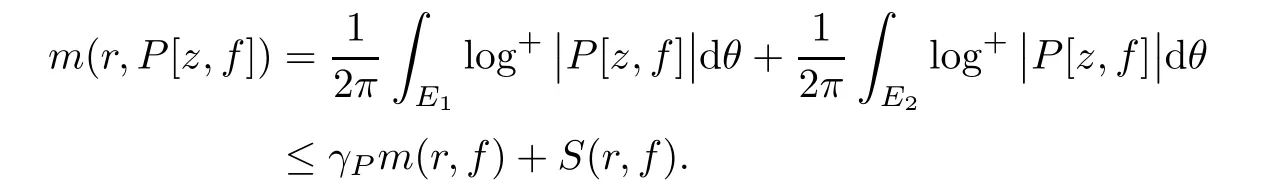
Next,we will give an estimation of counting function N(r,P[z,f])of poles of P[z,f].Obviously,each pole of function P[z,f]comes from the poles of functions f(z)or αλ(z)(λ ∈ I)in(1.3).Namely,each pole of function R(z,f)comes from the poles of functions f(z)or αλ(z)(λ∈I).Without loss of generality,we may assume that all poles of R(z,f)come from the poles of f(z).
Let nj(z0)be multiplicity of zero or pole of aj(z)at z0,(j=0,1,···,p).If z0is not a zero and pole of aj(z),then nj(z0)=0.Let mj(z0)be multiplicity of zero or pole of bj(z)at z0,(j=0,1,···,q).Denote M(z0)=max{n0(z0),···,np(z0),m0(z0),···,mq(z0)}.If z0is a pole with multiplicity k of f(z)and a pole of R(z,f),then from equation(1.3),z0is a pole of R(z,f)with multiplicity at most kΓP.Let
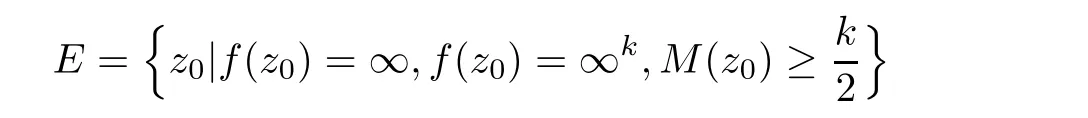
and N(r,E)denote the counting function of the poles(considering the multiplicity)of R(z,f)in E.Then from Lemma 2.3,we have N(r,E)=S(r,f).If M(z0)<,and then z0must be a pole of Q(z,f).At this case,z0is an analytic point of R(z,f)or a pole of R(z,f)with multiplicity not greater than k max{p?q,0}+M(z0).Hence,we have
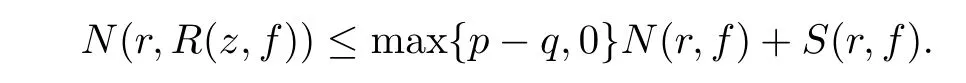
Namely,
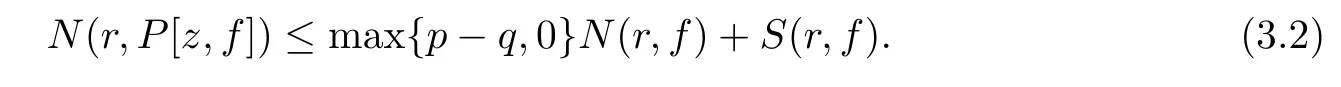
Therefore,
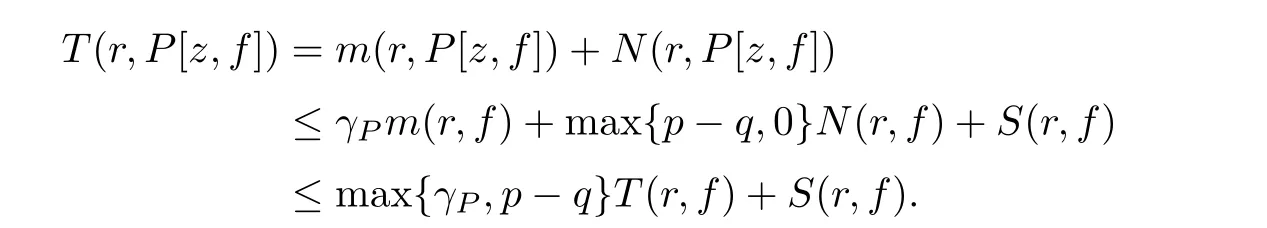
By Lemma 2.1 and the above inequality,we get
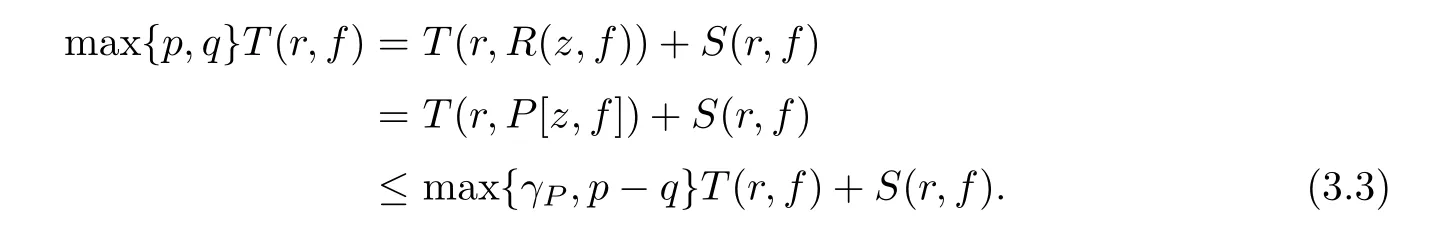
On the other hand,because all the poles of function P[z,f]come from the poles of function f(z)and its coefficients αλ(z)(λ ∈ I),and every pole of multiplicity k of f(z),possibly except the pole of αλ(z),is a pole with multiplicity at mostthus
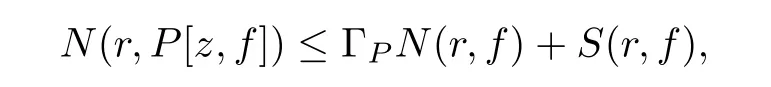
we also have
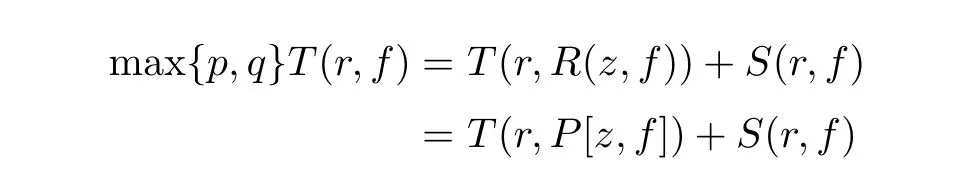
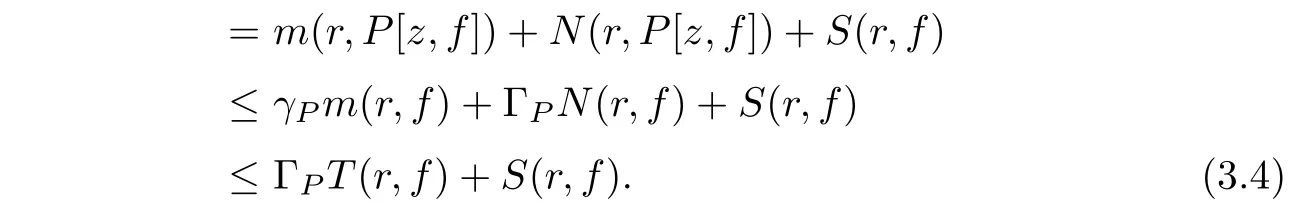
Hence,we obtain max{p,q}≤ΓP.
Now,we are going to show that p>q.If p≤q,then by Lemma 2.2,we have m(r,P[z,f])=S(r,f).According to(3.2),N(r,P[z,f])=S(r,f)when p≤q.Thus,we obtain
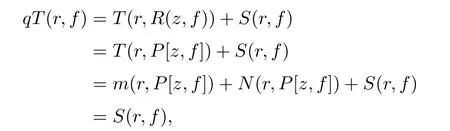
which implies that p=q=0,so this is impossible.Thus,we have p>q.
Next,we shall deal with two cases.
Case 1p?q≥ΓP.Then by(3.4),we have q≤p?ΓP≤ΓP?ΓP=0,thus q=0.
Case 2p?q< ΓP.Select now γ ∈ C,such that
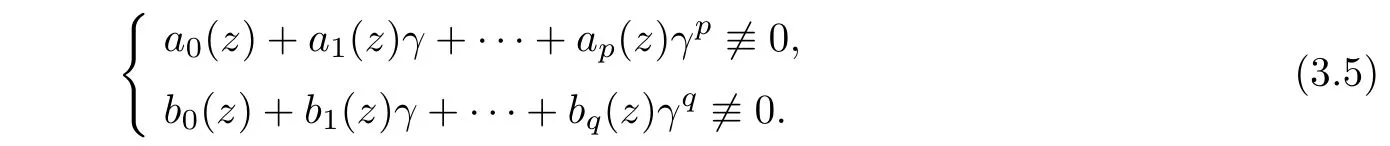
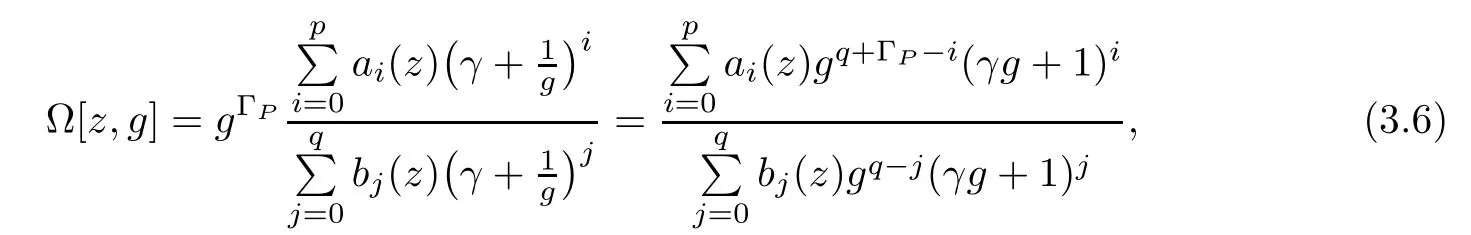
where ?[z,g]is a differential polynomial in g and its derivatives with meromorphic coefficients,and
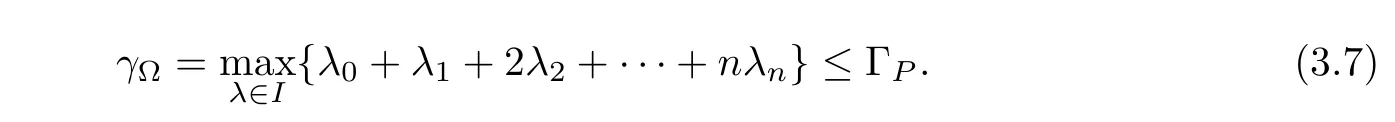
Obviously,g is an admissible solution of equation(3.6).By(3.5),we see that the nominator of(3.6)is of degree q+ΓP,while the denominator is of degree q.Clearly,the right-hand side of(3.6)is irreducible,otherwise,R(z,f)would be reducible.By the similar argument as in inequality(3.3),we have
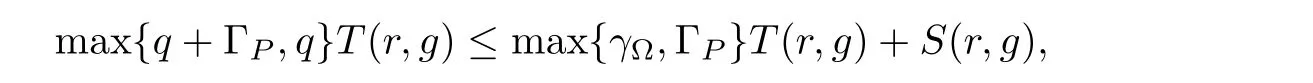
As γ?≤ ΓPby(3.7),we have q+ ΓP≤ ΓP,thus q=0.
Therefore,R(z,f)is reduced to a polynomial in f with meromorphic coefficients.We denote the degree of R(z,f)by d:=degfR(z,f).By the similar discussion as in(3.4),we obtain
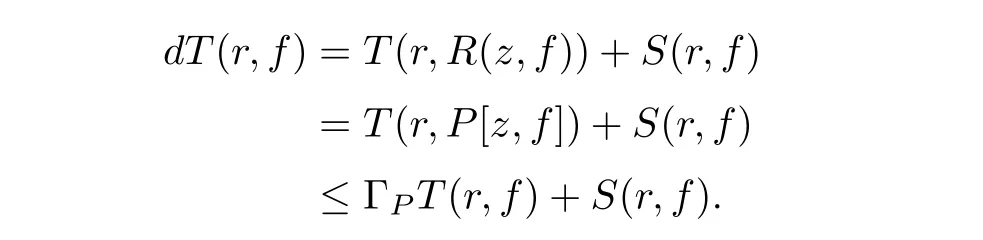
Therefore,we have d≤ ΓP.Thus,the proof of Theorem 1.3 is completed.
[1]Cherry W,Ye Z.Nevanlinna’s Theory of Value Distribution.Berlin:Springer-Verlag,2001
[2]Gackstatter F,Laine I.Zur theorie der gew?hnlichen differentialgleichungen im komplexen.Ann Polon Math,1980,38:259–287
[3]Halburd R G,Korhonen R J.Finite order meromorphic solutions and the discrete Painlevé equations.Proc London Math Soc,2007,94(3):443–474
[4]Hayman W K.Meromorphic Functions.Oxford:Clarendon Press,1964
[5]He Y Z,Laine I.The Hayman-Miles theorem and the differential equation(y′)n=R(z,y).Analysis,1990,10:387–396
[6]He Y Z,Xiao X Z.Algebroid functions and ordinary differential equations.Beijing:Science Press,1988
[7]Hille E.On some generalizations of the Malmquist theorem.Math Scand,1976,39:59–79
[8]Laine I.On the behaviour of the solutions of some first order differential equations.Ann Acad Sci Fenn Ser A,1971,497:1–26
[9]Laine I.Nevanlinna theory and complex differential equations.Berlin:Walter de Gruyter,1993
[10]Malmquist J.Sur les fonctionsà un nombre fini des branches définies par les équations différentielles du premier ordre.Acta Math,1913,36:297–343
[11]Rieth J V.Untersuchungen gewisser Klassen gew?hnlicher Differentialgleichungen erster und zweiter Ordnung im Komplexen[D].Aachen,1986
[12]Steinmetz N.Eigenschaften eindeutiger L?sungen gew?hnlicher Differentialgleichungen im Komplexen[D].Karlsruhe,1978
[13]Yang C C.A note on Malmquist’s theorem on first order differential equations.Yokohama Math J,1972,20:115–123
[14]Yosida K.A generalization of Malmquist’s theorem.J Math,1993,9:253–256
——和張建軍主任的《畫堂春·吟秋》
 Acta Mathematica Scientia(English Series)2018年2期
Acta Mathematica Scientia(English Series)2018年2期
- Acta Mathematica Scientia(English Series)的其它文章
- EXISTENCE AND BLOW-UP BEHAVIOR OF CONSTRAINED MINIMIZERS FOR SCHR?DINGER-POISSON-SLATER SYSTEM?
- STABILITY AND BIFURCATION ANALYSIS OF ADELAYED INNOVATION DIFFUSION MODEL?
- ON A CLASS OF DOUGLAS FINSLER METRICS?
- SOLUTIONS TO BSDES DRIVEN BY BOTH FRACTIONAL BROWNIAN MOTIONS AND THE UNDERLYING STANDARD BROWNIAN MOTIONS?
- LIOUVILLE THEOREM FOR CHOQUARD EQUATION WITH FINITE MORSE INDICES?
- THE GLOBAL ATTRACTOR FOR A VISCOUS WEAKLY DISSIPATIVE GENERALIZED TWO-COMPONENT μ-HUNTER-SAXTON SYSTEM?
