THE GLOBAL ATTRACTOR FOR A VISCOUS WEAKLY DISSIPATIVE GENERALIZED TWO-COMPONENT μ-HUNTER-SAXTON SYSTEM?

Lei ZHANG(張磊)Bin LIU(劉斌)

School of Mathematics and Statistics,Hubei Key Laboratory of Engineering Modeling and Scientific Computing,Huazhong University of Science and Technology,Wuhan 430074,China

E-mail:lzhang890701@163.com;binliu@mail.hust.edu.cn

1 Introduction

The μ-Hunter-Saxton(μHS)equation

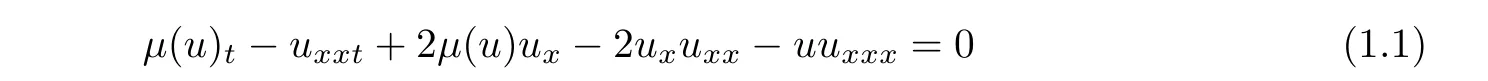
was first introduced by Khesin et al[34]to model the evolution of rotators in liquid crystals with self-interaction and external magnetic field,and the unknown function u(x,t)is a timedependent function on the circle S=R/Z andμ(u)=RSudx denotes its mean.With the interactions of rotators and external magnetic field,it is shown[34]that the(μHS)equation is a generalization of the rotator equation.In[34],the(μHS)equation is also constructed to describe the geodesic flow on Ds(S)with the right-invariant metric given at the identity by the following inner product

Moreover,in[34,38],it is proved that the(μHS)equation is bi-Hamiltonian and also admits both periodic one-peakon solution and the multi-peakons.The(μHS)equation(1.1),called μ-Camassa-Holm equation[25],is closely related to the following celebrated Camassa-Holm(CH)shallow water wave equation,

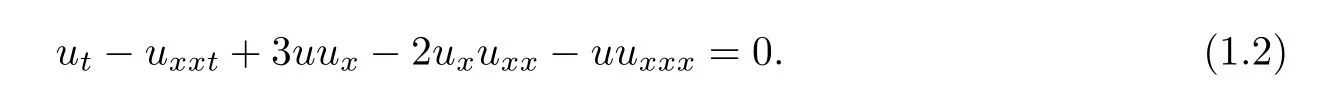
The(CH)equation was originally introduced to model the unidirectional propagation of shallow water waves over a flat bottom[6,32].Moreover,the(CH)equation is also a model for the propagation of axially symmetric waves in hyperelastic rods[11,16].It is shown that the(CH)equation is completely integrable[3,5,6,12–14]and also has a bi-Hamiltonian structure[19,39].The(CH)equation gives rise to geodesic flow of a certain invariant metric on the Bott-Virasoro group[33].Its solitary waves are peaked[7].The peaked solitons are orbital stable[10],and the explicit interaction of the peaked solitons is given in[4].Moreover,the(μHS)equation can be viewed as a generalized equation lying mid-way between the(CH)equation and the Hunter-Saxton(HS)equation given by

The(HS)equation was first introduced for rotators in liquid crystals[28],which describes the propagation of weakly nonlinear orientation waves in a massive nematic liquid crystal.In[48],it is shown that the orientation of the molecules can also be characterized by the vectors field(cosu(x,t),sinu(x,t)).The(HS)equation can be regarded as the limit of the(CH)equation arising in a different physical context[29].Similar to the(CH)equation,the(HS)equation is also completely integrable[29]and has a bi-Hamiltonian structure[32,40].For the other article related to the(HS)equation,see for example[28,39,48]and the references therein.

Recently,parallel to the(CH)equation and the(HS)equation mentioned above,the(μHS)equation(1.1)has been extended to the following generalized two-componentμ-Hunter-Saxton(gμHS2)system(see for example[21])

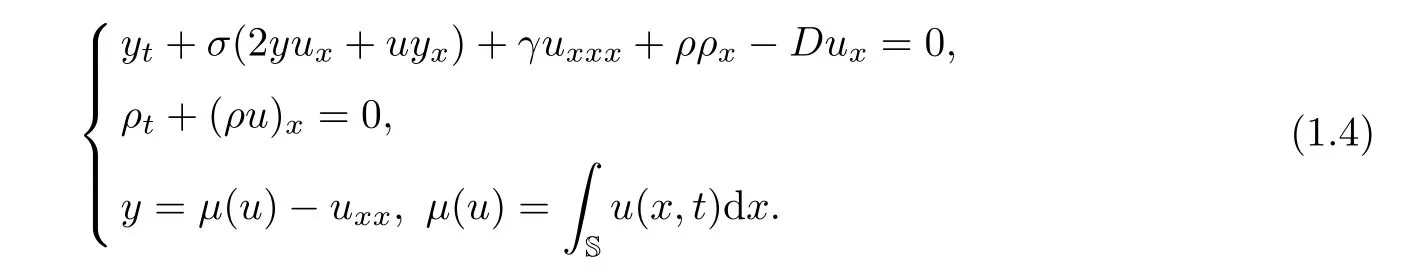
The unknown functions u(x,t)and ρ(x,t)are time-dependent periodic functions on the unit circle S=R/Z;andμ(u)is the mean of u on S,σ∈R is the new free parameter,and D≥0.By utilizing the tri-Hamiltonian duality approach[21,40],the(gμHS2)system can be derived from the bi-Hamiltonian structures of the Ito equation[30].It is known that the(gμHS2)system has two Hamiltonians which are provided by

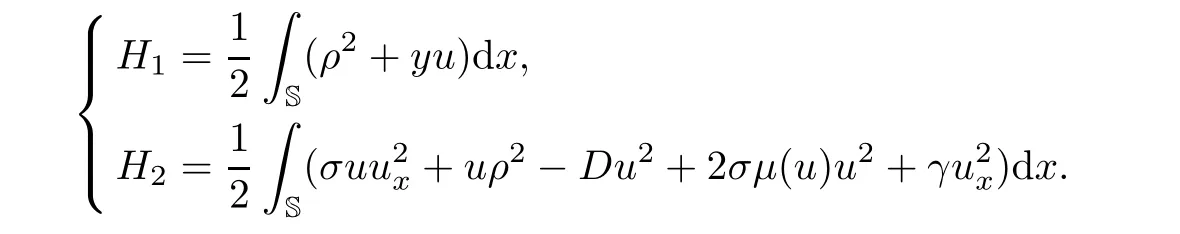
It is obvious that,by taking σ =1,system(1.4)is reduced to the two-component μ-Hunter-Saxton(μHS2)system[49],which can be regarded as a μ-version of the two-component Dullin-Gottwald-Holm system[26].It is shown in[49]that the(μHS2)system is a bi-variational equation and a bi-Hamiltonian Euler equation.For the other mathematical results related to the(μHS2)system,we can refer the readers to[35–37].Generally speaking,it is difficult to avoid energy dissipation mechanisms in a real world.In this physical sense,very recently,Wang et al[47]considered the following weakly dissipative(gμHS2)system in the periodic setting,

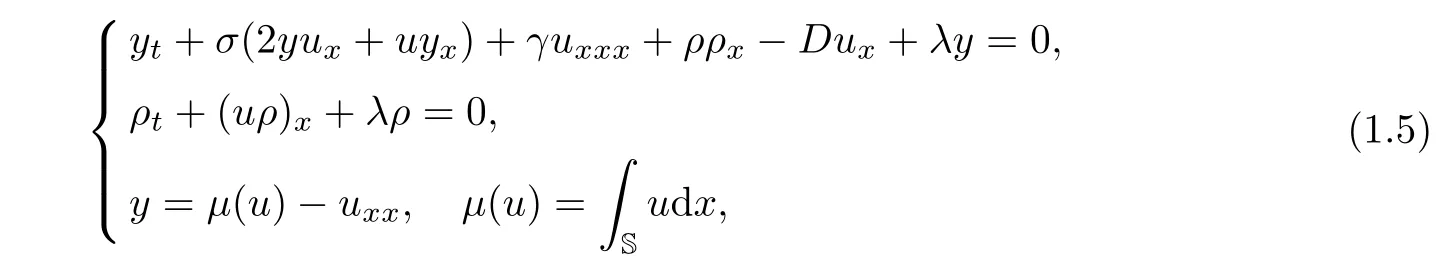
where S=R/Z is the unit circle,and λy(x,t)and λρ(x,t)are the weakly dissipative terms with the dissipative parameter λ ＞ 0.It is quite interesting to investigate the effect of the dissipative parameter λ in the blow-up phenomena and the global existence of solutions.In[47],the authors investigated the wave-breaking criterion for the solutions with certain initial data and give a sufficient condition for the global solutions.

Closely related to the previous(gμHS2)system,by taking σ =1 and D= γ =0,we then obtain the following two componentμ-Camassa-Holm system

which can be viewed as a mid-way between the two-component Camassa-Holm(CH2)system and the two-component Hunter-Saxton(HS2)system.On the one hand,the(CH2)system was originally introduced as a bi-Hamiltonian model by Olver and Rosenau[40],which is integrable and has a Lax pair formulation as well as the(CH)equation.The(CH2)system is related to the first negative flow of the AKNS hierarchy via a reciprocal transformation,which has the peakon and multi-kink solitons and is integrable in the sense that it has Lax pair[9,18].Mathematical properties of this system have also been investigated in many works;see,for example,[8,17,22–24].On the other hand,The(HS2)system can be regarded as a special case of the Gurevich-Zybin system[27]related to the nonlinear one-dimensional dynamics of nonlinear ion-acoustic waves and dark matter.Moreover,the(HS2)system is the high-frequency limit(t,x) → (∈t,∈x)of the generalized two-component Camassa-Holm(gCH2)system[8]as∈→ 0.Using Ivanov’s modeling method,one can derive the(gCH2)system from the shallow water theory with nonzero constant vorticity;see,for example,[31].

MotivationIn the field of in finite dimensional dynamical systems,it is very important to discuss the existence of global attractors for the semi-group of solution operator governed by some concrete partial differential equations.During the past decades,many works have been devoted to this problem,and we shall cite here some of them which are related to this article.For example,in[41,42],Tian etc.studied the existence of the global attractor for the viscosity Degasperis-Procesi equation and the viscous Fornberg-Whitham equation,where the viscous terms were given by second order differential operators.The existence of global attractor for the two-dimensional weakly damped KdV equation in belt field is studied in[43].In[1],Alarcon and Iorio obtained the existence of global attractors for a class of nonlinear dissipative evolution equations.Ding and Tian[15]obtained the existence of global attractor for a dissipative(CH)equation in H2.Tian and Xu[44,45]studied the global attractor for viscous two-component(CH)equations and viscous coupled(CH)equations,respectively.In[50],Zong obtain the global attractor for the two-component π-Camassa-Holm equations with viscous terms,which can be regarded as a generalized formulation for the(CH2)system and was first introduced by Lenells as a geodesic equation on a K?hlerian manifold.

Being directly inspired by the literature mentioned above,it is naturally to ask that does the(gμHS2)system has also global attractor in some appropriate function space?From the mathematical point of view,answering this question is very conducive for us to understand the long time behavior of the(gμHS2)system.However,to the best known of our knowledge,it seems that this problem for the(gμHS2)system has not been studied up to now.Hence,the major contribution of this thesis is devoted to studying the previous problem.More precisely,under the period boundary conditions,we shall investigate the existence of the global attractor for the following viscous weakly dissipative(gμHS2)system,

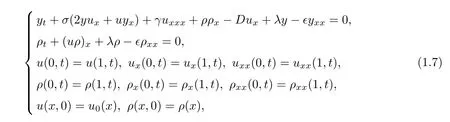
where

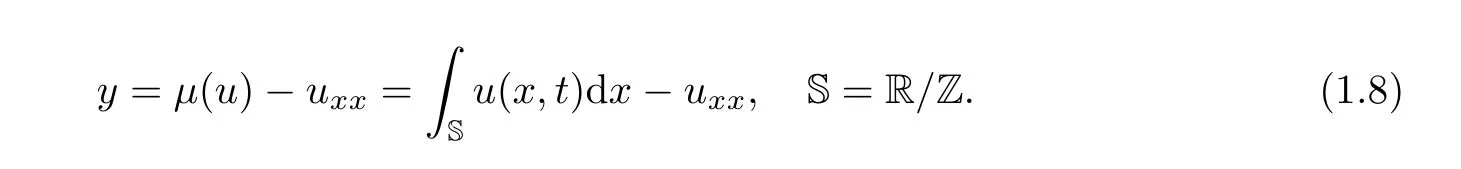
The viscous terms in(1.7)are given by the second order differential operators ∈yxxand ∈ρxxfor ?∈＞ 0.And we are interested in the effect of the weakly dispersive terms λy and λρ to the viscous(gμHS2)system.In the next sections,we shall first investigate the existence of global solution to system(1.7)using the Galerkin procedure and several complex mathematical prior estimates.Then,we show that semi-group of the solution has a bounded absorbing set,and further prove that the viscous weakly dissipative(gμHS2)system has a global attractor.

NotationLet H=L2(S)be the usual Lebesgue space with the norm|·|and inner product 〈·,·〉H.For m ∈ N+,we denote by Hm(S)the Sobolev space equipped with the norm‖u‖Hm=|?mu|,where ? is the first-order differential operator.represents the k-order differential operator,k=1,2,3,···.For convenience,if m=1,the norm in H1(S)is denoted by ‖ ·‖.Moreover,we also denote ?xu=ux,=uxx,=uxxx,and so on.The norm of the space L∞(?)is given by ‖u‖∞=esssupx∈S|u(x)|.

The plan of the remaining sections is as follows.In Section 2,we recall some well-known definitions and lemmas and give the main results in this work.Section 3 is devoted to the proof of the existence of weak solution using the Galerkin procedure and some complex uniformly estimates.In Section 4,we prove that the solution semigroup{S(t)}t≥0has a bounded absorbing set.Finally,by the compactness method,we prove that{S(t)}t≥0has a global attractor in H2×H2.

2 Main Results

For the sake of completeness of the article,let us recall some definitions and results of the in finite dimensional dynamical systems.For more details,we refer the readers to[2,46].

Definition 2.1Let B be a bounded subset of X and U a set containing B.The set B is called a absorbing set in U,if for every bounded set B0?U,there exists t0(B0)＞0 such that S(t)B0? B,for?t≥ t0(B).

Definition 2.2A compact subset A?X is called a global attractor if(i)A is invariant,that is,S(t)A=A,t≥0;(ii)A attracts every bounded subset of X,that is,for any bounded B?X,then we have

Lemma 2.3Let X be a Banach space,{S(t)}t≥0:X→ X is a semigroup such that S(t+ τ)=S(t)·S(τ),t,τ≥ 0;S(0)=I.If the following conditions are satisfied:

(1)For?R ＞ 0,there exists C(R)＞ 0 such that‖S(t)u‖ ≤ C(R),?t≥ 0 and ‖u‖X≤ R;

(2){S(t)}t≥0has a bounded absorbing set B0? X;

(3)For each bounded set B?X,there exists t0(B)＞0 such that the setcompact in X.Then,{S(t)}t≥0has a global attractor A in X.Moreover,

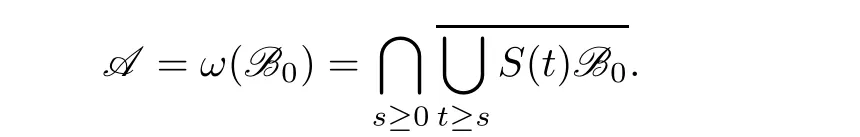
Lemma 2.4Assume that g(t),y(t),andFor?r＞0 and t≥t0,there exist constants r1,r2,r3＞0 such that

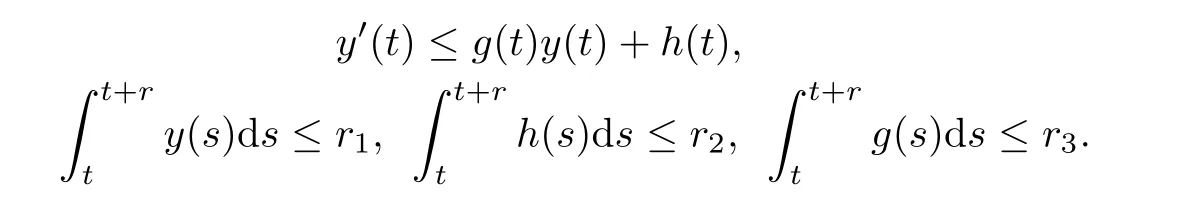
Then,we have

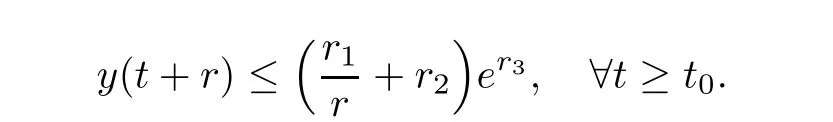
The main results in this article can be stated as follows.

Theorem 2.5Assume that(u0,ρ0)∈ H2(S)×H2(S),then system(1.7)admits a global solution in H2(S)×H2(S).

Theorem 2.6Let{S(t)}t≥0be the semi-group of the solution operator of the system(1.7)defined by(u,ρ)=S(t)(u0,ρ0)=(S1(t)u0,S2(t)ρ0).If(u0,ρ0) ∈ H2(S)× H2(S),then the semi-group{S(t)}t≥0has a bounded absorbing set.

Theorem 2.7Assume that(u0,ρ0)∈ H2(S)×H2(S),then the semi-group of the solution operator{S(t)}t≥0of the dynamical system possesses a global attractor in H2(S)× H2(S).

3 Proof of Theorem 2.1

ProofWe shall apply the Galerkin procedure to prove Theorem 1.1.Defining the operator A by Au= ?Δu,where Δ is the Laplace operator given by Δu=.As[μ(u)]x=we have[μ(u)?uxx]xx= ?A2u.System(1.7)thus can be transformed into the following in finite dimensional dynamical system:

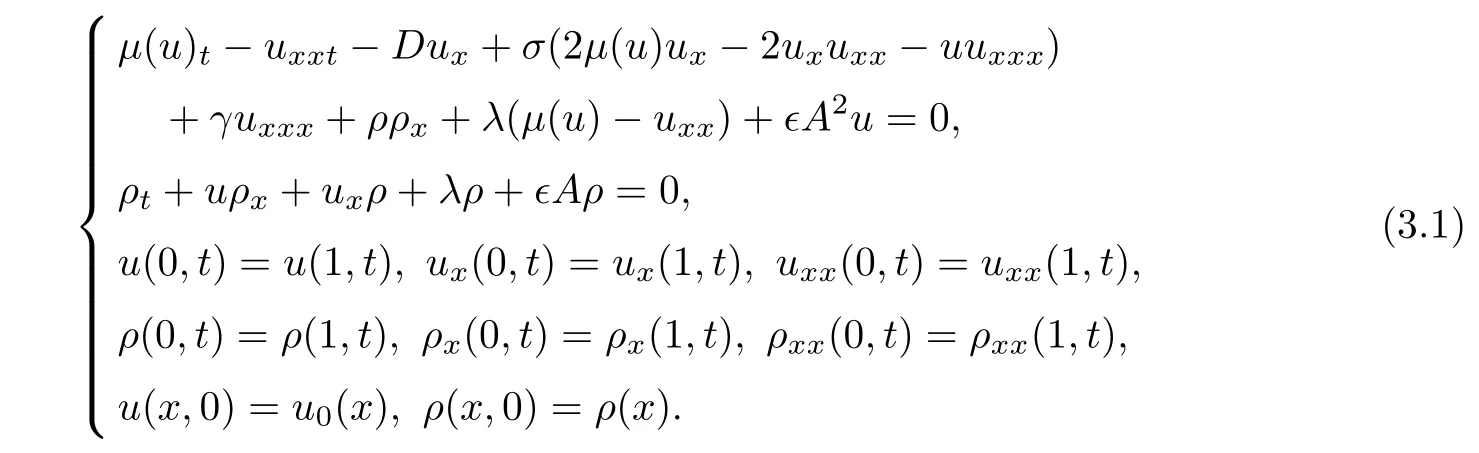
It is clear that the differential operator A is a linear unbounded self-adjoint operator in H,so we can define the powers Asof A for s∈R.The space D(As)is a Hilbert space endowed with the norm ‖As·‖H.Let{ωi}i∈N+be the orthogonal bases in H,which are the eigenfunctions of the operator A with the eigenvalues{λi}i∈N+such that(for example,[51,Chapter 3])

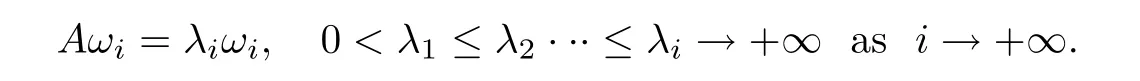
For?m ∈ N+,let us define the ansatz space Hm=span{ω1(x),ω2(x),···,ωm(x)}and Pmthe orthogonal projection from H to Hm.The Galerkin procedure for(3.1)can be formulated as the following ordinary differential system:

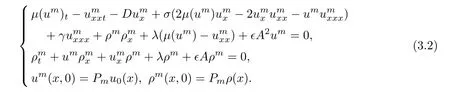
By means of the classical theory of ordinary differential equations,it can be concluded that system(3.2)admits an unique solution in a time interval[0,Tmax).In the sequel,we shall obtain a serious of uniform estimates which are independent of the time for the approximating solution,this indicates that the local solution is actually a global solution,that is,Tmax=+∞.

Multiplying the first equation of(3.2)by umand integrating with respect to the space variable x in S,one can obtain

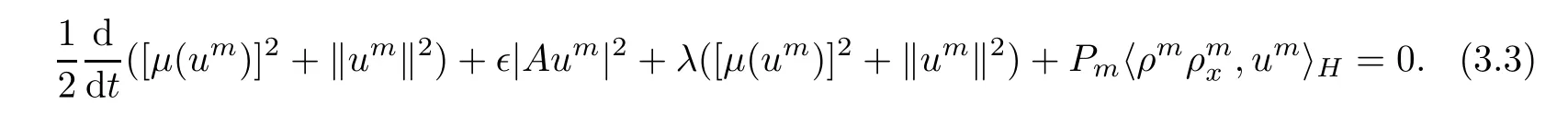
In fact,it is obvious that

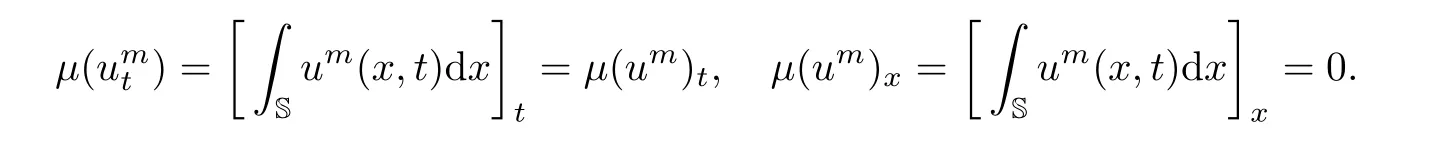
Moreover,using the period boundary conditions,we have

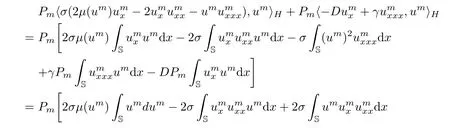
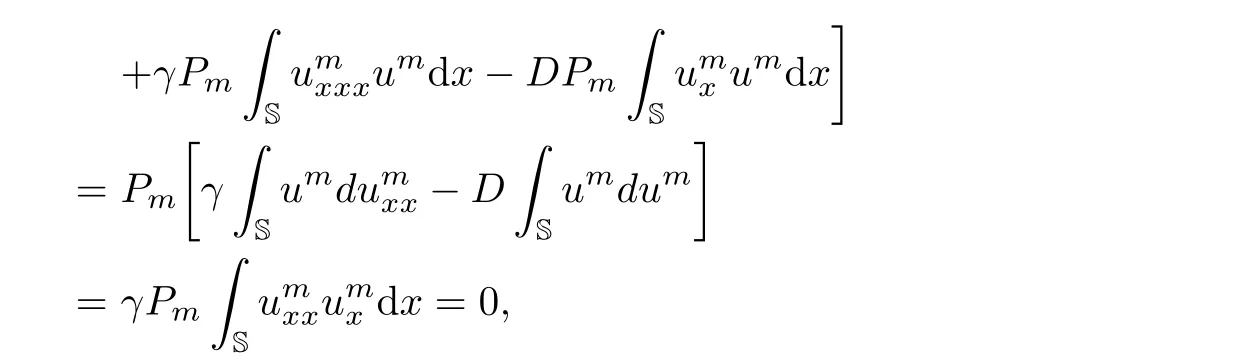
and

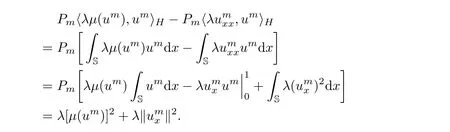
Multiplying the second equation of(3.2)by ρm,then integrating with respect to x on the circle S,we can deduce that

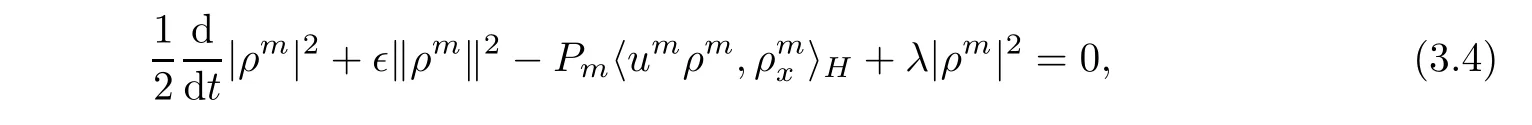
where we have utilized the fact that

Then,it deduce from(3.3)and(3.4)that

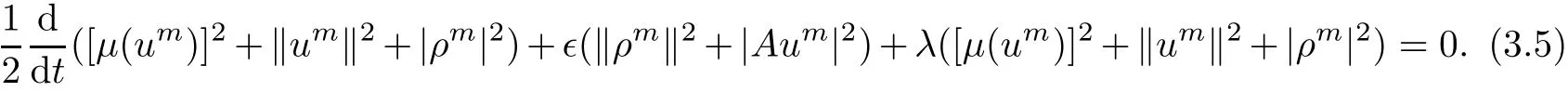
By means of the Poincaré inequality,it is not difficult to find that

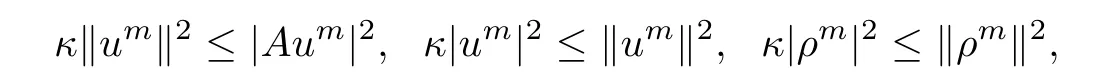
where κ is a positive constant.Then,we can deduce from(3.5)that

where c1=min{2∈κ,2λ}is a positive constant.Combining the Gromwall’s inequality and the previous inequality,there exists a nonnegative constant c2such that

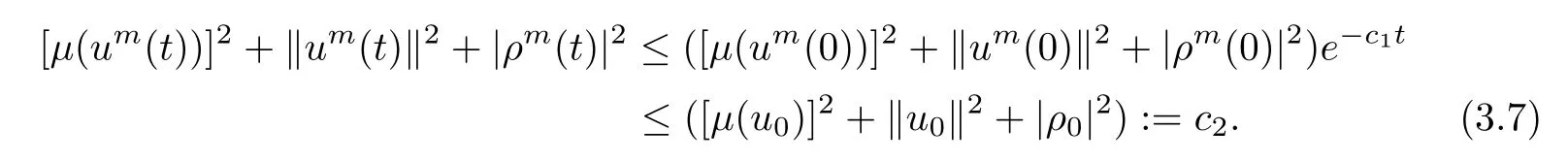
For?r＞ 0,by integrating both sides of(3.5)on the time interval[t,t+r],we obtain

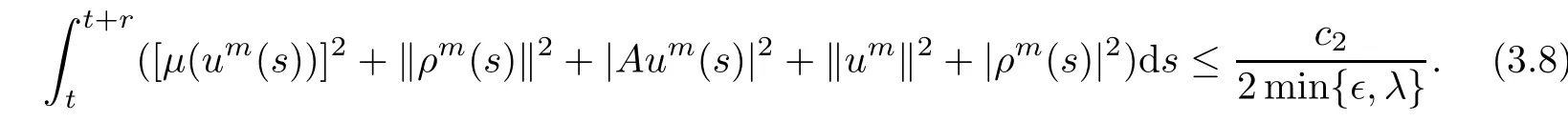
Multiplying the first equation of(3.2)by Aumand taking the inner product in H,we obtain

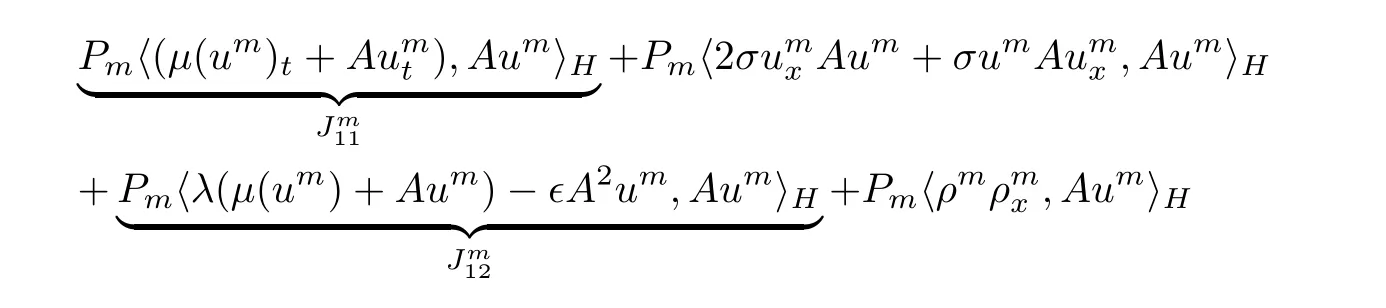
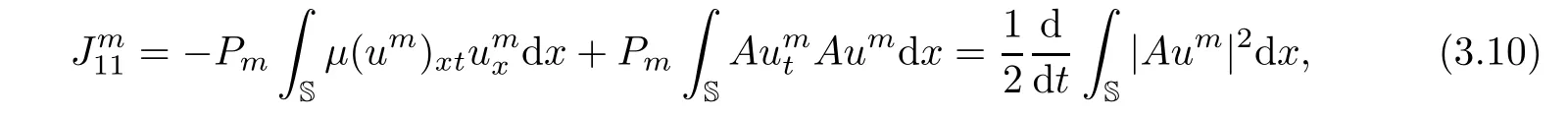
and

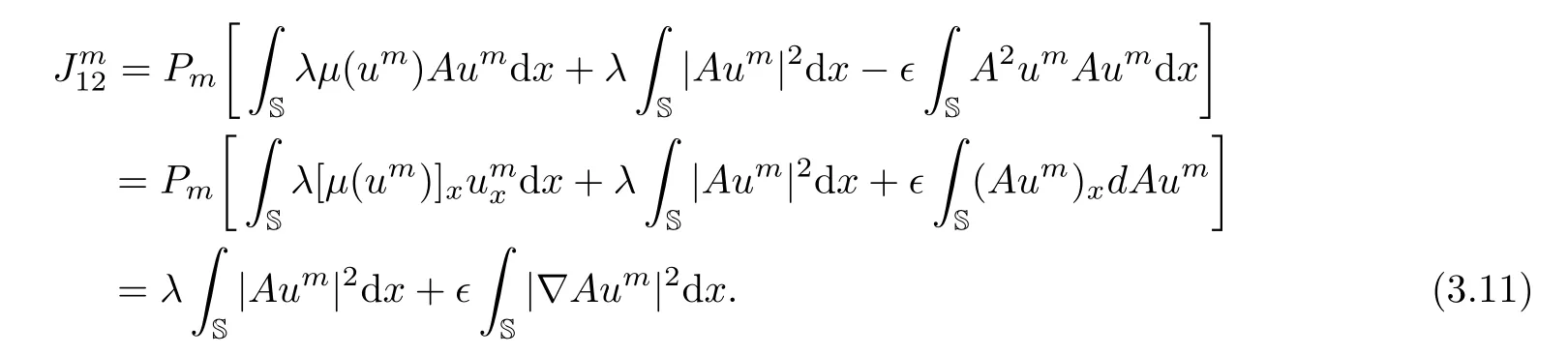
And it follows from the period boundary conditions that

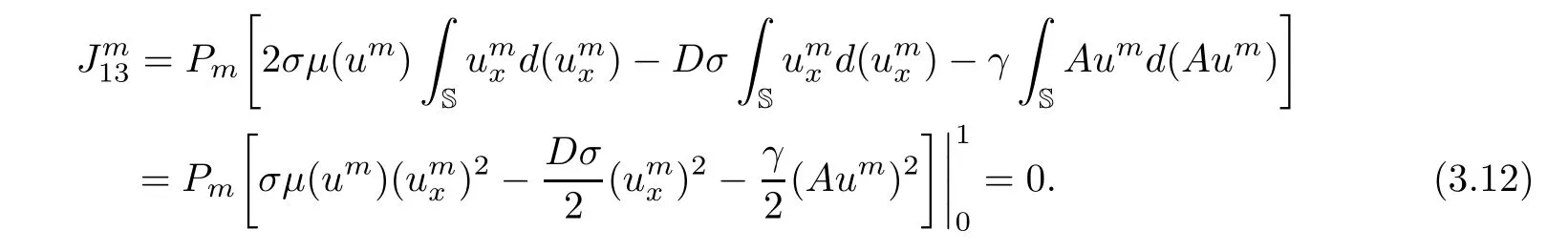
Multiplying the second equation of(3.2)by Aρmand integrating on the circle S,we obtain

Then,from(3.9)–(3.13),we can deduce that

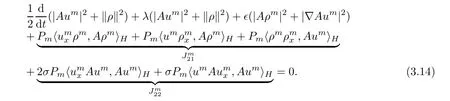
Utilizing the Agmon’s inequality(for example,[46,Chapter 2]),where δ is a positive constant,the inner product terms in(3.14)can be estimated as follows:

and

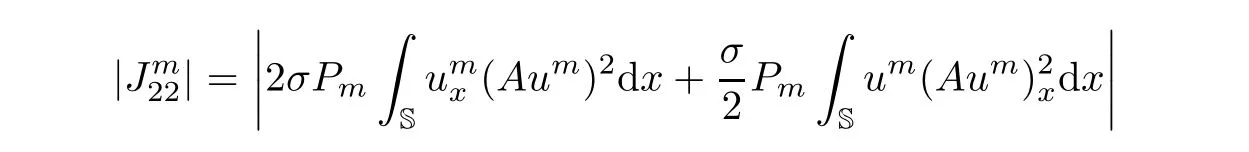
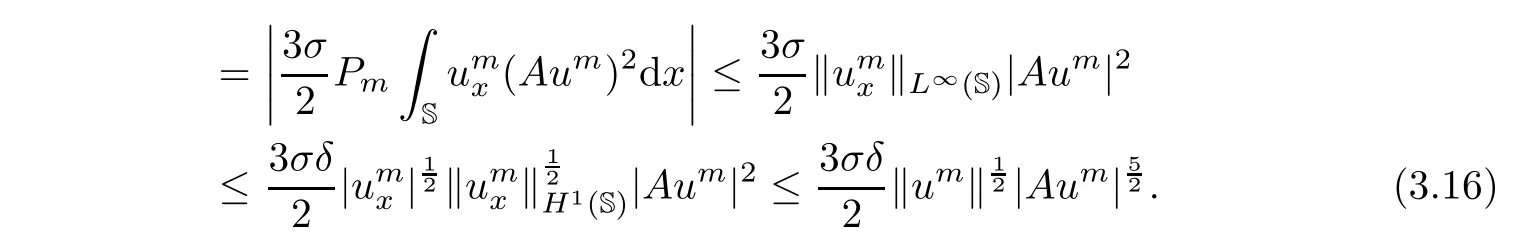
Using the Young’s inequality,it then follows from(3.14)? (3.16)that

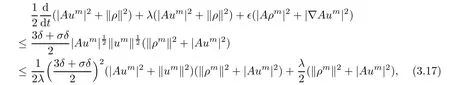
which indicates that

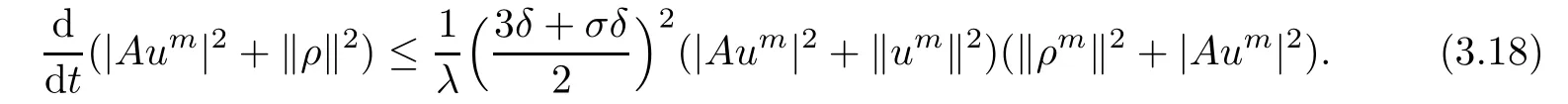
From(3.7)and(3.8),it is clear that

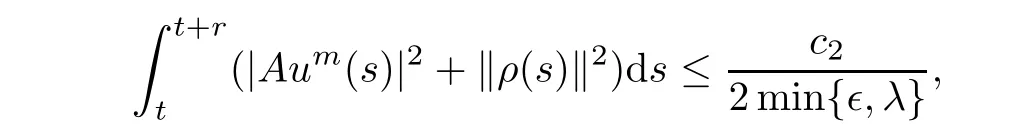
and

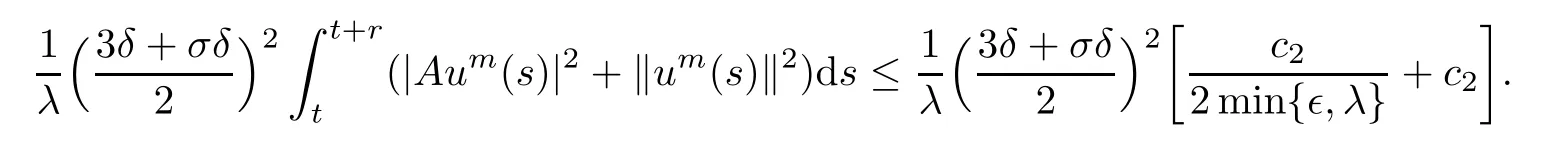
By applying the uniformly Gronwall inequality(see Lemma 2.2),we obtain

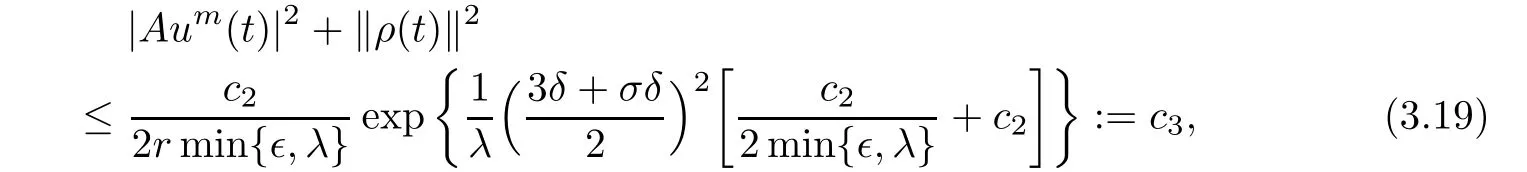
for t∈ [t0+r,∞),where c3is a nonnegative constant independent of t.Integrating both sides of(3.17)from t to t+r,we obtain

where c4is a nonnegative constant which is independent of t.

Multiplying the first equation of(3.2)by A2umand then taking inner product.we have

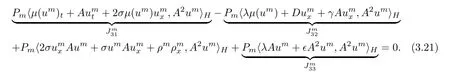
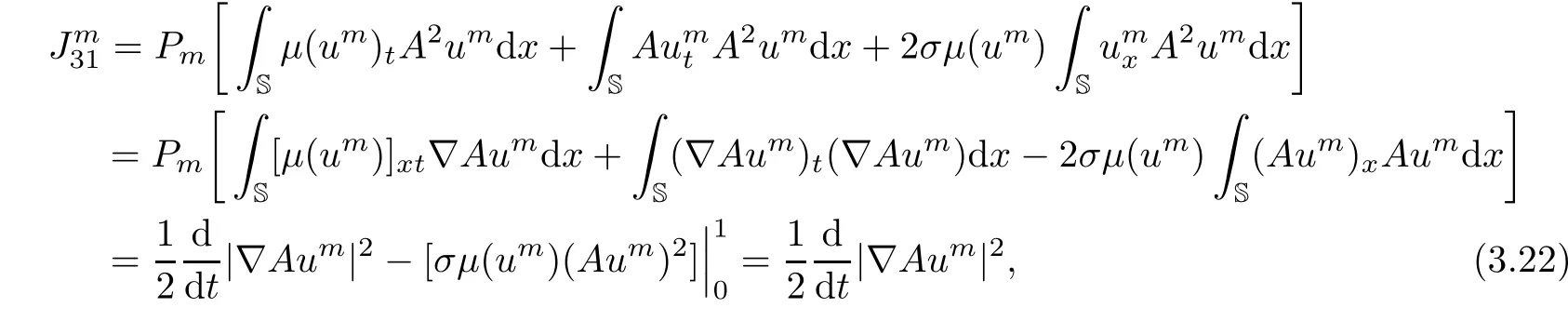
and

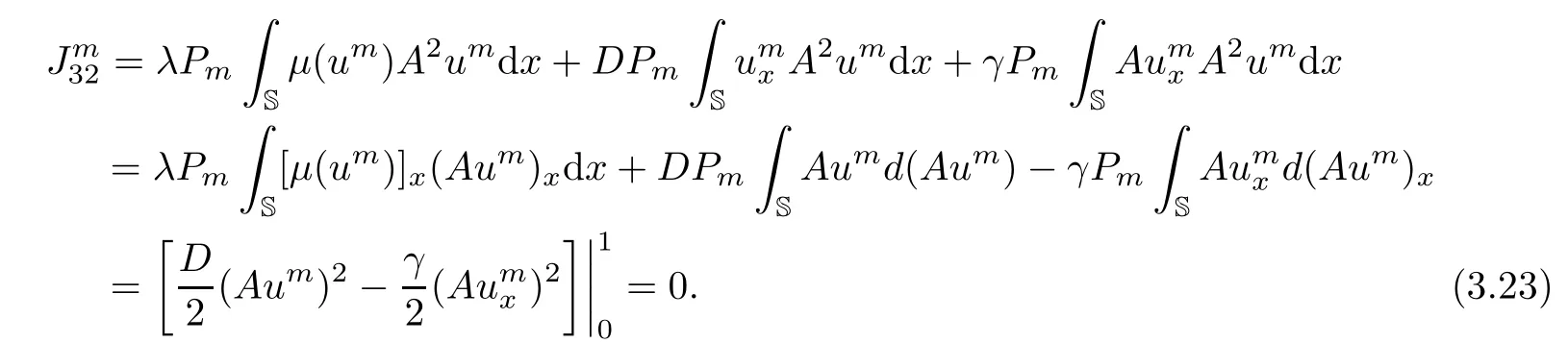
Moreover,from the boundary conditions,direct calculation shows that

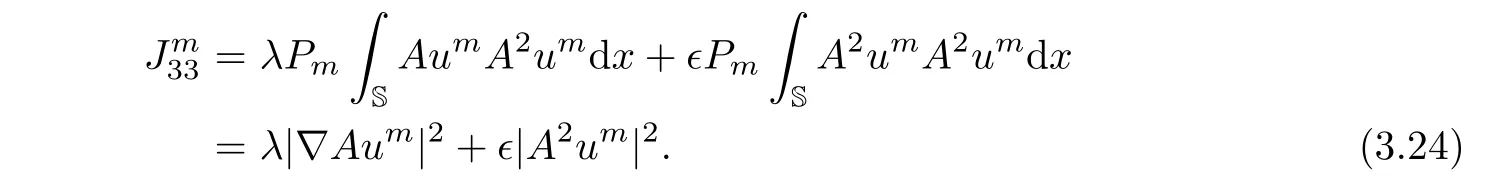
It thus transpires from(3.21)–(3.24)that

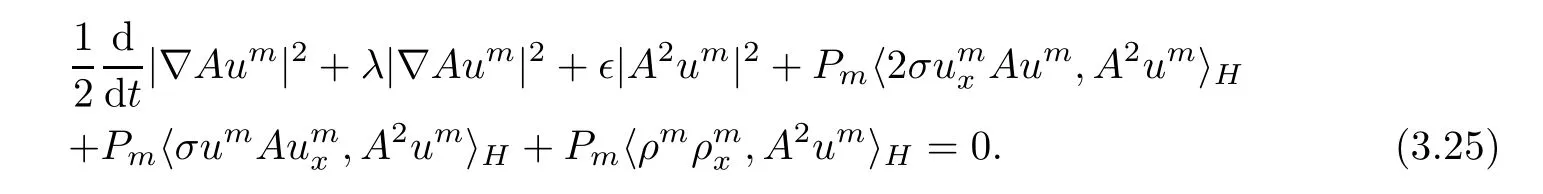
Multiplying the second equation of(3.2)by A2ρmand integrating on the circle with respect to x,we get

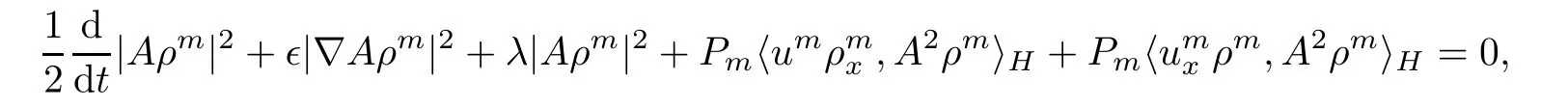
which combined with equality(3.25)yields that

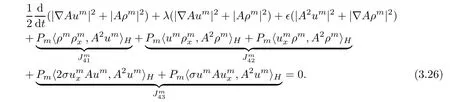
Using the Agmon’s inequality and the Sobolev embedding theorem,we estimate the inner product terms in(3.26)as follows:

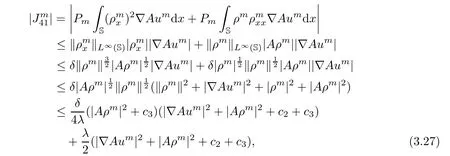
where the uniformly estimates(3.7)and(3.19)are used.Similarly,from the Poincaré inequality and the Agmon inequality,we have

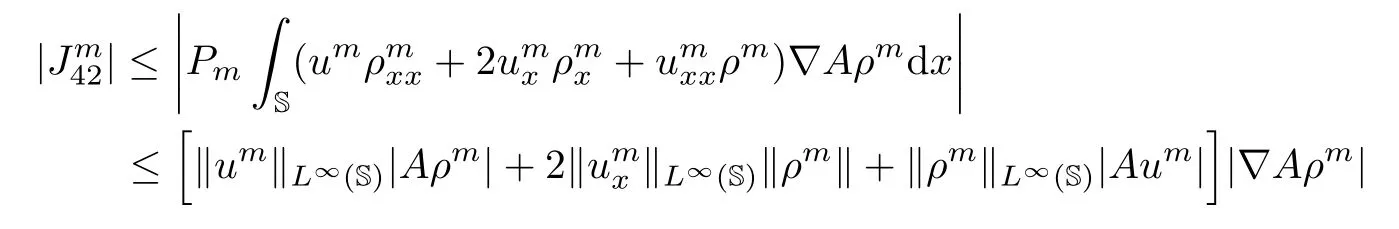
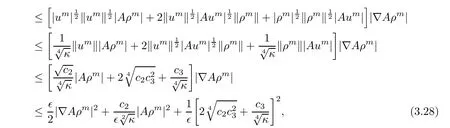
and

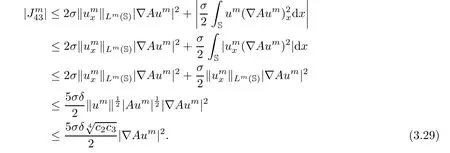
Thereby,it transpires from the estimates(3.26)?(3.29)that

Noting that for?r＞ 0,it follows from(3.20)that

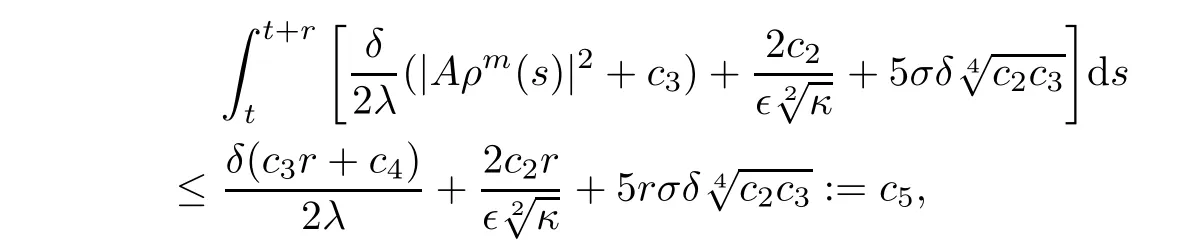
and

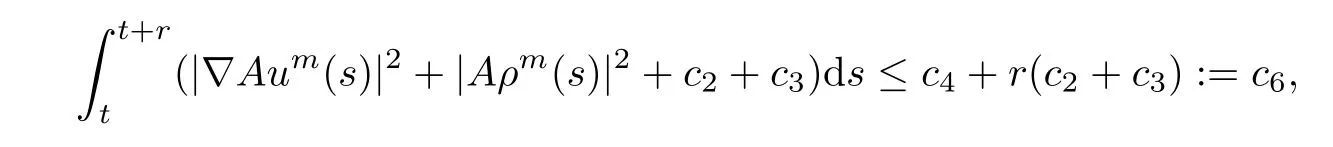
where c5,c6≥0 are constants independent of t.By(3.30)and using the uniformly Gronwall inequality,we get

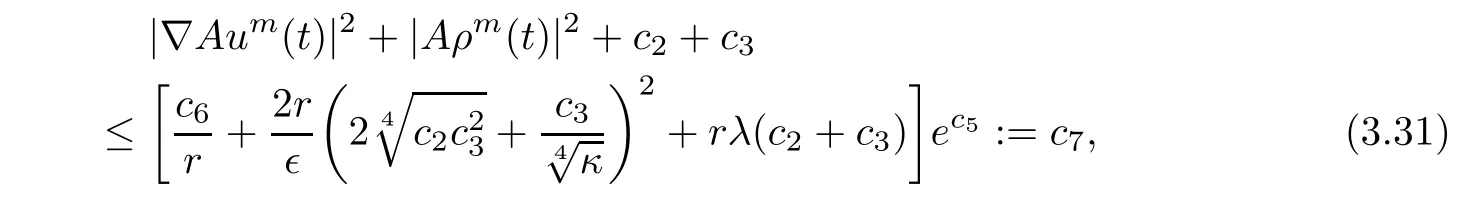
for t∈ [t0+r,∞)and c7is a nonnegative constant independent of t.Integrating the both sides of(3.30)from t to t+r,we obtain

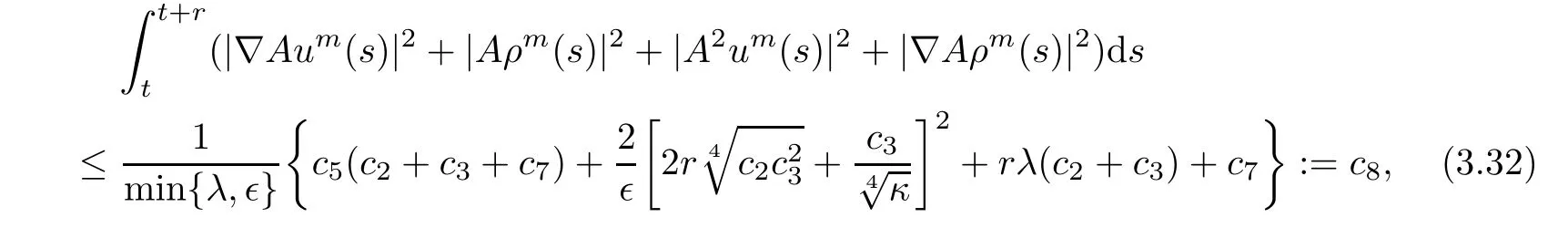
where c8is a nonnegative constant which is also independent of t.By using the similar method as we used above,we can also get the uniformly estimate|A2um(t)|2+|?Aρm(t)|2≤ c9,where c9is a nonnegative constant.Hence,from the above analysis and the Poincaré inequality,it is clear that the following bounds hold:

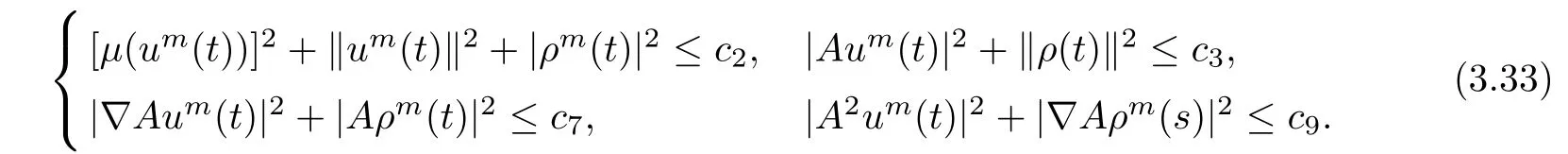
Noting that y=u ? uxx,it follows from(3.33)that|ym|,‖ym‖,|Aym|and|ρm|,‖ρm‖,|Aρm|are all uniformly bounded.Thus,we can deduce from equations(3.2)that the sequences{d(um)/dt}m∈N+and{d(ρm)/dt}m∈N+are also uniformly bounded.

In the sequel,we shall pass to the limit as m→∞to prove the existence of solution.Indeed,by using the Aubin-Lions compactness theorem(for example,[51,Theorem 3.1.1 of Chapter 3]),there exist subsequences of{um}m∈N+,{ym}m∈N+,and{ρm}m∈N+,still denoted by themselves for convenience,such that um→u,ym→y,and ρm→ρ,as m→∞.Hence,it just remains to verify that the functions u,y,and ρ are solutions to system(1.7).Indeed,for?? ∈ D(A),it follows from the first ordinary differential equation of(3.2)that

On the one hand,it is clear that Pm?→ ? and PmA?→A? strongly in H as m → ∞.By(3.33),it is not difficult to verify that

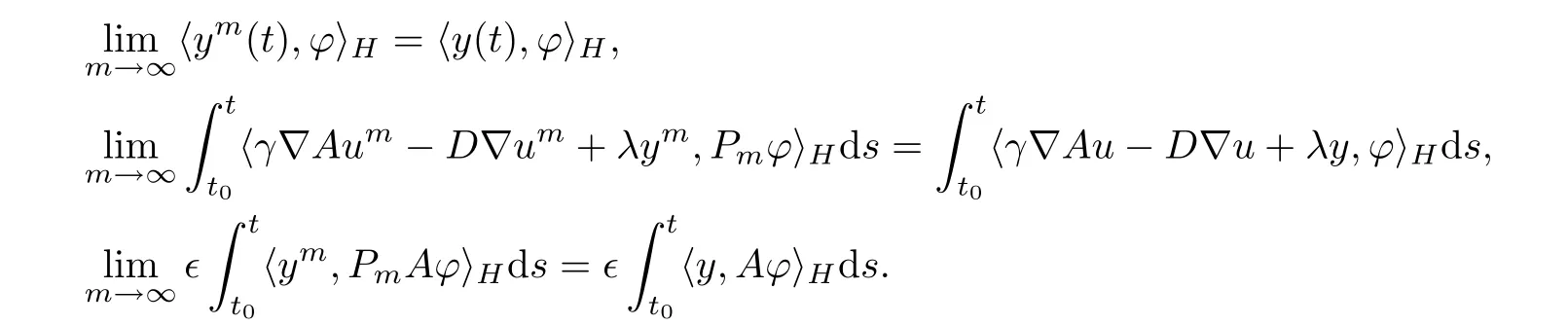
On the other hand,we have

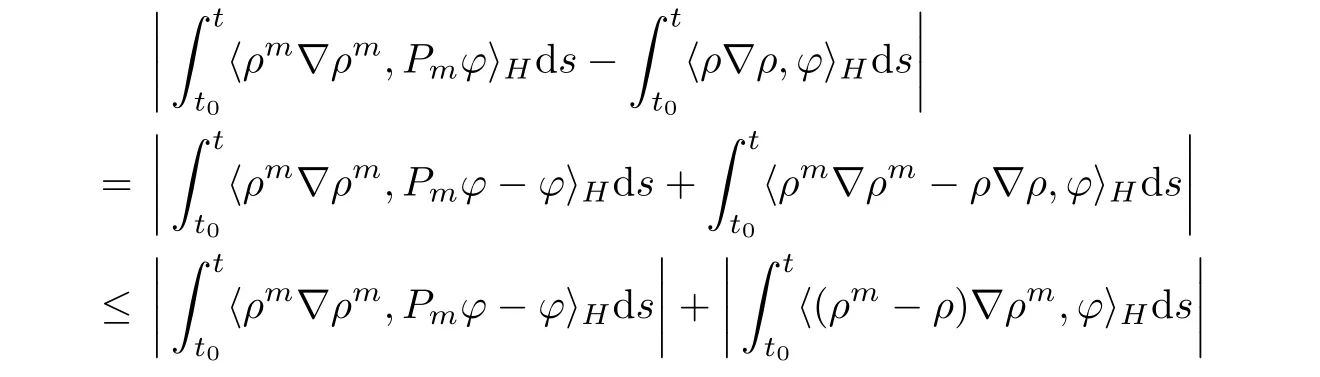
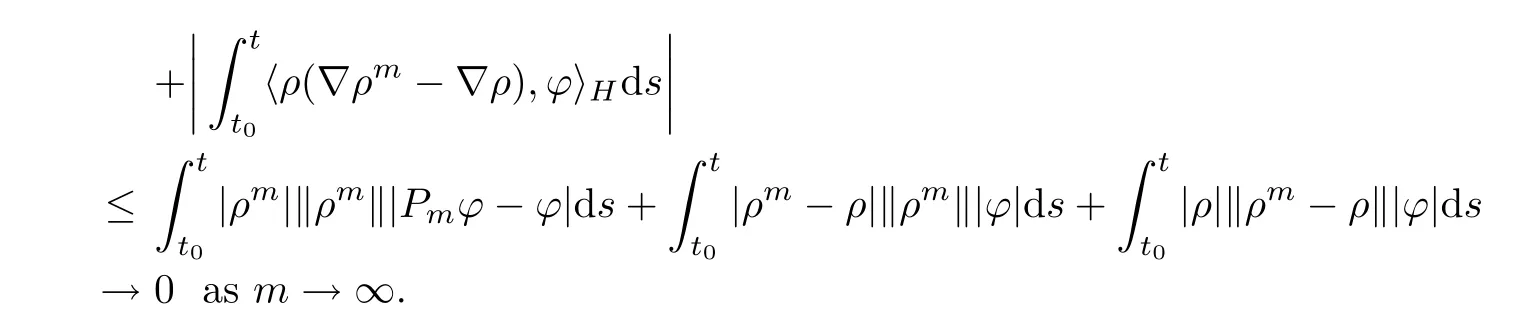
By the similar argument,we can also deduce that

Thereby,by passing to the limit as m→∞in(3.34),we get

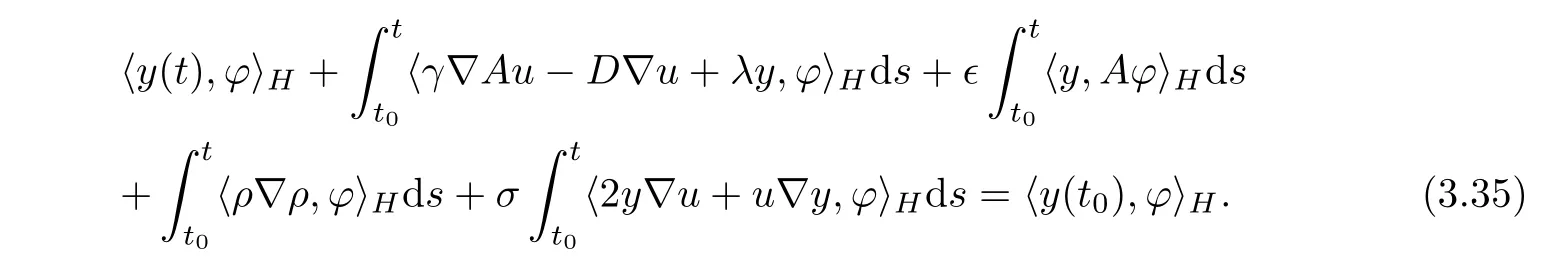
Next,from the second ordinary differential equation of(3.2),for?? ∈ D(A),we obtain

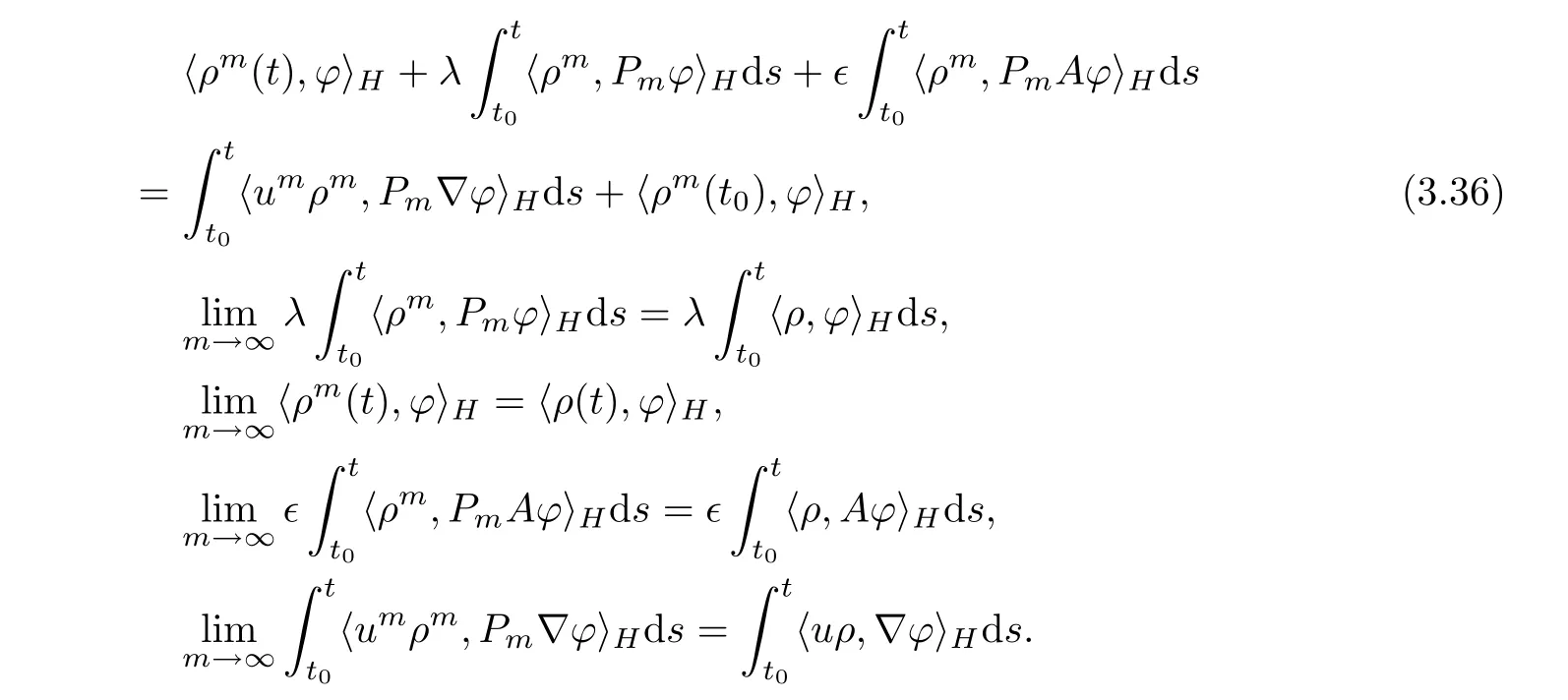
Hence,by passing to the limit as m→∞in(3.36),we get

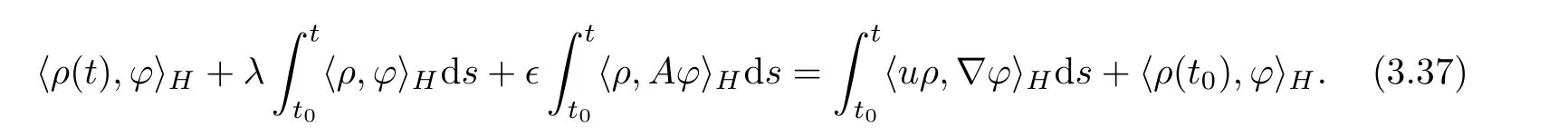
From the all analysis above,we can conclude the existence of the global solution to the system(1.7),and this completes the proof of Theorem 2.1.

4 Proof of Theorem 2.2

ProofThanks to the conclusion of Theorem 2.1,we can define the semi-group of the solution operator{S(t)}t≥0:H2× H2→ H2× H2such that S(t+ τ)=S(t)·S(τ),S(0)=I,t,τ＞ 0,and(u,ρ)=S(t)(u0,ρ0)=(S1(t)u0,S2(t)ρ0).Now,we are in a position to prove Theorem 2.2,that is,the semigroup{S(t)}t≥0has a bounded absorbing set.

Multiplying the first equation of(3.1)by u and integrating on the circle S,we obtain

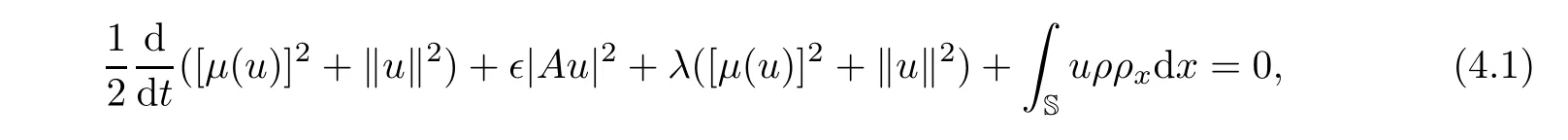
where we have used the fact that

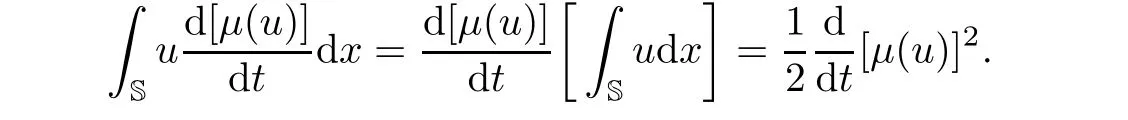
And from the period boundary conditions,we have

and

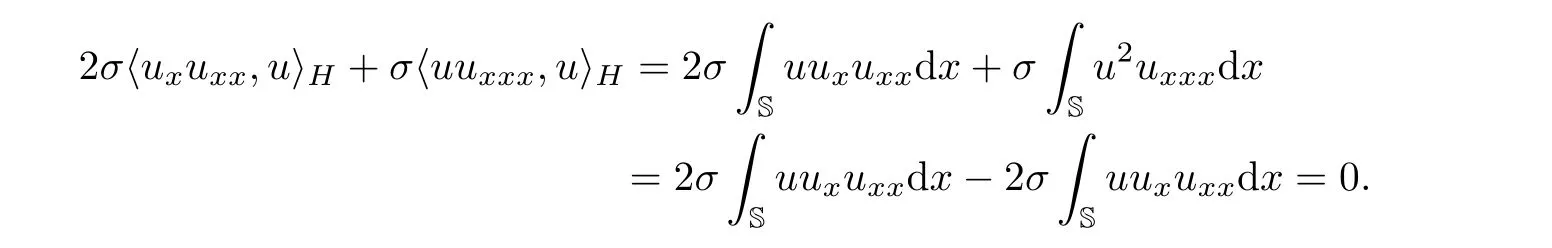
Multiplying the second equation by ρ and integrating with respect to x on the circle S,we get

Note that

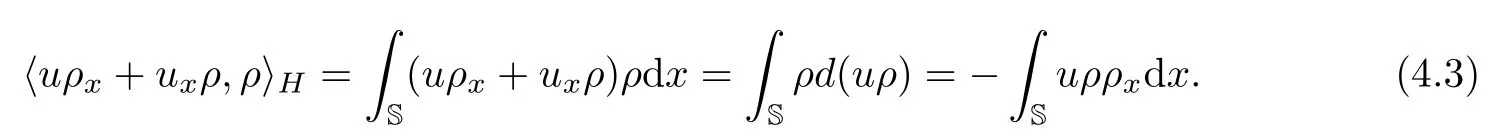
It then follows from(4.1)–(4.3)that

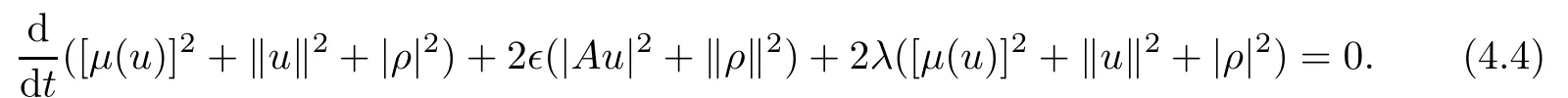
By means of the Gronwall inequality,we deduce from(4.4)that

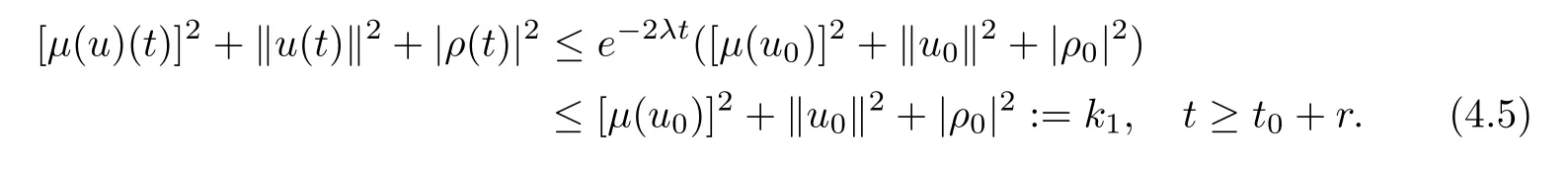
Here and throughout the proof of Theorem 2.2,we shall denote by ki,i=1,2,···some nonnegative constants which are independent of t.Then,integrating the both sides of(4.4)on the time interval[t,t+r]yields that

Multiplying the first equation of(3.1)by Au and integrating on the circle S,we obtain

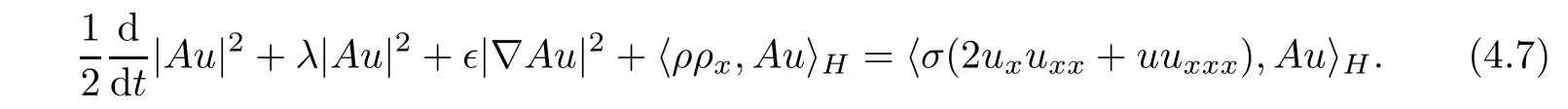
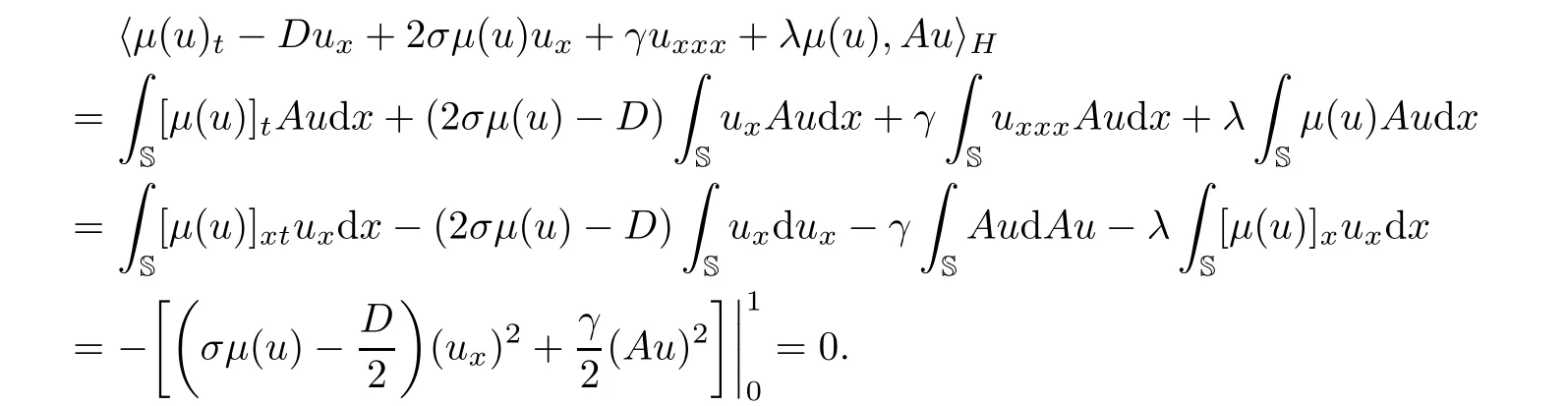
Multiplying the second equation of(3.1)by Aρ and integrating on S,we have

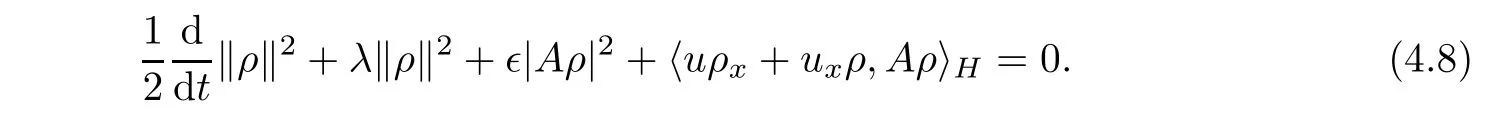
Combining(4.7)and(4.8),we get

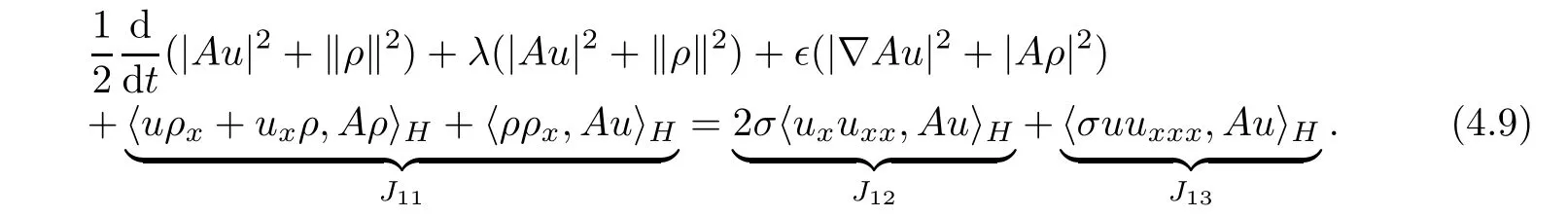
Utilizing the Agmon inequalityand the period boundary conditions,we can estimate that

Similarly,for the terms J12and J13,we have

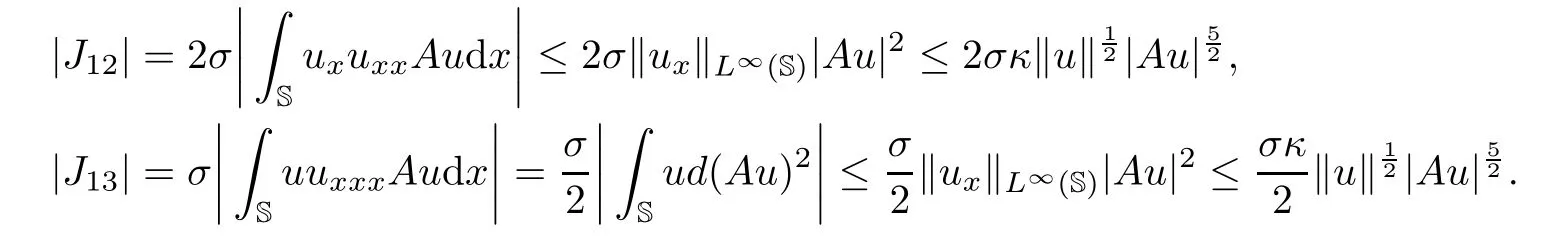
Hence,by means of the Young inequality,we can deduce from(4.9)that

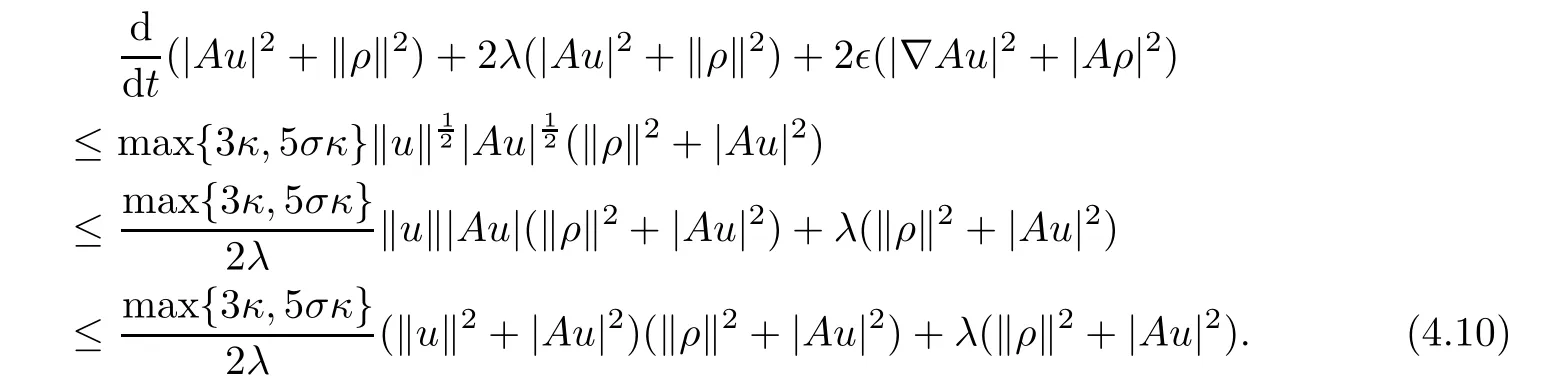
Noting that for?r＞ 0,it follows from(4.6)that the following two integrations are bounded:

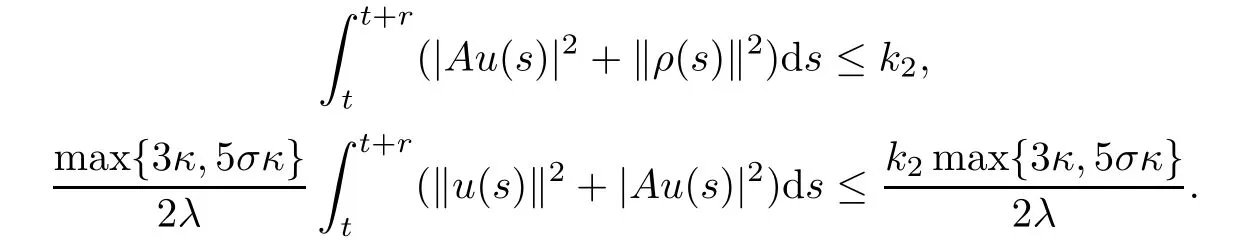
By applying the uniformly Gronwall inequality,we obtain

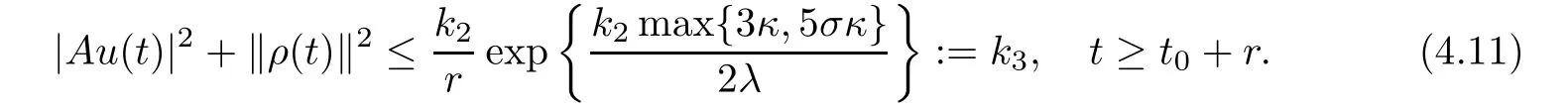
Integrating the both sides of(4.10)from t to t+r,we obtain

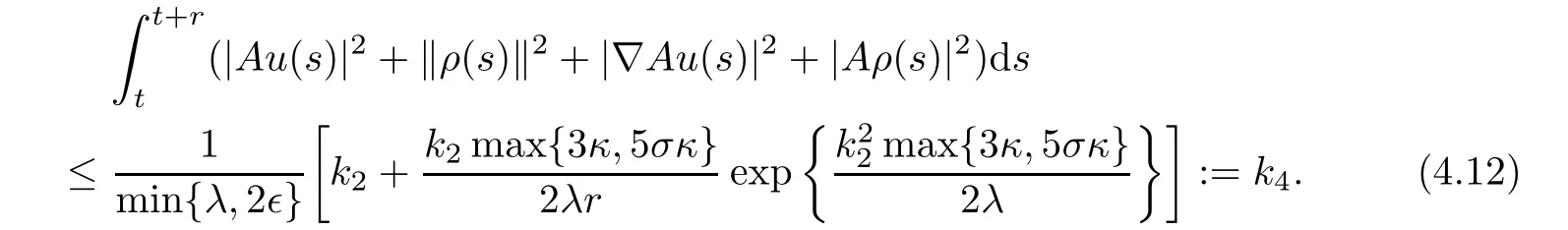
By using the Poincaré inequality κ‖u‖2≤ |Au|2and κ|u|2≤ ‖u‖2,we deduce from(4.5)and(4.11)that|ρ(s)|, ‖ρ(s)‖,|u(s)|,and ‖u(s)‖ are uniformly bounded.Recalling that the solution operator{S(t)}t≥0is defined by(u(t),ρ(t))=S(t)(u0,ρ0)=(S1(t)u0,S2(t)ρ0).From the above analysis,it deduces that if the initial data(u0,ρ0)∈ H2× H2,then the semigroup{S(t)}t≥0is uniformly bounded in L2(S)and H1(S).That is to say,setting B(0,R)the ball which is centered at 0 of radius R in L2(S)and H1(S),then S1(t)u0,S2(t)ρ0∈ B(0,R)for?t≥ t0+r.

We now prove that the semigroup{S(t)}t≥0is a mapping from H2×H2to itself and admits an absorbing set B(0,R)with appropriate radius R.In fact,multiplying the first equation of(3.1)by A2u and integrating with respect to x on the circle S,we obtain

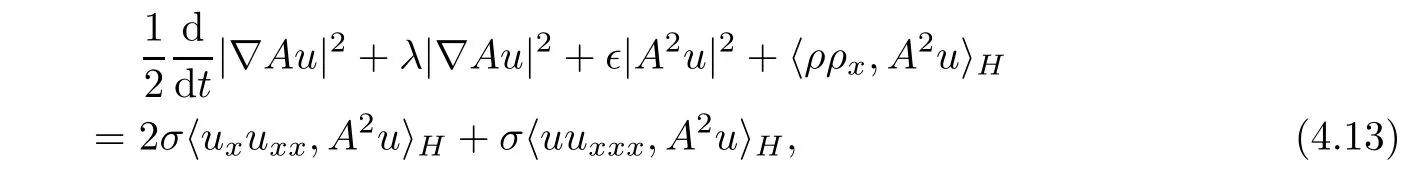
where we have used the fact that

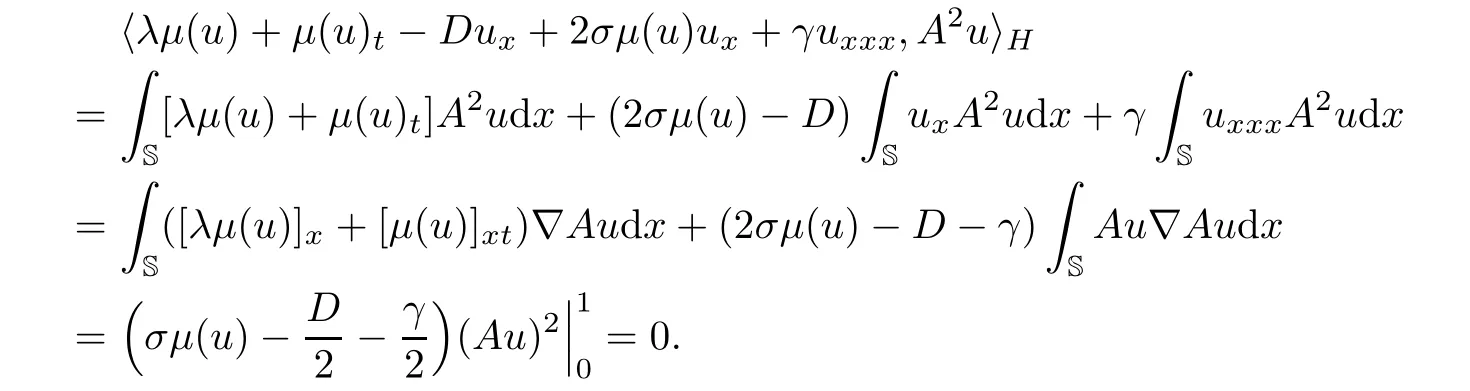
Multiplying the second equation of(3.1)by A2ρ and integrating with respect to x on the circle S,we can deduce that

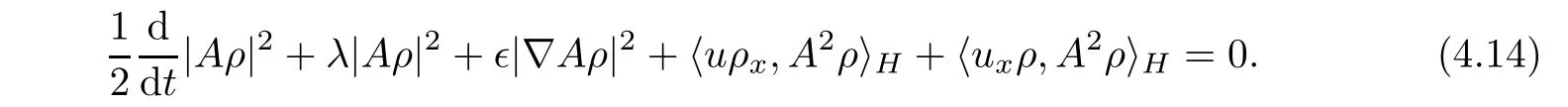
Combining(4.13)and(4.14),we get

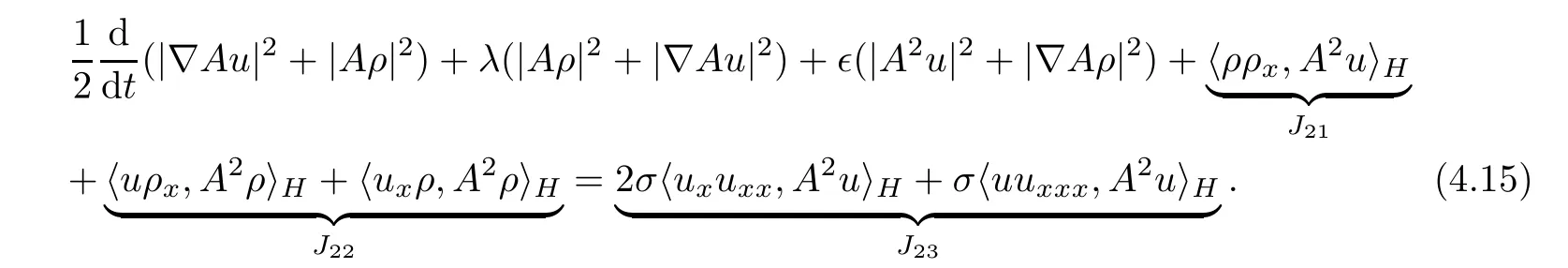
Next,we shall estimate the inner product terms in(4.15)respectively.For J21,integrating by parts,it then follows from the Agmon inequality that

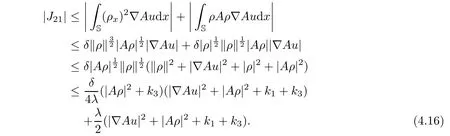
For J22,by applying the Agmon inequality,it follows from(4.5)and(4.11)that

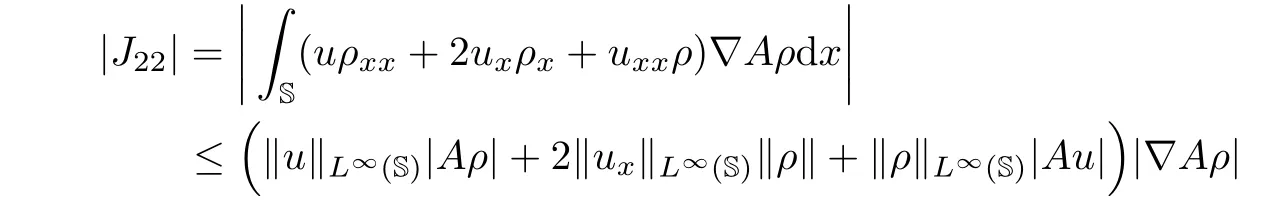
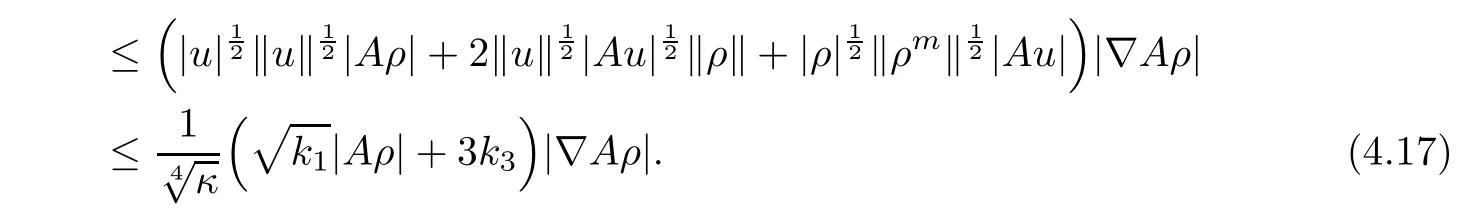
Similarly,we can estimate the term J23as follows:

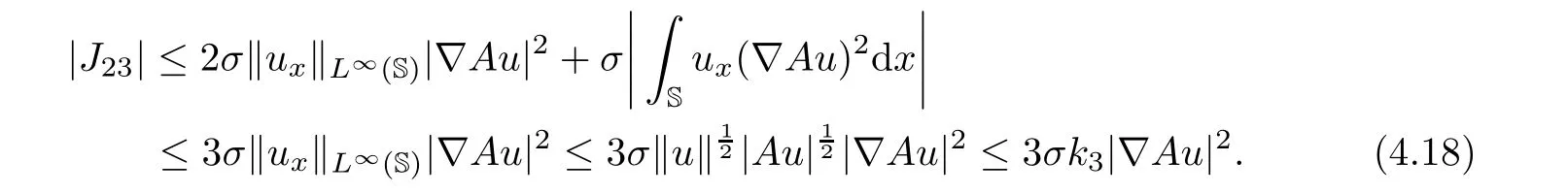
Then,from(4.15)–(4.18),we deduce

which implies that

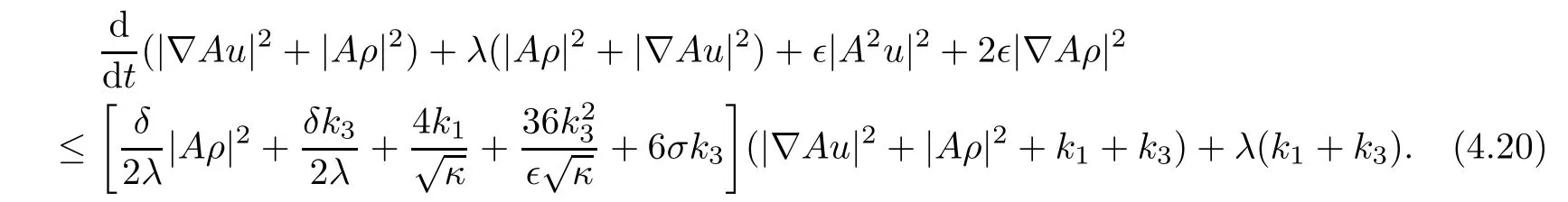
Note that

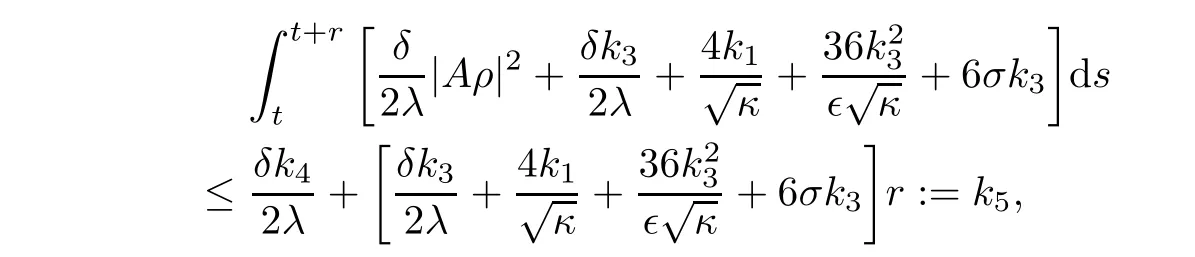
and

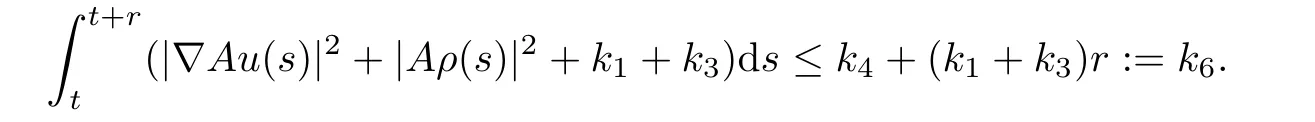
Utilizing the uniformly Gronwall inequality,we get

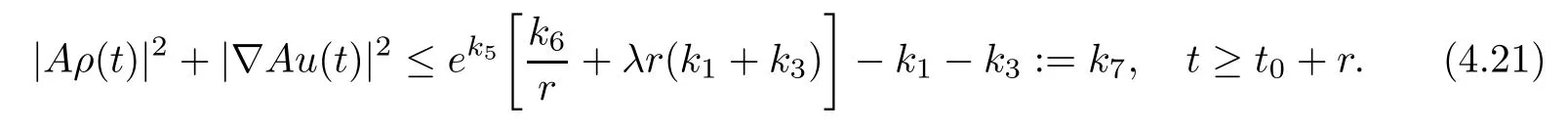
Integrating the both sides of(4.20)on the interval[t,t+r],we obtain

From the above analysis,we obtain|Au(t)|2≤ k3and|Aρ(t)|2≤ k7.This means that the semi-group mapping S(t):(u0,ρ0)→ (u(t),ρ(t))is uniformly bounded in H2× H2.Choosing the open ball B(0,R)∈H2with the radiusthen for any bounded set B?H2×H2,we have S(t)B?B(0,R)2for t≥t0+r,which means that the open ball B(0,R)2is a bounded absorbing set of{S(t)}t≥0in H2× H2.Thus,this completes the proof of Theorem 2.2.

5 Proof of Theorem 2.3

ProofBy Lemma 2.1,it just remains to prove the compactness of the solution operator S(t).Multiplying the first equation of(3.1)by t2Δ2Au and integrating with respect to x on the circle S,we can deduce that

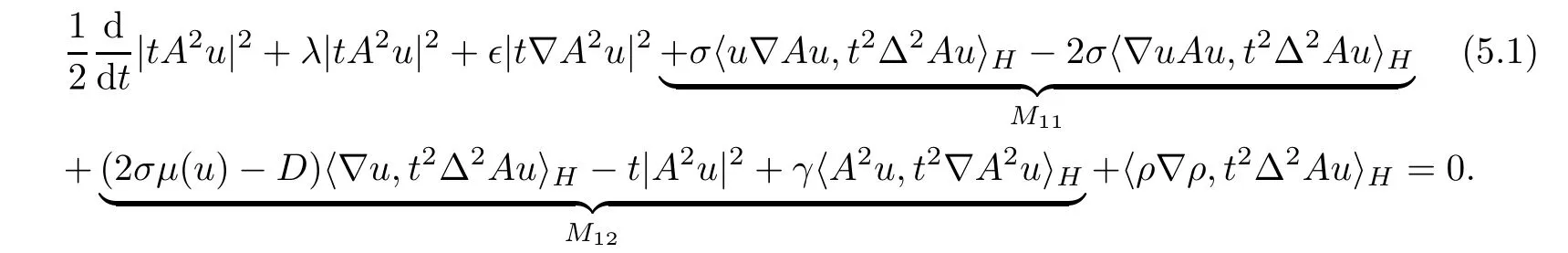
Moreover,by the period boundary conditions and integrating by parts,we can estimate that

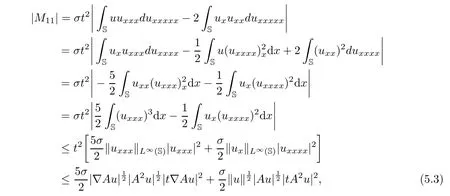
and

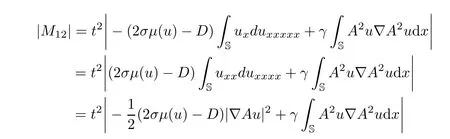
Multiplying the second equation of(3.1)by t2Δ2Aρ and integrating with respect to x on S,we can deduce that

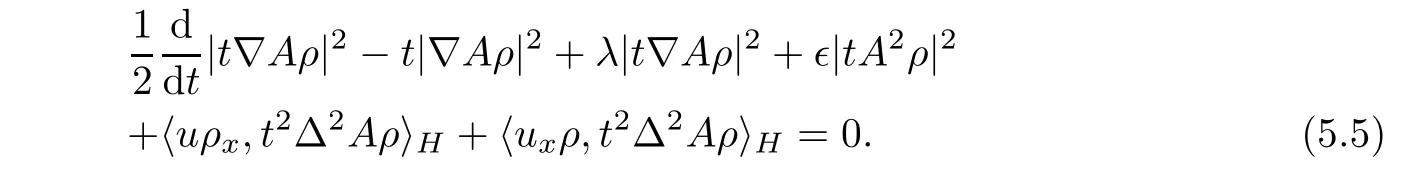
To obtain the uniformly estimate,we need to deal with the term M21= 〈ρ?ρ,t2Δ2Au〉H+〈uρx,t2Δ2Aρ〉H+ 〈uxρ,t2Δ2Aρ〉H.Indeed,it follows from the Sobolev inequality that

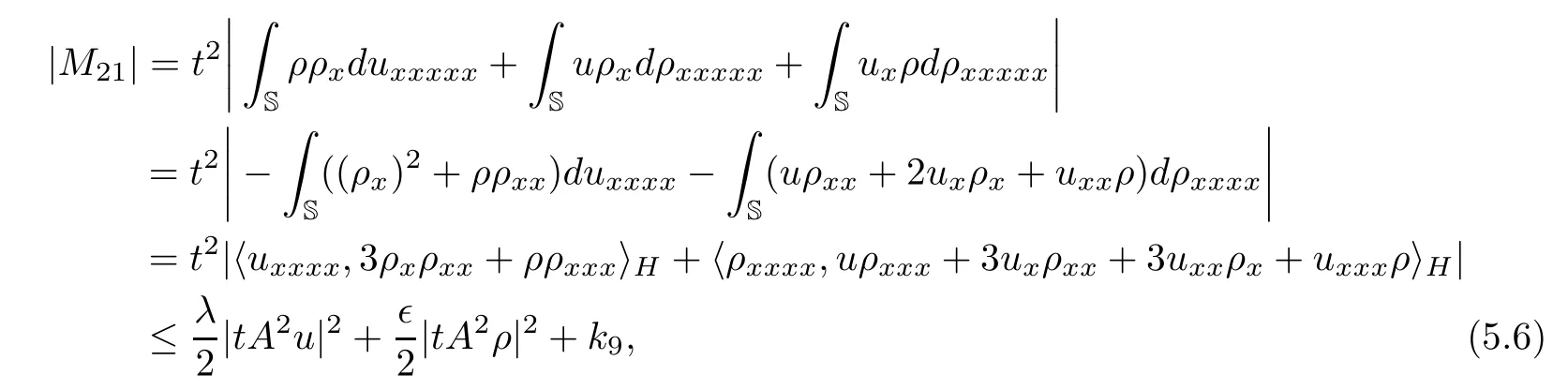
where k9is a nonnegative constant depend on|ρ|,‖ρ‖,|Aρ|,|u|,‖u‖,|Au|,|?Au|,t.Hence,it follows from the analysis(5.1)–(5.6)that

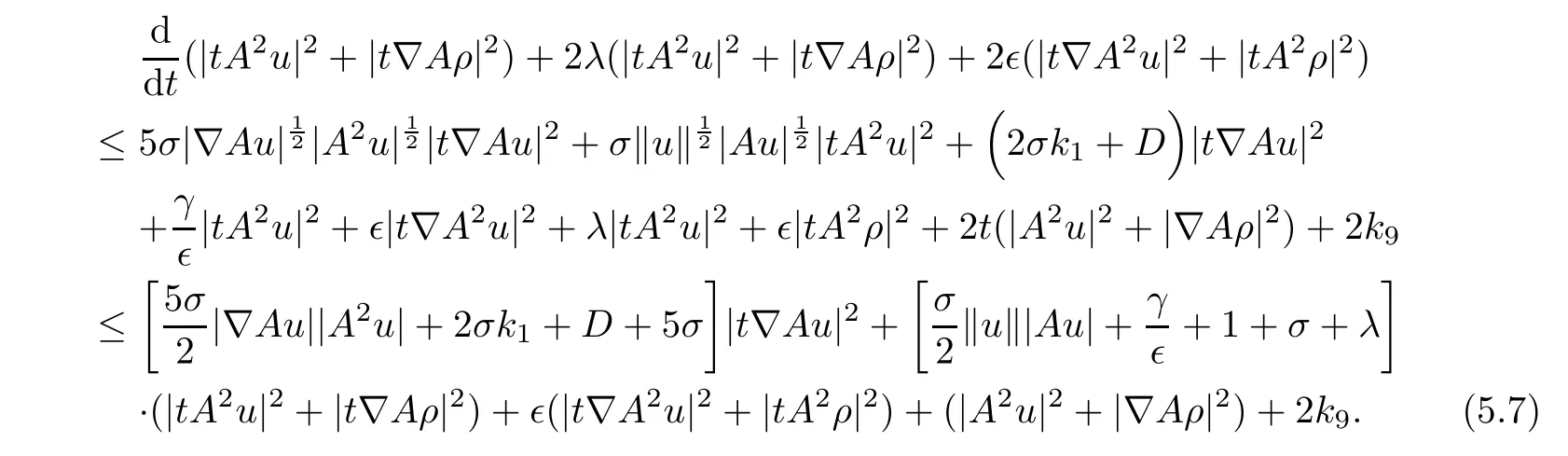
Using the Poincaré inequality,we deduce from(5.7)that

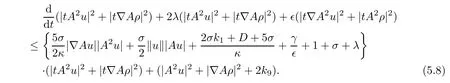
Defining the functions as follows:

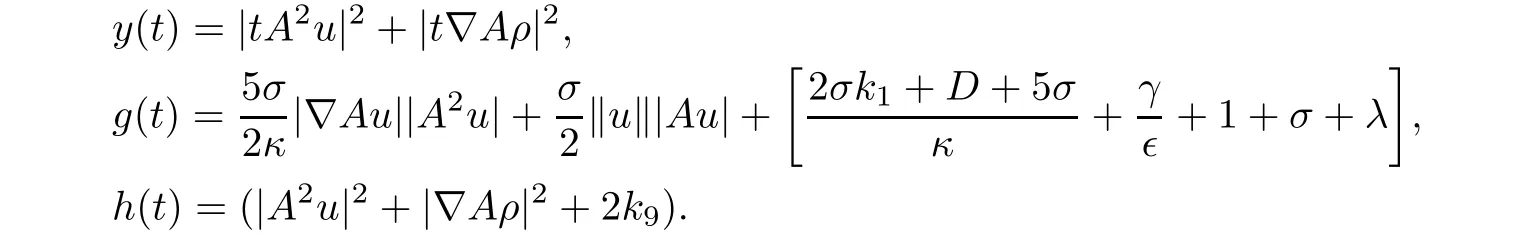
Utilizing estimates(4.6),(4.12),and(4.22),we obtain

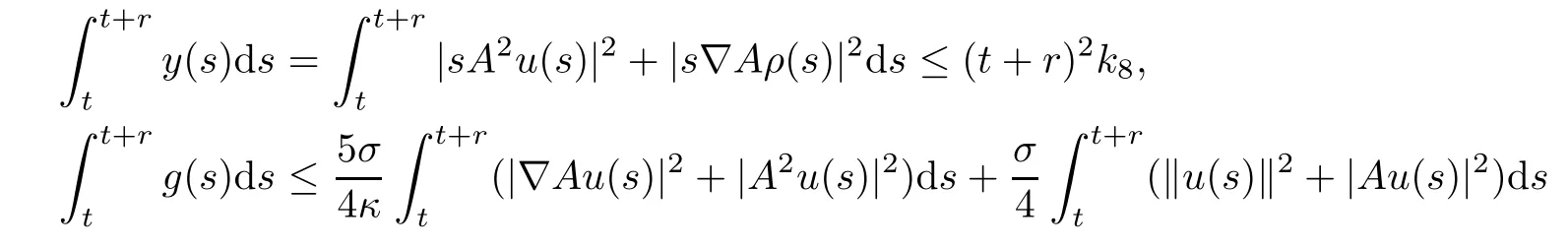
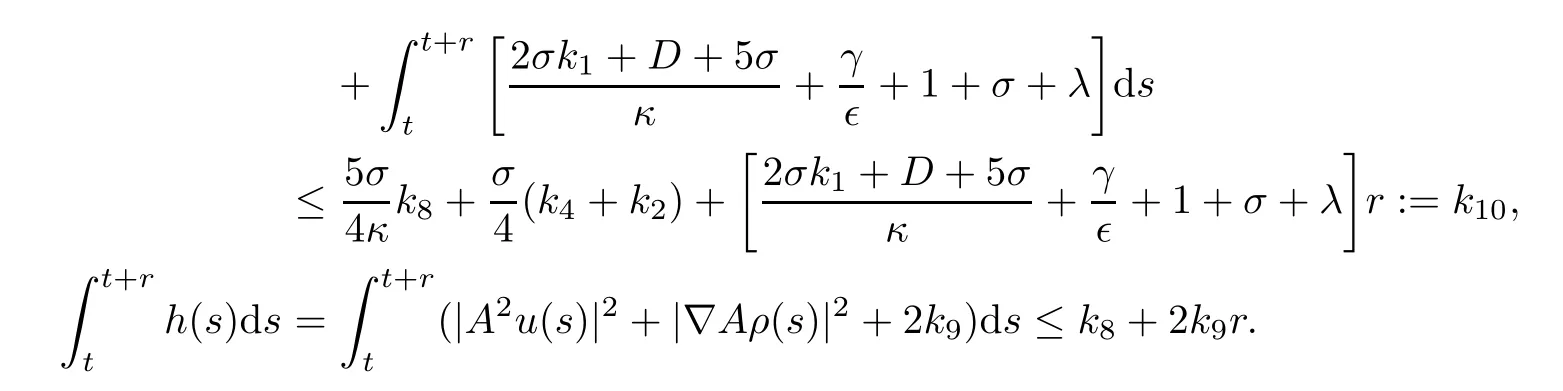
Applying the uniformly Gronwall inequality and the Poincaré inequality,we deduce that

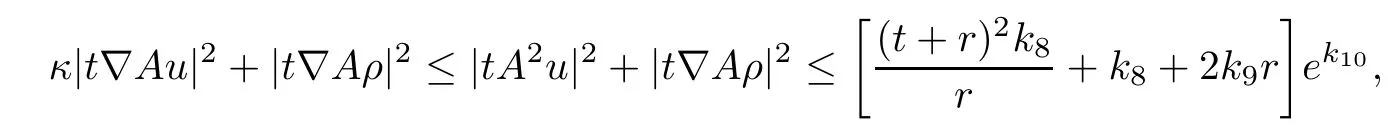
where κ is a positive constant as before.It thus transpires that

Noting that the space H3×H3is compactly embedded into H2×H2,for any bounded set B of H2×H2,by means of the Ascoli-Arzela theorem,it follows from(5.9)and(5.10)that there exists a t0=t0(B)＞0 such that the semigroup S(t)is uniformly compact,that is,is relatively compact in H2×H2.Hence,Lemma 2.1 can be applied to guarantee the existence of the global attractor A in H2×H2.

Indeed,the global attractor is given by the ω-limit set of B(0,R)2as A= ω(B(0,R)2),where B(0,R)is the open ball with radiusobtained in the proof of Theorem 2.2.Thus,the proof of Theorem 2.3 is completed.

[1]Alarcon E A,Iorio R J.The existence of global attractors for a class of nonlinear dissipative evolution equations.Proceedings of the Royal Society of Edinburgh Section A:Mathematics,2005,135(5):887–913

[2]Babin A V,Vishik M I.Attractors of Evolution Equations//Attractors of evolution equations.North-Holland,1992

[3]de Monvel A B,Shepelsky D.Riemann-Hilbert approach for the Camassa-Holm equation on the line.Comptes Rendus Mathematique,2006,343(10):627–632

[4]Beals R,Sattinger D H,Szmigielski J.Multi-peakons and a theorem of Stieltjes.Inverse Problems,1999,15(1):L1–L4

[5]Constantin A,McKean H P.A shallow water equation on the circle.Communications on Pure and Applied Mathematics,1999,52(8):949–982

[6]Camassa R,Holm D D.An integrable shallow water equation with peaked solitons.Physical Review Letters,1993,71(11):1661–1664

[7]Camassa R,Holm D D,Hyman J M.A new integrable shallow water equation.Advances in Applied Mechanics,1994,31:1–33

[8]Chen R M,Liu Y.Wave breaking and global existence for a generalized two-component Camassa-Holm system.International Mathematics Research Notices,2010,2011(6):1381–1416

[9]Chen M,Zhang Y.A two-component generalization of the Camassa-Holm equation and its solutions.Letters in Mathematical Physics,2006,75(1):1-15

[10]Constantin A,Strauss W A.Stability of peakons.Communications on Pure and Applied Mathematics,2000,53(5):603–610

[11]Constantin A,Strauss W A.Stability of a class of solitary waves in compressible elastic rods.Physics Letters A,2000,270(3):140–148

[12]Constantin A.On the scattering problem for the Camassa-Holm equation//Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.The Royal Society,2001,457(2008):953–970

[13]Constantin A.On the inverse spectral problem for the Camassa-Holm equation.Journal of Functional Analysis,1998,155(2):352–363

[14]Constantin A,Gerdjikov V S,Ivanov R I.Inverse scattering transform for the Camassa-Holm equation.Inverse Problems,2006,22(6):2197–2207

[15]Ding D,Tian L.The attractor in dissipative Camassa-Holm equation.Acta Mathematicae Applicatae Sinica,2004,27(3):536–545

[16]Dai H H.Model equations for nonlinear dispersive waves in a compressible Mooney-Rivlin rod.Acta Mechanica,1998,127(1/4):193–207

[17]Escher J,Lechtenfeld O,Yin Z.Well-posedness and blow-up phenomena for the 2-component Camassa-Holm equation.Discrete and continuous dynamical systems,2007,19(3):493–513

[18]Falqui G.On a Camassa-Holm type equation with two dependent variables.Journal of Physics A:Mathematical and General,2005,39(2):327–342

[19]Fuchssteiner B,Fokas A S.Symplectic structures,their B?cklund transformations and hereditary symmetries.Physica D:Nonlinear Phenomena,1981,4(1):47–66

[20]Wei F,Da-Jun Z.The Hamiltonian structures ofμ-equations related to periodic peakons.Chinese Physics Letters,2013,30(8):080201

[21]Fuchssteiner B.Some tricks from the symmetry-toolbox for nonlinear equations:generalizations of the Camassa-Holm equation.Physica D:Nonlinear Phenomena,1996,95(3/4):229–243

[22]Guan C,Yin Z.Global existence and blow-up phenomena for an integrable two-component Camassa-Holm shallow water system.Journal of Differential Equations,2010,248(8):2003–2014

[23]Gui G,Liu Y.On the global existence and wave-breaking criteria for the two-component Camassa-Holm system.Journal of Functional Analysis,2010,258(12):4251–4278

[24]Gui G,Liu Y.On the Cauchy problem for the two-component Camassa-Holm system.Mathematische Zeitschrift,2011,268(1):45–66

[25]Gui G,Liu Y,Zhu M.On the wave-breaking phenomena and global existence for the generalized periodic Camassa-Holm equation.International Mathematics Research Notices,2011,2012(21):4858–4903

[26]Guo F,Gao H,Liu Y.On the wave-breaking phenomena for the two-component Dullin-Gottwald-Holm system.Journal of the London Mathematical Society,2012,86(3):810–834

[27]Gurevich A V,Zybin K P,Gnedin N Y,et al.Nondissipative gravitational turbulence.Zh Eksp Teor Fiz,1988,94:3–25

[28]Hunter J K,Saxton R.Dynamics of director fields.SIAM Journal on Applied Mathematics,1991,51(6):1498–1521

[29]Hunter J K,Zheng Y.On a completely integrable nonlinear hyperbolic variational equation.Physica D:Nonlinear Phenomena,1994,79(2/4):361–386

[30]Ito M.Symmetries and conservation laws of a coupled nonlinear wave equation.Physics Letters A,1982,91(7):335–338

[31]Ivanov R.Two-component integrable systems modelling shallow water waves:the constant vorticity case.Wave Motion,2009,46(6):389–396

[32]Johnson R S.Camassa-Holm,Korteweg-de Vries and related models for water waves.Journal of Fluid Mechanics,2002,455:63–82

[33]Kolev B.Poisson brackets in Hydrodynamics.Discrete and Continuous Dynamical Systems-Series A,2007,19(3):555–574

[34]Khesin B,Lenells J,Misio lek G.Generalized Hunter-Saxton equation and the geometry of the group of circle diffeomorphisms.Mathematische Annalen,2008,342(3):617–656

[35]Liu J,Yin Z.On the Cauchy problem of a periodic 2-componentμ-Hunter-Saxton system.Nonlinear Analysis:Theory,Methods&Applications,2012,75(1):131–142

[36]Liu J.The Cauchy problem of a periodic 2-componentμ-Hunter-Saxton system in Besov spaces.Journal of Mathematical Analysis and Applications,2013,399(2):650–666

[37]Liu J,Yin Z.Global weak solutions for a periodic two-componentμ-Hunter-Saxton system.Monatshefte für Mathematik,2012,168(3/4):503–521

[38]Lenells J,Misio lek G,Ti?glay F.Integrable evolution equations on spaces of tensor densities and their peakon solutions.Communications in Mathematical Physics,2010,299(1):129–161

[39]Lenells J.Conservation laws of the Camassa-Holm equation.Journal of Physics A:Mathematical and General,2005,38(4):869–880

[40]Olver P J,Rosenau P.Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support.Physical Review E,1996,53(2):1900–1906

[41]Tian L,Fan J.The attractor on viscosity Degasperis-Procesi equation.Nonlinear Analysis:Real World Applications,2008,9(4):1461–1473

[42]Tian L,Gao Y.The global attractor of the viscous Fornberg-Whitham equation.Nonlinear Analysis:Theory,Methods&Applications,2009,71(11):5176–5186

[43]Tian L,Tian R.The attractor for the two-dimensional weakly damped KdV equation in belt field.Nonlinear Analysis:Real World Applications,2008,9(3):912–919

[44]Tian L,Xu Y,Zhou J.Attractor for the viscous two-component Camassa-Holm equation.Nonlinear Analysis:Real World Applications,2012,13(3):1115–1129

[45]Tian L,Xu Y.Attractor for a viscous coupled Camassa-Holm equation.Advances in Difference Equations,2010,2010(1):512812

[46]Temam R.In finite-dimensional dynamical systems in mechanics and physics.Springer Science&Business Media,2012

[47]Wang F,Li F,Chen Q.Wave breaking and global existence for a weakly dissipative generalized twocomponent μ-Hunter-Saxton system.Nonlinear Analysis:Real World Applications,2015,23:61–77

[48]Yin Z.On the Structure of Solutions to the Periodic Hunter-Saxton Equation.SIAM Journal on Mathematical Analysis,2004,36(1):272–283

[49]Zuo D.A two-componentμ-Hunter-Saxton equation.Inverse Problems,2010,26(8):085003

[50]Zong X,Sun S.On the global attractor of the two-component π-Camassa-Holm equation with viscous terms.Nonlinear Analysis:Real World Applications,2014,20:82–98

[51]Zheng S.Nonlinear evolution equations.CRC Press,2004