Solving Fractional Integro-Differential Equations by Using Sumudu Transform Method and Hermite Spectral Collocation Method
Y. A. Amer, A. M. S. Mahdy, and E. S. M. Youssef
1 Introduction
A lot of problems can be modeled by fractional integro-differential equations from various sciences and engineering applications. In addition to the fact that many problems cannot be found analytical solutions to them and therefore, once you get a solution is a result of a good result solutions, using numerical methods, will be very helpful. Recently, several numerical methods to solve fractional integro-differential equations (FIDEs) [Zedan,Tantawy, Sayed et al. (2017); Oyedepo, Taiwo, Abubakar et al. (2016); Wang and Zhu(2017)] have been given. Since the example collocation method for solving the nonlinear fractional Langevin equation [Bhrawy and Alghamdi (2012); Yang, Chen and Huang(2014)]. A Chebyshev polynomials method is introduced in Bhrawy et al. [Bhrawy and Alofi(2013)], Doha et al. [Doha, Bhrawy and Ezz-Eldien (2011)], Irandoust-pakchin et al.[Irandoust-pakchin, Kheiri and Abdi-mazraeh (2013)] for solving multiterm fractional orders differential equations and nonlinear Volterra and Fredholm Integro-differential equations of fractional order. The authors in Rathore et al. [Rathore, Kumar, Singh et al.(2012)] applied variational iteration method for solving fractional Integro-differential equations with the nonlocal boundary conditions and more methods in Wang et al. [Wang,Han and Xie (2012)], Lin et al. [Lin, Gu and Young (2010)].
In this paper Sumudu transform method [Wang, Han and Xie (2012); Lin, Gu and Young(2010); Singh and Kumar (2011); Ganji (2006); Hashim, Chowdhurly and Mawa (2008);He (1999); Liao (2005); Amer, Mahdy and Youssef (2017)] and Hermite spectral collocation method [Andrews (1985); Solouma and Khader (2016); Bagherpoorfard and Ghassabzade (2013)]; Bojdi, Ahmadi-Asl and Aminataei (2013); Brill (2002); Bialecki(1993); Dyksen and Lynch (2000); He (1999)] is applied to solving fractional integro differential equations.
In this paper, we are concerned with the numerical solution of the following linear fractional integro-differential equation [Bhrawy and Alofi(2013); Doha, Bhrawy and Ezz-Eldien (2011); Irandoust-pakchin, Kheiri and Abdi-mazraeh (2013); Mohammed (2014)]:
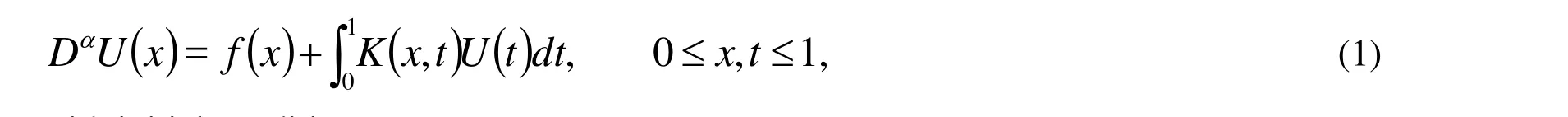
with initial conditions:

2 Basic definitions of fractional calculus
In this section, we present the basic definitions and properties of the fractional calculus theory, which are used further in this paper
Definition 1:A real functionis said to be in the spaceif there exists a real numbersuch thatwhereand it is said to be in the spaceif
Definition 2:The Caputo fractional derivative operatorof orderis defined in the following form [El-Sayed and Salman (2013); El-Sayed and Salman (2013); Elsadany and Matouk (2015)]:

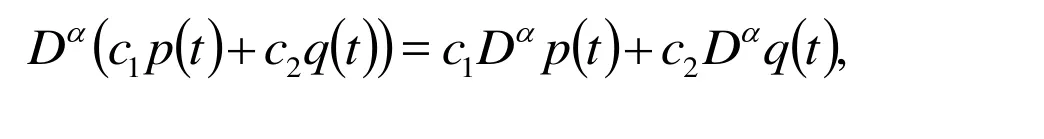
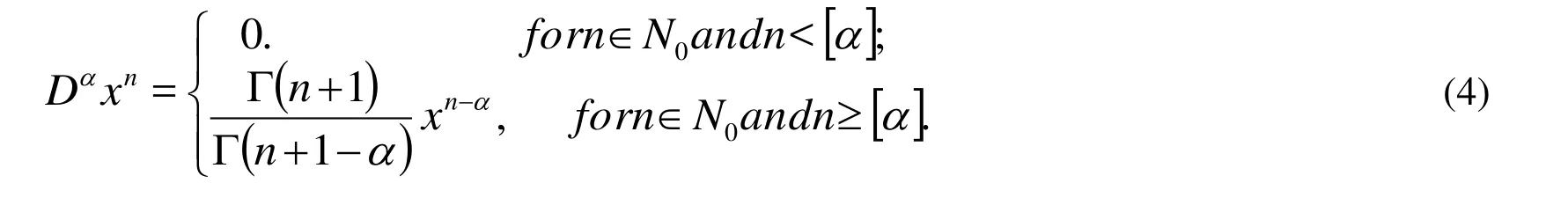
Definition 3:The Sumudu transform is defined over the set of functions [Singh and Kumar(2011); Ganji (2006)]
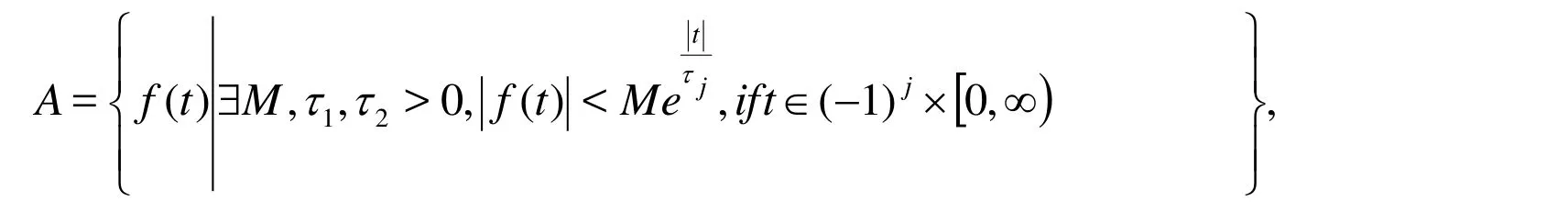
by the following formula:
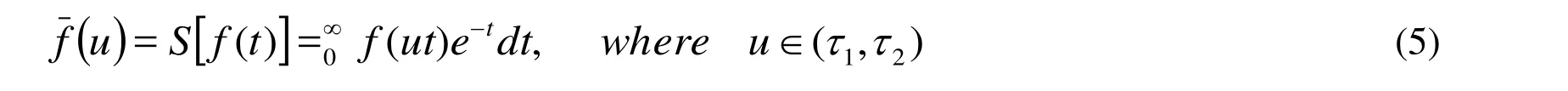
where
Some special properties of the sumudu transform are as follows [Belgacem and Karaballi(2006)]:
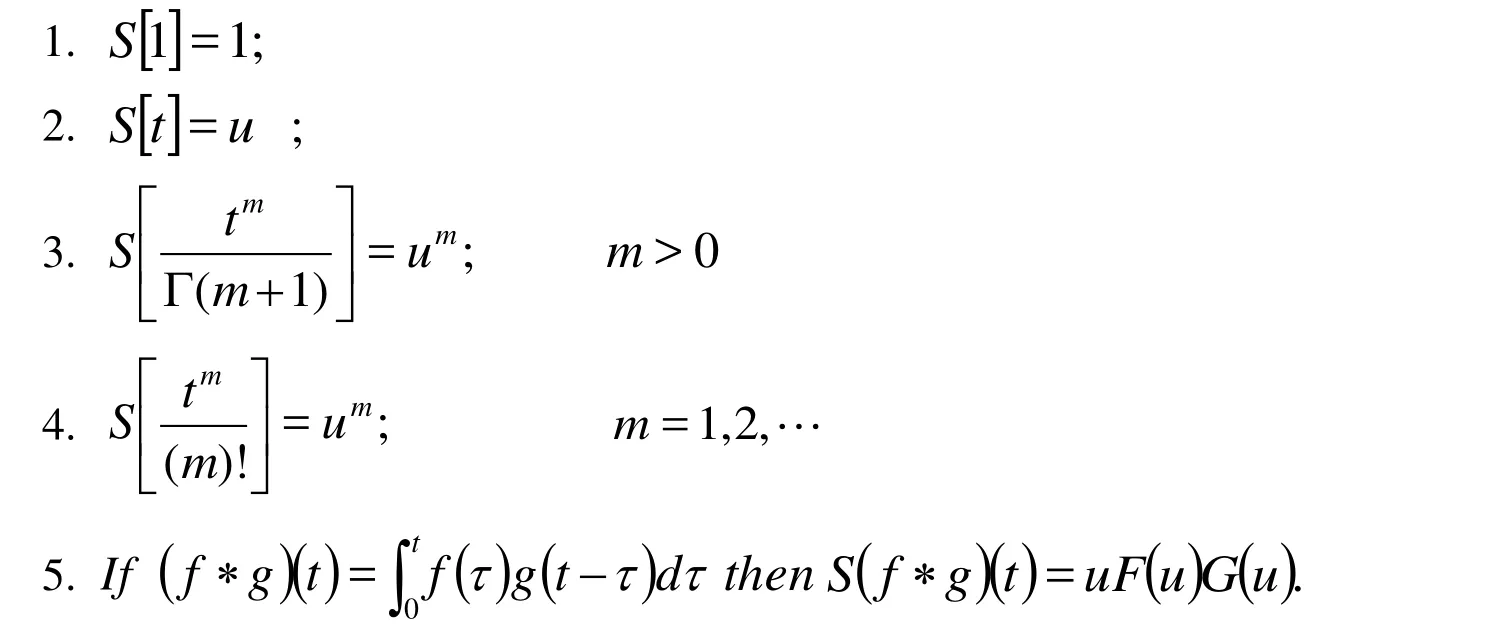
Definition 4:The Sumudu transform of Caputo fractional derivative is defined as follows[Amer, Mahdy and Youssef (2017); Belgacem and Karaballi (2006)]:

Theorem:[Singh and Kumar (2011); Amer, Mahdy and Youssef (2017)]
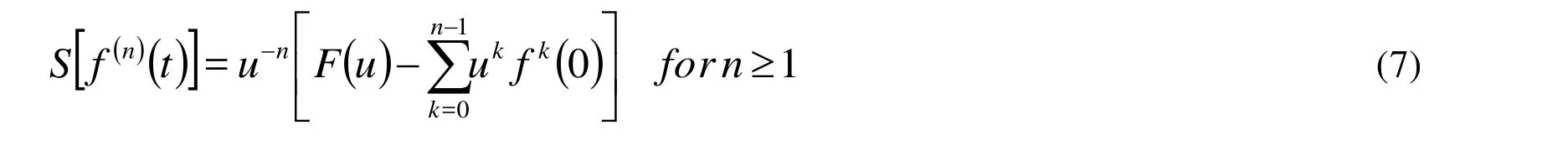
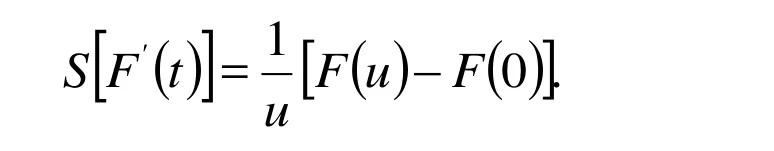
This theorem is very important to calculate approximate solution of the problems and for more details in Singh et al. [Singh and Kumar (2011)], Amer et al. [Amer, Mahdy and Youssef (2017)]
Definition 5:The Hermite polynomials are given by Andrews [Andrews (1985)], Solouma et al. [Solouma and Khader (2016)], Bagherpoorfard et al. [Bagherpoorfard and Ghassabzade (2013)], Bojdi et al. [Bojdi, Ahmadi-Asl and Aminataei (2013)], Brill [Brill(2002)], Bialecki [Bialecki (1993)], Dyksen et al. [Dyksen and Lynch (2000)], He [He(1999)]:

A lot of the properties of these polynomials are:
The Hermite polynomials evaluated at zero argumentand are have called Hermite number as follows: [Andrews (1985); Solouma and Khader (2016)]
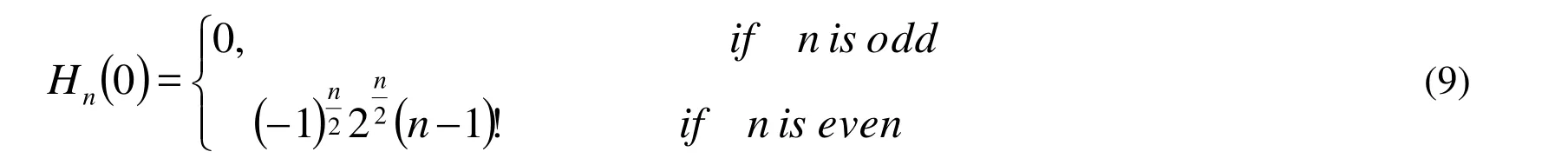

3 The homotopy perturbation sumudu transform method
In order to elucidate the solution procedure of this method, we consider a general fractional nonlinear differential equation of the form [Singh and Kumar (2011); Ganji (2006);Hashim, Chowdhurly and Mawa (2008); He (1999); Liao (2005); Amer, Mahdy and Youssef (2017)]:

Applying the Sumudu transform (denoted throughout this paper by) on both sides of Eq.(11), we have
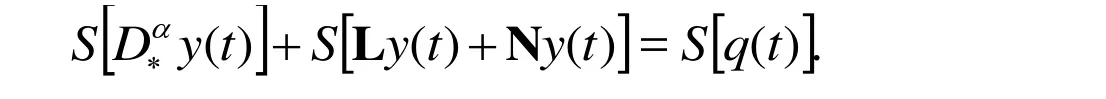
Using the property of the Sumudu transform and the initial conditions in Eq. (12), we have
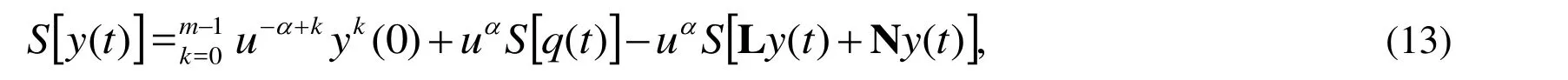
Operating with the Sumudu inverse on both sides of Eq. (13) we get



for some Adomian’s polynomials, which can be calculated with the formula [Ghorbani(2009); Jafari and Daftardar-Gejji (2006)]

Substituting Eq. (15) and (17) in Eq. (14), we get
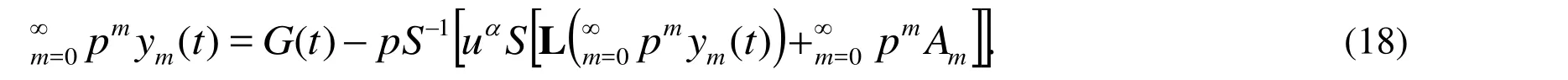
Equating the terms with identical powers of, we can obtain a series of equations as the follows:
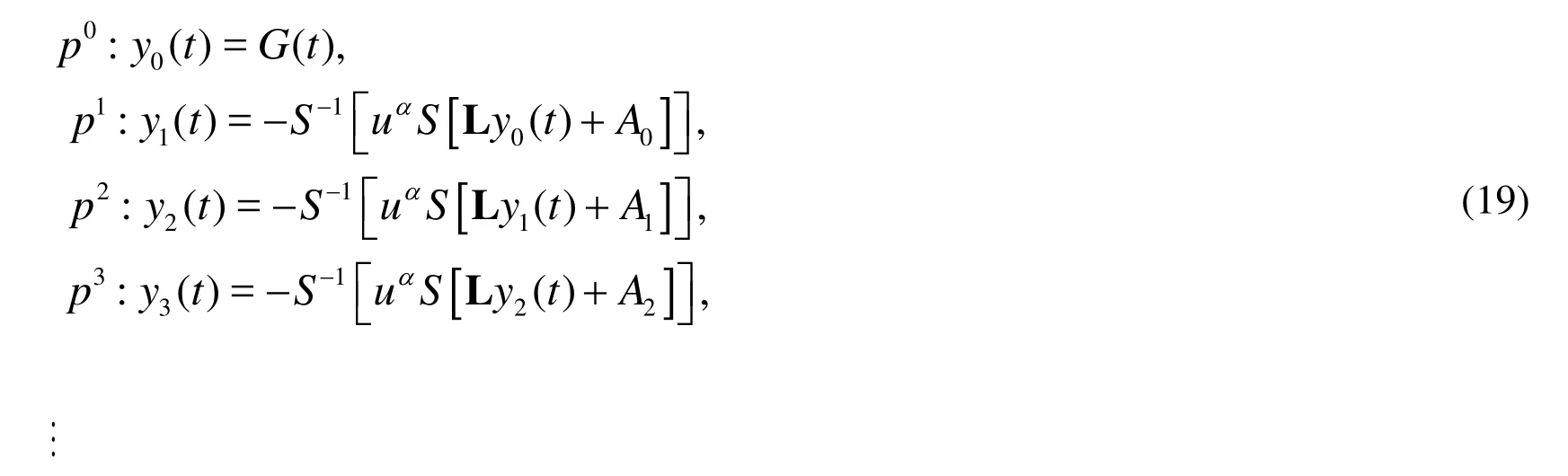
Finally, we approximate the analytical solutionby truncated series as

4 Basic idea of hermite collocation method
In this section the Hermite collocation method is applied to study the numerical solution of the fractional Integro-differential (1).
This method is based on approximating the unknown functionas

At first by Substituting (21) into (1) we obtain
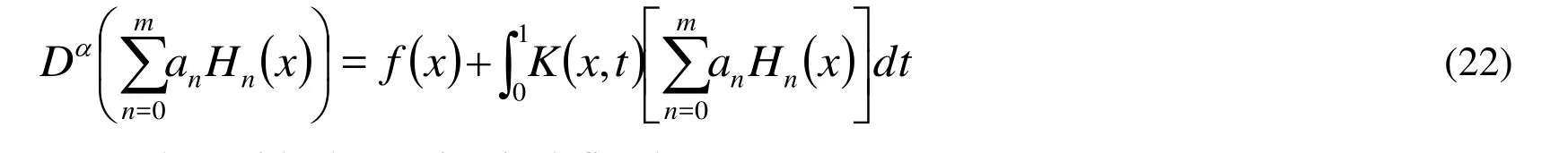
Hence the residual equation is defined as:
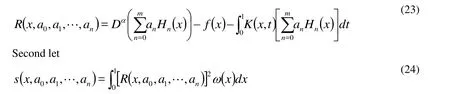
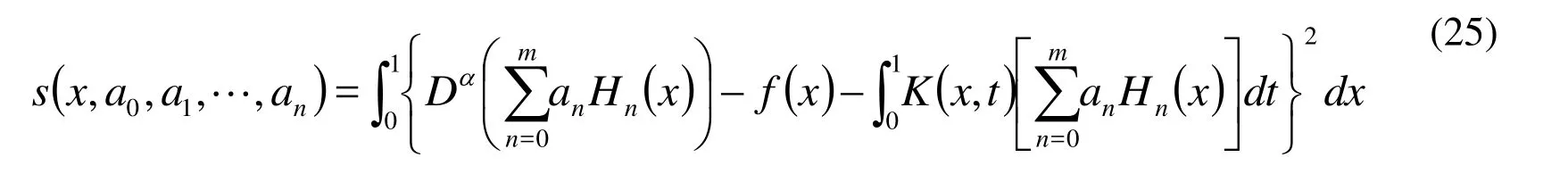
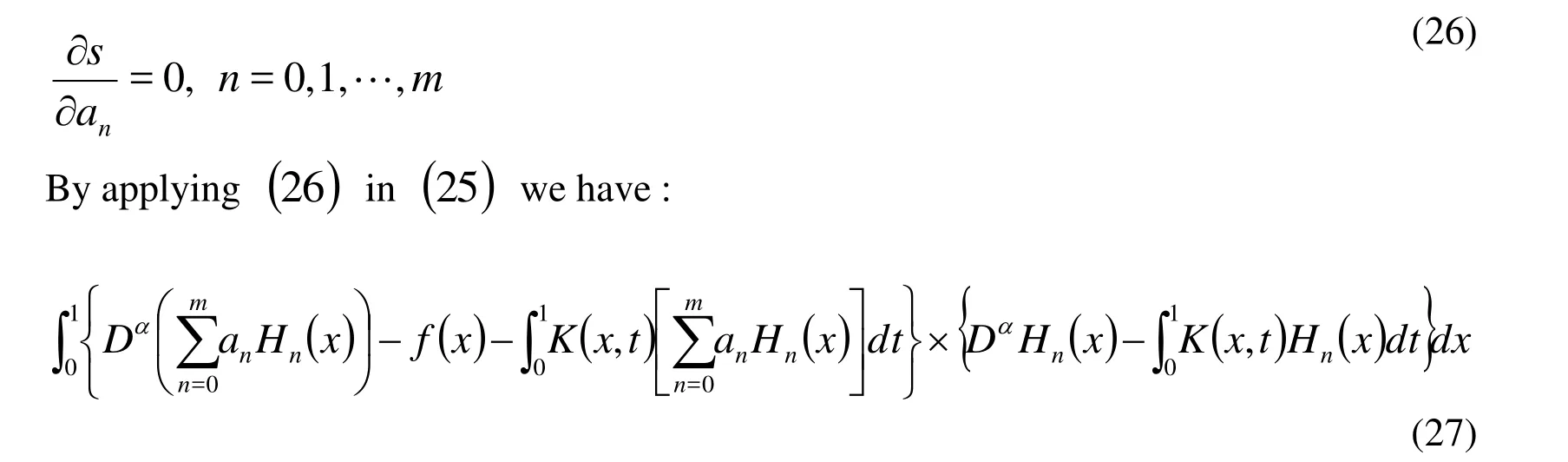
By evaluating the above equation forwe can obtain a system of (n+1)linear equations with (n+1) unknown coefficients, after calculate the coefficientwe substitute in Eq. (21) then we get the solution of)
5 Applications
In this section, to illustrate the method and to show the ability of the method two examples are presented.
Example (1):Cosider the fractional integro-differential equations as

(i)First by using Sumudu transform method
By taking the Sumudu transform on both sides of Eq. (28), thus we get
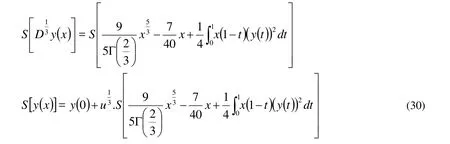
Using the property of the Sumudu transform and the initial condition in Eq. (30), we have

Operating with the Sumudu inverse on both sides of Eq. (31) we get
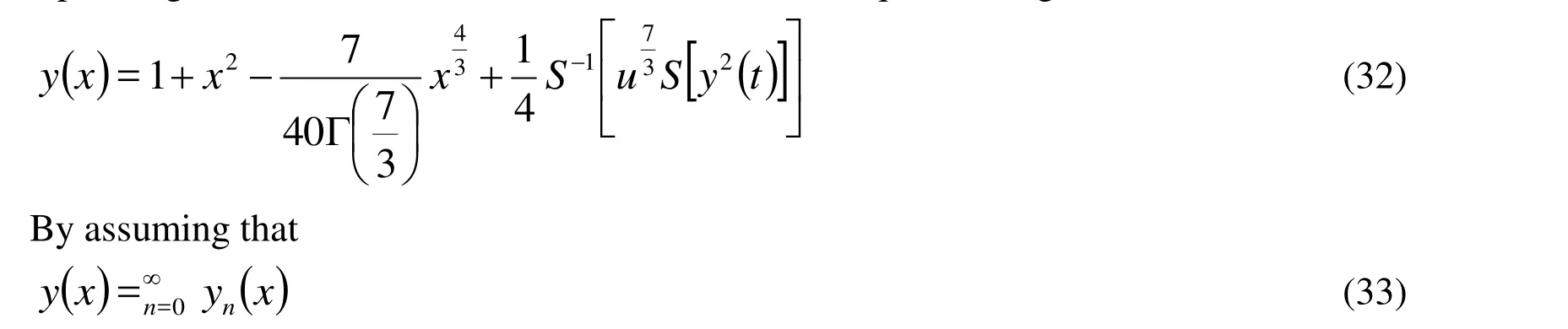
By substituting Eq. (33) in Eq. (32) we have

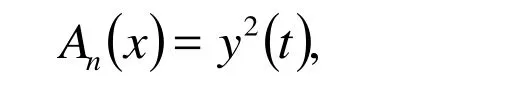
The few components of the Adomian polynomials are given as follows:
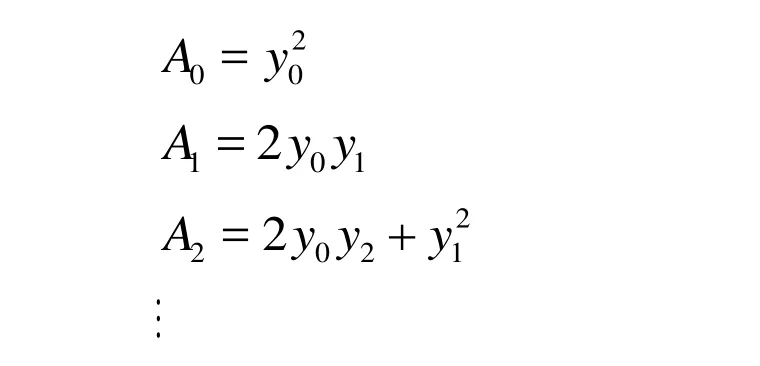
Then we have

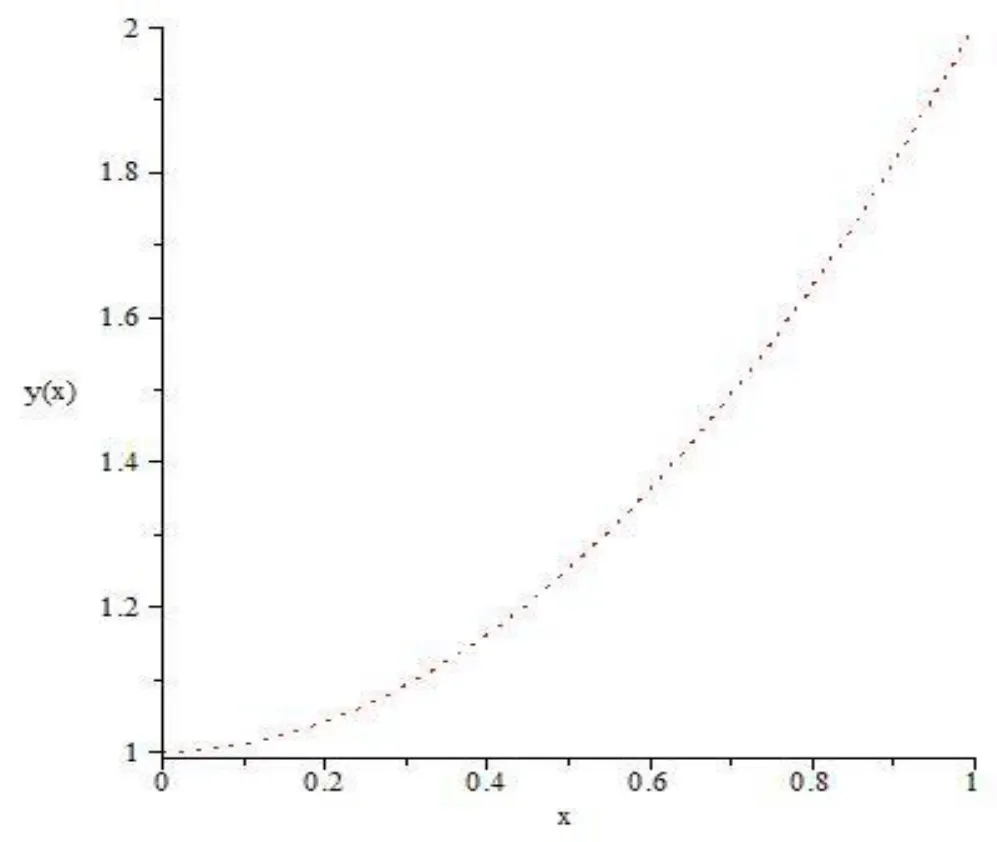
Figure 1: The behavior of y(x) by HPSTM
(ii)By sing Hermite spectral collocation method
First By assuming the approximate of the solution ofwith m=2 as:

Second by Substituting (36) into (28) we obtain
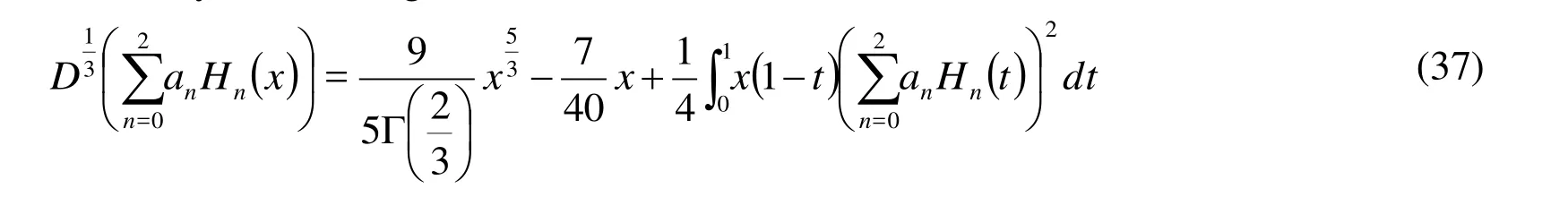
Hence the residual equation is defined as:
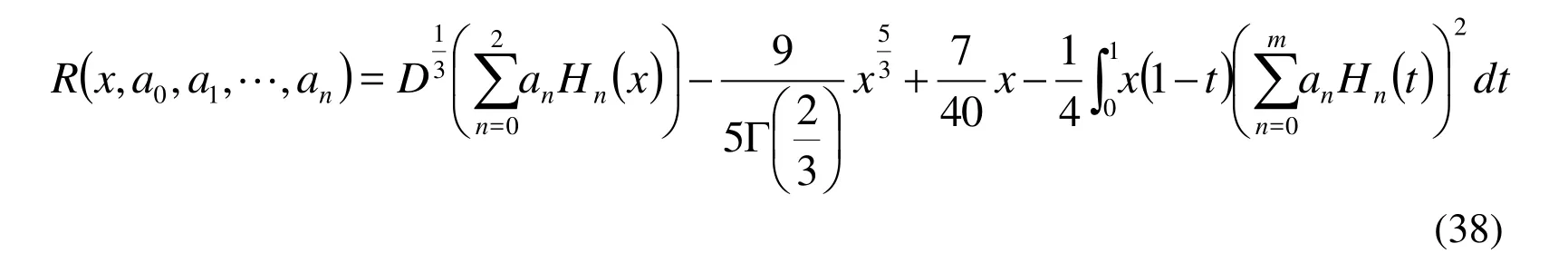
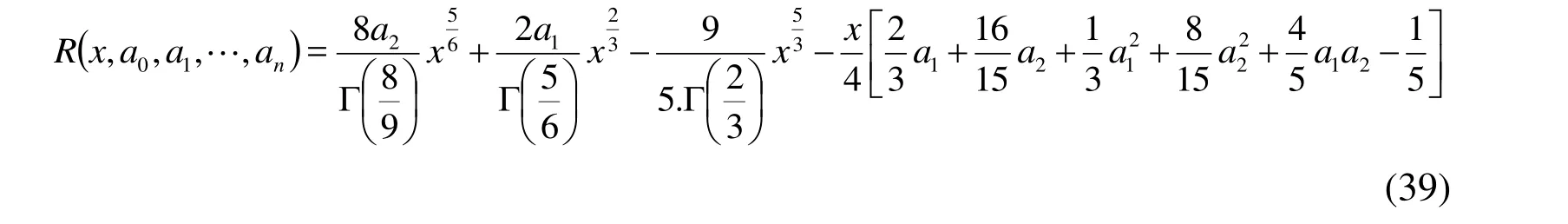
Second let
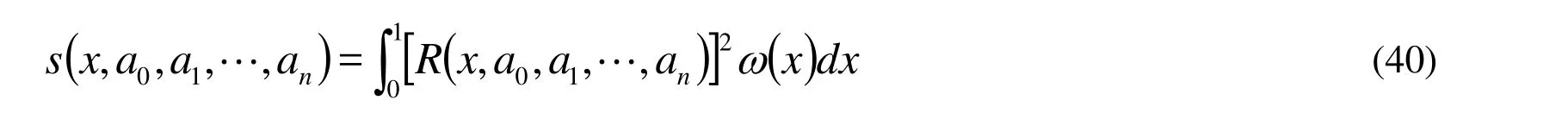
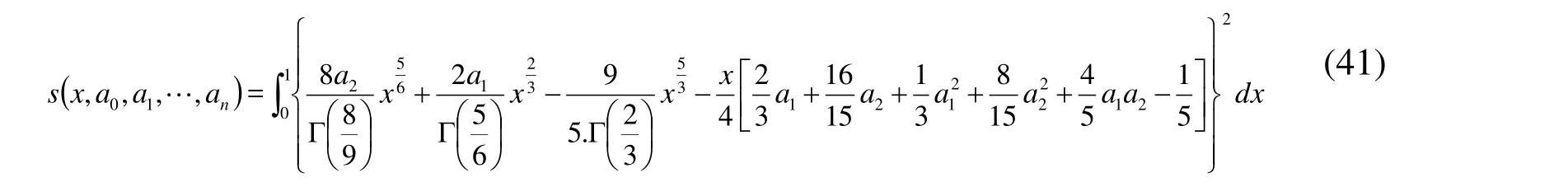
The minimum value of S is obtained by setting

By applying (42) in (41) we have:
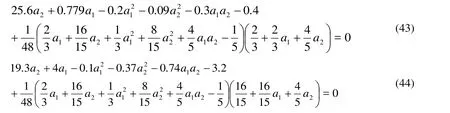
From the initial condhtion y(0)=1 and from Eq. (7) we get

By solving the Eq. (43)-(45) we get the values ofand substituting in Eq.(36) we get the solution as series:

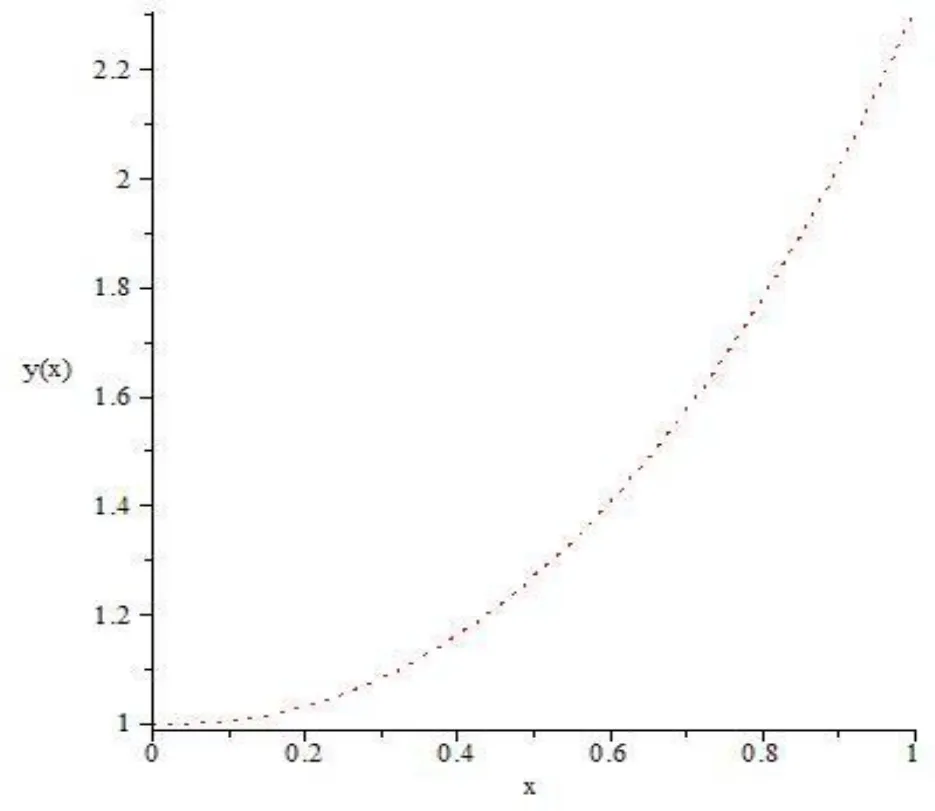
Figure 2: The behavior of y(x) by Hermite collocation method
It is no doubt that the efficiency of this approach is greatly enhanced by the calculation further terms of yby using by using Sumudu transform method and Hermite spectral collocation method.As shown in Fig. 1 and Fig. 2.
Example (2):Consider the systems of fractional integro-differential type as :
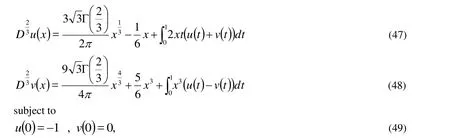
By using the properities of Gamma function of the two Eq. (47), (48) become
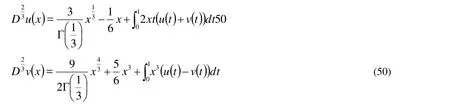
(i)First by using Sumudu transform method
By taking the Sumudu transform on both sides of Eq. (50), thus we get
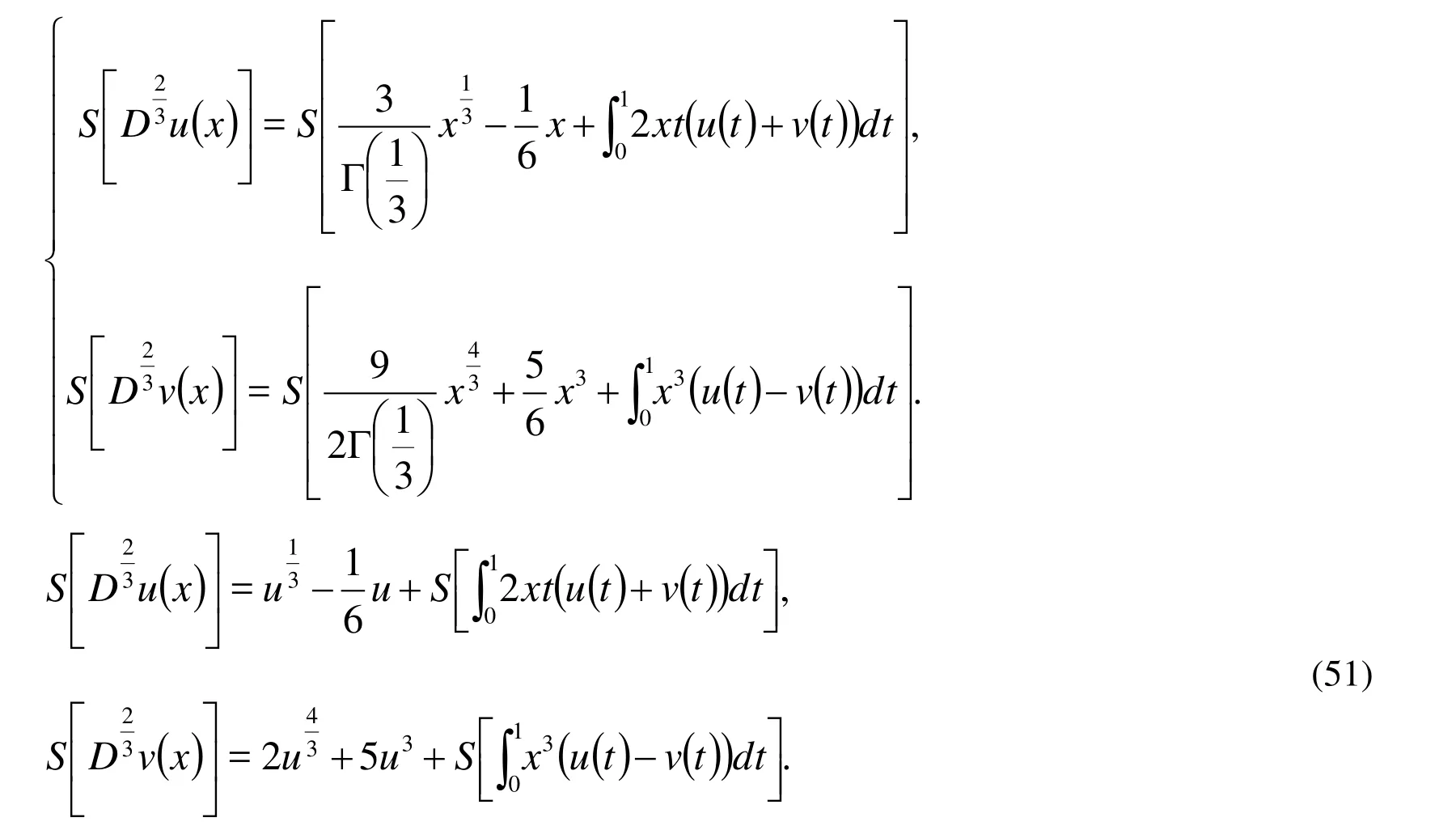
Using the property of the Sumudu transform and the initial condition in Eq. (49), we have
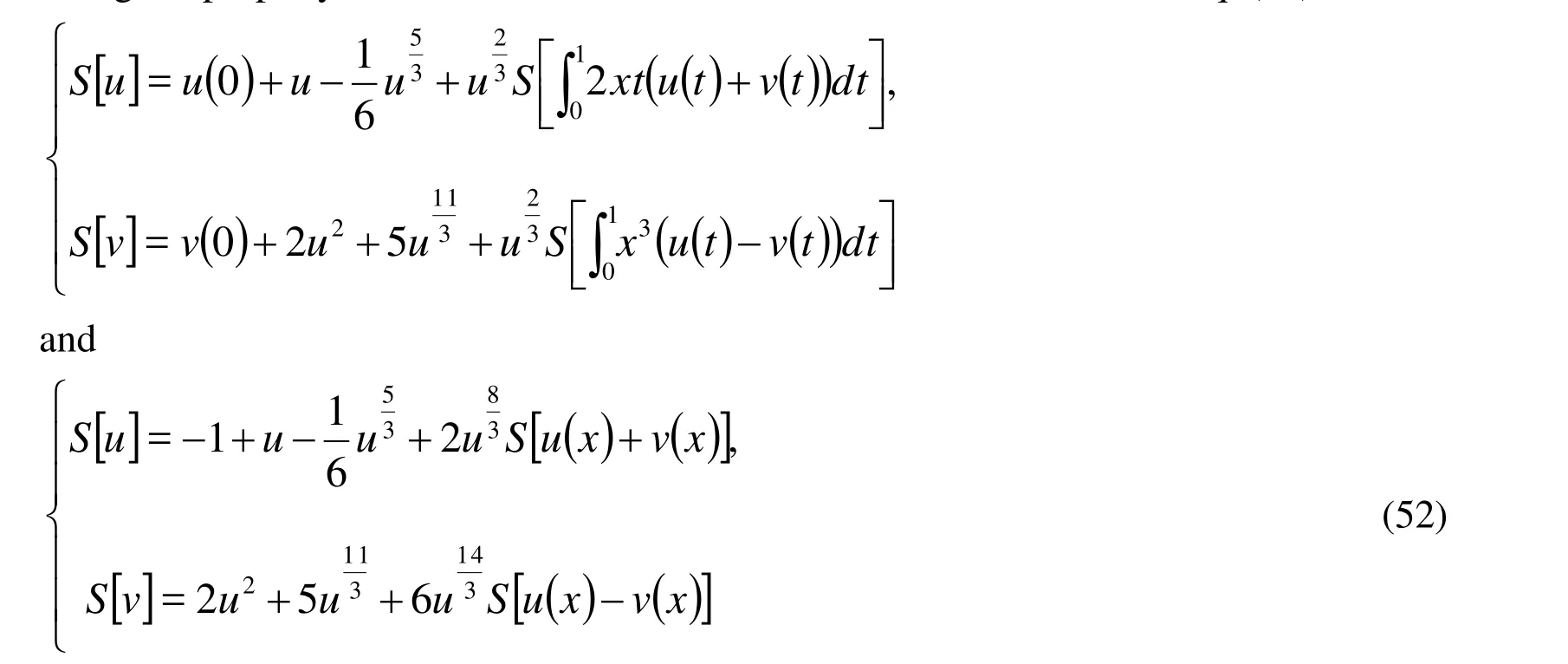
Operating with the Sumudu inverse on both sides of Eq. (52) we get
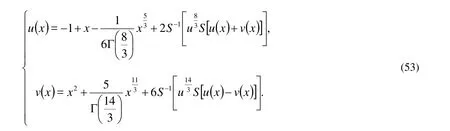
By assuming that

By substituting Eq. (54) in Eq. (53) we have

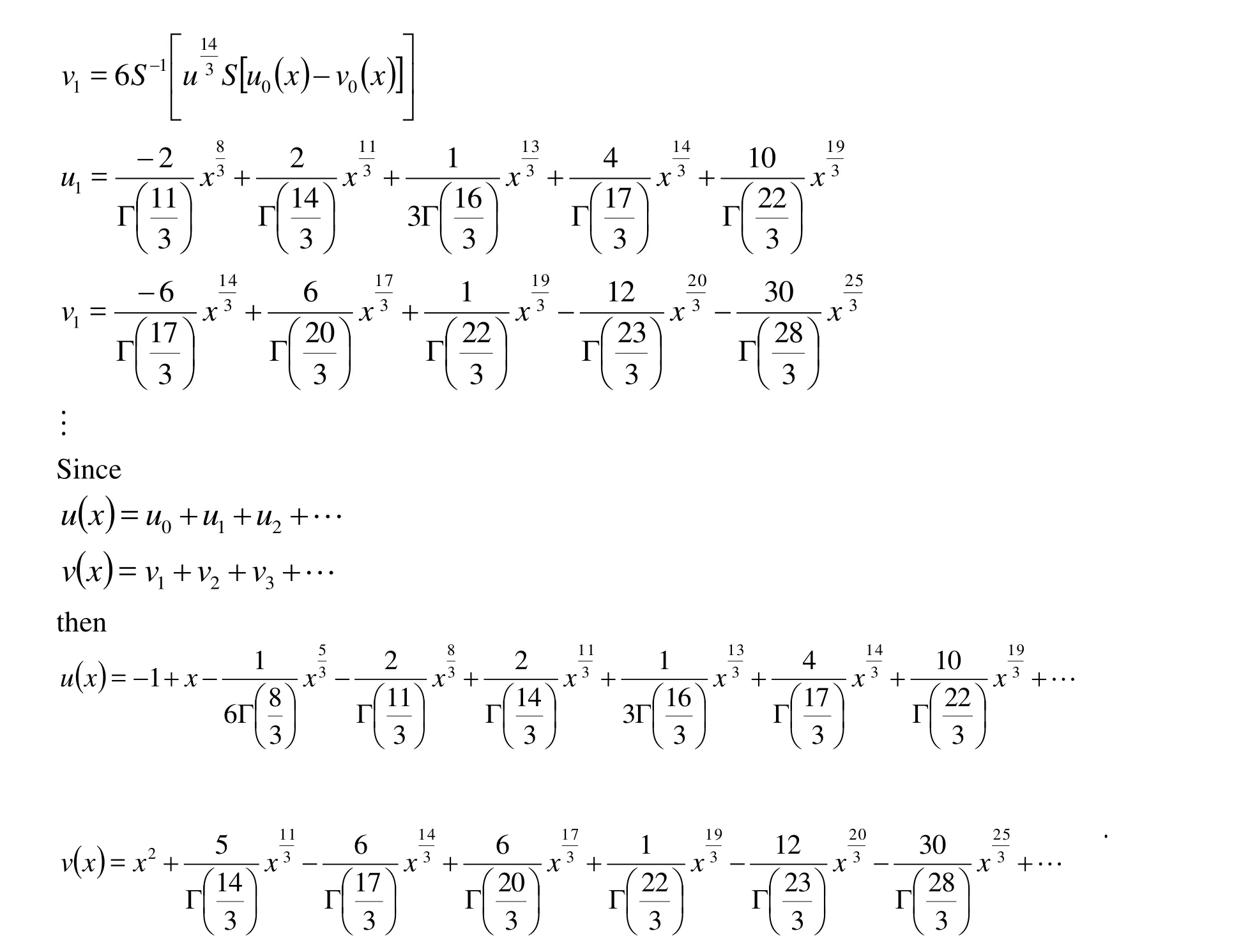
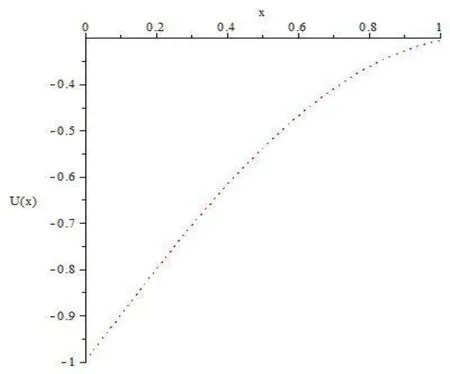
Figure 3: The behavior of u(x) by HPSTM
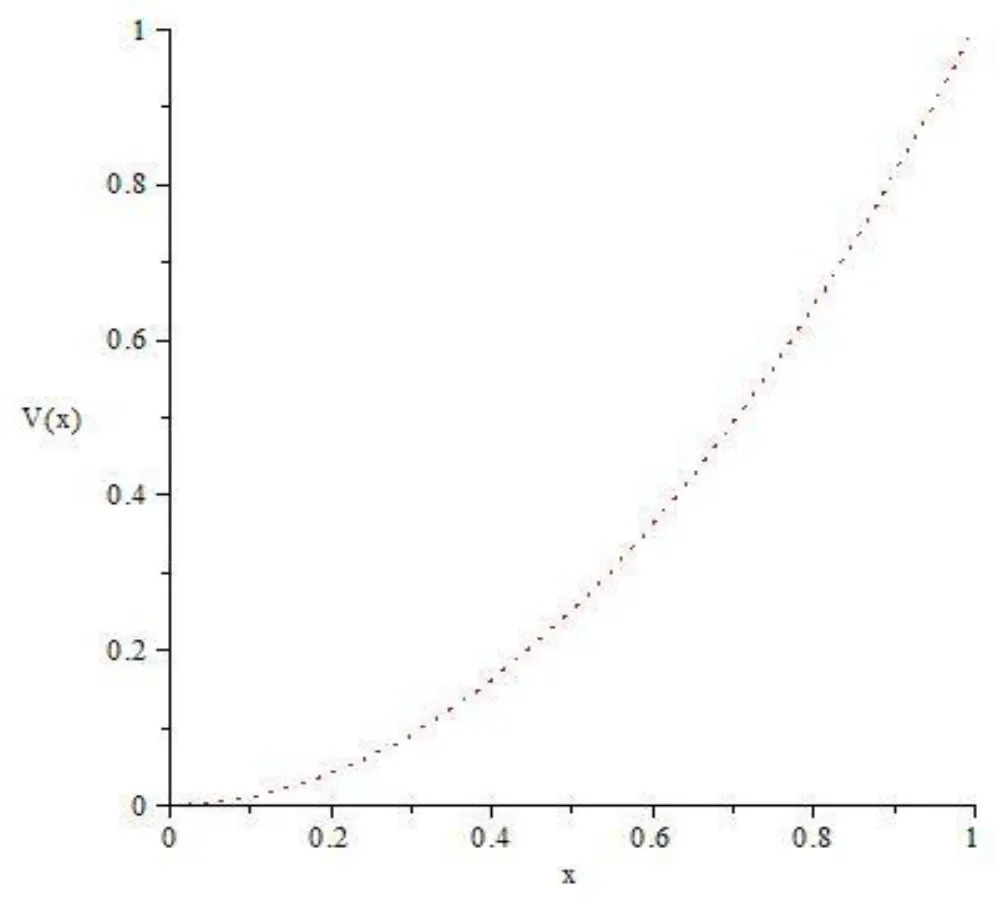
Figure 4: The behavior of v(x) by HPSTM
(ii)By sing Hermite spectral collocation method
First By assuming the approximate of the solution ofwith m=2 as:

Second by Substituting (57) into (50) we obtain
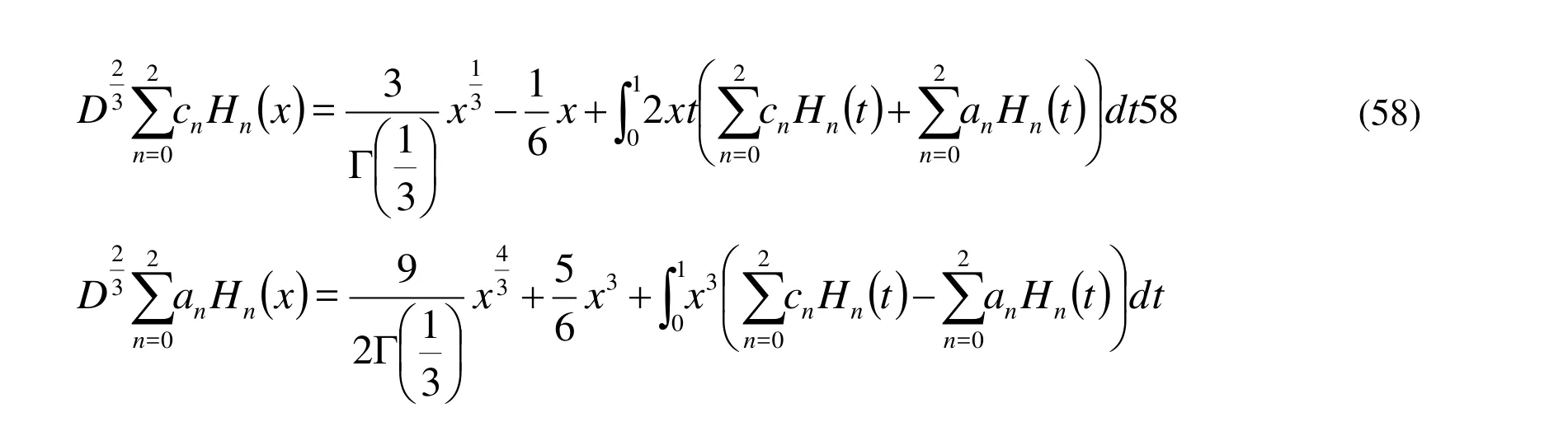
Hence the residual equation is defined as:
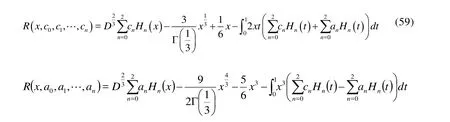
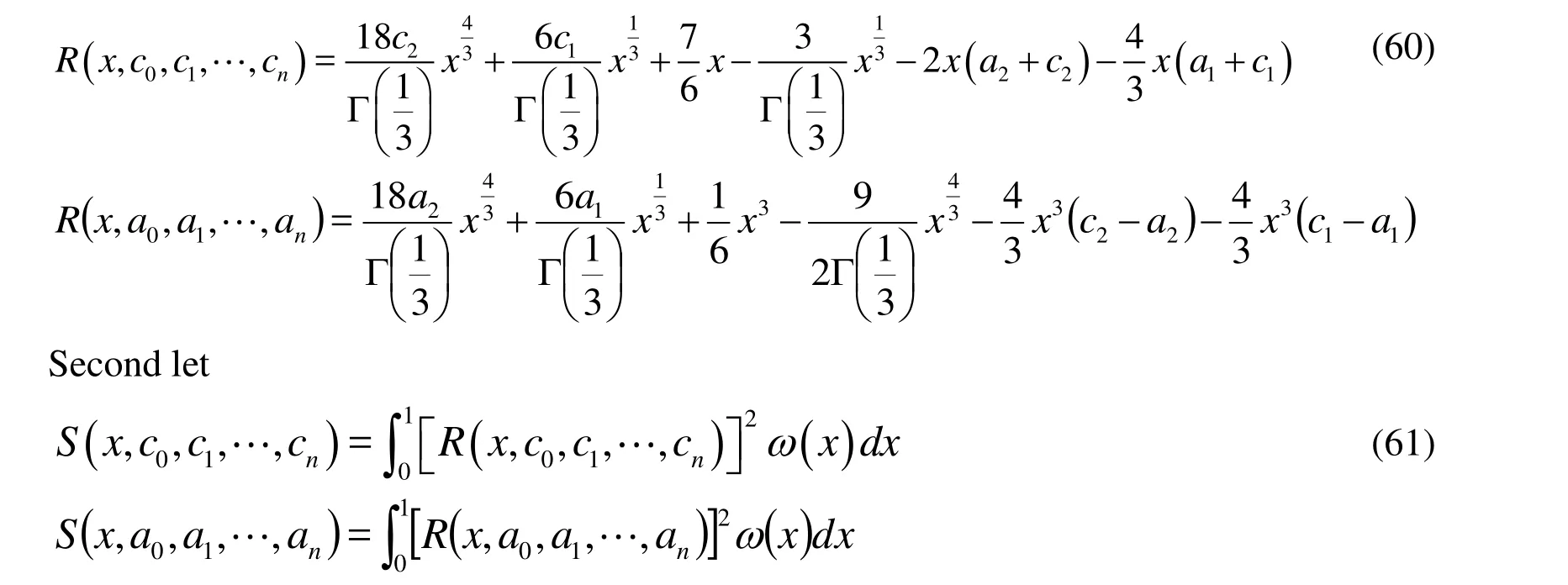
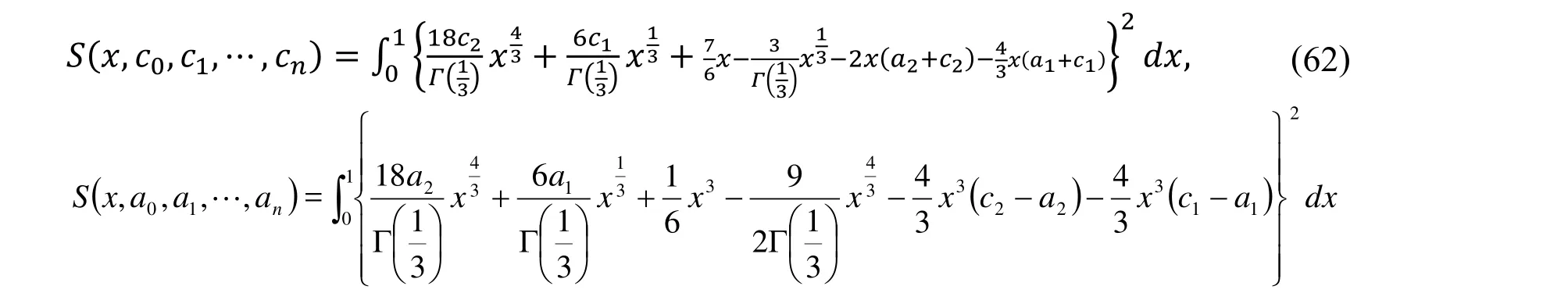
The minimum value of S is obtained by setting


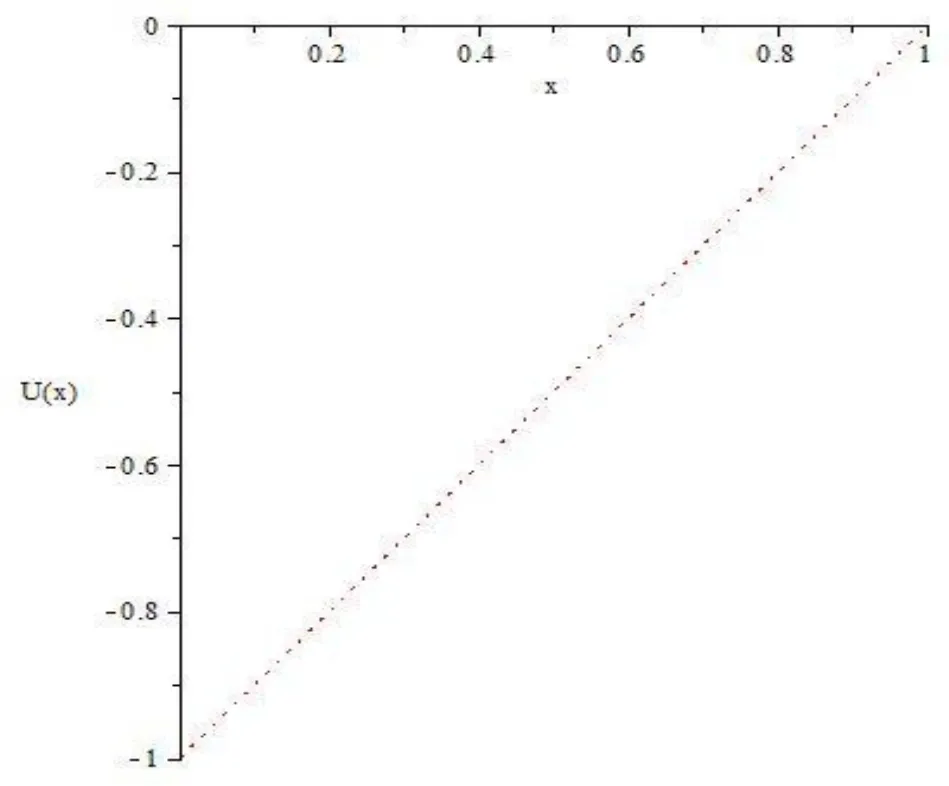
Figure 5: The behavior of u(x) by Hermite collocation method
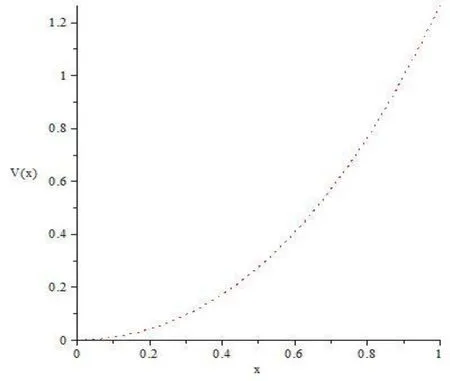
Figure 6: The behavior of v(x) by Hermite collocation method
It is no doubt that the efficiency of this approach is greatly enhanced by the calculation further terms of uby using by using Sumudu transform method and Hermite spectral collocation method. As In Fig. 3 and Fig. 4 show the The behavior of uby using Sumudu transform method and in Fig. 5 and Fig. 6. show the The behavior of uby using the Hermite collocation method.
6 Conclusions
The main aim of this paper is to know that the sumud transform method and Hermite spectral collocation method are of the most important and simplest methods used in solving linear and nonlinear differential equations. This method have been successfully applied to systems of fractional integro-differential equations.in this method we do not need to do the difficult computation for finding the Adomian polynomials. Generally speaking, the proposed method is promising and applicable to a broad class of linear and nonlinear problems in the theory of fractional calculus.
Agarwal, R. P.; El-Sayed, A. M. A.; Salman, S. M.(2013): Fractional-order Chua’s system: discretization, bifurcation and chaos.Advances in Difference Equations, vol. 2013,pp. 320.
Amer, Y. A.; Mahdy, A. M. S.; Youssef, E. S. M.(2017): Solving systems of fractional differential equations using sumudu transform method.Asian Research Journal of Mathematics, vol. 7, no. 2, pp. 1-15.
Andrews, L. C.(1985):Special functions For engineers and applied mathematical.Macmillan publishing company, New York.
Bagherpoorfard, M.; Ghassabzade, F. A.(2013): Hermite matrix polynomial collocation method for linear complex differential equations and some comparisons.Journal of Applied Mathematics and Physics, vol. 1, pp. 58-64.
Belgacem,F. B. M.; Karaballi, A. A.(2006): Sumudu transform fundamental properties in vestigations and applications.Journal of Applied Mathematics and Stochastic Analysis,vol. 2006, pp 1-23, doi:10.1155/JAMSA/2006/910832005.
Bhrawy, A. H.; Alghamdi, M. A.(2012): A shifted Jacobi-Gauss-Lobatto collocation method for solving nonlinear fractional Langevin equation involving two fractional orders in different intervals.Boundary Value Problems, vol. 2012, pp. 62.
Bhrawy, A. H.; Alofi, A. S.(2013): The operational matrix of fractional integration for shifted Chebyshev polynomials.Applied Mathematics Letters, vol. 26, no. 1, pp. 25-31.
Bialecki, B.(1993): A fast domain decomposition poisson solver on a rectangle for Hermite bicubic orthogonal spline collocation.Siam Journal Numerical Analysis, vol. 30,pp. 425-434.
Bojdi, Z. K.; Ahmadi-Asl, S.; Aminataei, A.(2013): Operational matrices with respect to Hermite polynomials and their applications in solving linear differential equations with variable coeffcients.Journal of Linear and Topological Algebra, vol. 2, no. 2, pp. 91-103.
Brill, S. H.(2002): Analytic solution of Hermite collocation discretization of the steady state convection-diffusion equation.International Journal of Differential Equations and Applications, vol. 4, no. 2, pp. 141-155.
Doha, E. H.; Bhrawy, A. H.; Ezz-Eldien,S. S.(2011): Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations.Applied Mathematical Modelling, vol. 35, no. 12, pp. 5662-5672.
Dyksen, W. R. ; Lynch, R. E.(2000): A new decoupling technique for the Hermite cubic collocation equations arising from boundary value problems.Mathematics and Computers in Simulation, vol. 54, pp. 359-372.
Elsadany, A. A.; Matouk, A. E.(2015): Dynamical behaviors of fractional-order Lotka-Voltera predator-prey model and its discretization.Applied Mathematics and Computation,vol. 49, pp. 269-283.
El-Sayed, A. M. A.; Salman, S. M.(2013): On a discretization process of fractional order Riccati’s differential equation.Journal of Fractional Calculus and Applications, vol. 4, no.2, pp. 251-259.
Funaro, D.(1992):Polynomial approximations of differential equations. Springer-Verlag.Ganji, D.(2006): The application of He’s homotopy perturbation method to nonlinear equations arising in heat transfer.Physics Letters A, vol. 355, pp. 337-341.
Ghorbani, A.(2009): Beyond, Adomian polynomials: He polynomials.Chaos Solitons &Fractals, vol. 39, no. 3, pp. 1486-1492.
Hashim, I.; Chowdhurly, M.; Mawa, S.(2008): On multistage homotopy perturbation method applied to nonlinear biochemical reaction model.Chaos, Solitons & Fractals, vol.36, pp. 823-827.
He, J.(1999): Homotopy perturbation technique.Computer Methods in Applied Mechanics and Engineering, vol. 178, no. 3-4, pp. 257-262.
He, J.(1999): Homotopy perturbation technique.Computer Methods in Applied Mechanics and Engineering, vol. 178, no. 3-4, pp. 257-262.
Irandoust-pakchin, S.; Kheiri, H.; Abdi-mazraeh, S.(2013): Chebyshev cardinal functions: an effective tool for solving nonlinear Volterra and Fredholm integro differential equations of fractional order.Iranian Journal of Science and Technology Transaction A: Science, vol. 37, no. 1, pp. 53-62.
Jafari, H.; Daftardar-Gejji, V.(2006): Solving a system of nonlinear fractional differential equations using Adomian decomposition.Journal of Computational and Applied, vol. 196, no. 2, pp. 644-651.
Liao, S.(2005): Comparison between the homotopy analysis method and homotopy perturbation method.AppliedMathematics and Computation, vol. 169, pp. 1186-1194.
Lin,C. Y.; Gu, M. H.; Young, D. L.(2010): The time-marching method of fundamental solutions for multi-dimensional telegraph equations.Computers, Materials & Continua,vol. 18, no. 1, pp. 43-68.
Mohammed,D. S.(2014): Numerical solution of fractional integro-differential equations by least squares method and shifted chebyshev polynomial.Mathematical Problems in Engineering,vol. 2014.
Oyedepo, T.; Taiwo, O. A.; Abubakar, J. U.; Ogunwobi, Z. O.(2016): Numerical studies for solving fractional integro-differential equations by using least squares method and bernstein polynomials.Fluid Mechanics: Open Access, vol. 3, no. 3.
Rathore, S.; Kumar, D.; Singh, J.; Gupta, S.(2012): Homotopy analysis sumudu transform method for nonlinear equations.International Journal of Industrial Mathematics,vol. 4, no. 4, pp. 301-314.
Singh, J.; Kumar, D.(2011): Homotopy perturbation sumudu transform method for nonlinear equations.Advances in Applied Mathematics and Mechanics,vol. 4, no. 4, pp. 165-175.
Solouma, E. M.; Khader, M. M.(2016): Analytical and numerical simulation for solving the system of non-linear fractional dynamical model of marriage.International Mathematical Forum, vol. 11, no. 8, pp. 875-884.
Wang, L.; Han, X.; Xie, Y.(2012): A new iterative regularization Method for solving the dynamic load identification problem.Computers, Materials & Continua, vol. 31, no. 2,pp.113-126.
Wang, Y.; Zhu, L.(2017): Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method.Advances in Difference Equations, doi:10.1186/s13662-017-1085-6.
Yang, Y.; Chen, Y.; Huang, Y.(2014): Spectral-collocation method for fractional Fredholm integro-differential equations.Journal of the Korean Mathematical Society, vol.51, no. 1, pp. 203-224.
Zedan, H. A.; Tantawy, S. S.; Sayed, Y. M.(2017): New solutions for system of fractional integro-differential equations and Abel’s integral equations by chebyshev spectral method.Mathematical Problems in Engineering, vol. 2017.
 Computers Materials&Continua2018年2期
Computers Materials&Continua2018年2期
- Computers Materials&Continua的其它文章
- Coverless Information Hiding Based on the Molecular Structure Images of Material
- Solution of Algebraic Lyapunov Equation on Positive-Definite Hermitian Matrices by Using Extended Hamiltonian Algorithm
- Joint Bearing Mechanism of Coal Pillar and Backfilling Body in Roadway Backfilling Mining Technology
- The Influence of the Imperfectness of Contact Conditions on the Critical Velocity of the Moving Load Acting in the Interior of the Cylinder Surrounded with Elastic Medium
