The Influence of the Imperfectness of Contact Conditions on the Critical Velocity of the Moving Load Acting in the Interior of the Cylinder Surrounded with Elastic Medium
M. Ozisik, M. A. Mehdiyev and S. D. A kb .0arov,
1 Introduction
The development and successful application of modern high-speed underground trains and other types of underground moving wheels requires fundamental study of the corresponding dynamic problems. As usual, underground structures into which such high-speed wheels move are modelled as infinite hollow cylinders surrounded by an elastic or viscoelastic medium. Consequently, the aforementioned dynamical problems can be modelled as the problem of the moving pressure acting on the internal surface of an infinite hollow cylinder surrounded by an elastic or viscoelastic medium. The present paper is concerned namely with these types of problems and it studies the dynamics of the moving point-located, with respect to the cylinder axis, normal forces which are uniformly distributed in the circumferential direction acting on the inner surface of the circular cylinder which is surrounded by an elastic medium.
It should be noted that, in general, the main issue in the investigations of the moving load acting on layered systems is the determination of both the critical velocity of this moving load under which resonance type behavior takes place and of the influence of the problem parameters on the values of this velocity. At the same time, another issue which is also important is to determine the rules of attenuation of the perturbations of the stresses and displacements caused by the moving load with the distance from the point at which this load acts.
Now we consider a brief review of related investigations regarding layered systems and note that the first attempt in this field was made by Achenbach et al. [Achenbach, Keshava and Hermann (1967)] in which the dynamic response of the system consisting of the covering layer and half plane to a moving load was investigated with the use of the Timoshenko theory for describing the motion of the plate. However, the motion of the half-plane was described by using the exact equations of the theory of linear elastodynamics and the plane-strain state was considered. It was established that critical velocity exists in the cases where the plate material is stiffer than that of the half-plane material. Reviews of later investigations, which can be taken as developments of those started in the paper by Achenbach et al. [Achenbach, Keshava and Hermann (1967)], are described in the papers by Dieterman et al. [Dieterman and Metrikine (1997)] and by Metrikine et al. [Metrikine and Vrouwenvelder (2000)]. At the same time, in the paper by Dieterman et al. [Dieterman and Metrikine (1997)], the critical velocity of a point-located time-harmonic varying and unidirectional moving load which acts on the free face plane of the plate resting on the rigid foundation, was investigated. The investigations were made within the scope of the 3D exact equations of the linear theory of elastodynamics and it was established that as a result of the time-harmonic variation of the moving load,two types of critical velocities appear: the first (the second) of which is lower (higher)than the Rayleigh wave velocity in the plate material. Later, similar results were also obtained by Akbarov et al. [Akbarov and Salmanova (2009)], Akbarov et al. [Akbarov and Ilhan (2009)], and Akbarov et al. [Akbarov, Ilhan and Temugan (2015)], which were also discussed in the monograph by Akbarov [Akbarov (2015)].
The aforementioned paper by Metrikine et al. [Metrikine and Vrouwenvelder (2000)]deals with the study of the surface vibration of the layer resting on the rigid foundation and containing a beam on which the moving load acts. In this paper, a two-dimensional problem is considered and the motion of the layer is described by the exact equations of elastodynamics, however, the motion of the beam is described by the Euler-Bernoulli theory. At the same time, it is assumed that the material of the layer has a small viscosity and three types of load are examined, namely constant, harmonically varying and a stationary random load. Note that all the investigations carried out in the papers by Metrikine et al. [Metrikine and Vrouwenvelder (2000)], and Dieterman et al. [Dieterman and Metrikine (1997)] are based on the concept of the critical velocity which is determined through the dispersion diagrams of the corresponding wave propagation.
Up to now, a certain number of investigations have also been made related to the dynamics of the moving load acting on the prestressed system. For instance, in the paper by Kerr [Kerr (1983)], the initial stresses on the values of the critical velocity of the moving load acting on an ice plate resting on water were taken into account. In this paper,the motion of the plate is described by employing the Kirchhoff plate theory and it is established that the initial stretching (compression) of the plate along the load moving direction causes an increase (a decrease) in the values of the critical velocity.
Moreover, in the paper by Metrikine et al. [Metrikine and Dieterman (1999)], under investigation of the lateral vibration of the beam on an elastic half-space due to a moving lateral time-harmonic load acting on the beam, the initial axial compression of this beam is also taken into consideration. In this investigation, the motion of the beam is written through the Euler-Bernoulli beam theory, however, the motion of the half-space is described by the 3D exact equations of elastodynamics and it is assumed there are no initial stresses in the half-space.
The influence of the initial stresses acting in the half-plane on the critical velocity of the moving load which acts on the plate which covers this half-plane was studied in the papers by Babich et al. [Babich, Glukhov and Guz (1986, 1988, 2008a)]. Note that in these studies, the plane strain state was considered and the motion of the half-plane was written within the scope of the three-dimensional linearized theory of elastic waves in initially stressed bodies (see Guz [Guz (1999, 2004)]). However, the motion of the covering layer, which does not have any initial stresses, as in the paper by Achenbach et al. [Achenbach, Keshava and Hermann (1967)], was written by employing the Timoshenko plate theory and the plane-strain state is considered. For more detail, we note that in the paper by Babich et al. [Babich, Glukhov and Guz (1986)], the corresponding boundary value problem for the highly-elastic compressible half-plane was solved by employing the Fourier transformation with respect to the spatial coordinate along the plate-lying direction. Numerical results on the critical velocity of the moving load were presented for the case where the elasticity relations of the half-plane material are described through the harmonic potential. In the other paper by Babich et al. [Babich,Glukhov and Guz (1988)], the same problem which was considered in the paper by Babich et al. [Babich, Glukhov and Guz (1986)] was solved by employing the complex potentials of the three-dimensional linearized theory of elastic waves in initially stressed bodies, which are developed and presented in the monograph by Guz [Guz (1981)]. Note that in the papers by Babich et al. [Babich, Glukhov and Guz (1986, 1988)], the subsonic regime was considered. However, in the papers by Babich et al. [Babich, Glukhov and Guz (2008a)], the foregoing investigations of these authors were developed for the supersonic moving velocity of the external load for the case where the material of the half-plane is incompressible [Babich, Glukhov and Guz (2008a)] as well as for the case where this material is compressible [Babich, Glukhov and Guz (2008b)].
Furthermore, in the works of the first author of the present paper and his collaborators,the investigations of the problems related to the dynamics of the moving load acting on the layered systems were developed and under these investigations not only the motion of the half-plane but also the motion of the covering layer was written within the scope of the exact equations of the three-dimensional linearized theory of elastic waves in initially stressed bodies. Some of these works are as follows.
In the paper by Akbarov et al. [Akbarov, Guler and Dincoy (2007)], the influence of the initial stresses in the covering layer and half-plane on the critical velocity of the moving load acting on the plate covering the half-plane, was studied. The same moving load problem for the system consisting of the covering layer, substrate and half-plane was studied in the paper by Dincsoy et al. [Dincsoy, Guler and Akbarov (2009)]. The dynamics of the system consisting of the orthotropic covering layer and orthotropic half plane under action of the moving and oscillating moving load were investigated in the papers by Akbarov et al. [Akbarov and Ilhan (2008, 2009)] and the influence of the initial stresses in the constituents of this system on the values of the critical velocity was examined in the paper by Ilhan [Ilhan (2012)]. Moreover, in the paper by Akbarov et al.[Akbarov and Salmanova (2009)], the dynamics of the oscillating moving load acting on the pre-strained bi-layered slab made of highly elastic material and resting on a rigid foundation was studied. The 3D problems of the dynamics of the moving and oscillating moving load acting on the system consisting of a pre-stressed covering layer and halfspace were considered in the paper by Akbarov et al. [Akbarov, Ilhan and Temugan(2015)] and, in particular, it was established that the minimal values of the critical velocities determined within the scope of the 3D formulation coincide with the critical velocity determined within the scope of the corresponding 2D formulation. These and other related results were also detailed in the monograph by Akbarov [Akbarov (2015)].Finally, we note the paper by Akbarov et al. [Akbarov, Ilhan and Temugan (2015)] in which the dynamics of the lineally-located moving load acting on the hydro-elastic system consisting of elastic plate, compressible viscous fluid and rigid wall were studied.It was established that there exist cases under which the critical velocities appear.
Note that related non-linear problems regarding the moving and interaction of two solitary waves was examined in the paper by Demiray [Demiray (2014)] and other ones cited therein. At the same time, non-stationary dynamic problems for viscoelastic and elastic mediums were studied in the papers by Ilyasov [Ilyasov (2011)], Akbarov[Akbarov (2010)] and other works cited in these papers. Moreover, it should be noted that up to now it has been made considerable number investigations on fluid flow-moving around the stagnation-point (see the paper by Aman et al. [Aman and Ishak (2014)] and other works listed therein). Some problems related to the effects of magnetic field and the free stream flow-moving of incompressible viscous fluid passing through magnetized vertical plate were studied by Ashraf et al. [Ashraf, Asghar and Hossain (2014)].
The investigations related to the fluid-plate and fluid-moving plate interaction were considered the papers by Akbarov et al. [Akbarov and Panachli (2015)] and Akbarov et al.[Akbarov and Ismailov (2015, 2016)].
It follows from the foregoing brief review that almost all investigations on the dynamics of the moving and oscillating moving load relate to flat-layered systems. However, as noted in the beginning of this section, cases often occur in practice in which it is necessary to apply a model consisting of cylindrical layered systems, one of which is the hollow cylinder surrounded by an infinite or finite deformable medium under investigation of the dynamics of a moving or oscillating moving load. It should be noted that up to now some investigations have already been made in this field. For instance, in the paper by Abdulkadirov [Abdulkadirov (1981)] and others listed therein, the low-frequency resonance axisymmetric longitudinal waves in a cylindrical layer surrounded by an elastic medium were investigated. Note that under “resonance waves” the cases under which the relationoccurs, is understood, whereis the wave propagation velocity andis the wavenumber. It is evident that the velocity of these “resonance waves” is the critical velocity of the corresponding moving load. Some numerical examples of“resonance waves” are presented and discussed. It should be noted that in the paper by Abdulkadirov [Abdulkadirov (1981)], in obtaining dispersion curves, the motion of the hollow cylinder and surrounding elastic medium is described through the exact equations of elastodynamics, however, under investigation of the displacements and strains in the hollow cylinder under the wave process, the motion of the hollow cylinder is described by the classical Kirchhoff-Love theory.
Another example of the investigations related to the problems of the moving load acting on the cylindrical layered system is the investigation carried out in the paper by Zhou et al. [Zhou, Deng and Hou (2008)] in which the critical velocity of the moving internal pressure acting in the sandwich shell was studied. Under this investigation, two types of approaches were used, the first of which is based on first order refined sandwich shell theories, while the second approach is based on the exact equations of linear elastodynamics for orthotropic bodies with effective mechanical constants, the values of which are determined by the well-known expressions through the values of the mechanical constants and volumetric fraction of each layer of the sandwich shell.Numerical results on the critical velocity obtained within these approaches are presented and discussed. Comparison of the corresponding results obtained by these approaches shows that they are sufficiently close to each other for the low wavenumber cases,however, the difference between these results increases with the wavenumber and becomes so great that it appears necessary to determine which approach is more accurate.It is evident that for this determination it is necessary to investigate these problems by employing the exact field equations of elastodynamics within the scope of the piecewise homogeneous body model, which is also used in the present paper.
Finally, we note the works by Hung et al. [Hung, Chen and Yang (2013); Hussein,Fran? ois, Schevenels et al. (2014); Yuan, Bostrom and Cai (2017)] and others listed therein, in which numerical and analytical solution methods have been developed for studying the dynamical response of system consisting of the system consisting of the circular hollow cylinder and surrounding elastic medium to the moving load acting on the interior of the cylinder. However, the main aim of these investigations is the study of a displacement distribution of the surrounding elastic medium caused by the moving load and the analyses related to the critical velocity and to the response of the interface stresses to the moving load are almost completely absent. Moreover we note the development in recent years numerical methods based on various type finite elements and applied for investigations of the dynamics and statics of the related bi-material elastic and piezoelectric systems (see, for instance the papers by Fan et al. [Fan, Zhang, Dong et al.(2015)], Babuscu [Babuscu (2017)], Wei et al. [Wei, Chen, Chen et al. (2016)] and others listed in these papers.
With this we restrict ourselves to reviewing related investigations, from which it follows that up to now there have not been any systematic investigations on the dynamics of the moving internal pressure acting on the hollow cylinder surrounded by an elastic medium carried out within the scope of the piecewise homogeneous body model by employing the exact field equations of linear elastodynamics. There have not been any systematic investigations not only for the cases where between the constituents of the “hollow cylinder+surrounding infinite elastic medium” system the imperfect contact conditions exist but also in the cases where these conditions are perfect. There are also no results on the interface stress and displacement distributions caused by this moving load. Namely these and other related questions are studied in the present paper.
It should be noted that the related study of the axisymmetric forced vibration of the“hollow cylinder+surrounding infinite elastic medium” system under perfect and imperfect contact between the constituents is carried out in the paper by Akbarov et al.[Akbarov and Mehdiyev (2017)].
2 Mathematical Formulation of the Problem
Consider a hollow circular cylinder with thicknesswhich is surrounded by anelastic medium. We associate the cylindrical and cartesian systems of coordinatesand(Fig. 1) with the central axis of this cylinder. Assume that the external radius of the cross section of the cylinder isand on its inner surface axisymmetric uniformly distributed normal forces act in the circumferential direction moving with constant velocity which is point-located with respect to the cylinder central axis.Within this framework, we investigate the axisymmetric stress-strain state in this system by employing the exact equations of the linear theory of elastodynamics within the scope of the piecewise homogeneous body model. Below, the values related to the cylinder and to the surrounding elastic medium will be denoted by upper indices (2) and (1),respectively.
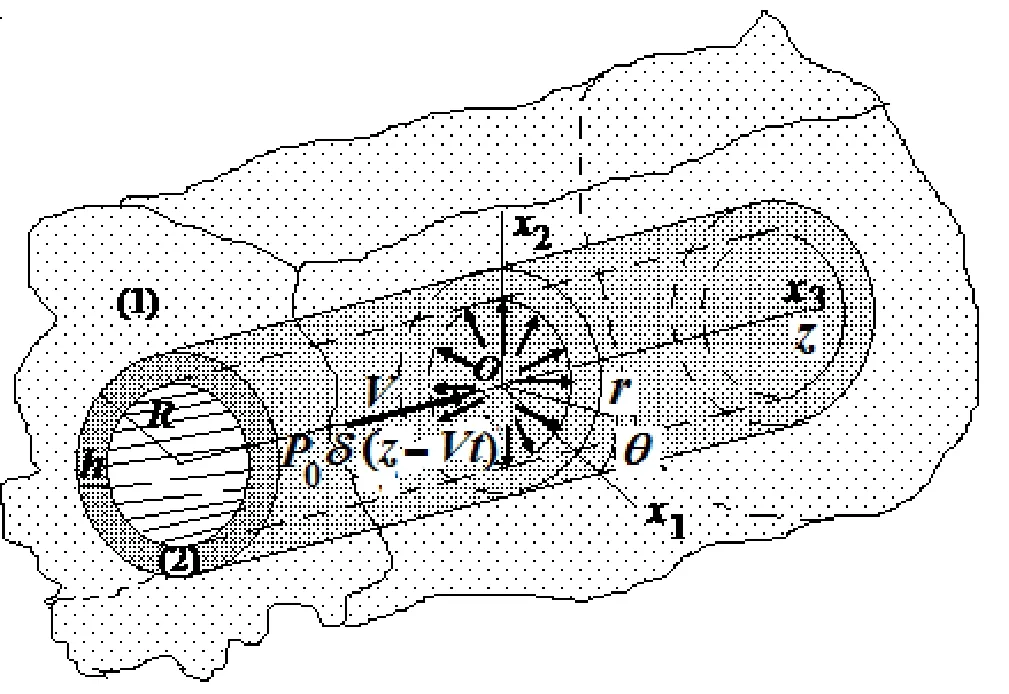
Figure 1: The sketch of the elastic system under consideration
We suppose that the materials of the constituents are homogeneous and isotropic.We write the field equations and contact conditions as follows.
Equations of motion:
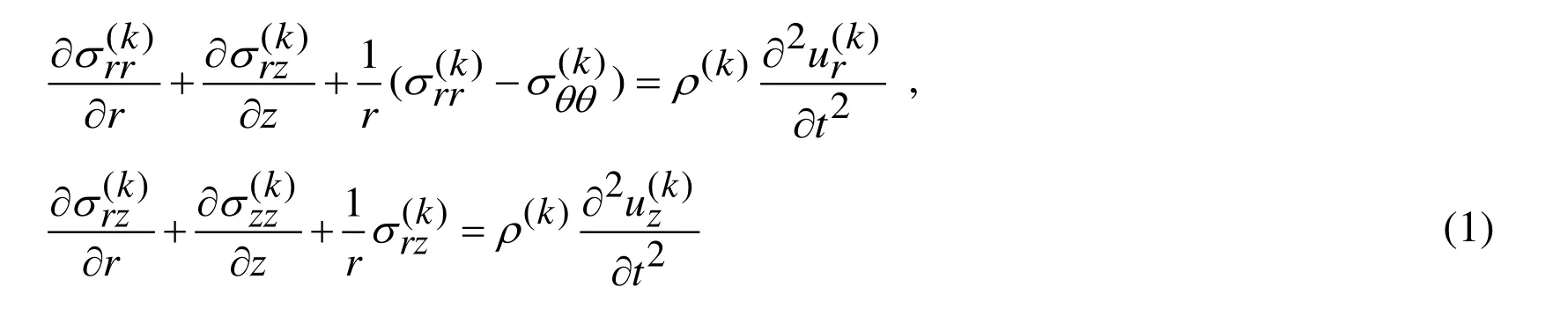
Elasticity relations:
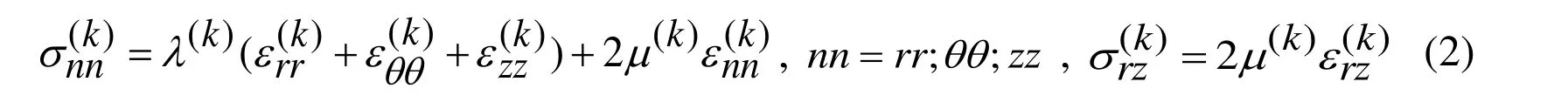
Strain-displacement relations:
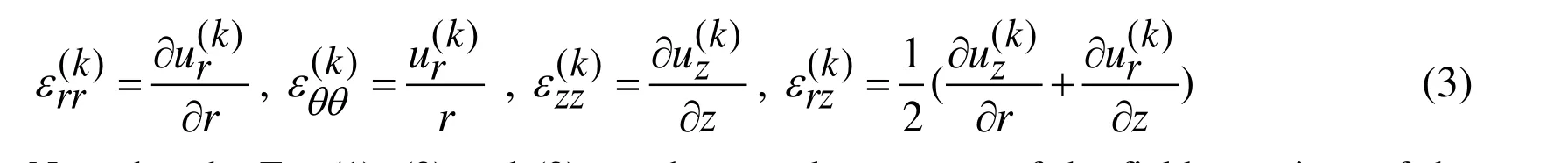
Note that the Eq. (1), (2) and (3) are the complete system of the field equations of the linear theory of elastodynamics in the case under consideration and in these equations conventional notation is used.
Consider the formulation of the boundary and contact conditions. According to the foregoing description of the problem, the boundary conditions on the inner face surface of the cylinder can be formulated as follows.
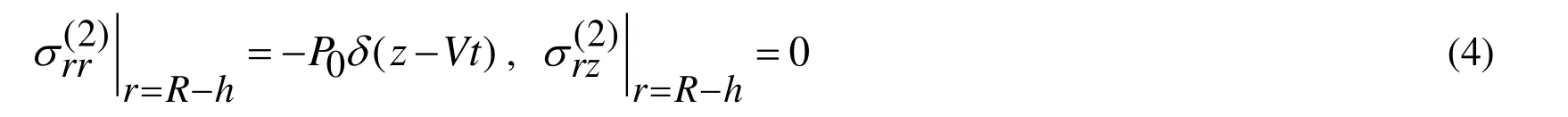
We assume that the contact conditions with respect to the forces and radial displacement are continuous and can be written as follows:
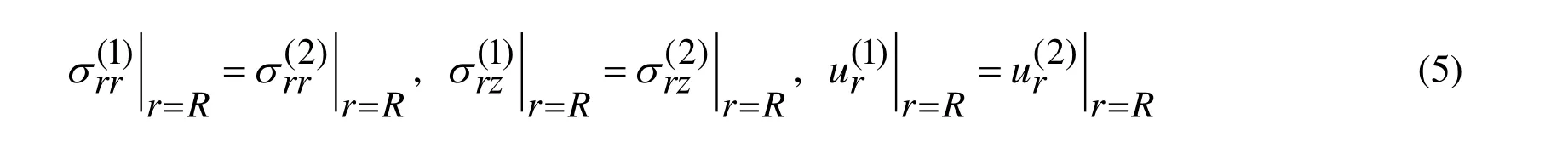
At the same time, we assume that shear-spring type imperfection occurs in the contact conditions related to the axial displacements and, according to Akbarov [Akbarov (2015)]and others listed therein, these conditions are formulated by the following equation:

We will also assume that
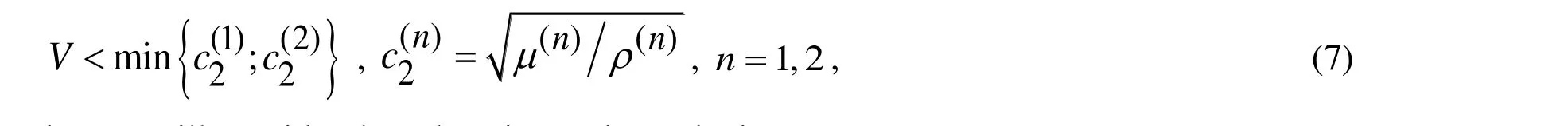
i.e. we will consider the subsonic moving velocity.
According to (7), we can write that
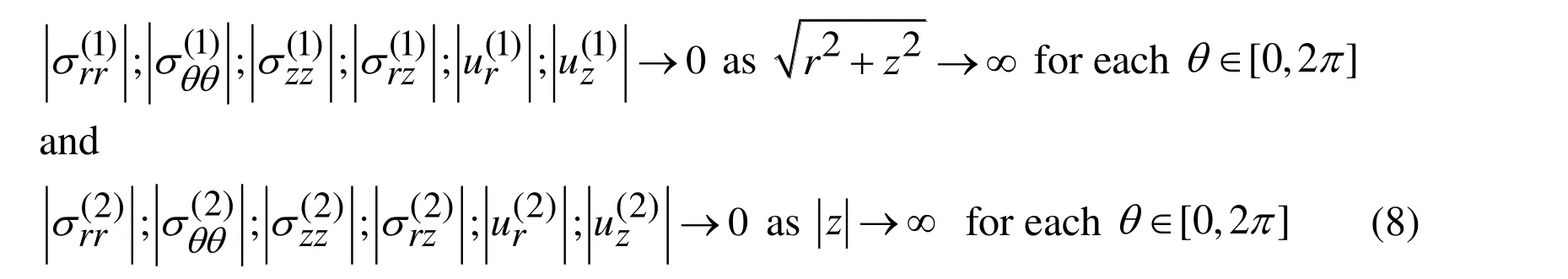
This completes formulation of the problem and consideration of the governing field equations.
3 Method of solution
For solution to the problem formulated above we use the well-known, classical Lame (or Helmholtz) decomposition (see, for instance, Eringen et al. [Eringen and Suhubi (1975)]):
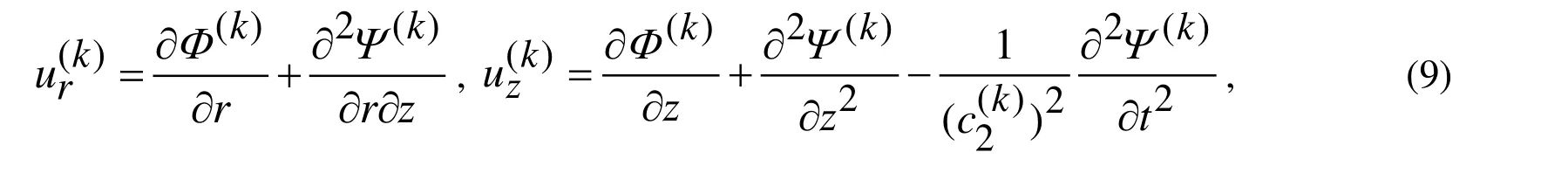

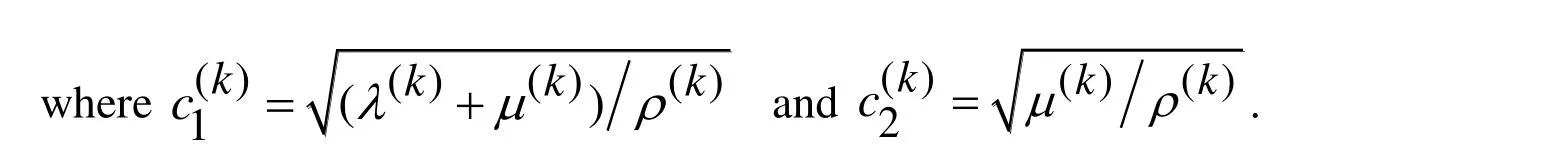
We use the moving coordinate system

which moves with the loading internal pressure and by rewriting the Eq. (10) with the coordinatesand, we obtain:
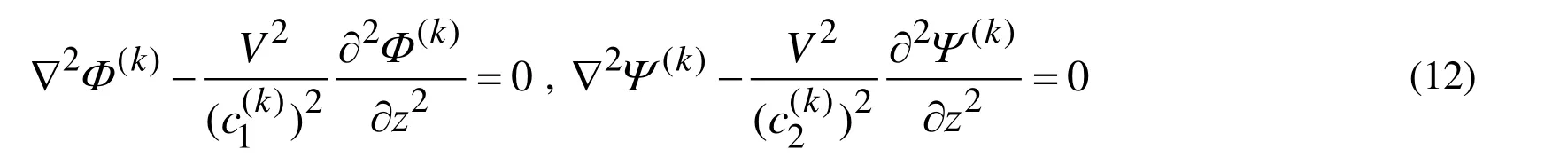

but the other relations and conditions in (1-8) remain valid in the new coordinates determined by (11).
Below we will use the dimensionless coordinatesandinstead of the coordinatesand, respectively and the over-bar inandwill be omitted.
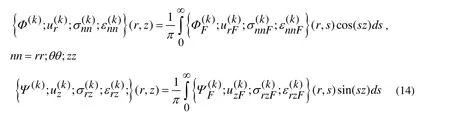
Substituting the expressions in (14) into the foregoing equations, relations and contact and boundary conditions, we obtain the corresponding ones for the Fourier transformations of the sought values. Note that after this substitution, the relation (2), the first and second relation in (3), the second condition in (4) and all the conditions in (5)and (6) remain as for their Fourier transformations. However, the third and fourth relation in (3) and the condition (13) and the relations in (9) transform to the following ones:
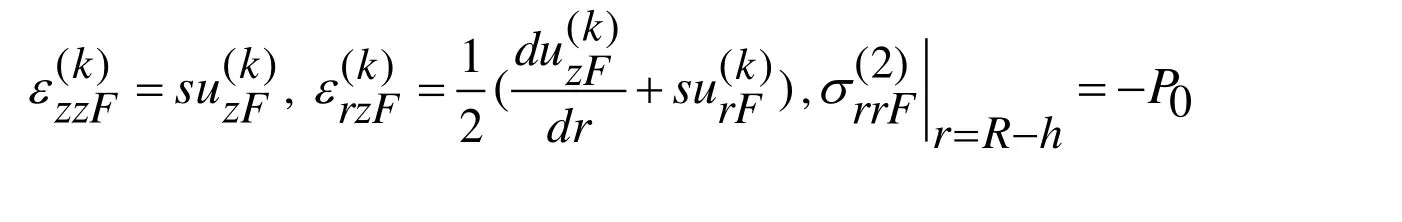
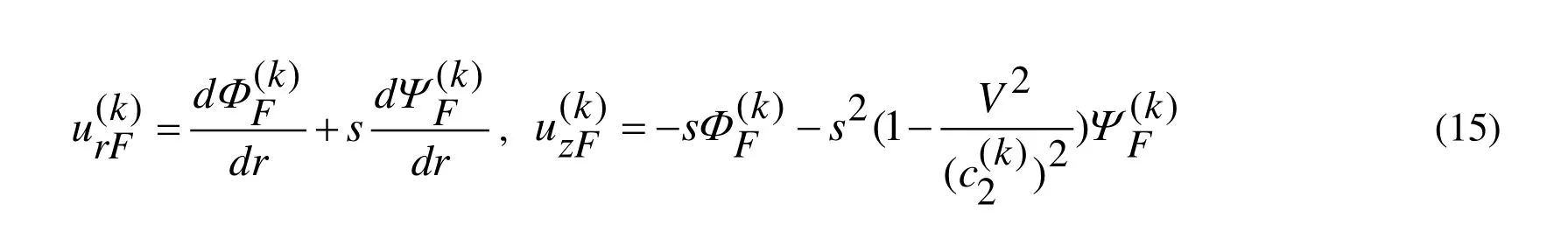
Moreover, after the aforementioned substitution we obtain the following equations forandfrom the equations in (12).
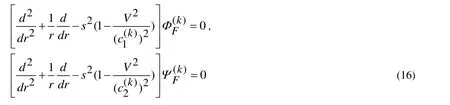
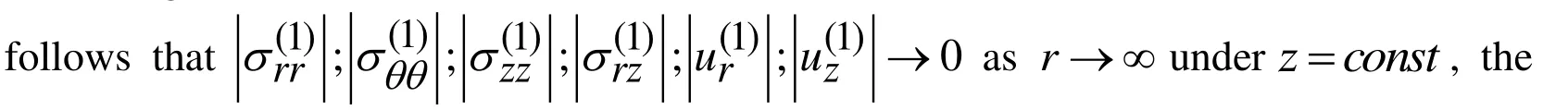

Thus, using the expressions (2), (3), (9), (15) and (17) we obtain the following expressions of the Fourier transformations of the sought values.
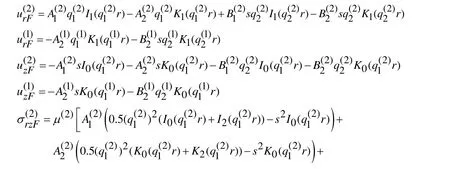



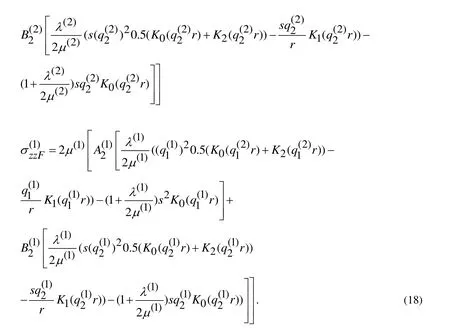
Thus, using the expressions in (18) we attempt to satisfy the Fourier transformations of the conditions (13) and (4-6), according to which, the following expressions can be written.
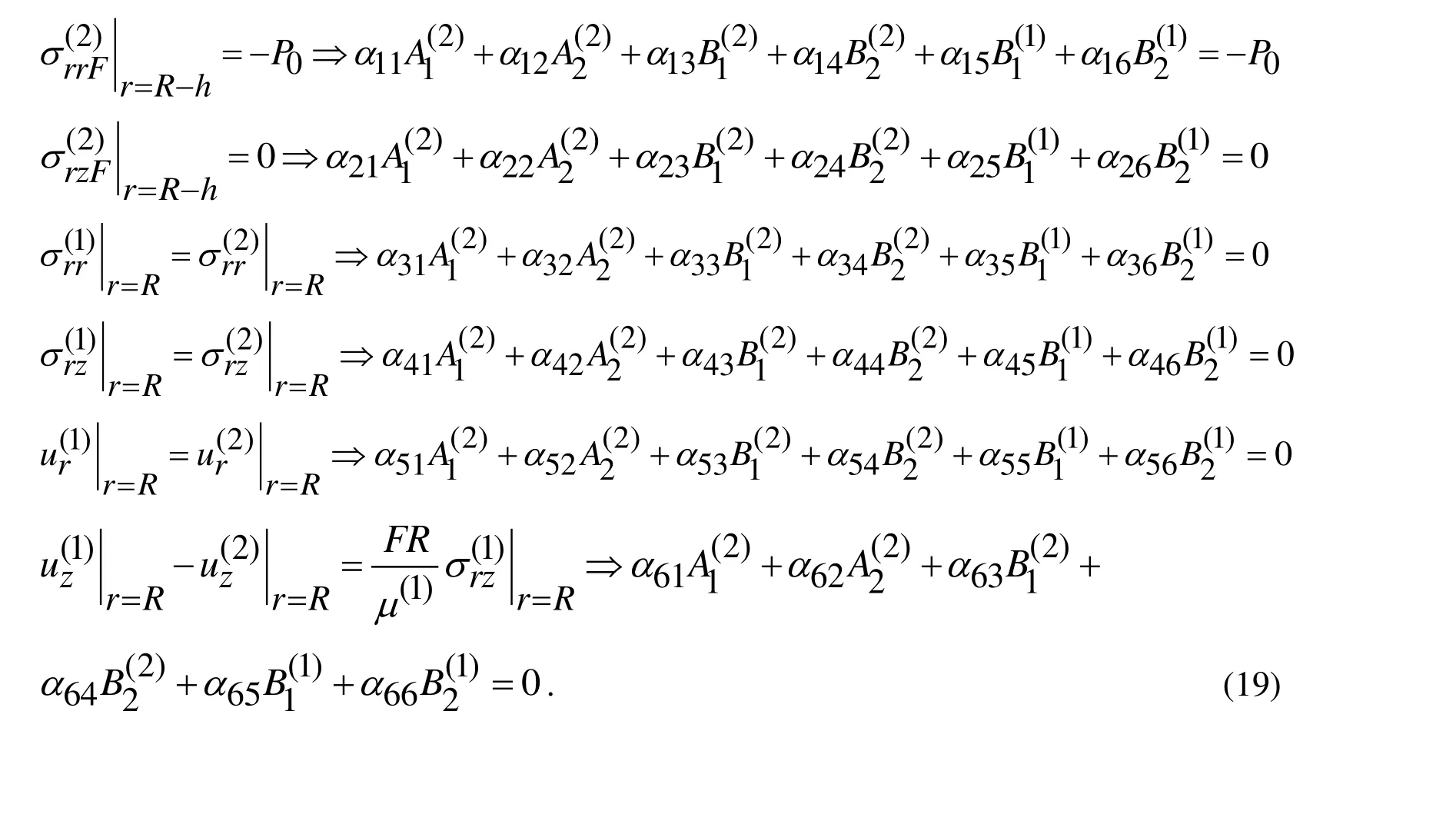
This completes the consideration of the solution method.
4 Numerical results and discussions
4.1 The criteria and algorithm for calculation of the critical velocity
First we consider the criterion for determination of the critical velocity under which the values of the stresses and displacements become infinity and resonance-type behavior occurs. For this purpose, we detail the expressions of the unknown constantsandwhich are obtained from the Eq. (19) and can be presented as follows:
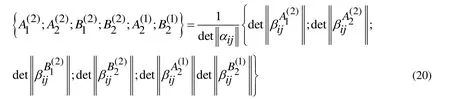

has roots with respect to the Fourier transformation parameterand as a result of the solution of the equation (21), the relationis obtained. It is obvious that if the order of this root is one, then the integrals in (18) at the vicinity of this root can be calculated in Cauchy’s principal value sense. However, if there is a root the order of which is two, then the integrals in (18) have infinite values and namely the velocities corresponding to this root are called the critical velocity. In other words, the critical velocity is determined as the velocity corresponding to the case where

It should also be noted that if we rename the Fourier transformation parameterwith the wavenumber and the load moving velocity with the wave propagation velocity, then the Eq. (21) coincides with the dispersion equation of the corresponding near-surface wave propagation problem. So, the relationobtained from the solution of the Eq. (21),which is made by employing the well-known “bisection” method, is also the dispersion relation of the near-surface wave. Therefore, in some investigations (for instance in the paper by Abdulkadirov [Abdulkadirov (1981)] the critical velocity is renamed as“resonance waves” and is determined from the dispersion curves of the corresponding wave propagation problem.
This completes the consideration of the criteria and algorithm for determination of the critical velocity under which the resonance-type phenomenon takes place.
4.2 Algorithm for calculation of the integrals in (18)
First of all, we note that the integrals in (18) and similar types of integrals are called wavenumber integrals, for calculation of which, special algorithms are employed. These algorithms are discussed in the works by Akbarov [Akbarov (2015)], Jensen et al. [Jensen,Kuperman, Porter et al. (2011)], Tsang [Tsang (1978)] and others listed therein.According to these discussions, in the present investigation we prefer to apply the Sommerfeld contour integration method. This method is based on Cauchy’s theorem on the values ofthe analytic functions over the closed contour, and according to this theorem the contour is “deformed” into the contour(Fig. 2), which is called the Sommerfeld contour in the complex planeand in this way the real roots of the Eq. (21) are avoided under calculation of the wavenumber integrals.
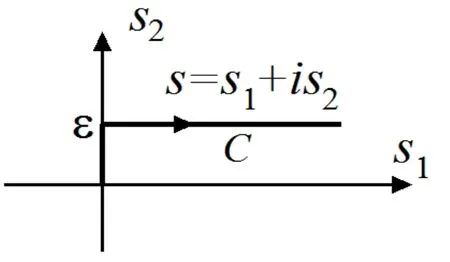
Figure 2: The sketch of the Sommerfeld contour
Thus, according to this method, the integrals in (18) are transformed into the following ones.
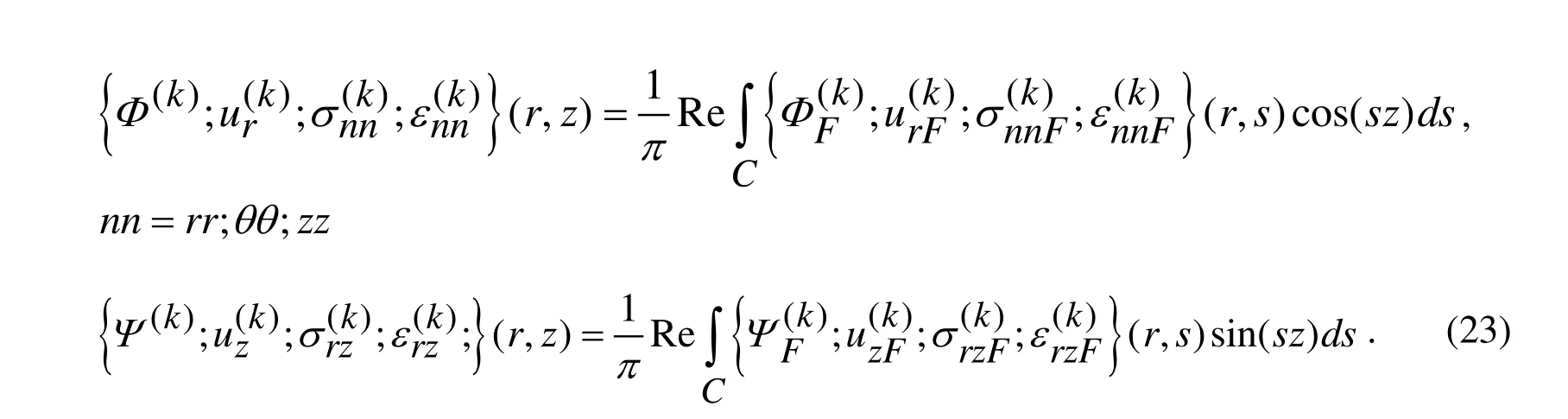
Taking the configuration of the contourgiven in Fig. 2, we can write the following relations.
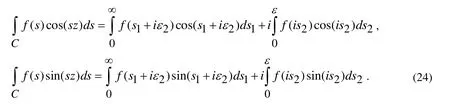
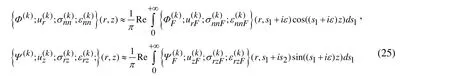
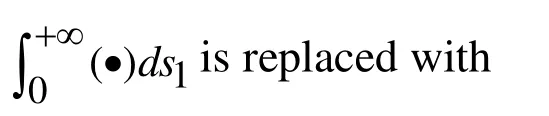
4.3 Numerical results related to the critical velocity
All numerical results which will be considered in the present subsection are obtained through the solution to the Eq. 21. First, we consider the numerical results obtained in the following two cases:
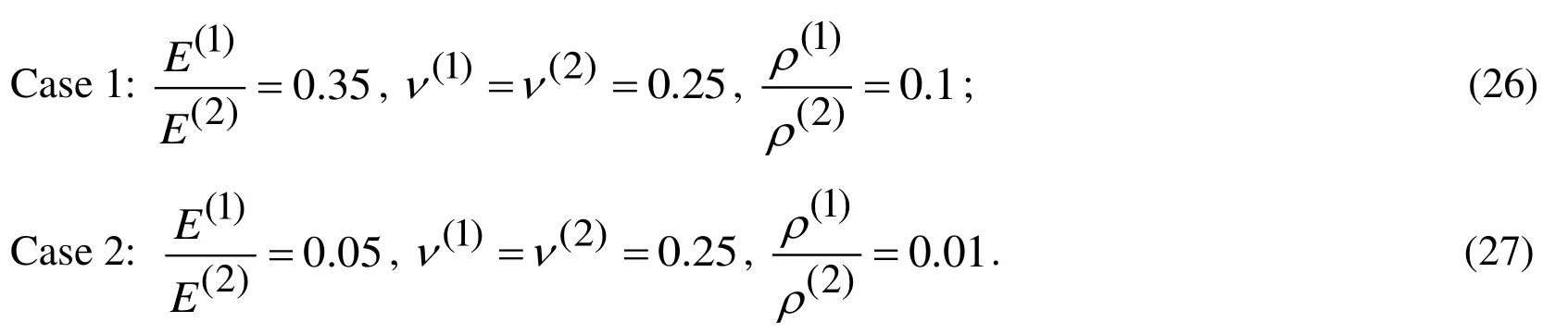
Note that these cases were also considered in the paper by Abdulkadirov [Abdulkadirov(1981)] within the assumption thatand the existence of the critical velocity was observed in Case 1 (in Case 2) under(under) in (6), i.e. under full slipping imperfect (perfect) contact conditions between the hollow cylinder and surrounding elastic medium. In the present investigation we obtain numerical results notonly for the cases whereand, but also for the cases whereand. The graphs of the dependencies between the dimensionless critical velocityand the imperfection parameterconstructed underare given in Fig.3 and 4 for Case 1 and Case 2, respectively.
It follows from these graphs that the results obtained in the present paper in these particular cases coincide with the corresponding ones obtained in the paper by Abdulkadirov [Abdulkadirov (1981)] and in addition, these results show that there exist the following relations:
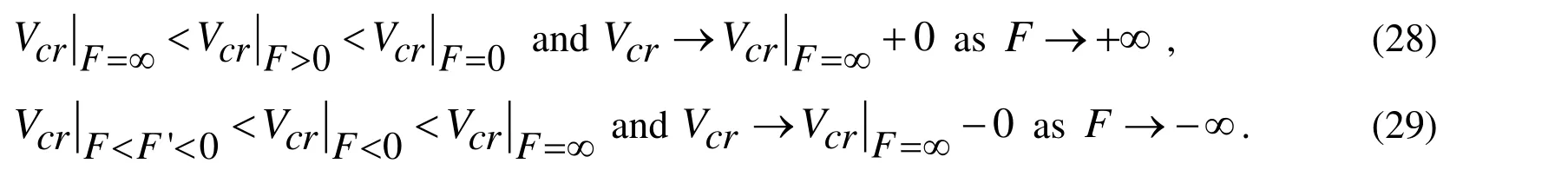
Note that the aforementioned coinciding of the present results obtained in the particular cases with the corresponding ones given in the paper by Abdulkadirov [Abdulkadirov(1981)] proves the reliability of the calculation algorithm and PC programs used in the present investigation.
Now we attempt to explain the meaning ofwhich is in the relation (29) and for this purpose, as an example, we consider the corresponding dispersion curves obtained in Case 2 for the first lowest mode and given in Fig. 5. To prevent misunderstandings, we note that under construction of the graphs given in Fig. 5, the cases whereare also considered and in these cases in the solution of the corresponding equations considered above, the functionsandin (17) are changed withandrespectively, whereandare Bessel functions of the first and second kind of theorder. However, the critical velocities are determined from the results which relate to the subsonic velocity of the moving load,i.e. to the cases where.
Thus, we turn to the analyses of the results given in Fig. 5 which show that in the case where, the dispersion curves are limited to the dispersion curves obtained in the case where(upper limit) and in the case where(lower limit). However, in the case where, the dispersion curve of the first mode has two branches. The first branch has cut off valuesafter which the wave propagation velocities in this branch are less than those obtained in the perfect contact case, i.e. by denoting the wave propagation velocity for the first branch throughwe can write the following relation:

However, the second branch of the dispersion curve has no cut off value ofand the wave propagation velocity of this branch (denote it by) is less than that obtained in the perfect contact case, i.e. for the second branch we can write the following relation:

Moreover, it follows from Fig. 5 that the point at whichon the first branch of the dispersion curves appears after a certain value of the parameter(denote this value by). For instance, in the case under consideration, it can be seen thatNamely, this value of the parameterenters into the relation (29).
We also note the meanings of the cases whereandwhere under selected forms of the contact condition (6), the case wheremeans that ifthen the displacement of the hollow cylinder along theaxis at the interface surface is greater (less) than that of the surrounding elastic medium. Analogically, the casemeans that under satisfaction of the foregoing conditions, the displacement of the hollow cylinder along theaxis on the interface surface is less (greater) than that of the surrounding elastic medium. It is evident that each of these cases has real application fields and therefore the results obtained in the cases wherealso have a real physico-mechanical meaning.
We recall that the foregoing results were obtained in the case where. It shouldnoted that similar types of results are also obtained in the other values of the ratio. As an example of this, in Fig. 6 and 7 the graphs of the dependence betweenand the parameterconstructed underare given for Case 1 (26)and Case 2 (27), respectively. It follows from thesegraphs that the foregoing conclusions on the character of the influence of the parameter on the values of the critical velocity do not depend on the ratioin the qualitative sense.
Now we consider in more detail the results illustrating the influence of the ratioon the values of the critical velocity obtained in the cases whereand. These results, i.e. the values ofare givenin Tab. 1 and 2 for Case 1 and Case 2,respectively under various values of the ratio . It follows from these tables that the values of the critical velocity decrease monotonically with decreasing of the ratio,and the magnitude of this decrease in Case 2 is more considerable than in Case 1.
As noted above, the influence of the ratioon the values of the critical velocity in Case 2 is more considerable than in Case 1. We think that theon the critical velocity in Case 2 is caused by the ratiowhich is significantly less than in Case 1. This explanation is also proven with the data given in Tab. 4 which show the values of the dimensionless critical velocity in the cases whereandunderandfor various values ofand. Thus, it follows from Tab. 4 that a decrease in the values ofandcauses a decrease in the values of the critical velocity, and the magnitude of the influence ofon the values of this velocity become more considerable with decreasing of the ratio.
This completes consideration of the results related to the critical velocity.
Note that the results detailed in the foregoing eight paragraphs and corresponding numerical results used in this detailing can be taken as a part of the main contribution of the present paper into the related investigations. The other part of this contribution is detailed in the next subsection
4.4 Numerical results related to the stress and displacement distributions

All numerical results which will be considered inthe present subsection are obtained inthe perfect contact case, i.e. in the case where in (6). According to the results given in Fig. 5, in the cases whereunderthe integrated expressions do not have any singularity over an arbitrary integrated interval. However, in this case the integrated expressions have the fast oscillating terms-or, and this also causes difficulties in the convergence sense of the integrals in (25). This difficulty can also be prevented by the use of the Sommerfeld contour integration method which is also used in the present study. As a result of the corresponding numerical investigations, it is established that in the accuracy and convergence senses it is enough to assume that in the integrals in (25). Note that the values of the integrals calculated for each value of the parameterselected from the intervalcoincide with each other with accuracy. Under obtaining the numerical results considered below, it is assumed that.

Figure 3: The dependence of the critical velocity on the imperfection parameter
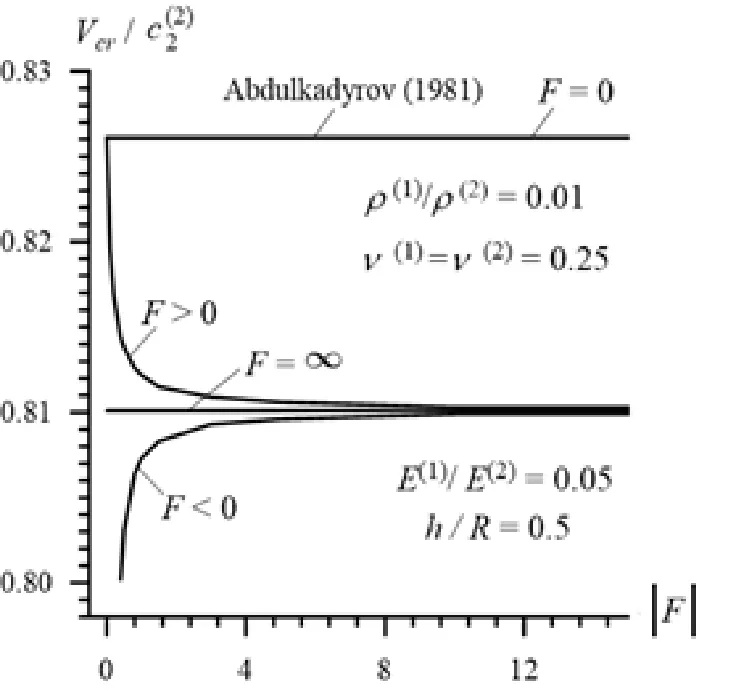
Figure 4: The dependence of the critical velocity on the imperfection parameter
Table 1: The values of the dimensionless critical velocity in the cases where(upper number) and(lower number)

Table 1: The values of the dimensionless critical velocity in the cases where(upper number) and(lower number)
?
Table 2: The values of the dimensionless critical velocity

Table 2: The values of the dimensionless critical velocity
?
Thus, we analyze the numerical results obtained within the scope of the foregoing assumptions and calculation algorithm. First we consider the graphs ofthe dependence between the dimensionless normal stress calculated at point (whereis determined through the expression (32)) and dimensionless load moving velocity. These graphs for Case 1 (26) and Case 2 (27) are given in Fig. 10 and 11, respectively.The graphs of the same dependence for the dimensionless shear stress, where

Table 3: The values of the dimensionless critical velocity obtained for various
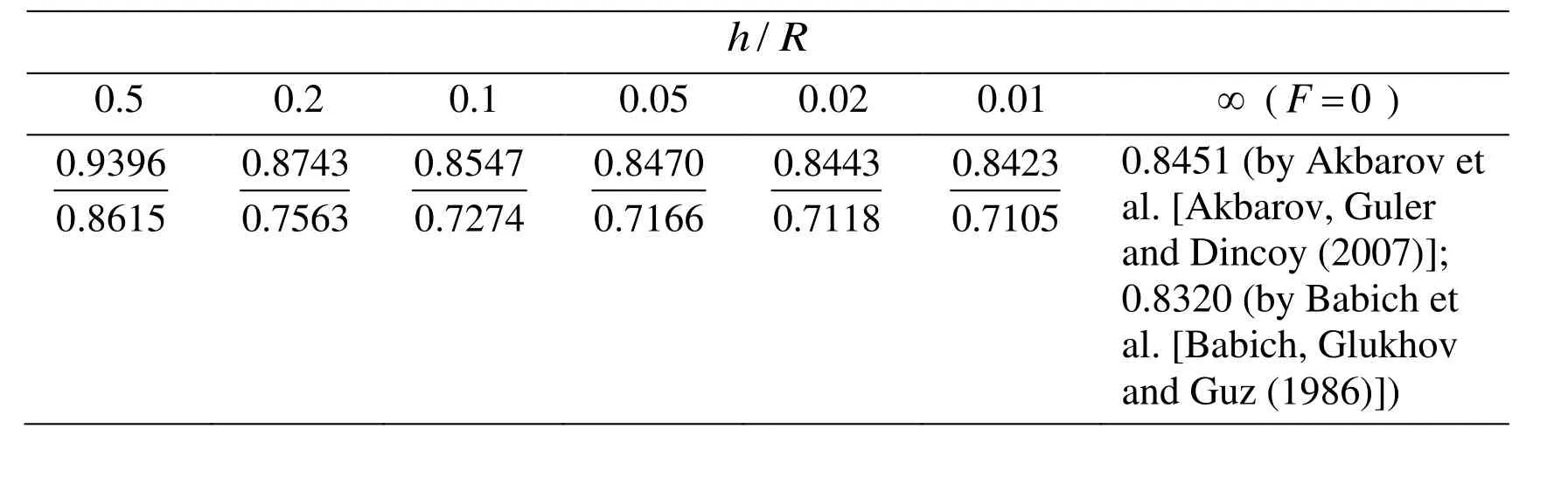
Table 3: The values of the dimensionless critical velocity obtained for various
?
Table 4: The influence of the ratios and on the values of the dimensionless critical velocity under, in the cases where(upper number) and(lower number).
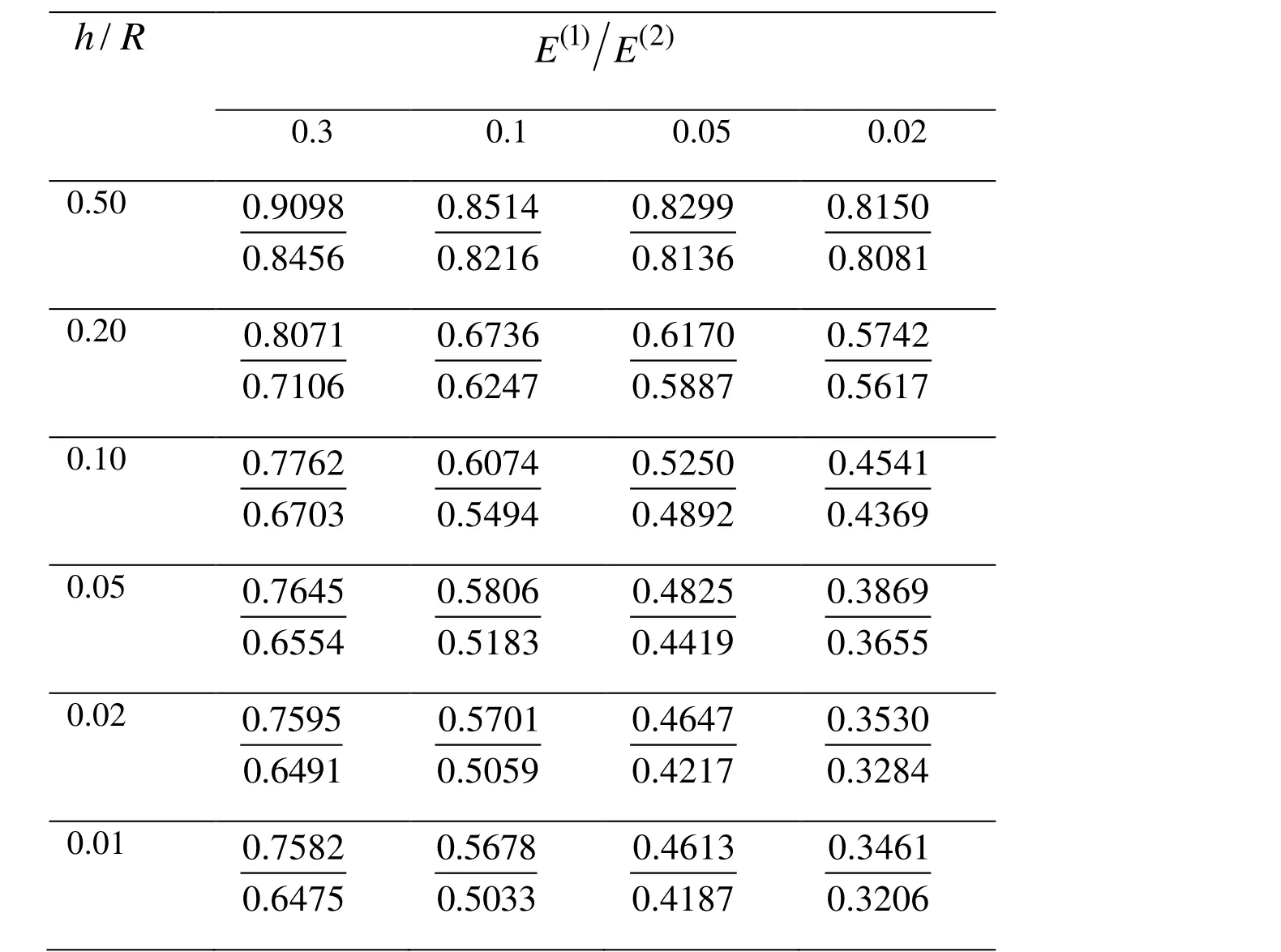
Table 4: The influence of the ratios and on the values of the dimensionless critical velocity under, in the cases where(upper number) and(lower number).
?
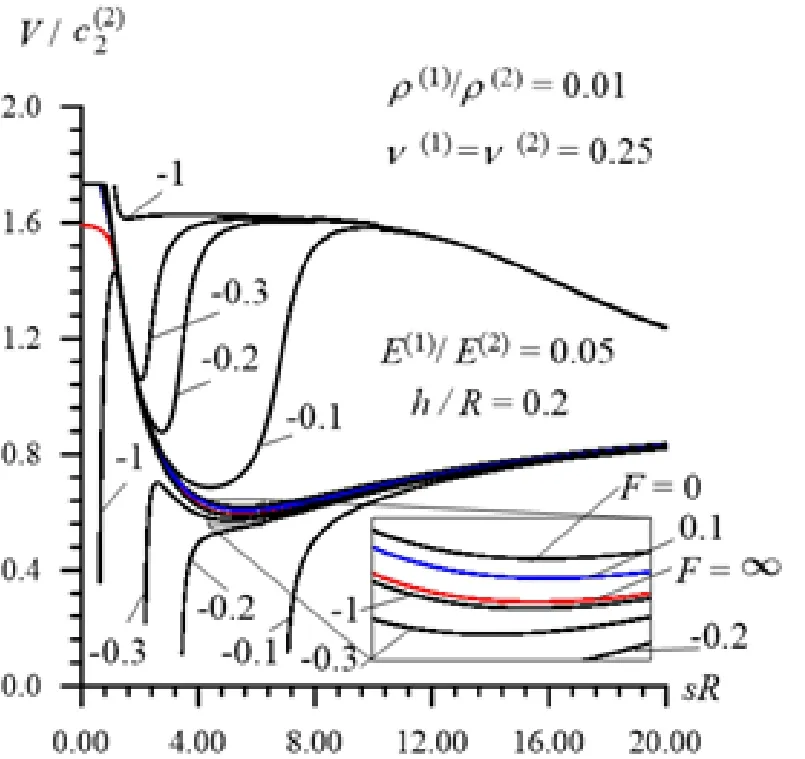
Figure 5: The influence of the imperfection parameter on the dispersion curves in Case 2 (27) under
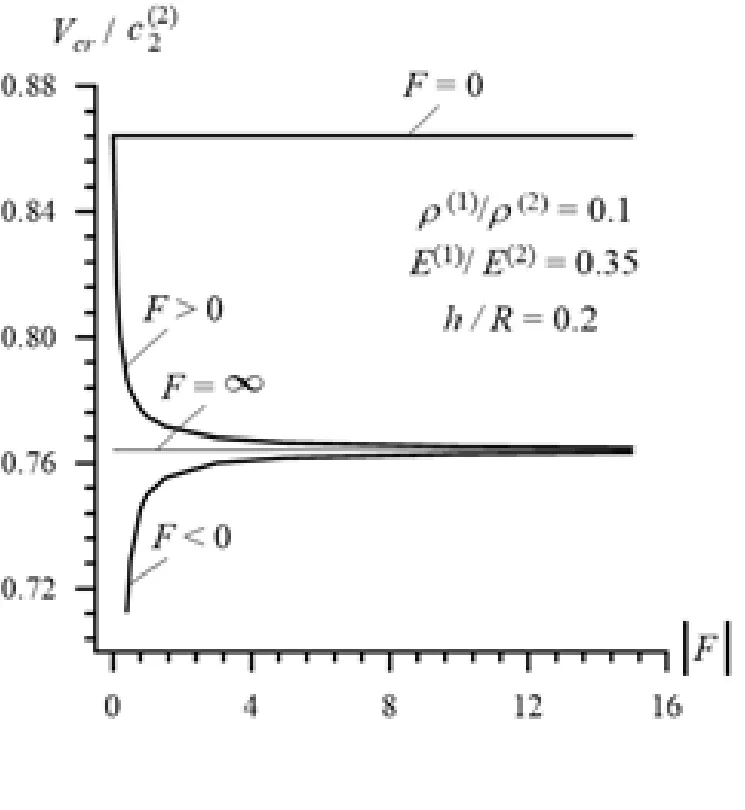
Figure 6: The dependence of the critical velocity on the imperfection parameter in Case 1 (26) under
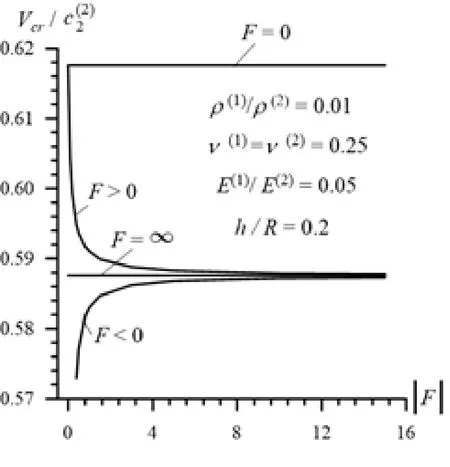
Figure 7: The dependence of the critical velocity on the imperfection parameter in Case 2 (26) under
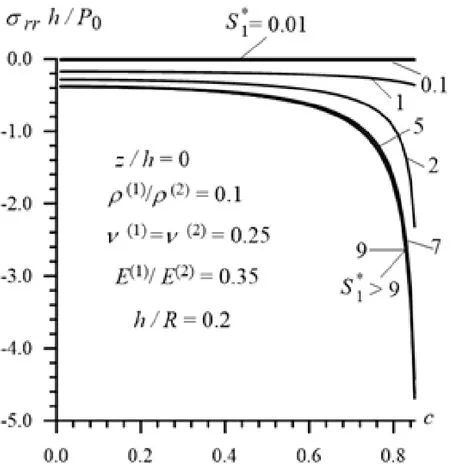
Figure 8: Convergence of the respect to the integration interva
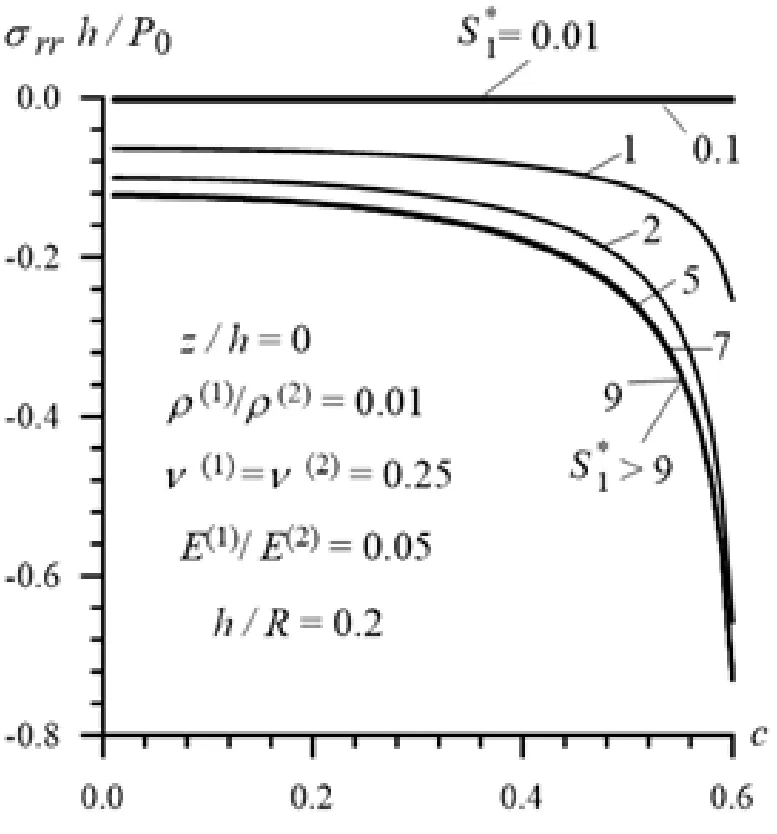
Figure 9: Convergence of the results with respect to the integration interval
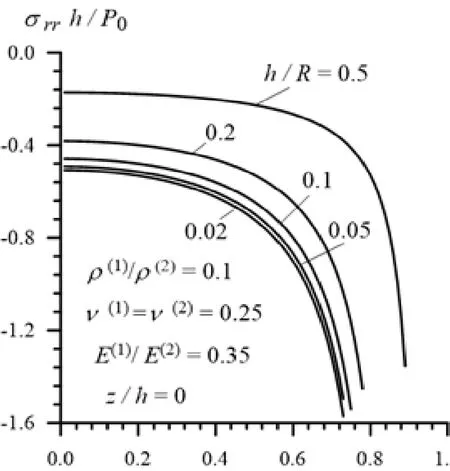
Figure 10: Dependence of the interface normal stress load moving velocity in Case 1
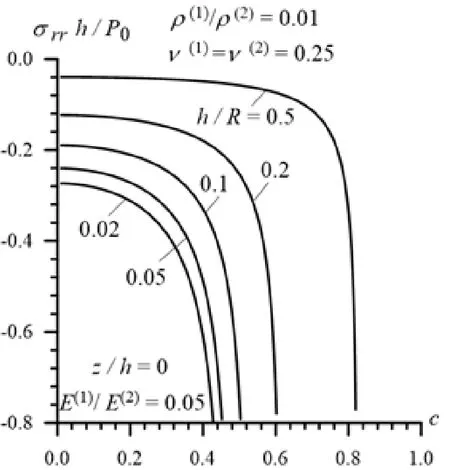
Figure 11: Dependence of the interfaceload moving velocity in Case 2
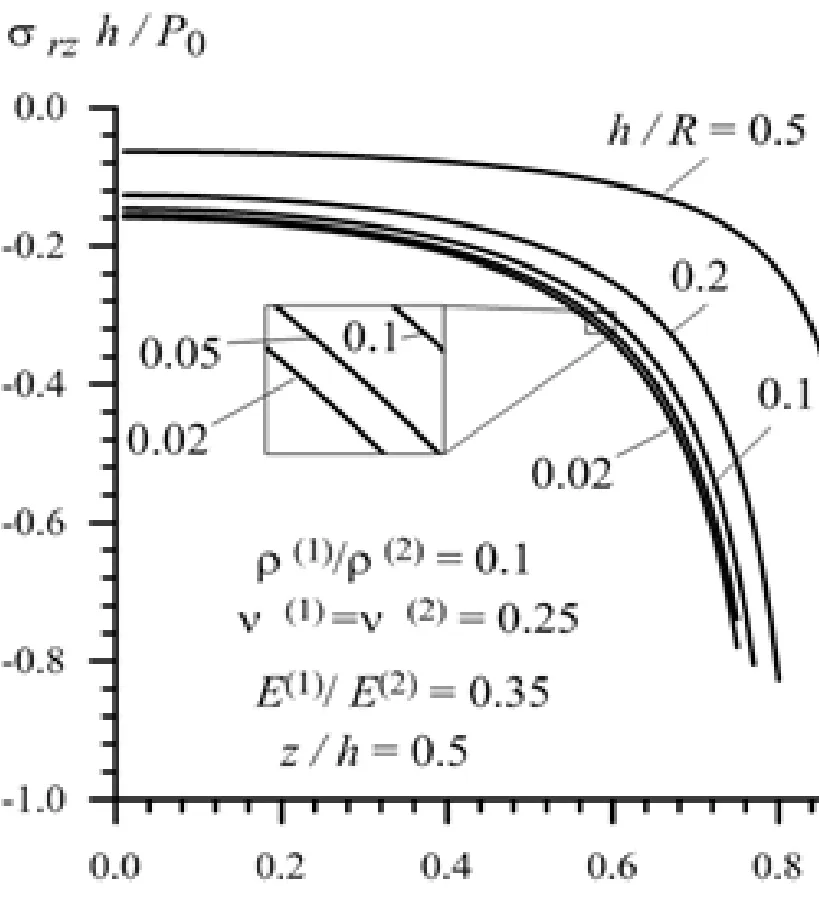
Figure 12: Dependence of the interfaceload moving velocity in Case 1
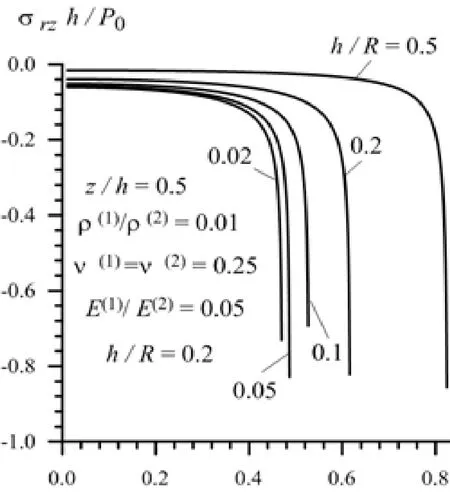
Figure 13: Dependence of the interface
Now we consider the results related to the distribution of the stressesand displacements on the interface surface with respect to the dimensionless coordinate . The diagrams of these distributions for the stress() are given in Fig. 16 and 17 (in Fig. 18 and 19)in Case 1 and Case 2, respectively for the various values of the ratio. The same distributions for the displacement(=(for the displacement(=) are given in Fig. 20 and 21 (in Fig. 22 and 23) also in Case 1 and Case 2, respectively under various. It follows from these figures that the absolute values of the stresses and displacements after some insignificant “oscillations”are dicey.
Thus, it follows from Fig. 10-13 that both in Case 1 and in Case 2 the absolute values of the stresses increase monotonically with the load moving velocity c. It should be noted that in Case 2 the absolute values of the stresses increase more rapidly than those in Case 1 as . Analyses of these and other numerical results allow us to conclude that the character of the foregoing dependencies does not depend not only on the ratiobut also on the ratio. In connection with this we consider the graphs given in Fig.14 and 15 which illustrate the foregoing dependence for the stressesand,respectively for various values ofunder,and. Thus, it follows from Fig. 14 and 15 that the dependence between the stresses and load moving velocity is monotonic for each selected value of the ratio. Moreover, it follows from these results that the absolute values of the normaland shearstresses decrease with decreasing of the ratio. Note that these results agree in the qualitative sense with the corresponding results related to the dynamics of the moving load acting on the layered half-space and discussed in the monograph by Akbarov [Akbarov (2015)] and in other works listed therein. Moreover,these results agree also with the well-known mechanical and engineering considerations and can be taken as validation in a certain sense of the used calculation algorithm and PC programs.
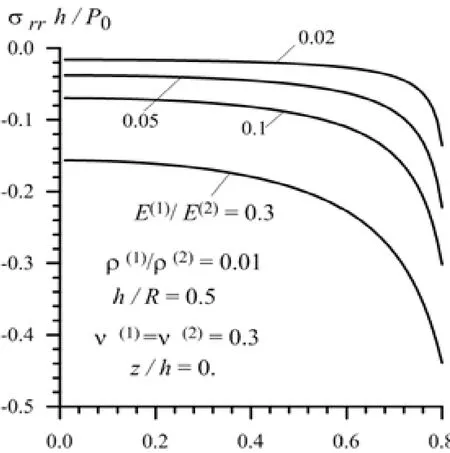
Figure 14: The influence of the modulus of elasticity of the cylinder material on the dependence between and in Case 1

Figure 15: The influence of the modulus of elasticity of the cylinder material on the dependence betweenand in Case 1
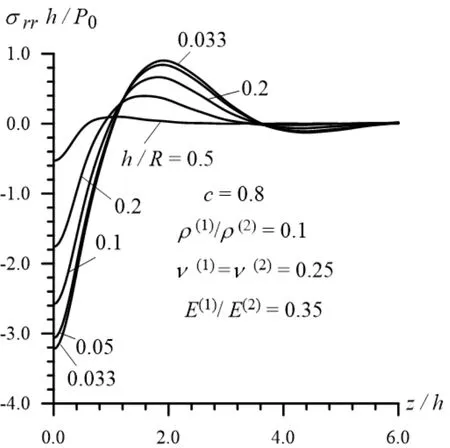
Figure 16: The distribution of the normal

Figure 17: The distribution of the normal
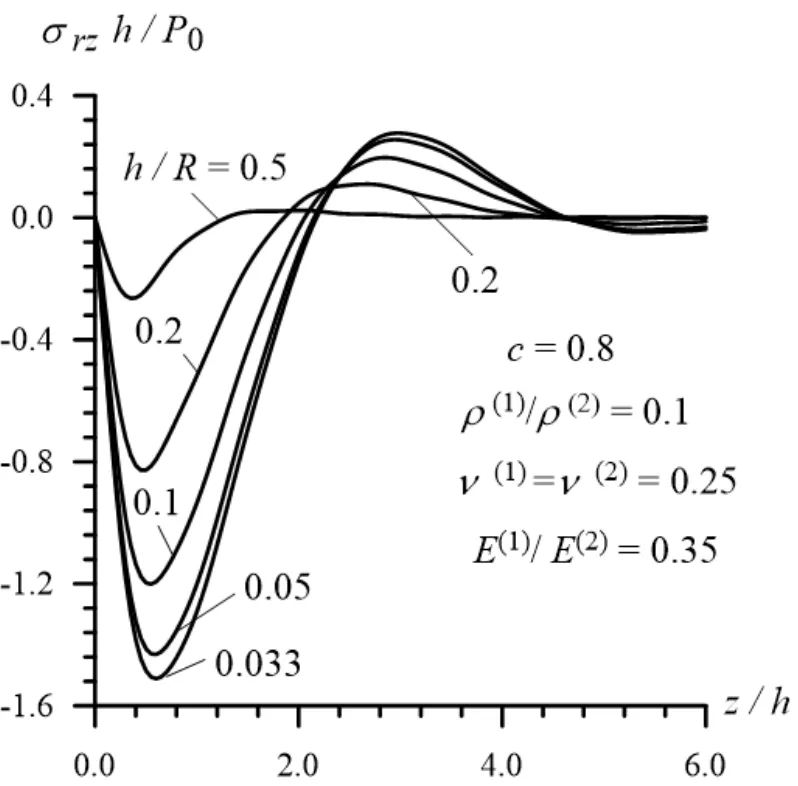
Figure 18: The distribution of the shear
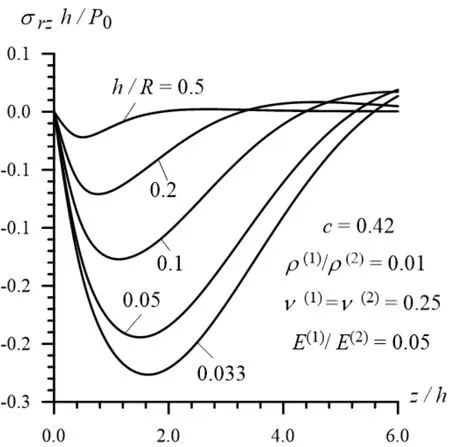
Figure 19: The distribution of the shear
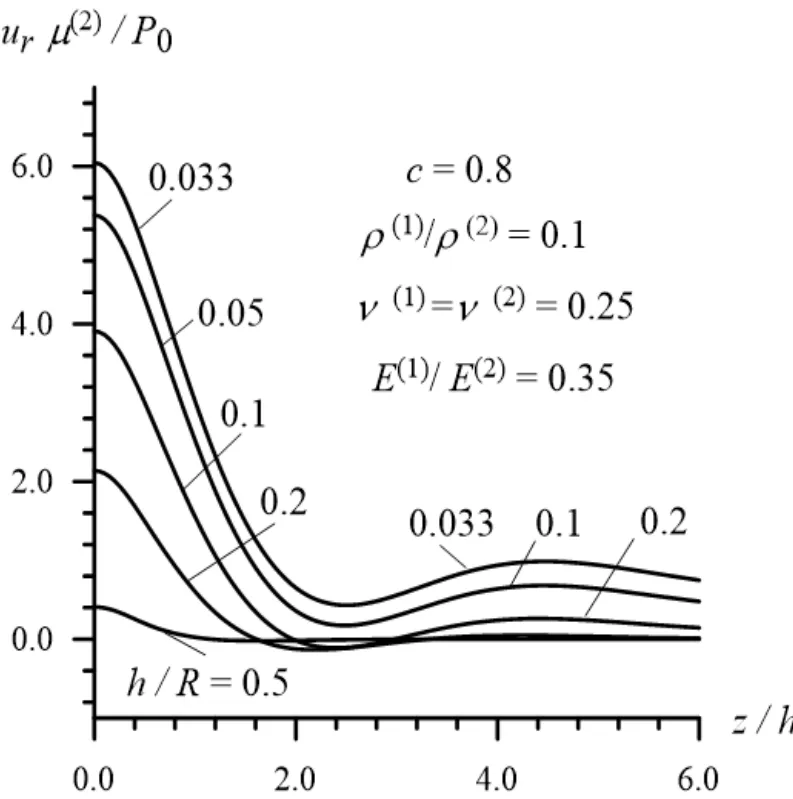
Figure 20: The distribution of the radial
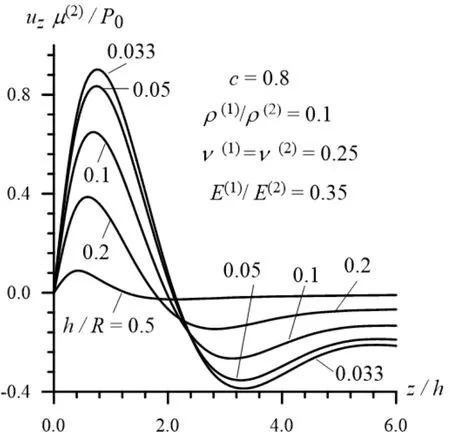
Figure 22: The distribution of the radial

Figure 23: The distribution of the radial
5 Conclusions
Thus, in the present paper the dynamics of the moving axisymmetric and rotationally,uniformly distributed point, located with respect to the cylinder axis, moving internal pressure acting on the internal face of the hollow cylinder surrounded by an elastic medium has been investigated within the scope of the piecewise homogeneous body model by employing the exact equations of elastodynamics. It is assumed that the contact conditions between the cylinder and surrounding elastic medium have shear-spring type imperfection. The subsonic regime is considered and for solution of the corresponding boundary value problem both the method of moving the coordinate system and the Fourier transformation, with respect to the coordinate directed along the cylinder axis in the moving coordinate system, are applied. Analytical expressions for the Fourier transformations of the sought values are determined and the algorithm for determination of the critical velocity and inverse Fourier transformations are discussed. Numerical results on the critical velocity and the stress and displacement distribution on the interface surface between the cylinder and surrounding elastic medium are presented and discussed. Analyses of these numerical results allow us to make the following concrete conclusions:
- In the case where the shear-spring type imperfection is given, as in (6) the following two states appear: a) ifthen the critical velocity obtained for eachis limited with the corresponding critical velocity obtained in the cases where(upper limit) and (lower limit); and b) ifthen after a certain value of(denoted by) the critical velocity is obtained, the values of which are less than those obtained in the case whereand decrease monotonically as;
- The values of the critical velocity decrease with increasing of the external radius of the cross section of the cylinder under constant thickness and approach the critical velocity obtained for the corresponding system consisting of the covering layer and half-plane;
- The increase in the values of the modulus of elasticity of the material of the hollow cylinder causes a decrease in the values of the critical velocity;
- The absolute values of the interface normal and shear stresses increase monotonically with load moving velocity for the relatively greater values of the ratio of the modulus of elasticity of the surrounding material to the modulus of elasticity of the cylinder material. However, the dependence of the stresses on the load moving velocity becomes non monotonic with decreasing of the ratio of the modulus of elasticities;
- The absolute values of the interface stresses and displacements increase with external radius of the cross section of the cylinder under fixed thickness;
- An increase in the values of the modulus of elasticity of the cylinder material causes a decrease in the absolute values of the interface normal and shear stresses;
- The attenuation of the interface stresses and displacements with respect to time(or with the distance from the point at which the moving load acts) becomes more significant with increasing of the modulus of elasticity of the cylinder material.
Abdulkadirov, S. A.(1981): Low-frequency resonance waves in a cylindrical layer surrounded by an elastic medium.Journal of Mining Science, vol. 80, pp. 229-234.
Achenbach, J. D.; Keshava, S. P.; Hermann, G.(1967): Moving load on a plate resting on an elastic half-space.Transactions of the ASME. Series E, Journal of Applied Mechanics, vol. 34, no. 4, pp. 183-189.
Akbarov, S. D.(2010): Dynamical (time-harmonic) axisymmetric stress field in the prestretched non-linear elastic bi-layered slab resting on the rigid foundation.TWMS Journal of Pure and Applied Mathematics,vol. 1, no. 2, pp. 146-154.
Akbarov, S. D.(2015):Dynamics of pre-strained bi-material elastic systems: Linearized three-dimensional approach.Springer, New-York.
Akbarov, S. D.; Guler, C.; Dincoy, E.(2007): The critical speed of a moving load on a pre-stressed load plate resting on a pre-stressed half-plan.Mechanics of Composite Materials, vol. 43, no. 2, pp. 173-182.
Akbarov, S. D.; Ilhan, N.(2008): Dynamics of a system comprising a pre-stressed orthotropic layer and pre-stressed orthotropic half-plane under the action of a moving load.International Journal of Solids and Structures,vol. 45, no. 14-15, pp. 4222-4235.
Akbarov, S. D.; Ilhan, N.(2009): Dynamics of a system comprising an orthotropic layer and orthotropic half-plane under the action of an oscillating moving load.International Journal of Solids and Structures, vol. 46, no. 21, pp. 3873-3881.
Akbarov, S. D.; Ilhan, N.; Temugan, A.(2015): 3D Dynamics of a system comprising a pre-stressed covering layer and a pre-stressed half-space under the action of an oscillating moving point-located load.Applied Mathematical Modelling, vol. 39, pp. 1-18.
Akbarov, S. D.; Ismailov, M. I.(2015): Dynamics of the moving load acting on the hydro-elastic system consisting of the elastic plate, compressible viscous fluid and rigid wall.Computers, Materials & Continua, vol. 45, no. 2, pp. 75-105.
Akbarov, S. D.; Ismailov, M. I.(2016): Frequency response of a pre-stressed metal elastic plate under compressible viscous fluid loading.Applied Mathematics and Computation, vol. 15, no. 2, pp. 172-188.
Akbarov, S. D.; Mehdiyev, M. A.(2017): Forced vibration of the elastic system consisting of the hollow cylinder and surrounding elastic medium under perfect and imperfect contact.Structural Engineering & Mechanics, vol. 62, pp. 113-123.
Akbarov, S. D.; Panachli, P. G.(2015): On the discrete-analytical solution method of the problems related to the rynamics of hydro-elastic systems consisting of a pre-strained moving elasticplate, compressible viscous fluid and rigid wall.Computer Modeling in Engineering & Sciences, vol. 108, no. 2, pp. 89-112.
Akbarov, S. D.; Salmanova, K. A.(2009): On the dynamics of a finite pre-strained bilayered slab resting on a rigid foundation under the action of an oscillating moving load.Journal of Sound and Vibration, vol. 327, no. 3-5, pp. 454-472.
Aman, T.; Ishak, A.(2014): Stagnation-point flow and heat transfer over a nonlinearly stretching sheet in a micropolar fluid with viscous dissipation.Applied Mathematics and Computationvol. 13, no. 2, pp. 230-238.
Ashraf, M.; Asghar, S.; Hossain, M. A.(2014):The computational study of the effects of magnetic field and free stream veloc?ty oscillation on boundary layer flow past a magnetized vertical plate.Applied Mathematics and Computation, vol. 13, no. 2, pp. 175-193.
Babich, S. Y.; Glukhov, Y. P.; Guz, A. N.(1986): Dynamics of a layered compressible pre-stressed half-space under the influence of moving load.International Applied Mechanics, vol. 22, no. 6, pp. 808-815.
Babich, S. Y.; Glukhov, Y. P.; Guz, A. N.(1988): To the solution of the problem of the action of a live load on a two-layer half-space with initial stress.International Applied Mechanics, vol. 24, no. 8, pp. 775-780.
Babich, S. Y.; Glukhov, Y. P.; Guz, A. N.(2008a): Dynamics of a pre-stressed incompressible layered half-space under load.International Applied Mechanics, vol. 44,no. 3, pp. 268-285.
Babich, S. Y.; Glukhov, Y. P.; Guz, A. N.(2008b): A dynamic for a pre-stressed compressible layered half-space under moving load.International Applied Mechanics,vol. 44, no. 4, pp. 388-405.
Babuscu Yesil, U.(2017): Forced and Natural Vibrations of an Orthotropic Pre-Stressed Rectangular Plate with Neighboring Two Cylindrical Cavities.Computers, Materials &Continua,vol. 53, no. 1, pp. 1-23.
Demiray, H.(2014): A note on the interactions of nonlinear waves governed by the generalized Boussinesq equation.Applied Mathematics and Computation, vol. 13, no. 3,pp. 376-380.
Dieterman, H. A.; Metrikine, A. V.(1997): Critical velocities of a harmonic load moving uniformly along an elastic layer.Journal of applied mechanics-transactions of the asme, vol. 64, pp. 596-600.
Dincsoy, E.; Guler, C.; Akbarov, S. D.(2009): Dynamical response of a prestrained system comprising a substrate and bond and covering layers to moving load.Mechanics of composite materials, vol. 45, no. 5, pp. 527-536.
Eringen, A. C.; Suhubi, E. S.(1975):Elastodynamics, Finite motion, vol. I; Linear theory, vol. II, Academic Press, New-York.
Fan, Q.; Zhang, Y.; Dong, L.; Li, S.; Atluri, S. N.(2015): Static and dynamic analysis of laminated thick and thin plates and shells by a very simple displacement-based 3-d hexahedral element with over-integration.Computers, Materials & Continua,vol. 47, no.2, pp. 65-88.
Guz, A. N.(1981):Brittle fracture of the materials with initial stresses.Naukova Dumka,Kiev (in Russian).
Guz, A. N. (1999):Fundamentals of the three-dimensional theory of stability of deformable bodies.Springer-Verlag, Berlin Heidelberg.
Guz, A. N.(2004):Elastic waves in bodies with initial (residual) stresses. A.C.K., Kiev(in Russian).
Hung, H. H.; Chen, G. H.; Yang, Y. B.(2013): Effect of railway roughness on soil vibrations due to moving trains by 2.5D finite/infinite element approach.Engineering Structures, vol. 57, pp. 254-266.
Hussein, M. F. M.; Fran? ois, S.; Schevenels, M.; Hunt, H. E. M.; Talbot, J. P. et al.(2014): The fictitious force method for efficient calculation of vibration from a tunnel embedded in a multi-layered half-space.Journal of Sound and Vibration,vol. 333, pp.6996-7018.
Ilhan, N.(2012): The critical speed of a moving time-harmonic load acting on a system consisting a pre-stressed orthotropic covering layer and a pre-stressed half-plane.Applied Mathematical Modelling, vol. 36, no. 8, pp. 3663-3672.
Ilyasov, M. X.(2011): Dynamical torsion of viscoelastic cone.TWMS J. Pure Appl.Math.,V.2, N.2, pp. 203-220.
Jensen, F. B.; Kuperman, W. A.; Porter, M. B.; Schmidt, H.(2011):Computational ocean acoustic,2nd ed. Springer, Berlin.
Kerr, A. D.(1983): The critical velocity of a load moving on a floating ice plate that is subjected to in-plane forces.Cold Regions Science and Technology, vol. 6, no. 3, pp.267-274.
Metrikine, A. V.; Dieterman, H. A.(1999): Lateral vibration of an axially compressed beam on an elastic half-space due to a moving lateral load.European Journal of Mechanics-A/Solids, vol. 18, pp. 147-158.
Metrikine, A. V.; Vrouwenvelder, A. C. W. M.(2000): Surface ground vibration due to a moving load in a tunnel: two-dimensional model.Journal of Sound and Vibration, vol.234, no. 1, pp. 43-66.
Tsang, L.(1978): Time-harmonic solution of the elastic head wave problem incorporating the influence of Rayleigh poles.The Journal of the Acoustical Society of America, vol. 65, no.5, pp. 1302-1309.
Wei, X.; Chen, W; Chen, B.; Chen, B.; Chen, B. et al.(2016): B-Spline Wavelet on Interval Finite Element Method for Static and Vibration Analysis of Stiffened Flexible Thin Plate.Computers, Materials & Continua, vol. 52, no. 1, pp. 53-71.
Yuan, Z.; Bostrom, A.; Cai, Y.(2017): Benchmark solution for vibration from a moving point source in a tunnel embedded in a half-space.Journal of Sound and Vibration, vol. 387, pp. 177-193.
Zhou, J. X.; Deng, Z. C.; Hou, X. H.(2008): Critical velocity of sandwich cylindrical shell under moving internal pressure.Applied Mathematics and Mechanics, vol. 29, no.12, pp. 1569-1578.
 Computers Materials&Continua2018年2期
Computers Materials&Continua2018年2期
- Computers Materials&Continua的其它文章
- Coverless Information Hiding Based on the Molecular Structure Images of Material
- Solution of Algebraic Lyapunov Equation on Positive-Definite Hermitian Matrices by Using Extended Hamiltonian Algorithm
- Solving Fractional Integro-Differential Equations by Using Sumudu Transform Method and Hermite Spectral Collocation Method
- Joint Bearing Mechanism of Coal Pillar and Backfilling Body in Roadway Backfilling Mining Technology
