保持二次算子的可加映射

孟紅葉,吉國興

(陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,陜西 西安 710119)

保持二次算子的可加映射

孟紅葉,吉國興

(陜西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,陜西 西安 710119)

設(shè)X是具有無限重復(fù)度的無限維或維數(shù)不小于3的有限維復(fù)Banach空間,B(X)是X上全體有界線性算子組成的Banach代數(shù).首先證明了單位算子不能表示成3個平方冪零算子之和,利用算子分塊矩陣技巧獲得了平方冪零算子的本質(zhì)特征.以此特征為基礎(chǔ),刻畫了B(X)上雙邊保持二次算子可加滿射的結(jié)構(gòu).

二次算子;冪等算子;平方冪零算子;可加映射

1 引言

近幾十年來,許多學(xué)者都致力于矩陣代數(shù)或算子代數(shù)上的保持問題的研究[1-3,5-9,11].特別是刻畫保持平方冪零算子,冪等算子等重要算子類的線性或可加映射.眾所周知,平方冪零算子和冪等算子是特殊的二次算子.Mourad Oudghiri和Khalid Souilah刻畫了B(H)上雙邊保持二次算子的線性映射,其中B(H)是復(fù)Hilbert空間H上有界線性算子的全體.文獻(xiàn)[4]指出無限維Hilbert空間是具有無限重復(fù)度的.從這方面出發(fā),本文主要考慮了B(X)上雙邊保持二次算子的可加映射問題,其中B(X)是具有無限重復(fù)度的無限維或維數(shù)不小于3的有限維復(fù)Banach空間X上有界線性算子的全體.

下面引入一些概念和記號.設(shè)C是復(fù)數(shù)域,X是具有無限重復(fù)度的無限維或維數(shù)不小于3的有限維復(fù)Banach空間,X?是X的對偶空間.B(X)表示X上全體有界線性算子組成的Banach代數(shù),Mn(C)表示全體n×n復(fù)矩陣組成的代數(shù).F(X),N2(X),P(X)和F1(X)分別表示B(X)中的有限秩算子,平方冪零算子,冪等算子和一秩算子組成的集合.設(shè)T∈B(X),用kerT,rankT和T?分別表示T的核,T的秩和T的伴隨算子.

設(shè)T∈B(X),如果存在a,b∈C使得(T?aI)(T?bI)=0,則稱T是二次算子.用A2(X)表示B(X)中全體二次算子組成的集合.由文獻(xiàn)[8]的公式2.1,可得

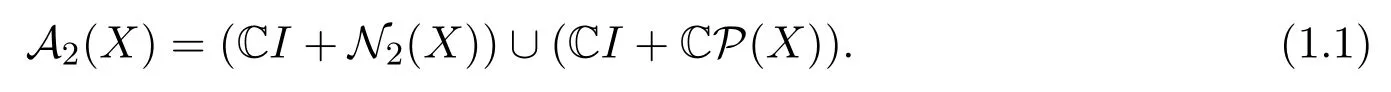
對任意的x∈X,f∈X?{0},表示X上一秩算子,即

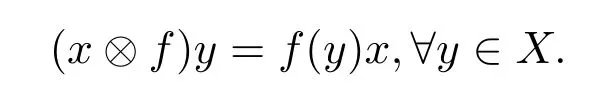
注意到任意的一秩算子都是二次算子且

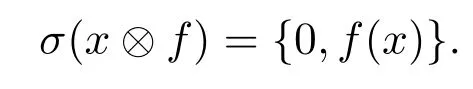
顯然,f(x)=0當(dāng)且僅當(dāng)是平方冪零算子;f(x)=1當(dāng)且僅當(dāng)是冪等算子.

本文的主要結(jié)論如下:

定理 1.1設(shè)X是具有無限重復(fù)度的復(fù)Banach空間且Φ:B(X)→B(X)是可加滿射,

則以下敘述等價.

(1)Φ雙邊保持二次算子;

(2)存在c∈C{0},X上的有界線性(或共軛線性)算子A以及B(X)上的可加映射f使得對任意的T∈B(X),有

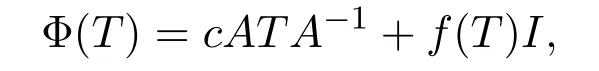
或存在c∈C{0},從X?到X上的有界線性 (或共軛線性)算子A以及B(X)上的可加映射f,使得對任意的T∈B(X),有

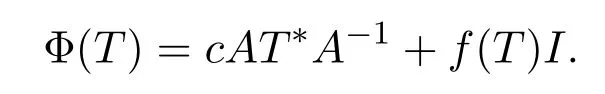
定理 1.2設(shè)n≥3且Φ:Mn(C)→Mn(C)是可加滿射,則以下敘述等價.

(1)Φ雙邊保持二次算子;

(2)存在c∈C{0},C上的環(huán)自同構(gòu)τ,非奇異矩陣A∈Mn(C)以及可加映射?:Mn(C)→C使得對任給的(tij)∈Mn(C),有

(i)Φ((tij))=cA(τ(tij))A?1+?((tij))In或

(ii)Φ((tij))=cA(τ(tij))trA?1+?((tij))In.

2 二次算子的基本性質(zhì)

這部分給出了二次算子的一些基本性質(zhì),為了提高可讀性和完整性,本文給出基本的證明.

引理 2.1設(shè)I∈B(X)是單位算子,則I不能表示成三個平方冪零算子的和.

證明假設(shè)存在Ni∈N2(X)(i=1,2,3)使得

不失一般性,設(shè)Ni/=0(i=1,2,3).令X1=kerN1.首先證明X1是Ni(i=1,2,3)的不變子空間.顯然,X1是N1的不變子空間.由

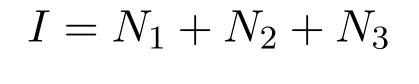
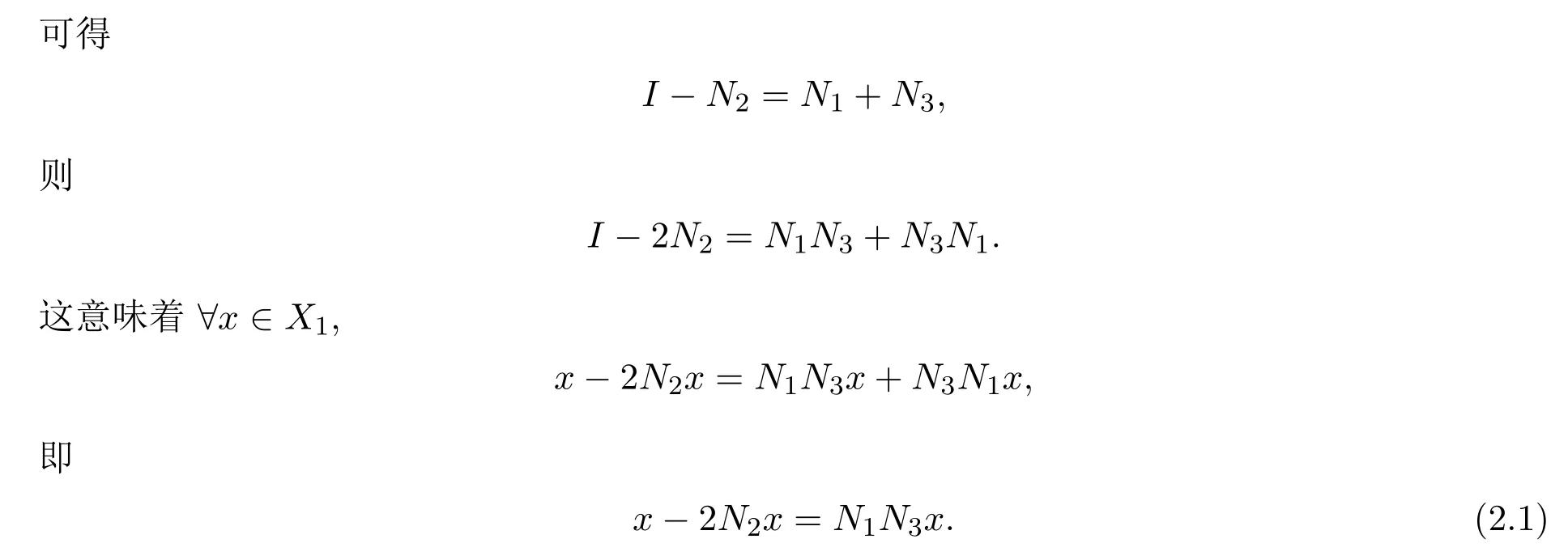
等式(2.1)兩邊分別左乘N1得N1x=2N1N2x,即N1(N2x)=0.因此,N2x∈kerN1=X1.類似地,可以證明X1是N3的不變子空間.

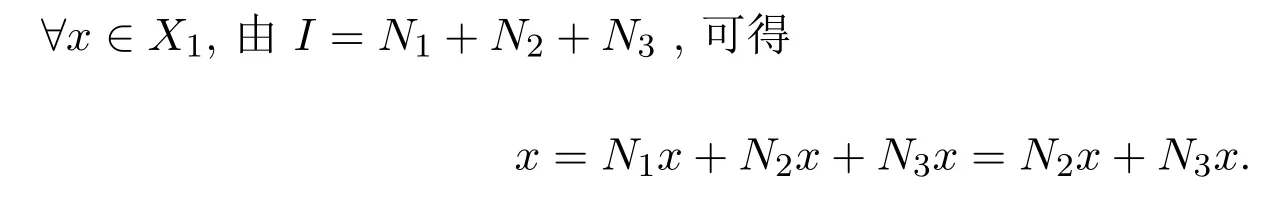
根據(jù)X1是Ni(i=1,2,3)的不變子空間,則N2x,N3x∈X1.因此,

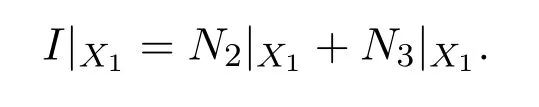
這與單位算子I不能表示成兩個平方冪零算子的和相矛盾.綜上所述,單位算子I不能表示成三個平方冪零算子的和.

接下來給出一秩冪等算子和平方冪零算子的線性組合是二次算子的充分必要條件.記

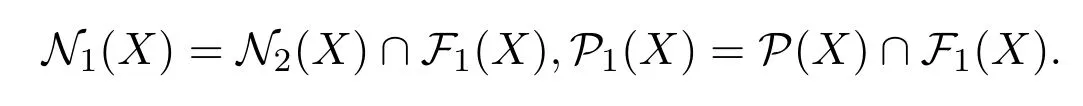
定理 2.2設(shè)N∈N2(X),P∈P1(X),則以下敘述是等價的:

(1)cP+N∈A2(X),其中c∈C{0};

(2)N=PN,NP=0,或N=NP,PN=0.

證明取P=x?f∈P1(X),其中x∈X,f∈X?使得f(x)=1.

(1)?(2).設(shè)存在c∈C{0}使得cP+N∈A2(X),則由文獻(xiàn) [8]的命題 2.2可知存在a∈C使得

其中β=ac?1.下面來證明β=0.假設(shè)β/=0.分兩種情況來考慮.

(i)當(dāng)dimX=∞時.由等式(2.2)可得:

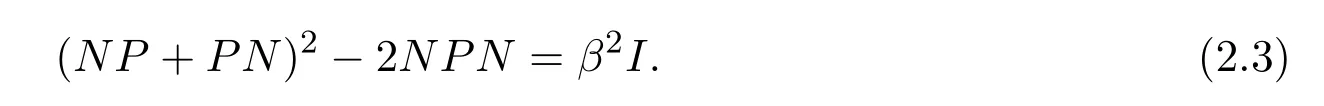
由于rank(NP+PN)2?2NPN＜∞而rankβ2I=∞,矛盾.

(ii)當(dāng)dimX=n＜∞時.等式(2.2)兩邊分別求跡可得

給等式(2.2)兩邊分別左乘P有?PNP=βP,給上式兩邊也分別求跡可得：tr(NP)=?β.結(jié)合等式 (2.4)可知 tr(I)=2,這與 dimX≥3相矛盾.因此,β=0且N=NP+PN.等式(2.2)兩邊分別左乘N得NPN=0.根據(jù)得Nx=0或N?f=0.如果Nx=0,

則

如果N?f=0,則

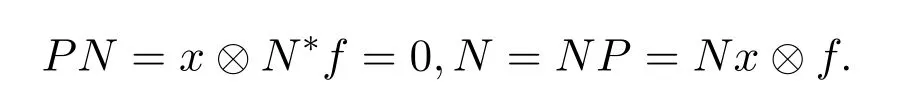
(2)?(1)顯然,N是一秩算子.如果N=NP,PN=0,則存在c∈C{0}使得

因此,cP+N∈A2(X).同理,如果N=PN,NP=0,則存在c∈C{0}也有cP+N∈A2(X).

定理 2.3設(shè)A,B∈N2(X)且rankA＞1,rankB＞1,假定對任給的有限秩算子F,A+F∈CI+N2(X)當(dāng)且僅當(dāng)B+F∈CI+N2(X),則存在α∈C{0}使得B=αA.

證明首先證明kerA=kerB且AB=BA=0.

對任給的x∈kerA,則在空間分解X={x}˙+X1,下,A和B有如下的矩陣表示:

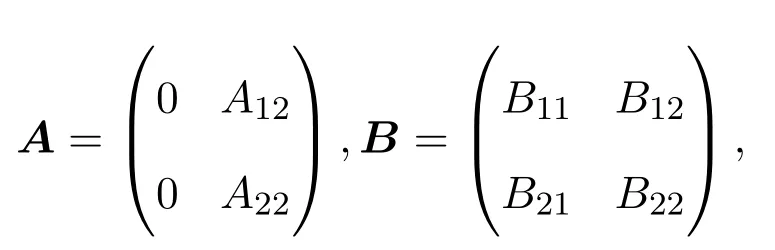
其中rankA12≤1且B11是常數(shù).由A,B∈N2(X)可得

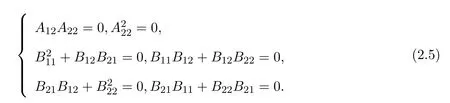
下面分兩種情況討論.

(i)當(dāng)A12/=0時.對α∈C{0},令

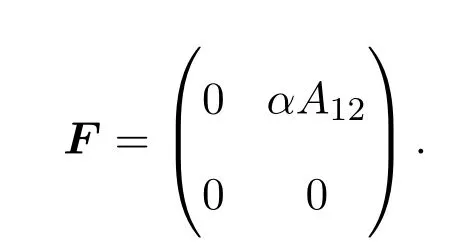
顯然,A+F∈N2(X)?CI+N2(X),進(jìn)而可得B+F∈CI+N2(X),所以存在λ∈C,N∈N2(X)使得B+F=λI+N.由引理2.1可得λ=0.因此,B+F=N.這意味著

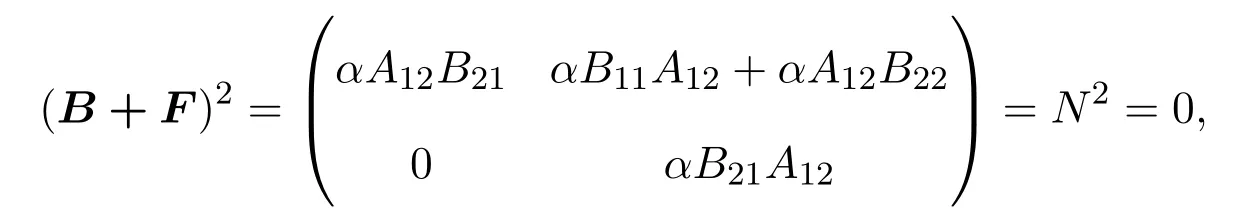
即A12B21=0,B21A12=0且B11A12+A12B22=0.因此,B21=0,結(jié)合等式 (2.5)可得.由于B11是常數(shù),則B11=0.因此,Bx=0,即x∈kerB.

(ii)當(dāng)A12=0時.則存在y∈X使得Ay/=0.令x1=Ay.則x1∈kerA.在空間分解下,A有如下的矩陣表示

由Ay/=0可得.類比情形(i)可知Bx1=0.令x2=x+x1∈kerA.由x,y,Ay線性無關(guān)得x2,x,y也線性無關(guān).所以存在f∈X?使得f(x2)=1且f(x)=f(y)=0.令X3=kerf.顯然,x,y∈X3.在空間分解下,A有如下矩陣表示

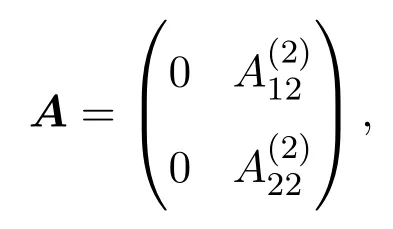
假設(shè)存在x∈X使得Ax和Bx線性無關(guān),則Ax,x和Bx也線性無關(guān).令

顯然,X4是A和B的不變子空間.在空間分解下,A和B有如下的矩陣表示

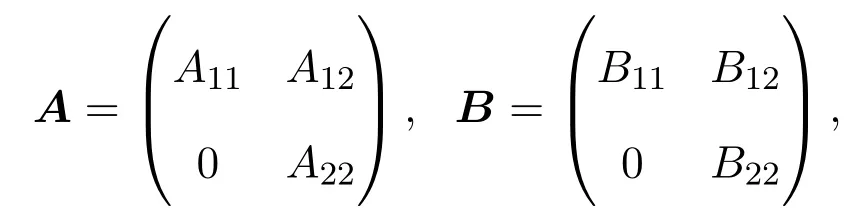
其中

令

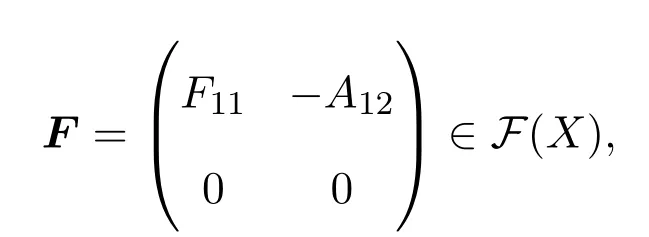
其中

且a/=0.則

因此,B+F∈CI+N2(X).然而,

3 主要定理及證明

為了證明本文的主要定理,首先給出下面的引理,其證明過程與文獻(xiàn)[8]的推論3.1類似.

引理 3.1設(shè)Φ:B(X)→B(X)是雙邊保持A2(X)的可加滿射,則

(1)Φ(CI)=CI.

(2)Φ是單射.

(3)Φ雙邊保持CI+N2(X).

定理 1.1的證明只需證明(1)?(2).由引理3.1可知Φ是雙邊保持A2(X)的可加雙射,下面來完成定理的證明.

第一步:Φ(CI+CP1(X))=CI+CP1(X)且 Φ(CI+N1(X))=CI+N1(X).

首先證明

Φ(CI+CP1(X))=CI+CP1(X).

任取P∈P1(X).不妨設(shè),其中x∈X,f∈X?且f(x)=1.則Φ(P)∈CI+CP(X).不失一般性,設(shè) Φ(P)=λI+μQ,其中λ,μ∈C,μ/=0,Q∈P(X).因為 Φ(P)是二次算子,所以存在λ1,λ2∈C 且λ1/=λ2使得 (Φ(P)? λ1)(Φ(P)?λ2)=0.則在空間分解

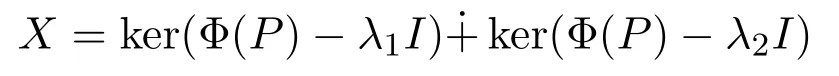
下,Φ(P)有如下的矩陣表示:

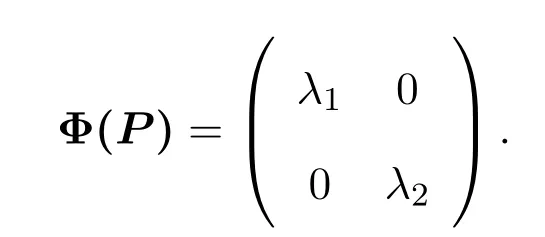
下面證明:

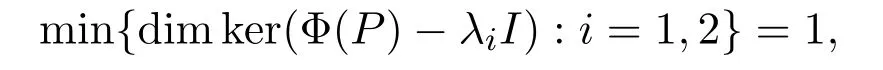
這意味著Q∈P1(X).則Φ(CI+CP1(X))?CI+CP1(X).如果

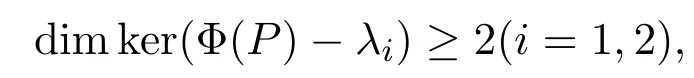
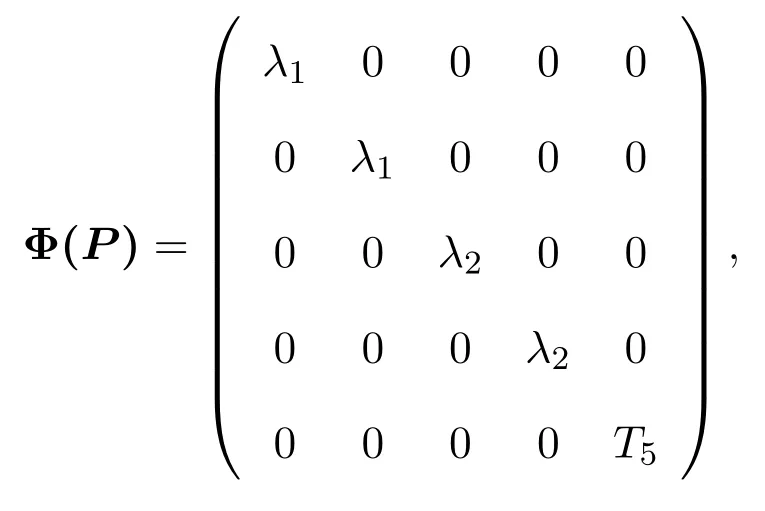
其中dimXi=1(i=1,2,3,4).對任給的a,b,c,d∈C{0},取

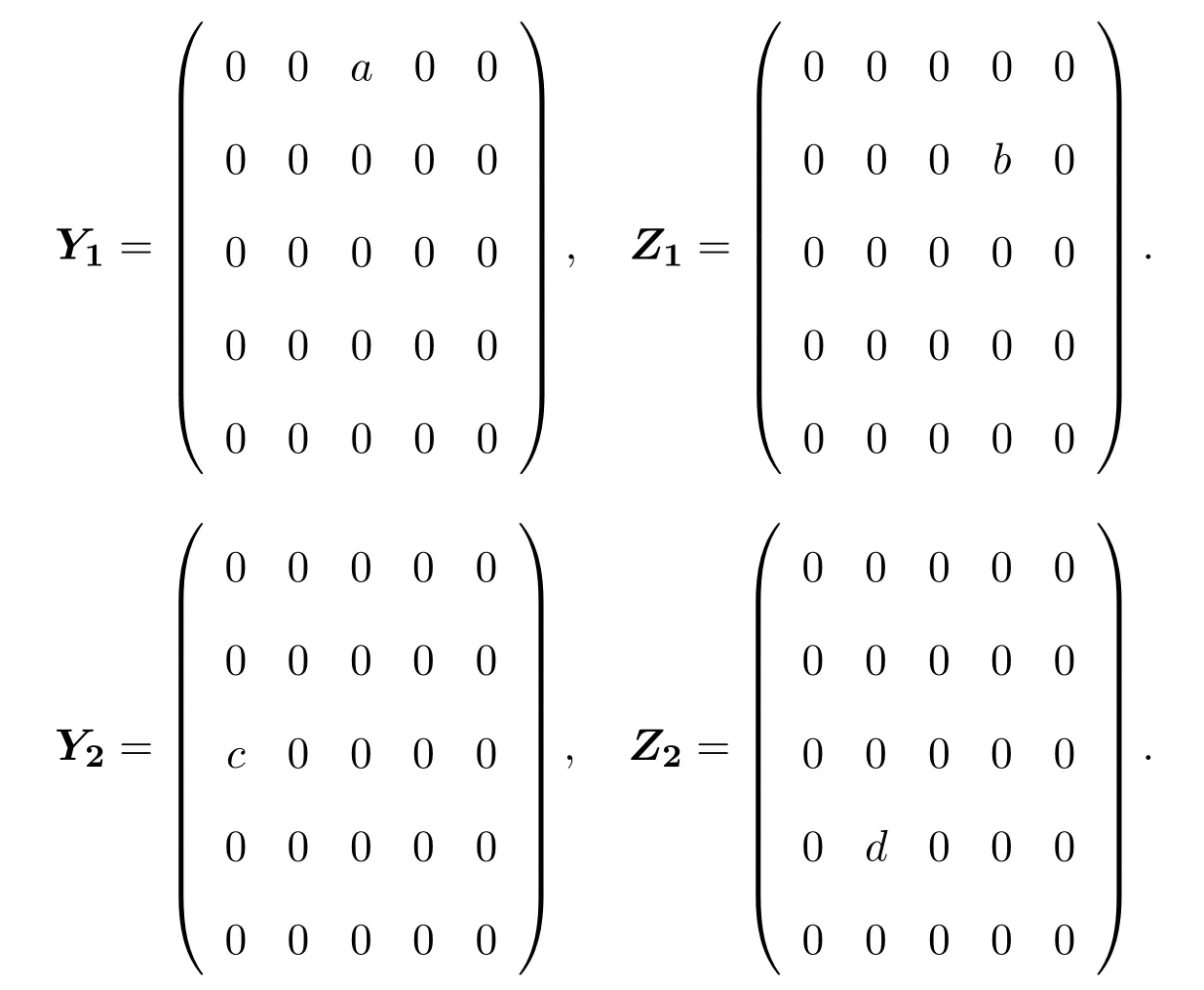
令

則Ti和Φ(P)相似,因此,Ti∈A2(X).因為Yi,Zi∈N2(X)且Φ雙邊保持CI+N2(X),所以

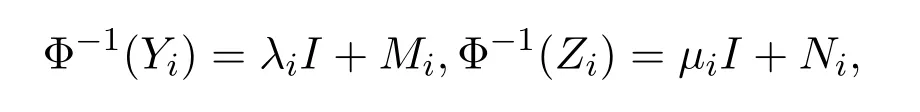
其中λi,μi∈C,Mi,Ni∈N2(X).由Yi+Zi∈N2(X)可得Mi+Ni∈N2(X).注意到

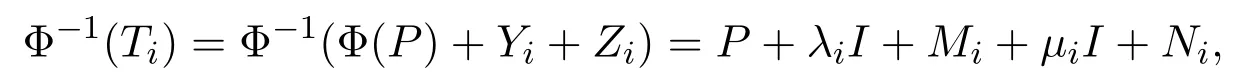
則P+Mi+Ni∈A2(X).根據(jù)a,b,c,d的任意性,結(jié)合定理2.2可得

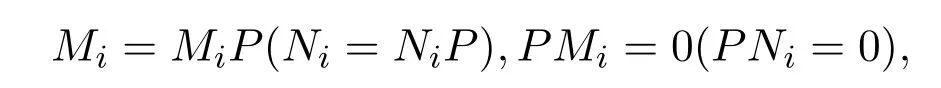
或

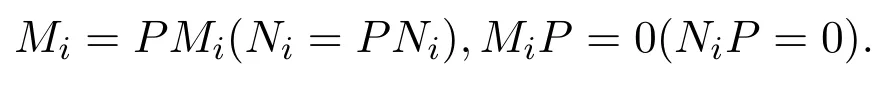
下列敘述之一成立:

(1)如果Mi=MiP,PMi=0,則Ni=NiP,PNi=0,反之亦然;

(2)如果Mi=PMi,MiP=0,則Ni=PNi,NiP=0,反之亦然.

假設(shè)Mi=MiP,PMi=0.因為P+Mi+Ni∈A2(X),根據(jù)定理2.2可得:Mi+Ni是一秩算子,

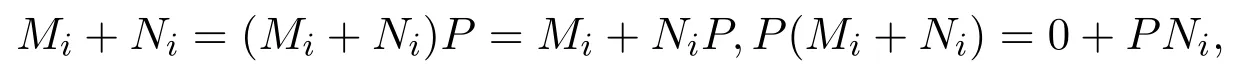
或

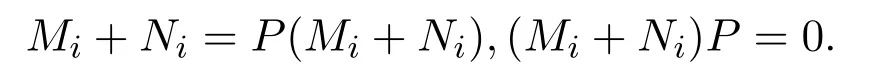
如果Ni=PNi和NiP=0成立,則 (Mi+Ni)P=Mi和P(Mi+Ni)=Ni成立,矛盾.因此,Ni=NiP,PNi=0.同理,反之也成立.類似地,如果Mi=PMi和MiP=0成立,則Ni=PNi和NiP=0成立.

下列的論斷成立:

(3)如果M1=M1P,PM1=0,則M2=PM2,M2P=0,反之亦然;

(4)如果N1=N1P,PN1=0,則N2=PN2,N2P=0,反之亦然.

事實上,如果M1=M1P,PM1=0和M2=M2P,PM2=0同時成立,則

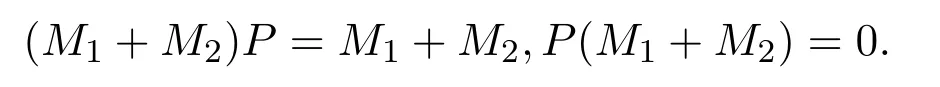
在這種情況下,

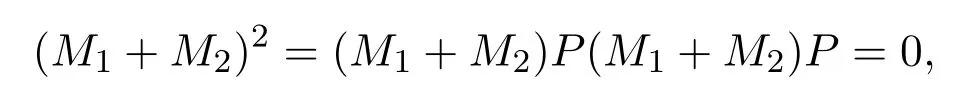
即M1+M2∈N2(X).根據(jù)定理2.2可得P+M1+M2∈A2(X).因為

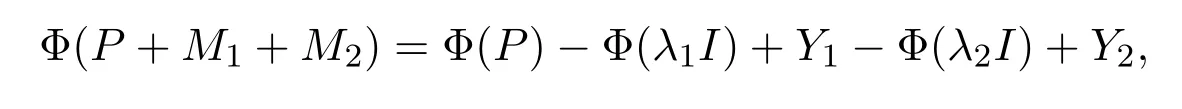
則由引理3.1和Φ雙邊保持A2(X)可得Φ(P)+Y1+Y2∈A2(X).然而,通過選擇合適的a和c可使 Φ(P)+Y1+Y2的譜包含異于λ1和λ2的其它元素,這與 Φ(P)+Y1+Y2∈A2(X)相矛盾.因此,如果M1=M1P,PM1=0,則M2=PM2,M2P=0.同理,反之也成立.類似地,如果N1=N1P,PN1=0,則N2=PN2,N2P=0.

另一方面,因為 Φ(P)+Y1+Z2∈A2(X)且

則P+M1+N2∈A2(X).由定理2.2可得:M1+N2是一秩算子,

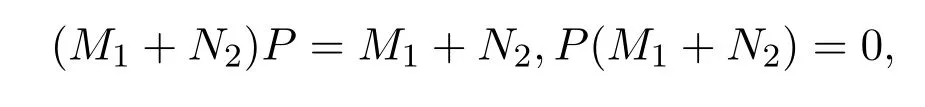
或

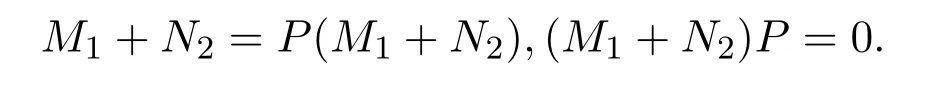
不失一般性,假設(shè)

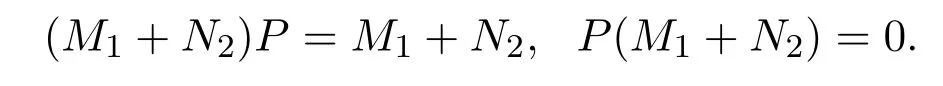
類似地,M1=M1P,PM1=0和N2=N2P,PN2=0同時成立,矛盾.

因此,min{dimker(Φ(P)?λiI):i=1,2}=1.故

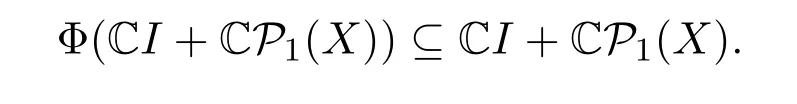
同理,Φ?1(CI+CP1(X))?CI+CP1(X).因此,Φ(CI+CP1(X))=CI+CP1(X).

下面來證明

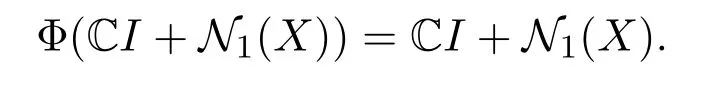
對任給的N∈N1(X),不妨設(shè)且g(x)=0.取f∈X?使得f(x)=1.令

由

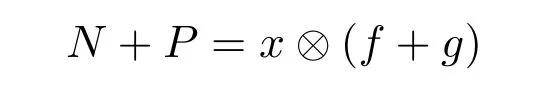
可得N+P是二次算子,則存在λ1,λ2,μ1∈C,N1∈N2(X),Q1∈P1(X)使得

根據(jù)Φ雙邊保持二次算子可得M+μ1Q1是二次算子.由定理2.2可知M∈N1(X),即

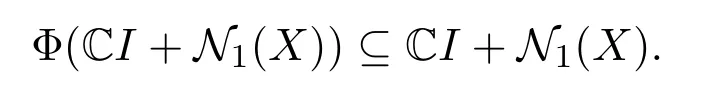
同理,Φ?1(CI+N1(X))?CI+N1(X).因此,Φ(CI+N1(X))=CI+N1(X).

注意到第一步對于X是有限維的情況也是成立的.

第二步:存在c∈C{0},X上有界線性(或共軛線性)算子A以及F(X)上的可加映射f,使得對任給的F∈F(X)有

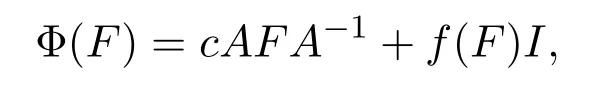
或存在c∈C{0},從X?到X的有界線性(或共軛線性)算子A以及F(X)上的可加映射f,使得對任給的F∈F(X)有

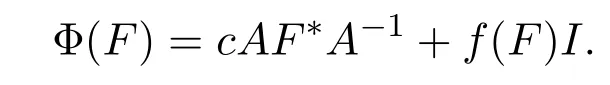
其中ai,μi∈C,yi∈X,gi∈X?滿足gi(yi)=0或者gi(yi)=1.定義

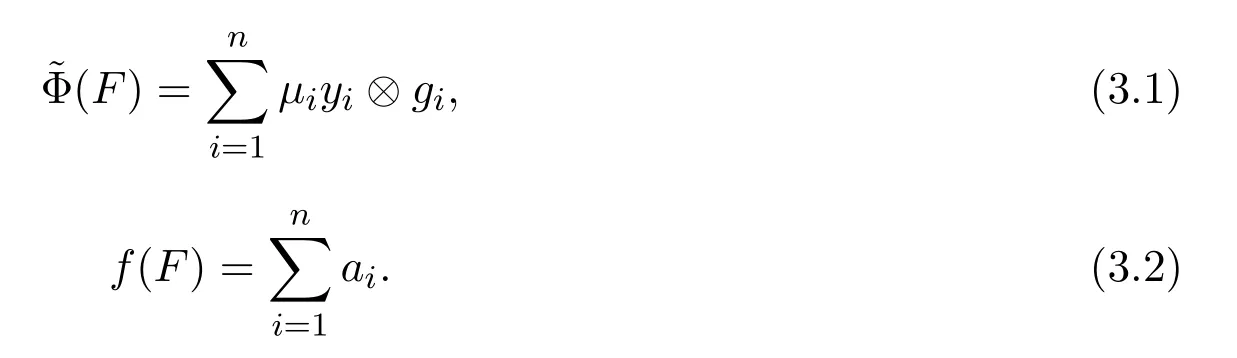
根據(jù)X是無限維和

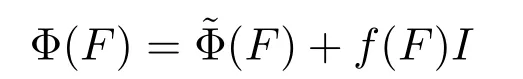
可得F的表示和f(F)是獨立的.因此,和f是可加的.

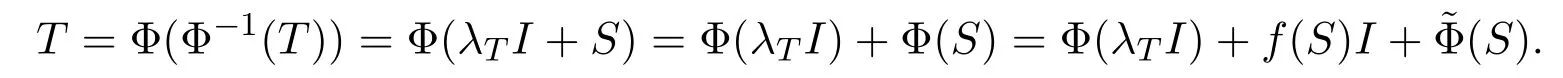
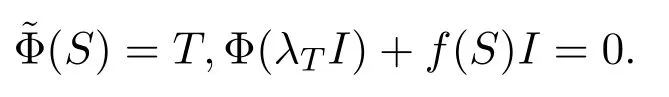
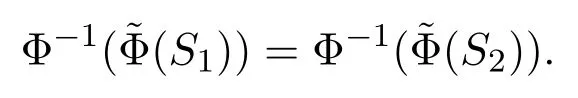
因而存在λ1,λ2∈C使得

則

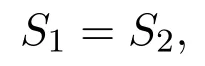
(i)存在環(huán)自同構(gòu)τ:F→F以及τ-擬線性雙射A:X→X和C:X?→X?使得

對所有x∈X及f∈X?都成立;

(ii)存在環(huán)自同構(gòu)τ:F→F以及τ-擬線性雙射A:X?→X和C:X→X?使得

對所有x∈X及f∈X?都成立.

顯然,

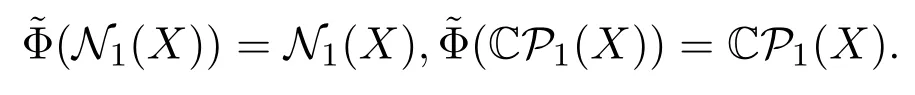
則存在c∈C{0}使得對所有的x∈X和f∈X?都有

類似于文獻(xiàn) [5]的定理 2.5.2的證明可知A是有界線性 (或共軛線性)算子.因此,對任意的和y∈X有

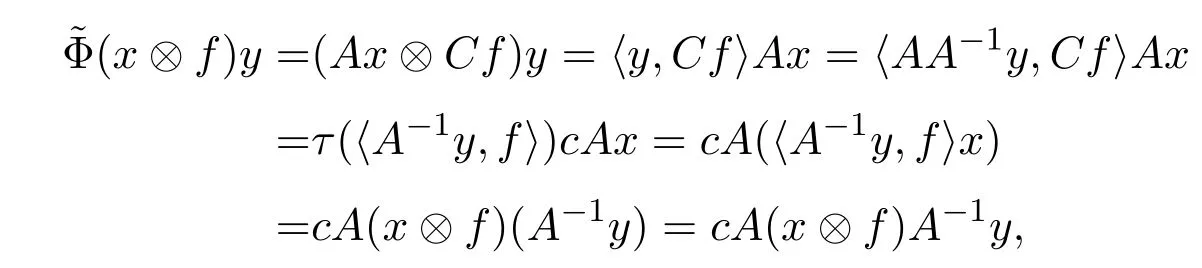
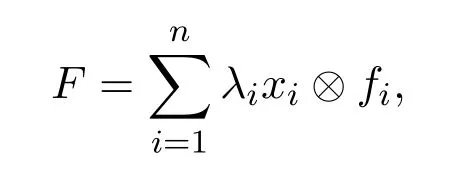
其中λi∈C,xi∈X,fi∈X?.則

故對任給的F∈F(X)有Φ(F)=cAFA?1+f(F)I.

第三步:對任給的N∈N2(X)有 Φ(N)=cλNI+cANA?1,其中c,λN∈C.

定義

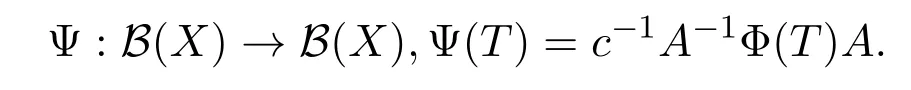
顯然,Ψ是雙邊保持二次算子的可加雙射,且對任給的F∈F(X)有

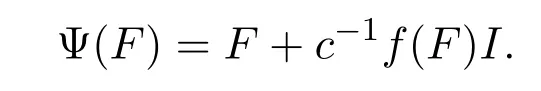
根據(jù)Φ雙邊保持CI+N2(X)可得Ψ也雙邊保持CI+N2(X).則對無限秩算子N∈N2(X),存在λN∈C,M∈N2(X)使得 Ψ(N)=λNI+M,注意到 rankM＞1.因為 Ψ 雙邊保持CI+N2(X),所以存在F∈F(X)使得

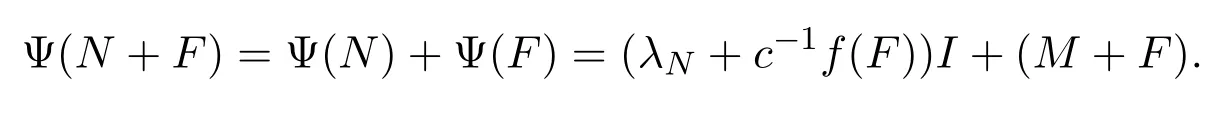
則N+F∈CI+N2(X)當(dāng)且僅當(dāng)M+F∈CI+N2(X).由定理2.3可得:存在α∈C{0}使得M=αN.因此,Ψ(N)=λNI+αN.

下面只需要證α=1即可.取x∈X使得Nx/=0.則在空間分解X={Nx}˙+X6下,N有如下矩陣表示

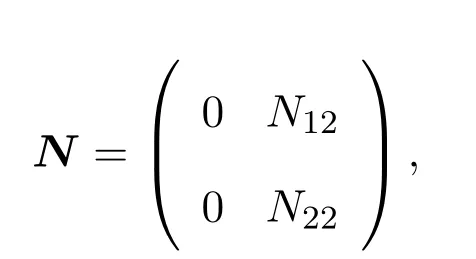
其中N12是一秩的,且N12/=0.令

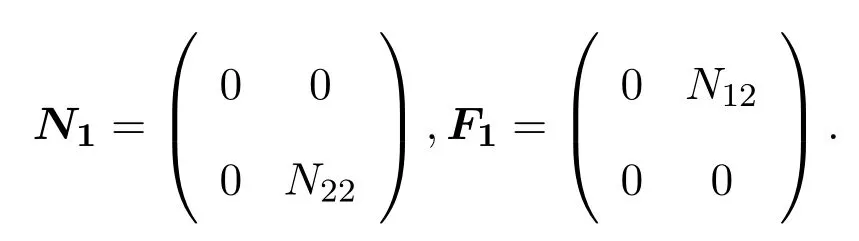
顯然,N1,F1∈N2(X)且F1∈F(X).則 Ψ(N1)=λN1I+βN1,其中λN1,β∈C.因為

結(jié)合 Ψ(N)=λNI+αN可得

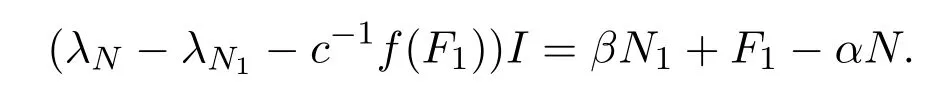
再由引理2.1可知

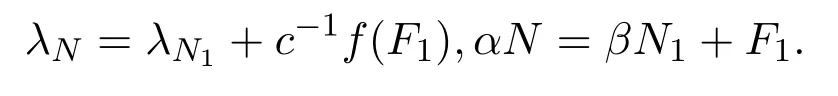
因為αN=βN1+F1+N1?N1=(β ?1)N1+N,所以 (α?1)N=(β ?1)N1.由于N/=N1,則α=1,β=1.因此,對任給的N∈N2(X)有 Ψ(N)=λNI+N.

第四步:存在c∈C{0},X上的有界線性(或共軛線性)算子A以及B(X)上的可加映射f,使得對任意的T∈B(X),有

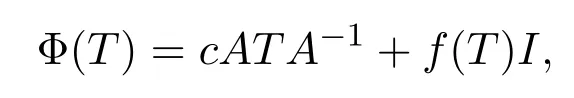
或存在c∈C{0},從X?到X上的有界線性 (或共軛線性)算子A以及B(X)上的可加映射f,使得對任意的T∈B(X),有 Φ(T)=cAT?A?1+f(T)I.

事實上,如果還存在n(n≤8)個平方冪零算子使得,則

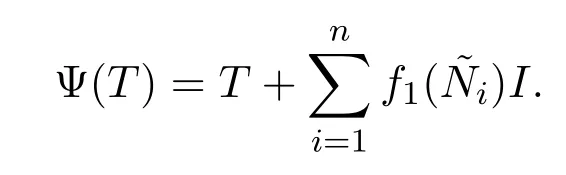
由 (3.3)可得

則定義

顯然,f2是可加映射.因此,Ψ(T)=T+f2(T)I,?T∈B(X).定義

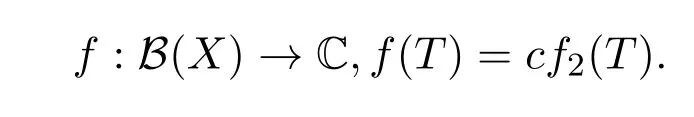
根據(jù)f2是可加映射可知f是可加映射.因此,對任給的T∈B(X),

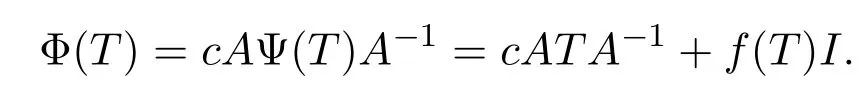
類似地,對于情形(ii)有

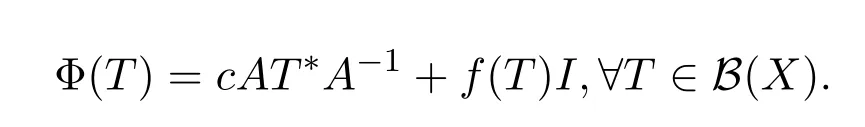
定理 1.2的證明只需要證明(1)?(2).取

是所有跡為零的矩陣組成的集合,N1是所有一秩冪零矩陣組成的集合.我們知道sln(C)是N1可加張成的空間.注意到定理1.1第一步的證明對X是維數(shù)不小于3的有限維也成立.因此,

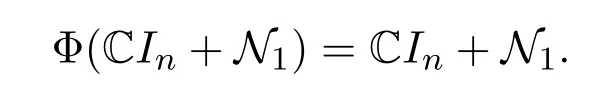
即對任給的N∈N1,存在f(N)∈C和?Φ(N)∈N1使得

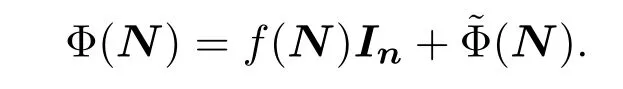
將f和延拓到sln(C)上.事實上,對任給的T∈sln(C),如果存在Tij∈N1使得

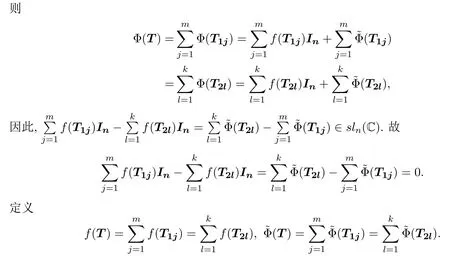
顯然,f和是可加的,且,?T∈sln(C).

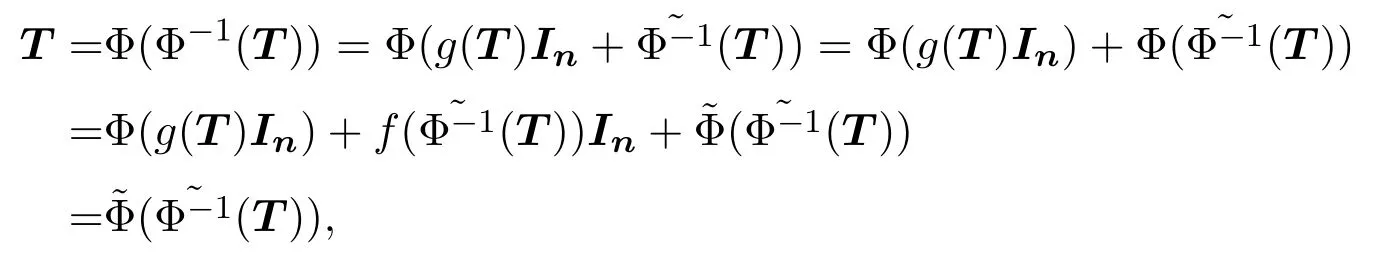
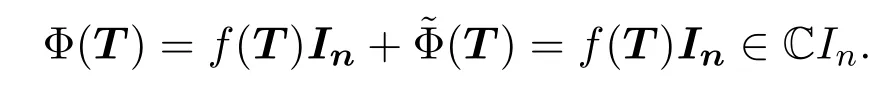
故由引理3.1可得T=0,即?Φ是雙邊保持一秩冪零性的可加雙射.由文獻(xiàn)[2]中的定理 2.4可得:存在 C上的環(huán)自同構(gòu)τ,可逆矩陣A∈Mn(C)以及c∈C{0}使得對任給的(tij)∈sln(C)有

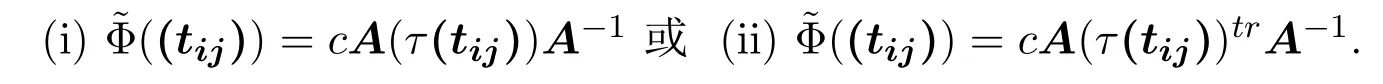
假設(shè) (i)成立,對T=(tij)=n?1tr(T)In+(T?n?1tr(T)In)∈Mn(C)有

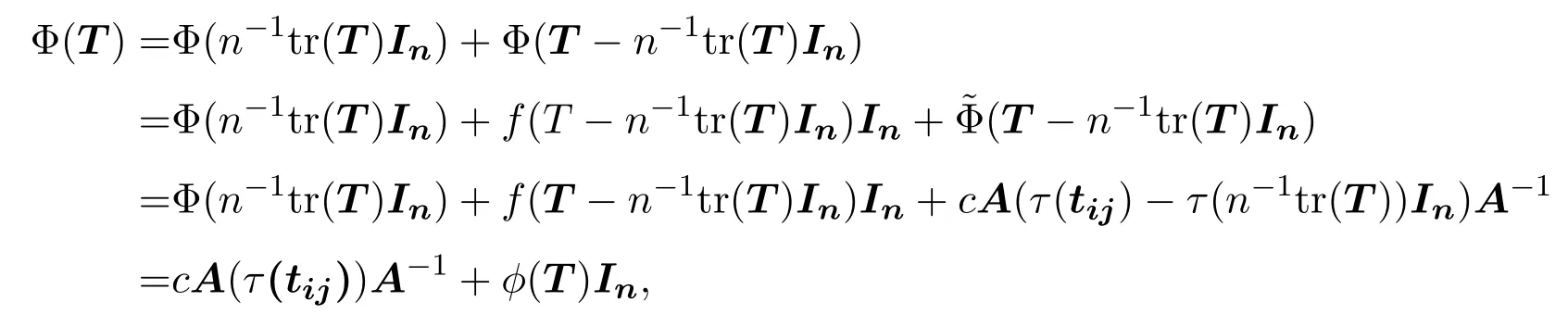
其中

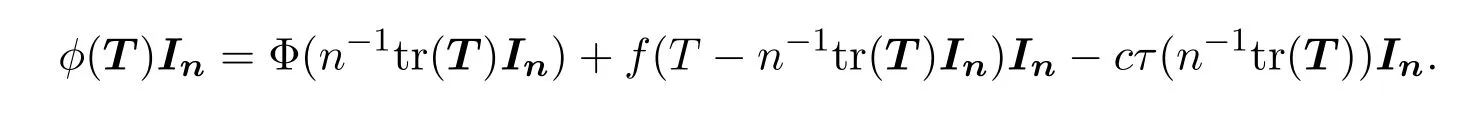
顯然,?是可加的.即定理1.2(2)的(i)是成立的.如果(ii)成立,則定理1.2(2)的(ii)成立.

[1]Bai Zhaofang,Hou Jinchuan.Linear maps and additive maps that preserve operators annihilated by a polynomoal[J].Math.Anal.Appl.,2002,271:139-154.

[2]Bai Zhaofang,Hou Jinchuan.Additive maps preserving nilpotent operators or spectral radius[J].Acta.Math.Sin,(Engl.Ser.),2005,21:1167-1182.

[3]Cao Chongguang,Zhang Xian.Additive operators preserving idempotent matrices over fi elds and applications[J].Linear Algebra Appl.,1996,248:327-338.

[4]Hadwin L B.Local multiplications on algebras spanned by idempotents[J].Linear and Multilinear Algebra,1994,37:259-263.

[5]侯晉川,崔建蓮.算子代數(shù)上線性映射引論[M].北京:科學(xué)出版社,2002.

[6]Kuzma B.Additive idempotence preservers[J].Linear Algebra Appl.,2002,335:103-117.

[7]Omladic M,ˇSemrl P.Additive mappings preserving operators of rank one[J].Linear Algebra Appl.,1993,182:239-256.

[8]Oudghiri M,Souilah K.Linear preservers of quadratic operators[J].Mediterranean Journal of Mthematics,2016,13:4929-4938.

[9]ˇSemrl P.Linear mappings preserving square-zero matrics[J].Bull.Australian Math.Soc.,1993,48:365-370.

[10]Jin-hsien W,Wu Peiyuan.Sums of square-zero opeators[J].Studia Mathematica,1991,99:115-127.

[11]Wu Jing,Li Pengtong,Lu Shijie.Additive mappings that preserve rank one nilpotent operators[J].Linear Algebra Appl.,2003,367:213-224.

[12]Wu Peiyuan.Additive combimations of special operators[J].Functional Analysis and Operator Theory,1994,30:337-361.

Additive maps preserving quadratic operators

Meng Hongye,Ji Guoxing
(Department of Mathematics and Information Science,Shaanxi Normal University,Xi′an 710119,China)

LetXbe an in fi nite dimensional complex Banach space with in fi nite multiplicity or a fi nite dimensional Banach space with dimX≥3 andB(X)be the Banach algebra of all bounded linear operators onX.In this paper,we fi rst prove that identity operator is not the sum of three square-zero operators,the block operator matrix technique is used to obtain the essential feature of square-zero operators.Based the given feature,we characterize the structure of additive surjective maps onB(X)that preserve quadratic operators in both directions.

quadratic operator,idempotent operator,square-zero operator,additive map

2010 MSC:47B49,47L10

O177.1

A

1008-5513(2017)06-0600-15

10.3969/j.issn.1008-5513.2017.06.006

2017-11-21.

國家自然科學(xué)基金(11371233).

孟紅葉(1992-),碩士生,研究方向：算子代數(shù)與算子理論.