General Solutions for Hydromagnetic Free Convection Flow over an In finite Plate with Newtonian Heating,Mass Diffusion and Chemical Reaction

Constatin Fetecau,Nehad Ali Shah,and Dumitru Vieru

1Academy of Romanian Scientists,Bucuresti 050094,Romania

2Abdus Salam School of Mathematical Sciences GC,University Lahore,54600,Pakistan

3Technical University of Iasi,Iasi 700050,Romania

1 Introduction

Natural or free convection flows are abundantly met in nature.They are particularly important in oceanic and atmospheric circulation, filtration processes,cooling of nuclear reactors,solar energy collectors and arise in fluids when the temperature changes imply variations of the density leading to buoyancy forces which affect their motion.Details about the applications of free convection flows can be found in the books of Ghoshdastidar[1]and Nield and Bejan[2]but one of the oldest and interesting studies regarding the free convection from a heated vertical plate is that of Turnbull[3]in presence of an electric field.Such flows,which are also affected by the differences in concentration,have been extensively studied due to their multiple applications in engineering and environmental processes.The study of free convection flow in the presence of magnetic field is also important in polymer industry,metallurgy,astrophysics and geophysics and the first authors who took into consideration the effects of magnetic field in their work seem to be Soundalgekaret al.[4]

Hydromagnetic flows combined with heat and mass transfer by free convection have been studied by many authors due to their diverse applications in science and technology.The mass transfer,that means the transport of a constituent between two regions having different concentrations,is the basis of many biological and chemical processes.[5]It also appears in the theory of stellar and solar structures.On the other hand,in the last time,hydromagnetic free convection flows involving heat and mass transfer with chemical reaction received a special attention(see for instance the recent works of Reddyet al.[6?7]Raoet al.,[8]Srihari and Chirra Kesava Reddy,[9]Pattnaik and Biswal,[10]Sethet al.[11]and therein references).They are important in different areas of sciences and engineering and usually occur in magnetohydrodynamic power generation systems,cooling of nuclear reactors,power and cooling systems as well as in petro-chemical industry.

However,the heat transfer characteristics are strongly dependent on the thermal boundary conditions,and in all above-mentioned papers the free convection flows are driven by a prescribed surface temperature or prescribed surface heat flux.Merkin[12]was the first author who assumed that the flow is set up by Newtonian heating from the surface.In such flows,which are also called conjugate convective flows and have important applications in many ture.Effects of Newtonian heating on the free convection lf ow of a viscous fluid along an in finite vertical or horizontal plate embedded in a porous medium have been studied by Lesnicet al.[14?15]and Popet al.[16]Other interesting solutions,in the absence of mass transfer,have been also established by Chaudhary and Jain,[17]Mebine and Adigio,[18]Narahari and Ishak,[19]Daset al.[20]and Hussananet al.[21]The effects of mass transfer on such flows have been studied by Narahari and Nayan,[22]Narahariet al.,[23]Narahari and Dutta[24]and Hussananet al.[25?26]However,none of these works took into consideration,heat source or chemical reaction.Free convection flows with Newtonian heating and mass diffusion in which the plate applies a shear stress to the fluid or slip effects are taken into consideration have been studied by Vieruet al.,[27]Khanet al.,[28]and Fetecauet al.[29]An interesting mathematical study of the free convection with dissipative heating has been developed by Sheremetet al.[30]

The main purpose of this work is to provide a general study of hydromagnetic free convection flow of an engineering devices,[13]the rate of heat transfer from the plate surface is proportional to the local surface temperaincompressible viscous fluid over a moving in finite vertical plate with Newtonian heating,heat source and chemical reaction.Radiative and porous effects are not taken into consideration but,according to Magyari and Pantokratoras[31]and Fetecauet al.,[32]they can be immediately included by a simple rescaling of Prandtl number and magnetic parameter.Exact analytical solutions are established for the dimensionless velocity and concentration fields and the corresponding Sherwood number and skin friction coefficient.They can generate exact solutions for any flow of this type and,for illustration,three special cases are considered and some known results from the literature are recovered or corrected.The in fluence of physical parameters on some flows with technical relevance is graphically underlined and discussed.Contributions of mechanical,thermal and concentration components of velocity on the fluid motion are together brought to light for motions due to a highly accelerating plate.The required time to reach the steady-state for cosine or sine oscillations of the concentration on the boundary is also determined.

2 Mathematical Formulation of the Problem

Let us consider the hydromagnetic free convection flow of an electrically conducting,incompressible viscous fluid with Newtonian heating and mass diffusion over a moving in finite non conducting vertical flat plate(Fig.1).At the initial momentt=0,both the fluid and the plate are at rest with the same temperatureT∞and the species concentrationC∞.After timet=0+the plate,whose concentration is raised or lowered to the valueC∞+Cwg(t),is moving in its plane against the gravitational field with an arbitrary velocityUf(t).HereCwandUare constants while the dimensionless functionsf(·)andg(·)are piecewise continuous andf(0)=g(0)=0.A transverse magnetic field of uniform strengthB,whose magnetic lines of force are fixed relative to the fluid,acts perpendicular to the plate and the magnetic Reynolds number is assumed to be small enough so that the induced magnetic field can be neglected.

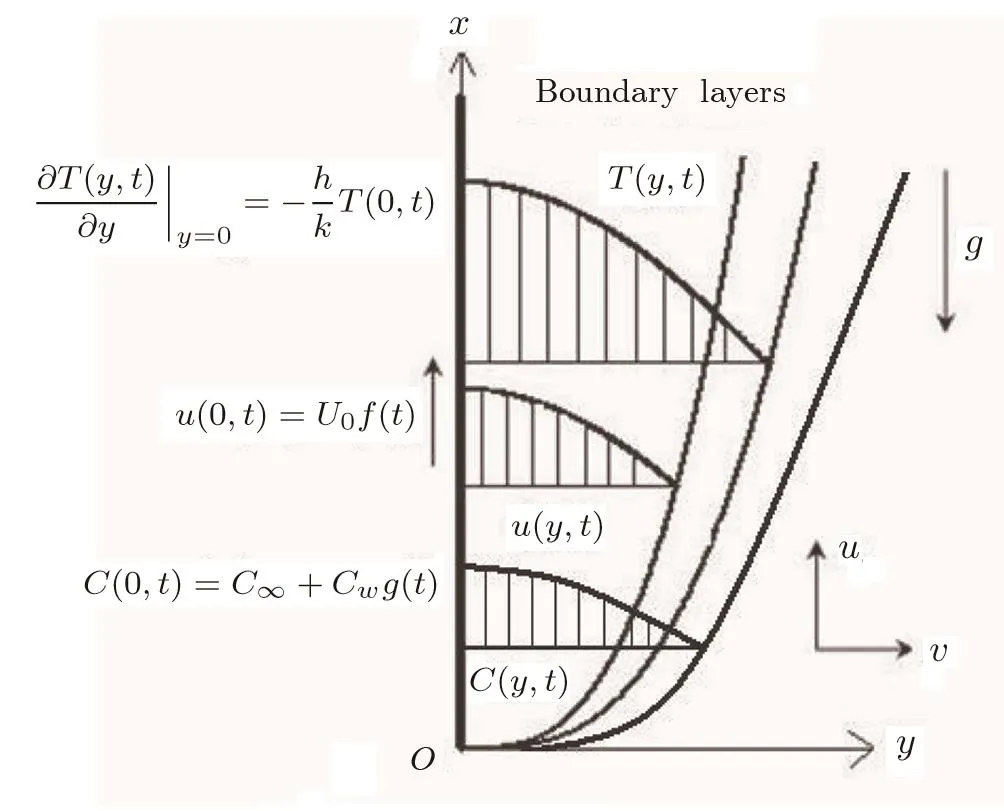
Fig.1 Schematic diagram of the flow con figuration.

Radiative and porous effects are not taken into consideration but,as we already mentioned,they can be immediately included by a simple rescaling of Prandtl number,respectively the magnetic parameter.Our results are obtained in the presence of heat source and chemical reaction,but the viscous dissipation is neglected due to its small size.This assumption can be justi fied by small velocities usually encountered in free convection flows.[33]In these conditions,choosing a suitable Cartesian coordinate system and using the usual Boussinesqs approximation,our flow is governed by the following partial differential equations[10](the inertia terms are also neglected)

whereu,T,andCare velocity,temperature and species concentration of the fluid,νis the kinematic viscosity,gis the acceleration due to gravity,βTis the thermal expansion coefficient,βCis the volumetric coefficient of concentration expansion,σis electrical conductivity,ρis fluid density,cpis the speci fic heat at constant pressure,kis the thermal conductivity,Qis the heat generation or absorption coefficient,Dis the chemical molecular diffusivity andRis chemical reaction parameter.

The corresponding initial and boundary conditions are:

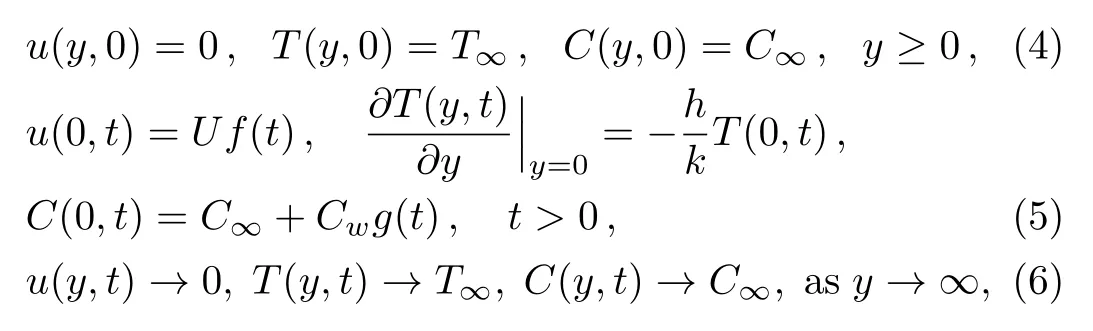
wherehis the heat transfer coefficient for Newtonian heating.

By introducing the dimensionless variables and functions

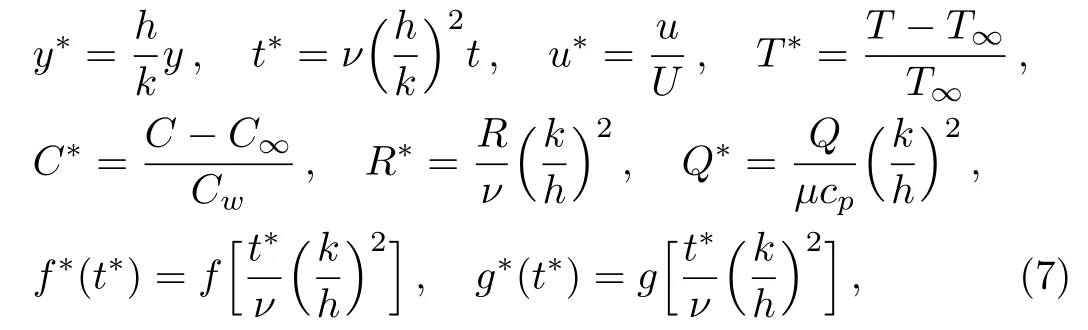
and dropping out the star notation,we attain to the following dimensionless initial boundary values problem:

are the thermal Grashof number,the mass Grashof number,the buoyancy ratio parameter,the magnetic parameter,the Prandtl number and the Schmidt number,respectively.Of course,the characteristic velocityUhas been taken to be equal with(gβT/νU)(k/h)2T∞.

It is worth pointing out thatPrandScare transport parameters representing the thermal diffusivity,respectively the mass diffusivity whileNgives the relative contribution of the mass transport rate on the flow into consideration.[24]AsβCcan be positive or negative[34]andβTis a positive quantity,Ncan be also positive or negative.IfNis positive,the mass and thermal buoyancy forces act in the same direction.In the contrary case,the two forces are opposite.Of course,N=0 in the absence of mass diffusion.

3 Solution of the Problem

The temperature fieldT(y,t)corresponding to this problem has been already determined by Vieruet al.[27]in a problem with shear stress on the boundary.Our interest here,is to determine the velocity and concentration fields as well as the corresponding Sherwood number and the skin friction coefficient whenT(y,t)is known.For completion,the thermal boundary layer thickness will be also determined.To do that,the Laplace transform technique will be used and the corresponding Laplace transform(Ref.[27],Eq.(19))

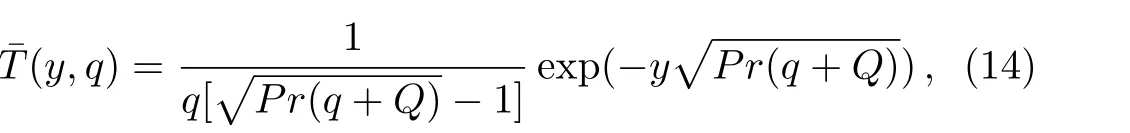
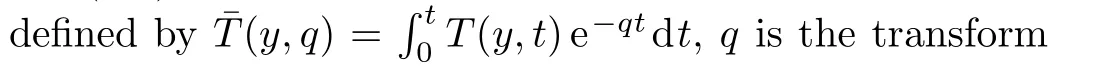
In order to determine the differential equation describing the thickness of the thermal boundary layer,[35]we integrate Eq.(9)with respect toyfrom zero to in finity,respectively toδ1T,whereδ1Tis the thermal layer thickness,introduce the measure of thermal layer

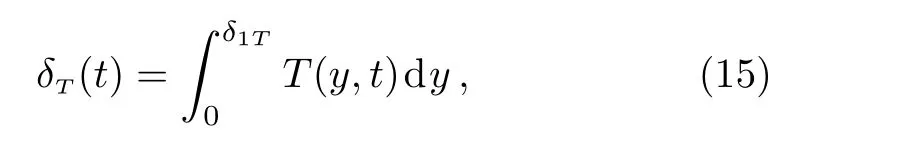
and use the boundary conditions(12)2and(13)2.The obtained equation is

Applying the Laplace transform to Eq.(16)and using Eq.(14)as well as the fact thatδT(0)=0,we find that

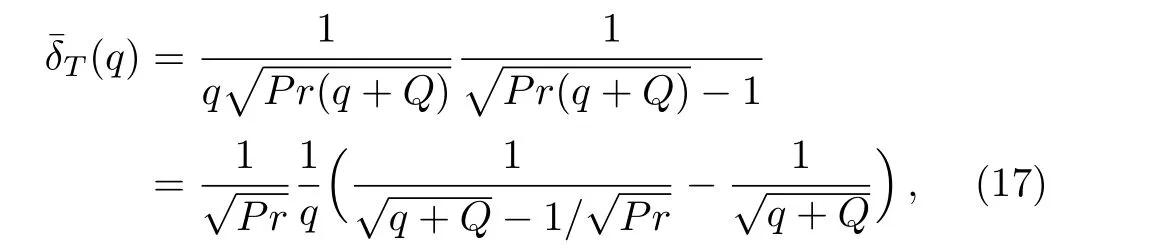
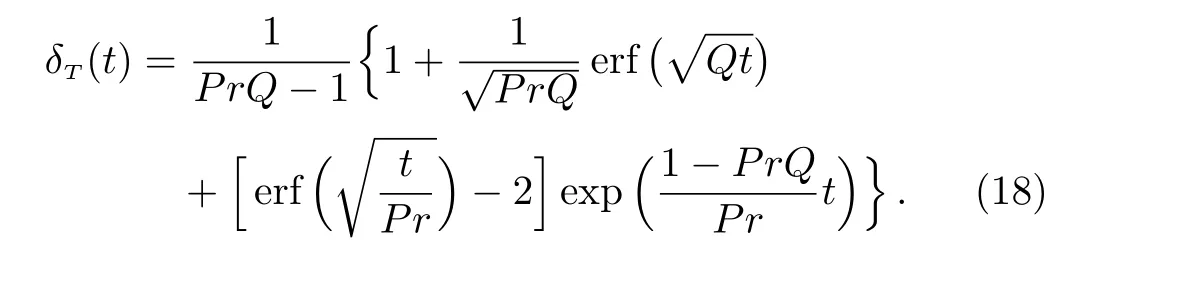
3.1 Species Concentration

Applying the Laplace transform to Eq.(10)and using the corresponding initial and boundary conditions,we find that

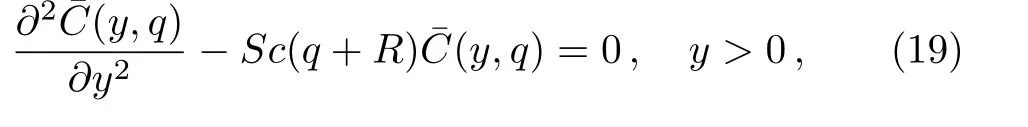
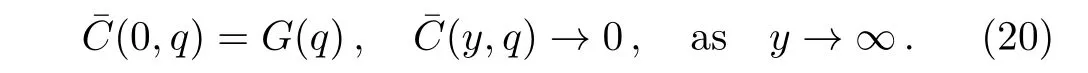
Here,G(q)is the Laplace transform ofg(t)andqis the transform parameter.

The solution of the ordinary differential equation(19)subjected to the boundary conditions(20),is given as

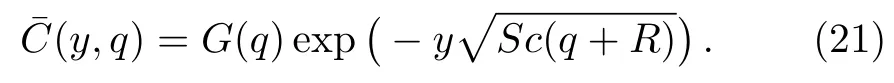
Applying the inverse Laplace transform to Eq.(21)and using Eq.(A1)from Appendix,the fact thatL?1{qG(q)}=g′(t)ifg(0)=0 and the convolution theorem,we find that

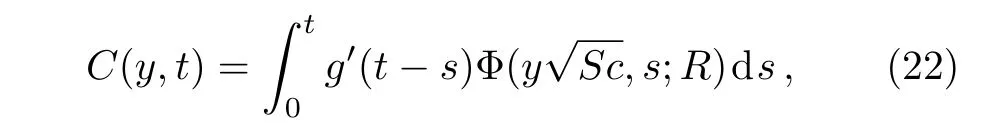
where the function Φ is de fined in Appendix.

The rate of mass transfer from the plate to fluid,in terms of Sherwood number,is given by

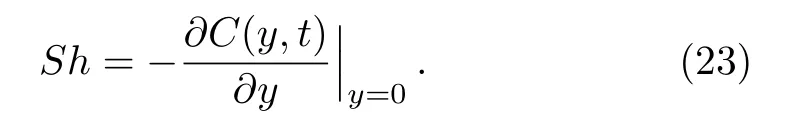
Introducing the equality(22)into Eq.(23),we find that

Now,we integrate Eq.(10)across the concentration layer from zero to in finity,respectively toδ1C,whereδ1Cis the concentration layer thickness,introduce the measure of the concentration boundary layer

and use the boundary conditions(12)3and(13)3.It results that

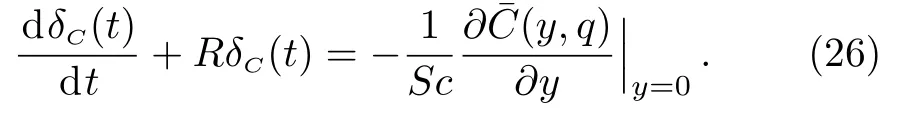
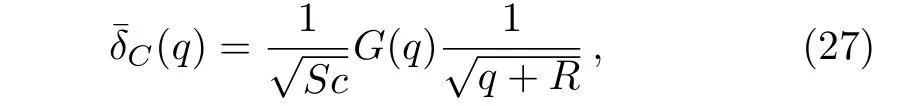
whose inverse Laplace transform is

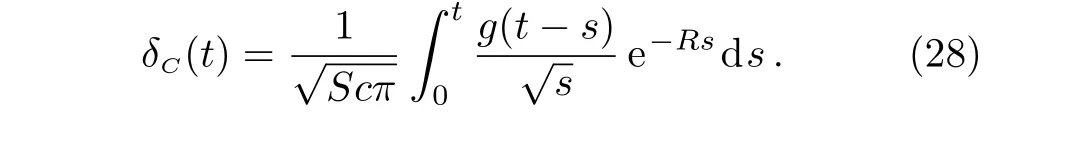
3.2 Velocity Field

Applying the Laplace transform to Eq.(8)and bearing in mind the corresponding initial and boundary conditions,it results that

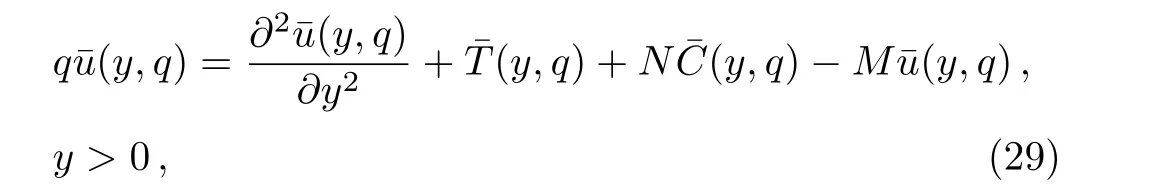
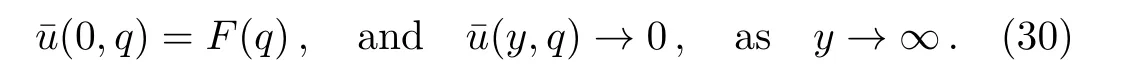
Introducing Eqs.(14)and(21)into Eq.(29),it results that

The solution of the ordinary differential equation(31)with the boundary conditions(30),is given by

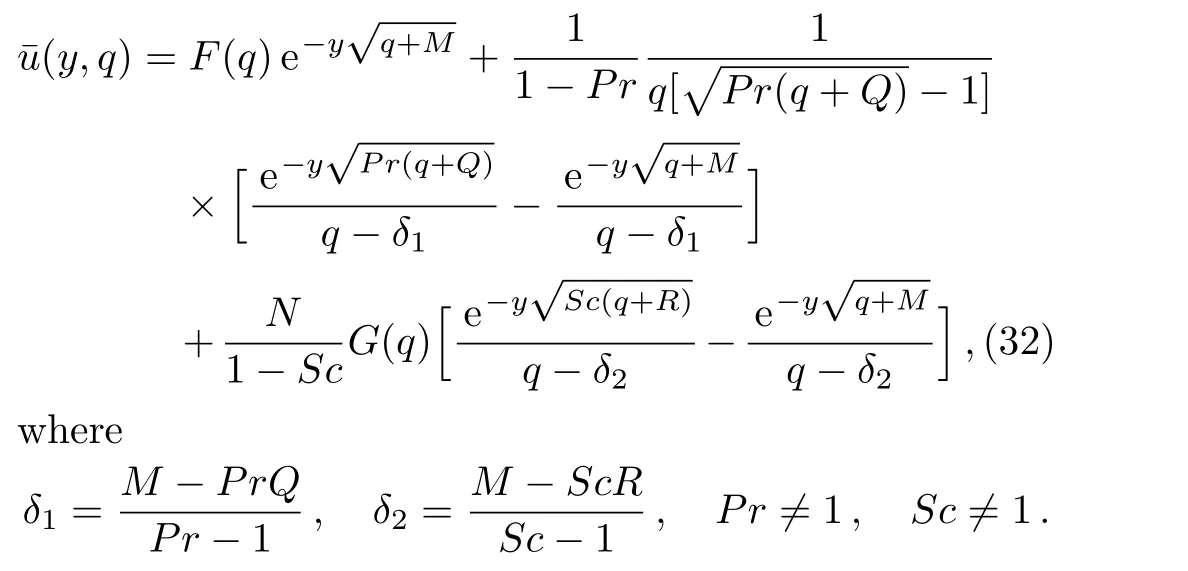
Applying the inverse Laplace transform to Eq.(32)and using again the convolution theorem and Eq.(A2)from Appendix,we find the velocity field under the form

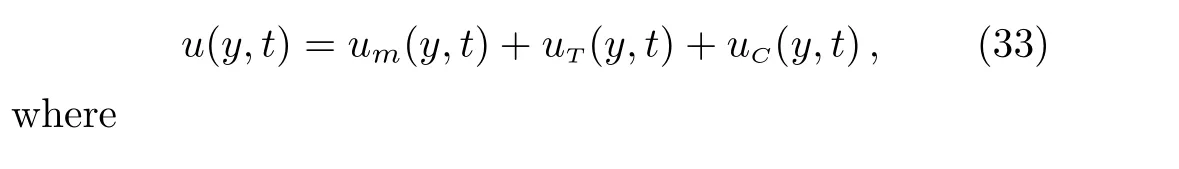
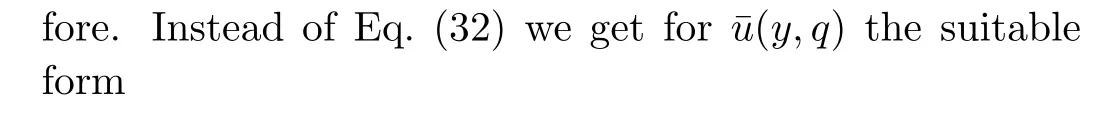
Appling the inverse Laplace transform to Eq.(37),um(y,t)remain unchanged while the thermal and concentration components of velocity become(see Eqs.(A1)and(A3)1)

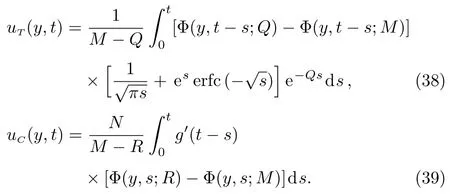
Another physical entity of interest is the skin friction coefficient at the plate[7,10]

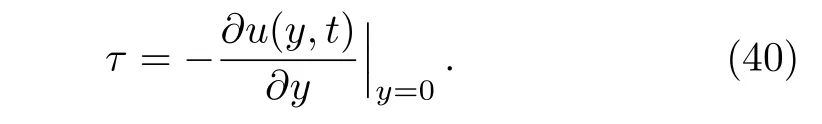
Introducing Eq.(33)in Eq.(40),we find the skin friction coefficient

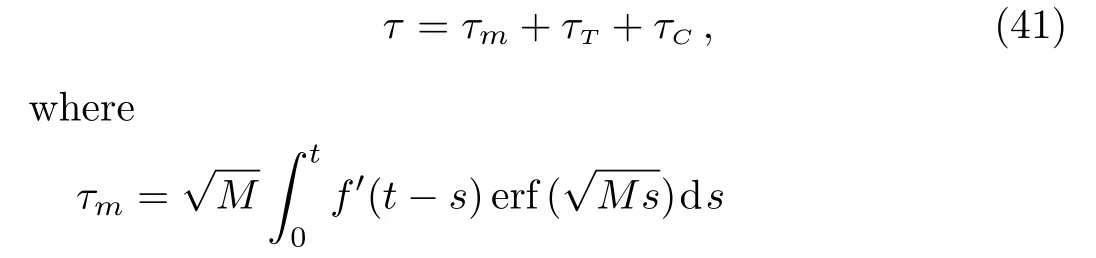
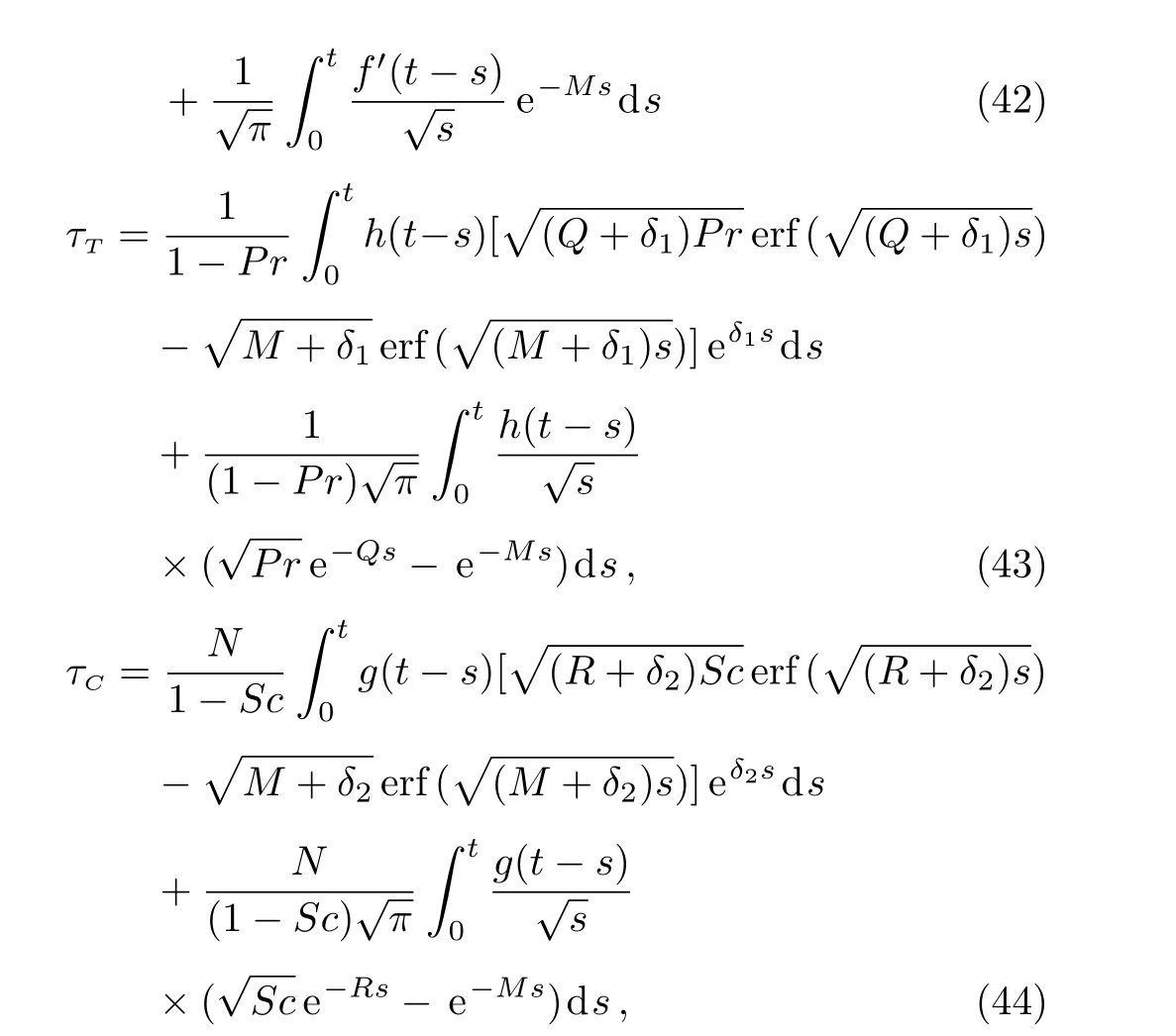
are its mechanical,thermal and concentration components.

Thedifferentialequation describing thevelocity boundary layer thickness,namely

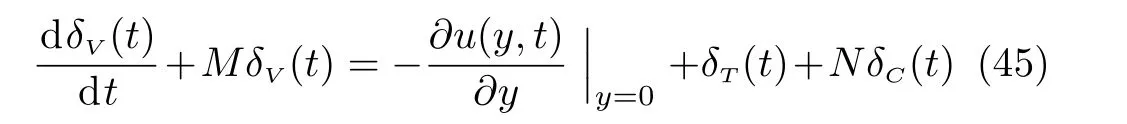
is obtained integrating Eq.(8)across the velocity boundary layer and following the same line as before for temperature and concentration.The solution of this differential equation with the initial conditionδV(0)=0 can be also obtained by means of the Laplace transform technique.

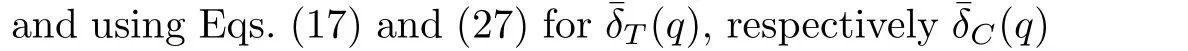
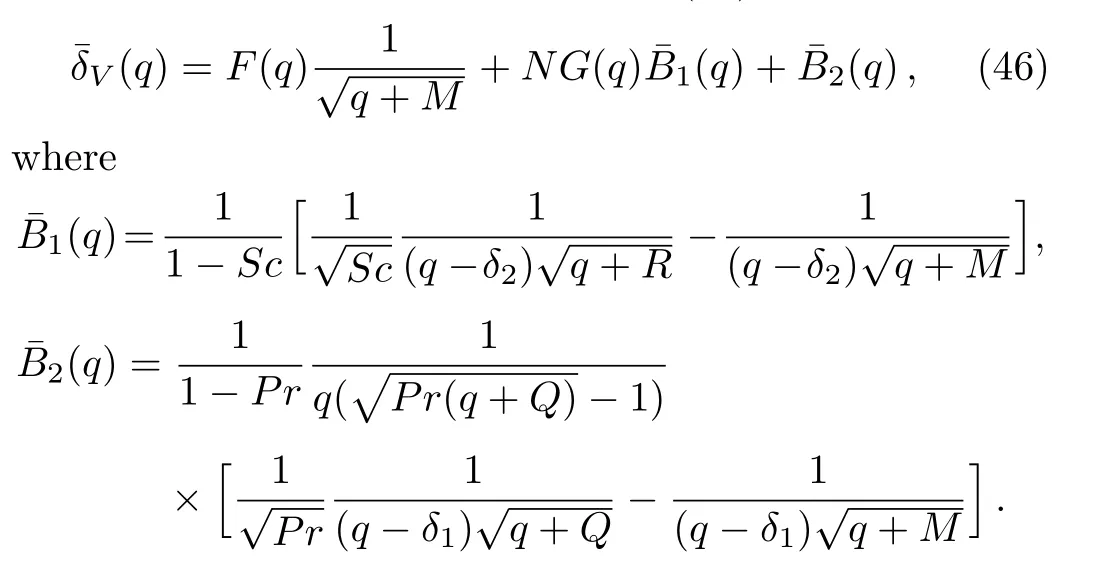
Applying the inverse Laplace transform to Eq.(46),and using Eqs.(A2)and(A3)2,it results

4 Special Cases with Engineering Applications

As we previously mentioned,the general expressions that have been here obtained for velocity,concentration,Sherwood number and the skin friction coefficient can generate exact solutions for any hydromagnetic free convection flow of this type.In order to validate their correctness,as well as to get some physical insight of certain fundamental flows with possible engineering applications,three special cases are considered and some results from the existing literature are recovered or corrected.

Case 1Uniform Motion and Constant Concentration of the Plate

By substituting the functionsf(·)andg(·)byH(·)(the Heaviside unit step function)in Eqs.(22),(34),and(36)and bearing in mind the fact that

whereδ(·)is the Dirac delta function,we find the dimensionless fluid concentration

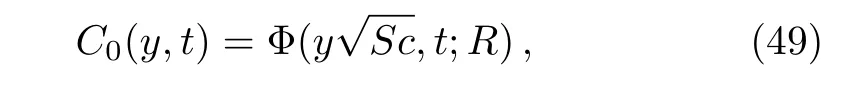
and the mechanical and concentration components of ve-

corresponding to the hydromagnetic free convection flow over an in finite plate,which is maintained at a constant concentration and is moving in its plane with a constant velocity.The thermal component of velocity remain unchanged while the expressions ofC0(y,t)andum0(y,t)are identical to those obtained in(Ref.[6],Eqs.(12)and(16)).

The corresponding Sherwood number,namely

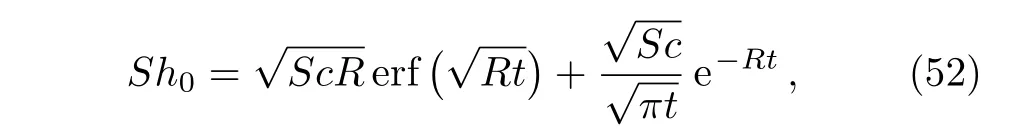
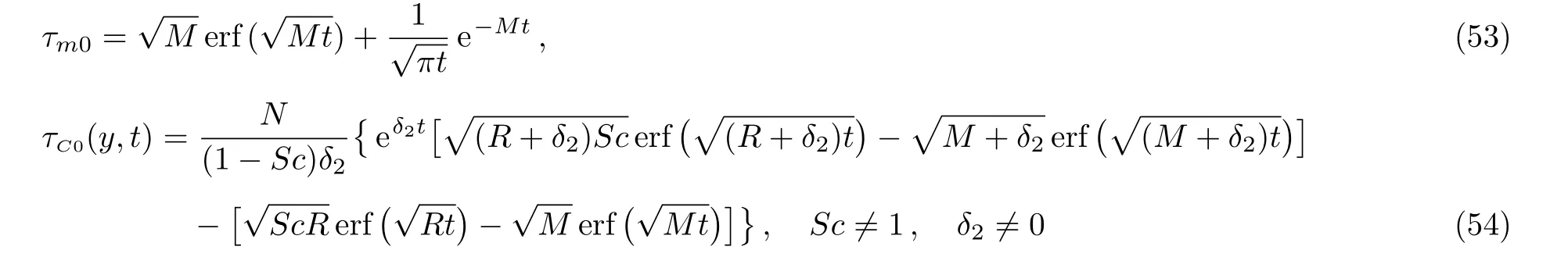
are obtained substitutingf(t)byH(t)in Eqs.(42)and(44).As expected,Eq.(53)is identical to the first term of Eq.(19)from Ref.[6].In the absence of magnetic effects and chemical reaction,Eqs.(49),(50),(52),and(53)take the simple forms

which are well known in the literature.

By now substitutingf(t)andg(t)byH(t)in Eqs.(28)and(47),the expressions of the thickness of the corresponding boundary layers are obtained.The concentration boundary layer thickness,for instance,has the simple form

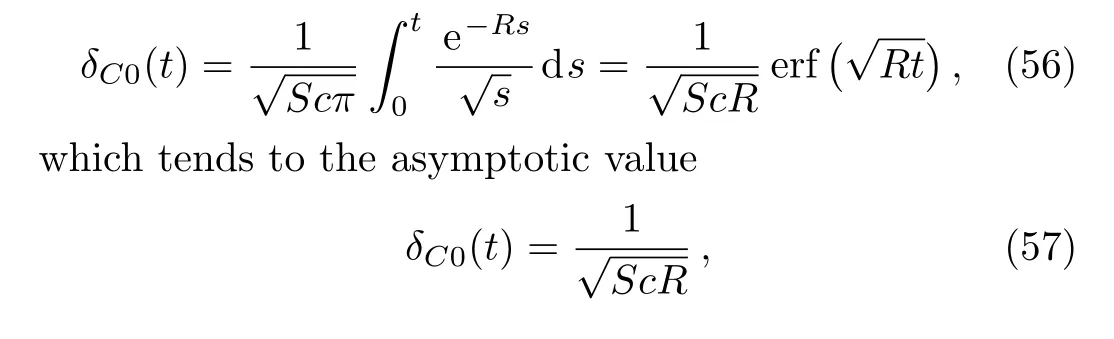
whent→∞.

Case 2Accelerated Plate with Ramp-Type Concentration

By now lettingf(t)=g(t)H(t)ta(a＞0)into Eqs.(22),(34),and(36),we find solutions

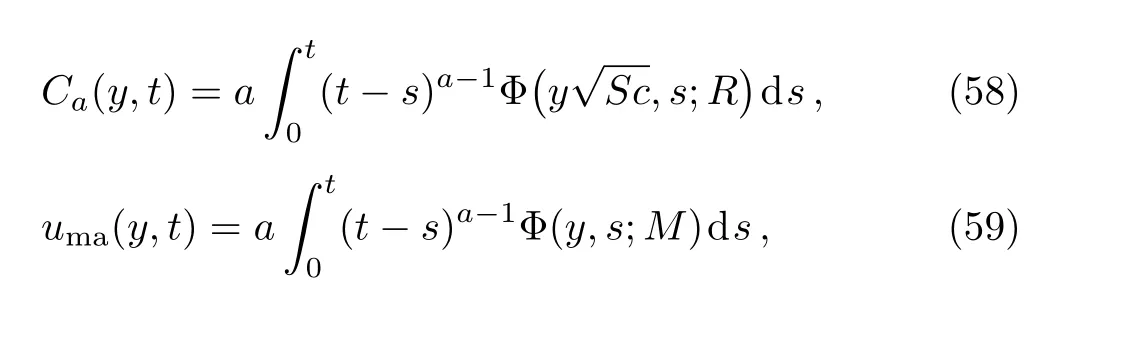
corresponding to the hydromagnetic free convection flow due to a slowly(a＜1),constantly(a=1)or highly(a＞1)accelerating plate with ramp-type concentration.[36]Of course,the corresponding velocity field is

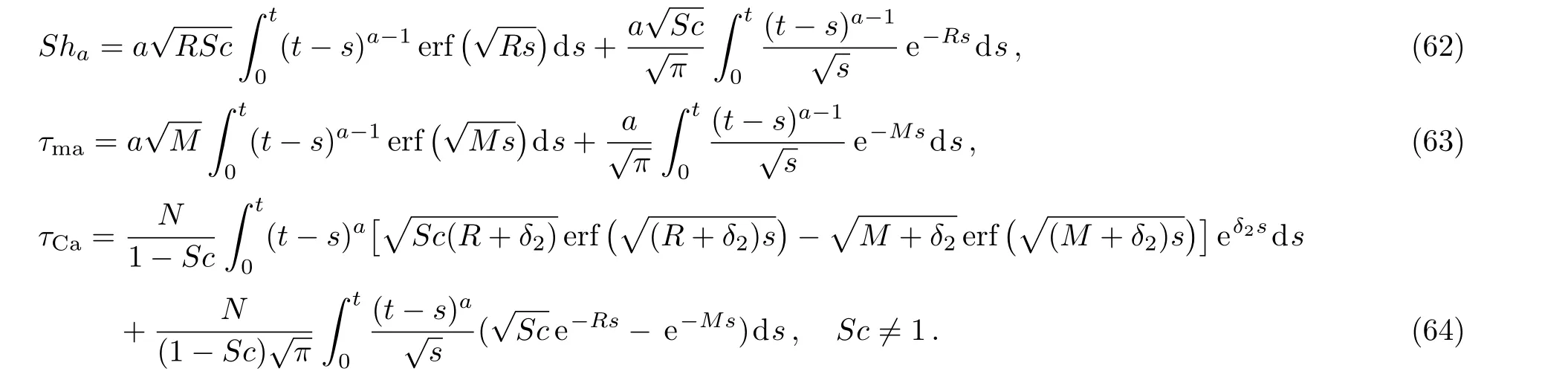
whereuT(y,t)is given by Eq.(35).

Making the same substitutions in Eqs.(24),(42),and(44),we find that

Of a special interest is the casea=1 corresponding to the free convection flow due to a constantly accelerating plate.By makinga=1 in Eqs.(58)–(60),and(62)–(64)and using Eqs.(A4)–(A9),it results that

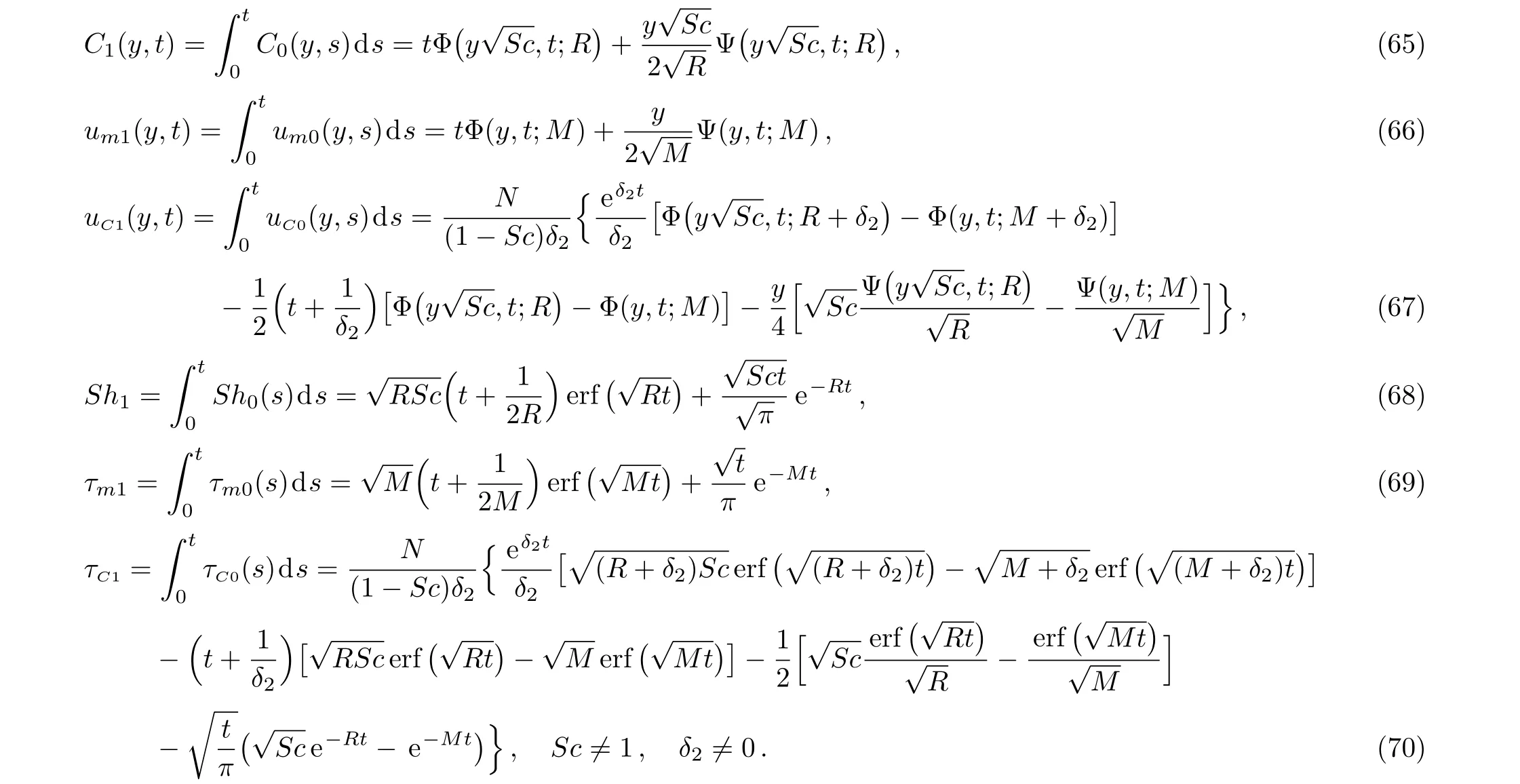
It is worth pointing out the fact thatum1(y,t)from Eq.(66)is identical to the result of Reddyet al.(Ref.[6]Eq.(17)and Sethet al.(Ref.[37],Eq.(2.11))while the expression ofτm1from Eq.(69)corrects the similar result of Ref.[6].The corresponding expressions of the associated boundary layers thickness can be immediately obtained puttingf(t)=g(t)=H(t)tain Eqs.(28)and(47).Fora=1 Eq.(28)reduces to

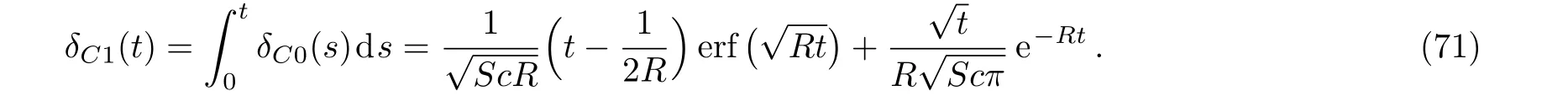
Case 3Oscillating Plate with Oscillatory Concentration

Let us now assume that the plate,with oscillatory concentration on the boundary,is oscillating in its plane with the same frequencyωas well as the concentration.The dimensionless solutions corresponding to the free convection flow due to cosine or sine oscillations of the concentration on the boundary,namely

are obtained substitutingf(t)andg(t)byH(t)cos(ωt)orH(t)sin(ωt)in Eqs.(22),(24),(34),(36),(42),and(44),respectively.As expected,the solutions(72)–(77)reduce to those given by Eqs.(49)–(54)if the frequencyωof oscillations tends to zero(foruCc(y,t),uC0(y,t)andτCc,τC0see also the general solutions(36)and(44)).Furthermore,all solutions corresponding to this subsection can be written as a sum of steady-state(permanent)and transient solutions.The steady-state solutions corresponding toCc(y,t)andCs(y,t),for instance,can be given by the equalities(see also Eq.(A10))

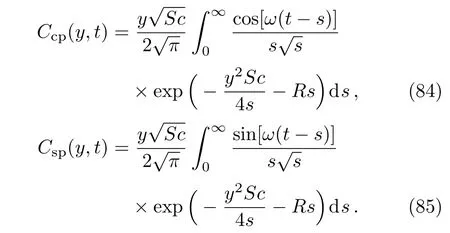
Moreover,lengthy but straightforward computation show that these solutions can be written in the simple forms(see Eqs.(A11)and(A12))

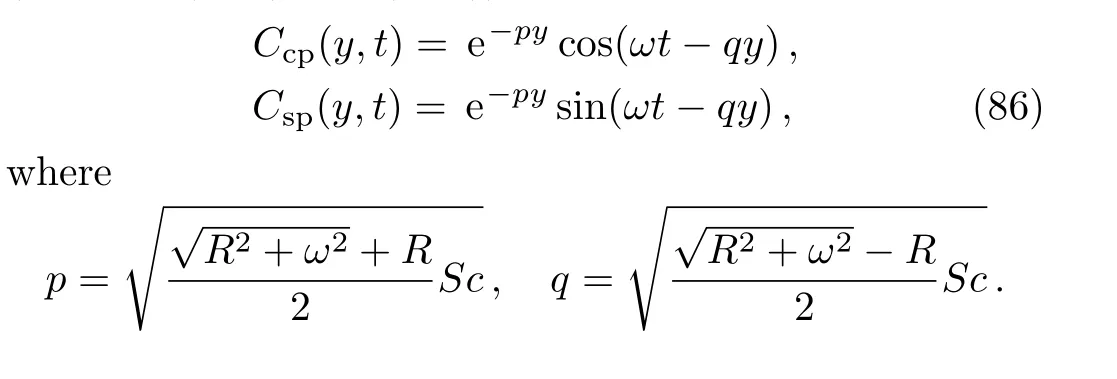
5 Numerical Results and Discussions

In order to gain some physical insight of results that have been here obtained and to avoid repetition,the effects of buoyancy ratio parameter(N),heat generation or absorption coefficient(Q),Schmidt number(Sc)and chemical reaction parameter(R)on dimensionless concentration and velocity fields are graphically underlined in Figs.2–7 for fluid motions induced by a highly accelerating plate(f(t)=H(t)t3/2)with ramp-type concentration(g(t)=H(t)ta).Variations of Sherwood number(Sh)with respect toScandRare presented in Fig.8 while the diagrams of the skin friction coefficientτagainsttare given in Fig.9.Finally,for completion,the contributions of mechanical,thermal and concentration components of velocity on the fluid motion are brought to light by Fig.10 and the required time to reach the steady-state of mass transfer is graphically obtained in Figs.11 and 12 for flows with cosine or sine oscillations of concentration at the plate.Time variation of thermal or concentration boundary layer thickness is presented in Figs.13 and 14 for different values of physical parameters when the species concentration is constant on the boundary.

Fig.2 Pro files of the dimensionless concentration C1(y,t)against y for R=1.5,t=0.5,and 1 with different values of Sc.

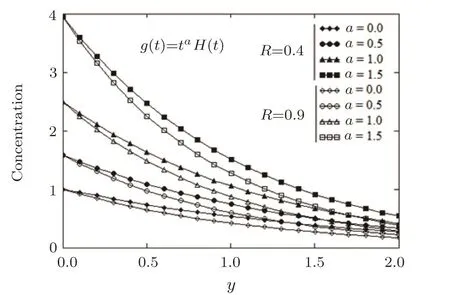
Fig.3 Pro files of the dimensionless concentration Ca(y,t)against y for t=2.5,Sc=0.8,R=0.4,and 0.9 with different values of a.

Pro files of the concentrationCa(y,t)againstyare presented in Figs.2 and 3 for different values ofSc,R,aand the timet.The species concentration,as expected,is an increasing function with respect toaandtbut it decreases for increasing values ofScandR.As it is known,[5]a diminution in the Schmidt numberScmeans an increase in mass diffusivity which enhances the species concentration in fluid.Consequently,an increase ofScorRlowers the concentration level of the fluid.In all cases,the concentration pro files smoothly descend from maximum values on the wall to the zero value for large values ofy.

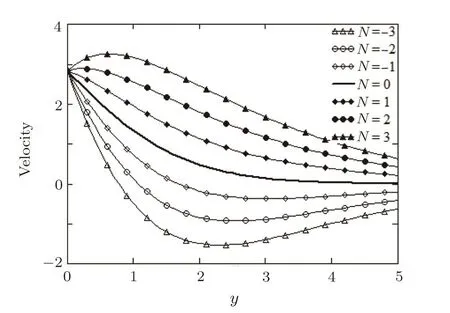
Fig.4 Pro files of the dimensionless velocity u3/2(y,t)against y at time t=2,M=0.2,Pr=1.5,Q=0.7,Sc=0.2,R=0.3,and different values of N.

Fig.5 Pro files of the dimensionless velocity u3/2(y,t)against y at time t=2,for M=1,N=2,Pr=1.5,Sc=0.5,R=0.7,and different values of Q.

Numerical values of the fluid velocityua(y,t),given by Eq.(61),are graphically displayed in Figs.4–7 fora=3/2 the plate concentrationC(0,t)=tH(t)and different value of physical parameters.Velocity pro files againstyare presented in Fig.4 for aiding(N＞0)and opposing(N＜0)flows at the timet=2.In the first case,when thermal and mass buoyancy forces act in the same direction,the fluid velocity increases for increasing values ofNas a result of the growth of concentration.N=0 implies the mass Grashof numberGm=0 and the mass diffusion phenomenon is absent.IfN＜0,the mass buoyancy forces are negative and the fluid velocity is signi ficantly diminished.However,it increases for increasing values ofN.For positive values ofNgreater than a criticalNcvalue(about 1.9),in the plate vicinity,the fluid velocity increases from the common value on the wall up to a maximum value and then decreases to the stream value for large values ofy.

Effects of the heat generation or absorption coefficientQon the fluid motion are displayed in Fig.5.The presence of heat generation(Q＜0)generates thermal energy,which increases the fluid temperature.As a result,the fluid velocity increases due to the increasing thermal buoyancy force.An opposite effect appears in the case of heat absorption.More exactly,due to the heat absorption(Q＞0),the fluid temperature diminishes and the thermal buoyancy force decreases.This implies a reduction of fluid velocity with increasing values ofQ.However,in the case of heat generation,for eachQless than a critical valueQc(about?0.5),the fluid velocity increases from the common value on the plate up to a maximum value and then smoothly decreases to the zero value for increasing values ofy.

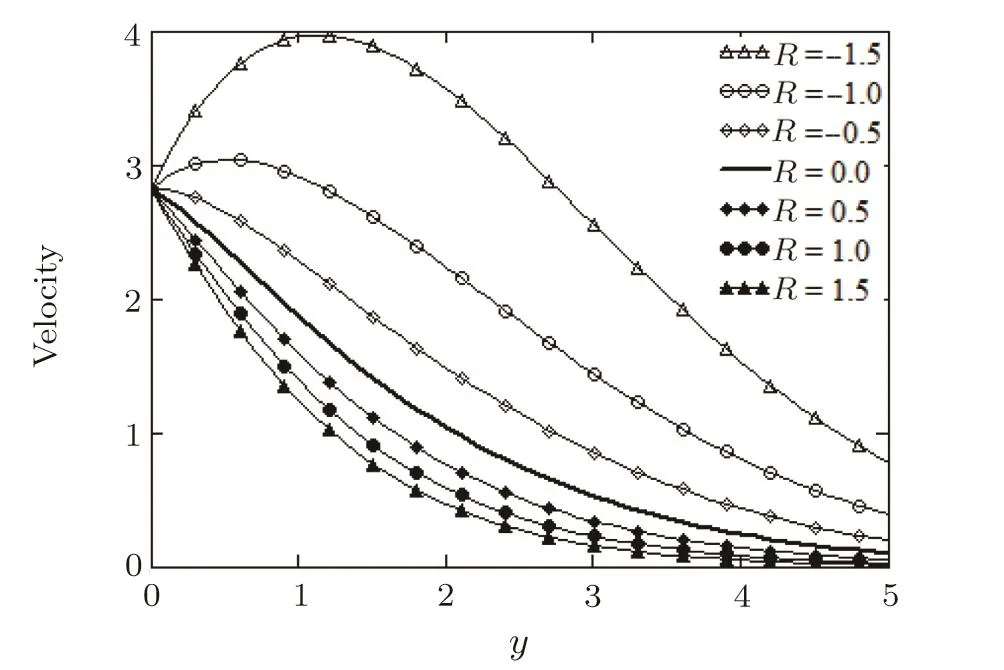
Fig.6 Pro files of the dimensionless velocity u3/2(y,t)against y at time t=2,for M=1,N=2,Pr=1.5,Q=0.5,Sc=0.5,and different values of R.

Figure 6 displays the in fluence of chemical parameterRon the fluid velocity.The presence of destructive chemical reaction(R＞0),as it results from Fig.3,diminishes the species concentration and implicitly reduces the mass buoyancy force.As a result,the fluid velocity decreases for increasing values ofR.Of course,an opposite trend appears in the case of non-destructive chemical reactions whenR＜0.Variations of the fluid velocity are also presented in Fig.7 for two values ofPrand different values ofScwhile the other parameters are fixed.From this figure,it clearly results that the velocity is a decreasing function both withPrandSc.Consequently,the viscous forces predominate thermal diffusion or mass diffusion effects for increasing values of Prandtl,respectively Schmidt number.

The variation of Sherwood numberShin time is graphically presented in Fig.8 at different values ofScandRfor flows with ramp-type surface concentration.It is found that the rate of mass transfer at the plate is an almost linearly increasing function oft.It also increases for increasing values ofScandR.Consequently,the destructive chemical reaction enhances the rate of mass transfer at the plate.An opposite effect produces the increase of the chemical molecular diffusivityD.

Figure 9 shows the skin friction coefficient variation againsttunder the in fluence ofQandN,respectivelyRandPr.The skin friction coefficient is an increasing function with respect tot,Q,N,Prand decreases for increasing positive values ofR.It increases almost linearly intforN=3 withQ=0.6 and 0.7 orPr=3.5 withR=0.5,1.0 and 1.5.From physical point of view,it means that a destructive chemical reaction diminishes the viscous drag at the plate while the heat absorption enhances it.Fig.9Variation of skin frictionτgiven by Eq.(41)againsttforM=0.4,Sc=0.5,f(t)=t3/2,g(t)=tand different values ofQ,N,R,andPr.

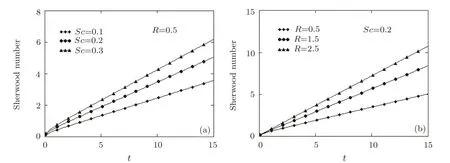
Fig.8 Variation of Sherwood number Sh,given by Eq.(68),with respect to Sc and R.

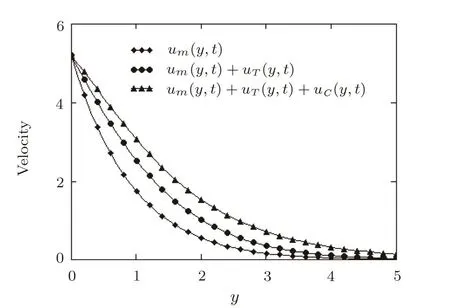
Fig. 10 Pro filesofthe dimensionlessvelocities um3/2(y,t),um3/2(y,t)+uT(y,t),and um3/2(y,t)+uT(y,t)+uC(y,t)against y for Pr=1.5,Q=0.5,Sc=0.5,R=0.7,M=0.6,N=2,and t=3.

In order to evaluate the importance of thermal or mass diffusion effects on free convection flows of viscous fluids,the contributions of mechanical,thermal and concentration components of velocityu3/2(y,t)on the fluid motion are together brought to light in Fig.10.As it clearly results from this figure,each component signi ficantly influences the fluid velocity and cannot be neglected.

In Figs.11 and 12,the required time to reach the steady-state for mass diffusion is graphically determined for flows with cosine or sine oscillations of concentration at the plate for two values of chemical reaction parameterR.This is the time after which the diagrams of starting solutions(72)or(78)are almost identical to those of steadystate solutions(86)1,respectively(86)2.At small values oft,the difference between the corresponding solutions is signi ficant but it quickly dissapears and the required time to reach the steady-state is higher for sine in comparison to cosine oscillations of concentration at the wall.This is obvious,because at timet=0 the concentration level at the plate is zero for sine oscillations.Furthermore,as it clearly results from these figures,the presence of destructive chemical reaction improves this time for increasing values ofR＞0.

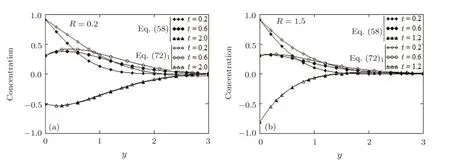
Fig.11 Required time to reach the steady-state of mass transfer for cosine oscillations of concentration at the plate at Sc=0.9 and ω =2π/3.

Figures 13 and 14 bring to light the time variation of the thickness of thermal or concentration boundary layers with respect toPrandQ,respectivelyScandRandg(t)=H(t).In all cases,the boundary layer thickness signi ficantly increases up to a critical value oft(aroundt=10)and then rapidly tends to the asymptotic value.The thermal boundary layer thickness is a decreasing function with respect toProrQand it rather reaches the asymptotic value for greater values of these parameters.A similar behavior appears from Fig.14 for the concentration boundary layer thickness with regard toRandSc.

Fig.12 Required time to reach the steady-state of mass transfer for sine oscillations of concentration at the plate at Sc=0.9 and ω =2π/3.

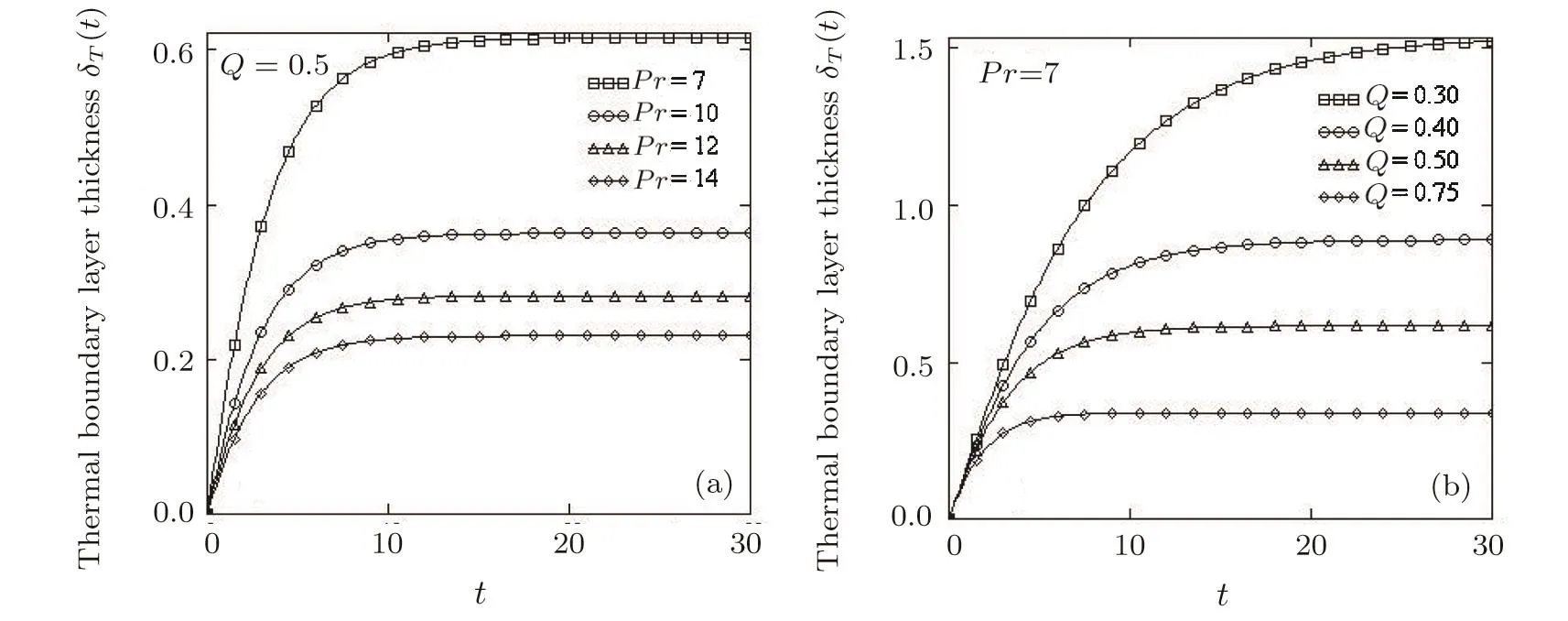
Fig.13 Time variation of thermal boundary layer thickness for different values of Prandtl number Pr and heat generation/obsorption parameter Q.

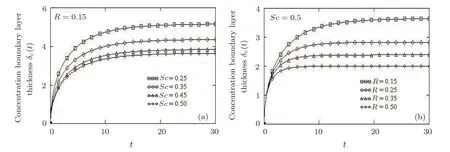
Fig.14 Time variation of thermal boundary layer concentration for different values of Schmidt number Sc and chemical reaction parameter R.

6 Conclusions

Hydromagnetic free convection flow of an electrically conducting,incompressible viscous fluid over a moving infinite vertical plate with Newtonian heating,heat source,mass diffusion and chemical reaction is completely solved.Exact analytic solutions are established for velocity,con-centration,Sherwood number and skin friction coefficient when the plate is moving in its plane with an arbitrary velocity and the concentration at the wall is a timedependent function.They satisfy all imposed initial and boundary conditions and can generate exact solutions for any free convection flow of this type.For illustration,as well as to get some physical insight of the obtained results,three special cases with technical relevance are considered and some results from the existing literature are recovered or corrected.Radiative and porous effects are not taken into consideration but they can be immediately included by a simple rescaling of Prandtl number and magnetic parameter.[31?32]

The solutions corresponding to the motion due to a plate with uniform velocity(Stokes first problem)and constant concentration at the wall,as well as those induced by a constantly accelerating plate with ramp-type concentration at the wall,[36]are presented in simple forms in terms of exponential function and error function or complementary error function of Gauss.In addition,the solutions of the second problem can be written as simple integrals of the similar solutions corresponding to the first problem of Stokes.The solutions corresponding to motions due to an oscillating plate(Stokes second problem)with oscillatory concentration at the wall can be written as sum of steady-state(permanent)and transient solutions.These solutions,which are independent of the initial conditions but satisfy the boundary conditions and governing equations,are important for those who want to eliminate the transients from their experiments.Moreover,as it was to be expected,all solutions corresponding to cosine oscillations of the plate and of the concentration at the wall reduce to the similar solutions of Stokes first problem when the oscillation frequencyωtends to zero.

Finally,in order to bring to light some physical penetration of results that have been obtained,the diagrams of dimensionless concentration and velocity fields,Sherwood number and skin friction coefficient are presented in different situations for typical values of pertinent parameters.However,in order to avoid repetition,their pro files have been here presented and discussed only for variations of physical parametersN,Q,ScandRwith ramp-type concentration at the wall.Contributions of mechanical,thermal and concentration components of velocity on the fluid motion are together underlined for motions due to highly accelerating plate.The required time to reach the steady-state of mass diffusion for cosine or sine oscillations of the concentration at the plate has been graphically determined and the main results that have been here obtained are:

(i)The problem in consideration has been completely solved.Obtained results can generate exact solutions for any free convection flow of this type.

(ii) Species concentration is increasing function in time and ramp-type parametera.

(iii) The increase of mass diffusivity brings up the concentration level of the fluid while the presence of destructive chemical reaction diminishes it.

(iv)For aiding flows(N＞0),velocity of the fluid is increasing function with respect toN.An opposite trend appears in the case of opposing flows when(N＜0).

(v)Heat absorption(Q＞0)causes a reduction of velocity for increasing value ofQ.This is due to the fact the fluid temperature diminishes and the thermal buoyancy force decreases.A reverse trend appears in the presence of heat generationQ＜0.

(vi)Destructive chemical reaction(R＞0)reduces the mass buoyancy force and the fluid velocity decreases for increasing values ofRthrough the boundary layer region.The non-destructive chemical reaction(R＜0)enhances the fluid velocity.

(vii)Destructive chemical reaction enhances the rate of mass transfer at the plate.

(viii)The presence of heat absorption enhances the viscous drag at the plate while the destructive chemical reaction diminishes it.

(ix)Mechanical,thermal or concentration effects signi ficantly in fluence the fluid motion and they cannot be neglected.

(x)Required time to reach the steady-state for the mass transfer is higher for sine in comparison to cosine oscillations of concentration of the plate and it is improved in the presence of destructive chemical reaction.

(xi)Thermal or concentration boundary layer thickness signi ficantly increases up to a critical value oftand then it rather reaches the asymptotic value for greater values ofQorPr,respectivelyRorSc.It is a decreasing function with respect to each of the respective parameters.

Appendix

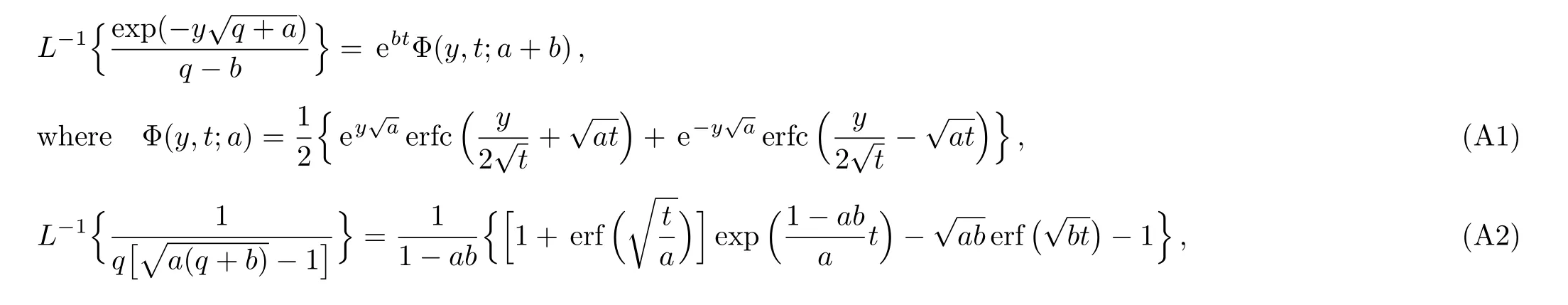
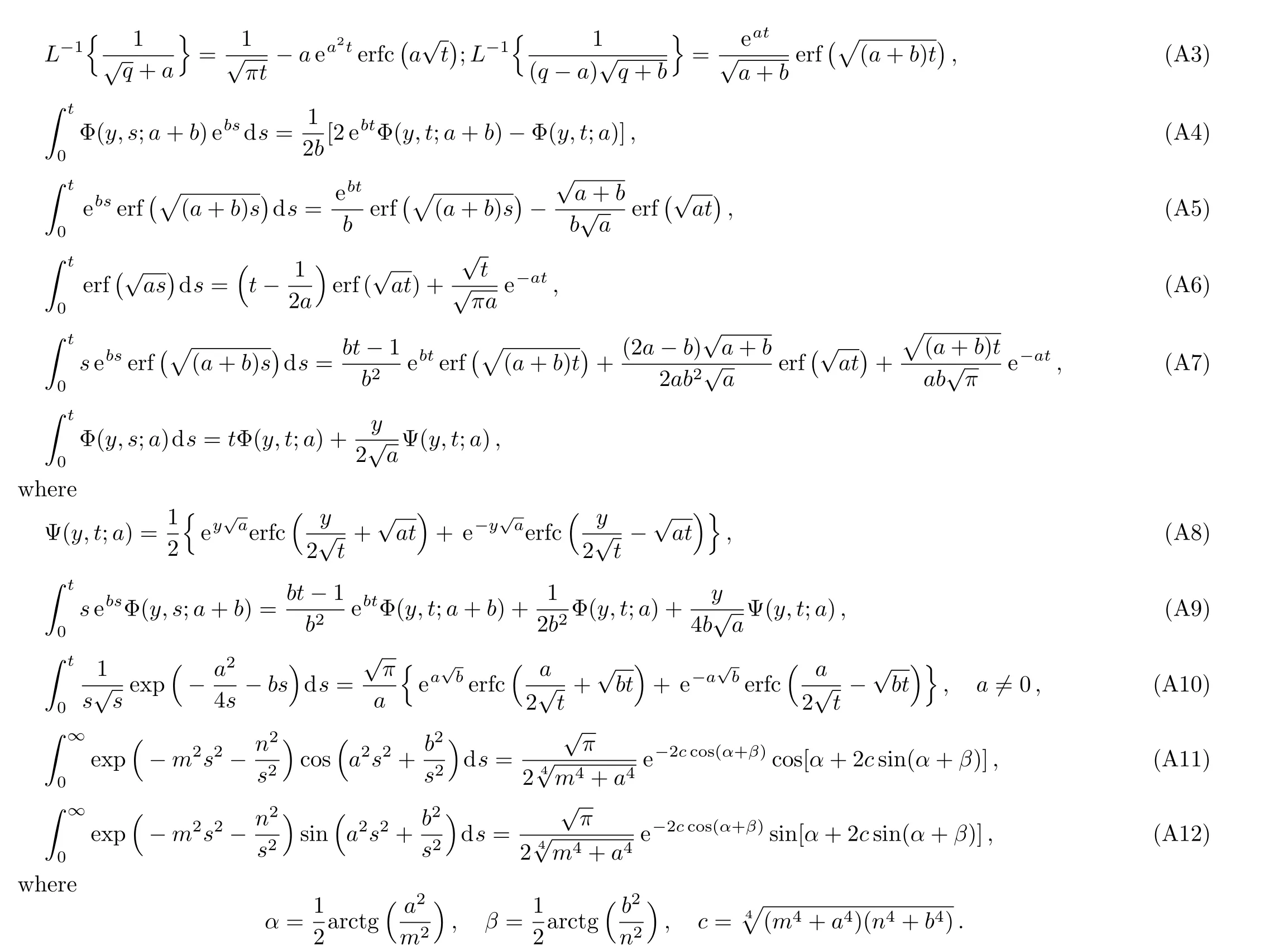
The author Nehad Ali Shah is highly thankful and grateful to Abdus Salam School of Mathematical Sciences,GC University,Lahore,Pakistan and Higher Education Commission of Pakistan,for generous supporting and facilitating this research work.

[1]P.S.Ghoshdastidar,Heat Transfer,Oxford University Press,Oxford(2004)p.225.

[2]D.A.Nield and A.Bejan,Convection in Porous Media,Springer,Verlag,New York(2006)pp.94-97.

[3]R.J.Turnbull,Phys.Fluids 12(1969)2255.

[4]V.M.Soundalgekar,S.K.Gupta,and N.S.Birajdar,Nucl.Eng.Des.53(1979)339.

[5]N.Ahmed and M.Dutta,Int.J.Phys.Sci.8(2013)254.

[6]T.S.Reddy,M.C.Raju,and S.V.K.Varma,J.Appl.Fluid Mech.6(2013)443.

[7]T.S.Reddy,M.C.Raju,and S.V.K.Varma,Journal of Computational and Applied Research in Mechanical Engineering(JCARME)3(2013)53.

[8]B.M.Rao,G.V.Reddy,M.C.Raju,and S.V.K.Varma,IOSR J.Appl.Phys.(IOSR-JAP)3(2013)22.

[9]K.Srihari,Chirra Kesava Reddy,Int.J.Mech.Eng.3(2014)1.

[10]P.K.Pattnaik and T.Biswal,Walailak J.Sci.Technol.12(2015)749.

[11]G.S.Seth,B.Kumbhakar,and S.Sarkar,Int.J.Eng.Sci.7(2015)94.

[12]J.H.Merkin,Int.J.Heat Fluid Flow 15(1994)392.

[13]V.Rajesh,Int.J.Heat Mass Tran.85(2012)221.

[14]D.Lesnic,D.B.Ingham,and I.Pop,Int.J.Heat Mass Tran.42(1999)2621.

[15]D.Lesnic,D.B.Ingham,and I.Pop,J.Porous Media 3(2000)227.

[16]I.Pop,D.Lesnic,and D.B.Ingham,Hybrid Methods Eng.2(2000)31.

[17]R.C.Chaudhary and P.Jain,J.Eng.Phys.Thermophys.80(2007)954.

[18]P.Mebine and E.M.Adigio,Turk.J.Phys.33(2009)109.

[19]M.Narahari and A.Ishak,J.Appl.Sci.11(2011)1096.

[20]S.Das,C.Mandal,and R.N.Jana,Int.J.Comput.Appl.41(2012)36.

[21]A.Hussanan,M.I.Anwar,F.Ali,I.Khan,and S.Sha fie,Heat Trans.Res.45(2014)119.

[22]M.Narahari and M.Y.Nayan,Turkish J.Eng.Env.Sci.35(2011)187.

[23]M.Narahari,R.Pendyala,and M.Y.Nayan,AIP Conference Proceedings 1482(2012)340.

[24]M.Narahari and B.K.Dutta,Chem.Eng.Commun.199(2012)628.

[25]A.Hussanan,Z.Ismail,I.Khan,and S.Sha fie,Materials Sciences and Application,2013,doi:104236/msa.2013.

[26]A.Hussanan,Z.Ismail,I.Khan,A.G.Hussein,and S.Sha fie,Eur.Phys.J.Plus 129(2014)1.

[27]D.Vieru,Corina Fetecau,C.Fetecau,and Nait Nigar,Z.Naturforsch.69a(2014)714.

[28]A.Khan,I.Khan,and S.Sha fie,Jurnal Teknologi(Sciences and Engineering)78(2016)71.

[29]C.Fetecau,D.Vieru,Fetecau Corina,and I.Pop,Eur.Phys.J.Plus 130(2015)1.

[30]M.A.Sheremet,T.Grosan,and I.Pop,Eur.J.Mech.B/Fluid 53(2015)241.

[31]E.Magyari and A.Pantokratoras,Int.Commun.Heat Mass Transfer 38(2011)554.

[32]C.Fetecau and S.Akhter,Bull.Inst.Polit.Iasi,Sect.Matematica,Mecanica Teoretica,Fizica LIX 3(2013)15.

[33]G.R.Pande,G.A.Georgantopoulos,and C.L.Goudas,Astrophys.Space Sci.60(1979)125.

[34]M.Turkyilmazoglu and I.Pop,Int.J.Heat Mass Tran.55(2012)7635.

[35]A.S.Dorfman,Conjugate Problems in Convective Heat Transfer,CRC Press,Boca Raton,London,New York(2010).

[36]C.J.Toki and J.N.Tokis,Z.Angew.Math.Mech.87(2007)4.

[37]G.S.Seth,S.M.Hussain,and S.Sarkar,Journal of Egyptian Mathematical Society 23(2015)197.