In finite Conservation Laws,Continuous Symmetries and Invariant Solutions of Some Discrete Integrable Equations?

Yu-Feng Zhang(張玉峰),Xiang-Zhi Zhang(張祥芝),and Huan-He Dong(董煥河)

1College of Mathematics,China University of Mining and Technology,Xuzhou 221116,China

2College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao 266590,China

1 Introduction

Blaszak,et al.[1]adopted the R-matrix method to have obtained some differential-difference integrable systems with a few lattice fields,including the well-known Toda lattice equation.Through the very natural set of Casimir functions on a Lie algebrag,which consists of some shift operators,some Hamiltonian structures expressed by Poisson tensors,of some lattice equations were obtained.Furthermore,Blaszak,et al.[2?3]applied two different methods for the construction of(2+1)-dimensional integrable lattice- field and field Hamiltonian dynamical systems.The first method is based on the central extension procedure.[1]The second method is called the operand formulism.With the help of Casimir functions,Hamiltonian structures of some(2+1)-dimensional integrable lattice systems were obtained.Special emphasis on that the central extension approach presented in Ref.[2]is a powerful tool for generating(2+1)-dimensional continuous and discrete integrable systems via the introduced Lax pairs and Novikov–Lax equations.Based on these works,[1?3]we want to introduce two types of Lie algebras constituting shift operators,which generalize the shift operator given by Zhu,et al.,[4]and utilize Lax pairs and Novikov–Lax equations to generate a few differential-difference systems,including the Toda lattice equation and a Toda-type equation.Next,we expand different variations of Casimir functions and make use of Poisson tensors to produce Hamiltonian structures of some lattice systems obtained by us.Finally,we employ two methods for deducing in finite conservation laws of some differential-difference equations presented in the paper.The first method starts from spectral equations and introduces new functions expressed by spectral functions with various lattices[5?7]to deduce in finite conservation laws of integrable lattice equations.The second method proposed by Goktas,et al.[8]is to assume given a local conservation laws

whereρnis the conserved density andJnis the associated flux,then the use of a new algorithm generates theρnandJnpresented in Eq.(1).But in the paper we extend the way to a three- filed lattice equation for deducing infinite conservation laws.Besides,we apply the Lie-point transformation group of difference equations to investigate some continuous symmetries and invariant exact solutions of the Toda-type equation obtained in the paper.Blaszak,et al.[1]once gave two basic types of reductions of the Lie algebragas follows

Zhu,et al.[4]introduced a shift operator

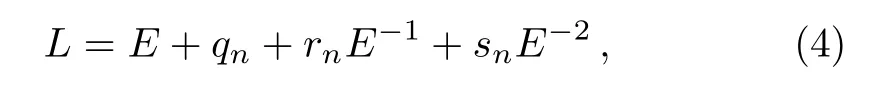
from which two Blaszak–Marciniak lattice hierarchies were obtained,and furthermore,the corresponding in finite conservation laws were derived.It is easy to see the shift operator(4)is a special form of Eq.(2).In the paper,we can generalize(4)to the following two shift operators

Obviously,Eqs.(5)and(6)are special forms of Eqs.(2)and(3),respectively.However,operator(5)was introduced in Ref.[9]so that some integrable systems and sone resulting properties were discussed.Therefore,we only start from Eq.(6)to deduce integrable discrete equations and some properties.

2 Some Discrete Lattice Equations

Assume that a Lax equation presents

Then the corresponding(2+1)-dimensional lattice hierarchy can be given by

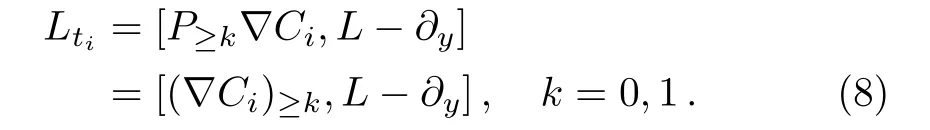
In what follows,we apply the shift operator(6)and the case where Lax equation(7)is given by takingk=1 to deduce integrable lattice hierarchies.A simpler case is to takeq=1,Eq.(7)along with Eq.(6)leads to the following lattice systems

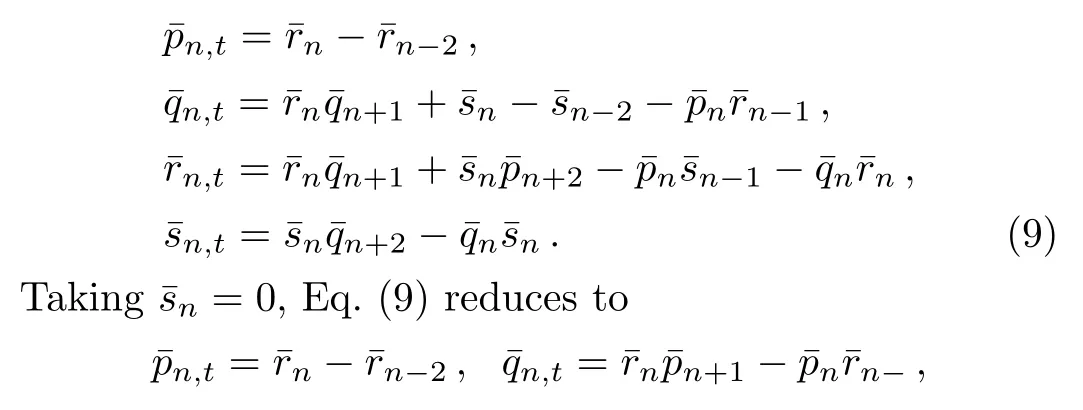
Again settingˉrn=ˉpn=0,Eq.(9)becomes

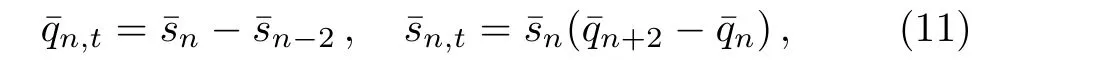
which is called Toda-type system.

The second equation of Eq.(11)can be written as

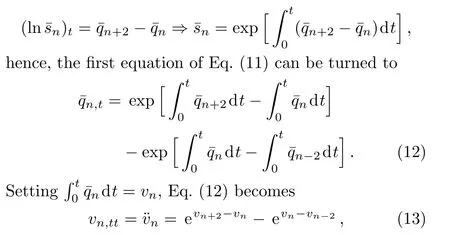
which is another form of Eq.(11),greatly similar to the standard Toda lattice equation.

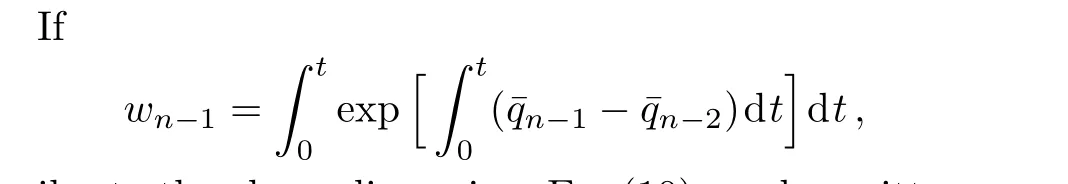
similar to the above discussion,Eq.(10)can be written as

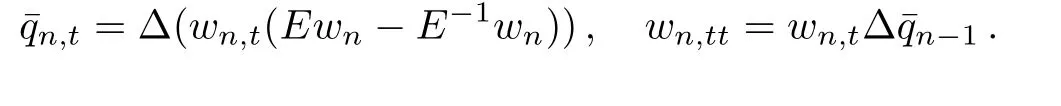
3 Hamiltonian Structures of the Integrable Lattice Systems

Blaszak,et al.[1?3]adopted the Casimir functions of Lie-Poisson brackets to infer Hamiltonian structures of some differential-difference equations.In the section we want to generate Hamiltonian structures of system(9)expressed by Poisson tensors.For Eq.(9),employing the method presented in Ref.[10]yields

which is the Hamiltonian form of Eq.(9).

4 Some in finite conservation laws

Zhu[5]once started from shift operators to discuss infinite conservation laws for some lattice hierarchies.It follows that papers[6?7]further investigated generation of discrete integrable hierarchies and in finite conservation laws for some lattice equations.References[5–7]and[8]have presented the conservation laws of some discrete equations.In what follows,we want to generate conservation laws to the Toda-type equation(13),we shall find that the results obtained in the paper are different from those of the standard Toda lattice equation.Set

Usually,a local conservation of discrete system

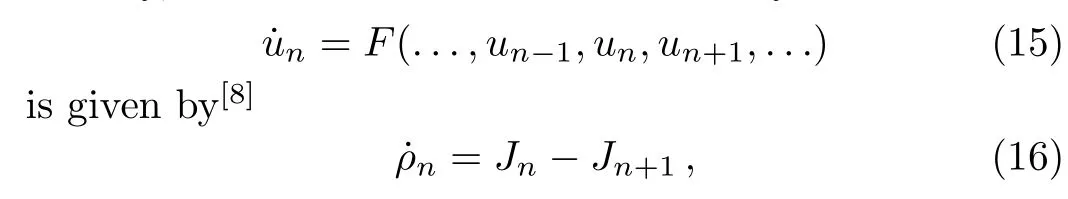
which is Eq.(1),whereρnis the conserved density,andJnis the associated flux.Assumem1andm2are monomials,m1andm2are called equivalent ifm1=m2?ΔMn,denoted bym1～=m2,whereMndepends onunand its shifts.Given a notation called weight of variableun,which is de fined by equating to the number of derivatives with respect tot,the rank of a monomial is de fined as the total weight of the monomials,again in terms of derivatives with respect tot.Based on this,in order to be the same rank for two equations in Eq.(14),we require that

where we have de finedw(?t)=1.

Starting from Eq.(17),we could generate many conserved densities and the associated fluxes.For example,we can consider the case where rank=3.Construction of a set of monomials has rank less than 3,which is denoted by

Next,we want to turnGinto a setH,which has the same rank for ever element

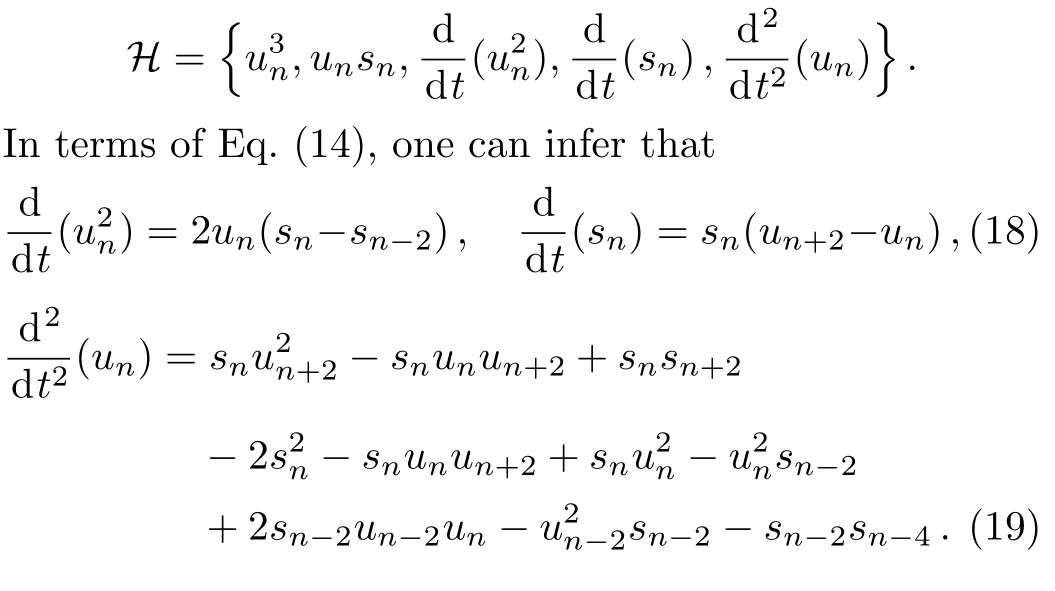
Substituting Eqs.(18)and(19)intoHand utilizing equivalence of monomials de fined as above,Hreduces to a new set

which has the same rank for every element inA.We make a linear combination for elements inAas follows

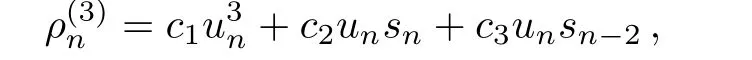
whereci(i=1,2,3)are to be determined.A direct calculation gives

hence,the associated flux presents

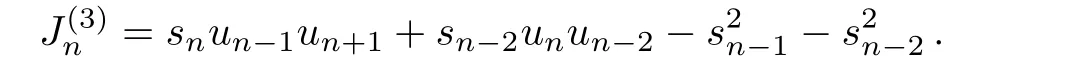
Obviously,ρ(3)nandJ(3)nare different from the corresponding conserved densities and the flux of the standard Toda lattice system presented in Ref.[8]:

Similar steps could lead to the conservation laws of the lattice system(14)when rank=4,5,...,here we do not want to further discuss them in detail.In what follows,we only discuss a few conservation laws of the three- field lattice system(10).In order to be convenient for writing,we rewrite the system as follows

yieldsw(sn)=1,w(un)=1/2,w(vn)=3/2.Consider the case where rank=1/2:G={un},hence we setρ(1/2)n=cun.Then

Next,we consider the case where rank=1,the homogenous rank set isG={sn}.Setρ1n=csn,then it is easy to get that

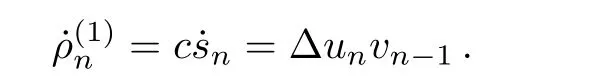
Therefore,the conserved density isρ(1)n=snwhenc=1,the associated flux presentsJ(1)n=?unvn?1. As for rank=3/2,4,...are concerned,we could produce the corresponding conservation laws by similar approach as above,here we omit them.

5 Continuous Symmetries and Invariant Solutions of the Toda-Type Equation

In the section we discuss some continuous symmetries of the(1+1)-dimensional Toda-type equation(13)and its corresponding(2+1)-dimensional Toda-type equations.First of all,we discuss the symmetries and exact solutions of the first case.Denote

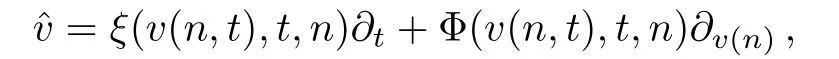
then its second prolongation presents

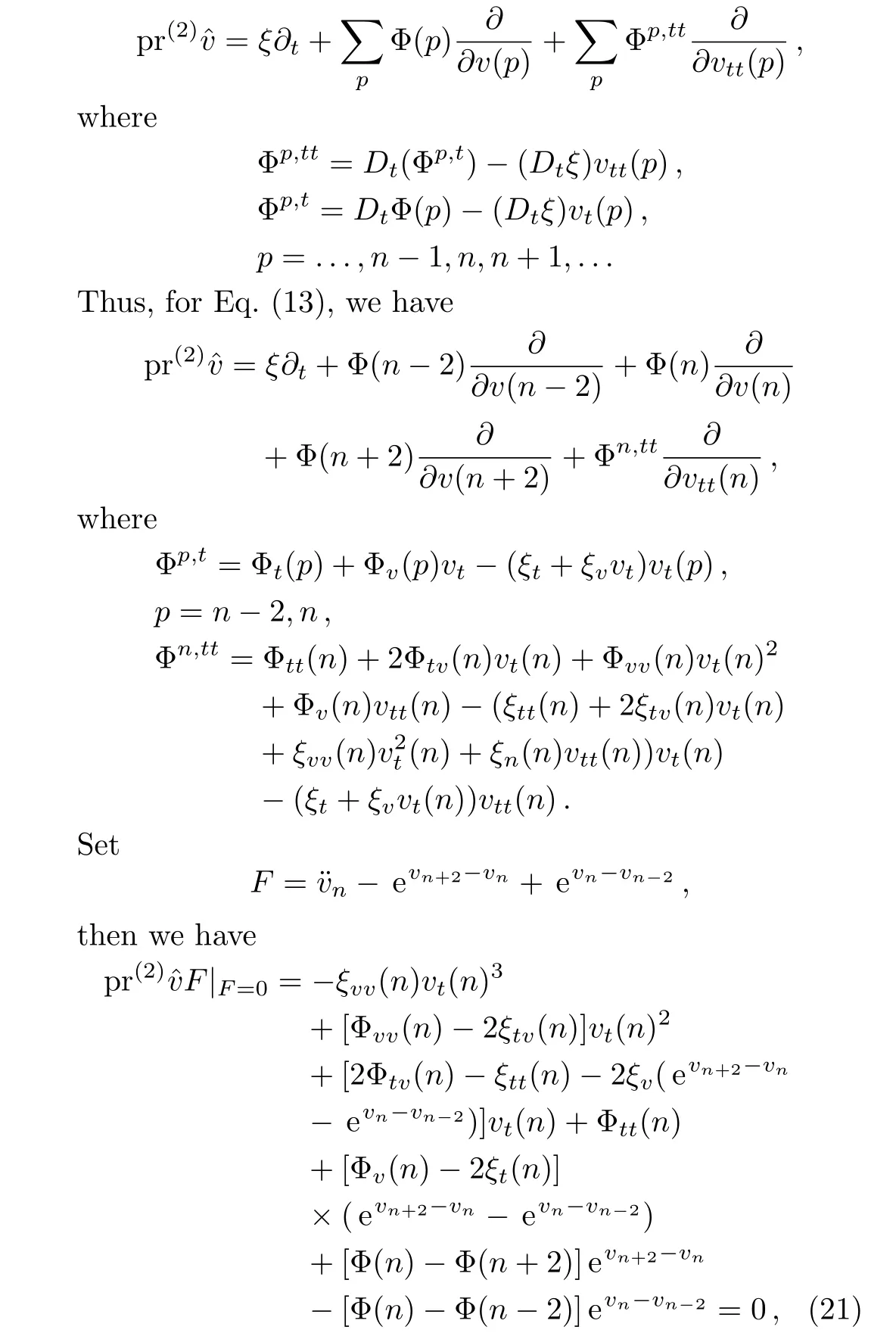
from which we get the following equations

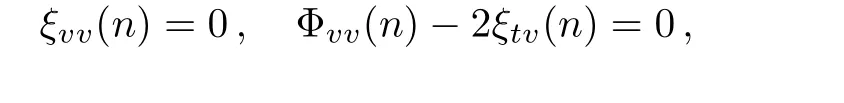
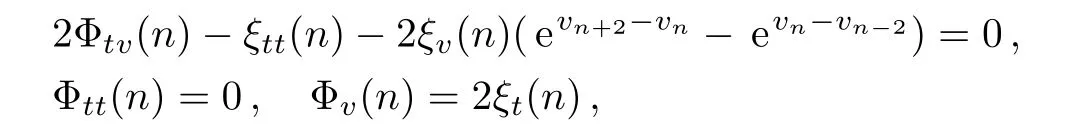
which have a special solution

wherea,b,care arbitrary functions,andβ(n)is also an arbitrary function only depending onn.It is easy to find that a special solution to Eq.(13)presents

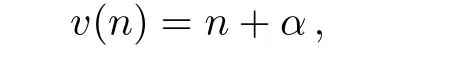
hereαis an arbitrary integer number,α∈Z,andZstands for integer set.Therefore,we take

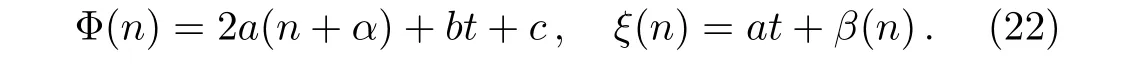
Substituting Eq.(22)into Eq.(21),we find Eq.(21)identically holds.Therefore,the in finitesimal operator of the Lie transformation group of Eq.(13)can be written as

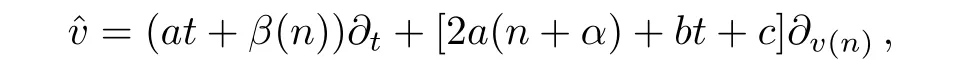
from which we can get a Lie subalgebra of the Lie algebraA1:

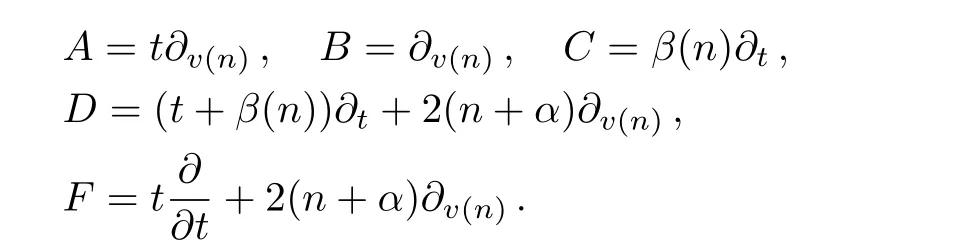
Obviously,hereFis a special case ofD.It is easy to verify that the commutation relations amongA,B,C,Fare as follows

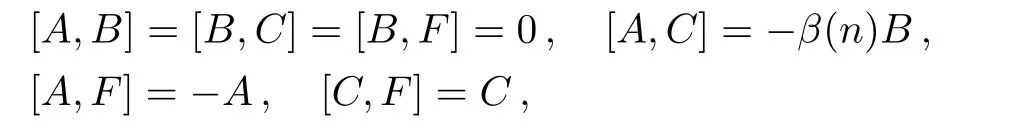
which is the same with that presented in Ref.[8].In what follows,we shall find that the invariant solutions of transformation groups of Eq.(13)are different from those of the standard Toda lattice equation.From the Lie subalgebra{F},we have

whereM(n)is an integration constant. Substituting Eq.(23)into Eq.(13)yields that

whereδis a constant independent ofn,t.Thus,an invariant solution of Eq.(13)is obtained as follows

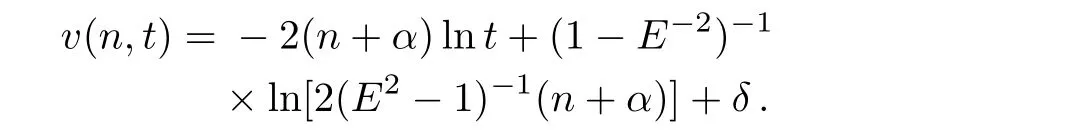
Next,we shall discuss the second case,that is,the symmetries of the(2+1)-dimensional Toda-type equation.For the sake,we must derive it by using the operator(6)and the Lax equation(8).Here the operator(?Ci)/=kis replaced with(Lq)≥kfor the computational conveniences.Takingk=1,the Lax equation(8)becomes that

Letq=1,we can deduce a(2+1)-dimensional integrable system in terms of Eq.(24)

which is the resulting(2+1)-dimensional Toda-type equation corresponding to the(1+1)-dimensional case(13).

In what follows,we would like to look for the symmetries of Eq.(29).Assume that

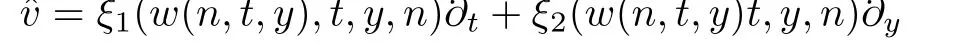
In details,the coefficients as above present that

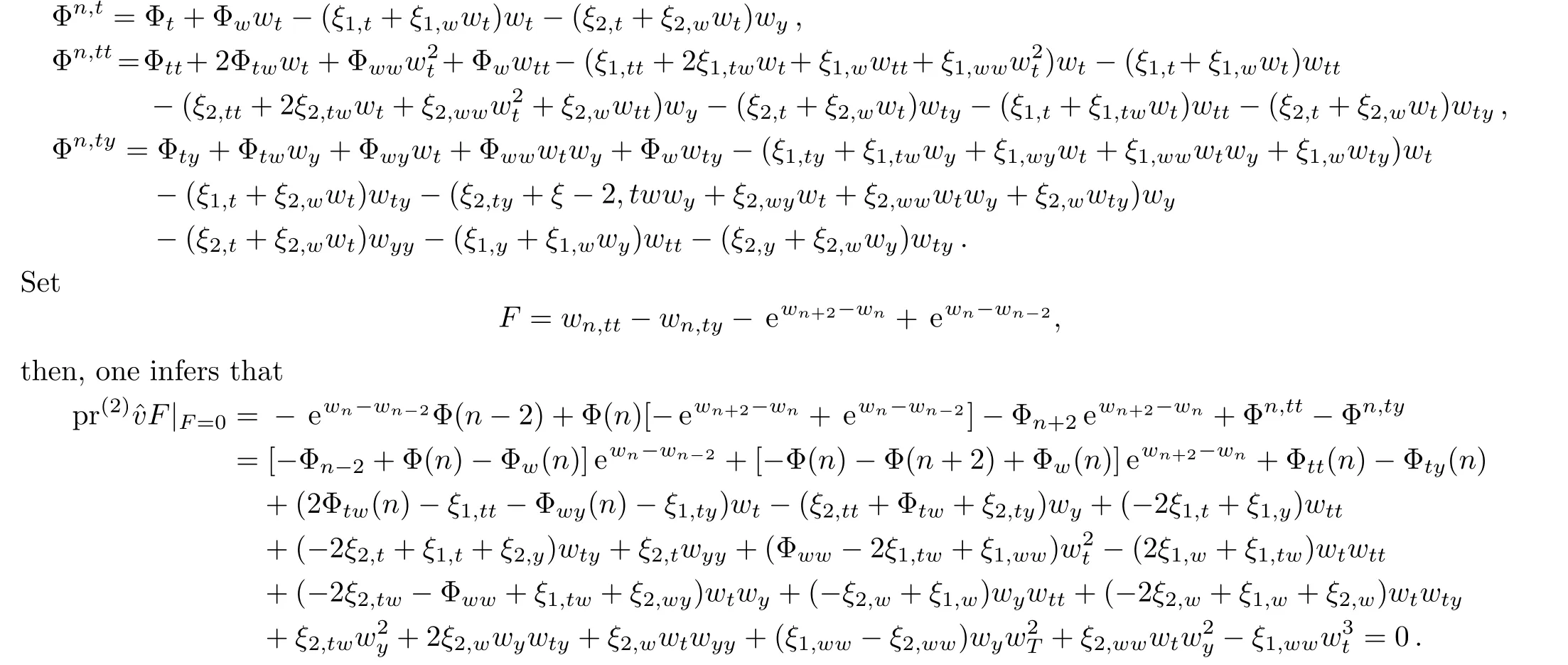
Set the coefficients of the above expression to be zero,an over-determined set of partial differential equations is obtained,whose special solution presents that

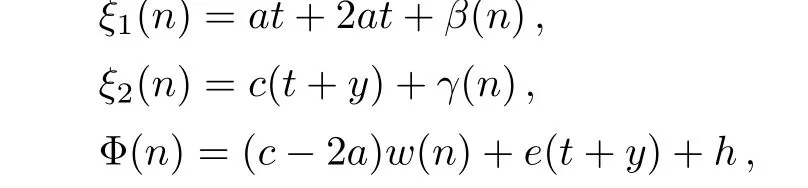
wherea,c,e,f,hare all constants independent ofn,and theβ(n),γ(n)are arbitrary functions inn.Thus,we obtained the symmetry operator of the(2+1)-dimensional

Toda-type differential-difference equation as follows

Similar to the case of(1+1)-dimensional Toda-type equation(13),as long as taking different parameter valuesa,c,e,f,h,β(n),γ(n),we could obtain different Lie algebras for which some surface solutions of the(2+1)-dimensional Toda-type equation by making use of Eq.(32).In addition,if takingq=2 in Eq.(25),we could deduce other new(2+1)-dimensional differential-difference equations whose symmetries could be derived similar to the courses presented as above.Here we omit the explicit computing results.

6 Conclusion

With the help of new shift operators introduced in the paper,we have obtained some(1+1)-and(2+1)-dimensional integrable differential-difference equations and derived some properties,such as the Hamiltonian structures,symmetries and part of surface solutions.By applying the approach we could discuss the similar properties of the other difference equations including(1+1)and(2+1)dimensions.In the forthcoming days,we hope to apply the approach presented combining the ideas in Refs.[11–13]to further study various aspects of difference equations.

The authors are grateful to the reviewer for his appreciated revised suggestions.

[1]M.Blaszak and K.Marciniak,J.Math.Phys.35(1994)4661.

[2]M.Blaszak,A,Szum,and A.Prykarpatsky,Reports on Math.Phys.44(1999)37.

[3]M.Blaszak and A.Szum,J.Math.Phys.42(2001)225.

[4]Z.N.Zhu and H.C.Huang,J.Phys.A 32(1999)4171.

[5]Z.N.Zhu,arXiv:nln/0311035v1,19,Nov.(2003),18 pages.

[6]Y.F.Zhang,et al.,Z.Naturforsch.A 72(2017)77.

[7]Y.F.Zhang and X.J.Yang,J.Nonlinear Sci.Appl.9(2016)6126.

[8]¨U.Goktas,W.Hereman,and G.Erdmann,Phys.Lett.A 236(1997)30.

[9]H.W.Tam and Z.N.Zhu,J.Phys.A 49(2007)13031.

[10]Y.F.Zhang,I.Muhammad,and C.Yue,Commun.Theor.Phys.68(2017)463.

[11]S.Y.Lou,Y.Shi,and D.J.Zhang,Physics 38(2016)1.

[12]E.G.Fan and Z.H.Yang,Int.J.Theor.Phys.48(2009)1.

[13]Z.J.Qiao and R.G.Zhou,Phys.Lett.A 235(1997)35.