Plane Vibrations in a Transversely Isotropic Infinite Hollow Cylinder Under Effect of the Rotation and Magnetic Field

F. S. Bayones and A. M. Abd-Alla

1 Introduction

The analysis of the dynamic problems of elastic bodies is an important and interesting research field for engineers and scientists. It is concerned with determining the strength and load carrying ability of engineering structures, including buildings, bridges, cars,planes, and thousands of machine parts that most of us never see. It is especially important in the fields of mechanical, civil, aeronautical and materials engineering.However, little attention has been given to the problem of the wave propagation in the isotropic circular cylinder. [Boukhari, et al. (2016)] studied an efficient shear deformation theory for wave propagation of functionally graded material plates. [Tounsi, et al. (2016)]investigated a new simple three-unknown sinusoidal shear deformation theory for functionally graded plates. [Yahia, et al. (2015)] discussed the wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories. [Bellifa, et al. (2016)] investigated the bending and free vibration analysis of functionally graded plates using a simple shear deformation theory and the concept the neutral surface position. [Draiche, et al. (2016)] studied a refined theory with stretching effect for the flexure analysis of laminated composite plate. [Mahmoud, et al. (2011)]investigated the effect of the rotation on the radial vibrations in a non-homogeneous orthotropic hollow cylinder. [Abd-Alla, et al. (2008)] studied the effect of the non-homogenity on the composite infinite cylinder of isotropic material. [Bourada , et al.(2015)] studied a new simple shear and normal deformations theory for functionally graded beams. [Gaoab et al. (2013)] investigated the wave propagation in poroelastic hollow cylinder immersed in fluid with seismoelectric effect [Hebali, et al. (2014)]investigated the a new quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. [Hou, et al.(2006)] discussed the transient responses of a special non-homogeneous magneto-electroelastic hollow cylinder for axisymmetric plane strain problem. [Bennoun, et al. (2016)]studied a novel five variable refined plate theory for vibration analysis of functionally graded sandwich plates.[Bounouara, et al. (2016)] studied a nonlocal zeroth-order shear deformation theory for free vibration of functionally graded nanoscale plates resting on elastic foundation. [Meziane (2014)] investigated an efficient and simple refined theory for buckling and free vibration of exponentially graded sandwich plates under various boundary conditions. [Marin and Lupu(1998)] investigated the harmonic Vibrations in Thermoelasticity of Micropolar Bodies. [Marin (2010)] studied the doma in of influence theorem for microstretch elastic materials. [Marin (2010)] discussed the harmonic vibrations in thermoelasticity of microstretch materials. [Marin (1997)] investigated the weak solutions in elasticity of dipolar bodies with voids. [Hutchinson and El-Azhary(1986)] investigated the vibrations of free hollow circular cylinder. [Abd-Alla and Farhan(2008)] studied the effect of the non-homogeneous on the campsite infinite cylinder of isotropic material. [Chen, et al. (2005)] studied the free vibration of non-homogeneous transversely isotropic magneto-electro-elastic plates. [Buchanan (2003)] discussed the free vibration of an infinite magneto-electro-elastic cylinder. [Abd-Alla, et al. (2015)]investigated the wave propagation in fibre-reinforced anisotropic thermoelastic medium subjected to gravity field. The extensive literature on the topic is now available and we can only mention a few recent interesting investigations in Refs. [Abd-Alla and Mahmoud (2012), Abd-Alla, et al.( (2013), (2017)), Bayones and Abd-Alla (2017)].

The main objective of the present research is to determine the eigenvalues of the natural frequency of the transversely isotropic infinite hollow cylinder for different boundary conditions in the cases of harmonic vibrations under effect the in rotation and magnetic field after determining the displacement components and stress components. The numerical results of the frequency equation are discussed in detail for homogeneous material and the effect of rotation and magnetic field for different cases by figures.

2 Formulation of the problem

Let us consider the electromagnetic field governs by Maxwell equations, under consideration that the medium is a perfect electric conductor taking into account absence of the displacement current (SI) in the from is in [Abd-Alla and Mahmoud (2012)].

where

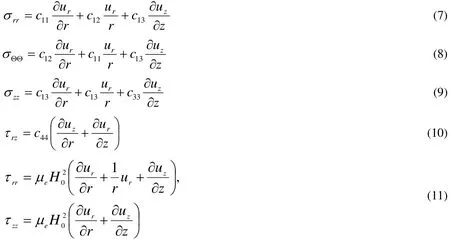
where

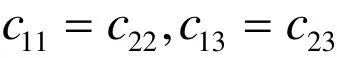
The elasto-dynamic equations in rotating medium as:

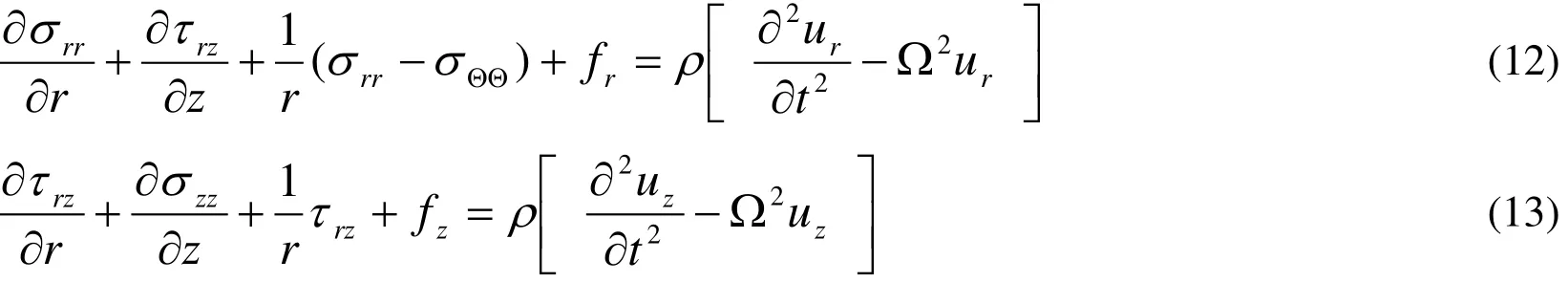
where frand fzare Lorenz’s force-are defined by

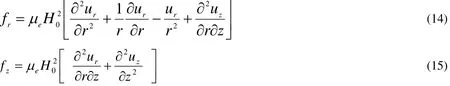
Substituting from Eqs.(1)-( 10) into Eqs.( 12) and (13), we

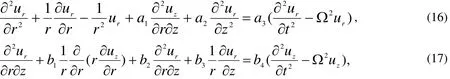
where

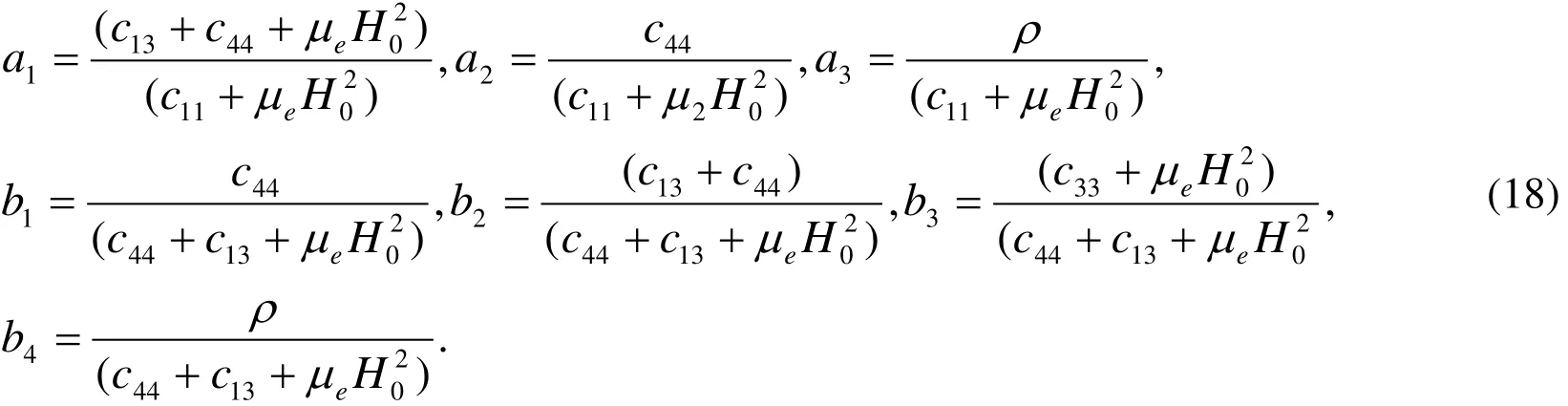
3 - Solution of the problem

By [Morse and Feshbach (1953)], is the displacement vector u can be written

where the two functions Φand Ψare known in the theory of elasticity, by Lame’s potentials rotational and rotational parts of the displacement vectorrespectively. The cylinder being bounded by the curved surface, therefore the stress distribution includes the effect of both Φand Ψ. It is possible to take only one component of the vectorto be nonzero as

From Eqs.(16) and (17), we obtain

Substituting from Eqs. (21) and (22) into Eq. (16), we get two independent equations for Φand Ψas follows:

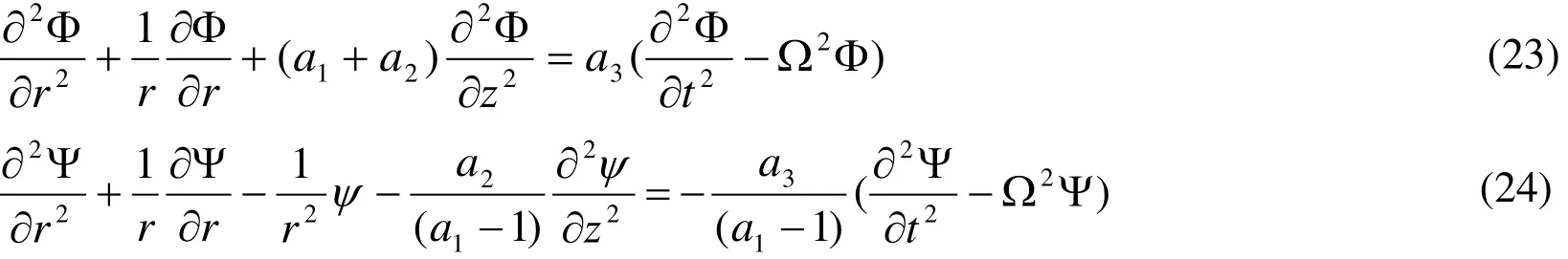
To study the propagation of harmonic waves in the z-direction, we assume a solution in the form

where γis the wave number,ωis the angular frequency.

Substituting from Eq. (25) into Eqs. (23) and (24) we have

and

where

The solution of Eqs. (26) and (27) can be written in the following form:

where A1, A2, B1and B2are arbitrary constants,J0and Y0are Bessel functions of the first and second kind of order zero, respectively,J1and Y1denote cylindrical Bessel’s functions of the first and second kind of order one respectively. From Eqs. (29), (30) and(25) we get

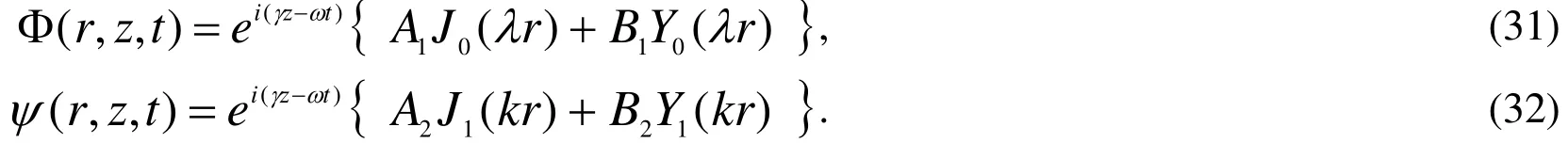
Substituting from Eqs.(31) and (32) into Eqs.(21) and (22) we obtain

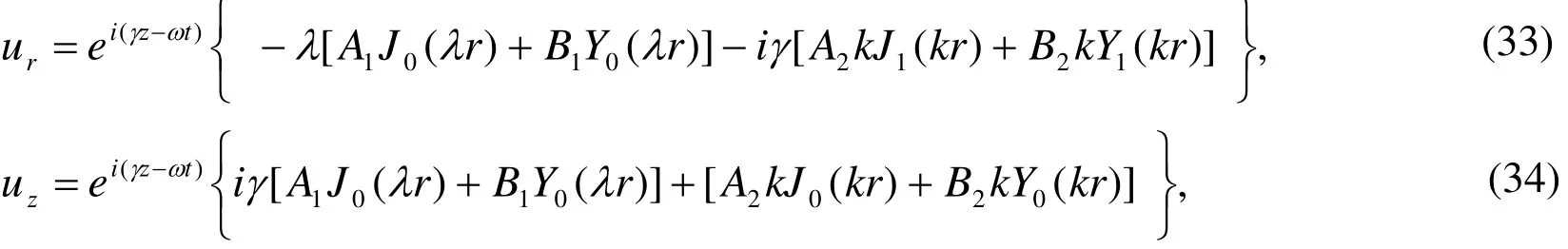
Substituting from Eqs.(33) and (34) into Eqs.(7) , (10) and (11), we get

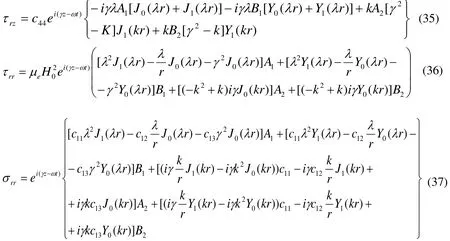
In the following sections of the hollow circular cylinders with three different boundary conditions are performed.

4 Boundary conditions and frequency Equations

In this case, we are going to obtain the frequency equation for the boundary conditions.We consider the following transformations the boundary

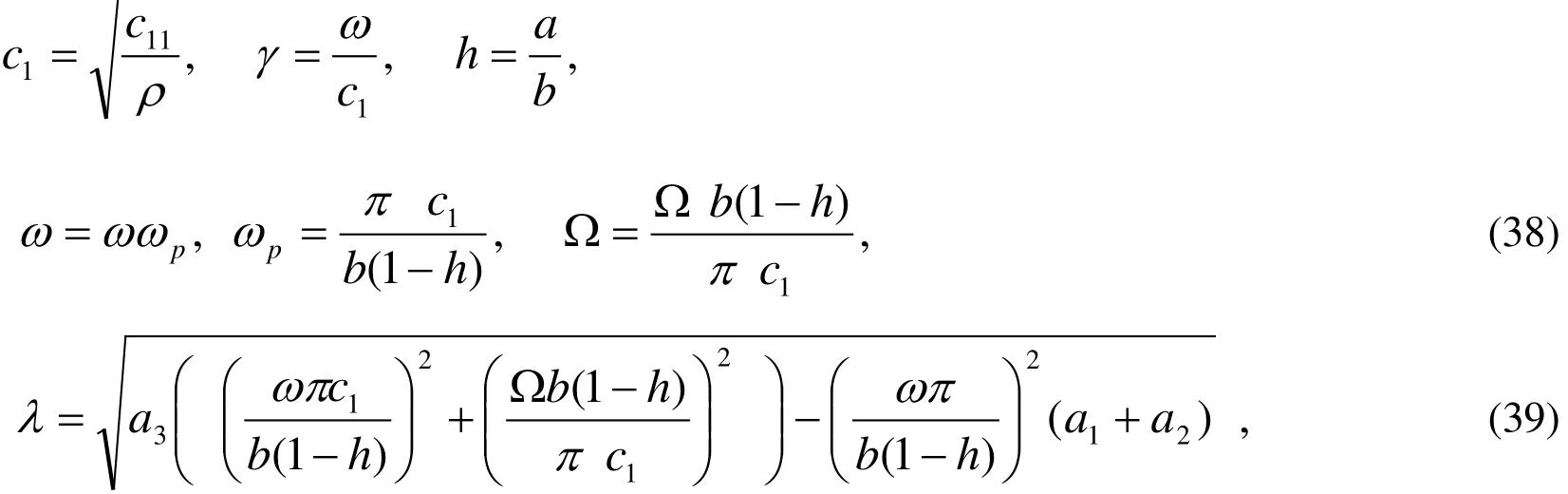
To make all the quantities in (33)-(39), where λ,k do there frequency dimensions.

4.1 Plane vibrations cylindrical body-free surface traction:

In this case, we have

Which corresponds to the free inner and outer surfaces respectively. From Eqs.(35)- (41),we obtain four homogeneous linear equations in A1, B1,A2and B2

These are a set of four homogeneous algebraic equations involving four unknown integration constants A1, B1,A2and B2.For a nontrivial solution of these equations, the determinant of the coefficient matrix must vanish. The zero determinant of the coefficient matrix will give the frequency equation for the surface waves. Thus,elimination of these unknowns would give us the frequency equations

where

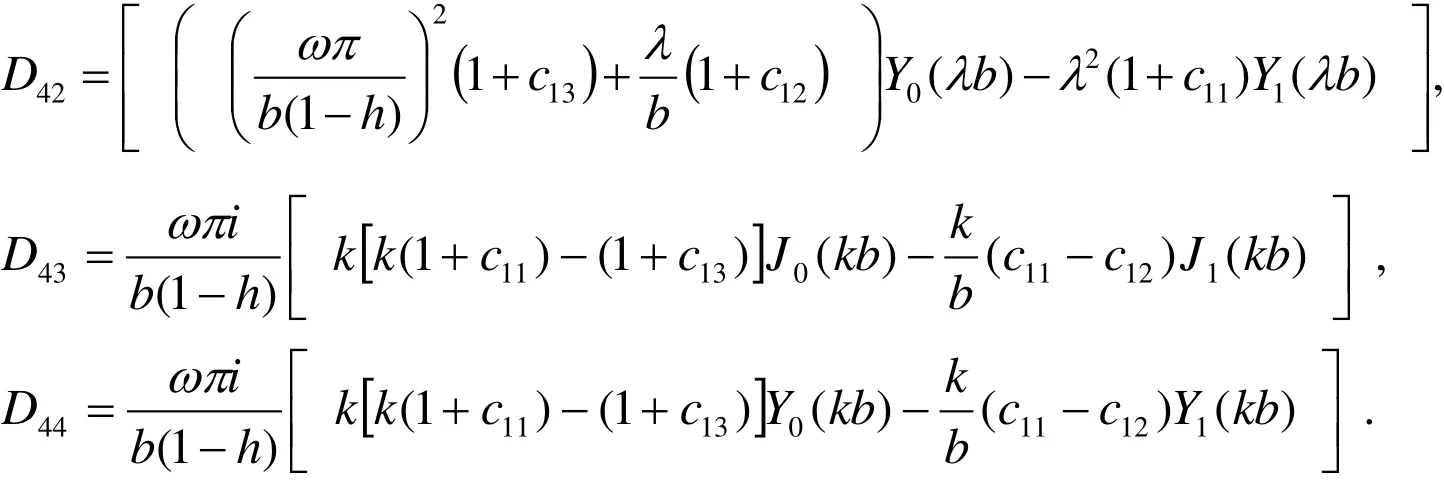
The roots of Eq. (46) gives the values of natural frequency for the free? surfaces of the cylinder.N

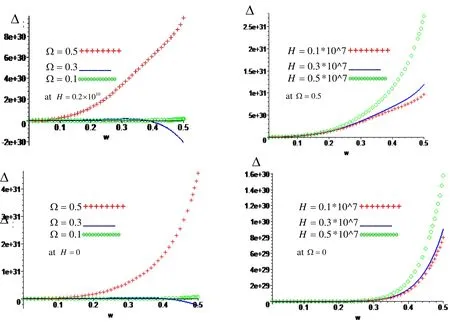
Figure 1: Variation of ?with respect to frequency ωwith effect and neglect respectively of rotation ?and magnetic field H .

4.2 Plane vibrations of cylindrical body of fixed boundary conditions:

In this case, we have

which correspond to the fixed inner and outer surfaces respectively. From Eqs.(33), (34),(38), (39),(40), (47) and (48), we get

These are a set of four homogeneous algebraic equations involving four unknown integration constants A1, B1,A2and B2.The condition for a nontrivial solution of these equations is that the determinant of the coefficients of these integration constants must vanish, which leads to the following frequency equation:

where

The roots of Eq. (53) gives the values of natural frequency for the free surfaces of the cylinder.

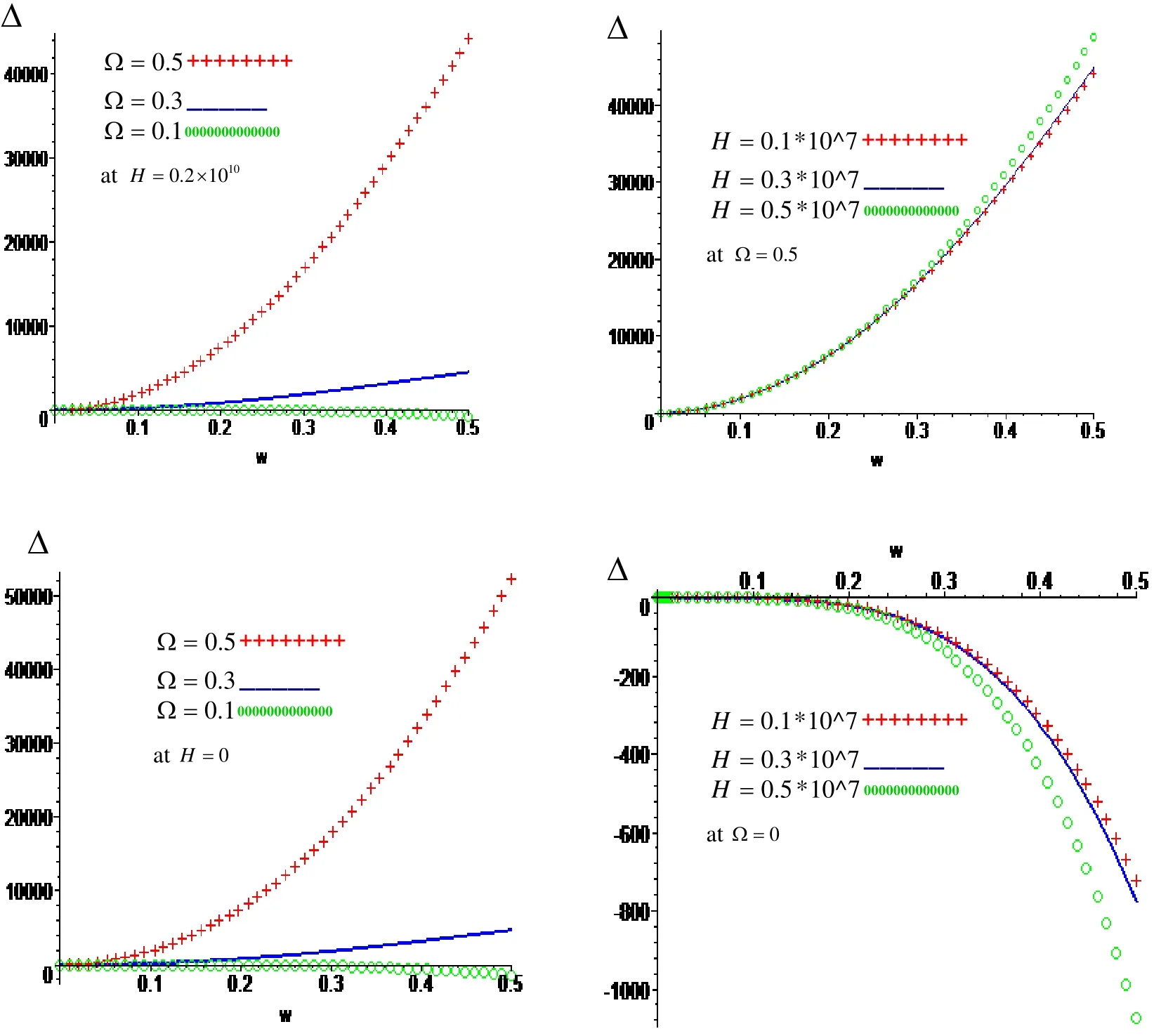
Figure 2:Variation of ?with respect to frequenc ωwith effect and neglect respectively of rotation ?and magnetic field H .

4.3 Plane vibrations of cylindrical body with mixed boundary Conditions

In this application , we apply the mixed boundary conditions which consist of two kinds of boundary conditions, the first requires that the displacements vanish at the inner surface and the outer surface is traction-free i.e.,

while the second requires that the inner surface is traction-free and the displacements vanish at the outer surface, i.e.

4.4 Free outer surface and fixed inner surface

In this case, from Eqs. (33)–(40) and (54), we get

These are a set of four homogeneous algebraic equations involving four unknown integration constants A1, B1,A2and B2.The condition for a nontrivial solution of these equations is that the determinant of the coefficients of these integration constants must vanish, which leads to the following frequency equation:

where

The roots of Eq. (60) gives the values of natural frequency for the free outer surface and fixed inner surface of the cylinder.

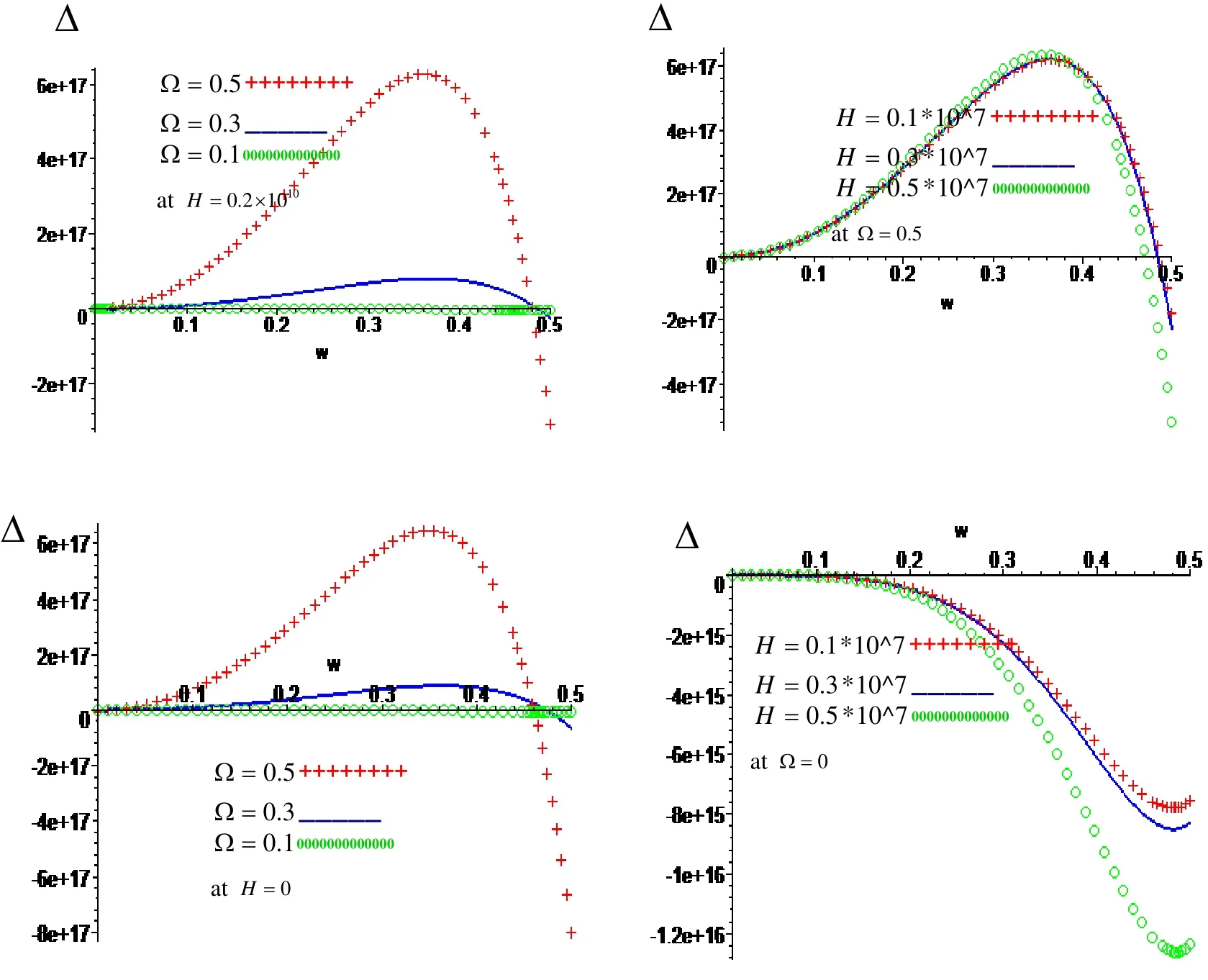
Figure 3: Variation of ?with respect to frequenω with effect and neglect respectively of rotation ?and magnetic field H .

5 Free inner surface and fixed outer surface

In this case, from Eqs. (33)-(40) and (55), we get

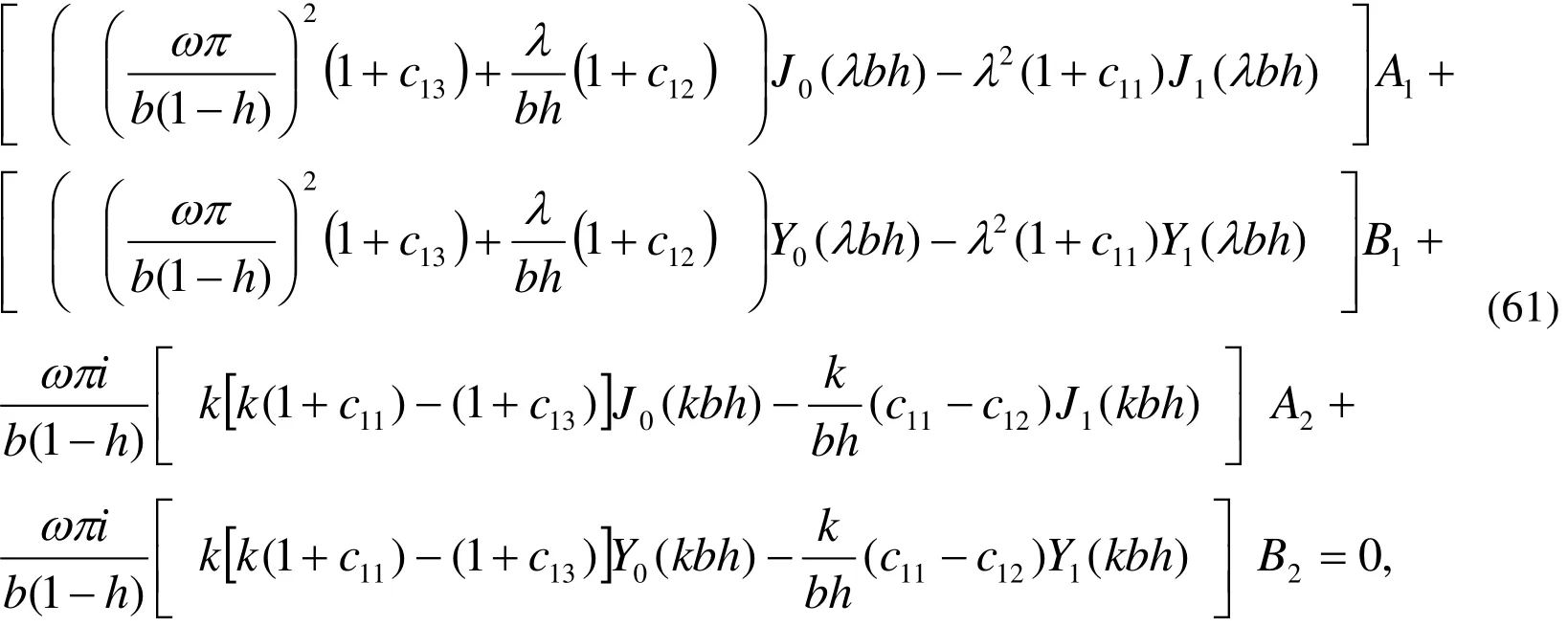
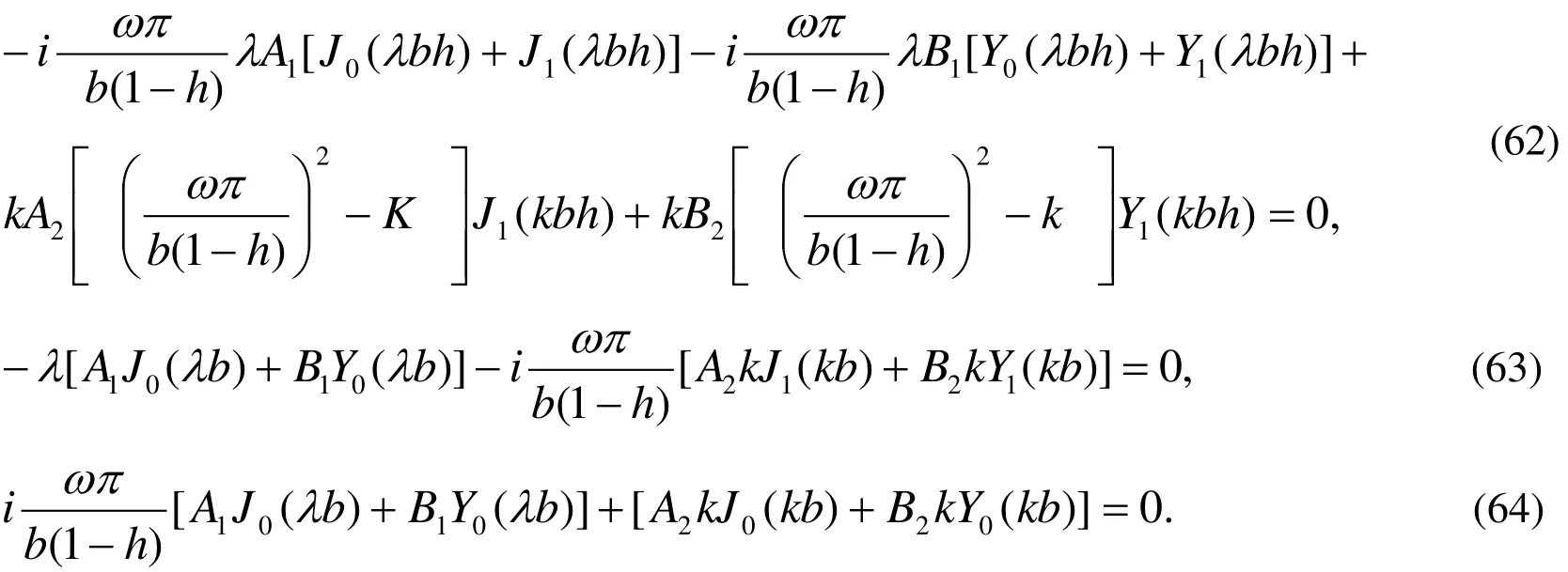
These are a set of four homogeneous algebraic equations involving four unknown integration constants A1, B1,A2and B2.The condition for a nontrivial solution of these equations is that the determinant of the coefficients of these integration constants must vanish ,which leads to the following frequency equation:

where

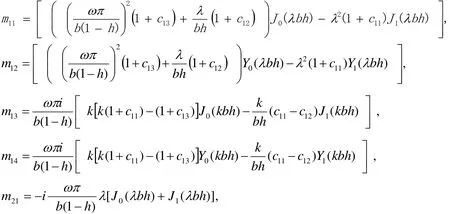
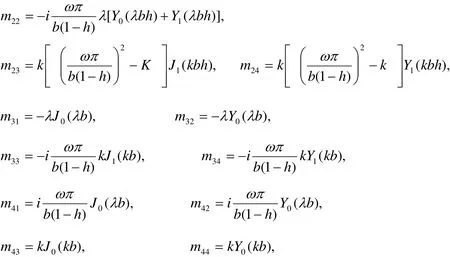
The roots of Eq. (65) gives the values of natural frequency for the free surfaces of the cylinder.

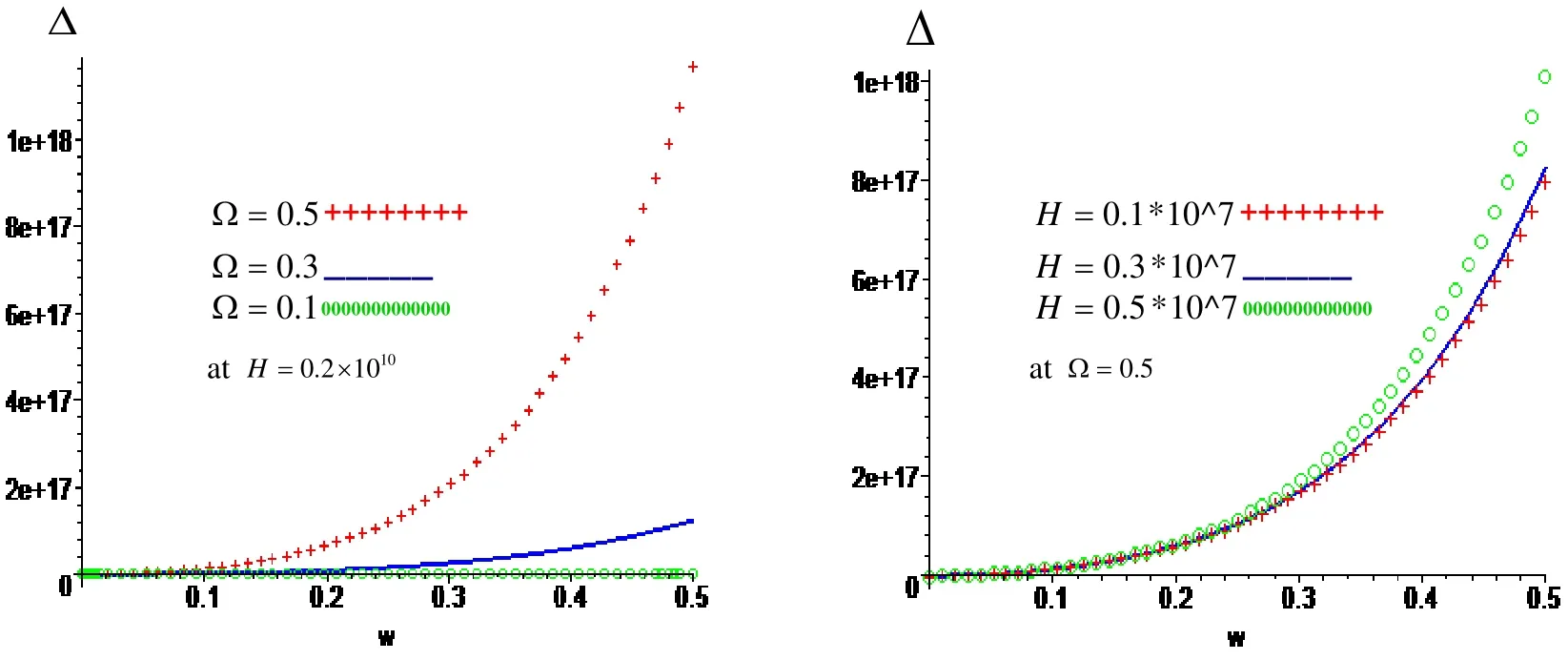
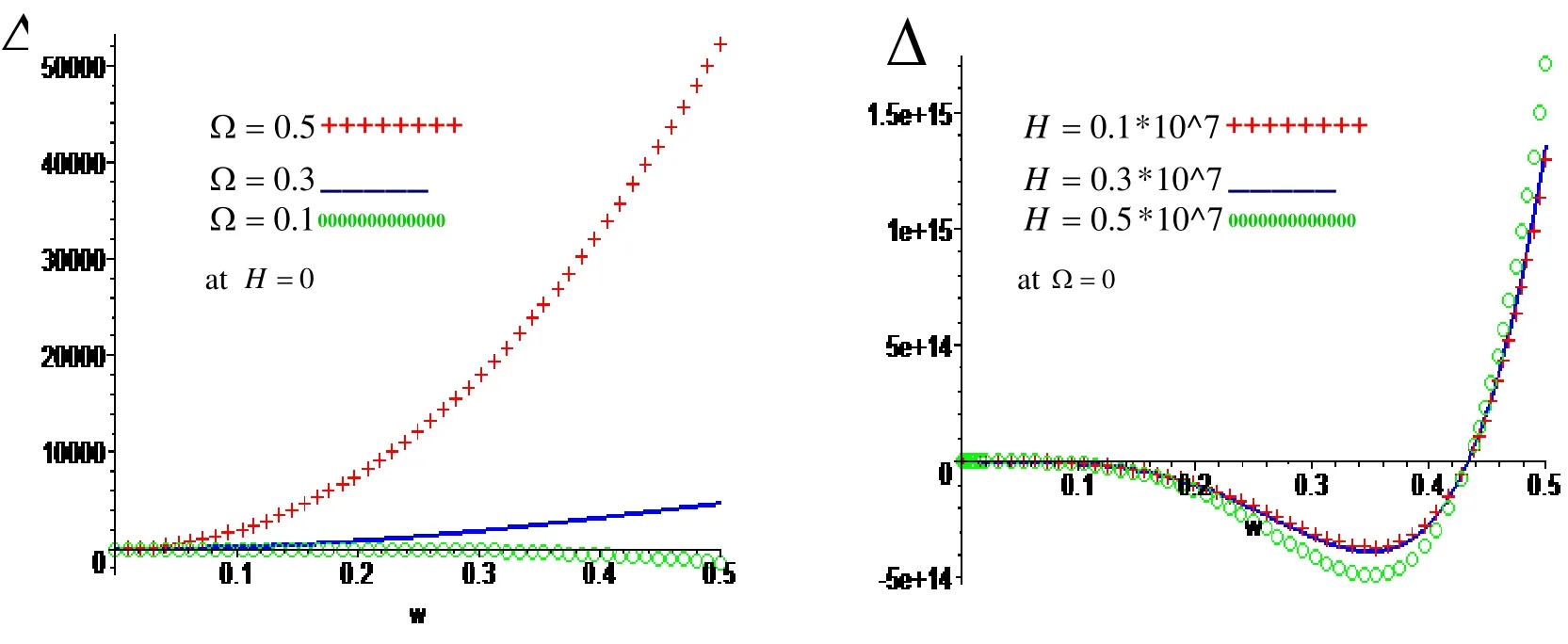
Figure 4: Variation of ?with respect to frequencyω with effect and neglect respectively of rotation ?and magnetic field H .

6 Numerical results and discussion

Here, we shall investigate the frequency equations given by Eqs. (46), (53), (60) and (65)numerically for a particular model. Since these equations are an implicit function relation of natural frequency ω, therefore one can proceed to find the variation of natural frequency (the eigenvalues) with rotation ?and magnetic field H , the cylinder has the following geometric and material constants given by [Chen, et al. (2005)].

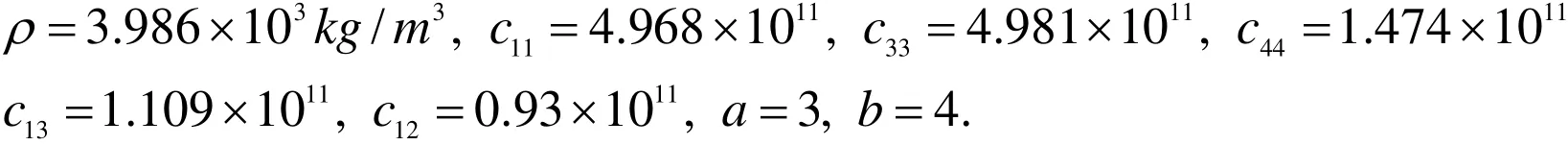
The variations are shown in Figures. (1)- (4), respectively.

Figure.1: show that the variation of the magnitude of the frequency equation ?with respect to frequency ωfor different values of rotation ?and magnetic field H at free surface traction. The magnitude of the frequency equation increases with increasing of rotation and frequency, while it dispersion at ?=0.3 in the presence and absence of magnetic field, while it increases with increasing of magnetic field in the presence and absence of the rotation.

Figure.2: show that the variation of the magnitude of the frequency equation ?with respect to frequency ωfor different values of rotation ?and magnetic field H at a fixed surface. The magnitude of the frequency equation increases with increasing of rotation and frequency in the presence and absence of magnetic field, while it increases with increasing of magnetic field and frequency in the presence of the rotation, while it decreases with increasing of magnetic field and frequency in the absence of rotation.

Figure.3: show that the variation of the magnitude of the frequency equation ?with

respect to frequency ωfor different values of rotation ?and magnetic field H at Free outer surface and fixed inner surface. The magnitude of the frequency equation increases with increasing of rotation in the presence and absence of magnetic field, while it increases and decreases with increasing of frequency in the presence and absence of the magnetic field, as well as it increases with increasing of magnetic field in the interval[0,0.3], while it decreases with increasing of magnetic field in the interval[0.3,0.5]and it increases and decreases with increasing of frequency in the presence of rotation,while it decrease with increasing of magnetic field and frequency in the absence of rotation.

Figure.4: show that the variation of the magnitude of the frequency equation ?with respect to frequency ωfor different values of rotation ?and magnetic field H at Free inner surface and fixed outer surface. The magnitude of the frequency equation increases with increasing of rotation and frequency in the presence and absence of magnetic field, while it dispersion at ?=0.1, as well as it increases with increasing of magnetic field and frequency in the presence of the rotation, while it increases and decreases with increasing of magnetic field and frequency in the absence of rotation.

7 Conclusions

1. Harmonic vibrations of an elastic cylinder have been studied using a half-interval method. The governing equations in cylindrical coordinates are recorded for future reference. The magnitude of the frequency equations has been obtained under the effect of rotating ?and magnetic field H . The numerical results of the natural frequency are obtained and represented graphically in detail for different cases.

2. All the physical quantities satisfy the boundary conditions.

3. The magnetic field and rotation play a significant role in the distribution of all the physical quantities.

4. The results presented in this paper will be very helpful for researchers in structures and material science, designers of new materials and the study of the phenomenon of rotation and magnetic field is also used to improve the conditions of oil extractions.Finally, if the rotation and magnetic field are neglected, the relevant results obtained are deduced to the results obtained by [Abd-Alla et al. (2013)].

Abd-Alla, A. M.; Abo-Dahab, S. M., Bayones, F. S. (2015): Wave propagation in fibrereinforced anisotropic thermoelastic medium subjected to gravity field, Structural Engineering and Mechanics, vol. 53, 76-90.

Abd-Alla, A.M.; Farhan, A.M. (2008): Effect of the non-homogeneous on the campsite infinite cylinder of orthotropic material , J. Physics Letters A, vol. 372, pp. 756-760.

Abd-Alla, A.M.; Nofal, T.A.; Farhan A.M.(2008): Effect of the non-homogenity on the composite infinite cylinder of isotropic material, Physics Letters A, vol. 372, pp. 4861-4864.

Abd-Alla, A.M.; Abo-Dahab, S.M.; Khan, A. (2017):Rotational effect on thermoelastic Stoneley, Love and Rayleigh waves in fibre-reinforced anisotropic general viscoelastic media of higher order , Structures Engineering and Mechanics, vol.61,pp.221-230.

Abd- Alla, A. M.; Mahmoud, S. R. (2012): Analytical solution of wave propagation in a non-homogeneous orthotropic rotating elastic media, Journal of Mechanical Science and Technology, vol. 26, pp.917-926.

Abd-Alla, A.M. ; Yahya, G.A.; Mahmoud, S.R. (2013): Effect of magnetic field and non-homogeneity on the radial vibrations in hollow rotating elastic cylinder, Meccanica,vol.47, pp.76-88.

Buchanan, G.R. (2003) Free vibration of an infinite magneto-electro-elastic cylinder, J.Sound and Vibration, vol. 268, pp. 413-426.

Bayones, F.S. ; Abd-Alla, A.M. (2017):Eigenvalue approach to two dimensional coupled magneto-thermoelasticity in a rotating isotropic medium, Results in Physics,vol.7, pp.2941-2949.

Bounouara, F.; Benrahou,K.H.;Belkorissat, I.;Tounsi , A. (2016): A nonlocal zerothorder shear deformation theory for free vibration of functionally graded nanoscale plates resting on elastic foundation, Steel and Composite Structures, vol. 20, 2, pp.227 - 249.

Bellifa, H.; Benrahou, K. H. ; Hadji, L.; Houari,M. S. A. ; Tounsi, A. (2016):Bending and free vibration analysis of functionally graded plates using a simple shear deformation theory and the concept the neutral surface position, J. Braz. Soc. Mech. Sci.Eng., vol. 38, 1, pp. 265-275.

Bennoun, M.; Houari,M. S. A.;Tounsi , A. (2016): A novel five variable refined plate theory for vibration analysis of functionally graded sandwich plates, Mechanics of Advanced Materials and Structures, vol. 23, 4, pp.423 - 431.

Boukhari, A.; Hassen, A.A.; Tounsi, A.; Mahmoud, S.R. (2016): An efficient shear deformation theory for wave propagation of functionally graded material plates,Structural Engineering and Mechanics, vol. 57, 5, PP.837-859.

Bourada,M.; Kaci,A.; Ahmed,H. M. S.;Tounsi , A. (2015): A new simple shear and normal deformations theory for functionally graded beams, Steel and Composite Structures, vol.18, 2, pp.409 -423.

Chen, W. Q.; Lee, K. Y.; Ding, H. J. (2005): On free vibration of non-homogeneous transversely isotropic magneto-electro-elastic plates, J. Sound and Vibration, vol. 279,pp.237- 251.

Draiche,K.; Tounsi, A. ; Mahmoud, S.R. (2016): A refined theory with stretching effect for the flexure analysis of laminated composite plates", Geomechanics and Engineering, vol. 11, 5, pp. 671-690.

Gaoab ,W.; Cuia,Z.; Wanga,K.(2013): Wave propagation in poroelastic hollow cylinder immersed in fluid with seismoelectric effect,Journal of Sound and Vibration,vol. 332, 20, pp.5014-5028.

Hebali, H.;Tounsi , A.; Houari,M. S.A.;Bessaim, A. (2014): A new quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates, ASCE J. Engineering Mechanics, vol. 140, pp.374 - 383.

Hou, P.F.; Ding, H.J.; Leung, A.Y.T. (2006):The transient responses of a special nonhomogeneous magneto-electro-elastic hollow cylinder for axisymmetric plane strain problem, Journal of Sound and Vibration, vol. 291,1, pp.19-47.

Hutchinson, J.R.; El-Azhary, S.A. (1986): Vibrations of free hollow circular cylinder, J.Applied Mechanics, vol. 53, pp. 641-646.

Mahmoud, S.R.; Abd-Alla, A.M. and AL-Shehri, N.A. (2011): Effect of the rotation on the radial vibrations in a non-homogeneous orthotropic hollow cylinder, Int. J. of Modern Physics B, vol.25, pp. 3513-3528.

Marin, M. and Lupu, M. (1998): On Harmonic Vibrations in Thermoelasticity of Micropolar Bodies, Journal of Vibration and Control, vol.4, pp. 507-518.

Marin, M. (2010): A domain of influence theorem for microstretch elastic materials,Nonlinear, Analysis: Rea World Applications, vol. 11, pp. 3446-3452.

Marin,M. (2010):Harmonic vibrations in thermoelasticity of microstretch materials, J.Vibr. Acoust., ASME, vol. 132, 4, pp.1-6.

Marin, M. (1997):On weak solutions in elasticity of dipolar bodies with voids ,J. Comp. Appl. Math., vol. 82 (1-2), 291-297, 1997

Meziane,M. A.A.;Abdelaziz, H.H.;Tounsi , A. (2014): An efficient and simple refined theory for buckling and free vibration of exponentially graded sandwich plates under various boundary conditions, J. Sandw. Struct. Mater., vol.16, 3, 293-318.

Morse, P. M.; Feshbach, H.(1953): Methods of theoretical physics, Part I, McGraw-Hill, New York|.

Tounsi, A. ;Ahmed, H.;Bessaim, A. (2016): A new simple three-unknown sinusoidal shear deformation theory for functionally graded plates, Steel and Composite Structures,vol.22, 2, pp. 257 - 276.

Yahia,S. A.; Hassen,A. A.; Ahmed,H. M. S.;Tounsi, A. (2015): Wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories, Structural Engineering and Mechanics, vol. 53, 6, pp.1143 - 1165.