STRONGLY CONVERGENT ITERATIVE METHODS FOR SPLIT EQUALITY VARIATIONAL INCLUSION PROBLEMS IN BANACH SPACES?
Shih-sen CHANG(張石生)
Center for General Education,China Medical University,Taichung 40402,China
Lin WANG(王林)
College of Statistics and Mathematics,Yunnan University of Finance and Economics, Kunming 650221,China
Lijuan QIN(秦麗娟?)
Department of Mathematics,Kunming University,Kunming 650214,China
Zhaoli MA(馬招麗)
School of Information Engineering,College of Arts and Science Yunnan Normal University, Kunming 650222,China
STRONGLY CONVERGENT ITERATIVE METHODS FOR SPLIT EQUALITY VARIATIONAL INCLUSION PROBLEMS IN BANACH SPACES?
Shih-sen CHANG(張石生)?
Center for General Education,China Medical University,Taichung 40402,China
E-mail:changss2013@163.com
Lin WANG(王林)
College of Statistics and Mathematics,Yunnan University of Finance and Economics, Kunming 650221,China
E-mail:wl64mail@aliyun.com
Lijuan QIN(秦麗娟?)
Department of Mathematics,Kunming University,Kunming 650214,China
E-mail:annyqlj@163.com
Zhaoli MA(馬招麗)
School of Information Engineering,College of Arts and Science Yunnan Normal University, Kunming 650222,China
E-mail:kmszmzl@126.com
The purpose of this paper is to introduce and study the split equality variational inclusion problems in the setting of Banach spaces.For solving this kind of problems,some new iterative algorithms are proposed.Under suitable conditions,some strong convergence theorems for the sequences generated by the proposed algorithm are proved.As applications, we shall utilize the results presented in the paper to study the split equality feasibility problems in Banach spaces and the split equality equilibrium problem in Banach spaces.The results presented in the paper are new.
the split equality variational inclusion problem in Banach space;split feasibility problem in Banach space;split equilibrium problem in Banach spaces
2010 MR Subject Classifcation47J25;47H09;65K10
1 Introduction
Let C and Q be nonempty closed and convex subsets of real Hilbert spaces H1and H2, respectively.The split feasibility problem(SFP)is formulated aswhere A:H1→ H2is a bounded linear operator.In 1994,Censor and Elfving[1]frst introduced the(SFP)in fnite-dimensional Hilbert spaces for modeling inverse problems which arise from phase retrievals and in medical image reconstruction[2].It was found that the (SFP)can also be used in various disciplines such as image restoration,computer tomograph and radiation therapy treatment planning[3–5].The(SFP)in an infnite dimensional real Hilbert space can be found in[2,4,6–10].
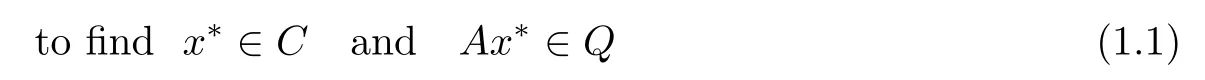
Recently,Moudaf[11–13]introduced the following split equality feasibility problem(SEFP):
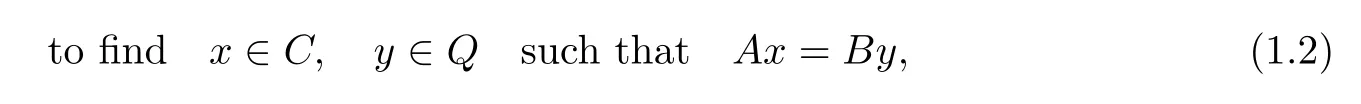
where A:H1→H3and B:H2→H3are two bounded linear operators.Obviously,if B=I (identity mapping on H2)and H3=H2,then(1.2)reduces to(1.1).The kind of split equality feasibility problems(1.2)allows asymmetric and partial relations between the variables x and y. The interest is to cover many situations,such as decomposition methods for PDEs,applications in game theory and intensity-modulated radiation therapy.
In order to solve split equality feasibility problem(1.2),Moudaf[11]introduced the following simultaneous iterative method

and under suitable conditions he proved the weak convergence of the sequence{(xn,yn)}to a solution of(1.2)in Hilbert spaces.
Attempt to introduce and consider the split feasibility problem and split common null point problem in the setting of Banach spaces have recently been made.In 2015,Takahashi [14]frst introduced and considered such problems in Banach spaces.By using hybrid methods and Halpern’s type methods and under suitable conditions some strong and weak convergence theorems for such problems are proved in Banach spaces.The results presented in[14]seem to be the frst outside Hilbert space.
Motivated by the above works and related literatures,the purpose of this paper is to introduce and study the following split equality variational inclusion problems in the setting of Banach spaces.
Let H1and H2be two real Hilbert spaces and F be a real Banach space.Let A:H1→F,B:H2→F be two bounded linear operators and A?and B?be the adjoint mappings of A and B,respectively.In the sequel we always denote by F(K)the fxed point set of a mapping K.Let Ui:Hi→2Hi,i=1,2 be a maximal monotone mapping.The resolvent of Uiis defned by
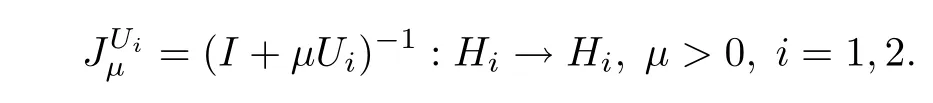
The“so-called”split equality variational inclusion problems in Banach spaces(SEVIP)is to fnd

In the sequel,we always denote bythe solution set of(SEVIP)(1.4).
Next we give some examples of(SEVIP)(1.4).
Example 1.1Split equality feasibility problem in Banach spaces.
Let H1,H2be two real Hilbert spaces and F be a real Banach space.Let C?H1and Q?H2be two nonempty closed convex subsets and A:H1→F,B:H2→F be two bounded linear operators.The“so-called”“split equality feasibility problem in Banach space”(SEFP) is to fnd
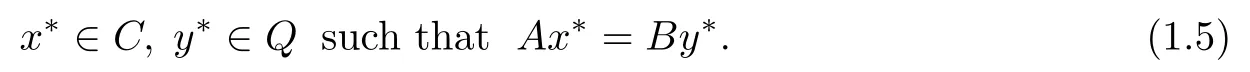
Let iCand iQbe the indicator function of C and Q,respectively,i.e.,
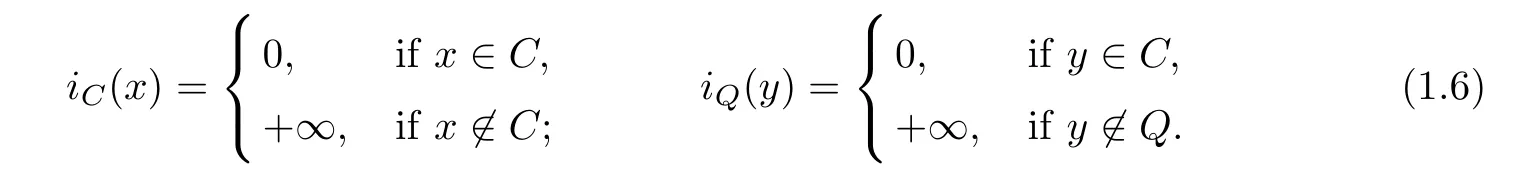
Denote by NC(x)and NQ(y)the normal cone of C and Q at x and y,respectively,
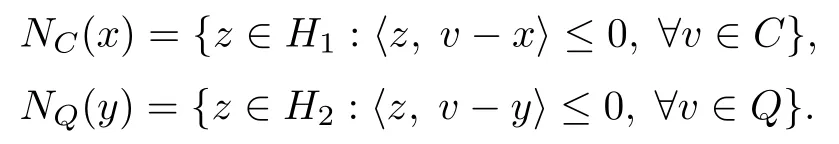
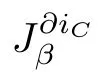

where
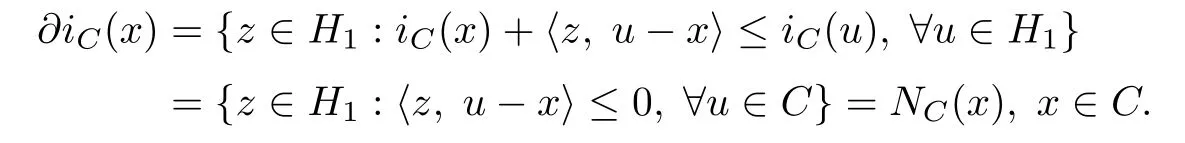
Hence we have
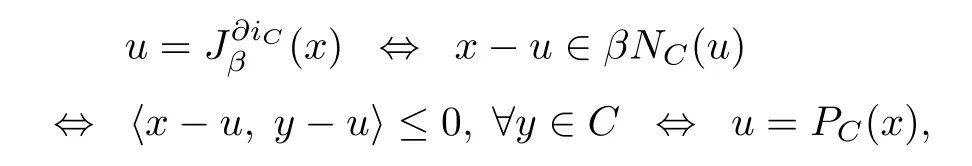
where PCis the metric projection from H1onto C.This implies thatfor any β>0. Similarly,we also havefor any β>0.Therefore the(SEFP) (1.5)is equivalent to the following split equality variational inclusion problem in Banach space, i.e.,to fnd x?∈H1,and y?∈H2such that
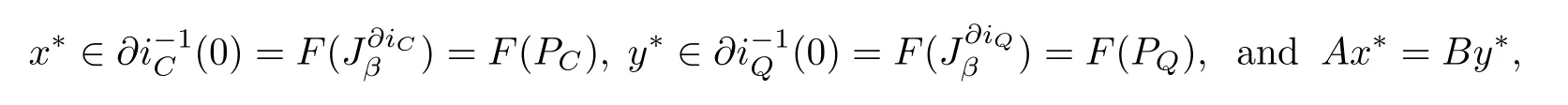
Example 1.2Split equality equilibrium problem in Banach space.
Let D be a nonempty closed and convex subset of a real Hilbert space H.A bifunction g:D×D→(?∞,+∞)is said to be a equilibrium function,if it satisfes the following conditions
(A1)g(x,x)=0 for all x∈D;
(A2)g is monotone,i.e.,g(x,y)+g(y,x)≤0 for all x,y∈D;
(A3)limsupt↓0g(tz+(1?t)x,y)≤g(x,y)for all x,y,z∈D;
(A4)for each x∈D,y 7→g(x,y)is convex and lower semi-continuous.
The“so-called”equilibrium problem with respective to the equilibrium function g is
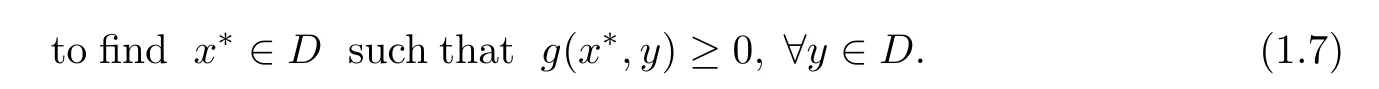
Its solution set is denoted by EP(g).
For given λ>0 and x∈H,the resolvent of the equilibrium function g is the operator Rλ,g:H→D defned by
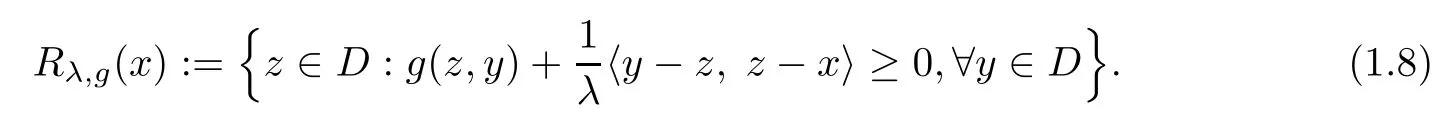
Proposition 1.3(see[15]) The resolvent operator Rλ,gof the equilibrium function g has the following properties:
(1)Rλ,gis single-valued;
(2)F(Rλ,g)=EP(g)and EP(g)is a nonempty closed and convex subset of D;
(3)Rλ,gis a frmly nonexpansive mapping.
Let h,g:D×D→(?∞,+∞)be two equilibrium functions and F be a real Banach space. For given λ>0,let Rλ,hand Rλ,gbe the resolvent of h and g(defned by(1.8)),respectively.
The”so-called”split equality equilibrium problem in Banach space with respect to h,g,D and F is to fnd x?∈D,y?∈D such that
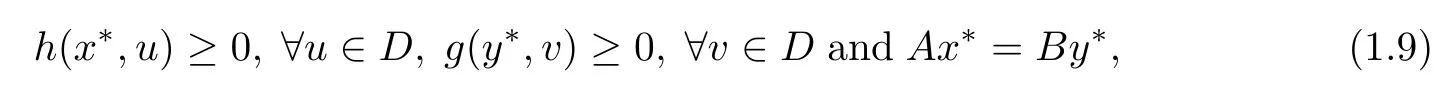
where A,B:D→F are two linear and bounded operators.
By Proposition 1.3,the split equality equilibrium problem in Banach space(1.9)is equivalent to fnd x?∈D,y?∈D such that for each λ>0,
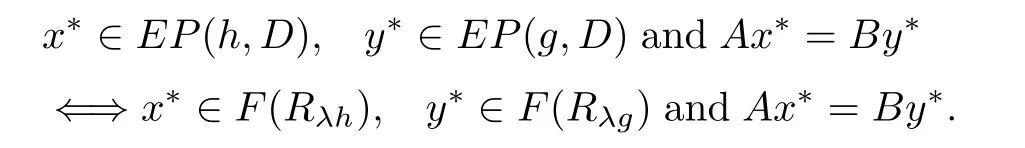
Letting C=F(Rλh),Q=F(Rλg),by Proposition 1.1,C and Q both are nonempty closed and convex subset of D.Hence problem(1.9)is equivalent to the following split equality feasibility problem
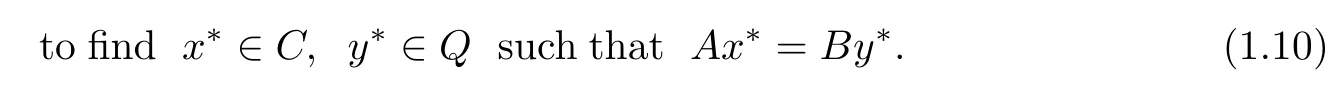
By using Example 1.1,we know that problem(1.10)is equivalent to the following split equality variational inclusion problem in Banach space
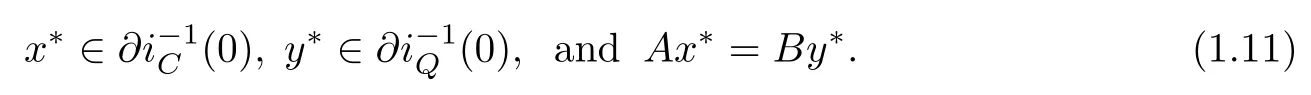
For solving(SEVIP)(1.4),in Section 2,we propose a new type iterative algorithm.Under suitable conditions some strong convergence theorems for the sequences generated by the algorithm to approximate a solution of(SEVIP)(1.4)are proved.As an application,we shall utilize our results to study the split equality feasibility problem and the split equality equilibrium problem in Banach spaces.The results presented in the paper are new which extend and improve the corresponding results announced by Censor et al.[1,3–5,16],Moudafet al.[11–13],Eslamian and Latif[17],Chen et al.[18],Chuang[19],Chang,Wang[20],Chang, Agarwai[21]and Chang et al.[22],Naraghirad[23],Tang,China,Liu[24].
2 Strong Convergence Theorems for Split Equality Variational Inclusion Problems in Banach Spaces
Throughout this section we always assume that
1.F is a real smooth Banach space and JFis the duality mapping of F defned by
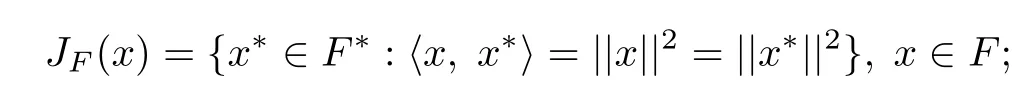
2.H1,H2are two real Hilbert spaces;
3.A:H1→F,B:H2→F are two bounded linear operators and A?:F?→H1and B?:F?→H2are the adjoint mappings of A and B,respectively;
4. Ui:Hi→2Hi,i=1,2 is a maximal monotone mapping.The resolventof Uiis defned by:
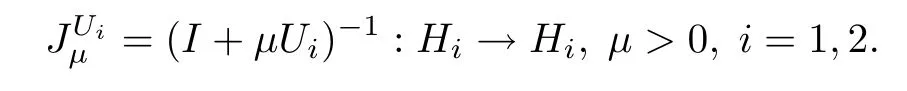
It is easy to know that if Ui:Hi→2Hi,i=1,2 is a maximal monotone mapping,then the resolventof Uiis nonexpansive andwhereis the set of zero points of Uiandis the the set of fxed points of
We are now in a position to give the following main result.
Theorem 2.1Letand A,B,A?,B?be the same as above.Denote by C1=H1,Q1=H2.For given x1∈C1and y1∈Q1,let the iterative sequence{xn}and{yn}be generated by
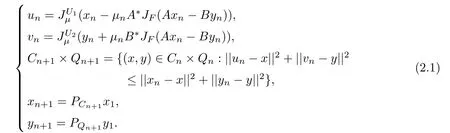

then the sequence{(xn,yn)}converges strongly to some point(x?,y?)∈?,where||A||(resp. ||B||)is the norm of the operator A(resp.B),therefore||A||=||A?||and||B||=||B?||.
Proof(I)First we prove that for each n≥1,??Cn×Qn.
In fact,for any(p,q)∈? we haveHence(p,q)∈C1×Q1.If for some n≥2,(p,q)∈Cn×Qn,next we prove that(p,q)∈Cn+1×Qn+1.In fact,from(2.1)we have

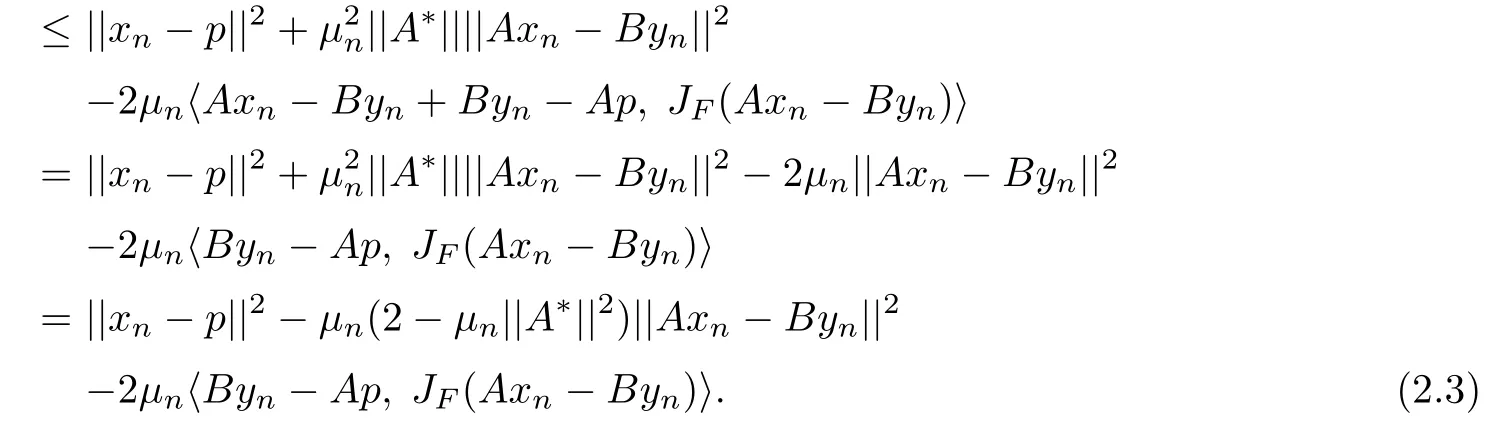
Similarly,we can also prove that
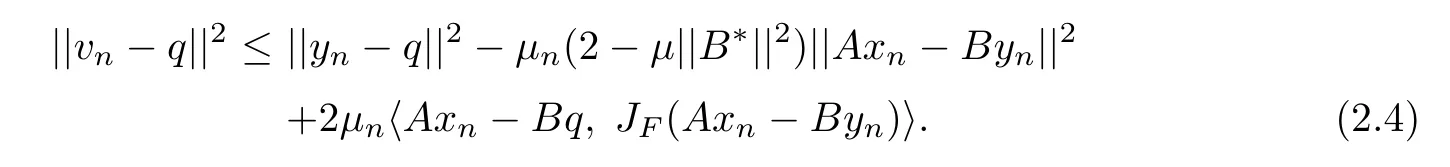
Add up(2.3)and(2.4).After simplifying and noting Ap=Bq,we have
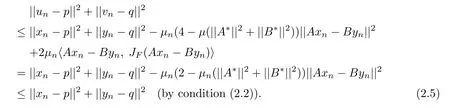
This implies that(p,q)∈Cn+1×Qn+1and so ??Cn×Qn,?n≥1.
(II)Now we prove that{xn}and{yn}is a Cauchy sequence in H1and H2,respectively.
Indeed,by the defnition of Cnand Qn,n≥1,it is easy to know that all of them are nonempty closed and convex subsets.Therefore the sequences{xn}and{xn}are well defned.
Since
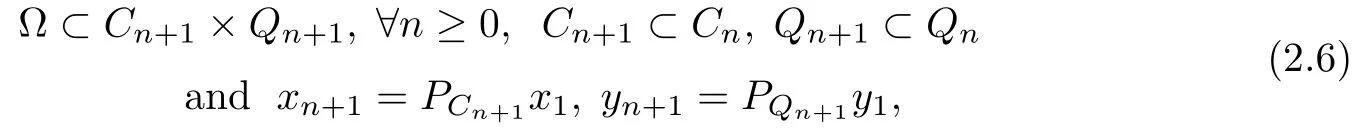
we have

This implies that{xn}and{yn}are bounded.
Furthermore,it follows from(2.1)that
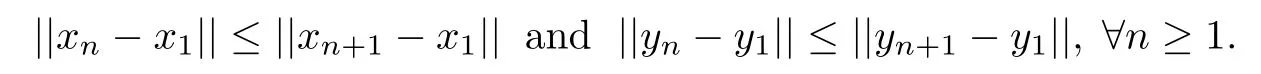
Therefore{||xn?x1||}and{||yn?y1||}are convergence sequences.For any positive integers n,m≥1,since xm=PCmx1,by the property of projection operator,we have
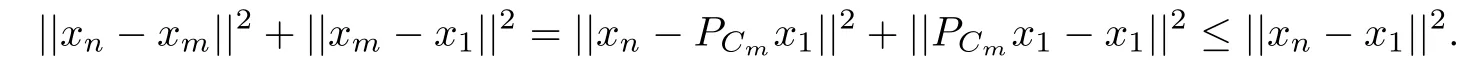
Therefore we have
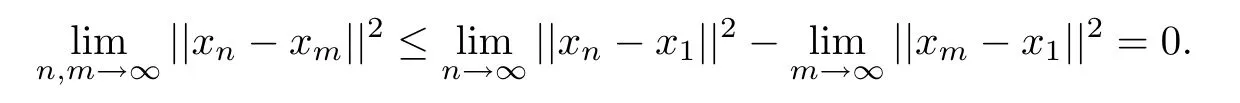
This shows that{xn}is a Cauchy sequence in H1.By the same way we can also prove that {yn}is a Cauchy sequences in H2.Without loss of generality,we can assume that xn→x?and yn→y?.
(III)Now we prove that(x?,y?)∈?.
In fact,since(xn+1,yn+1)∈Cn+1×Qn+1,it follows from(2.1)that
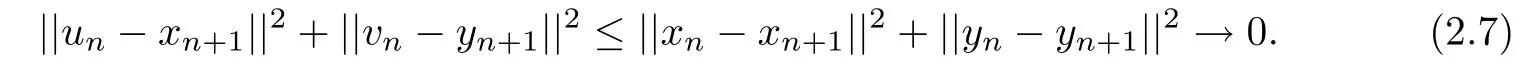
Hence
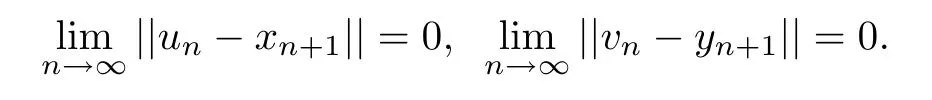
Therefore we have un→x?and vn→y?.Furthermore,it follows from(2.5)that
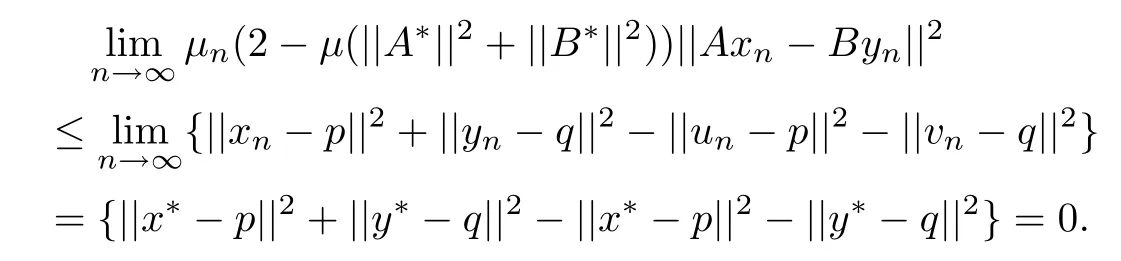
By virtue of condition(2.2),we have
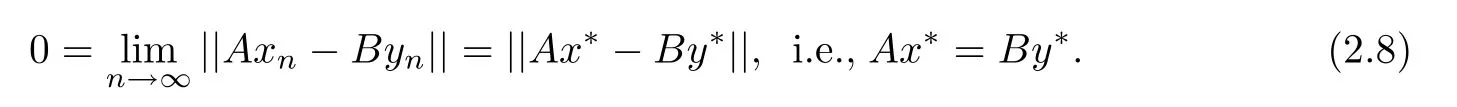
It follows from(2.7)and(2.8)that

3 Application to Split Equality Feasibility Problems in Banach Spaces
In this section we shall utilize Theorem 2.1 to study the split equality feasibility problems in Banach spaces
Let H1,H2be two real Hilbert spaces and F be a real Banach space.Let C?H1and Q?H2be two nonempty closed convex subsets and A:H1→F,B:H2→F be two bounded linear operators and A?and B?be the adjoint operators of A and B,respectively.As pointed out in Section 1,Example 1.1,that the“so-called”“split equality feasibility problem in Banach space”(SEFP)is to fnd
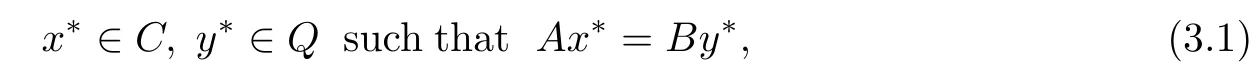
which is equivalent to the following split equality variational inclusion problem in Banach space, i.e.,to fnd
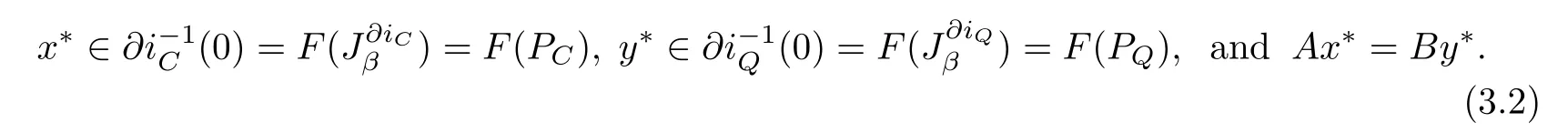
Therefore from Theorem 2.1 we can obtain the following.
Theorem 3.1Let H1,H2,F,C,Q,A,B be the same as above.Let A?and B?be the adjoint operators of A and B respectively.Denote by C1=C,Q1=Q.For given x1∈C1andy1∈Q1,let the iterative sequence{xn}and{yn}be generated by
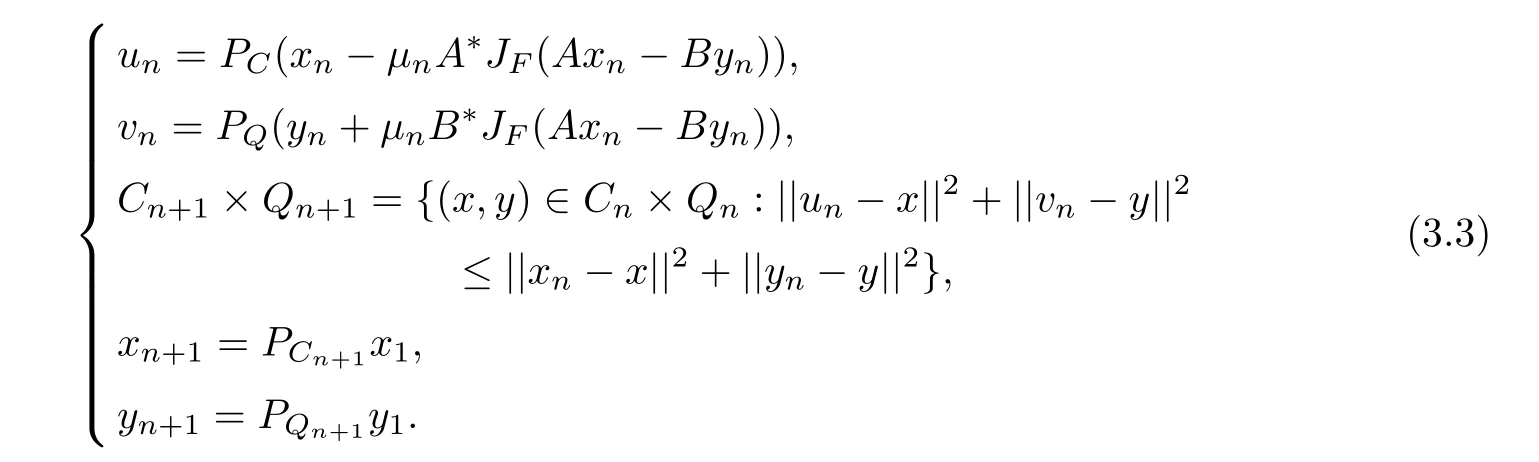
If the solution set ?1:={(p,q)∈C×Q,Ap=Bq}of(SEVIP)(3.1)is nonempty and the following condition is satisfed

then the sequence{(xn,yn)}converges strongly to some point(x?,y?)∈?1.
4 Application to Split Equality Equilibrium Problems in Banach Spaces
In this section we shall utilize Theorem 2.1 to study the split equality equilibrium problems in Banach spaces.
Let H1,H2be two real Hilbert spaces,and F be a real Banach space.Let h:H1×H1→R and g:H2×H2→R be two equilibrium functions.Let A:H1→F and B:H2→F be two bounded linear operators with adjoint operator A?and B?,respectively.For given λ>0,let Rλ,h,and Rλ,gbe the resolvents of h and g(defned by(1.8)),respectively.
As pointed out in Section 1,Example 1.2,that the split equality equilibrium problem with respective to h,g in Banach space is to fnd x?∈H1,y?∈H2such that

which is equivalent
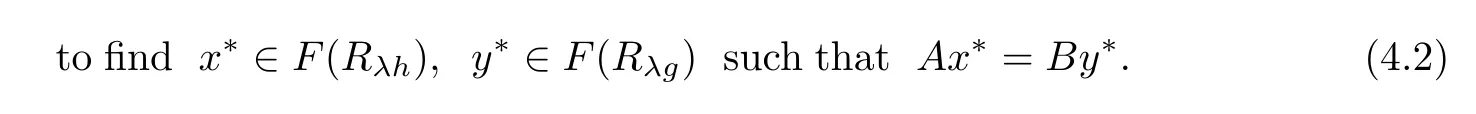
Letting C=F(Rλh),Q=F(Rλg),by Proposition 1.3,C and Q are nonempty closed and convex subset of H1and H2,respectively.Hence problem(4.2)is equivalent to the following split equality feasibility problem in Banach space

By using Example 1.1 in Section 1,we know that problem(4.3)is equivalent to the following split equality variational inclusion problem in Banach space
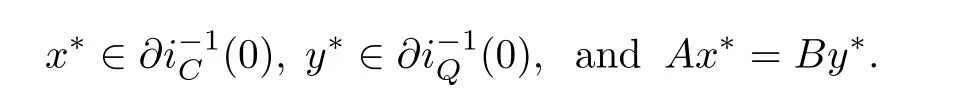
Hence the following result can be obtained from Theorem 2.1 immediately.
Theorem 4.1Let H1,H2,F,C,Q,h,g,A,B,A?,B?,,RλhRλgbe the same as above.Denote by C1=C,Q1=Q.For given x1∈C1and y1∈Q1,let the iterative sequence{xn}and{yn}be generated by
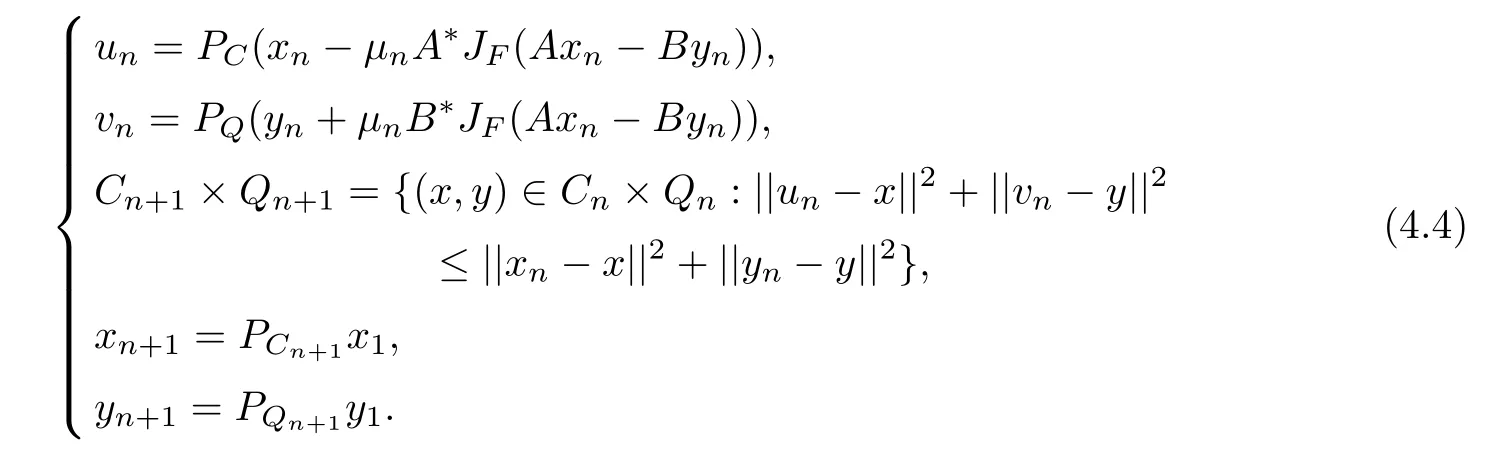
If the solution set ?2:={(p,q)∈C×Q,Ap=Bq}of(SEVIP)(4.3)is nonempty and the following condition is satisfed

then the sequence{xn,yn}converges strongly to some point(x?,y?)∈?2.
[1]Censor Y,Elfving T.A multiprojection algorithm using Bregman projections in a product space.Numer Algorithms,1994,8:221–239
[2]Byrne C.Iterative oblique projection onto convex subsets and the split feasibility problem.Inverse Problem, 2002,18:441–453
[3]Censor Y,Bortfeld T,Martin N,Trofmov A.A unifed approach for inversion problem in intensitymodulated radiation therapy.Phys Med Biol,2006,51:2353–2365
[4]Censor Y,Elfving T,Kopf N,Bortfeld T.The multiple-sets split feasiblility problem and its applications. Inverse Problem,2005,21:2071–2084
[5]Censor Y,Motova A,Segal A.Perturbed projections ans subgradient projiections for the multiple-sets split feasibility problem.J Math Anal Appl,2007,327:1244–1256
[6]Xu H K.A variable Krasnosel’skii-Mann algorithm and the multiple-sets split feasibility problem.Inverse Problem,2006,22:2021–2034
[7]Yang Q.The relaxed CQ algorithm for solving the split feasibility problem.Inverse Problem,2004,20: 1261–1266
[8]Zhao J,Yang Q.Several solution methods for the split feasibility problem.Inverse Problem,2005,21: 1791–1799
[9]Chang S S,Cho Y J,Kim J K,Zhang W B,Yang L.Multiple-set split feasibility problems for asymptotically strict pseudocontractions.Abst Appl Anal,2012,2012:Article ID 491760
[10]Chang S S,Wang L,Tang Y K,Yang L.The split common fxed point problem for total asymptotically strictly pseudocontractive mappings.J Appl Math,2012,2012:Article ID 385638
[11]MoudafA.A relaxed alternating CQ algorithm for convex feasibility problems.Nonlinear Anal,2013,79: 117–121
[12]MoudafA,Al-Shemas Eman.Simultaneouss iterative methods forsplit equality problem.Trans Math Prog Appl,2013,1:1–11
[13]MoudafA.Split monotone variational inclusions.J Optim Theory Appl,2011,150:275–283
[14]Takahashi W.Iterative methods for split feasibility problems and split common null point problems in Banach spaces//The 9th International Conference on Nonlinear Analysis and Convex Analysis.Thailand, Jan:Chiang Rai,2015:21–25
[15]Blum E,Oettli W.From optimization and variational inequalities to equilibrium problems.Math Stud, 1994,63:123–145
[16]Censor Y,Segal A.The split common fxed point problem for directed operators.J Convex Analysis,2009, 16:587–600
[17]Eslamian M,Latif A.General split feasibility problems in Hilbert spaces.Abst Appl Anal,2013,2013: Article ID 805104
[18]Chen R D,Wang J,Zhang H W.General split equality problems in Hilbert spaces.Fixed Point Theory Appl,2014,2014:35
[19]Chuang C S.Strong convergence theorems for the split variational inclusion problem in Hilbert spaces. Fixed Point Theory Appl,2013,2013:350
[20]Chang S S,Wang L.Strong convergence theorems for the general split variational inclusion problem in Hilbert spaces.Fixed Point Theory Appl,2014,2014:171
[21]Chang S S,Agarwal Ravi P.Strong convergence theorems of general split equality problems for quasinonexpansive mappings.J Ineq Appl,2014,2014:367
[22]Chang S S,Wang L,Tang Y K,Wang G.Moudaf’s open question and simultaneous iterative algorithm for general split equality variational inclusion problems and general split equality optimization problems. Fixed Point Theory Appl,2014,2014:215
[23]Naraghirad E.On an open question of Moudaffor convex feasibility problem in Hilbert spaces.Taiwan J Math,2014,18(2):371–408
[24]Tang J F,Chang S S,Liu M.General split feasibility problems for two families of nonexpansive mappings in Hilbert spaces.Acta Math Sci,2016,36B(2):602–613
?Received July 17,2015;revised April 18,2016.This work was supported by the National Natural Science Foundation of China(11361070)and the Natural Science Foundation of China Medical University,Taiwan.
?Corresponding authors:Shih-sen CHANG.
 Acta Mathematica Scientia(English Series)2016年6期
Acta Mathematica Scientia(English Series)2016年6期
- Acta Mathematica Scientia(English Series)的其它文章
- NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS?
- THREE SOLUTIONS FOR A FRACTIONAL ELLIPTIC PROBLEMS WITH CRITICAL AND SUPERCRITICAL GROWTH?
- SHARP ESTIMATES OF ALL HOMOGENEOUS EXPANSIONS FOR A SUBCLASS OF QUASI-CONVEX MAPPINGS OF TYPE B AND ORDER α IN SEVERAL COMPLEX VARIABLES?
- MULTIPLICITY RESULTS FOR A NONLINEAR ELLIPTIC PROBLEM INVOLVING THE FRACTIONAL LAPLACIAN?
- EXISTENCE AND UNIQUENESS OF NON-TRIVIAL SOLUTION OF PARABOLIC p-LAPLACIAN-LIKE DIFFERENTIAL EQUATION WITH MIXED BOUNDARIES?
- PROPERTIES OF THE MODIFIED ROPER-SUFFRIDGE EXTENSION OPERATORS ON REINHARDT DOMAINS?
