b-度量空間中壓縮型映象的公共不動點定理

劉麗亞,谷峰

(杭州師范大學數(shù)學系,浙江 杭州 310036)

b-度量空間中壓縮型映象的公共不動點定理

劉麗亞,谷峰

(杭州師范大學數(shù)學系,浙江 杭州 310036)

在完備的b-空間中,建立一個壓縮型映象,研究公共不動點的存在性和唯一性,得到了一個新的公共不動點定理.舉例證明了在b-空間中的新結果,改進了當前文獻中的結果.

完備b-空間;壓縮映象;公共不動點;弱相容

1 引言和預備知識

Czerwik在文獻[1-2]中介紹了b-度量空間的概念,最近,文獻[3-13]在b-度量空間中研究了滿足一定壓縮條件的非線性算子的不動點的存在性問題,得到了一些新結果.

受上述文獻的啟發(fā),本文介紹b-度量空間的定義,主要在完備b-度量空間中研究壓縮型映射不動點存在性問題,得到了幾個新的不動點定理,本文的結果推廣了一些已知的相關結果,而且也是度量空間中某些經(jīng)典結果在b-度量空間的進一步推廣.在介紹主要結果之前,先介紹一些基本概念和已知結果.

定義1.1[1]設X是一非空集,令d：X×X→R+滿足：

(b-1)d(x,y)=0,若x=y;

(b-2)d(x,y)=d(y,x),?x,y∈X且x≠y;

(b-3)d(x,y)≤s(d(x,z)+d(z,y)),?x,y,z∈X,s≥1.

則稱函數(shù)d是X上的一個b-度量,或稱d是X上的一個b-度量,稱(X,d)為b-度量空間,s為其系數(shù).

定義1.2[8]設X是一非空集,(X,d)是b-度量空間,點列{xn}?X.

引理1.1[8]設X是一非空集,(X,d)是具有參數(shù)s≥1的b-度量空間,序列{xn},{yn}?X分別收斂于X中的兩點x,y,則有

特別的,當x=y時,有l(wèi)imn→∞d(xn,yn)=0.此外,?z∈X,有

引理1.2[8]設(X,d)是一個b-度量空間,序列{xn},{yn}?X,如果

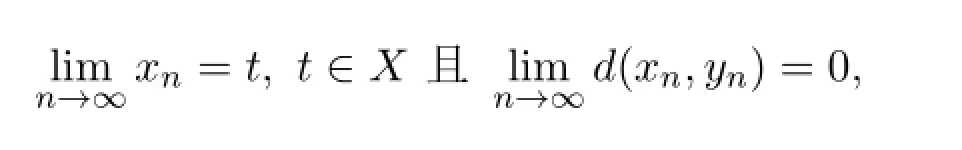
則

注 1.1[14]設X是一非空集,(X,d)是b-度量空間.在X中存在三個偏序關系和令A,B,C,D,E,F：X→X是X中的六個自映象.

其中x∈X.

定義1.3[14]設X是一非空集,(X,d)是b-度量空間,是X上的一偏序關系.序列{xn},{yn}?X分別收斂于X中的兩點x,y,即

定義1.4[14]設是定義在b-度量空間(X,d)中的兩個偏序關系.令A,B,C,D,f,g：X→X是X中的六個自映象.稱f是(A,B,C,D,g?1,?2)穩(wěn)定的,如果滿足下列條件：

定義1.5[13]b-度量空間(X,d)中的自映象對(f,g)稱為是弱相容的,若fx=gx,x∈X,就有fgx=gfx,即d(fx,gx)=0?d(fgx,gfx)=0.

2 主要內(nèi)容

該文處處假設以下兩種類型的函數(shù)：

定理2.1設X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的三個偏序關系.函數(shù)f,g,S,T,A,B,C,D,E,F,I：X→X為X上的11個的自映象,其中I表示X中的恒等映象,且滿足以下條件：

定理2.2設X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的三個偏序關系.函數(shù)f,g,S,T,A,B,C,D,E,F,I：X→X為X上的11個自映象,其中I表示X中的恒等映象,且滿足以下條件：

如果f,g,S和T其中之一在(X,d)上是閉區(qū)間,則當(f,S)和 (g,T)是弱相容時,這時f,g,S,T有唯一的公共不動點.

證明與定理2.1的證明方法類似,同理也可證得.

定義2.1[14]設X是一非空集,(X,d)是b-度量空間,其中是定義在X上的兩個偏序關系.令A,B,C,D,f：X→X是X中的5個自映象.稱g是 (A,B,C,D,f)穩(wěn)定的,如果滿足下列條件：

注 2.1在定理2.1中,令函數(shù)S,T為X中的恒等映像I.即可得到以下結果.

推論2.1設X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的三個偏序關系.函數(shù)f,g,A,B,C,D,E,F,I：X→X為X上的9個自映象,其中I表示X中的恒等映象,且滿足以下條件：

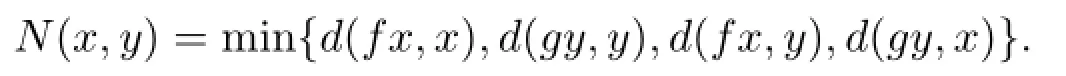
如果f和g其中之一在(X,d)中是閉區(qū)間,則f,g有唯一的公共不動點.

注 2.2[5]在推論2.1中,令函數(shù)f,g為X中的同一個映像T,即可得到以下結果.

推論 2.2設X是一非空集,(X,d)是完備的b-度量空間,s≥1為其系數(shù).其中為(X,d)上的兩個偏序關系.函數(shù)T,A,B,C,D：X→X為X上的五個自映象,且滿足以下條件：

3 非線性方程解的唯一性

令推論2.1中的A,B,C,D,E,FI為X中的恒等映象,定義偏序關系

在以上情形中,我們可以考慮方程組的解的存在性情況.

規(guī)定X=C[0,T]為所有[0,T]上的連續(xù)函數(shù)全體,現(xiàn)在我們考慮下列積分方程組在[0,T]中解的存在情況.

這里函數(shù)G1,G2：[0,T]×[0,T]×X→R+.

在X中定義b-度量為

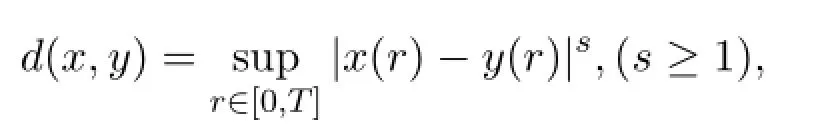
其中2s-1為其系數(shù).

假設在b-度量空間(X,d)中滿足以下條件：

定理3.1在條件(a)-(c)下,可證得方程(32)在X中存在唯一解.

[1]Czerwik S.Contraction mappings in b-metric spaces[J].Acta Math.Inform.Univ.Ostrav.1993,1,5-11.

[2]Czerwik S.Nonlinear set-valued contraction mappings in b-metric spaces[J].Atti.Sem.Math.Fis.Univ.Modena.,1998,46(2)：263-276.

[3]Aghajani A,Abbas M,Roshan JR.Common fixed point of generalized weak contractive mappings in partially ordered b-metric spaces[J].Math.Slovaca,2014,4：941-960.

[4]Akkouchi M.Common fixed point theorems for two self mappings of a b-metric space under an implicit relation[J].Hacet.J.Math.Stat.,2011,40(6)：805-810.

[5]Bota M F,Karapinar E,Mlesnite O.Ulam-Hyers stability results for fixed point problems via φ-ψcontractive mapping in b-metric space[J].Abstr.Appl.Anal.,2013,Article ID 825293.

[6]Bota M F,Karapinar E.A note on Some results on multi-valued weakly Jungck mappings in b-metric space[J].Cent.Eur.J.Math.,2013,11：1711-1712.

[7]Aydi H,Bota M F,Karapinar E,et al.A common fixed point for weak φ-contractions on b-metric spaces[J].Fixed Point Theory 2012,13(2)：337-346.

[8]Boriceanu M,Bota M,Petrusel A.Multi-valued fractals in b-metric spaces[J].Cent.Eur.J.Math., 2010,8(2)：367-377.

[9]Aydi H,Bota M,Karapinar E,et al.A common fixed point for weak φ-contractions on b-metric spaces[J].Fixed Point Theory,2012,13(2)：337-346.

[10]Bota M.Molnar A,Varga C.On Ekeland’s variational principle in b-metric spaces[J].Fixed Point Theory, 2011,12(2)：21-28.

[11]Boriceanu M.Strict fixed point theorems for multi-valued operators in b-metric spaces[J].International Journal of Modern Mathematics,2009,4(3)：285-301.

[12]Aghajani A,Abbas M,Roshan J R.Common fixed point of generalized weak contractive mappings in partially ordered b-metric spaces[J].Math.,2012,64(1)：941-960.

[13]Roshan J R,Shobkolaei N,Sedghi S,et al.Common fixed point of four maps in b-metric spaces[J].Hacettepe Journal of Mathematics and Statistics,2014,43(4)：613-624.

[14]Jleli,Samet.A fixed point problem under two constraint inequalities[J].Fixed Point Theory and Applications,2016,2016(1)：1-14.

A common fixed point theorem of contractive mappings in b-metric spaces

Liu Liya,Gu Feng
(Department of Mathematics,Hangzhou Norm University,Hangzhou 310036,China)

In complete b-metric spaces,by establishing a new contractive condition,we obtain the existence and the uniqueness of fixed point theorem,We also provide illustrative examples in support of our new results in b-metric spaces.The result obtained in this paper differ from the recent relative results in the literature.

complete b-metric space,contractive mappings,common fixed point,weak compatible

O178

A

1008-5513(2016)06-0591-15

10.3969/j.issn.1008-5513.2016.06.005

2016-09-01.

國家自然科學基金(11071169);浙江省自然科學基金(Y6110287).

劉麗亞(1990-),碩士生,研究方向：應用非線性分析.

谷峰(1960-),教授,研究方向：應用非線性分析.

2010 MSC:47H10,54H25