SECONDARY CRITICAL EXPONENT AND LIFE SPAN FOR A DOUBLY SINGULAR PARABOLIC EQUATION WITH A WEIGHTED SOURCE?

Pan ZHENG(鄭攀)Department of Applied Mathematics,Chongqing University of Posts and Telecommunications,Chongqing 400065,ChinaE-mail:zhengpan@cqupt.edu.cnChunlai MU(穆春來)College of Mathematics and Statistics,Chongqing University,Chongqing 401331,ChinaE-mail:clmu2005@163.comXuegang HU(胡學(xué)剛)Department of Applied Mathematics,Chongqing University of Posts and Telecommunications,Chongqing 400065,ChinaE-mail:huxg@cqupt.edu.cnFuchen ZHANG(張付臣)College of Mathematics and Statistics,Chongqing Technology and Business University,Chongqing 400067,ChinaE-mail:zhangfuchen1983@163.com

?

SECONDARY CRITICAL EXPONENT AND LIFE SPAN FOR A DOUBLY SINGULAR PARABOLIC EQUATION WITH A WEIGHTED SOURCE?

Pan ZHENG(鄭攀)
Department of Applied Mathematics,Chongqing University of Posts and Telecommunications,Chongqing 400065,China
E-mail:zhengpan@cqupt.edu.cn
Chunlai MU(穆春來)
College of Mathematics and Statistics,Chongqing University,Chongqing 401331,China
E-mail:clmu2005@163.com
Xuegang HU(胡學(xué)剛)
Department of Applied Mathematics,Chongqing University of Posts and Telecommunications,Chongqing 400065,China
E-mail:huxg@cqupt.edu.cn
Fuchen ZHANG(張付臣)
College of Mathematics and Statistics,Chongqing Technology and Business University,Chongqing 400067,China
E-mail:zhangfuchen1983@163.com

AbstractThis paper deals with the Cauchy problem for a doubly singular parabolic equation with a weighted source

where N≥1,1＜p＜2,m＞max{0,3?p?pN}satisfying 2＜p+m＜3,q＞1,andα＞N(3?p?m)?p.We give the secondary critical exponent on the decay asymptotic behavior of an initial value at in finity for the existence and non-existence of global solutions of the Cauchy problem.Moreover,the life span of solutions is also studied.

Key wordslife span;secondary critical exponent;doubly singular parabolic equation; weighted source;blow-up

2010 MR Subject Classi fi cation35K55;35K65;35B40

?Received September 15,2014;revised November 20,2014.The first author was partially supported by the Doctor Start-up Funding and Natural Science Foundation of Chongqing University of Posts and Telecommunications(A2014-25 and A2014-106);partially supported by Scienti fi c and Technological Research Program of Chongqing Municipal Education Commission(KJ1500403)and the Basic and Advanced Research Project of CQCSTC(cstc2015jcyjA00008);the second author was partially supported by NSFC(11371384);the fourth author was partially supported by NSFC(11426047),the Basic and Advanced Research Project of CQCSTC(cstc2014jcyjA00040)and the Research Fund of Chongqing Technology and Business University(2014-56-11).

1 Introduction

In this paper,we consider the following Cauchy problem for the doubly singular parabolic equation with a weighted source

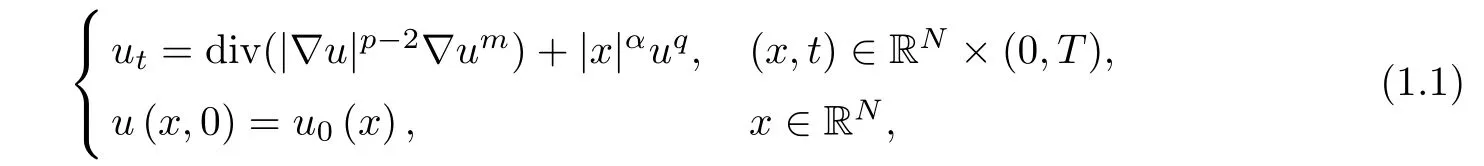
One of the particular features of problem(1.1)is that the equation is doubly singular.Hence,there is no classical solution in general and we introduce the following de finition of weak solution.

De finition 1.1A non-negative function u(x,t)de fined in RN×(0,T)is called a weak solution of Cauchy problem(1.1),if for every bounded open set ? with smooth boundary??,

for all 0≤t0≤t≤T and all test functionMoreover,

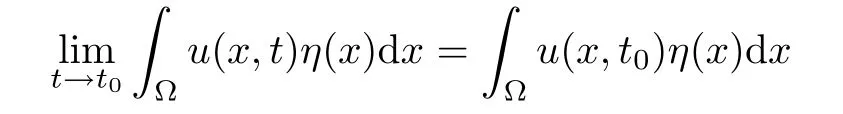
We denote

then T?is called the life span of the solution u(x,t).If T?=∞,the solution u(x,t)is global.

On the other hand,if T?＜∞,the solution u(x,t)is called blow-up in finite time T?.In[16],Liu and Wang obtained thatis the critical Fujita exponent of(1.1).Precisely,has the following properties:ifthen all solutions blow up in finite time,while both global and blow-up solutions exist ifThe critical Fujita exponent was first established by Fujita in[3].In recent years,the critical Fujita exponent for the parabolic equations were studied by many authors(see[1,2,4,7,14,15,18,23-28,30]and references therein).

In this paper,we mainly investigate the behavior of solution u(x,t)to(1.1),when the initial data u0(x)has slow decay near x=∞.For instance,in the following case

we are interested in the question of global existence and non-global existence of solutions to(1.1)in terms of M and a.The study of the secondary critical exponent originated from Lee and Ni in[11].In recent years,the secondary critical exponent and life span for the parabolic equations were also studied by many authors(see[5,8-10,12,19-22,35]and references therein).In particular,for the case p=2 and α=0 in(1.1),Guo et al.[6]obtained the secondary critical exponent for the following fast di ff usion equation in high dimensions

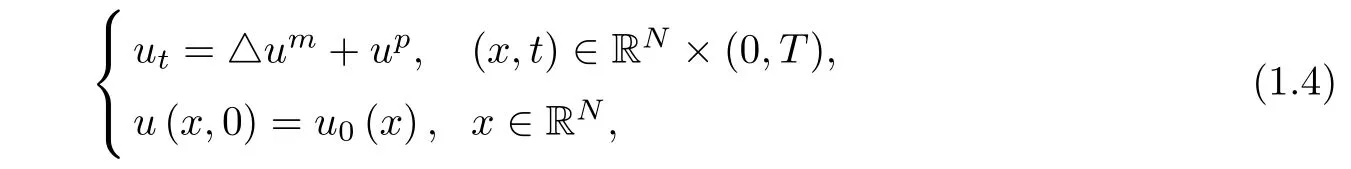
In[17],for the case α=0 in(1.1),Mi et al.studied a new critical exponent and life span for the following doubly degenerate p-Laplacian equation with slow decay initial values

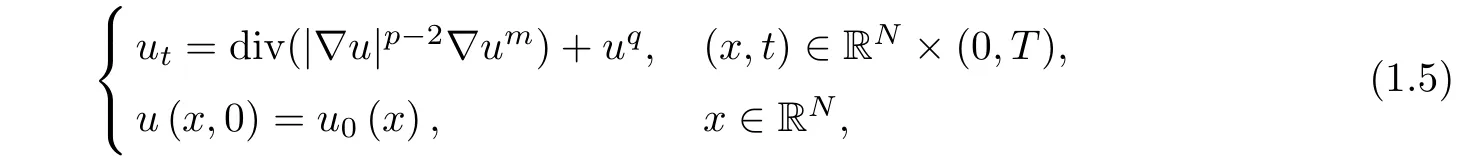
where p＞2,q＞1,m＞1 and obtained thatis secondary critical exponent of

Recently,for the case m=1 in(1.1),Yang et al.[29]also obtained thatthe secondary critical exponent,and gave estimates of life span for the case α=0.Moreover,for the degenerate parabolic equation with a weighted source,the reader can see the references[13,34].

Motivated by the above works,we investigate the secondary critical exponent and life span of solutions to the doubly singular parabolic problem(1.1).Due to the presence of double singularity,we have to overcome some new difficulties for problem(1.1).

Throughout the paper,we denote by Cb(RN)the space of all bounded continuous functions in RN.For a≥0,we de fi ne

Moreover,we let

Remark 1.1Since α＞N(3?p?m)?p,it is easy to see that

Our main results of this paper are stated as follows.

Theorem 1.1For q＞q?c,assume that u0(x)∈Φawith a∈(0,a?c),then the solution u(x,t)of problem(1.1)blows up in finite time.

Remark 1.2It follows from Theorems 1.1 and 1.2 that the numbergives another cut-o ff between the blow-up and global existence cases under the condition q＞Therefore,the numberis so-called new secondary critical exponent of problem(1.1).Unfortunately,for the critical casewe do not know whether the solution of(1.1)exists globally or blows up in finite time,moreover,we also do not give the asymptotic behavior of global solutions for problem(1.1)in this paper,so we will study them in our forthcoming work.

Remark 1.3When m=1,the results of Theorems 1.1 and 1.2 are consistent with those in[29].

Finally,we also consider the life span of blow-up solution for problem(1.1),and give the estimates of the life span.

Theorem 1.3Suppose that u0(x)=λ?(x)with λ＞0,?(x)∈Cb(RN)and α=0.

(i)If‖?‖∝=?(0)＞0,then there exists λ1≥0 such that,and

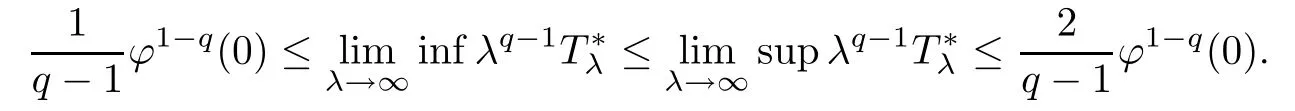
(ii)If‖?‖∝=then for any λ＞0 we havesatisfying

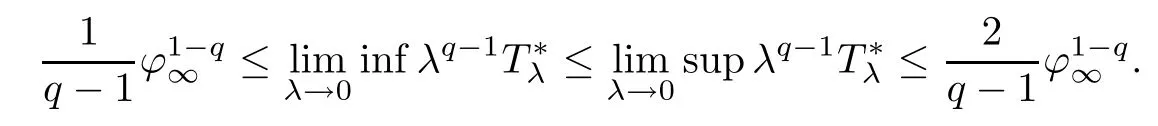
Remark 1.4Compared with those in[19,20],it follows from Theorem 1.3 that when α=0,the estimates of life spanare independent of the speed of di ff usion term,while it only depends on the power of the source term and initial data λ?(x).

Theorem 1.4Suppose that u0(x)=λ?(x)with λ＞0,?(x)∈Cb(RN)and α0.

(i)If‖?‖∝=?(0)＞0,then there exist λ1≥0 and a suitable positive constant

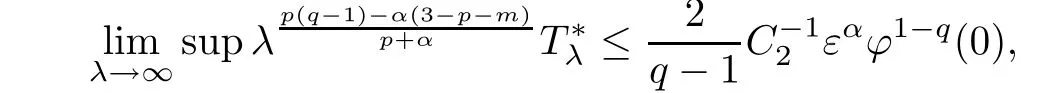
where the positive constants C1,C2are given in Section 2 below.

(ii)If‖?‖∝=then for any λ＞0,there exists a suitable positive constant

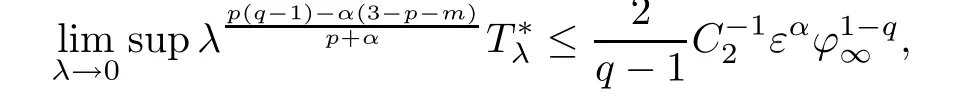
where the positive constants C1,C2are given in Section 2 below.

Remark 1.5In Theorem 1.4,we only give an upper estimate of life span for the case ofbut the lower estimate of the life span is an open problem.

This paper is organized as follows.In Section 2,by using the energy method,we shall obtain a blow-up condition,and prove Theorem 1.1.In Section 3,using the comparison principle,wecan construct a global supersolution to prove Theorem 1.2.Finally,we give the estimates of the life span,and prove Theorems 1.3 and 1.4 in Section 4.

2 Blow-up Case

In this section,by using energy methods,we will obtain a blow-up condition to(1.1).Therefore,we need to select a suitable test function as follows

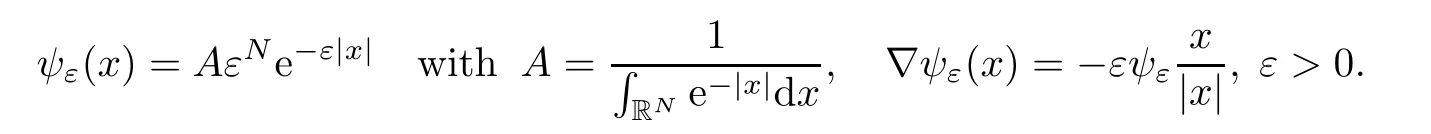
Proof of Theorem 1.1Suppose that u(x,t)is the solution of the Cauchy problem(1.1)and T is the blow-up time.Let

where 0＜3?p?m＜s＜1p,then we obtain

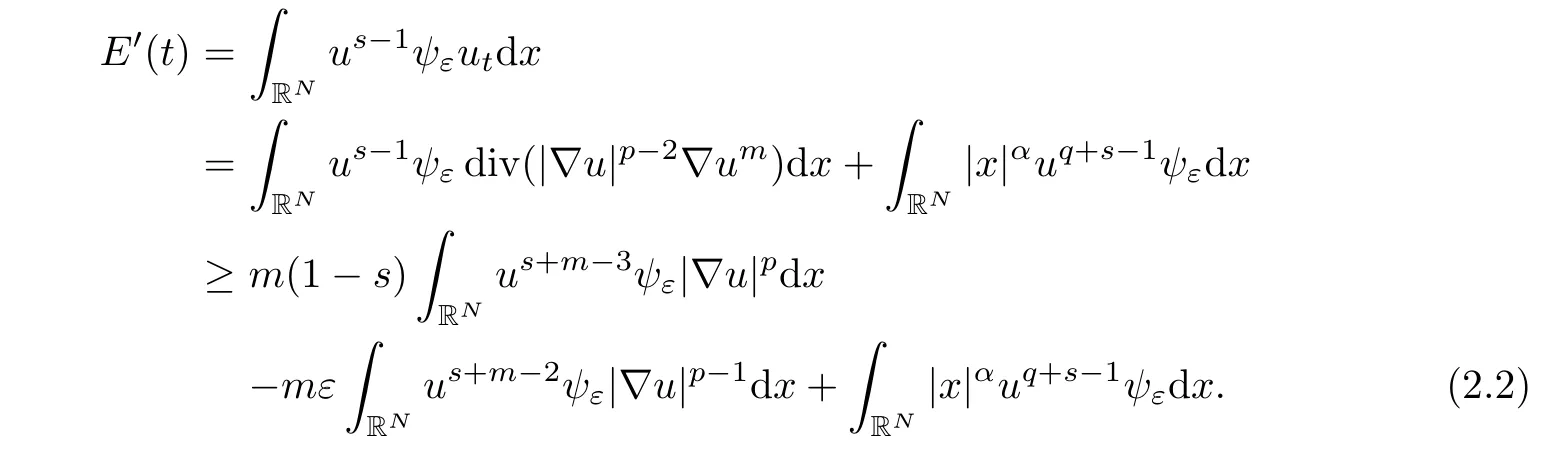
Using Young’s inequality,we have

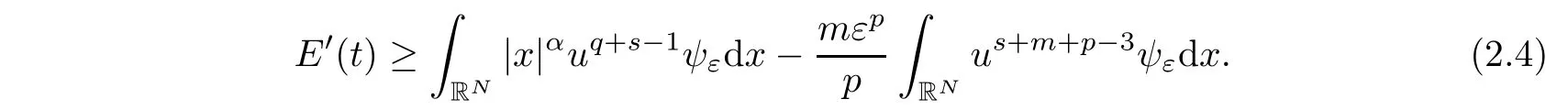
By using H?lder’s inequality,we obtain

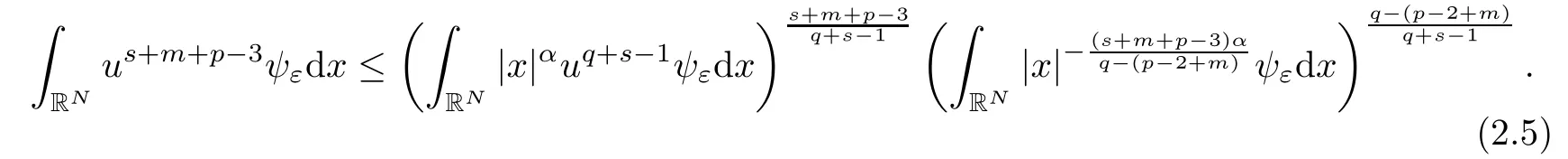
Therefore,by(2.4)and(2.5),we have

where

Applying H?lder’s inequality again,we obtain

where

Thus,it follows from(2.6)and(2.7)that

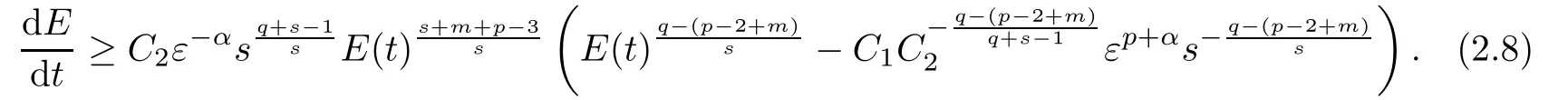
Therefore,we deduce from(2.8)that

as long as

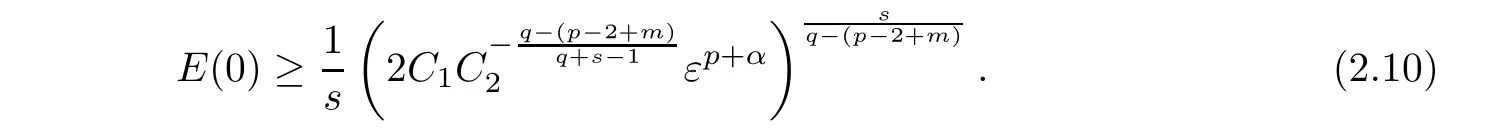
By(2.9),we have

Therefore,from(2.10)and(2.11),we obtain that u(x,t)blows up in finite timeand get an estimate on the blow-up time T of the solution u(x,t)as follows,

Finally,it remains to verify the blow-up condition(2.10).Since u0(x)∈Φafor some a∈there exist two positive constants M and R0＞1 such that u0(x)≥M|x|?afor all|x|≥R0,and we have

3 Global Existence

In this section,we shall prove Theorem 1.2 by constructing a global supersolution.

Proof of Theorem 1.2Similar to the arguments in[16],we will prove Theorem 1.2 by two cases:α≥0 and α＜0.

(i)We first consider the case of α≥0.Since ?(x)∈Φawiththere exists a constant K＞0 such that

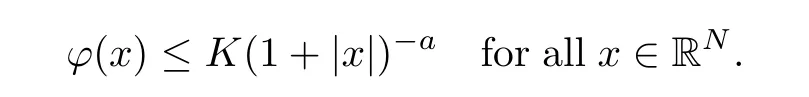
Let M＞K and consider the following Cauchy problem

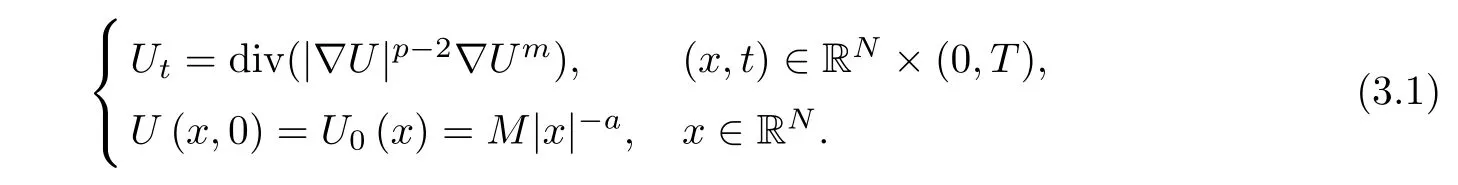
The existence and uniqueness of the solution to(3.1)were well established(see[31-33]).This solution UM,a(x,t)to(3.1)is given by the following form

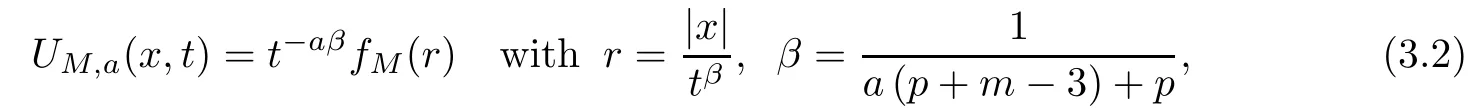
where the function fMis the positive solution of the problem

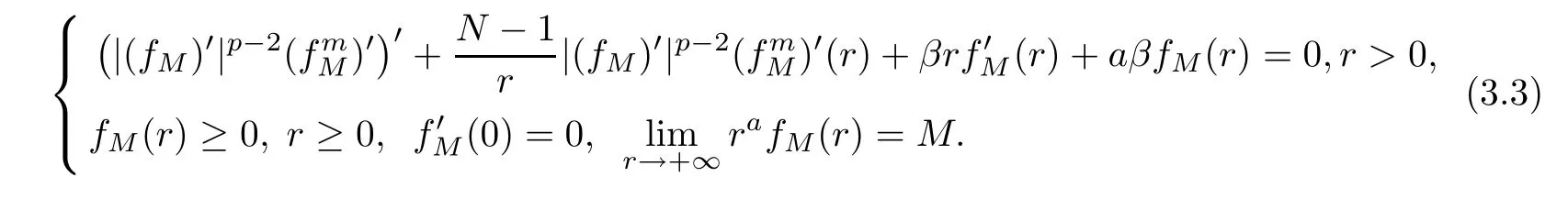
Let us begin with an estimate of UM,a(x,t).Since1＜p＜2,and α≥0,then we have

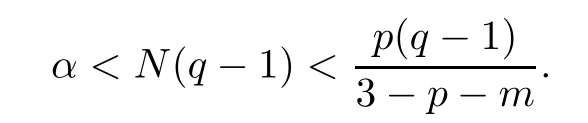
Therefore,there exists L=L(M,a)＞0 such that

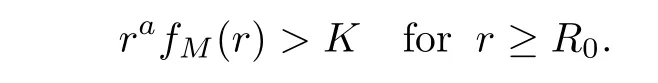
Set γ=fM(R0)=min{fM(r)|r∈[0,R0]}＞0,then it is easy to verify that ?(x)≤UM,a(x,t0)for all x∈RN,where t0∈(0,1)and

Let λ＞0,then w(x,t)=λUM,a(x,λp+m?3t+t0)is the solution of the following problem

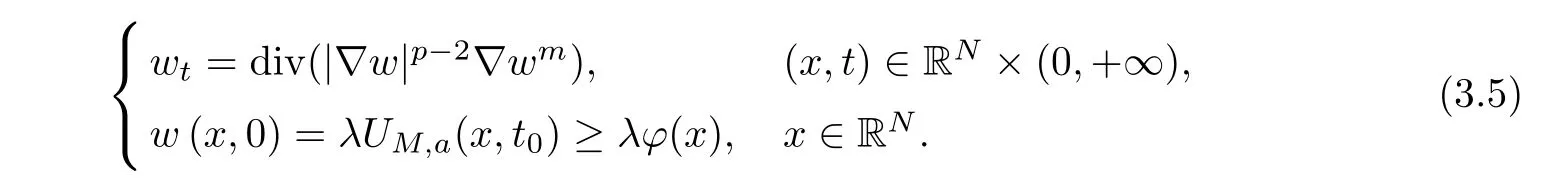
By(3.4),we have

Next,Set v(x,t)=A(t)w(x,B(t)),where A(t)and B(t)are solutions of the following problem

We shall prove that there exists a positive constant λ0=λ0(?)such that problem(3.6)has a global solution(A(t),B(t))with A(t)bounded in(0,∞)if λ∈(0,λ0).In fact,according to the standard theory of ODE,then the local existence and uniqueness of solution(A(t),B(t))of(3.6)holds.By(3.6),we have A′(t)＞0,A(t)＞1 for t＞0,furthermore,the solution is continuous as long as the solution exists and A(t)is finite.

From(3.6),when A(t)exists in[0,t],then B(t)is uniquely de fined by

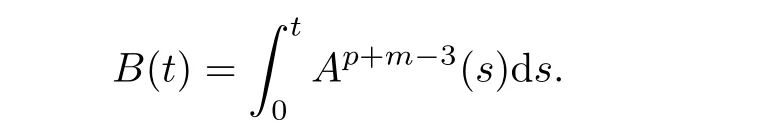
Since 2＜p+m＜3 and A(t)is increasing,we obtain

It follows from(3.6)to(3.8)that

Let λ0=λ0(?)be a positive constant de fined by

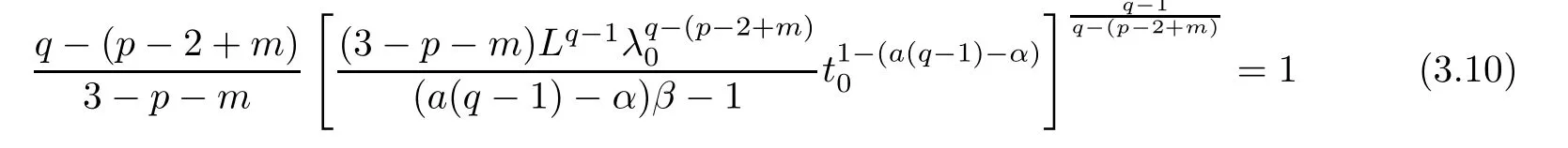
and for λ∈(0,λ0),we set

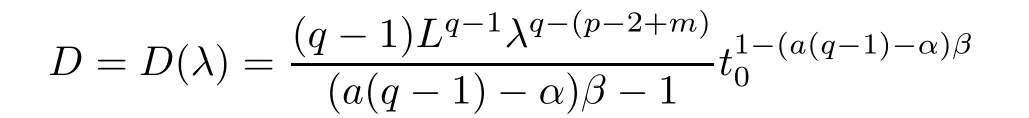
and

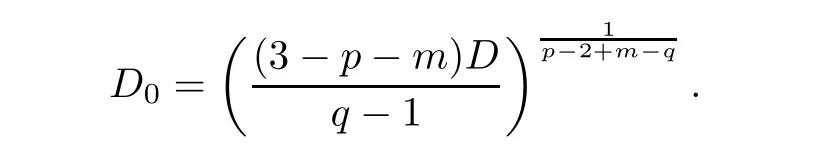
We introduce the function

Note that D＞0 and D0∈(1,+∞).Moreover,F(x)is continuous on(1,+∞)such that F(1)＜0,F(+∞)=?∞,anddue to λ∈(0,λ0).Finally,we claim thatA(t)＜D0as long as A(t)exists.Otherwise,if A(t)≥D0for some t,then there exists s≤t such that A(s)=D0and so F(A(s))＞0,which is contradiction to(3.9).

By a direct calculation,we obtain that v(x,t)satisfies

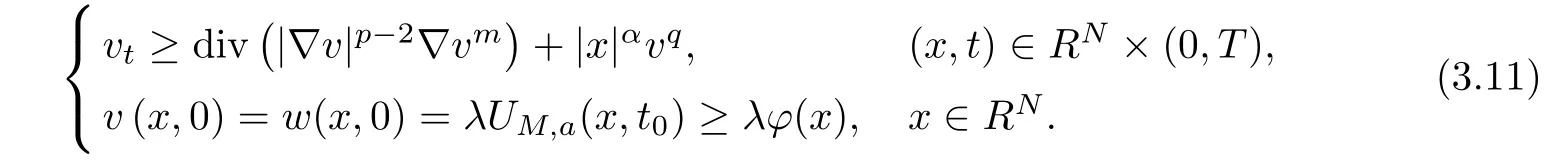
Therefore,by the comparison principle and(A(t),B(t))exists globally,we deduce that the solution u(x,t)of(1.1)with u0(x)=λ?(x)also exists globally and u(x,t)≤v(x,t)in RN×(0,T)if λ∈(0,λ0),where λ0is de fined as(3.10).

(ii)On the other hand,we shall discuss the case of α＜0 by constructing a global solution.Let

where

and g(ξ)satisfies the following problem

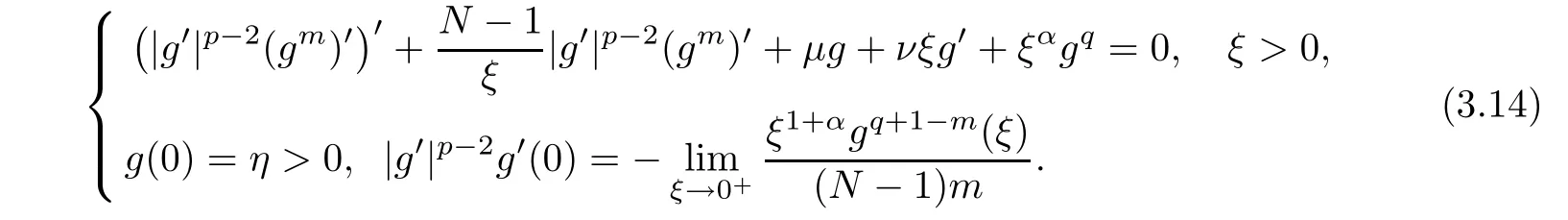
Then it is easy to check that u(x,t)satisfies the equation in(1.1).Moreover,it follows from Lemma 2 and Lemma 3 in[16]that for η＞0 sufficiently small,there exists a constant C0= C0(η)＞0 such that the unique positive solution g(ξ)∈C2[0,∞)of(3.14)satisfiesg′(ξ)＜0,and

Moreover,similar to arguments in[29],there exist constants M1,M2＞0 such that|g(ξ)|≤

According to the properties of g,then there exists λ0＞0 such thatTherefore,by the comparison principle,we obtain that the function u(x,t)is a global supersolution of(1.1).The proof of Theorem 1.2 is completed.

4 Life Span

In this section,we first give the estimates of the life spanof the solution to(1.1)both from below and above when α=0.Moreover,we also give the upper estimate of life spanwhen α0.To do this,we shall give a lower estimate of the life spanto(1.1)with α=0,which needs the following lemma.

Lemma 4.1(see[12,21])Let f(t)＞0 be a bounded continuous function of t＞0.Then the solution of the Cauchy problem

is given by

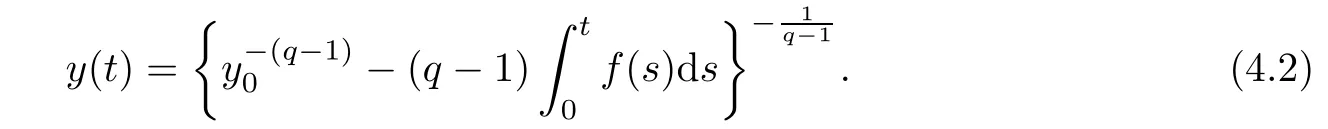
In order to obtain an upper estimate ofwe denote

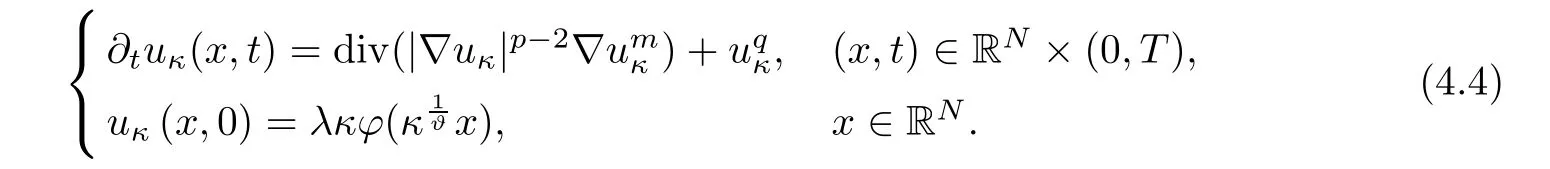
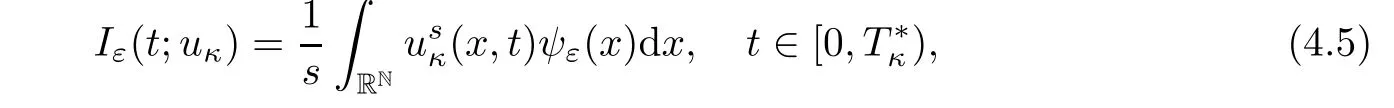
Lemma 4.2If Iε(0;uκ(x,0))satisfies

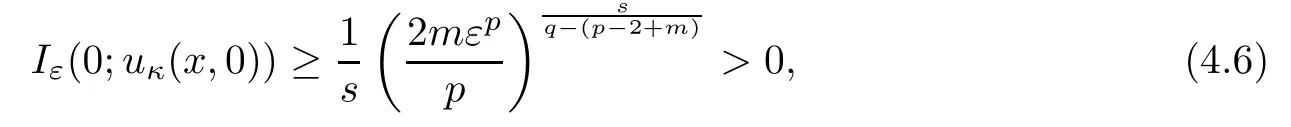
then the solution uκ(x,t)of(4.4)blows up in finite time,and we have

ProofThe proof is same as that in the proof of Theorem 1.1 for α=0 withand C2=1,thus we refrain us from repeating it here.

Proof of Theorem 1.3Step 1Let f(t)=1 and y0=‖u0‖∝=λ‖?(x)‖∝in Lemma 4.1,then y(t)is a supersolution of(1.1).By using the comparison principle,the solution u(x,t)of(1.1)exists at least up to the existence time of y(t),and we obtain

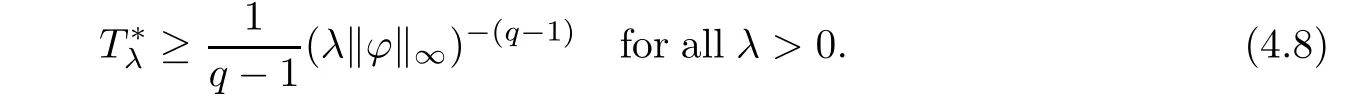
Step 2For the case‖?‖∝=?(0)＞0.Taking κ=λ?1in(4.3),and since

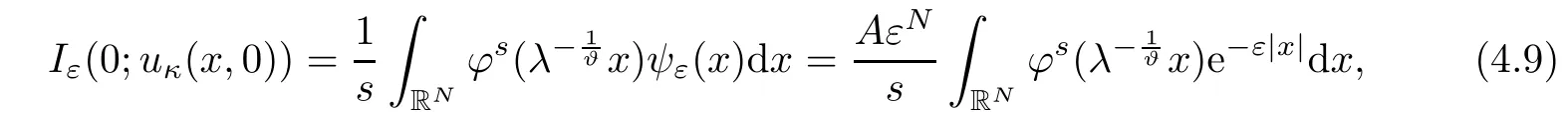
then for any fixed ε＞0,we have

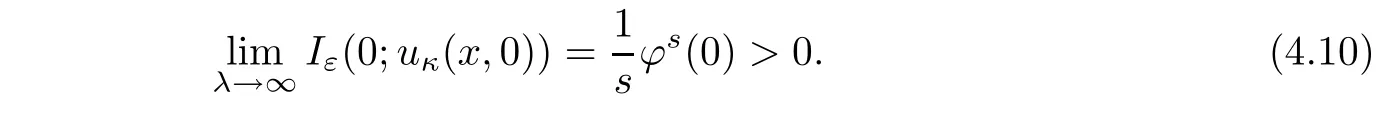
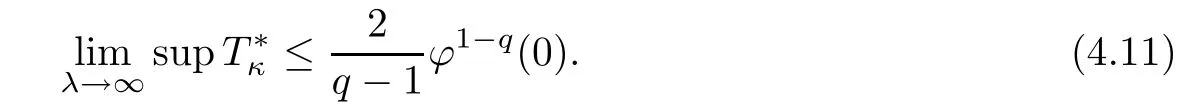
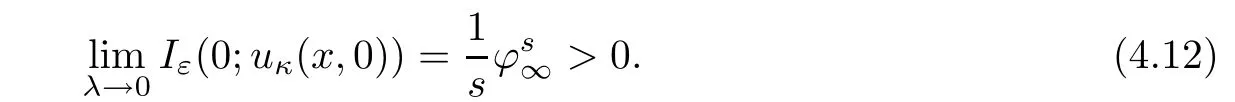
Hence,for any λ＞0,we choose a suitable positive constant ε such that(4.6)holds,by Lemma 4.2 and a similar method in Step 2,then we have

It follows from(4.8)and(4.13)that assertion(ii)holds.The proof of Theorem 1.3 is completed.

Finally,we will consider the life span of the blow-up solution to(1.1)with α0,and give the upper estimate of the life spanTo do this,we Let

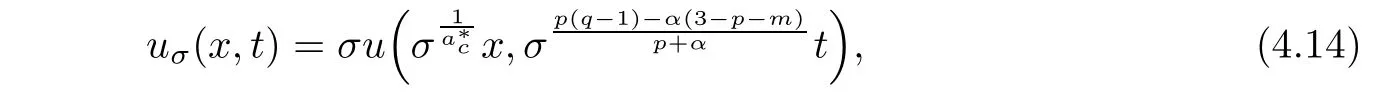
Lemma 4.3If Jε(0;uσ(x,0))satisfies

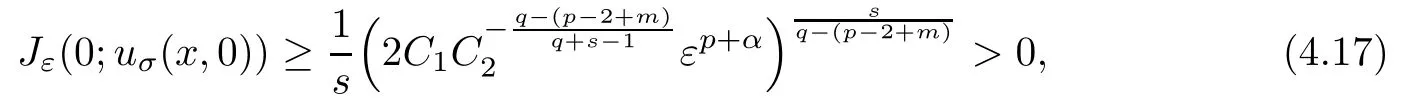
where C1and C2are de fined in Section 2,then the solution uσ(x,t)of(4.15)blows up in finite time,and we have

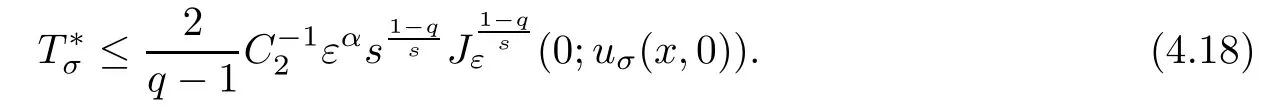
ProofThe proof is similar to that in Theorem 1.1,we omit it here.?

Proof of Theorem 1.4Step 1For the case‖?‖∝=?(0)＞0.Taking σ=λ?1in(4.14),and since

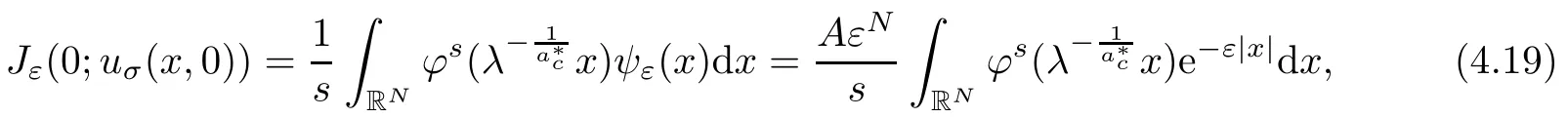
then for any fixed ε＞0,we have

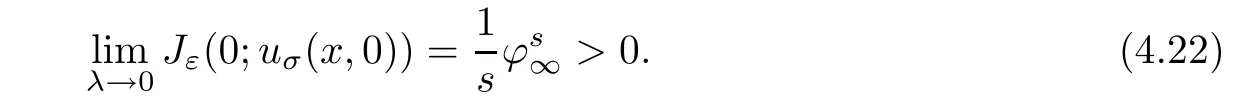
Hence,for any λ＞0,we choose a suitable positive constant ε such that(4.17)holds,by Lemma 4.3 and a similar method in Step 1,then we have

Therefore,it follows from(4.23)that assertion(ii)holds.The proof of Theorem 1.4 is completed.

References

[1]Afanas’eva N V,Tedeev A F.Fujita-type theorems for quasilinear parabolic equations in the case of slowly decaying initial data.Mat Sb,2004,195:3-22(in Russian);Translation in Sb Math 2004,195:459-478

[2]Deng K,Levine H A.The role of critical exponents in blow-up theorems:the sequel.J Math Anal Appl,2000,243:85-126

[3]Fujita H.On the blowing up of solutions of the Cauchy problem for ut=?u+uα+1.J Fac Sci Univ Tokyo Sec A,1966,16:105-113

[4]Galaktionov V A.Blow-up for quasilinear heat equations with critical Fujita’s exponents.Proc Roy Soc Edinburgh Sect A,1994,124:517-525

[5]Gui C,Wang X.Life span of solutions of the Cauchy problem for a semi-linear heat equation.J Di ff erential Equations,1995,115:166-172

[6]Guo J S,Guo Y J.On a fast di ff usion equation with source.Tohoku Math J,2001,53:571-579

[7]Guo W,Wang Z J,Du R M,Wen L S.Critical Fujita exponents for a class of nonlinear convection-di ff usion equations.Math Meth Appl Sci,2011,34:839-849

[8]Huang Q,Mochizuki K,Mukai K.Life span and asymptotic behavior for a semilinear parabolic system with slowly decaying initial values.Hokkaido Math J,1998,27:393-407

[9]Kobayashi Y.The life span of blow-up solution for a weakly coupled system of reaction-di ff usion.Tokyo J Math,2001,24:487-498

[10]Kobayashi Y.The behavior of the life span for solutions to the system of reaction-di ff usion equations.Hiroshima Math J,2003,33:167-187

[11]Lee T Y,Ni W M.Global existence,large time behavior and life span on solutions of a semilinear Cauchy problem.Trans Amer Math Soc,1992,333:365-378

[12]Li Y H,Mu C L.Life span and a new critical exponent for a degenerate parabolic equation.J Di ff erential Equations,2004,207:392-406

[13]Li Z P,Du W J.Life span and secondary critical exponent for degenerate and singular parabolic equations.Annali di Matematica,2014,193:501-515

[14]Liang Z L.Critical exponents for the evolution p-Laplacian equation with a localized reaction.Indian J Pure Appl Math,2012,43:535-558

[15]Liu C C.Critical exponent for a quasilinear parabolic equation with inhomogeneous density in a cone.Monatsh Math,2012,165:237-249

[16]Liu X F,Wang M X.The critical exponent of doubly singular parabolic equations.J Math Anal Appl,2001,257:170-188

[17]Mi Y S,Mu C L,Zeng R.Secondary critical exponent,large time behavior and life span for a quasilinear parabolic equation with slowly decaying initial values.Z Angew Math Phys,2011,62:961-978

[18]Mochizuki K,Mukai K.Existence and nonexistence of global solutions to fast di ff usions with source.Methods Appl Anal,1995,2:92-102

[19]Mu C L,Li Y H,Wang Y.Life span and a new critical exponent for a quasilinear degenerate parabolic equation with slow decay initial values.Nonlinear Anal RWA,2010,11:198-206

[20]Mu C L,Zeng R,Zhou S M.Life span and a new critical exponent for a doubly degenerate parabolic equation with slow decay initial values.J Math Anal Appl,2011,384:181-191

[21]Mukai K,Mochizuki K,Huang Q.Large time behavior and life span for a quasilinear parabolic equation with slowly decaying initial values.Nonlinear Anal,2000,39:33-45

[22]Pinsky R G.The behavior of the life span for solution to ut=?u+a(x)upin Rd.J Di ff erential Equations,1998,147:30-57

[23]Qi Y W.The critical exponents of degenerate parabolic equations.Sci China Ser A,1994,38:1153-1162

[24]Qi Y W.The critical exponents of parabolic equations and blow-up in RN.Proc Roy Soc Edinburgh Sect A,1998,128:123-136

[25]Qi Y W,Wang M X.Critical exponents of quasilinear parabolic equations.J Math Anal Appl,2002,267:264-280

[26]Wang L S,Yin J X,Wang Z J.Large time behavior of solutions to Newtonian fi ltration equations with sources.Acta Math Scientia,2010,30B:968-974

[27]Wang Z J,Yin J X,Wang L S.Critical exponent for non-Newtonian fi ltration equation with homogeneous Neumann boundary data.Math Meth Appl Sci,2008,31:975-985

[28]Winkler M.A critical exponent in a degenerate parabolic equation.Math Meth Appl Sci,2002,25:911-925

[29]Yang J G,Yang C X,Zheng S N.Second critical exponent for evolution p-Laplacian equation with weighted source.Math Comput Modelling,2012,56:247-256

[30]Yin J X,Jin C H,Yang Y.Critical exponents of evolutionary p-laplacian with interior and boundary sources.Acta Math Scientia,2011,31B:778-790

[31]Zhao J N.The asymptotic behavior of solutions of a quasilinear degenerate parabolic equation.J Di ff erential Equations,1993,102:33-52

[32]Zhao J N.The Cauchy problem for ut=div(|?u|p?2?u)when 2n/(n+1)＜p＜2.Nonlinear Anal TMA,1995,24:615-630

[33]Zhao J N.On the Cauchy problem and initial traces for the evolution p-Laplacian equation with strongly nonlinear sources.J Di ff erential Equations,1995,121:329-383

[34]Zheng P,Mu C L.Global existence,large time behavior and life span for a degenerate parabolic equation with inhomogeneous density and source.Z Angew Math Phys,2014,65:471-486

[35]Zheng P,Mu C L,Liu D M,Yao X Z,Zhou S M.Blow-up analysis for a quasilinear degenerate parabolic equation with strongly nonlinear source.Abstr Appl Anal,2012,2012:1-19