度量空間上自映射有異狀點的一個充要條件

王理峰,石艷玲

(1.南京鐵道職業(yè)技術(shù)學(xué)院 社科部,江蘇 南京 210031; 2.鹽城工學(xué)院 基礎(chǔ)部,江蘇 鹽城 224051)

度量空間上自映射有異狀點的一個充要條件

王理峰1,石艷玲2

(1.南京鐵道職業(yè)技術(shù)學(xué)院 社科部,江蘇 南京 210031; 2.鹽城工學(xué)院 基礎(chǔ)部,江蘇 鹽城 224051)

設(shè)f是N維度量空間到自身的可降自映射,給出了f有異狀點的一個充要條件為存在鏈回歸點但不是周期點,且f的ω-極限集與周期點集的交非空．

周期點; 鏈回歸點;ω-極限集; 異狀點

0 引言

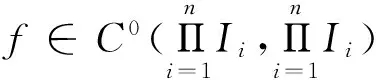
1 基本定義

設(shè)(X,ρ)為度量空間,其中ρ表示X上的度量．為了簡便通常將這個度量空間簡記為X,φ表示空集．f∈C0(X,X),f0表示恒等映射,對任意自然數(shù)n,定義fn=f°fn-1．如果映射f:X→X是一個連續(xù)映射,則稱f為空間X上的一個連續(xù)自映射．

定義1 設(shè)f是度量空間X上的一個連續(xù)自映射,x∈X:

1)點x成為f的一個周期點,如果?n∈N,使得fn(x)=x;點x成為f的一個n-周期點;如果?n∈N,使得fn(x)=x并且fk(x)≠x,(k=1,2,…,n-1)．f的周期點的全體記為P(f)．對于x∈X,集合O(x,f)={fn(x):n≥0}稱為x的軌跡,如果x∈P(f),則O(x,f)稱為一個周期軌跡．

2)點x稱為f的一個非游蕩點,如果?ε>0,?n∈N,?y∈Oε(x)使得fn(y)∈Oε(x)．并用Ω(f)表示f的所有非游蕩點的集合．

3)點y∈X稱為點x∈X關(guān)于f的ω-極限點,如果{fm(x)}有一個子列fmk(x)→y(k→+∞)．點x關(guān)于f的ω-極限點全體記為ω(x,f)．

4)點x稱為f的一個鏈回歸點,如果對?ε>0,存在自然數(shù)m和有限點列x0,x1,…,xm∈X,使得x0=xm=x并且ρ(f(xi),xi+1)<ε,i=0,1,2,…,m-1.并用CR(f)表示f的所有鏈回歸點的集合．

5)設(shè)x∈X,如果對x的任何鄰域V(x),存在自然數(shù)n,使得fn(x)∈V(x),則稱x為f的回歸點．記為R(f).

6)稱x∈X為f的幾乎周期點,如果對?ε>0,?n>0,s.t.,對任意整數(shù)q≥0存在自然數(shù)r,q≤r≤N+q,滿足ρ(fr(x),x)<ε,記f的幾乎周期點的全體為AP(f)．

7)設(shè)x∈X,如果滿足(i)x∈P(f),(ii)?P∈ω(x,f)∩P(f),(iii)?xk→P(k→∞)以及mk∈Z,使x=fmk(xk)(k=1,2,…,),則稱x為f的異狀點．

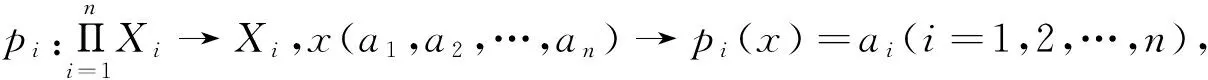
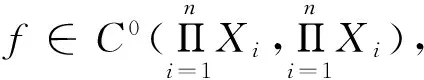
2 若干命題

命題1[1]設(shè)I=[0,1]是單位區(qū)間,f∈C0(I,I),則f有異狀點的充分必要條件是存在x∈CR(f)/P(f),使得ω(x,f)∩P(f)≠φ.

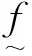
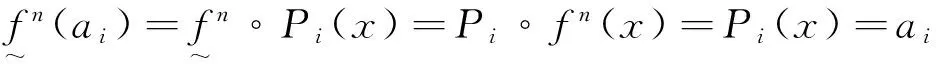
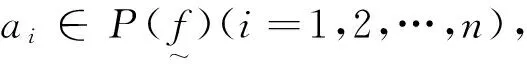
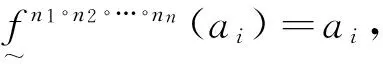
所以fn1°n2°…°nn(x)=x,即x∈P(f)．

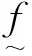
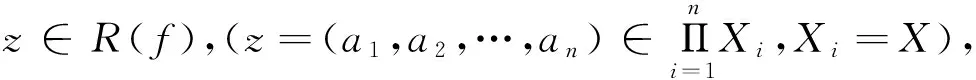
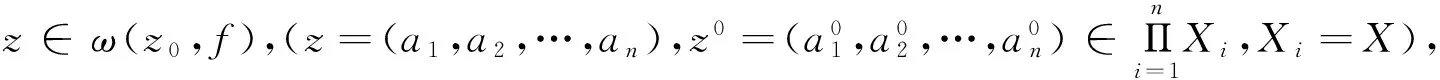
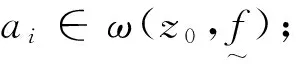
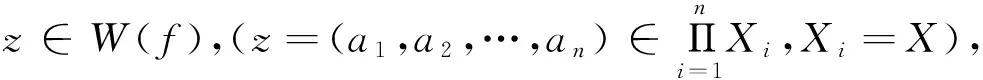
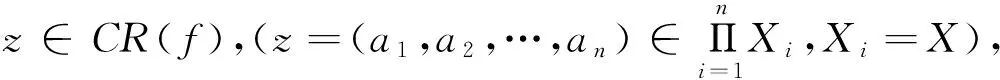
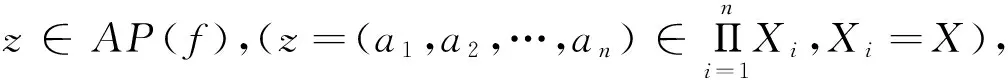
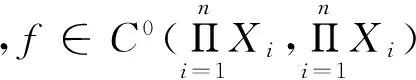
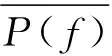
命題3的證明與文[3]中的證明類似．

3 定理及其證明

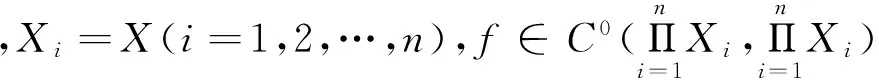
1)f有異狀點;

2)存在z∈CR(f)P(f),使得ω(z,f)∩P(f)≠φ．

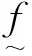
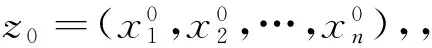
[1]熊金城.關(guān)于線段連續(xù)自映射鏈回歸點的一個注記[J]. 中國科學(xué)技術(shù)大學(xué)學(xué)報,1985(15):385-389.

[2]金渝光.有素周期點的一類正方形自映射[J]. 重慶師范大學(xué)學(xué)報:自然科學(xué)版,1993(2):51-54.

[3]杜瑞瑾.關(guān)于一類n維自映射的周期點集[J].重慶工商大學(xué)學(xué)報:自然科學(xué)版,2006,23(1):11-14

[4]劉喜玲.一類n維自映射有異狀點的特征[J].大慶師范學(xué)院學(xué)報,2007,27(2):12-14.

[5]張愛華,王堯.n維單體上的連續(xù)自映射有素周期點的條件[J]. 鞍山師范學(xué)院學(xué)報,2003(2):4-6.

[6]熊金城.線段映射的動力系統(tǒng):非游蕩集,拓?fù)潇匾约盎靵y[J].數(shù)學(xué)進(jìn)展,1988,17(1):1-11.

[7]金渝光.關(guān)于自映射的周期點集[J].重慶師范學(xué)院學(xué)報:自然科學(xué)版,1995,12(4):35-38.

[責(zé)任編輯：李春紅]

ANecessaryandSufficientConditionofHomoclinicPointsforaSelf-mappingontheMetricSpace

WANG Li-feng1,SHI Yan-ling2

(1.Dapartment of Social Science,Nanjing Railway Vocational and Technical College,Nanjing Jiangsu 210031,China)

(2.Basic Department,Yancheng Institute of Technology,Yancheng Jiangsu 224051,China)

Iffis a reduced self-mapping of theN-dimensional metric space to itself,Here this paper presents a necessary and sufficient condition forfwith homochinic points:Existences chain recurrent but not periodic point,and theω-limiting point set and periodic point set is nonempty intersection.

periodic point; chain recurrent;ω-limiting point; hoochinic point

2015-04-08

江蘇省普通高校研究生科研創(chuàng)新計劃項目(CXZZ12-0083); 江蘇省高校哲學(xué)社會科學(xué)基金項目(2014SJD283); 中國職教學(xué)會軌道交通專業(yè)委員會課題項目(201418)

王理峰(1981-),女,河南平頂山人,講師,碩士,研究方向為應(yīng)用數(shù)學(xué)及多元統(tǒng)計. E-mail:qingqingcaolf@163.com

O174

:A

:1671-6876(2015)03-0207-04