Three-dimensional simulation for problem of penetrative convection near the maximum density＊

HARFASH Akil J., ALSHARA Ahmed K.

1. Department of Mathematics, College of Sciences, University of Basrah, Basrah, Iraq,E-mail: akilharfash@gmail.com 2. Petroleum Department, College of Engineering, University of Misan, Misan, Iraq

Introduction

The phenomenon of penetrative convection, in which motion in a gravitationally unstable fluid layer penetrates into a stably-stratified layer, has attracted the attention of researchers in a number of disciplines including geophysics and astrophysics as well as fluid dynamics. A comprehensive book by Straughan[1]surveys areas in which this type of convection occurs and studies various properties of solutions to the mathematical models that have been used to describe this behavior. Mharzi et al.[2]dealt with applications in building design and heat transfer, Zhang and Schubert[3,4]were concerned with applications in astrophysics, and a very interesting application was highlighted in a study by Kaminski et al.[5], where they pointed out that penetrative convection above large lava flows may be responsible for enhancing the rise of volcanic plumes into the Earth’s stratosphere.

Mathematical models to describe penetrative convection, based on either an internal heat source or sink, or using a nonlinear density–temperature relationship in the buoyancy term, have been developed and analysed intensely[6,8-14]. Applications for some convection models have been developed and analysed by Rashidi et al.[15,16].

Assessing the onset and type of convection is crucial in understanding this system, which can be achieved by analysing both the linear instability and nonlinear stability thresholds of the governing model.Comparing these thresholds allows for the assessment of the suitability of linear theory to predict the physics of the onset of convection. In order to gain stability results we turn our attention to the highly adaptable energy method[1]. Nonlinear energy methods are particularly useful as they delimit the parameter region of possible subcritical instability (i.e., the region between the linear instability and nonlinear stability thresholds).Hence, quantifying the discrepancy between these two thresholds makes it possible to provide an assessment of the suitability of linear theory to predict the instability of convection. The aim of the present paper is to examine the problem of stability of convective motions in a fluid layer. More precisely, we determine critical Rayleigh numbers for linear and nonlinear convection in a fluid with two fixed surfaces, for which we adopt the cubic and fifth density law proposed by Merker et al.[17].

Since Merker et al.[17]introduced only linear in-stability results for the problem of penetrative convection with the cubic and fifth order equations and it is clear from the analytical methods of Veronis’[18]that sub-critical instabilities will exist, McKay and Straughan[19]concentrated on determining a nonlinear threshold below which there is stability. Since in all situations the sub-critical regions exist, our aim in this paper is to test the convection in these sub-critical regions. When the difference between the linear and nonlinear thresholds is very large, the comparison between these thresholds is very interesting and useful.Thus we test the stability analysis results of McKay and Straughan[19]in the situations which have very big subcritical region. We develop a three-dimensional simulation for the problem. To do this, firstly, we transform the problem to a velocity-vorticity formulation,then we use a second-order finite difference scheme.We use implicit and explicit schemes to enforce the free divergence equation. The size of the box is evaluated according to the normal mode representation.Moreover, we adopt the periodic boundary conditions for velocity and temperature in thex,ydimensions.

1. Governing equations

We adopt the following momentum, continuity,and energy equations:

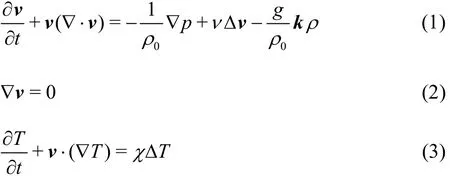
where standard notation is employed,v,p,g,ν,χ, Δ are respectively velocity, pressure, gravity constant, kinematic viscosity, thermal diffusivity and the Laplace operator, andk=(0,0,1).

The phenomenon of penetrative convection and its application to several areas of geophysical fluid dynamics and convection in stars were lucidly described by Veronis[18]who also analyzed in detail the linearized system and developed a weakly nonlinear finite amplitude analysis for two stress free boundaries.Veronis’ analysis was based on the density law in the body force term in the form

whereρ(T) is density,Ttemperature,ρ0the density at 4oC andα≈ 7.68× 10-6(oC)-2. One of Veronis’findings is that a finite amplitude solution exists for subcritical Rayleigh numbers. Veronis’ work based on Eq.(4) has directly or indirectly inspired many subsequent papers among which we mention Payne and Straughan[20]and Straughan[21].

Several studies have questioned whether the quadratic Eq.(4) is accurate enough. Merker et al.[7]formulated a density law with quintic temperature dependence. They compared their two relations to the more commonly-used quadratic one as advocated by Veronis[18]. On the basis of linear theory, Merker et al.suggested that their cubic law is about 10% more accurate than the quadratic one, whereas the quintic law yields an improvement of approximately 3%over the cubic law. McKay and Straughan[19]used the cubic and quintic laws of Merker et al. to describe penetrative convection in a fluid layer. They concluded that the cubic density relation is preferable to the quintic model since the quintic model leads to complicated mathematics for relatively little gain in accuracy.In fact, the cubic law has proved to be a popular choice since it is more accurate than the quadratic law but easier to implement than the quintic one (cf. McKay and Straughan[19]and references therein). However, in this paper we test Eq.(4) with a density law like

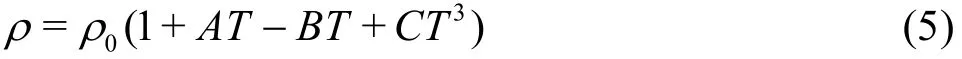
or even like

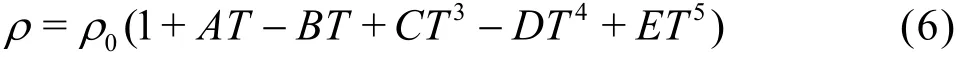
where0ρis the density of water at 0oC and the coefficientsA-Eare constants obtained by curve fitting to data points. Merker et al.[17]suggested the following values of coefficients in Eq.(5) for water:

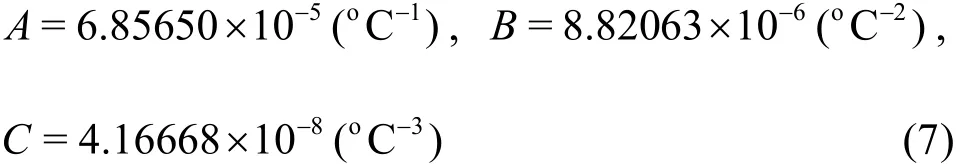
while in Eq.(6):

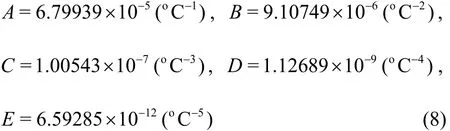
The temperature boundary conditions for the problem are

whereT1andT2are constants with 0≤T1≤4 schematically shown in Fig.1. The densityρ(T) in Eq.(1) will be replaced by either Eq.(5) or Eq.(6) , and firstly we replaceρ(T) by Eq.(5). Equations (1)-(3)possess the static solution

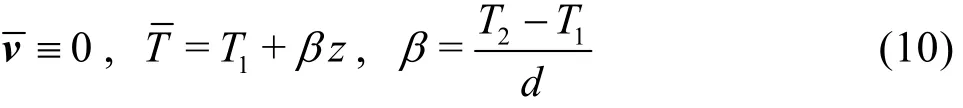
and hydrostatic pressure can be derived from Eq.(1) as

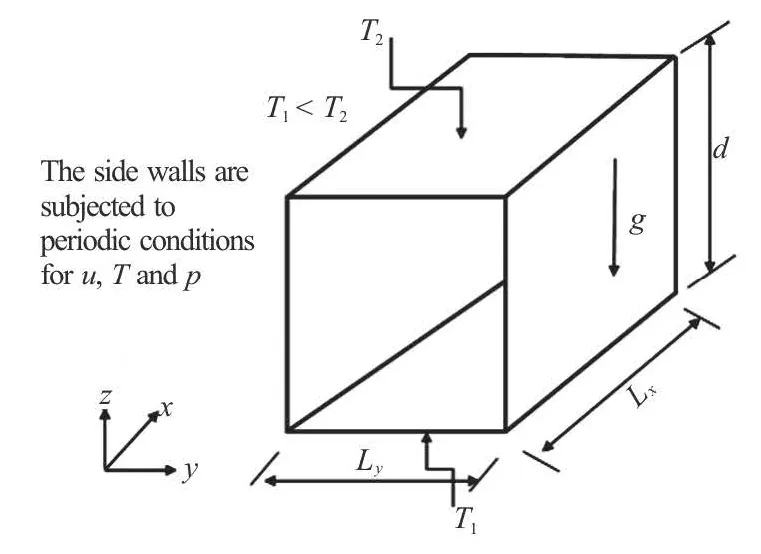
Fig.1 Schematic representation of the system

To assess the stability of the steady solution, we introduce a perturbation (ui,P,θ) to the steady-state solution, such that

and normalize the governing equations with scalings of

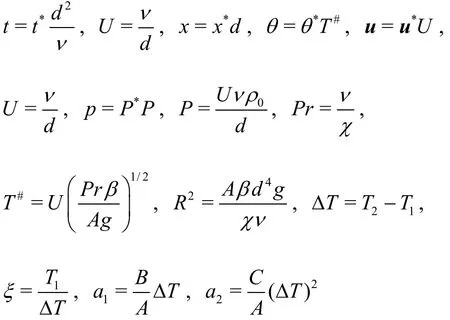
Next, substituting the perturbations and normalized variables into Eqs.(1)-(3), and dropping the stars we derive the system

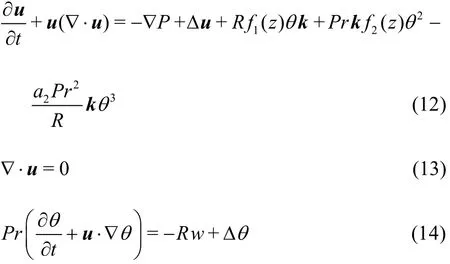
In these equations,w=u3andf1(z) andf2(z) are given by

andPris the thermal Prandtl number and 2=RaRis the thermal Rayleigh number. Now, we suppose the density term in the momentum equation is defined by Eq.(6) with the coefficients given by Eq.(8). The conduction solution whose stability we investigate is again defined by Eqs.(10) and (11), but whereρ()in Eq.(1) is determined from Eq.(6). The perturbation equations forui,θ,Pare found by normalization with the scalings for Eqs.(1)-(3), and here we additionally need

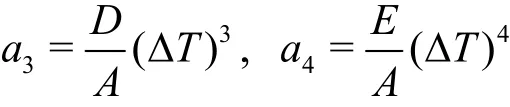
The normalized system of perturbation equations becomes

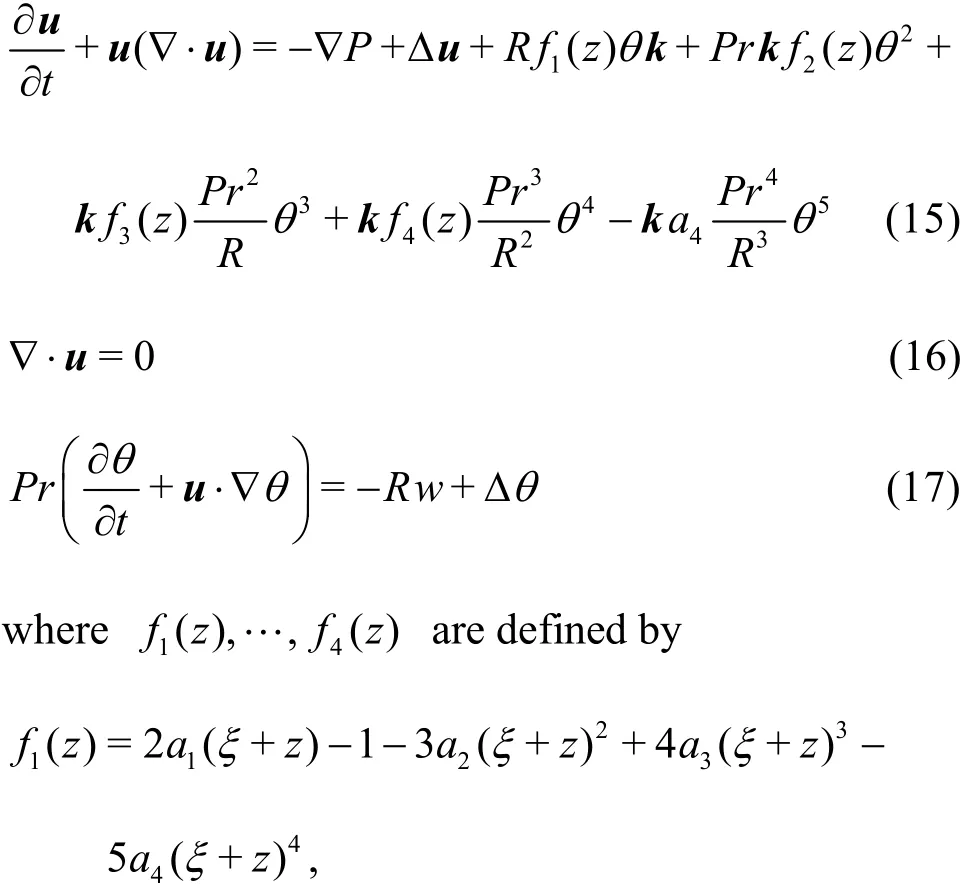
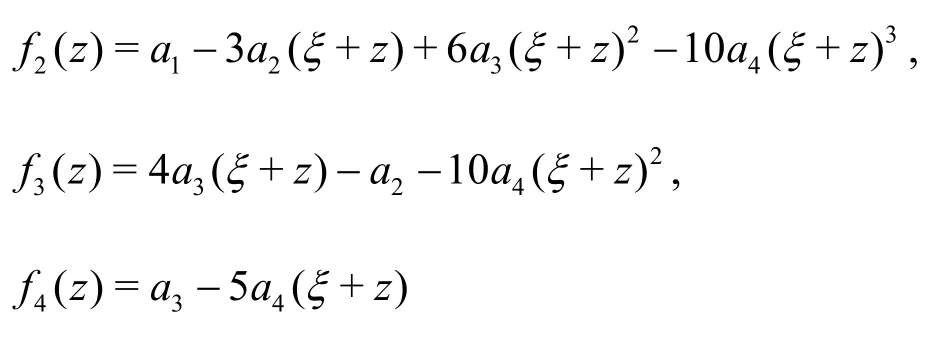
In both systems, the perturbed boundary conditions are given by

2. Velocity-vorticity formulation

In this section, we develop a three-dimensional approach to solve the time-dependent governing Eqs.(12)-(14) and (15)-(17) in order to assess the accuracy of the linear instability thresholds. A schematic diagram of the three-dimensional space (based on Fig.1) under consideration is given in the next section.

In this paper, we present an efficient, stable, and accurate finite difference scheme in the vorticity-vector potential formulation for computing the dynamics of viscous incompressible fluid. The emphasis is laid on three dimensions and nonstaggered grids. We introduce a second-order accurate method based on the vorticity-vector potential formulation with the nonstaggered grid whose performance on uniform grids is comparable with the finite scheme. We will pay special attention to how accurately the divergence-free conditions for vorticity, velocity and vector potential are satisfied. We will derive the three-dimensional analog of the local vorticity boundary conditions.

Now, we transform the momentum Eq.(12) and its normalized form (15) to the velocity-vorticity formulation. Here we will explain this transformation and then give the finite difference approximation just for Eq.(15) as the transformation and the numerical approximation of Eq.(12) can be given directly with the same procedure. By using the curl operator to Eq.(15), one gets the following dimensionless form of the vorticity transport equation:

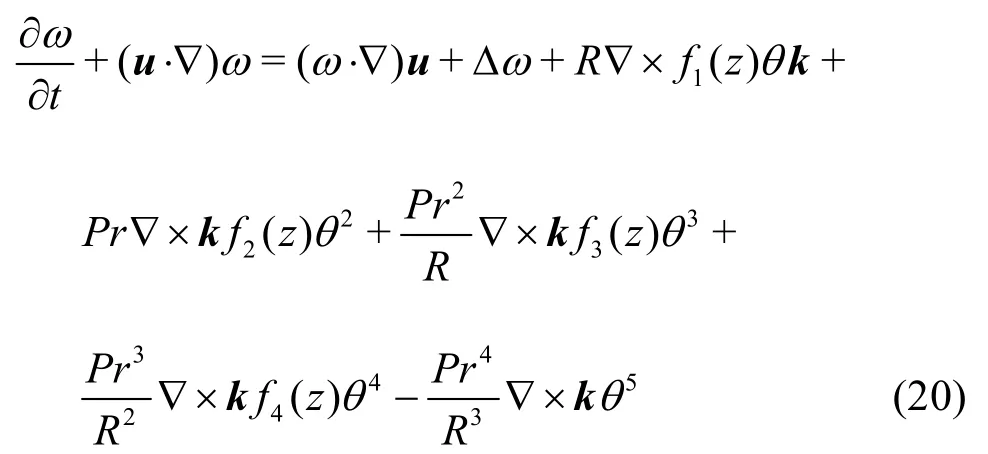
To calculate velocity from vorticity, it is convenient to introduce a vector potential,which may be looked upon as the three-dimensional counterpart of two-dimensional stream function. The vector potential are defined by

It is easy to show the existence of such a vector potential for a solenoidal vector field (▽ ·u=0). Such a vector potential can be required to be solenoidal, i.e.,

Substituting Eq.(22) into Eq.(21) and using Eq.(23) yield

The set of Eqs.(17), (20), (22) and (24) with appropriate boundary conditions are found to be a convenient form for numerical computations. The details on the boundary conditions for the vector potential and vorticity can be found in Ref.[7].

The first step in the numerical computation is to give the initial values for the vorticity vectors,Next, the Poisson Eq.(24) are discretized in space using a second-order central difference scheme. Then, we solve the resulted system using the Gause-Sidel iteration method to evaluateas follows:

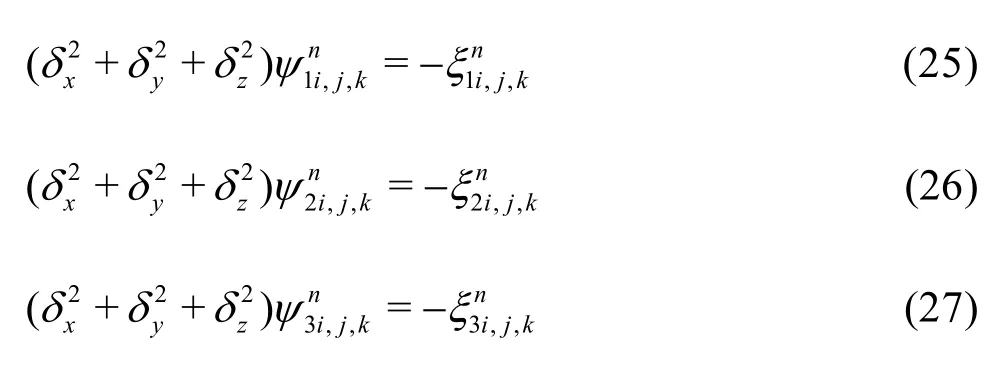
The next step is to evaluate the potential vectors at the boundary, i.e., we computeNow, the velocity vector can be calculated explicitly by using a second-order finite difference scheme to Eq.(22) as follows:

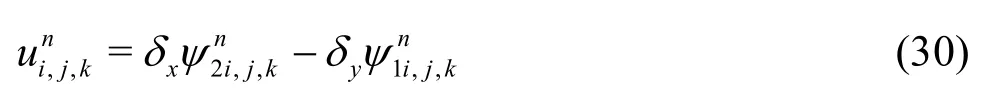
wherei,j,k=1,… ,m-1 andare the firstorder central difference operators. The vorticity transport Eq.(20) are discretized in time using the explicit scheme. The discretized form of Eq.(20) for the three vorticity components and the energy Eq.(17) can be written as

The temperature on the boundary can be computed explicitly using Eqs.(18)-(19). However, a secondorder implicit technique has been used to evaluated the vorticity vector at the boundary.

Here, we should mention that our scheme is flexible for various values ofRaand thus the grid resolution has been selected according to the value ofRa. We decrease the values of Δx, Δyand Δzas the value ofRaincreases. For our problem, we find that Δx= Δy= Δz=0.02 can give sufficiently accurate results.

3. Numerical results

As we mentioned in the introduction, McKay and Straughan[19]derived the eigenvalue system of linear instability and nonlinear stability analyses for the third- and fifth-order equation of state. Thus, to find the stability results, we use their eigenvalue system of linear instability and conditional nonlinear stability and solve the system using the Chebyshev collocation,finite element and finite difference methods. In use of the Chebyshev collocation method, we took 20-30 polynomials. Usually 25 polynomials were found to be sufficient but convergence was checked by changing the number of polynomials and examining the convergence of the associated eigenvector (which yielded the approximate associated eigenfunction). However,for the finite element method, we have checked the convergence and found that convergence to 8 decimal places is achieved with 3 elements and each element has 11 nodes. For the finite difference scheme the convergence is tested and we found that the convergence to 8 decimal places is achieved withh=0.001. It should be mentioned that we use these methods to solve our problem because their flexibility especially for problems which have variable coefficients and they give very accurate result. Moreover, the finite element method and Chebyshev collocation method have the performance of fast convergence.

Table 1 Critical Rayleigh and wavenumbers RaL, RaE,. Equation of state (5) holds

Table 1 Critical Rayleigh and wavenumbers RaL, RaE,. Equation of state (5) holds

T T1 RaL 2 2 a RaE Lx Ly L 7 2 94 158.09725 25.9560 56 337.87505 1.7 1.8 8 2 194 931.4136 37.1410 75 118.43636 1.7 1.3

Table 2 Critical Rayleigh and wavenumbers RaL, RaE,. Equation of state (6) holds

Table 2 Critical Rayleigh and wavenumbers RaL, RaE,. Equation of state (6) holds

T T1 RaL 2 2 a RaE Lx Ly L 7 2 100 922.7422 26.3910 50 519.33548 1.6 1.9 8 2 209 008.0329 37.8040 139 210.6888 1.4 1.5

In this section, letRaLandRaEdenote the critical Rayleigh numbers for linear instability and nonlinear stability theories. The corresponding critical wavenumbers of the linear instability will be denoted byaL. In Tables 1 and 2 we present numerical results of the linear instability and nonlinear stability analyses for Eqs.(5) and (6), respectively. The dimensions of the box, which are calculated according to the critical wavenumber, are shown in Tables 1 and 2. In these tablesLxandLyare box dimensions in thexandydirections, respectively. The box dimension in thezdirection is always equal to 1. We assume that the perturbation fields (u,θ,P) are periodic in thexandydirections and letdenote the periodicity cell, whereaxandayare the wavenumbers in thexandydirections, respectively.axandayare evaluated according to the critical wavenumbersaLwhere, where. The values ofLxandLyin Tables 1 and 2 may be rearranged to yield a number of possible solutions for each value of the critical wavenumbers. However, we select a solution so that these two values are similar to avoid any possible stabilization effect from walls.

For numerical solutions in three dimensions, we used Δt=5×10-5and Δx=Δy=Δz=0.02. The convergence criterion have been selected to make sure that the solutions arrive at a steady state. The convergence criterion is

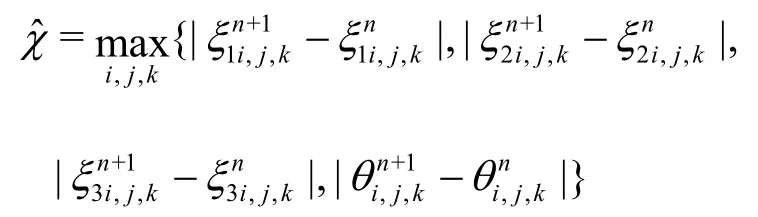
To solve Eqs.(25)-(27) using the Gauss-Seidel iteration method, in the first time step we give an initial value to the potential vector and denote,to be the potential vector. Then, using these initial values, we compute new values denoted byand use these values to evaluate new values. The program will continue in this process until the convergence criterion is satisfied,which is

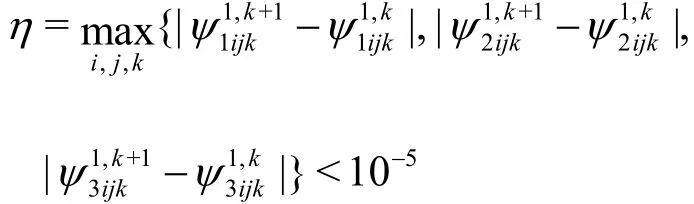
In the next time steps, the values ofin the time stepnwill be the initial values to the next time step.

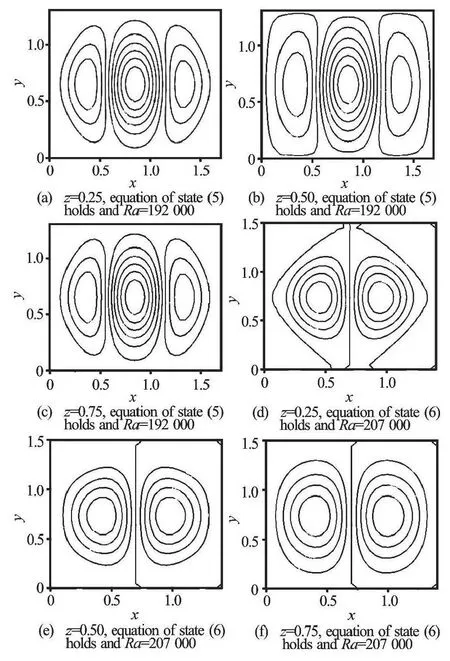
Fig.2 Contour plot of u at τ=6

In order to display the numerical results clearly,the temperature, velocity and vorticity contours are plotted in Figs.2-7 atτ=6,T2=8,T2=2,Ra=192 000 andRa=207000. In these figures, we use the mesh size of 86×66×51 forRa=192000 and 71×76×51 forRa=207000. Moreover, the temperature,velocity and vorticity contours are presented at the time levelτ=6 as the possibility of arriving at the solution to any steady state impossible. Figures 2-7 show the contours ofu,v,w,ζ1,ζ2andθ, respectively, atz=0.25,z=0.5 andz=0.75 in (a)-(c) of Figs.2-7 forRa=192000 and when Eq.(5)holds. Also, Figs.2-7 show the contours ofu,v,w,ζ1,ζ2andθ, respectively, atz=0.25,z=0.5 andz=0.75 in (d)-(f) of Figs.2-7 forRa=207000when Eq.(6) holds.

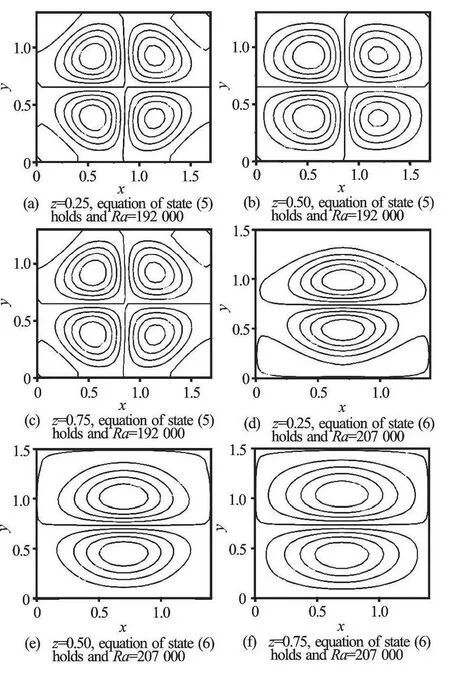
Fig.3 Contour plot of v at τ=6

Figure 2 presents the contours of perturbation velocityuin thex-yplane, which shows three rotating cells in each case. The contours ofuatz=0.25 andz=0.75 (Figs.2(a) and 2(c)) are identical, due to symmetric the boundary conditions atz=0 and(=0)du. The maximum ofuoccurs at the center of cells, also the middle cell (positionz=0.75) gives the minimum ofu(=0.036uat the center of cell),and the rotating cells become bigger and the cells move progressively toward the boundaries, because the far way from the boundary condition atz=0 andd. Generally, Figs.2(a)-2(c) show three rotating cells,and the cell at the center (middle) is rotating counter clockwise CCW (positive sign), while the sides cells are similar and rotating clockwise CW (negative sign),which may return to symmetric conditions for thexandy-axes. Figures 2(d)-(2f) exhibit that the number of rotating cells is reduced to two cells (CW and CCW)and symmetric about they-axis. This may return to the large value of =207000Raand the degree of density is 5, which gives the results more sensitive to buoyancy effect. Also, from Fig.2, we observed that the magnitudes of rotating cells decrease with increasing Rayleigh number (Figs.2(a)-2(c),Ra=192000 and Figs.2(d)-2(f),Ra=207000), and the number, magnitudes and volumes of rotating cells for the case of Eq.(6) are smaller than those for the case of Eq.(5).

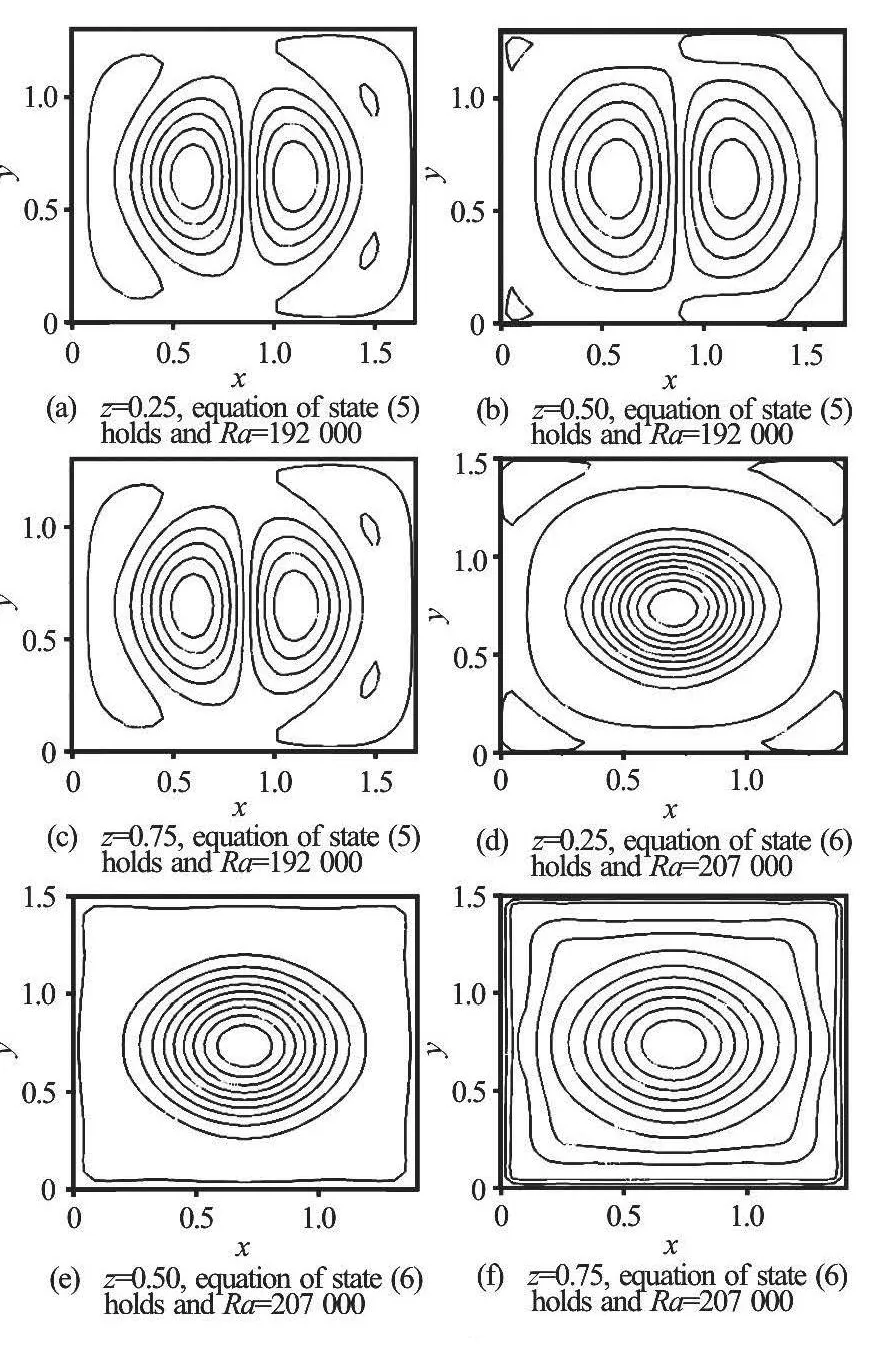
Fig.4 Contour plot of w at τ=6

Figure 3 shows the contours of perturbation velocityvin thex-yplane. Figures 3(a)-3(c) show formulated four rotating cells (CW and CCW) and have mirror images about thex- andy-axes, and the sign of contours is symmetric about diagonal. Figures 3(a) and 3(c) are approximately similar because symmetric boundary conditions atz=0 andd. Figures 3(d)-3(f) illustrate that the number of cells are reduced to two rotating cells (CW and CCW) flatting toward the horizontal boundaries, this may return to be sensitive to the degree of polynomial ofρ(T), and the cells are symmetric about thex-axis. Generally, the maxima ofvfor all cells appear at the centre of cells.

Figure 4 illustrates the contours of perturbation velocitywin thex-yplane. Figures 4(a)-4(c) show there are two opposite rotating cells (CW and CCW),and the minimum appears atz=0.5 due to the long distance from the boundaries, while the equation of state gives signal rotating cell flatting atz=0.25 andz=0.75.

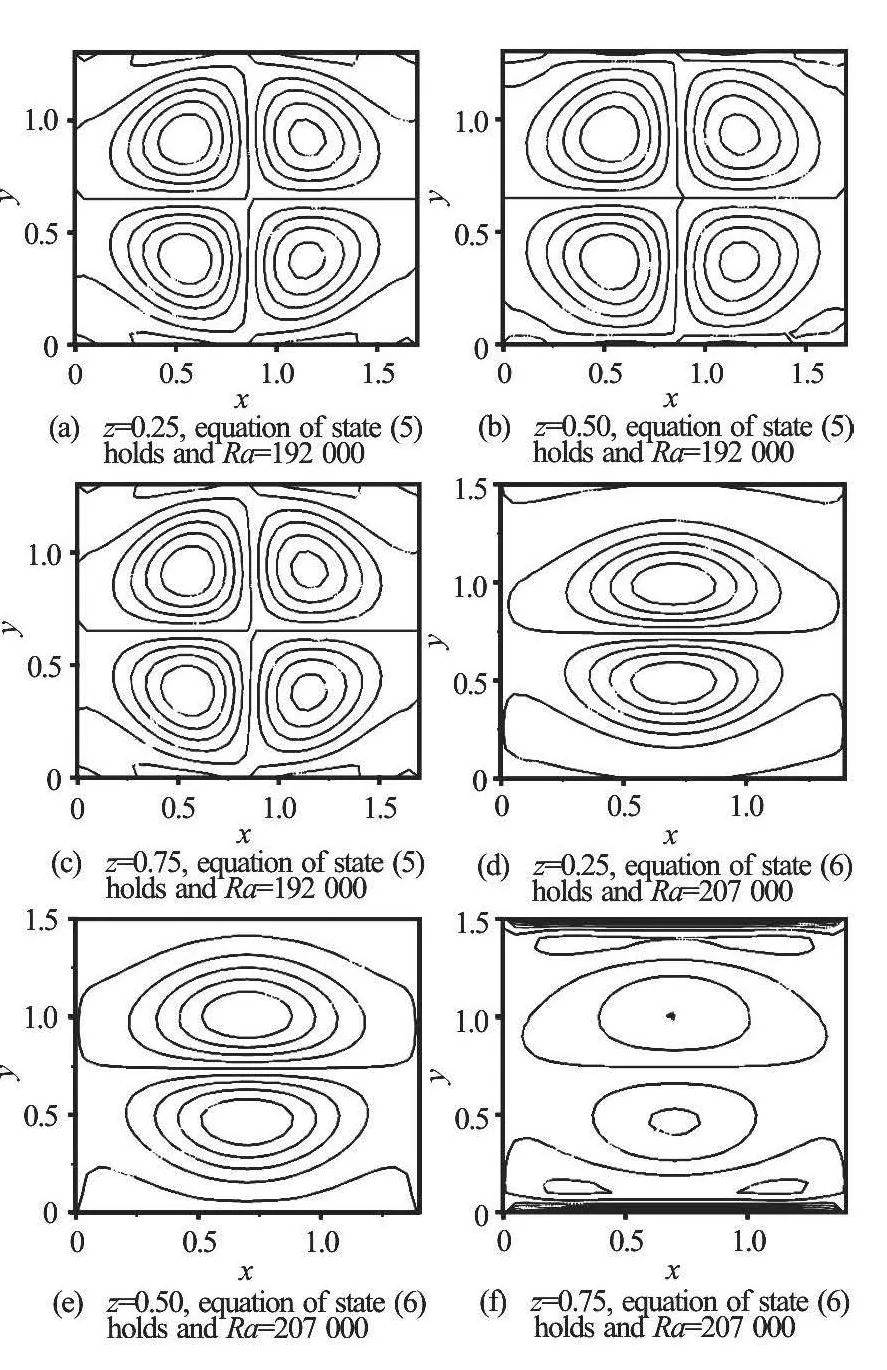
Fig.5 Contour plot of 1ξ at τ=6

Figure 5 indicates the contours of=0.5(?w/?y-?v/?z). Figures 5(a)-5(c) exhibit that the vorticityhas four identical rotating cells and the maximum magnitude atz=0 andz=0.75 (= ±0 .74).Also, the cells have mirror image about thex-axis(horizontal) andy-axis (vertical), while the symmetry of sign is about the diagonals. Figure 5(d)-5(f) indicate that the cells are reduced to two flatting rotating cells, and these cells are approximately symmetric about thex-axis (horizontal) and one of cells is rotating CW and the other CCW.

Figure 6 gives the contours of=0.5(?u/?z-?w/?x). Figures 6(a)-6(c) indicate that there are three rotating cells of the vorticity, and the middle cell possessses the maximum of(1.6,- 0.54,1.6) forz=0.25, 0.5, 0.7, respectively. Figures 6(d)-6(f)shows that the number of cells are reduced to two rotating cells, one being rotating CW and the other CCW, and the maximum is 0.22, while in Figs.6(a),6(b) and 6(d), it is 1.6, which may be returned to use the equation of state (6). On the other hand, there are no identical properties between Fig.6(f) and Fig.6(d),while in Fig.6(a) and Fig.6(c) are symmetric.

Fig.6 Contour plot of 2ξ at τ=6

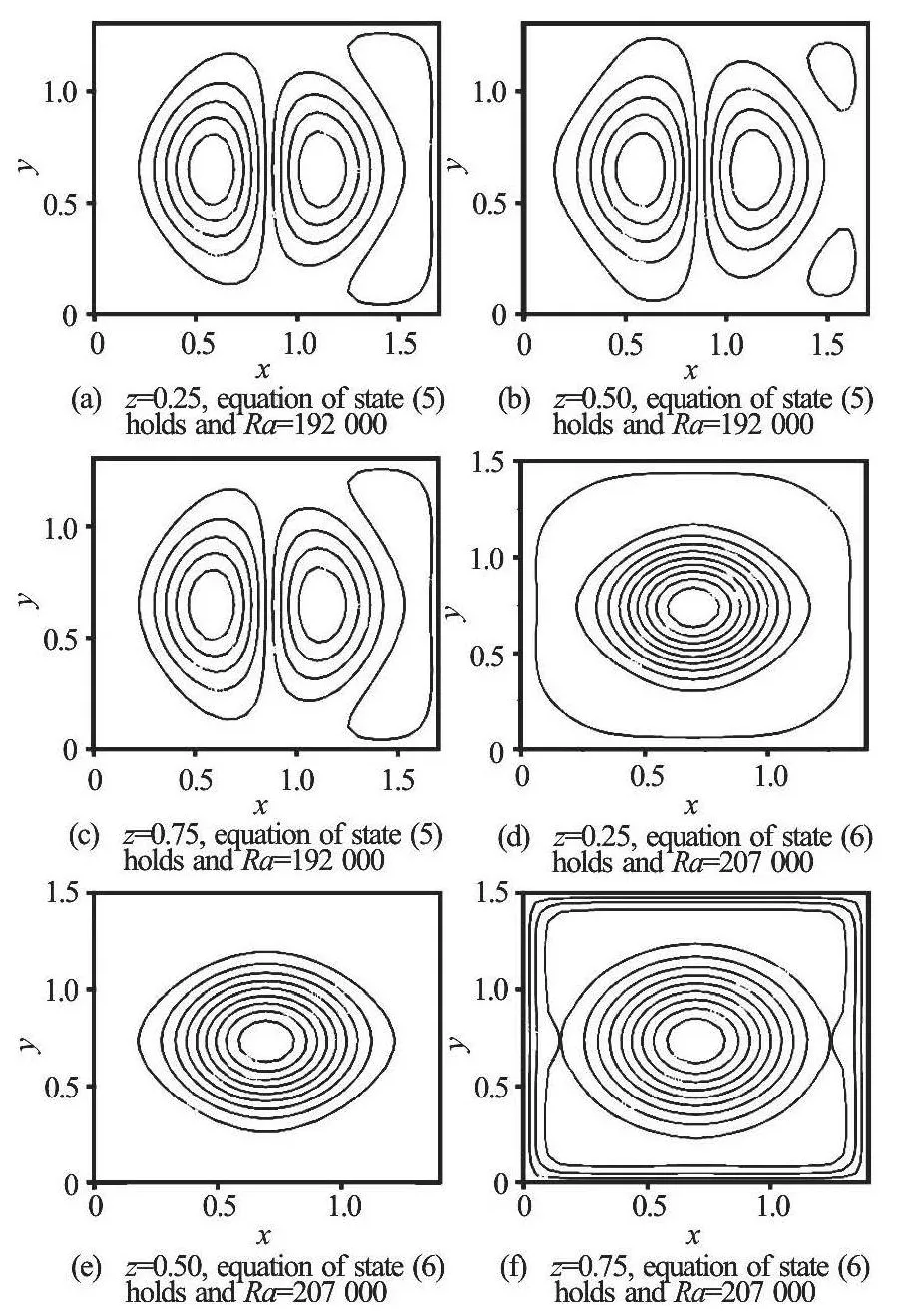
Fig.7 Contour plot of θ at τ=6

Finally, Fig.7 plots the contours ofθat three positions,z=0.25, 0.5 and 0.75. Figures 7(a)-7(c)show two inidentical cells of isothermθ, one of cell being positive, while the other being negative, and the magnitudes ofθatz=0.25 andz=0.75 are larger than atz=0.5. The maximum ofθin the Figs.6(a)-6(c) is equal to 0.53 and minimum difference ofθ(negative) is -0.59 at the equation of state (5). For Figs.7(d)-7(e), there is a single cell, the centers of cells in Figs,7(d) and (f) is different from the outer of cell (the sign ofθis changed from the negative one to the positive one and verse virus). The equation of state (6) gives smaller value ofθthan the equation of state (5), and the number of cells are less than that using the equation of state (5).Also, the valueRa=19 200 and 207 000 is near the value of linear instabilityRaL, which makes the perturbation (u,θ,π) fluctuating about mean valueV=0 and.

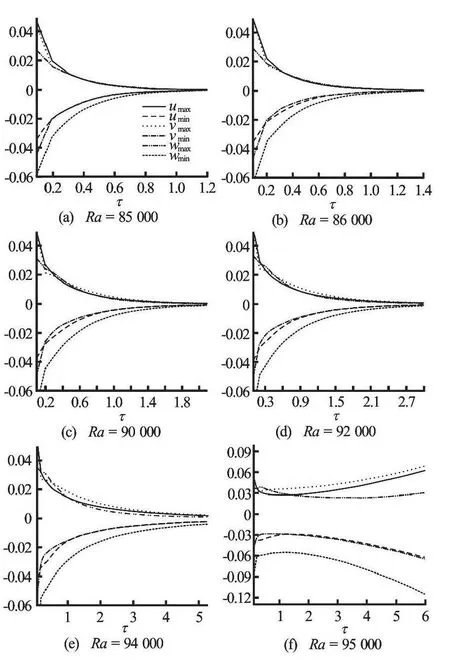
Fig.8 Equation of state (5) holds and T2=7, T1=2, RaL=94 158.09725, RaE=56337.87505

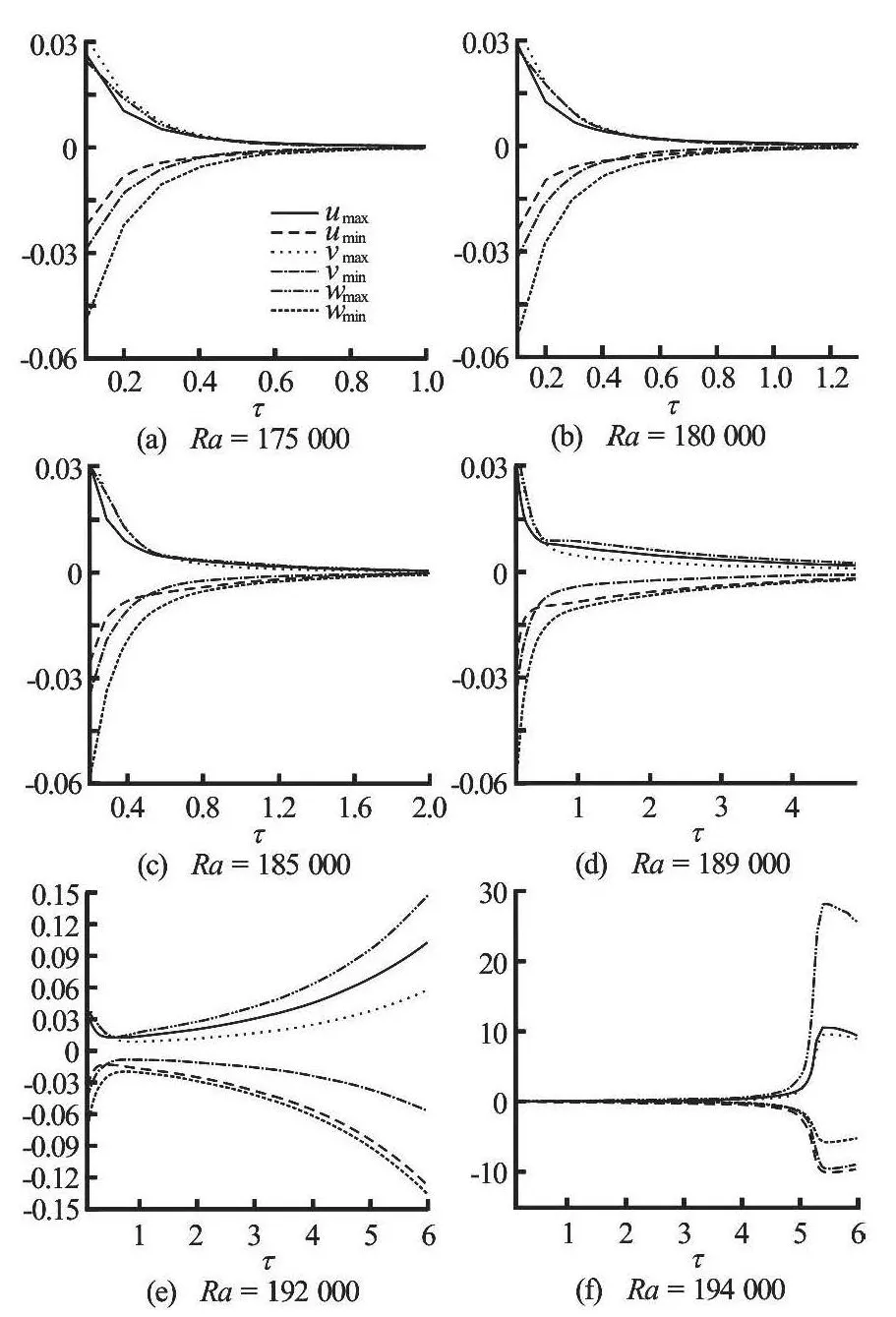
Fig.9 Equation of state (5) holds and T2=8, T1=2, RaL=194 931.4136, RaE=75118.43636

In Figs.8-11, we show a summary of the numerical results where we present the maximum and minimum values of velocities versus time. In Fig.8, we selectT2=7,T2=2 and Eq.(5), and then according to the stability analysis we haveRaL=94158.09725,RaE=56337.87505,Lx=1.7 andLy=1.8. Here, it is clear that we have very large subcritical stability region as there is a big difference between the critical Rayleigh numbers given by the linear and non-linear theories. From Fig.8, forRa=85000, we can see that the solutions satisfy the convergence criterion atτ=1.26325 and thus the solution arrives at the basic steady state within a short time. However, forRa=86 000,Ra=90000,Ra=92000 andRa=94 000, the program needsτ=1.4611,τ=2.19635,τ=3.03985andτ=5.36525, respectively, to arrive at the basic steady state, which implies that the required time to arrive at a steady state increases with increasing values ofRauntil the solution does not arrive at any steady state. Finally, forRa=95000, the solutions do not arrive at any steady state and the program stops atτ=6. ForRa=95000, we let the program run for a significant period to test the convection’s long time behaviour. We see that the values of the velocities increase atτ=8, and then decrease atτ=12 and continue to oscillate. Here, according to the numerical results, the linear instability threshold isvery close to the actual threshold, i.e., the solutions arrive at the basic steady state before the linear instability threshold.

The results of Figs.9-10 indicate that the stability behaviour is absolutely similar to the stability behaviour of Fig.8, as we found that the linear instability threshold is very close to the actual threshold. In Fig.9,the equation of state (5) holds, the critical Rayleigh numbers forT2=8,T2=2 were computed, leading to the following stability results:RaL=194931.4136,RaE=75118.43636,Lx=1.7 andLy=1.3. In this case, the difference between the critical Rayleigh numbers of linear and non-linear theories is very large.Figure 9 shows that forRa=175000,Ra=180000,Ra=185000 andRa=189000 the solutions go to the basic steady state and satisfy the convergence criteria atτ=1.07975,τ=1.3994,τ=2.07785andτ=4.97595, respectively. Moreover, atRa=192 000 andRa=194000, the basic steady state atτ=6 could not be achieved and the solutions can not arrive at any steady state and the program stops atτ=6. ForRa=192000 andRa=194000, the convection exhibits oscillating behaviour and the access to a stable state is impossible.

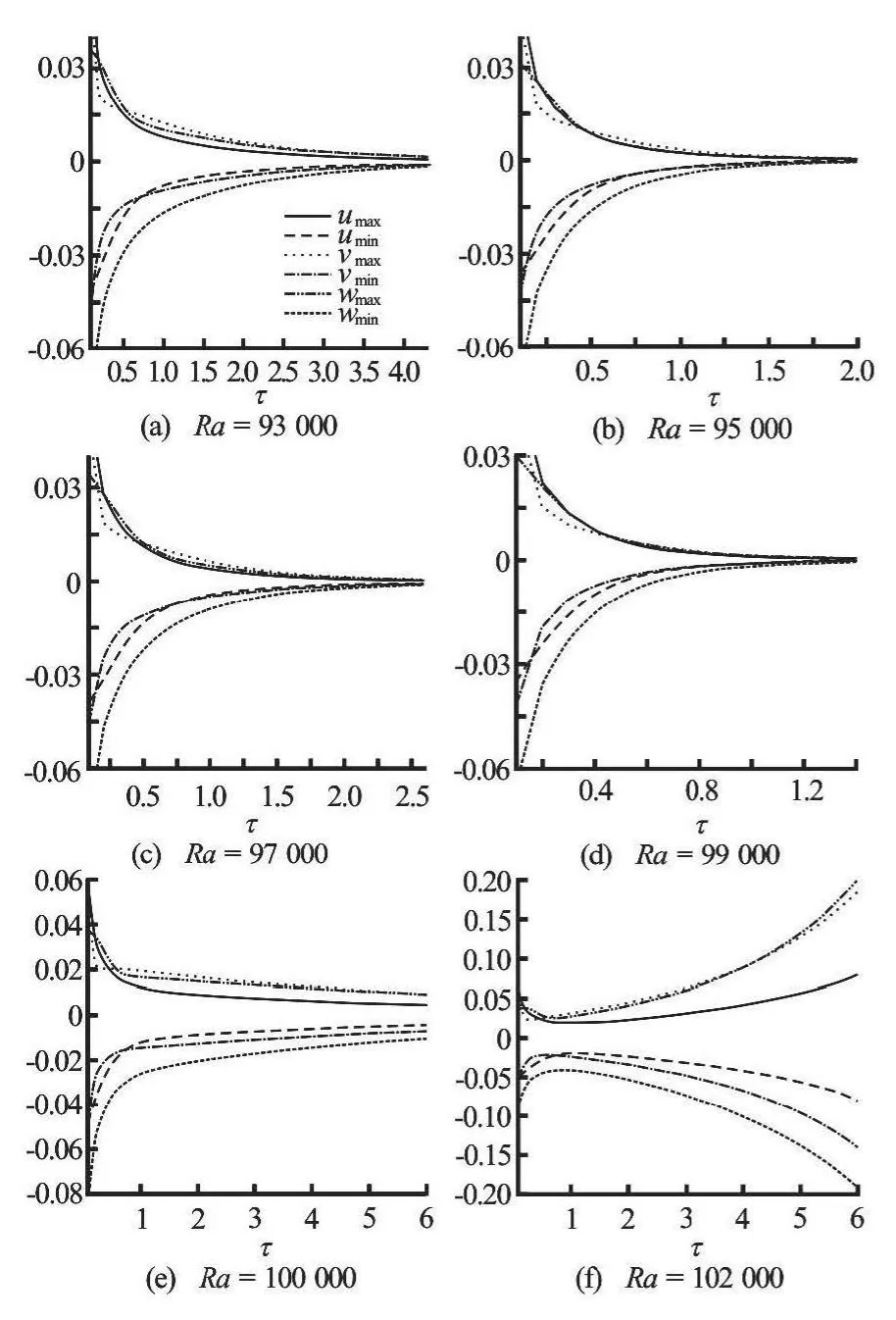
Fig.10 Equation of state (6) holds and T2=7, T1=2, RaL=10 0922.7422, RaE=50519.33548

Figure 10, shows the Rayleigh numbers forT2=7,T2=2, with Eq.(6). This leads to the following stability results:RaL=100922.7422,RaE=505 19.33548,Lx=1.6 andLy=1.9. As can be seen, the difference between the critical Rayleigh numbers of linear and nonlinear theories is considerable, with Fig.10 showing that forRa=93000,Ra=95 000,Ra=97000 andRa=99000 the solutions arrive at the basic steady state soon and satisfy convergence criteria atτ=1.48615,τ=2.0029,τ=2.6761 andτ=4.3067, respectively. Moreover, atRa=100000, the basic steady state atτ=6 could not be reached, but there is a decrease in the solutions’values and therefore to reaching a basic steady state at the next time levels is expected. Furthermore, forRa=102000, the solutions could not arrive at any steady state and the program does not progress beyondτ=6. ForRa=102000, the convection exhibits oscillating behaviour and access to a stable state is impossible.

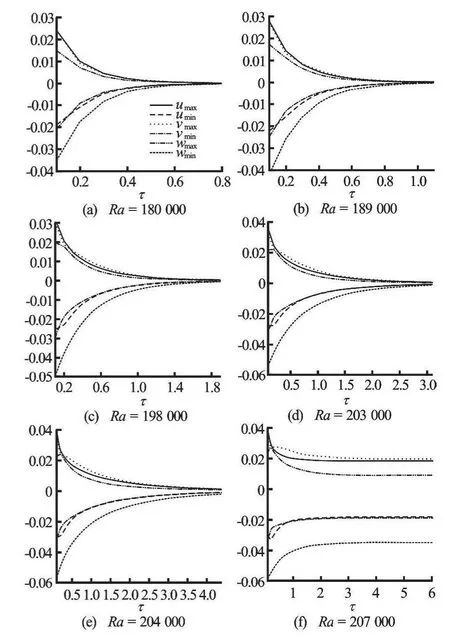
Fig.11 Equation of state (6) holds and T2=8, T1=2, RaL=209 008.0329, RaE=139210.6888

In Fig.11, we selected the parameters as follows:T2=8,T2=2, where Eq.(6) holds, then we get thefollowing stability results:RaL=209008.0329,RaE=139210.6888,Lx=1.4 andLy=1.5. In this case, there is a considerable difference between the critical Rayleigh numbers of linear and nonlinear theories. Figure 11 shows that forRa=180000,Ra=189000,Ra=198000,Ra=203000 andRa=204000 the solutions for the basic steady state are found in short time and the convergence criteria atτ=0.83465,τ=1.1397,τ=1.92,τ=3.15965andτ=4.45135, respectively are satisfied. Moreover, atRa=207000, the basic steady state atτ=6 was not accessed. Solutions forRa=207000, could not arrive at any steady state and the program stops atτ=6.ForRa=207000, the convection exhibits oscillating behaviour and the access to a stable state is impossible.

4. Conclusions

In this paper we have investigated the problem of penetrative convection with the cubic and fifth-order equations of state proposed by Merker et al.[1]. Regions of very large subcritical instabilities, i.e., where agreement between the linear instability thresholds and nonlinear stability thresholds is poor, are studied by solving the full three-dimensional system. The results indicate that the linear threshold accurately predicts the onset of instability in the basic steady state. However, the required time to arrive at the steady state increases significantly as the Rayleigh number tends to the linear threshold.

For three-dimensional simulations, numerically,we find that the convection has three different patterns.The first picture, whereRalies betweenRaLandRaE, is that the solutions perturbations vanish, sending the solution back to the steady state, before the linear thresholds are reached. The required time to arrive at the steady state increases as the value ofRaincreases. The second picture, whereRais close toRaLis that solutions can tend to a steady state which is different from the basic steady state. In the third picture, whereRais very close orRa＞RaL,the solutions do not arrive at any steady state and oscillate.

In the previous literatures, the general believe was that the linear analysis provides limited tangible evidence on the behaviour of the nonlinear system[2],so in such cases only instability can be deduced from the linear thresholds, as any potential growth in the nonlinear terms is not considered. By employing a nonlinear stability analysis, the discrepancy between these two thresholds makes it possible to provide an assessment of the suitability of linear theory to predict the onset of convection. However, for the system which we study in this paper, we find that the linear analysis provides a very good prediction of the behaviour of the nonlinear system for very large subcritical regions where we find the solution arrive at the basic steady state before the actual threshold which is very close to the linear threshold.

[1] STRAUGHAN B. The energy method, stability, and nonlinear convection[M]. 2nd Edtion. New York, USA:Springer, 2004.

[2] MHARZI M., DAGUENET M. and DAOUDI S. Thermosolutal natural convection in a vertically layered fluid-porous medium heated from the side[J]. Energy Conversion Management, 2000, 41(10): 1065-1090.

[3] ZHANG K. K., SCHUBERT G. Teleconvection: Remotely driven thermal convection in rotating stratified spherical layers[J]. Science, 2000, 290(5498): 1944-1947.

[4] ZHANG K. K., SCHUBERT G. From penetrative convection to teleconvection[J]. Astrophysical Journal,2002, 572(1): 461-476.

[5] KAMINSKI E., CHENET A.-L. and JAUPART C. et al.Rise of volcanic plumes to the stratosphere aided by penetrative convection above large lava flows[J]. Earth Planetary Science Letters, 2011, 301(1-2): 171-178.

[6] HARFASH A. J., HILL A. A. Simulation of three dimensional double-diffusive throughflow in internally heated anisotropic porous media[J]. International Journal of Heat Mass Transfer, 2014, 72(3): 609-615.

[7] HARFASH A. J. Three dimensions simulation for the problem of a layer of non-Boussinesq fluid heated internally with prescribed heat flux on the lower boundary and constant temperature upper surface[J]. International Journal of Engineering Science, 2014, 74(1): 91-102.

[8] HARFASH A. J. Three-dimensional simulations for convection in a porous medium with internal heat source and variable gravity effects[J]. Transport Porous Media, 2014, 101(2): 281-297.

[9] HARFASH A. J. Three dimensional simulation of radiation induced convection[J]. Applied Mathematics and Computation, 2014, 227(2): 92-101.

[10] HARFASH A. J. Three-dimensional simulations for convection problem in anisotropic porous media with nonhomogeneous porosity, thermal diffusivity, and variable gravity effects[J]. Transport Porous Media,2014, 102(1): 43-57.

[11] HARFASH A. J. Three dimensional simulations for penetrative convection in a porous medium with internal heat sources[J]. Acta Mechanica Sinica, 2014, 30(2):144-152.

[12] HARFASH A. J. Convection in a porous medium with variable gravity field and magnetic field effects[J].Transport Porous Media, 2014, 103(3): 361-379.

[13] HARFASH A. J. Three dimensional simulations and stability analysis for convection induced by absorption of radiation[J]. International Journal of Numerical Methods for Heat and Fluid Flow, to appear.

[14] HARFASH A. J. Stability analysis of penetrative convection in anisotropic porous media with variable permeability[J]. Journal of Non-Equilibrium Thermodynamics, to appear.

[15] RASHIDI M. M., MOHIMANIAN POUR S. A. and HAYAT T. et al. Analytic approximate solutions for steady flow over a rotating disk in porous medium with heat transfer by homotopy analysis method[J]. Computers and Fluids, 2012, 54(2): 1-9.

[16] RASHIDI M. M., ABELMAN S. and FREIDOONI MEHR N. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid[J]. International Journal of Heat and Mass Transfer, 2013, 62(7):515-525.

[17] MERKER G. R., WAAS R. and GRIGULL U. Onset of convection in a horizontal water layer with maximum density effects[J]. International Journal of Heat Mass Transfer, 1979, 22(79): 505-515.

[18] VERONIS G. Penetrative convection[J]. Astrophysical Journal, 1963, 137: 641-663.

[19] MCKAY G., STRAUGHAN B. Nonlinear energy stability and convection near the density maximum[J]. Acta Mechanica, 1992, 95(1-4): 9-28.

[20] PAYNE L. E., STRAUGHAN B. Unconditional nonlinear stability in penetrative convection[J]. Geophysical and Astrophysical Fluid Dynamics, 1987, 39(1): 57-63.

[21] STRAUGHAN B. Finite amplitude instability thresholds in penetrative convection[J]. Geophysical and Astrophysical of Fluid Dynamics, 1985, 34(1): 227-242.