Some Results of a Certain Odd Perfect Number
ZHANG Si-bao
(Department of Mathematics,Kashi Teacher’s College,Kashi 844006,China)
Some Results of a Certain Odd Perfect Number
ZHANG Si-bao
(Department of Mathematics,Kashi Teacher’s College,Kashi 844006,China)
Def i ne the total number of distinct prime factors of an odd perfect number n as ω(n).We prove that if n is an odd perfect number which is relatively prime to 3 and 5 and 7,then ω(n)≥107.And using this result,we give a conclusion that the third largest prime factor of such an odd perfect number exceeds 1283.
odd perfect numbers;the total number of distinct prime factors;the third largest prime factor
§1.Introduction
Let σ(n)denote the sum of the positive divisors of n.We say that n is a perfect number if and only if σ(n)=2n.The theory of even perfect numbers is well-known,Euclid proved that if Mpis prime,then n=is perfect number,and Euler proved that every even perfect number is of this form,where p is prime and Mpis Mersenne prime.Up to now,we have found 47 even perfect numbers.On the other hand,it is not known whether any odd perfect numbers(opn)exists.A very famous result,originally proved by Euler,is that every opn n(if it exists)must be of the form n=where π and pi(1≤i≤s)are distinct odd primes and βiare positive integers,π≡α≡1(mod 4)[1].
De fi ne the total number of distinct prime factors of an opn n as ω(n).Some results concerning ω(n),can be found in[2-4].If n is an opn which is relatively prime to 3,then ω(n)≥16 ([2]).If n is an opn which is relatively prime to 3 and 5,then ω(n)≥15[3].S B ZHANG[4]extended this result,and proved that if n is an opn which is relatively prime to 3 and 5,then ω(n)≥17.If n is an opn which is relatively prime to 3 and 5 and 7,then ω(n)≥27[3].The main purpose of this paper is to extend these results and to study the third largest prime factor of it.
§2.Preliminaries
In order to prove the theorems,we need the following three lemmas.
Lemma 2.1[5]If n=is an opn,where π≡α≡1(mod 4),then the distinct odd primes pi(1≤i≤s)are not satisfy with pi≡1(mod 4).
Lemma 2.2[6]The largest prime factor of an opn exceeds 108.
Lemma 2.3[7]The second largest prime factor of an opn exceeds 104.
§3.Main Results and Proofs
Let n denote an opn and assume that it is relatively prime to 3 and 5 and 7.Write nfor the standard factorization of n,where s=ω(n)and pi(1≤i≤s)are distinct odd primes of increasing order and βi(i≤i≤s)are positive integers.
Theorem 3.1If n is is an opn which is relatively prime to 3 and 5 and 7,then ω(n)≥107.
ProofIn order to prove the theorem,it suffices to show that the case s=106 is impossible. We prove by contradiction and assume that s=106.According to the Equ σ(n)=2n,since σ is multiplicative,we have that,
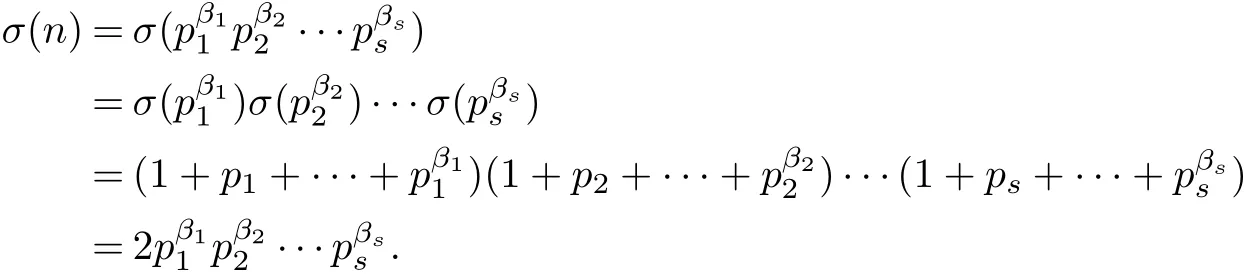
Therefore,
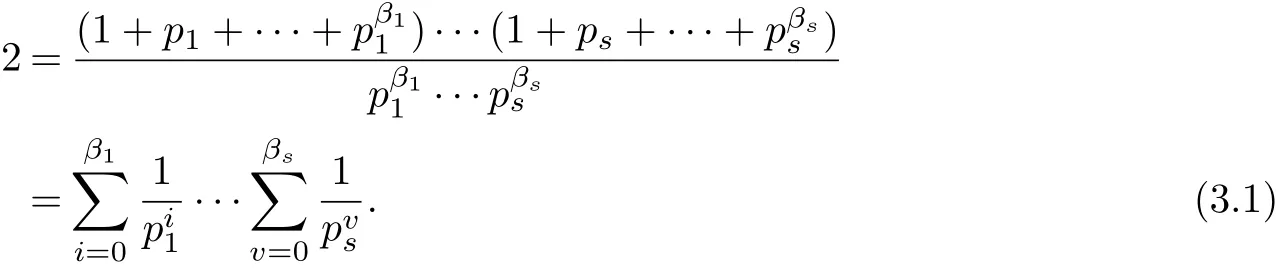
Noting that
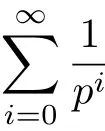
is a convergent series and

we have that
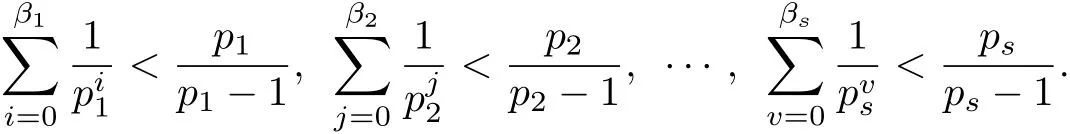
By Lemma 2.1,n is relatively prime to 3 and 5 and 7,and then 13 is the least odd prime with pi≡1(mod 4).So,the other odd prime divisors of n should be of the form p≡3(mod 4). According to Lemma 2.2,we know that there are primes which exceed 108and according to Lemma 2.3,we know that there are primes which exceed 104.Note that 10007 is the f i rst prime which exceeds 104,with 10007≡3(mod 4);and100000007 is the f i rst prime which exceeds 108, with 100000007≡3(mod 4).So,we can let X and Y as follow,

where
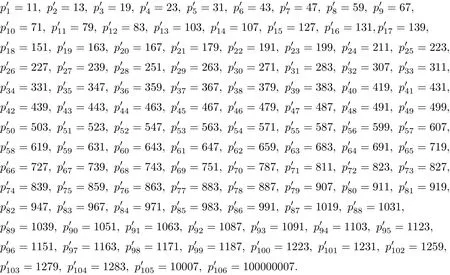
We also note that the function f(x)=is a monotone-decreasing function for x∈[11,∞). If piis di ff erent with,where pi∈X andY,then

which is contradict to the Equ(3.1).This completes the proof.
Using this result,we give a result as follows.
Theorem 3.2The third largest prime factor of an odd perfect number which is relatively prime to 3 and 5 and 7 exceeds 1283.
[1]DICKSON L E.History of Theory of Number[M].Washington:Carnegie Institution,1919.
[2]ZHANG Si-bao,DENG Yong.Number ω(n)of a kind of odd perfect number,s distinct prime factors[J]. Journal of the Graduate School of the Chinese Academy of Science,2011,28(4):548-550.
[3]KARL K,NORTON.Remarks on the number of factors of an odd perfect number[J].Acta Arith,1961,(6): 365-374.
[4]ZHANG Si-bao.On the number of distinct prime factors of a kind of 2nd order perfect number[J].Journal of Jiangnan University,2010,9(3):353-355.
[5]LIU Xiu-sheng.Some results on perfect number[J].Journal of Hubei Adult Education Institute,2001,(3): 48-49.
[6]GOTO T,OHNO Y.Odd perfect numbers have a prime factor exceeding 108[J].Math Comp,1981,(77): 1859-1868.
[7]COHEN G L,SORLI R M.On the number of distinct prime factors of odd perfect number[J].Journal of Discrete Algorithms,2003,(1):21-35.
tion:11N25,11Y70
CLC number:O156.1Document code:A
1002–0462(2014)02–0167–04
date:2011-11-14
Supported by the Science Foundation of Kashgar Teacher’s College(112390)
Biography:ZHANG Si-bao(1978-),male,native of Xiajiang,Jiangxi,a lecturer of Kashi Teacher’s College, M.S.D.,engages in number theory.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Outer P(ρ,σ)-set’s Random Characteristic and Application
- On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables
- Biserial Incidence Algebras
- Bicriteria Scheduling on a Series-Batching Machine to Minimize Makespan and Total Weighted Completion Time with Equal Length Job
- Characterizing C6+P2-graphic Sequences
- Properties for Certain Subclasses of Analytic Functions Associated with Generalized Multiplier Transformation
