Properties for Certain Subclasses of Analytic Functions Associated with Generalized Multiplier Transformation
LI Zong-tao,GUO Dong
(1.Foundation Department,Guangzhou Civil Aviation College,Guangzhou 510403,China;2.Foundation Department,Chuzhou Vocational and Technical College,Chuzhou 239000,China)
Properties for Certain Subclasses of Analytic Functions Associated with Generalized Multiplier Transformation
LI Zong-tao1,GUO Dong2
(1.Foundation Department,Guangzhou Civil Aviation College,Guangzhou 510403,China;2.Foundation Department,Chuzhou Vocational and Technical College,Chuzhou 239000,China)
In this paper,we introduce certain new subclasses of analytic functions def i ned by generalized multiplier transformation.By using the dif f erential subordination,we study and investigate various inclusion properties of these classes.Also inclusion properties of these classes involving the integral operator are considered.
analytic functions;subordination;convolution;multiplier transformation;inclusion properties
§1.Introduction
Let A denote the class of functions in the open unit disk U={z:|z|<1},normalized by

A analytic function f(z)is subordinate to analytic function g(z),written as f(z)?g(z),if there exists a analytic function w(z)in U such that w(0)=0 and|w(z)|<1 and f(z)=g(w(z)).
The convolution of two analytic functionsdef i ned by

Let N be the class of all analytic functions φ(z)which are univalent in U and for which φ(U)is convex with φ(0)=1 and Re{φ(z)}>0 in U.
Making use of the principle of subordination between analytic functions,we introduce the subclasses S?(ξ,φ),K(ξ;φ)and C(ξ,ρ;φ,ψ)of the class A,0≤ξ,ρ<1 and φ,ψ∈N,which are def i ned by

and
We note that

Set the function

For a=1,

which is discussed in[1].
Analogous to[1],the following operator is introduced




The following relations are easily derived that

Next,by using the operator Ika,c(λ,μ)f(z),we introduce the following subclasses of analytic functions for 0≤ξ,ρ<1 and φ,?∈N
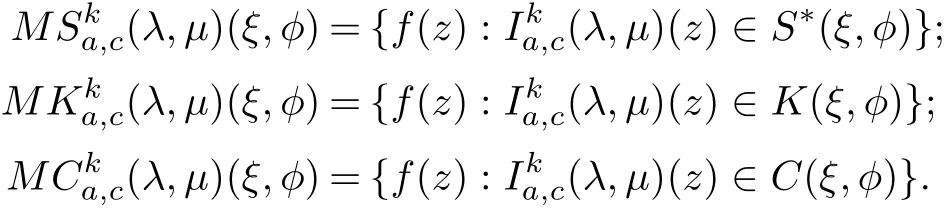
We also note that

§2.Inclusion Properties Involving(λ,μ)f
In order to prove our results,we shall make use of the following known results.
Lemma 2.1[4]Let φ be convex univalent in U with φ(0)=1 and R{κφ(z)+η}>0(κ,η∈?).If p is analytic in U with p(0)=1,then
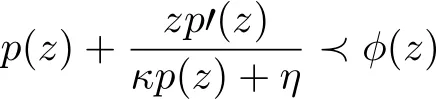
implies

Lemma 2.2[5]Let φ be convex univalent in U and w be analytic in U with R{w(z)}≥0. If p is analytic in U with p(0)=φ(0),then

implies
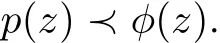
For simplicity,unless otherwise mentioned we shall writeλ,μ)f(z)=Ikf(z)throughout this paper.
Theorem 2.1If φ∈N and Re{(1?ξ)φ(z)+(ξ?1)+>0,then
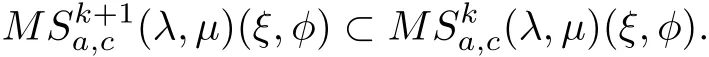

where p is analytic in U with p(0)=1.
Rearranging(1.4),we have

Dif f erentiating(2.2)and multiplying by z gives that


Theorem 2.2If φ∈N and Re{(1?ξ)φ(z)+(ξ?1)+>0,then
ProofBy using(1.6)and Theorem 2.1,it follows that

which proves Theorem 2.2.
Theorem 2.3If φ,ψ∈N and Re{(1?ξ)φ(z)+(ξ?1)+}>0,then



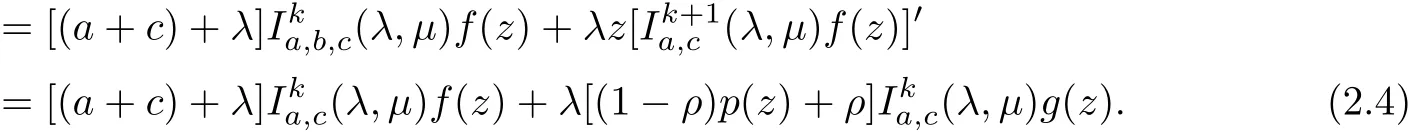
Dif f erentiating(2.4)with z and multiplying by z,we get


Applying(1.4)again,we have

From(2.5)and(2.6),we have

Since h(z)?ψ(z)and Re{(1?ξ)φ(z)+(ξ?1)+>0,then Re{(1?ξ)h(z)+(ξ?1)+}>0.
Theorem 2.4If k,c,λ≥0,μ≥1,then

where φ∈N.
Make use of the dif f erentiation on both sides in(2.7)and set p(z)we have

Sinceμ≥1,φ(z)∈N,Re{φ(z)+(μ?1)}>0,using Lemma 2.1,we get p(z)?φ(z).Thus, f(z)∈(λ,μ,φ).The proof is complete.
By using similar manner,we obtain the following results.
Theorem 2.5If k,c,λ≥0,μ≥1,then
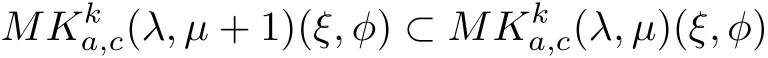
and

where φ∈N.
§3.Inclusion Properties Involving Integral Operators
In this section,we present integral-preserving properties of general Bernardi-Libera-Livington integral operator def i ned by[6-9]

From(3.1),we have

Theorem 3.1Let δ>?1 and φ(z)∈N with Re[(1?ξ)φ(z)+δ+ξ]>0.If f∈(λ,μ)(ξ,φ),then


where p is analytic in U with p(0)=1.
From(3.2)and(3.3),we have

Taking the dif f erentiation on the both sides of(3.4)and multiplying by z,we obtain

Applying Lemma 2.1 to(3.5),we conclude that Fδ(f)(z)∈(λ,μ)(ξ,φ).
Similarly applying(1.6)and Theorem 3.1,we have the following result.
Theorem 3.2Let δ>?1 and φ(z)∈N with Re[(1?ξ)φ(z)+δ+ξ]>0.If f∈MKka,c(λ,μ)(ξ,φ),then

Theorem 3.3Let δ>?1 and φ(z)∈N with Re[(1?ξ)φ(z)+δ+ξ]>0.If f∈(λ,μ)(ξ,ρ,φ,ψ),then

ProofLetf(z)∈MCka,c(λ,μ)(ξ,ρ,φ,ψ),then there exists a function g(z)∈(λ,μ) (ξ,φ)such that

We set
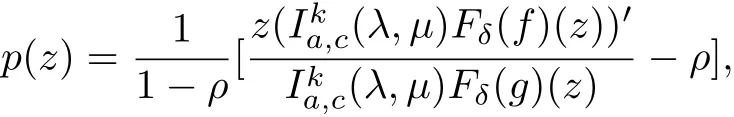
where p(z)is analytic in U with p(0)=1.Since g(z)∈(λ,μ)(ξ,φ),we have from Theorem 3.1,that Fδg(z)∈(λ,μ)(ξ,φ).Using(3.2)we obtain

By simple calculations,we get


Applying Lemma 2.1 to(3.7),we can show that p(z)?ψ(z)so that f(z)∈(λ,μ) (ξ,ρ,φ,ψ),which proves Theorem 3.3.
[References]
[1]OMAR R,HALIM S A.Subclasses of analytic functions associated with generalised multiplier transformations[J].ISRN Mathematical Analysis,Vol 2012,Article ID 632429,9 pages,2012,doi:10.5402/2012/632429.
[2]DARUS M,FAISAL I.Inclusion properties of certain of analytic functions[J].Revista Notas de Matematica, 2011,7(305):66-75.
[3]KWON O,CHO N.Inclusion properties for certain subclasses of analytic functions def i ned by a multiplier transformation[J].Eur J Pure Appl Math J,2010,3:1124-1136.
[4]ENIGENBERG P,MILLER S S,MOCANU P T,et al.On a Briot-Bouquet dif f erential subordination[J]. General Inqualities,1983,3:339-348.
[5]MILLER S S,MOCANU P T.Dif f erential subordination and univalent functions[J].The Michigan Mathematical Journal,1981,28:157-171.
[6]BERNARDI S D.Convex and starlike univalent functions[J].Transactions of the American Mathematical Society,1969,135:429-446.
[7]JUNG I B,KIM Y C,SRIVASTAVA H M.The Hardy space of analytic functions associated with certain one-parameter families of integral operators[J].Journal of Mathematical Analysis and Applications,1993, 176(1):138-147.
[8]LIBERA R J.Some classes of regular univalent functions[J].Proceedings of the American Mathematical Society,1965,16:755-758.
[9]LIVINGTON A E.On the radius of univalence of certain analytic functions[J].Proceedings of the American Mathematical Society,1966,17:352-357.
tion:30C45
CLC number:O174.51Document code:A
1002–0462(2014)02–0257–08
date:2012-10-25
Supported by the Natural Science Foundation of Department of Education of Anhui Province(KJ2012Z300)
Biographies:LI Zong-tao(1970-),male,native of Taian,Shandong,a lecturer of Guangzhou Civil Aviation College,M.S.D.,engages in theory of functions;GUO Dong(1976-),male,native of Linyi,Shandong,a lecturer of Chuzhou Vocational and Technical College,M.S.D.,engages in complex analysis.
 Chinese Quarterly Journal of Mathematics2014年2期
Chinese Quarterly Journal of Mathematics2014年2期
- Chinese Quarterly Journal of Mathematics的其它文章
- Some Results of a Certain Odd Perfect Number
- Outer P(ρ,σ)-set’s Random Characteristic and Application
- On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables
- Biserial Incidence Algebras
- Bicriteria Scheduling on a Series-Batching Machine to Minimize Makespan and Total Weighted Completion Time with Equal Length Job
- Characterizing C6+P2-graphic Sequences
