Characterizing C6+P2-graphic Sequences

HU Li-li

(Department of Mathematics and Information Science,Zhangzhou Teacher’s College,Zhangzhou 363000 China)

Characterizing C6+P2-graphic Sequences

HU Li-li

(Department of Mathematics and Information Science,Zhangzhou Teacher’s College,Zhangzhou 363000 China)

For a given graph H,a graphic sequence π=(d1,d2,···,dn)is said to be potentially H-graphic if π has a realization containing H as a subgraph.In this paper,we characterize the potentially C6+P2-graphic sequences where C6+P2denotes the graph obtained from C6by adding two adjacent edges to the three pairwise nonadjacent vertices of C6.Moreover,we use the characterization to determine the value of σ(C6+P2,n).

graph;degree sequence;potentially C6+P2-graphic sequences

§1.Introduction

We consider f i nite simple graphs.Any undef i ned notation follows that of Bondy and Murty[1].The set of all non-increasing nonnegative integer sequence π=(d1,d2,···,dn)is denoted by NSn.A sequence π∈NSnis said to be graphic if it is the degree sequence of a simple graph G of order n;such a graph G is referred to as a realization of π.Let GSndenote the set of all graphic sequences in NSn.Let Ckand Pkdenote a cycle on k vertices and a path on k+1 vertices,respectively.Let σ(π)be the sum of all the terms of π.A graphic sequence π is said to be potentially H-graphic if it has a realization G containing H as a subgraph. Let G?H denote the graph obtained from G by removing the edges set E(H),where H is a subgraph of G.In the degree sequence,rtmeans r repeats t times.

For a given graph H,Gould,Jacobson and Lehel[2]considered the following problem:determine the smallest even integer σ(H,n)such that every n-term positive graphic sequence π=(d1,d2,···,dn)with σ(π)≥σ(H,n)is potentially H-graphic.For many kinds of graph H,the problem of determining the smallest degree sum that yields potentially H-graphic sequences has been solved,see also review articles[6,8].

In the research of degree sequence,a harder question is to characterize the potentially H-graphic sequences without zero terms.Yin and Chen[9]characterized the potentially K2,4-graphic sequences.Yin et al[10]characterized the potentially K6-graphic sequences.Hu and Lai[4]characterized the potentially K3,3and K6?C6-graphic sequences.In this paper,we characterize the potentially C6+P2-graphic sequences where C6+P2denotes the graph obtained from C6by adding two adjacent edges to the three pairwise nonadjacent vertices of C6. Moreover,we use the characterization to determine the value of σ(C6+P2,n).

§2.Preliminaries

Let π=(d1,···,dn)∈NSn,1≤k≤n.Let

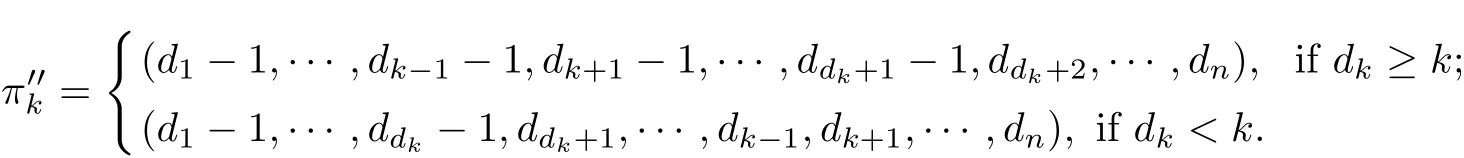
For a nonincreasing nonnegative integer sequence π=(d1,d2,···,dn),we write m(π)and h(π)to denote the largest positive term of π and the smallest positive term of π,respectively. We need the following results.

Theorem 2.1[2]If π=(d1,d2,···,dn)is a graphic sequence with a realization G containing H as a subgraph,then there exists a realization G0of π containing H as a subgraph so that the vertices of H have the largest degrees of π.

Theorem 2.2[7]If π=(d1,d2,···,dn)is a sequence of nonnegative integers with 1≤m(π)≤2,h(π)=1 and even σ(π),then π is graphic.

Lemma 2.3[3]If π=(d1,d2,···,dn)is a nonincreasing sequence of positive integers with even σ(π),n≥4,d1≤3 and π/=(33,1),(32,12),then π is graphic. Lemma 2.4[5]π is graphic if and only if π0is graphic. The following corollary is obvious.

Corollary 2.5Let H be a simple graph.If π0is potentially H-graphic,then π is potentially H-graphic.

§3.Main Theorems

Theorem 3.1Let n≥6,π=(d1,d2,···,dn)∈GSn.Then π is potentially C6+P2-graphic if and only if the following conditions hold

(1)d1≥4,d3≥3 and d6≥2;

(2)d1=n?1 implies d4≥3;

(3)π=(d1,d2,d3,2i,1n?3?i)implies d1+d2+d3≤n+i+3;in particular,if d3=3,then d1+d2≤n+i?2;

(4)π/=(n?t,k,32,2k?2?t,1n?k+t?2),where t+4≤k≤n?1 and 1≤t≤k?4;

(5)π/=(44,22),(4,32,24),(4,32,25).

ProofFirst we show the necessity.Assume that π=(d1,d2,···,dn)is potentially C6+P2-graphic.(1)and(5)are obvious.Let G be a realization of π which contains C6+P2and let v∈V(G)with degree d(v)=d1.Then G?v1contains P4.Thus,G?v1contains at least three vertices with degree at least 2.Therefore,d1=n?1 implies d4≥3.Hence,(2)holds.If π=(d1,d2,d3,2i,1n?3?i)is potentially C6+P2-graphic,then according to Theorem 2.1,there exists a realization G of π containing C6+P2as a subgraph so that the vertices of C6+P2have the largest degrees of π.Therefore,the sequence π1=(d1?4,d2?3,d3?3,2i?3,1n?3?i) obtained from G?(C6+P2)is graphic.It follows d1?4+d2?3+d3?3≤2+2(i?3)+n?3?i, i.e.,d1+d2+d3≤n+i+3.In particular,if d3=3,then d1?4+d2?3≤2(i?3)+n?3?i, i.e.,d1+d2≤n+i?2.Hence,(3)holds.If π=(n?t,k,32,2k?2?t,1n?k+t?2)is potentially C6+P2-graphic,then according to Theorem 2.1,there exists a realization G of π containing C6+P2as a subgraph so that the vertices of C6+P2have the largest degrees of π.Therefore, the sequence π2=(n?t?4,k?3,1,2k?4?t,1n?2?k+t)obtained from G?(C6+P2)must be graphic.It follows n?t?4+k?3+1≤2+2(k?4?t)+(n?2?k+t),i.e.,0≤?2,a contradiction.Hence,(4)holds.

Now we prove the sufficiency.Suppose π=(d1,d2,···,dn)∈GSnsatis fi es the conditions (1)～(5).Our proof is by induction on n.We fi rst prove the base case where n=6.Since π/=(44,22),(52,32,22),then π is one of the following:(56),(54,42),(53,42,3),(53,33),(52,44), (52,43,2),(52,42,32),(52,4,32,2),(52,34),(5,44,3),(5,43,3,2),(5,42,33),(5,42,3,22), (5,4,33,2),(5,35),(5,33,22),(46),(45,2),(44,32),(43,32,2),(43,23),(42,34),(42,32,22), (4,34,2),(4,32,23).It is easy to check that all of these are potentially C6+P2-graphic.Now suppose that the sufficiency holds for n?1(n≥7),we will show that π is potentially C6+P2-graphic in terms of the following cases.

Case 1dn≥4.It is easy to check that π0=,···,satis fi es(1)～(5).Thus, by the induction hypothesis,π0is potentially C6+P2-graphic,and hence so is π. Case 2dn=3.Consider π0=(,···,)where≥3 and≥2.Clearly, π0satis fi es(2),(3),(5).If π0also satis fi es(1)and(4),then by the induction hypothesis,π0is potentially C6+P2-graphic and hence so is π.

If π0does not satisfy(1),then=3,so d1=4.It follows π=(4k,3n?k)where 1≤k≤3. Now we show that π is potentially C6+P2-graphic.

If k=1,then π=(4,3n?1)where n is odd.It is easy to see that(4,36)and(4,38)are potentially C6+P2-graphic.Let G1be a realization of(4,36)which contains C6+P2.If n≥11,then π1=(3n?7)is graphic by Lemma 2.3.Let G2be a realization of π1,then G1∪G2is a realization of(4,3n?1).Thus,π=(4,3n?1)is potentially C6+P2-graphic.With the same argument,one can easily show that(42,3n?2)and(43,3n?3)are also potentiallyC6+P2-graphic.

If π0does not satisfy(4),then π0is just(52,32,22).Hence π=(62,32,23)which contradicts dn=3.

Case 3dn=2.Consider π0=(),where≥3 and≥2.If π0satis fi es(1)～(5),then by the induction hypothesis,π0is potentially C6+P2-graphic and hence so is π.

If π0does not satisfy(1),there are three subcases

Subcase 3.2d01=d03=3.In this case,π=(42,3k,2n?2?k)where k≥1 and k is even or π=(4,3k,2n?1?k),where k≥3 and k is even.Now we show that these sequences are potentially C6+P2-graphic.

For the sequence π=(42,3k,2n?2?k),when k=2,π=(42,32,2n?4).It suffices to show π1=(2n?6,12)is graphic.By σ(π1)being even and Theorem 2.2,π1is graphic.If k=4, then π=(42,34,2n?6).It is easy to check that(42,34)is potentially C6+P2-graphic.Let G1be a realization of(42,34)which contains C6+P2.One can easily show that that(42,34,2) and(42,34,22)are potentially C6+P2-graphic.If n≥9,then G1∪Cn?6is a realization of (42,34,2n?6).In other words,(42,34,2n?6)is potentially C6+P2-graphic.We now consider k≥6.In this case,let π2=(42,34),π3=(3k?4,2n?2?k).If n≥10,then π3is graphic by Lemma 2.3.Let G2be a realization of π3,then G1∪G2is a realization of π.If n≤9,then π=(42,36,2)which is potentially C6+P2-graphic.Thus,π=(42,3k,2n?2?k)is potentially C6+P2-graphic.With the same argument as above,one can show that(4,3k,2n?1?k)is also potentially C6+P2-graphic.

If π0does not satisfy(2),then=n?2 and d=2.In this case,π=(n?1,33,2n?4).Since the residual sequence π10=(23,1n?4)obtain from π1by deleting the term n?1 is potentially P4graphic,thus π=(n?1,33,2n?4)is potentially C6+P2-graphic.

If π0does not satisfy(3),then π0=(2n?4)and＞2n?2.Thus, d1+d2+d3=+2＞2n,a contradiction.Moreover,if π0=(,3,2n?4)and＞2n?5,then d1+d2=d+2＞2n?3,a contradiction.Thus,π0satis fi es(3).

If π0does not satisfy(4),then π0=(n+t?3,n?1?t,32,2n?5).Since≤n?2,we have t=1,i.e.,π0=((n?2)2,32,2n?5).It follows π=((n?1)2,32,2n?4),which contradicts condition(4).Thus,π0satis fi es(4).

If π0does not satisfy(5),then π0=(44,22),(4,32,24),(4,32,25).Therefore,π is one of the following(52,42,23),(5,4,3,25),(43,25),(5,4,3,26),(43,26).It is easy to see that all of these are potentially C6+P2-graphic.

Case 4dn=1.Consider π0=(,···,d0n?1),where≥3 and≥2.If π0satis fi es (1)～(5),then by the induction hypothesis,π0is potentially C6+P2-graphic and hence so is π.

If π0does not satisfy(1),then=3.It follows d1=4,d2=d3=3,so π= (4,3k,2t,1n?1?k?t)where k≥2,k+t≥5,n?1?k?t≥1.We are going to show that π is potentially C6+P2-graphic.If k=2,then π=(4,32,2t,1n?3?t).Let π1=(2t?3,1n?3?t). By σ(π1)being even and Theorem 2.2,π1is graphic.Let G1be a realization of π1,then C6+P2∪G1is a realization of π=(4,32,2t,1n?3?t).Similarly,one can easily show that π=(4,3k,2t,1n?1?k?t)is potentially C6+P2-graphic for the cases k=3,4,5.When k≥6,let π2=(4,36),π3=(3k?6,2t,1n?1?k?t).Let G2be a realization of(4,36)which contains C6+P2. If n≥11 and π3/=(33,1),(32,12),then π3is graphic by Lemma 2.3.Let G3be a realization of π3,then G2∪G3is a realization of π.If π3=(33,1)or(32,12),then π=(4,39,1)or(4,38,12). If n≤10,then π is one of the following:(4,36,12),(4,36,2,12),(4,37,1),(4,37,2,1).It is easy to check that all of these are potentially C6+P2-graphic.Thus,π=(4,3k,2t,1n?1?k?t) is potentially C6+P2-graphic.

If π0does not satisfy(2),then=n?2 and=2.In this case,either d1=n?1, d4=2 or d1=d2=n?2,d4=2.But the former contradicts condition(2).For the latter, we have π=((n?2)2,d3,2i,1n?3?i).By π satis fi es(3),2(n?2)+d3≤n+i?3,i.e., i≥n?1+d3≥n+2,a contradiction.Hence,π0satis fi es(2).

If π0does not satisfy(3),then π0=(1n?4?i)and＞n+i+2.Thus, d1+d2+d3=+1＞n+i+3,a contradiction.Moreover,If π0=3,2i,1n?4?i) and＞n+i?3,then d1+d2=+1＞n+i?2,a contradiction.Thus,π0satis fi es(3).

If π0does not satisfy(4),then π0=(n?1?t,k,32,2k?2?t,1n?k+t?3).If n?1?t＞k+1, then π=(n?t,k,32,2k?2?t,1n?k+t?2),which contradicts condition(4).If n?1?t=k+1, then π0=(n?1?t,n?2?t,32,2n?2t?4,12t?1).Thus,π=(n?t,n?2?t,32,2n?2t?4,12t) or((n?1?t)2,32,2n?2t?4,12t),which contradicts condition(4).Thus,π0satis fi es(4).

If π0does not satisfy(5),then π0=(44,22),(4,32,24),(4,32,25).Therefore,π is one of the following

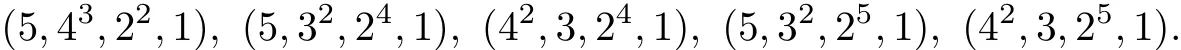
It is easy to see that all of these are potentially C6+P2-graphic.

§4.Application

In this section,we will use the above theorem to fi nd exact value of σ(C6+P2,n).

CorollaryIf n≥6,then σ(C6+P2,n)=4n?2.

ProofFirst we claim that for n≥6,σ(C6+P2,n)≥4n?2.Take π1=((n?1)2,32,2n?4), then σ(π1)=4n?4 and it is easy to see that π1is not potentially C6+P2-graphic by Theorem 3.1.Thus,σ(C6+P2,n)≥4n?4+2=4n?2.

Now we show that σ(C6+P2,n)≤4n?2.Let π be an n-term(n≥6)graphic sequence with σ(π)≥4n?2,we only need to show that π is potentially C6+P2-graphic.

If d1≤3,then σ(π)≤3n＜4n?2,a contradiction.Hence,d1≥4.

If d3≤2,then σ(π)≤2(n?1)+2(n?2)=4n?6＜4n?2,a contradiction.Hence,d3≥3.

If d6=1,then σ(π)=d1+d2+d3+d4+d5+(n?5)≤20+2(n?5)=2n+10＜4n?2, a contradiction.Hence,d6≥2.

If d1=n?1 and d4≤2,then σ(π)≤n?1+d2+d3+2(n?3)≤n?1+4+n?3+2n?6= 4n?6＜4n?2,a contradiction.

Since σ(π)≥4n?2,then π is not one of the following

(d1,d2,d3,2i,1n?3?i),(n?t,k,32,2k?2?t,1n?k+t?2),(44,22),(4,32,24),(4,32,25).

Thus,π satisf i es the conditions(1)～(5)in Theorem 3.1.Therefore,π is potentially C6+P2-graphic.

[1]BONDY J A,MURTY U S R.Graph Theory with Applications[M].Beijing:Science Press,1984.

[2]GOULD R J,JACOBSON M S,LEHEL J.Potentially G-graphic degree sequences[J].Combinatorics,Graph Theory and Algorithms,1999,1:451-460.

[3]HU Li-li,LAI Chun-hui.On potentially K5-Z4-graphic sequences[J].J of Zhangzhou Teacher’s College, 2009,22:10-12.

[4]HU Li-li,LAI Chun-hui.On potentially 3-regular graph graphic sequences[J].Utilitas Mathematica,2009, 80:33-51.

[5]KLEITMAN D J,WANG D L.Algorithm for constructing graphs and digraphs with given valences and factors[J].Discrete Math,1973,6:79-88.

[6]LAI Chun-hui,HU Li-li.Potentially Km-G-graphical sequences:a survey[J].Czechoslovak Maths Journal, 2009,59:1059-1075.

[7]LI Jiong-sheng,YIN Jian-hua.A variation of an extremal theorem due to Woodall[J].Southeast Asian Bulletin of Math,2001,25:427-434.

[8]LI Jiong-sheng,YIN Jian-hua.Extremal graph theory and degree sequences[J].Adv Math,2004,33:273-283.

[9]YIN Jian-hua,CHEN Gang.On potentially Kr1,r2,···,rm-graphic sequences[J].Utilitas Mathematica,2007, 72:149-161.

[10]YIN Meng-xiao,YIN Jian-hua.On potentially H-graphic sequences[J].Czechoslovak Mathematical Journal, 2007,57:705-724.

tion:05C07

CLC number:O157.5Document code:A

1002–0462(2014)02–0238–06

date:2012-09-18

Supported by the National Natural Science Foundation of China(11101358);Supported by the Project of Fujian Education Department(JA11165);Supported by the Project of Education Department of Fujian Province(JA12209);Supported by the Project of Zhangzhou Teacher’s College(SJ1104)

Biography:HU Li-li(1982-),female,native of Zhangzhou,Fujian,a lecturer of Zhangzhou Teacher’s College, M.S.D.,engages in graph theory.