Analytical and Numerical Studies of Quantum Plateau State in One Alternating Heisenberg Chain?

JIANG Jian-Jun(蔣建軍),LIU Yong-Jun(劉擁軍),TANG Fei(唐菲),YANG Cui-Hong(楊翠紅), and SHENG Yu-Bo(宇波)

1Department of Physics,Sanjiang College,Nanjing 210012,China

2School of Physics Science and Technology,Yangzhou University,Yangzhou 225002,China

3Department of Electronic and Information Engineering,Yangzhou Polytechnic Institute,Yangzhou 225127,China

4School of Physics and Optoelectroic Engineering,Nanjing University of Information Science and Technology,Nanjing 210044,China

5Institute of Signal Processing Transmission,Nanjing University of Postsand Telecommunications,Nanjing 210003,China

1 Introduction

Research relating to one-dimensional quantum antiferromagnetic spin chains has been an attractive f i eld in low-dimensional quantum magnetism.Usually,there are two kinds of uniform antiferromagnetic Heisenberg chains.One case is given by the spin chain with half integer spin,and another case is given by the spin chain with integer spin.The classical magnetic long-range order of these two chains disappears as a result of the strong quantum f l uctuations due to the low dimensionality.The half integer spin chain has a gapless spectrum and a power-law decay correlation function.By contrast,Haldane proposed in 1983 there is a gap between the ground state and the f i rst excited state for the integer spin chain and that the correlation function decays exponentially.[1]There are many theoretical studies that have subsequently validated Haldane’s conjecture.For example,the research on the AKLT model shows that each s=1 spin in the ground state can be viewed as two s=1/2 spins in the symmetric triplet state.[2]In Ref.[3],den Nijs and Rommelse proposed that,although the ground state of the integer spin chain is disordered,it possesses a hidden antiferromagnetic order,which can be measured by the string order parameter.It was pointed out by Kennedy and Tasaki that the hidden order is a discrete Z2×Z2symmetry.[4]Numerical results indicate that the spin gap in the s=1 spin chain is about 0.41J,where J is the strength of the antiferromagnetic interaction.[5]In addition to this evidence provided by theoretical calculations,the experimental evidence is that the m=0(m is the magnetization per site)magnetization plateau found in the compound[Ni(en)2(NO2)]ClO4,also shows the spin gap of the s=1 spin chain does exist.[6]

The magnetization plateau in the magnetization process,which is caused by the spin gap,is a very interesting quantum phenomenon in the spin chain.In 1997,Oshikawa,Yamanaka,and Aラeck pointed out that the necessary condition for the appearance of the magnetization plateau is

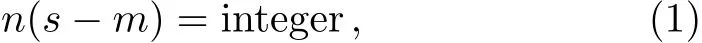
where n is the period of the ground state.[7]One typical example that satisf i es the above condition is the mixed spin chain.For example,the mixed spin(1,1/2)Heisenberg chain possesses the m=1/4 plateau state and it can be used to describe the properties of the actual oxamato compound NiCu(pba)(D2O)32D2O.[8?9]Another example is the bond alternating Heisenberg chain.Due to the diあerent spatial structures,diあerent alternating Heisenberg chains possess various magnetization plateaus.[10?16]For instance,the spin-1/2 tetrameric Heisenberg chain with alternating coupling ferromagnetic-ferromagneticantiferromagnetic-antiferromagnetic,which has been realized in the compound Cu(3-Clpy)2(N3)2,has the m=1/4 magnetization plateau.[11]

In the present paper,we study the behaviour of the magnetization plateau of an alternating Heisenberg spin chain by using the analytical coupled cluster method(CCM)and numerical density matrix renormalization group(DMRG)method.[5]The model is shown in Fig.1 and the Hamiltonian is

where S4i+j(j= ?3,?2,?1,0,and 1)is a spin-1/2 operator.J and αJ(α ≥ 1)denote the antiferromagnetic couplings.When α=1,the model(2)reduces to the isotropic Heisenberg chain in an external magnetic f i eld.In that case,the phase diagram of the model is exactly known and it only possesses the classical saturation plateau.[17]When α/=1,according to Eq.(1),model(2)may exhibit the m=0 and m=1/4 plateau states besides the m=1/2 plateau state.In the following discussion,our main goal is to study the eあect of modulating parameter α on the properties of the m=0 and m=1/4 plateau states that are caused by quantum f l uctuations.We now assume,without losing generality,that J=1 throughout the rest of this paper.

We now describe the organization of this paper.In the next section,the details of the application of CCM formalism to model(2)are described.In Sec.3,the application of the DMRG to the alternating chain is given.In Sec.4,the results of CCM and DMRG are presented.A summary is given in the f i nal section.

2 The Coupled Cluster Method Applied to the Alternating Heisenberg Chain

In recent years,a quite new method called CCM has been successfully applied to diあerent quantum spin chains.[18?30]Detailed descriptions of the CCM applied to quantum spin systems have been given in papers.[18,20?21]

We just focus on the application of CCM to m=0 plateau state of the alternating Heisenberg chain.When m=0,Hamiltonian(2)is equivalent to the following Hamiltonian

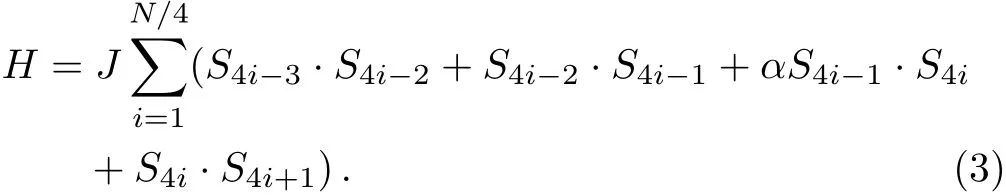
The critical f i eld hc1of model(2),at which the m=0 plateau state disappears,equals to the spin gap of Hamiltonian(3).So,we can use Hamiltonian(3)to investigate the properties of the m=0 plateau state.The starting point of any CCM calculation is to choose a model state|φ〉and this is often a classical spin state.So we choose the Neel state(···↑↓↑↓ ···)as the model state for model(3).Then we perform a rotation of the local axes of the“up” spins by 180°about the y-axis such that all spins in the model state align along the negative z-axis.After this rotation,the CCM parameterization of the ket ground state of model(3)is given by[20?21]

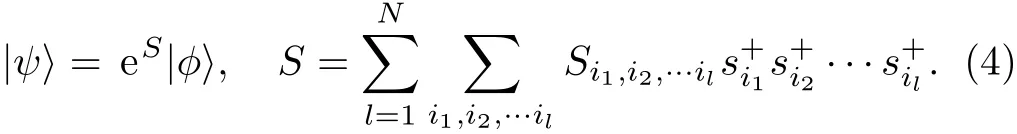
The CCM formalism is exact if all spin con fi gurations in the S correlation operator are considered,but it is impossible in practice.In this paper,a quite general approximation scheme called LSUBn is used to truncate the expansion of the operator S.[20?21]In the LSUBn approximation,only the con fi gurations including n or fewer correlated spins which span a range of no more than n contiguous lattice sites are retained.The fundamental confi gurations contained in the LSUBn approximation can be reduced by using the lattice symmetries and furthermore by the imposing that restriction that=0.We note that the ground state of model(3)lies in the subspace Stzol=0.The number of LSUBn con fi gurations is given in Table 1.

Table 1 Numberoffundamentalcon fi gurations of the LSUBn approximation with n={10,12,14}NFdenotes the number of the fundenmental con fi gurations for the ground state with Stzol=0,NFedenotes the number of the fundenmental con fi gurations for the excited state with Stzol=1.

Once the correlation coeきcients contained in the operator S have been found then one can use|ψ〉to calculate the ground state energy Egof Hamiltonian(3)by using the following formula

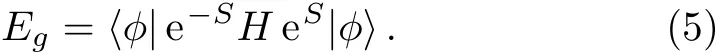
To obtain the correlation coeきcients contained in the operator S,one needs to solve the ket-state equations,which are given by[20?21]

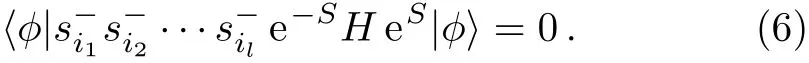
After these coupled equations are solved,the correlation coeきcients retained in the LSUBn approximation can be obtained.We can use the CCM ket-state correlation coeffi cients to calculate the ground state energy using formula(5).As the derivation of the coupled equations for higher orders of approximation is extremely tedious,we have developed our own programme by using Matlab to automate this process according to the method discussed in Ref.[21].The Matlab code with double precision was performed on a private computer.

Then,by applying an excitation operator Xelinearly to the ket-state wave function(4),an excited state wave function|ψe〉of model(3)can be obtained[20]

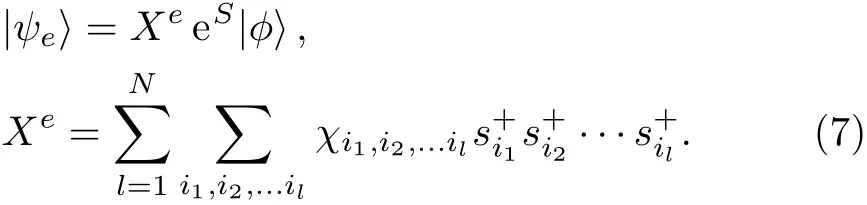
Analogously to the ground state,we also use the LSUBn approximation scheme to truncate the expansion of the operator Xe.One can fi nd the fundamental excited state con fi gurations retained in the LSUBn approximation by using the lattice symmetry and the restricted condition Stzol=+1 or?1.Table 1 also gives the number of such fundamental con fi gurations.

To get the excitation energy εe(εeis the diあerence between the excited state energy and the ground state energy),one can use the method introduced in Ref.[20]to obtain the LSUBn eigenvalue equations.Those equations with eigenvalues εeand corresponding eigenvectorsare as follows

The excitation energy gap Δ can be obtained from the lowest eigenvalue of Eq.(8).

Since the LSUBn approximation becomes exact in the limit n→∞,we need to extrapolate the LSUBn results to the limit n → ∞.[20?21]For the ground state energy,we use the following well-tested formula

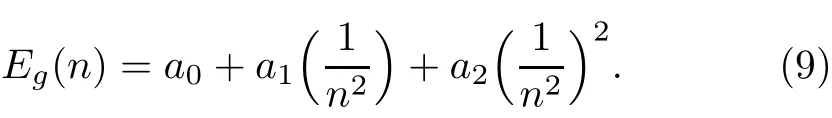
For the gap of the lowest-lying excitations,we use a matrix given by

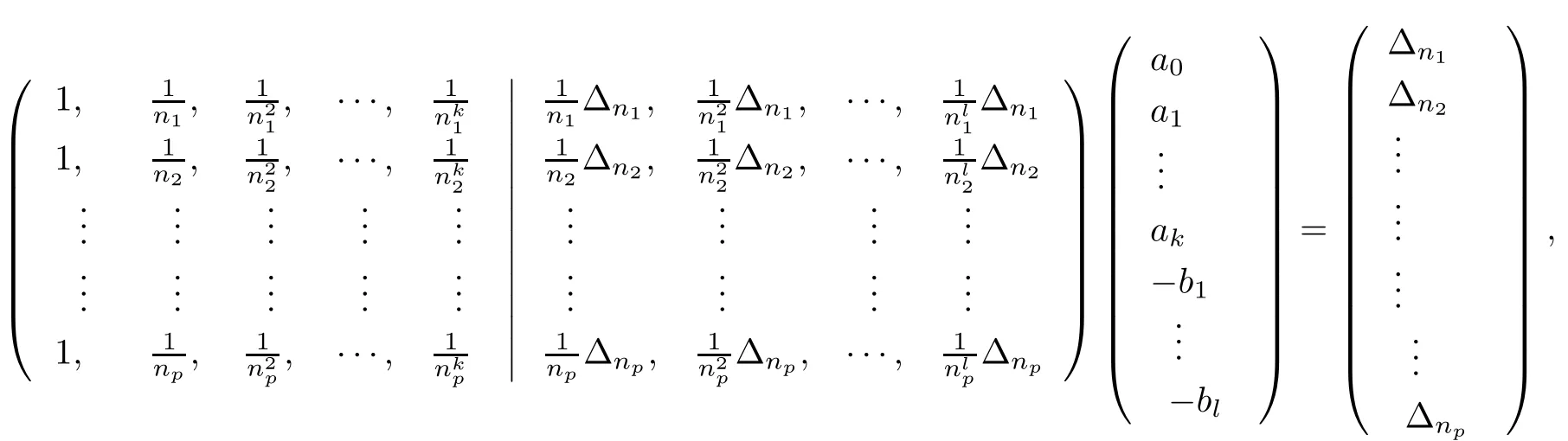
where k+l+1=p and the extrapolated value of Δnis given by a0.In this paper,we use n={10,12,14}for both extrapolation schemes described above.

3 The Application of the Density Matrix Renormalization Group to the Alternating Heisenberg Chain

In this section,we brief l y describe how to treat the alternating Heisenberg chain with the method of DMRG.Similar to the DMRG treatment of the dimerized spin chain,[31]the superblock of Hamiltonian(2)in our DMRG calculation is composed of four blocks S?a?E?b,where S and E are the“system”and “environment”blocks,while a and b denote the elementary blocks respectively added to S and E in each DMRG iteration.Blocks S and b are linked because we use periodic boundary condition in this paper.In the f i rst iteration of the DMRG calculation,both the system and environment blocks only contain one unit cell(4 sites).After one iteration,the system size of the superblock grows by 8 sites as we take one unit cell as the elementary block.1～4 sweeps were done to obtain accurate results.The DMRG programme code was also written in the Matlab environment and performed on a private computer.The number of the state kept per block is 180～240 and the highest errors are in the order of 10?7.

4 Results

4.1 The Magnetization Curve of the Alternating Heisenberg Chain

To f i nd the plateau state of model(2),we calculate the magnetization curve of that model by employing DMRG.Figure 2 displays the magnetization curve for a system size N=64 when α=1.5.Using the method introduced in Ref.[32],we also present the magnetization curve in the thermodynamic limit in Fig.2.It can be seen that,besides the m=0 plateau state in the parameter regime h≤hc1,a f i nite plateau appears at m=1/4.In the following discussion,we focus on the properties of the above two quantum plateau states.

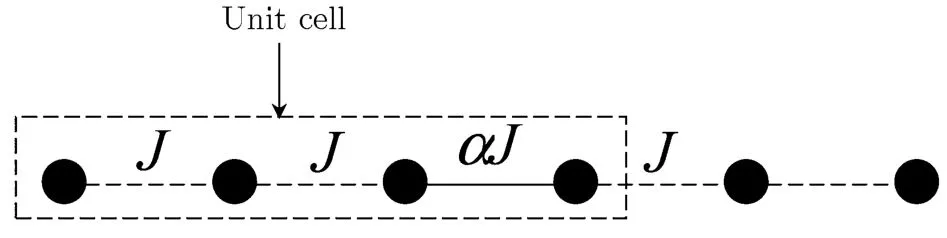
Fig.1 The structure of the alternating Heisenberg spin chain.

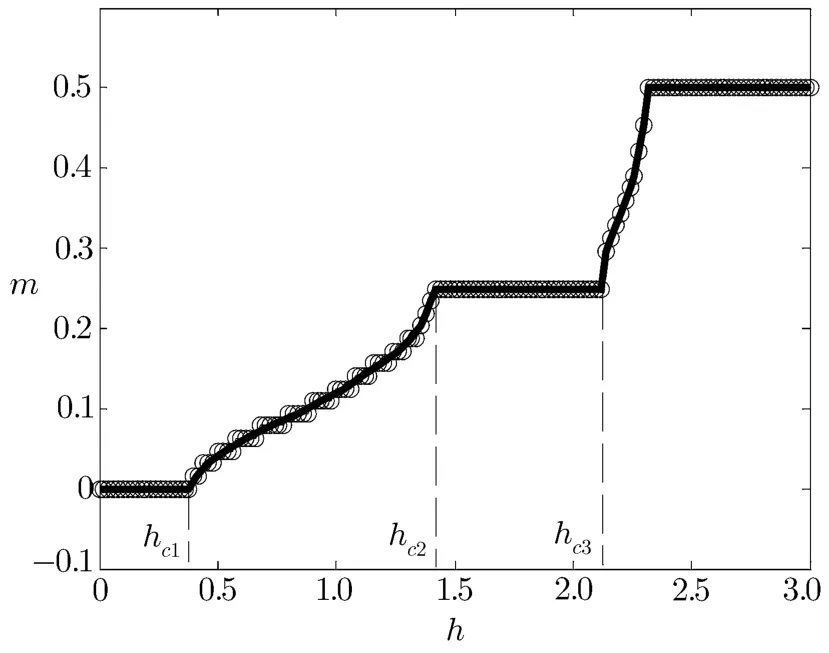
Fig.2 The magnetization m as a function of h when α=1.5.The line with circles represents the magnetization curve for the f i nite chain of N=64.The bold line is the result for the inf i nite chain.

4.2 The m=0 Plateau State

In this section,we discuss the behaviour of the m=0 plateau state,which is caused by the spin gap of Hamiltonian(3).The width of that state equals to the value of the critical f i eld hc1and it is given by

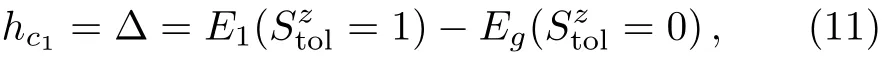
where E1and Egare the energies of the lowest-lying state with Stzol=1 and Stzol=0.When α=1,the spectrum of Hamiltonian(3)is gapless.Thus,model(2)does not possess the m=0 plateau state.In the case of large α or small α,the m=0 plateau state belongs to the dimerized state because the spin pairs S4i?3and S4i?2and the spin pairs S4i?1and S4itend to form singlet dimmers under that condition.One can reasonably predict that a quantum phase transition at a critical point αcbetween the gapless spin-liquid state and the gapped dimerized state occurs in Hamiltonian(3).As the m=0 plateau state only appears in the dimerized state parameter regime,we should f i nd the critical point αc.

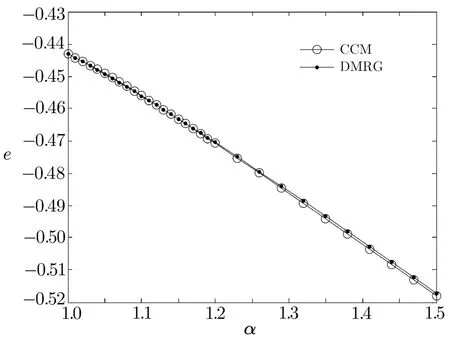
Fig.3 The GS energy per site e versus α using CCM and DMRG.

Fig.4 The second derivative of e,?d2e/dα2as a function of α.

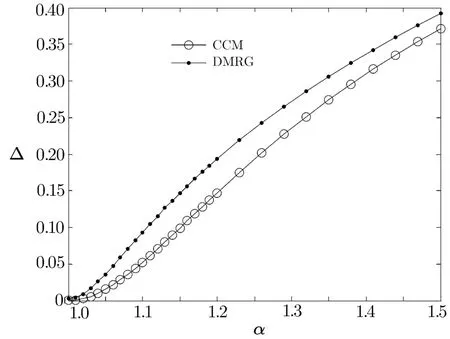
Fig.5 The spin gap Δ versus α using CCM and DMRG.

It is known that the ground state energy density e or its derivative may exhibit special property at the critical point.[33]We search f i rstly for quantum phase transition existing in the alternating chain by using the ground state energy of Hamiltonian(3).Figure 3 shows the ground state energy per site e=Eg/N obtained from CCM and DMRG.The energies calculated by DMRG are extrapolated to the thermodynamic limit by using the following formula with N=32,40,48,56,and 64 spins[34]

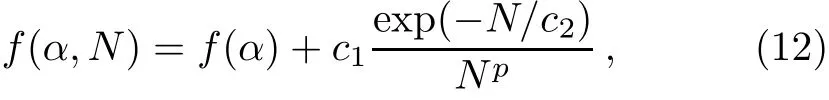
where p=2.When α=1,the energies per site obtained from DMRG and CCM are?0.443 146 and?0.443 138 respectively. They are both close to the exact result?0.443 147.[20]As shown in Fig.3,the ground state energy decreases as a result of increasing α and the results given by DMRG and CCM are in good agreement with each other.Since e changes continuously when α varies,its derivative is calculated.Figure 4 presents the second derivative of e obtained from DMRG.As is apparent in this f i gure,?d2e/dα2,all of the results for various lattice sizes,N,display a peak near α=1.Indeed,we see that the location of the peak moves nearer to α=1 and that the peak gets higher and shaper as N increases.Therefore,the second derivative of e can be used to detect the quantum phase transition in the alternating chain.

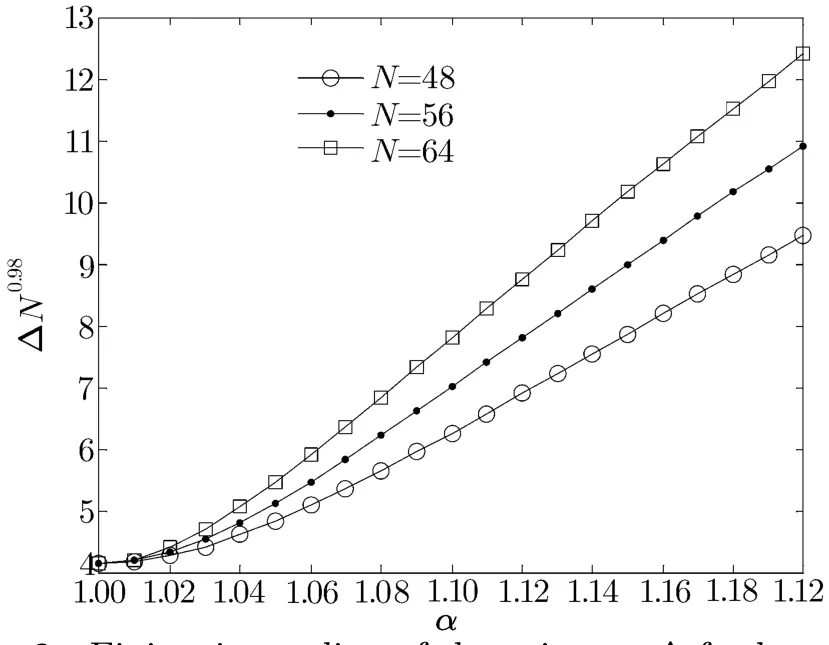
Fig.6 Finite size scaling of the spin gap Δ for lengths:N=48,56,64.

Next,the spin gap of the alternating chain Δ was also calculated by DMRG and CCM because the existence of a spin gap is an indication of a dimerized state.In order to extrapolate the results of DMRG,we use formula(12)with p=1.Figure 5 shows the results of the spin gap Δ as a function of α.From this graph,one can see the results of CCM are in qualitative agreement with those of DMRG.Moreover,the spin gap Δ increases as the parameter α increases,corresponding to the singlet dimer ground state.As shown in Fig.6,we plot ΔNβ1for diあerent chain sizes N as a function of α in order to determine the critical point αcprecisely.We use numerical results obtained from DMRG and we f i nd that all the curves cross at α =1,with the choice of a suitable exponent β1.This phenomenon means that the critical point of the alternating chain extracted from the operator Δ is αc=1.[35]

From the above analysis,one can conclude that the ground state of Hamiltonian(3)evolves from a spin-liquid state to a dimerized state when the parameter α changes across the critical point αc.Therefore,it possesses an m=0 plateau state with width Δ in the presence of a magnetic f i eld when α/=1.A similar phenomenon can also be observed in the dimerized spin chain.[36]

4.3 The m=1/4 Plateau State

We now discuss the eあect of the parameter α on the properties of the m=1/4 plateau state by using DMRG.That state occurs between two critical magnetic f i elds hc2and hc3.The critical f i elds hc2and hc3are respectively given by

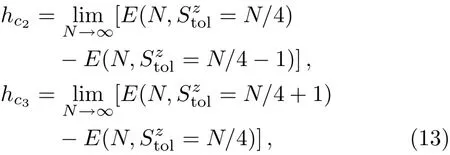
where E(N,Stzol)is the lowest energy in the subspace Stzol.

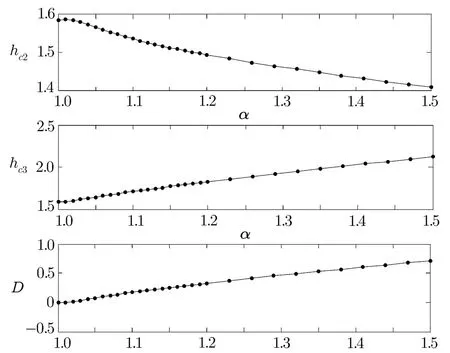
Fig.7 The critical magnetic f i elds hc2,hc3and the width of the plateau D obtained from DMRG as a function of α.

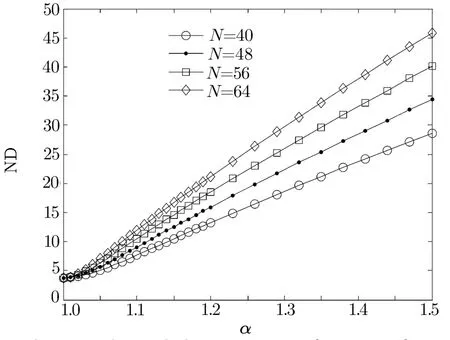
Fig.8 The scaled gap ND as a function of α.

Once these two critical fi elds have been calculated,the width of the plateau may be determined by using:D=hc3?hc2.We have calculated the above two critical fi elds for system sizes of N=32,40,48,56,and 64 by using DMRG.By using formula(12)with p=1,the bulk limit of the fi nite size results is obtained.The numerical results of the critical fi eld and the width of the plateau are plotted in Fig.7.As can be seen from this fi gure,the critical fi eld hc2decreases as α increases.By contrast,the critical fi eld hc3increases as α also increases.One sees also that the plateau occurs only when this parameter exceeds 1.To fi nd the critical point at which the plateau emerges precisely,we display the scaled gap ND of fi nite systems(N=40～64)in Fig.8.It is apparent that a fi nite plateau exists in the in fi nite system when α＞1 because ND increases with increasing N in this parameter region.[37]

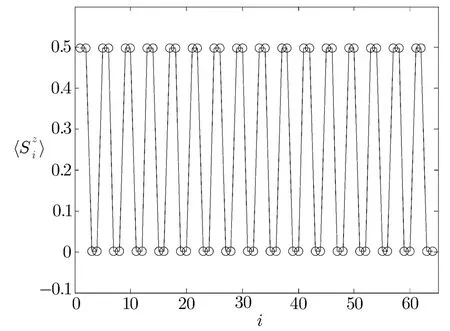
Fig.9 The expectation values 〈Szi〉for N=64 spins when α=10.

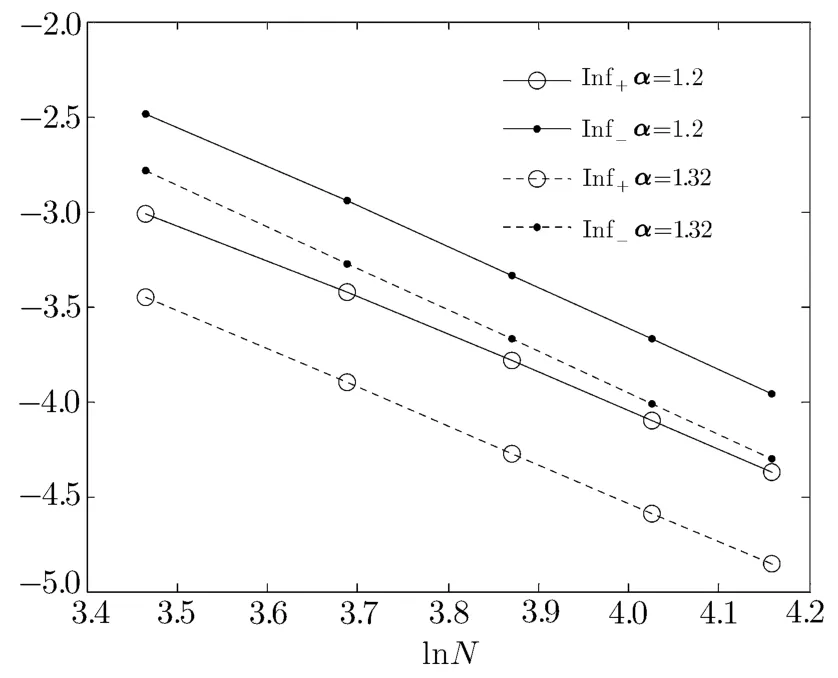
Fig.10 ln f+(lnf?)is plotted versus lnN.

To understand the mechanism for the m=1/4 plateau of the alternating chain,it is instructive to examine the case of large α limit.In this limit,two nearest spins connected by the αJ1interaction form a singlet dimer and the other two spins in a unit cell linked by J1interaction form a triplet dimer in subspace Stzol=N/4.Thus,in the m=1/4 plateau state,the expectation values〈Siz〉should be

To check this hypothesis,we present the expectation values 〈Szi〉,which are obtained by using DMRG for the N=64 system when α=10,in Fig.9.As is apparent in Fig.9,the behaviour of〈Szi〉obtained from DMRG favors the above mechanism for the m=1/4 plateau.

Lastly,we investigate the interesting critical behavior of the magnetization at m=1/4.In the vicinity of the critical f i elds hc2and hc3,the behavior of the magnetization m has the form[38?39]

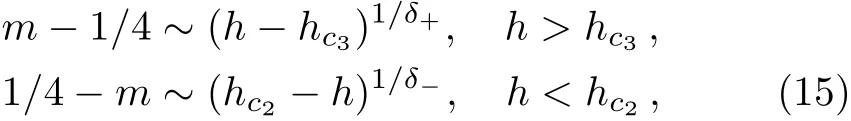
where δ+and δ?are the critical exponents,which can be used to describe the universality class of the phase transition induced by the f i eld.One can estimate the critical exponents by using two quantities f+(N)and f?(N),which are def i ned as[39]

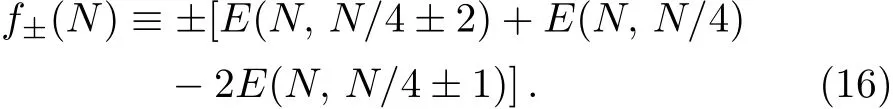
Once f+and f?are obtained, δ+and δ?can be determined from the slope of the lnf+～lnN and lnf?～lnN plot respectively.To avoid the large fi nite size eあect in the vicinity of the critical point,we only calculate the critical exponents when α≥1.2.Figure 10 shows the results of lnf±versus lnN.From this fi gure,we see that the calculated points fi t to a line very well.Thus,by a numerical fi tting, δ+and δ?can be estimated.The results of δ+and δ?are presented in Fig.11.From this fi gure,one can reasonably draw the conclusion that δ+= δ?=2,as expected for conventional one-dimensional gapped spin chains.[38]

Fig.11 The critical exponents δ+and δ? as a function of α.

5 Conclusions

In summary,we have investigated the properties of the quantum plateau state of the alternating Heisenberg chain by using CCM and DMRG methods.As the m=0 plateau state of Hamiltonian(2)is caused by the spin gap existing in Hamiltonian(3),we f i rst study the critical behaviour of Hamiltonian(3).The results for the second derivative of ground state energy per site obtained from DMRG show that a second order quantum phase transition happens at a critical point αc≈1.The results of the spin gap drawn from CCM and DMRG both indicate that the spin gap of Hamiltonian(3)opens up when the parameter α exceeds αc.By analyzing the scaling behavior of the spin gap,we f i nd that the precise value of αcis 1.Thus,when αc＞ 1,there is an m=0 plateau state in the alternating Heisenberg chain.

Due to its special spatial structure,the alternating Heisenberg chain also possesses an m=1/4 quantum plateau state that appears between two critical f i elds.Similar to the m=0 plateau state,the m=1/4 plateau state also appears when α＞1 and its width grows with the increase of α.By calculating the expectation values〈Szi〉using DMRG,we investigated the mechanism for the m=1/4 plateau state.The behavior of the magnetization m near the critical f i elds hc2and hc3exhibits a conventional critical behavior.

Acknowledgment

It is a pleasure to thank Dr.Damain Farnell for his careful reading of the manuscript and his valuable suggestions.

[1]F.D.M.Haldane,Phys.Rev.Lett.50(1983)1153.

[2]I.Aラeck,T.Kennedy,E.H.Lieb,and H.Tasaki,Phys.Rev.Lett.59(1987)799.

[3]M.den Nijs and K.Rommelse,Phys.Rev.B 40(1989)4709.

[4]T.Kennedy and H.Tasaki,Phys.Rev.B 45(1992)304.

[5]S.R.White,Phys.Rev.Lett.69(1992)2863.

[6]M.Yamashita,T.Ishii,and H.Matsuzaka,Coord.Chem.Rev.198(2000)347.

[7]M.Oshikawa,M.Yamanaka,and I.Aラeck,Phys.Rev.Lett.78(1997)1984.

[8]T.Sakai and S.Yamamoto,Phys.Rev.B 60(1999)4053.

[9]J.J.Jiang,Y.J.Liu,F.Tang,and C.H.Yang,Physica B 406(2011)781.

[10]W.Chen,K.Hida,and H.Nakano,J.Phys.Soc.Jpn.68(1999)625.

[11]H.T.Lu,Y.H.Su,L.Q.Sun,J.Chang,C.S.Liu,H.G.Luo,and T.Xiang,Phys.Rev.B 71(2005)144426.

[12]B.Gu,G.Su,and S.Gao,J.Phys.:Condens.Matter 17(2005)6081.

[13]S.S.Gong and G.Su,Phys.Rev.B 78(2008)104416.

[14]S.S.Gong,S.Gao,and G.Su,Phys.Rev.B 80(2009)014413.

[15]S.Mahdavifar and J.Abouie,J.Phys.:Condens.Matter 23(2011)246002.

[16]M.S.Naseri,G.I.Japaridze,S.Mahdavifar,and S.F.Shayesteh,J.Phys.:Condens.Matter 24(2012)116002.

[17]D.V.Dmitriev,V.Y.Krivnov,and A.A.Ovchinnikov,Phys.Rev.B 65(2002)172409.

[18]R.F.Bishop,J.B.Parkinson,and Y.Xian,Phys.Rev.B 44(1991)9425.

[19]R.F.Bishop,D.J.J.Farnell,and J.B.Parkinson,Phys.Rev.B 58(1998)6394.

[20]R.F.Bishop,D.J.J.Farnell,S.E.Kr¨uger,J.B.Parkinson,J.Richter,and C.Zeng,J.Phys.:Condens.Matter 12(2000)6887.

[21]D.J.J.Farnell,R.F.Bishop,and K.A.Gernoth,J.Stat.Phys.108(2002)401.

[22]D.J.J.Farnell,J.Schulenburg,J.Richter,and K.A.Gernoth,Phys.Rev.B 72(2005)172408.

[23]R.Darradi,J.Richter,K.A.Gernoth,and D.J.J.Farnell,Phys.Rev.B 72(2005)104425.

[24]D.Schmalfu?,R.Darradi,J.Richter,J.Schulenburg,and D.Ihle,Phys.Rev.Lett.97(2006)157201.

[25]R.F.Bishop,P.H.Y.Li,D.J.J.Farnell,and C.E.Campbell,Phys.Rev.B 79(2009)174405.

[26]D.J.J.Farnell,R.Zinke,J.Schulenburg,and J.Richter,J.Phys.:Condens.Matter 21(2009)406002.

[27]J.Richter,R.Darradi,J.Schulenburg,D.J.J.Farnell,and H.Rosner,Phys.Rev.B 81(2010)174429.

[28]D.J.J.Farnell,R.Darradi,R.Schmidt,and J.Richter,Phys.Rev.B 84(2011)104406.

[29]O.Goetze,D.J.J.Farnell,R.F.Bishop,P.H.Y.Li,and J.Richter,Phys.Rev.B 84(2011)224428.

[30]P.H.Y.Li,R.F.Bishop,D.J.J.Farnell,J.Richter,and C.E.Campbell,Phys.Rev.B 85(2012)085115.

[31]T.Papenbrock,T.Barnes,D.J.Dean,M.V.Stoitsov,and M.R.Strayer,Phys.Rev.B 68(2003)024416.

[32]K.Okamoto,T.Tonegawa,and M.Kaburagi,J.Phys.:Condens.Matter 15(2003)5979.

[33]Y.C.Tzeng,H.H.Hung,Y.C.Chen,and M.F.Yang,Phys.Rev.A 77(2008)062321.

[34]T.Barnes,E.Dagotto,J.Riera,and E.S.Swanson,Phys.Rev.B 47(1993)3196.

[35]G.De.Chiara,M.Lewenstein,and A.Sanpera,Phys.Rev.B 84(2011)054451.

[36]J.J.Jiang and Y.J.Liu,Physica B 403(2008)3498.

[37]N.Okazaki,J.Miyoshi,and T.Sakai,J.Phys.Soc.Jpn.69(2000)37.

[38]T.Sakai and M.Takahashi,Phys.Rev.B 57(1998)R8091.

[39]T.Sakai and H.Nakano,Phys.Rev.B 83(2011)100405(R).