Dynamical Properties of a Diluted Dipolar-Interaction Heisenberg Spin Glass?

ZHANG Kai-Cheng(張開成), LIU Yong(劉永),and CHI Feng(遲鋒)

1College of Mathematics and Physics,Bohai University,Jinzhou 121013,China

2State Key Laboratory of Metastable Materials Science&Technology and College of Science,Yanshan University,Qinhuangdao 066004,China

3College of Engineering,Bohai University,Jinzhou 121013,China

1 Introduction

Spin glass(SG)has long attracted much attention for its fascinating properties as well as the rich physics.[1]It is believed that the SG study can help people to better understand the glass state.Generally,when the frustrated system is cooled below certain freezing temperature,an SG transition occurs,accompanied by a series of slow relaxation phenomena.Much work has been done to understand the phase transition as well as the dynamical properties of SG.Up to now,theoretical understanding on SG properties mainly relies on the mean-f i eld solution based on replica symmetry breaking,[2]The meanfi eld solution predicted the system underwent a breaking of symmetry when the temperature was below the transition temperature,[2]which was manifested by recent numerical simulations.[3]However,the mean-f i eld method is only valid for the system with dimension d≥6,[4]which is not suitable for real SGs.For d＜6,a phenomenological droplet theory[5]based on domain growth gave some proper explanations on the dynamical properties of SG.However,it remains still unclear which theory can properly describe canonical SGs.It is found that canonical SGs can be better described by Heisenberg spins than Ising spins due to the large magnetic moments and weak anisotropy of spins in them.Numerical simulations have given the consistent critical values for the Ising and Heisenberg SGs respectively.[6?7]Surprisingly,the critical values measured from canonical SGs match neither of them.[8]It was suggested that the puzzles were caused by another hidden parameter-the chirality,which only arose in Heisenberg SG and represented the handedness caused by frustration among multiple neighbor spins.[9]The chirality in Heisenberg SG is interesting to study because it may or may not have the transition temperature coinciding with that of SG phase.Recently,much attention has been paid to the phase transitions in the three-dimensional Edward-Anderson(EA)Heisenberg SG.[11?13]Recent numerical simulations revealed that the chiral-glass(CG)phase did decouple from the SG phase at slightly higher temperature.[14?15]So far,the chirality is mainly studied in the EA Heisenberg model without any realistic analogy to real SGs,which possess both the site and bond disorder.For real SGs the site disorder brings a big trouble to the chirality due to the absence of translation invariance.So a new chirality must be def i ned and the underlying physics needs further clarif i cation.

One typical disordered SG is the doped LiHoxY1?xF4,where the host insulator LiHoF4shows ferromagnetism at low temperature due to dipolar interaction.As the nonmagnetic ions Y3+gradually substitute the magnetic ions Ho3+,the site disorder is introduced and the transition temperature of ferromagnetism continues to decrease until x?0.25.[16]Below it,the doped system was reported to undergo the transition from paramagnetic phase to SG phase.[17?18]Although earlier simulations gave negative reports on the existence of SG transition for the doped system with x＜0.25,[16]recent simulation revealed that an SG transition occurred for x=0.0625 and 0.125 by fi nite-size scaling analysis.[19]One may wonder whether the chirality exists in such dipolar SGs.According to the chirality theory,[11,20?21]the three-dimensional isotropic Heisenberg SG has the Z2×SO(3)symmetry,where Z2denotes the spin-ref l ection symmetry and SO(3)denotes the symmetry of global spin rotation.When the temperature decreases,the Z2symmetry is breaking f i rst,and this leads to the occurrence of CG transition.As the temperature further decreases,the following SO(3)symmetry breaking leads to SG transition.This is generally referred to as the spin-chirality decoupling.For the Heisenberg SG with random magnetic anisotropy,the system possesses only the Z2symmetry due to the presence of magnetic anisotropy.The chirality recouples to the spins via magnetic anisotropy.When the Z2symmetry is breaking,both CG and SG transitions occur together and this is called spin-chirality recoupling.[21]Therefore,if the chirality exists in the diluted dipolar SG,which has magnetic anisotropy due to dipolar interaction,a common transition temperature can be expected for both phases.

In this paper we investigate the nonequilibrium properties of both SG and CG phases in the diluted dipolar system by heat bath method.We intend to inspect whether the chirality has the same dynamical properties as the spins.If so,it means the chirality does recouple to the spins via magnetic anisotropy,otherwise,a spin-chirality decoupling occurs.By def i ning the chirality,we study the aging eあect as well as the time-dependent overlap correlation for both the spins and the chirality from dynamical perspective.By scaling,we f i nd that both phases have the same aging behavior and domain growth process,and their f i tting parameters are very closer.This means that a common transition temperature can be expected in the system.

2 Model,Method and Quantities

2.1 Model and Method

In much diluted spin glass,the system properties do not depend on the lattice type.Thus we consider a simple cubic(SC)lattice with size L×L×L,where spins randomly occupy the sites according to a probability p.To study the nonequilibrium properties,the system size should be large to avoid the global rotation of spins.[22]This generally brings no trouble to the short-range EA SG and the system size can reach as large as L=60.[23]However,the situation is much harder for the long-range dipolar SG.Due to the long-range interactions the whole computation increases proportionally to L6,which prohibits us to investigate large system.As we can reach,we set the parameters L=16 and p=0.125 in our simulation,which corresponds to a system with 512 spins.The Hamiltonian of the dipolar system can be written as[19,24]

where εdis the energy scale of the dipolar interaction,εd= μ0μ2s/(4πa3), μsis the spin moment and a is the lattice constant.rijis the spin separation between the i-th spin and the j-th spin,rij=|ri?rj|. σμiis theμ(μ =x,y,z)component of the i-th unit spin vector. δμvis the Kronecker symbol,which equals to one ifμ=v otherwise zero.For simplicity,we set εd/kB=1 in the simulations and the temperature takes the unit of εd/kB.We use the periodic boundary conditions in the simulation.Due to the long-range interactions,the simulation system interacts with the array of its images replicated along the space dimensions.If the i-th spin interacts with the j-th spin,it interacts with all the images of the j-th spin arrayed along the space dimensions.In such conditions,the selected spin also interacts with the images of itself,which is called self-interaction.Therefore,it is convenient to write the coupling strength as a 3 by 3 matrix,Lij.The matrix element can be written as[24]

where n is the lattice vector with n=L(kex+ley+mez).eμ(μ =x,y,z)is the unit vector along theμ axis and k,l,m are integers.The above summation is performed in the inf i nite space and it converges slowly and conditionally due to the dipolar interaction.To solve this problem,we use the Ewald summation technique[25]to calculate the coupling strength.The detailed summary of this technique can be found in Refs.[24,26].Note that the surface magnetization does not vanish in the thermodynamic limit and its contribution to the whole energy must be considered.[27]We use the metallic boundary conditions to erase the surface contribution.[24]This is equivalent to perform the summation in an inf i nite cylinder sample without considering the demagnetization eあect.[24]Consequently,the Hamiltonian of the interacting system can be simplif i ed as

The above summation is only performed in the simulation box L3.The interactions outside the simulation box are absorbed into the coupling matrix Lijautomatically.We use the heat bath method to update the spin conf i gurations.[28]This method directly produces the spin directions relative to the local molecular f i eld according to the Boltzmann distribution and hence eあectively updates the spin states.In the dynamic simulation,time is measured as the Monte Carlo sweeps(MCS)through all the spins.To reduce the statistical errors,all the simulations are averaged over 500 disorder realizations.

2.2 Quantities

In the site-ordered SG,the chirality is def i ned as the mixed product of three spins arrayed sequentially along certain axis.[9]This def i nition,however,can not be directly applied to the disordered SG due to the breaking of translation invariance.We notice that if one omits the directions of chirality,which is not necessary for the sitediluted case,the chirality can still be def i ned as[29]

where σi1and σi2are the nearest and next-nearest neighbors respectively with|ri1?ri|≤|ri2?ri|.If a spin has one more nearest neighbor,which is very rare for the case of low spin concentration,we randomly choose σi1and σi2from them.Due to the random spin occupations,the above triple spins are usually coplanar rather than collinear,therefore,the chirality def i ned above does not contain any f i xed direction.

Experimentally,the aging eあectwasoften observed by measuring the thermoremanent magnetization(TRM).[30?31]In simulations the autocorrelation function is often calculated to investigate the aging eあect.[32]The SG and CG autocorrelations of the diluted system can be written as

where N is the total number of spins.In the thermodynamic limits,the autocorrelation above is just the EA parameter,qEA=limt,tw,L→∞C(t+tw,tw).The angular brackets 〈···〉and the square brackets[···]mean the calculation takes thermal average and disorder average respectively.Furthermore,we calculate the overlap correlation function,which is also called four-point correlation,for both SG and CG phases.The SG and CG overlap correlation functions can be written as

where α and β are the indices of the system replicas.In the diluted case,the lattice does not possess translation invariance and the spins do not have constant neighbors.Therefore,Nris distance-dependent and represents the average neighbor number.

3 Results and Discussion

We use the following protocol to observe the aging effect.The system is f i rst quenched from high temperature to the goal temperature T0,then it waits at T0for some time tw,after that the time-dependent autocorrelations are calculated as the spin conf i guration evolves relatively to the reference one at time tw.We set T0=0.06 and 0.03,and at each temperature twtakes the values 102,103,104,105Monte Carlo sweeps(MCS).The SG autocorrelations versus the time are shown in Fig.1.It is noticed that the autocorrelations increase as the temperature decreases.The larger the waiting time is,the slower the autocorrelation decays.The autocorrelations decay slowly for t＜twwhile they decay fast for t＞tw.According to the droplet theory,[5]SG domains grow to the size of R(tw)after the system relaxes for tw.For t＜tw,spins mainly reverse in the domains and a quasi-equilibrium state can be observed.However,as the domains continue to grow,their sizes exceed R(tw)signif i cantly,and hence a nonequilibrium state is observed for t＞tw.It is also noticed that as the temperature decreases the autocorrelations show a plateau,which manifests that the EA order parameter qEAcan exist for a long time at low temperature with tw→ ∞.This behavior is similar to those observed in the EA Heisenberg model[23]and Ising model.[32]It was reported that the autocorrelations became stationary for the simulations of EA Heisenberg model if the lattice size was too small.[22?23]In our simulations,we do not observe this phenomenon even for t＞106MCS.This is because the dipolar interaction couples all the spins together and the system is more frustrated than the short-range EA model.The much hard relaxation was also observed in other simulations on dipolar systems.[19,24,29]

Fig.1 (Color online)SG autocorrelations versus the time for the dipolar system.The temperature takes 0.06 and 0.03.At each temperature,the system waits for 102,103,104,and 105MCS respectively.The error bars are about the symbol size.

Figure 2 presents the CG autocorrelations versus the time for diあerent temperatures.Due to the multi-spin product the CG autocorrelations are much smaller and usually one-order less than the SG ones,which is consistent with that of the EA Heisenberg model.[23]For t＜tw,the spin excitations mainly occur in the droplet,thus a slow decay is observed.However,for t＞tw,large droplets are excited and the autocorrelations decay much faster.For larger tw,the autocorrelations merge together and also show a plateau.The plateau is more obvious at lower temperature.This indicates the EA chiral order parameter exists for tw→∞.The larger the waiting time is,the slower the autocorrelation decays.These behaviors are similar to those of SG phase.

Fig.2 (Color online)CG autocorrelations versus the time for two temperatures,T=0.06,0.03.At each temperature the system relaxes for 105,104,103,102MCS respectively.The error bars are about the symbol size.

Since the chirality is another hidden degree of freedom,one may wonder whether it behaves distinctly from the SG phase.To obtain this information we try to scale the autocorrelations for both the spins and the chirality by the same scaling function.It was once suggested that the autocorrelations can be scaled by t/tw,[32?33]however,experiments often gave negative reports on this scaling method.[30]Alternatively,a combined aging method was proposed and widely used for the TRM scaling.[31,34]This method suggests that the decay can be combined by a stationary term A(τ0/t)αand an aging term f(λ/tμw).Thus the autocorrelation can be written as C(t+tw,tw)=A(τ0/t)α+f(λ/tμw),where A is a dimensionless constant and τ0is the microscopic f l ipping time;μ is the f i tting parameter.λ is theμ-dependent scaled variable which can be written as

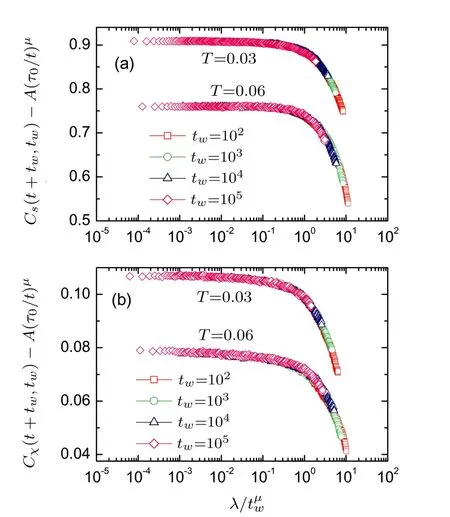
Fig.3(Color online)Scaling of the autocorrelations for both the spins(a)and the chirality(b).The error bars are about the symbol size.

Figure 3 shows the scaling for both the SG and CG autocorrelations. It is noticed that after the subtraction of the stationary term,all the autocorrelations collapse into a single curve,indicating the existence of twindependent universal scaling function.As the argument λ/tμwis less than one,the scaling function keeps horizontal,which manifests a quasi-equilibrium state exists and spins are excited locally.As λ/tμw＞ 1,the scaling function decreases rapidly,which indicates the system enters a nonequilibrium regime and large-droplet excitations occur for t? tw.According to the f i tting parameterμ,the aging can be divided into two types:one is subaging withμ＜1 and the other is superaging withμ＞1.Our results reveal that the superaging only occurs at the temperature well below the transition temperature.[29]The scaling parameters for both the spins and the chirality are listed in Table 1.The parameter A decreases when temperature decreases,indicating a reducing thermal f l ipping process.It can be seen thatμincreases as the temperature decreases for both cases,which is consistent with the results of the experiments[31]and the simulations of Heisenberg SG.[23,34]According to the previous studies,[23,33]a transition is expected to occur at f i nite temperature asμincreases fromμ＜1 toμ＞1.In our simulation,the fi tting parametersμfor both phases are larger than one at low temperature,which indicates both phases coexist.Note that the parameterμfor the SG phase is very close to that of the CG phase,indicating the similar aging behaviors.This means that the chirality does couple to the spins in the diluted dipolar SG.The dipolar interaction is responsible for the spin-chirality recoupling.Since below percolation limit,isolated spin blocks are present in the system.The spin blocks would have rotated randomly if the interaction was short-range,which would lead to the spin-chirality decoupling.However,due to the dipolar interaction,spin blocks couple together and the same aging behavior arises for both phases.

Table 1 The scaling parameters for both the SG and CG autocorrelations shown in Fig.3.

Furthermore,we investigate the evolvements of the overlap correlations as a function of the waiting time for both SG and CG phases.The temperature is set to be 0.06 and 0.03,at which the system relaxes for tw=10,102,103,104,and 105MCS.Figure 4 shows both the SG and CG overlap correlations versus the time for T=0.06.The overlap correlations decay very fast and become nearly negligible as r≥4,which manifests the domain size in the diluted dipolar system is very short compared with those in the EA Heisenberg SG.[23]The logscaled SG correlations decay with downward curvatures while the CG ones decay almost linearly as the distance increases.The decay of the SG correlation is diあerent from those of isotropic EA Heisenberg SG for its downward curvature.[23]This may be caused by the anisotropy of dipolar interaction.However,due to the multi-spin product,the anisotropic eあect is weakened for the CG overlap,which leads to the linear decay.The overlap correlations are less sensitive to the time variance compared with those of EA Heisenberg SG.[23]It is suggested the decay of correlation length obeys approximately the exponential function Θ(r,tw)=Ae?r/ξ(tw),[32]where ξ(tw)is the tw-dependent correlation length.The correlation length can be obtained by integration of the overlap correlation,ξ(tw)=A?1∫∞0Θ(r,tw)dr.The SG and CG correlation lengths versus the waiting time are shown in Fig.5.

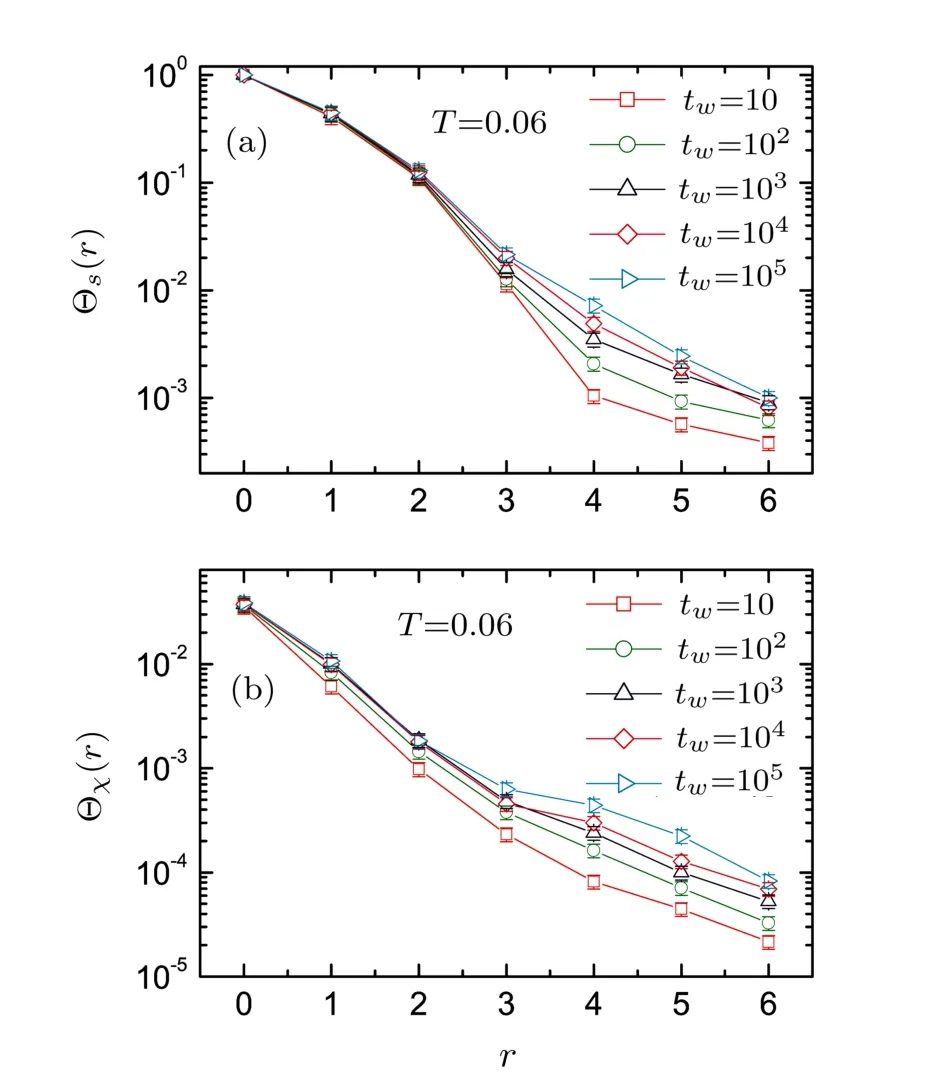
Fig.4 (Color online)The overlap correlations of both the spins(a)and the chirality(b)as a function of the spin separation.The temperature T=0.06 and the system waits for tw=10,102,103,104,105MCS respectively.The vertical axis is log-scaled.

Fig.5 (Color online)The SG(a)and CG(b)correlation lengths versus the log-scaled waiting time.The data are f i tted by power law.

Note that,for both cases the correlation lengths are much less than those in the EA Heisenberg SG,[23]which indicates the domains in dipolar SG are quite small.According to the droplet theory,[5]the domain size grows as the relaxing time elapses as ξ(tw) ∝ (lntw)1/Ψ,where Ψ is the exponent to describe the free-energy barrier of the droplet.By f i tting the correlation lengths with power law,the exponent Ψ can be obtained.For T=0.06 and 0.03,it takes the values 2.43 and 2.67 respectively for the SG phase;2.57 and 2.71 for the CG phase.The CG exponents are closer to the SG ones,indicating a similar growing process of domains.It also means that the chirality recouples to the spins and as a result both phases are ordered at the same freezing temperature.Due to the lack of barrier exponent of the EA Heisenberg SG,we only compare our results with those of the EA Ising SG.Our results show the exponent Ψ is larger than those obtained in the 3D Ising SG.[32?33]We explain it as follows:(i)As the system dimension increases,Ψ also increases,as can be seen from the previous studies.[33]For the dipolar-interaction case,the corresponding dimension is larger than three,thus Ψ is larger than those short-range Ising case.(ii)The heat bath method is more eきcient to relax the spins than the Metropolis method,therefore,correlation length calculated by the heat bath method often approaches to saturation much faster than the Metropolis method,thus contributes larger Ψ.

4 Conclusion

By de fi ning the chirality in the site-diluted case,we investigate the dynamical properties of the chirality as well as the spins in the diluted dipolar system by simulation.By scaling the autocorrelations we fi nd the SG and CG phases have the same aging behavior and closer aging parameters.Moreover,both phases have the same domain growth process.This means that the chirality does recouple to the spins via magnetic anisotropy and both phases are ordered at the same freezing temperature.We hope our study could be helpful for future investigations on this fi eld.

[1]K.Binderand and A.P.Young,Rev.Mod.Phys.58(1986)801.

[2]G.Parisi,J.Phys.A 13(1980)1101.

[3]L.Leuzzi,G.Parisi,F.Ricci-Tersenghi,and J.J Ruiz-Lorenzo,Phys.Rev.Lett.101(2008)107203.

[4]H.G.Katzgraber,D.Larson,and A.P.Young,Phys.Rev.Lett.102(2009)177205.

[5]D.J.Fisher and D.A.Huse,Phys.Rev.B 38(1988)373;Phys.Rev.B 38(1988)386.

[6]I.A.Campbell,K.Hukushima,and H.Takayama,Phys.Rev.Lett.97(2006)117202.

[7]L.A.Fernandez,V.Martin-Mayor,S.Perez-Gaviro,A.Tarancon,and A.P.Young,Phys.Rev.B 80(2009)024422.

[8]L.P.Levy and A.T.Ogielsky,Phys.Rev.Lett.57(1986)3288.

[9]H.Kawamura,Phys.Rev.Lett.68(1992)3785.

[10]H.Kawamura and D.Imagawa,Phys.Rev.Lett.87(2001)207203.

[11]D.Imagawa and H.Kawamura,Phys.Rev.Lett.92(2004)077204.

[12]L.W.Lee and A.P.Young,Phys.Rev.Lett.90(2003)227203.

[13]I.Campos,M.Cotallo-Aban,V.Martin-Mayor,S.Perez-Gaviro,and A.Tarancon,Phys.Rev.Lett.97(2006)217204.

[14]D.X.Viet and H.Kawamura,Phys.Rev.B 80(2009)064418.

[15]D.X.Viet and H.Kawamura,Phys.Rev.Lett.102(2009)027202.

[16]A.Biltmo and P.Henelius,Phys.Rev.B 76(2007)054423;Phys.Rev.B 78(2008)054437.

[17]C.Ancona-Torrres,D.M.Silevitch,G.Aeppli,and T.F.Rosenbaum,Phys.Rev.Lett.101(2008)057201.

[18]W.Wu,D.Bitko,T.F.Rosenbaum,and G.Aeppli,Phys.Rev.Lett.71(1993)1919.

[19]K.M.Tam and M.J.P.Gingras,Phys.Rev.Lett.103(2009)087202.

[20]D.Imagawa and H.Kawamura,Phys.Rev.B 70(2004)144412.

[21]H.Kawamura,J.Phys.Soc.Jpn.79(2010)011007.

[22]F.Matsubara,T.Shirakura,and S.Endoh,Phys.Rev.B 64(2001)092412.

[23]L.Berthier and A.P.Young,Phys.Rev.B 69(2004)184423.

[24]P.Stasiak and M.J.P.Gingras,arXiv:0912.3469

[25]P.Ewald,Ann.Phys.64(1921)253.

[26]S.W.De Leeuw,J.W.Perram,and E.R.Smith,Proc.R.Soc.London A 373(1980)27.

[27]Z.Wang and C.Holm,J.Chem.Phys.115(2001)6351.

[28]Y.Miyatake,M.Yamamoto,J.J.Kim,M.Toyanaga,and O.Nagai,J.Phys.C 19(1986)2539.

[29]K.C.Zhang,G.B.Liu,and Y.Zhu,Phys.Lett.A 375(2011)2041.

[30]V.S.Zotev,G.F.Rodriguez,G.G.Kenning,R.Orbach,E.Vincent,and J.Hammann,Phys.Rev.B 67(2003)184422.

[31]G.F.Rodriguez,G.G.Kenning,and R.Orbach,Phys.Rev.Lett.91(2003)037203.

[32]J.Kisker,L.Santen,M.Schreckenberg,and H.Rieger,Phys.Rev.B 53(1996)6418.

[33]L.Berthier and J.P.Bouchaud,Phys.Rev.B 66(2002)054404.

[34]O.V.Billoni,S.A.Cannas,and F.A.Tamarit,Phys.Rev.B 72(2005)104407.