Generation and evolution characteristics of the mushroom-like vortex generated by a submerged round laminar jet*

CHEN Yun-xiang (陳云祥), CHEN Ke (陳科), YOU Yun-xiang (尤云祥), HU Tian-qun (胡天群) State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China, E-mail: chenyunxiang@126.com

(Received August 6, 2013, Revised August 29, 2013)

Generation and evolution characteristics of the mushroom-like vortex generated by a submerged round laminar jet*

CHEN Yun-xiang (陳云祥), CHEN Ke (陳科), YOU Yun-xiang (尤云祥), HU Tian-qun (胡天群) State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China, E-mail: chenyunxiang@126.com

(Received August 6, 2013, Revised August 29, 2013)

This paper studies the formation mechanism and the evolution characteristics of the mushroom-like vortex generated by a submerged laminar round jet based on experiments, CFD simulation and a theoretical model. The results of the numerical simulations agree well with those obtained by the experiments, and three distinct stages are identified in the formation and evolution processes of the mushroom-like vortex: the starting, developing and decaying stages. Three non-dimensional parameters for such a mushroom-like vortex: the length of the jetL*, the vortex radiusR*and the circulation lengthd*, are introduced, and the variation characteristics of these parameters with respect to the non-dimensional timet*are quantitatively analyzed. In the starting stage,L*andd*increase linearly witht*whileR*approximately remains a constant. In the developing stage, a considerable self-similarity is observed, andL*,R*,d*have the same proportional relationship with respect tot*1/2regardless of the variations of the Reynolds number and the injection duration time. In the decaying stage,L*andR*are approximately proportional tot*1/5, whiled*nearly levels off at a constant. Furthermore, a theoretical model is proposed for the time evolution characteristics of the jet length, with predictions in good agreements with numerical and experimental results.

submerged round jet, mushroom-like vortex, evolution mechanism

Introduction

It is generally known that a kind of the special flow structures with a mushroom-like pattern exist in the images of the Ocean Remote Sensing Satellite[1]. Investigations show that such flow structures, in essence, are a class of large-scale vortexes and they originate from some momentum effects in the ocean[2]. It is generally believed that the mechanical effects of the propellers and the cooling water discharge of submarines are to transfer the momentum to the ambient fluid, which results in the formation of jet momentum wakes[3]. Under the impact of oceanic ambient environments, the jet momentum will generate a type of mushroom-like large-scale vortex or so called mushroom-like pattern. Generally, such a flow structure has a horizontal scale of 1 km-200 km, a vertical scale of 10 m-100 m and a decaying time of 1 d-30 d, and its image in the Ocean Remote Sensing Satellite is usually a pair of counter-rotating vortex dipoles[1]. Therefore, investigations to clarify the mechanism and the evolution characteristics of the mushroom-like vortex structure generated from a jet momentum under the impact of the oceanic ambient fluid are of significant military values for the development of non-acoustic remote sensing detection technology of submarines[2,4].

In the case of a homogenous fluid, it is shown that the flow characteristics of the jet momentum are related to the Reynolds numberRe. Specifically, whenRe＜300, the jet belongs to a laminar flow, whenRe>300, the jet becomes instable and some turbulent eddies appear at some distance away fromthe outlet of the jet nozzle. With the increase ofRe, the laminar boundary layer disappears gradually and the jet gradually evolves into a fully developed turbulence until the conical angle approximately becomes a constant. For turbulent jets, there are abundant coherent structures (e.g., the vortex ring, the single and double spiral vortex structures) which can easily trigger the instability of the shear layers[5]. For a stratified flow or shallow uniform fluids, the vertical motion of the momentum wake is restricted under the buoyancy effect generated by the density stratification, or the shallow water effect induced by the upper and lower boundaries of the water body, and hence the jet wake will develop into a quasi-two-dimensional largescale vortex[6-10].

For a viscous homogenous fluid, the laminar jet involves many nonlinear flow phenomena[11,12], for example, the jet liquid can cluster at its head to form a boot-like or mushroom-like pattern after maintaining a specific length under the impact of the ambient fluid. Moreover, the laminar jet can also be gradually stagnated by the ambient fluid in a finite length and evolves into an annular back flow.

It is demonstrated that the mushroom-like vortex is essentially a class of the annular back flows under the action of the ambient fluid. Afanasyev and Korabel[13]obtained an asymptotic theoretical solution of the mushroom-like pattern based on the Stokes approximation theory, which agrees well with the corresponding experimental results in the morphological structure, the motion track and the fluid field characteristics of the mushroom-like pattern. Further, Voropayev et al.[14]obtained an asymptotic theoretical solution for the collision problem of two mushroom-like vortex structures generated by two laminar round jets, which is also in good agreements with the corresponding experimental results.

As a whole, some understanding of the evolution mechanism and the associated features of such mushroom-like patterns is gained based on experimental results and theoretical asymptotical methods. However, during the evolution process of the round laminar jet, the jet length, the spiral annular vortex radius and the exterior envelope length change continually with respect to time, and these variation characteristics are not only related to the jet Reynolds number, but also to the duration time of the jet. They are of great significance for analyzing the appearance and the spatial distribution characteristics of the mushroom-like patterns in the remote sensing images. However, a clear understanding of these problems remains to be acquired so far.

With the growth in speed and capacity of modern supercomputers, the simulations based on the CFD method can now be a valuable supplement to the laboratory experiments. The CFD can achieve a high-resolution in space and time for the flow field along with details of the whole range of turbulent fluctuations. There were many successful studies for the formation and evolution characteristics of turbulent jets[15], however, those based on the CFD method in case of laminar jets are still few and far between.

This paper presents a combined experimental, CFD simulation and asymptotic theoretical investigation of the formation and evolution characteristics for the mushroom-like vortex generated by a submerged round laminar jet. In Section 1, the experimental facilities and methods are described. In Section 2, the CFD method is presented for numerically simulating the formation and evolution characteristics of a submerged round laminar jet. In Section 3, experimental and CFD simulation results are presented. In particular, three non-dimensional parameters for the mushroom-like vortex: the length of the jet, the radius of the mushroom-like vortex and the length of vortex circulation, are introduced, and the variation characteristics of these parameters with the non-dimensional time are quantitatively analyzed. Additionally, a theoretical model is proposed to account for the time evolution characteristics of the jet length for the mushroom-like vortex. Conclusions are made in Section 4.

1. Experimental setups

Experiments were performed in a transparent glass rectangular tank (L×B×H=1m×0.5 m× 0.6 m) filled with water at rest. The depth of the water layer isHo=0.5 m for all experiments presented here. Experimental apparatus includes a dyed liquid vessel, a separator vessel, an overflow collector, an electronic balance, an L-like jet nozzle, and a camera, as shown in Fig.1. The L-like nozzle has a diameterDof 0.0015 m and is horizontally placed at the half depth of the water, namely, a position of 0.25 m down the water surface. The density of the dyed liquid in the experiments isρ=1001kg/m3which is a little greater than that of the rest water, hence, a certain salt is added into the rest water to eliminate the difference.

Fig.1 Sketch of the experimental setup

In all experiments, the dyed liquid is first injected into the separator vessel until its level reaches theoverflow surface. Then the upper valve is opened, and the dyed liquid with a mass ofM0is then injected into the dyed liquid vessel to ensure a sustaining overflow status of the separator vessel before opening the lower valve. After these procedures, the lower valve is opened, then the dyed liquid is injected into the ambient fluid of the glass tank through the L-like jet nozzle under the action of the gravity, and a submerged horizontal round jet is formed. Because the dyed liquid in the separator vessel is always in the overflow state, the outlet velocity of the L-like jet nozzle keeps in a steady state during the injection.

whereu0denotes the average velocity of the nozzle outlet, which can be expressed as

The jet momentum is characterized by four parameters, namely, the momentum fluxJ, the kinematic viscosity coefficientν, the jet duration timeTinjand the evolution timet. Then three non-dimensional parameters can be obtained by use of these parameters, including the Reynolds number (Re), the non-dimensional jet duration timeand the non-dimensional timet*, respectively, as follows

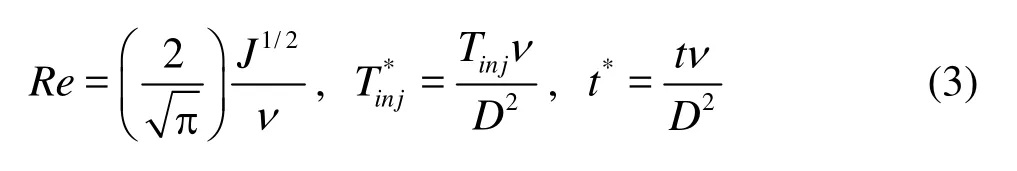
As we are interested in the formation mechanism and the evolution characteristics of the mushroom-like vortex generated by a submerged laminar round jet, a high resolution digital camera is used to record the overall process of the jet and is fixed over the glass tank, and some digital image processing techniques are employed to analyze the video records to get some qualitative and quantitative results of such a mushroom-like vortex.

2. Numerical setups

In the numerical simulations, a horizontal jet nozzle is placed in the rectangular container with its centerline located at the half depth of the ambient fluid. The length and the diameter of the horizontal jet nozzle are denoted byL0andD, respectively, the length of the rectangular container is 200Dand its width and depth are both 80D. With a Cartesian coordinate system, the origin is at the center of the nozzle outlet, theoxaxis coincides with the centerline of the nozzle with a positive direction pointing to right, theoyis perpendicular to the paper in the inward direction and theozis in the vertical direction, as shown in Fig.2.

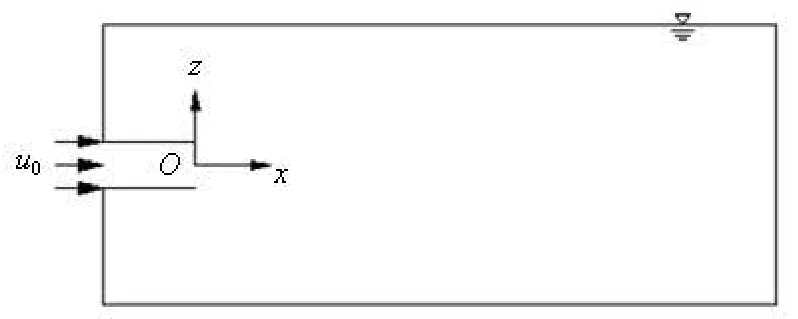
Fig.2 Sketch of the side view of the computational domain and its coordinate system

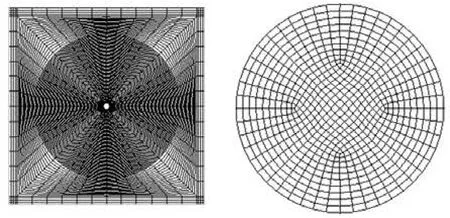
Fig.3 Sketch of transverse grid generation

The densities of the jet and the ambient fluids in the rectangular container are the same so that the two fluids could be regarded as a single phase fluid. The governing equations for the formation and the evolution of the jet in the ambient fluid can be expressed by the following incompressible Navier-Stokes equation.

Fig.4 Numerical results of the three-dimensional structures of the mushroom-like vortex atRe=160 and=2.2

wherepdenotes the dynamic pressure andudenotes the velocity vector.

A CFD method is used to numerically solve Eq.(4). The left end face of the nozzle is set as a velocity inlet with a velocityu0to provide a continual jet momentum during the jet duration timeTinj. The left end face of the rectangular container excluding the overlap part with the left side of the nozzle is also set as a velocity inlet with a zero velocity, its bottom and two side walls are nonslip stationary walls, while its right and top faces both are free outlets. The interior and exterior walls of the nozzle are both wall boundaries. In the beginning, the whole flow field is initialized by the inlet boundary conditions. Moreover, in order to ensure that the flow becomes fully developed at the nozzle outlet, the nozzle length is set to be longer than the flow development length in the tube, and we setL0=10D[17].

All grids are structured hexahedral elements. The computational domain is divided into three parts: the nozzle zone, the main zone and the outer zone. More precisely, the main zone is a ring-like structure with an outside diameter of 60D, which is divided into some hexahedral elements based on a uniform partition of the circumference and the radius, while the hexahedral grid in the outer zone is generated by dividing the area into many subdomains. The grid is made enough dense in the nozzle zone, and that in the outer zone is also made sufficiently dense. The grid number in the main zone isNx×Nr×NθwhereNxdenotes the grid number in the jet axial direction, andNrandNθdenote the grid numbers in the radial and circumferential directions, respectively. In the present simulations, the grid number in the main zone is 300× 120×48. Figure 3 illustrates the transverse mesh sketch of the computational domain, where the white spot in the left figure denotes the nozzle zone, and the details of the zone are shown in the right figure.

The commercial software Fluent is employed to solve Eq.(4) based on the grid generation as shown in Fig.3. Equation (4) is discretized by the Finite Volume Method. More precisely, the convective term is discretized by the 3-order Quadratic Upstream Interpolation for Convective Kinetics (QUICK) scheme whilst the 2-order central difference scheme is used to discretize the diffusion term, and the iteration of the pressure and velocity coupling is performed by the Pressure Implicit with Splitting of Operators (PISO) algorithm. The time step is Δt=0.0005s initially and then is increased gradually according to the convergence conditions in order to reduce the total computation time.

3. Results and discussions

The mushroom-like vortex is a type of flows generated by a submerged round jet in low Reynolds numbers. In general, the Reynolds numbers should be lower than 300 in order to keep a stable vortex. Keeping this in mind, three Reynolds numbers, namely,Re=36, 60 and 160, are chosen to consider the impact of the Reynolds numbers on the formation and evolution characteristics of the mushroom-like vortex. Besides, the jet duration time also has a significant influence on its formation and evolution characteristics so that two distinct non-dimensional time duration times, namely,=2.2 and 4.5, are chosen in the present computations.

3.1Formation mechanism

In this section, the formation mechanism and morphological characteristics of the mushroom-like vortex generated by a submerged round laminar jet will be first analyzed. Figure 4 and Fig.5 illustrate the numerical results of the formation and evolution processes of the mushroom-like vortex atRe=160 and=2.2. As shown in Fig.4 and Fig.5, the liquid discharged from the jet nozzle orderly evolves into a mushroom-like vortex in the ambient fluid. The flow patterns of the jet morphological structures are given in the Fig.6 for the case ofRe=160 and=2.2.

As shown in Fig.4(a) and Fig.5(a), when the jet starts, the jet liquid discharged from the horizontal nozzle moves along a longitudinal straight line and evolves into a symmetric columnar stream under theaction of the jet momentum. This stage is called the starting stage of the jet, and the flow pattern is shown in Fig.6(a). As shown in Fig.4(b) and Fig.5(b), the jet liquid clusters at the front of the main stream, and then a dome structure gradually comes into being at the front of the main stream accompanied with its transverse transportation due to the retardation of the ambient fluid. This stage is called the transition stage of the jet, and the flow pattern is shown in Fig.6(b).

Fig.5 Numerical results of the two-dimensional structures of the mushroom-like vortex atRe=160 and=2.2

Fig.6 Flow patterns of the mushroom-like vortex

After the transition stage is the developing stage, which contains three processes. The first process is shown in Fig.4(c) and Fig.5(c), when the jet liquid is entrained into the dome structure, mixes with the ambient fluid under the impact of the shear layer between the dome structure and the ambient fluid, and the corresponding flow pattern is displayed in Fig.6(c). The second process is shown in Fig.4(d) and Fig.5(d), during the bending process of the dome structure, the jet liquid gradually converts to an opposite back flow close to the main stream and covered by the dome structure, and the flow pattern of this situation is shown in Fig.6(d). In the third process (as shown in Fig.4(e) and Fig.5(e)), with plenty of the jet liquid entrained into the dome structure, the back flow becomes increasingly far away from the main stream and results in the continual expansion of the dome structure as well as the generation of the secondary back flow, and the flow pattern of this process is shown in Fig.6(e).

During the developing stage, the flow pattern is of a spiral vortex observed from a vertical view while the corresponding three-dimensional structure is of a spiral ring-like vortex. Because the exterior envelope of the spiral ring-like structure looks like an open mushroom umbrella and the main stream seems to be a mushroom stem, the flow is called a typical mushroom-like vortex. After the mushroom-like structure is fully formed, its geometrical sizes increase steadily with the continual injection of the jet liquid. Moreover, after the injection is completed, the main stream gradually vanishes while the remaining liquid continually enters the mushroom-like structure until all the jet liquid is absorbed into the inside of the vortex. Eventually, a stemless mushroom-like vortex appears, as shown in Fig.6(e).

As shown in Fig.4(f) and Fig.5(f), after all jet liquid is absorbed into the mushroom-like vortex, the main stream disappears completely and the vortex ring structure is gradually detached from the mushroom umbrella, and this situation is illustrated in Fig.6(f). As the spiral ring-like vortex cannot get the subsequent jet momentum, its development is restricted and the vortex starts to decay and is dissipated completely in the background fluid, and the stage is called the decaying stage of the jet.

To demonstrate the validation of the above numerical results, the experimental results are given in Fig.7, showing that the numerical results are in a good agreement with the experimental results. This fact implies that the present numerical simulation is reliable.

3.2Morphological characteristics

The investigation in the above section shows that there exist three distinct stages in the formation and evolution processes of the mushroom-like vortex. To make a quantitative analysis of its morphological characteristics, three characteristic parameters are defined: the length of the jetL, the radius of the mushroomlike vortexRand the length of the vortex circulationd. Figure 8 illustrates these characteristic parameters,where the length of the jet is defined as the distance between the head point of the jet and the nozzle outletO, the length of the vortex circulation is defined as the longitudinal distance from the head point of the jet to the back flow pointT,O′ denotes the virtual origin,T,GandMdenote the secondary back flow point, the geometry center and the momentum center, respectively.

Fig.7 Experimental results of the three-dimensional structures of the mushroom-like vortex atRe=160 and=2.2

Fig.8 The characteristics parameters of the mushroom-like vortex

Three parameters,Lref,Rrefanddref, are defined as the reference values ofL,Randd, which are chosen as the corresponding values att*=2.2. Then the non-dimensional length of the jetL*, the non-dimensional radius of the mushroom-like vortexR*and the non-dimensional circulationd*can be defined as follows

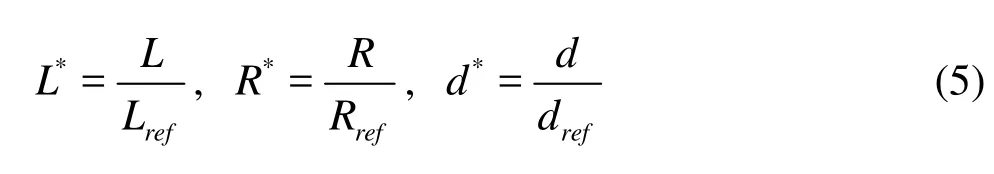
Figure 9 illustrates the numerical and experimental results of the time evolution ofL*,R*andd*where the variableS*representsL*,R*andd*. As shown in Fig.9,S*has different relationships with respect tot*during three distinct evolution stages, and there exist two distinct transition points which just divide the evolution curves into three sections corresponding to the three evolution stages: the starting, the developing and the decaying stages.

It can be seen from Fig.9 that the duration time of the starting stage is very short with a non-dimensional time of about=0.13. In this stage, when the jet fluid enters into the head zone of the vortex, there exists a shear layer between the jet and the ambient fluids due to the retardation of the ambient fluid. Hence, the envelope of the spiral ring-like vortex is essentially caused by the flow of the shear layer. During this process, with the increase of the injection flux entering the head area of the vortex, the radius of the dome structure changes but little. This means that the nondimensional radiusR*of the mushroom-like vortex is approximately a constant, while the non-dimensional lengthL*of the jet and the non-dimensional circulationd*then increase linearly with respect to the nondimensional timet*. When the starting stage reaches its end, a short-lived transition stage starts. Figure 9 shows that, in the transition stage, the circulationd*roughly levels at a constant, whileL*andR*increase linearly with respect tot*.

Fig.9 Comparison of the numerical results with experimental ones for the time evolutions ofL*,R*andd*atRe=160 and=2.2

In the starting stage,R*is almost a constant whileL*andd*both have approximately linear relationships with respect to the non-dimensional timet*with different slopes. On the other hand, in the transition stage,d*is nearly a constant whileL*andR*both increase linearly with the non-dimensional timet*but their slopes are also different. These mean thatL*,R*andd*are not self-similar or self-preserved. By contrast, in the developing stage as shown in Fig.9,L*,R*andd*show the same proportional relationship with respect tot*1/2. This means that the geometry structure of the mushroom-like vortex in the developing stage is self-similar or self-preserved. According to the data in Fig.9, such a self-similarity can be expressed in Eq.(6) by use of the data fitting method

Fig.10 Numerical and experimental results of the time evolutions ofL*,R*andd*for various combinations ofReand

According to its formation mechanism, the development of the laminar jet is maintained by the action of the continual jet momentum, and when such an action gradually vanishes after a certain time, the jet definitely cannot maintain its sustainable development and inevitably sinks into the decaying stage. It can be seen from Fig.9 that in the decaying stage, the variation characteristics ofL*,R*andd*with respect tot*change markedly, and there is not an obvious transition stage. More precisely,L*andR*are approximately proportional tot*1/5whiled*nearly levels off at a constant. This means that the geometry structure of the mushroom-like vortex does not have a self-similarity or self-preserved feature in this stage.

In order to further investigate the impact of various combinations ofReandon the characteristic parameters of the mushroom-like vortex, Fig.10 shows the experimental and numerical results for (Re,)=(160, 2.2), (60, 2.2), (36, 2.2) and (160, 4.5), respectively. It is shown thatL*,R*andd*have the same proportional relationships with respect tot*1/2like Eq.(6) in the developing stage for different (Re,) combinations. This means that the variations ofReandhave no effect on the self-similar characteristics of the mushroom-like vortex. It is further shown that the numerical results are in good agreements with the experimental ones under various combinations ofReand.

3.3Theoretical model

In this section, a theoretical model is proposed to derive a quantitatively accurate relationship between the length of the jet and the evolution time for the mushroom-like vortex in the developing stage. To this end, a cylindrical-coordinate system is used with itsx-axis in the centerline of the jet and its radial distance denoted byr. Based on the above assumptions, the velocity distribution of the three-dimensional free round jet can be expressed in Eq.(7) where the distance of the virtual origin is away from the jet outlet center, denoted byx0, and is introduced to meet the point momentum source assumption, and its value is determined byx0/D=1/4CVRe, whereCVis a constant with a value of 0.168[18]. In Eq.(7),ζis a nondimensional variable expressed byζ=γr/(x+x0) whereγis a constant to be determined, andumis the instantaneous longitudinal velocity component in the centerline of the jet.

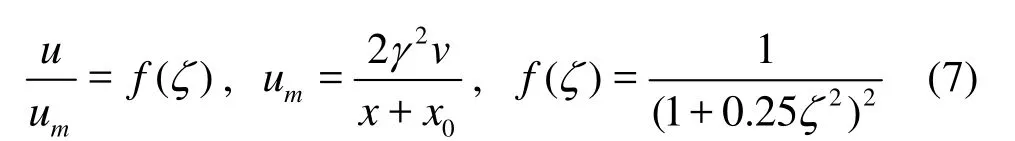
Moreover, because the pressure of the ambient fluid keeps a constant, the pressure gradient in thexdirection can be neglected. This means that the total momentum flux in thex-direction, denoted byJ, is independent of the distancexfrom the nozzle and canbe express as

According to Eq.(1), Eq.(7) and Eq.(8), it can be verified that the constantγ=Re/4. Substituting this value into the expression ofumin Eq.(7), and dividing it by the inlet velocityu0, the instantaneous longitudinal velocity component in the centerline of the jet can be obtained as shown in Eq.(9). Figure 11 shows a comparison of the numerical results with those based on Eq.(9), and the results show a very good agreement between them.

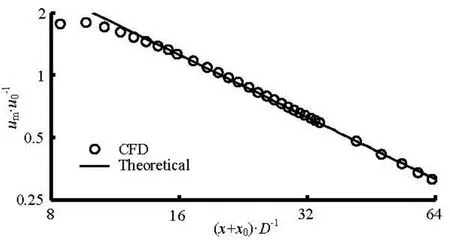
Fig.11 Comparison of numerical results with those based on the Eq.(9)

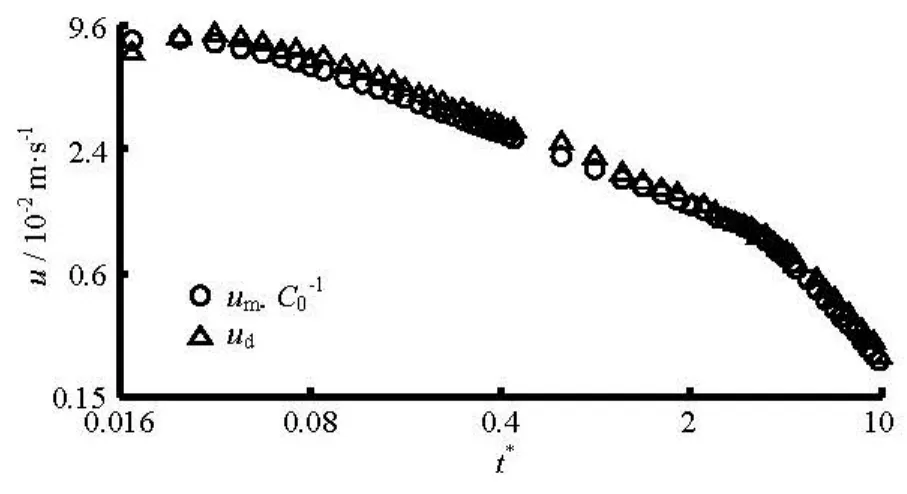
Fig.12 Comparison of numerical results with those based on the Eq.(10)

The translation velocity longitudinal component of the mushroom-like vortex is denoted byud. In the theory of the two-dimensional dipole vortex, it is known that the translation velocity has a fixed algebraic relationship with respect to the instantaneous longitudinal velocity in the centerline of the jet, which can be expressed by the following Eq.(10), whereC0is a constant with a value of 2.48. Figure 12 gives the comparison of the numerical results with those based on Eq.(10), showing a very good agreement between them.

In the developing stage, the length of the jet is much larger than the distance between the real and virtual origins so thatL=x+x0can be used to approximately represent the length of the jet. Based on the definition of the translation velocity of the mushroomlike vortex structure, one has

Fig.13 Comparison of results based on the theoretical models and the numerical and experimental results

According to the point momentum source and virtual origin assumptions, it can be shown thatL=x0fort=0. Solving Eqs. (9)-(11), theexpression of the jet length can be obtained as follows

Letbe the starting moment in the developing stage. It can be seen from Fig.9 that≈0.13. Noting that 4νt/D2=4t*≥4≈0.52?C C2=0.07 in the0Vdeveloping stage, Eq.(12) can be simplified as

On the other hand, in the developing stage of the mushroom-like vortex, Afanasyev and Korabel[13]deduced a theoretical model for the time evolution characteristics of the jet length based on the Stokes approximation theory as follows

Figure 13 illustrates the comparison of results based on the theoretical models (13) and (14) and the numerical and experimental results for three different Reynolds numbersRe=160, 60 and 36. It can be seen from Fig.13 that the present model has a better agreement than Afanasyev’s model for predicting the time evolution characteristics of the jet length.

4. Conclusions

A combined experimental, CFD simulation and asymptotic investigation is presented for the formation mechanism and evolution characteristics of the mushroom-like vortex generated by a submerged round laminar jet. Experimental and CFD simulation results show that there are three distinct stages in the formation and evolution processes of the mushroom-like vortex: the starting, developing and decaying stages. Moreover, the CFD simulations are in good agreements with the laboratory experiments for the variation characteristics of the non-dimensional characteristic parameters of the mushroom-like vortexL*,R*andd*against the non-dimensional timet*.

In the staring stage, the jet liquid shows the transverse transportation feature due to the retardation of the background fluid and the backflow liquid closely moves along with the main stream. Accordingly,L*andd*increase linearly with the non-dimensional timet*whileR*approximately remains a constant. In the developing stage, the backflow gradually flows away from the main stream and forms a secondary backflow, a considerable self-similarity is shown in this stage and this can be quantitatively represented by the same proportional relationships ofL*,R*andd*againstt*1/2. In the decaying stage, the mushroomlike structure starts to decay due to the lack of the supplementary jet momentum, whereL*andR*are approximately proportional tot*1/5, whiled*nearly levels off at a constant.

A theoretical model is proposed for the time evolution characteristics of the jet length, and the results based on the proposed model are in good agreements with the numerical and experimental ones. Moreover, the present model is in a better agreement than the Afanasyev’s model in predicting the time evolution characteristics of the jet length.

[1] IVANOV A. Y., GINSBURG A. I. Oceanic eddies in synthetic aperture radar images[J]. Journal of Earth System Science, 2002, 111(3): 281-295.

[2] Van HEIJST G. J. F., CLERCX H. J. H. Laboratory modeling of geophysical vortices[J]. Annual Review of Fluid Mechanics, 2009, 41: 143-164.

[3] MEUNIER P., SPEDDING G. R. Stratified propelled wakes[J]. Journal of Fluid Mechanics, 2006, 552: 229-256.

[4] WEI Gang, DAI Shi-qiang. Advances in Internal waves due to moving body in stratified fluid system[J]. Advances in Mechanics, 2006, 36(1): 111-124(in Chinese).

[5] FAN Quan-lin, WANG Xi-lin and ZHANG Hui-qiang et al. Coherent structures in turbulent round jets[J]. Advances in Mechanics, 2002, 32(1): 109-118(in Chinese).

[6] SOUS D., BONNETON N. and SOMMERIA J. Turbulent vortex dipoles in a shallow water layer[J]. Physics of Fluids, 2004, 16(8): 2886-2898.

[7] SOUS D., BONNETON N. and SOMMERIA J. Transition from deep to shallow water layer: Formation of vortex dipoles[J]. European Journal of Mechanics-B/ Fluids, 2005, 24(1): 19-32.

[8] PRAUD O., FINCHAM A. M. The structure and dynamics of dipolar vortices in a stratified fluid[J]. Journal of Fluid Mechanics, 2005, 544: 1-22.

[9] MEUNIER P., DIAMESSIS P. J. and SPEDDING G. R. Self-preservation in stratified momentum wakes[J]. Physics of Fluids, 2006, 18(10): 1-10.

[10] ZHU Min-hui, WANG Xiao-qing and CHEN Ke et al. Experiments on quasi-two-dimensional dipolar vortex streets generated by a moving momentum source in a stratified fluid[J]. Acta Physica Sinica, 2011, 60(2): 024702(in Chinese).

[11] O’NEIl P., SORIA J. and HONNERY D. The stability of low Reynolds number round jets[J]. Experiments in Fluids, 2004, 36(3): 473-483.

[12] KWON S. J., SEO I. W. Reynolds number effects on the behavior of a non-buoyant round jet[J]. Experiments in Fluids, 2005, 38(6): 801-812.

[13] AFANASYEV Y. D., KORABEL V. N. Starting vortex dipoles in a viscous fluid: Asymptotic theory, numerical simulations, and laboratory experiments[J]. Physics of Fluids, 2004, 16(1): 3850-3858.

[14] VOROPAYEV S. I., AFANASYEV Y. D. and KORABEL V. N. et al. On the frontal collision of two round jets in water[J]. Physics of Fluids, 2003, 15(11): 3429-3433.

[15] ZHAO Ping-hui, YE Tao-hong and ZHU Min-ming et al. Study of a large eddy simulation of a circular jet[J]. Journal of Engineering Thermophysics, 2012, 33(3): 529-532(in Chinese).

[16] LEE J. H. W., CHU V. H. Turbulent jets and plumes: A lagrangian approach[M]. Dordrecht, The Netherlands: Kluwer Academic Publisher, 2003, 6.

[17] DURST F., RAY S. and UNSAL B. et al. The development lengths of laminar pipe and channel flows[J]. Journal of Fluids Engineering, 2005, 127(6): 1154-1160.

[18] REVOELTA A., SáNOHEZ A. L. and LINáN A. The virtual origin as a first-order correction for the far-field description of la- minar jets[J]. Physics of Fluids, 2002, 14(6): 1821- 1824.

10.1016/S1001-6058(13)60425-4

* Project supported by the National Nature Science Foundation of China (Grant No. 11072153), the Foundation of State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University (Grant No. GP010819).

Biography: CHEN Yun-xiang (1987-), Male, Master

YOU Yun-xiang,

E-mail: youyx@sjtu.edu.cn