Inverse problem of bottom slope design for aerator devices*

WU Jian-hua (吳建華), FAN Bo (樊博)

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China,

E-mail: jhwu@hhu.edu.cn

XU Wei-lin (許唯臨)

State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China

(Received July 19, 2013, Revised July 23, 2013)

Inverse problem of bottom slope design for aerator devices*

WU Jian-hua (吳建華), FAN Bo (樊博)

College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China,

E-mail: jhwu@hhu.edu.cn

XU Wei-lin (許唯臨)

State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China

(Received July 19, 2013, Revised July 23, 2013)

Air entrainment is an effective approach to protect release works from cavitation damage. The traditional method of aerator device designs is that, for given flow conditions, the geometries of the aerator device are designed and then the effects are experimentally tested for cavitation damage control. The present paper proposes an inverse problem method of determining the bottom slopes in front of and behind an aerator if the requirements of air entrainment, flow conditions and some of aerator geometric parameters are given. An RBF neural network model is developed and the relevant bottom slopes are calculated in different conditions of flow and geometry on the basis of the data of 19 aerator devices from different discharge tunnels with safe operation. The case study shows that the methodology provides an effective way to design aerator devices under given target conditions.

air entrainment, bottom slope, inverse problem, neural network, discharge tunnel

Cavitation damage control has been a key issue for the design of a release work of hydropower projects. Early in 1953, Peterka conducted some laboratory experiments and deemed that the cavitation damage can be completely avoided when the air concentration of the flow near the surface of the release work reached 5%-8%[1]. The air entrainment has been used since inception and application of this methodology in the Grand Goulee Dam in America in 1960.

Generally, an aerator device is designed through amending its geometric parameters again and again in order to meet the conditions of the flow and to make sure the air concentration required for the whole range of the release work. However, so far as the forward problem of adjusting the system parameters, it is increasingly expected to directly determine their parameters according to the performance of a target system. The method is called inverse problem method.

The inverse problem was proposed by Huygens in 1673 when he conducted the directional design of the isochronous pendulum. Up to the 19th century, Abel promoted the inverse problems, and in recent decades, it was widely used in many fields, such as aircraft design[2], damage assessment of structures[3], geophysical remote measurement[4], and heat transfer[5].

It should be noticed that the ill-posed problem may occur when using the traditional method (like analytical methods) to solve inverse problems. The Artificial Neural Networks (ANN), with the characteristic massively parallel architecture and the ability to learn and generalize, can implement the function mapping between dependent variable and independent variable, and effectively fit or approximate the function relationship, so that the ill-posed problem could be solved if the input and output data are given.

The ANN methods have been used in the inverse problems, and the investigations and applications in the fields of hydraulics were reported: hydraulic design of earth dam cross section[6], and groundwater flow[7]. Luis and Abdalla constructed a data-driven model which can map the implicit relations between permeability and hydraulic head[8]. Zio[9]discussed the potential functions of ANN in solving parameter identification inverse problems of groundwater models. However, the inverse problems, with respect to thedesigns of the aerator device, have not been reported.

For an aerator device on discharge tunnels, its geometric and hydraulic parameters, including the ramp height and angle, bottom slope, flow discharge and velocity through the aerator, are related to the effects of the air entrainment. There are the complex nonlinear relationships among them.

In this study, based on the data collected from 19 aerator devices placed on different discharge tunnels with safe operation, the inverse problem of the bottom slope design of aerator devices will be solved using radial basis function neural network (RBF-NN).

The coefficient of the air entrainment is expressed by

whereQaandQare the flow discharges of the air and water, respectively. The unit discharge of the air through an aerator can be estimated by[10]

whereqa=Qa/B,Bis the chute width,Vois the mean flow velocity through the aerator,Lis jet length,Kis a constant. Equation (2) demonstrates that the value ofqais closely related to the jet lengthL. Generally,Lcan be expressed as[11]

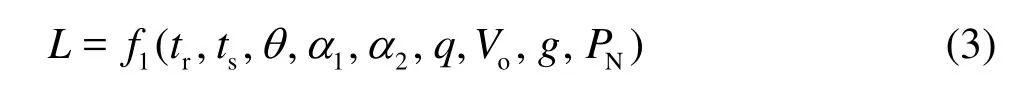
wheretrandtsare the heights of the ramp and step, respectively,θis the ramp angle, 1αand 2αare the bottom slopes in front of and behind the aerator, respectively,q=Q/B, is the unit discharge,g= 9.81 m/s2, is the gravitational acceleration,PNis the index of subpressure inside cavity.

When the influence ofPNis neglected and letts=0, Eq. (1) can be rewritten as

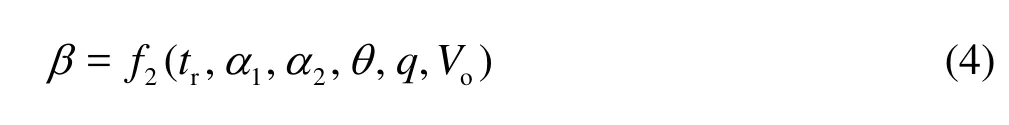
In fact, it is the protected distanceLcand the air concentrationCat the tail ofLcthat directly influence the effect of cavitation damage control. Thus, we have

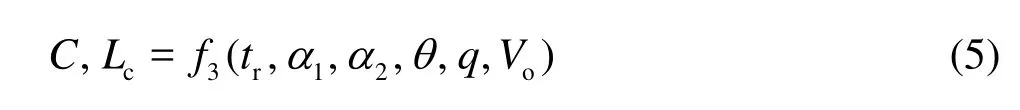
on the basis of Eq.(4).

Here, taking 1αand 2αfor example, the inverse problem of the bottom slope design of aerator devices will be investigated using the RBF-NN.

For the design of an aerator device, it is expected to directly determine the parameters of the aerator device. Thus, under the conditions of the effective air entrainment, Eq.(5) can be rewritten as

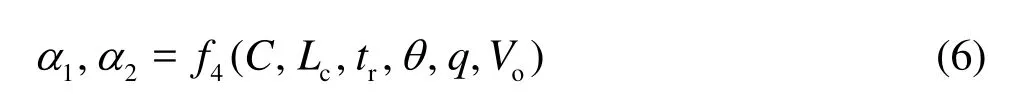
For the inverse problem of the bottom slope design, the input parameters were selected asC,Lc,tr,θ,q, andVo, and the output parameters as1αand 2α. The data of 19 aerator devices were collected from the different discharge tunnels with safe operation in order to establish and train the neural network, and the threshold values of the parameters are listed in Table 1. Here, since the established neural network is based on these data, those threshold values demonstrated the application conditions of the neural network.

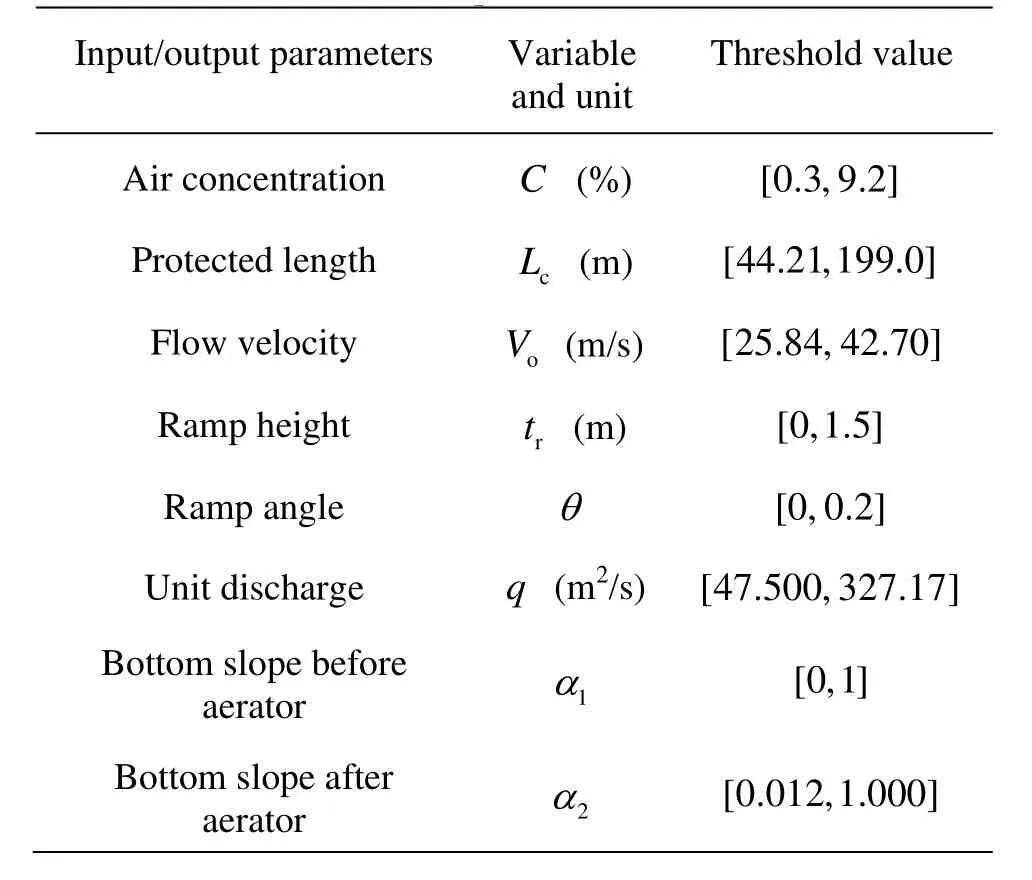
Table 1 Threshold value of parameters

The data were treated by the following linear normalization processing

whereis the input/output data after normalization processing,xiis the original input/output data, andxminandxmaxare the minimum and maximum values of the original data, respectively. After the normalization processing, the data is mapped in the interval [-1,1].

The neural network was trained according to the given input/output data, and the predictive parameters could be output. Then, the output values could be reverted to the real values by

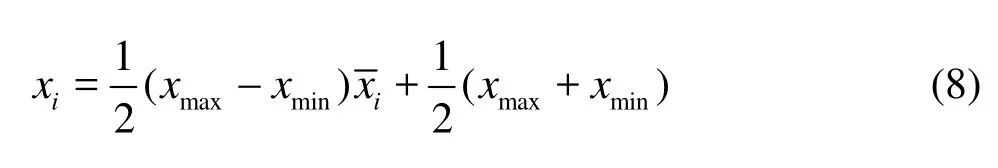
An RBF-NN is an ANN based on radial basis functions as transfer functions. In 1985, Powell introduced the multivariable interpolation radial basis function. Then, Broomhead and Lowe established the RBF-NN in 1988. This is a multilayer feed forward neural network, and has faster training speed and better adaptive data performance compared with the Back-Propagation Neural Network (BP-NN).

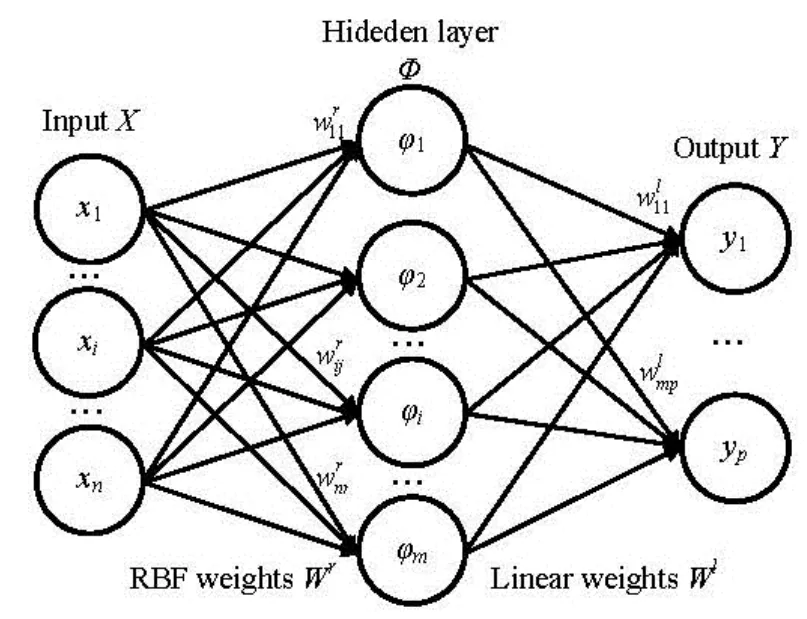
Fig.1 RBF-NN architecture

The RBF-NN obtains three layers, i.e., an input layer, a hidden layer and an output layer (see Fig.1). The neurons in the hidden layer use RBF as transfer function, called RBF neuron layer. There are different types of radial basis functions, and the Gaussian function was used in the present work, namely

rjand passes to thejth hidden neuron after the pretreatment process as follows

whereσjis the input of thejth hidden neuron,is the weight matrix, andis the pondage factor of RBF neurons. Commonly, dispersion constantc=0.8326/is used.

Inserting Eq.(10) and dispersion constantcinto Eq.(9) leads to thejth hidden layer neuron output

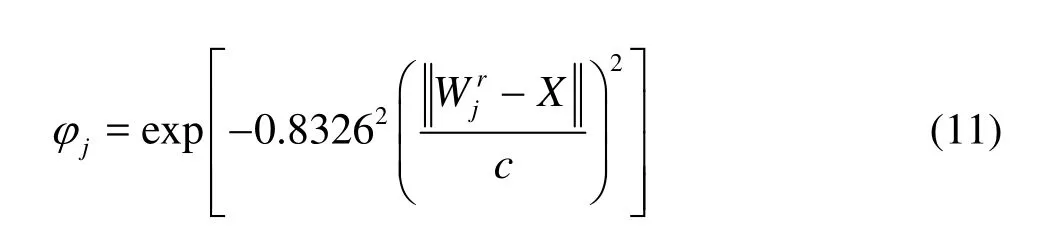
Equation (11) demonstrates that each hidden neuron generates an output on the basis of the distance between input vector and neuron weight vector, and there is the nonlinear transformation from the input layer to the hidden layer.

A case was designed to examine the inverse problem method presented in this study. The conditionsof the selected case are given as: the approach velocityVo=35 m/s, the ramp angleθ=1:10, the ramp heighttr=0.6 m, 0.8 m and 1.0 m, and the unit dischargeq=200 m2/s-280 m2/s. Estimate the minimum values of the bottom slopes (α1andα2) to meet the conditions of the air concentrationC≥2% in the protected range of 100 m.

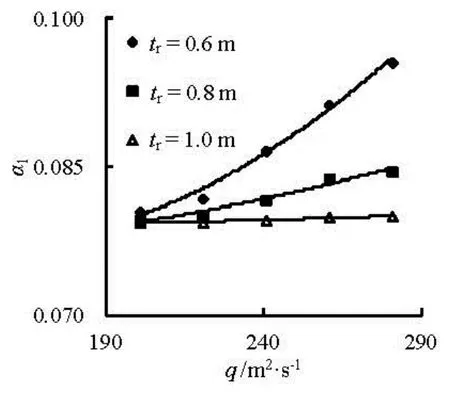
Fig.2 Variation of1αwithqat differenttr

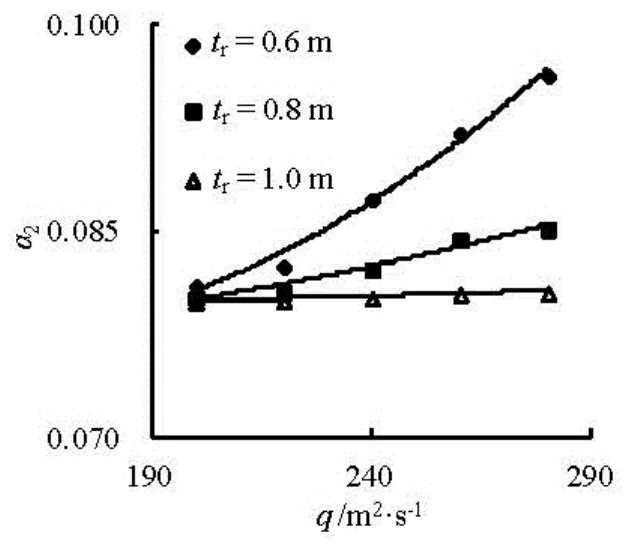
Fig.3 Variation of2αwithqat differenttr

Figures 2 and 3 show the variations of the bottom slopes in front of and behid the aerator (α1andα2) with the unit discharge (q) at different ramp heights (tr). It could be noticed that, the bottom slopes, bothα1andα2, have the similar change, and they all increase as the unit discharge increases. Secondly, the increment ofα1(orα2) is larger at the small ramp height than at large ramp height, such as the increment of 0.0151 fortr=0.6 m dropping to 0.0006 fortr= 1.0 m2when the discharge varies from 200 m2/s to 280 m/s (see Fig. 2). Thirdly, the bottom slope in front of the aerator is slight less than the one behind the aerator at the same conditions. Fortr=0.6 m, we haveα1=0.0805andα2=0.0812whenq= 200 m2/s, whileα1=0.0956andα2=0.0964atq=280 m2/s. The similar behavior occurs attr= 0.8 m and 1.0 m.

In summary, by means of the data of the 19 aerator devices, an RBF-NN was developed to solve the inverse problem of the bottom slope design of the aerator devices. Using this method, the minimum bottom slopes before and after the aerator devices could be estimated if the ramp height and angle of the aerator, approach velocity and unit flow discharge through the aerator, protected length and air concentration are given.

The case study shows that the present method provides an effective way to design an aerator device if the target conditions have been given.

[1] PETERKA A. J. The effect of entrained air on cavitation pitting[C]. Proceedings of the 5th IAHR Congress. Minneapolis, USA, 1953, 507-518.

[2] TRIVAILO P. M., DULIKRAVICH G. S. and SGARIOTO D. et al. Inverse problem of aircraft structural parameter estimation: Application of neural networks[J]. Inverse Problems in Science and Engineering, 2006, 14(4): 351-363.

[3] VALLABHANENI V., MAITY D. Application of radial basis neural network on damage assessment of structures[J]. Procedia Engineering, 2011, 14: 3104-3110.

[4] VLADIMIR M. K., HELMUT S. Some neural network applications in environmental sciences. Part I: Forward and inverse problems in geophysical remote measurements[J]. Neural Networks, 2003, 16(3-4): 321-334.

[5] DENG S., HWANG Y. Applying neural networks to the solution of forward and inverse heat conduction problems[J]. International Journal of Heat and Mass Transfer, 2006, 49(25-26): 4732-4750.

[6] XU Y. Q., UNAMI K. and KAWACHI T. Optimal hydraulic design of earth dam cross section using saturated-unsaturated seepage flow model[J]. Advances in Water Resources, 2003, 26(1): 1-7.

[7] RAJIB K B. Solving groundwater flow inverse problem using spread sheet solver[J]. Journal of Hydrologic Engineering, 2011, 16(5): 472-477.

[8] LUIS A. G., ABDALLA S. Using neural networks for parameter estimation in ground water[J]. Journal of Hydrology, 2006, 318(1-4): 215-231.

[9] ZIO E. Approaching the inverse problem of parameter estimation in groundwater models by means of artificial neural networks[J]. Progress in Nuclear Energy, 1997, 31(3): 303-315.

[10] NOVAK P., MOFFAT A. I. B. and NALLURI C. et al. Hydraulic structures[M]. 3rd Edition, London, UK: Spon Press, 2001.

[11] WU Jian-hua, RUAN Shi-ping. Cavity length below chute aerator[J]. Science in China, Series E: Technological Sciences, 2008, 51(2): 170-178.

10.1016/S1001-6058(13)60427-8

* Project supported by the National Natural Science Function of China (Grant No. 51179114).

Biography: WU Jian-hua (1958-), Male, Ph. D., Professor