脈沖積分—微分系統(tǒng)的Razumikhin型穩(wěn)定性定理

呂濯纓,鄭艷琳,張來(lái)亮

(1.山東科技大學(xué)公共課題部,山東濟(jì)南 250031;2.山東科技大學(xué)理學(xué)院,山東黃島 266510)

0 引 言

脈沖積分 —微分系統(tǒng)作為非線性脈沖微分系統(tǒng)的一個(gè)重要分支,在自然科學(xué)中有著廣泛的應(yīng)用背景,如物理學(xué)中的電路模擬器與生物學(xué)中的神經(jīng)網(wǎng)絡(luò)系統(tǒng)等.近年來(lái),學(xué)者們對(duì)其的研究也產(chǎn)生了一些成果[1-5].在對(duì)該系統(tǒng)的研究中,解的定性理論已有一定進(jìn)展,但解的穩(wěn)定性理論還僅有比較結(jié)果和極為少量的直接結(jié)果,而且在直接結(jié)果中對(duì)V函數(shù)要求條件較高.基于此,本文利用Lyapunov函數(shù)直接方法并借助研究泛函微分方程的Razumikhin技巧的思想,減弱了在脈沖點(diǎn)對(duì)V函數(shù)的限制條件,得到了脈沖積分 —微分系統(tǒng)零解的穩(wěn)定性的直接判定準(zhǔn)則.

考慮如下脈沖積分 —微分系統(tǒng),

其中:

(i)N為正整數(shù)集;

(ii)f:R+×S(ρ)×Rn在[tk,tk+1)×S(ρ)×Rn上連續(xù),S(ρ)={x∈Rn:|x|＜ρ},k∈N;

(iv)0＜t1＜t2＜ …＜tk＜ …,且tk→∞(k→∞);

(v)Jk(x):S(ρ)→Rn(?k∈N);

(vi)對(duì)上述ρ,存在ρ1:0＜ρ1≤ρ,使得當(dāng)x∈S(ρ1)時(shí),有 Jk(x)∈S(ρ);

(vii) K(t,t,0)≡0,f(t,0,0) ≡0,Jk(0) ≡0(?k∈N),保證系統(tǒng)(1)的零解存在.

另外,我們總假定f,Jk滿足一定條件以保證系統(tǒng)(1)的解整體存在唯一.

定義1 若函數(shù)V:R+×Rn→R+在 G上連續(xù)且滿足,

定義2 稱系統(tǒng)(1)的零解為:

(i)穩(wěn)定的,若對(duì) ?ε＞0,t0∈R+,?δ= δ(t0,ε)＞0,使當(dāng)|x0|＜δ時(shí),有|x(t,t0,x0)|≤ε,t≥t0;

則稱函數(shù)V∈V0.若V∈V0,則,

(ii)一致穩(wěn)定的,若(i)中的δ與t0無(wú)關(guān);

(iii)吸引的,若對(duì) ?ε＞0,t0∈R+,?δ= δ(t0)＞0,T= T(t0,ε)＞0,使當(dāng)|x0|＜δ時(shí)有, |x(t,t0,x0)|≤ε,t≥t0+T;

(iv)一致吸引的,若(iii)中的δ,T均與t0無(wú)關(guān);

(v)漸近穩(wěn)定的,若(i)與(iii)同時(shí)成立;

(vi)一致漸近穩(wěn)定的,若(ii)與(iv)同時(shí)成立.為方便起見(jiàn),我們引入下列記號(hào):

K={a∈C[R+,R+]:a(s)關(guān)于s嚴(yán)格單增,且 a(0)=0};

Ω1={P∈C[R+,R+]:P(s)關(guān)于s非減, P(s)＞s,s＞0,且 P(0)=0};

Ω2={H∈C[R+,R+]:H(s)關(guān)于s非減, H(s)＞0,s＞0,且 H(0)=0}.

1 主要結(jié)果

定理 設(shè)存在函數(shù)V∈V0,a,b∈K,P∈Ω1及 H∈Ω2滿足:

(i)a(|x|)≤V(t,x)≤b(|x|),(t,x)∈[t0,∞)×S(ρ);

(ii)對(duì)所有 k∈N及x∈S(ρ1)有,

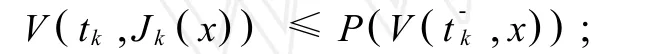
(iii)對(duì)系統(tǒng)(1)的任意解 x(t),當(dāng)V(s,x(s))≤P(V(t,x(t))),t′≤s≤t,t′≥t0時(shí),有,

其中,g:[t0,∞)→R+局部可積;

(iv)?τ＞0,λ＞0,使得對(duì) ?k∈N有,2τ＜tk-tk-1≤λ,同時(shí),對(duì)任意μ＞0,有,

則系統(tǒng)(1)的零解是一致漸近穩(wěn)定的.

證明 ?ε:0＜ε≤ρ1,?δ=δ(ε)＞0,滿足, P(b(δ))≤a(ε).?t0∈R+,不妨設(shè),t0∈[tk-1, tk),記V(t)=V(t,x(t)),則當(dāng)|x0|＜δ時(shí),有,

即,|x(t0)|＜ε.

下證,

首先證明,

若不然,?t—∈(t0,tk),使得 V(t—)＞ b(δ)＞ V(t0),則令,

那么,由V在(t0,tk)上連續(xù)知,V(t＊)=b(δ),D+V(t＊)＞0,且V(t)≤V(t＊),t∈[t0,t＊],于是,

由(iii)知,

矛盾,故(2)成立.

由(2)及(ii)知,

同理可證,

然后證明,

先證,?t＊∈[tk,tk+1)滿足,

若不然,對(duì)所有 t∈[tk,tk+1)有,

由式(3)與(6)有,

由(iii)知,

于是,

又由式(3)與(6)有,

則,

與(iv)矛盾,故式(5)成立.

然后再證,

由式(3)知,

由(iii)知,D+V(t—)＜0,矛盾,故式(8)成立.

由式(8)及(ii)有,

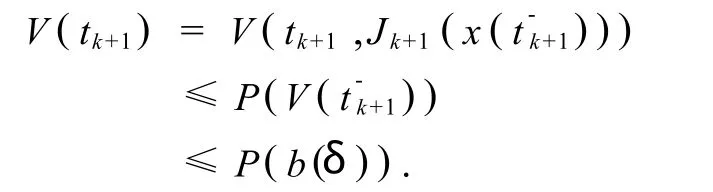
又由式(3)知,

同理可證,

由數(shù)學(xué)歸納法知,對(duì)于j=0,1,2,…,有,

從而,

因此,|x(t)|＜ε,t≥t0,即系統(tǒng)(1)的零解是一致穩(wěn)定的.

由系統(tǒng)(1)零解的一致穩(wěn)定性知,對(duì)于ε=ρ1,?ρ＞0,滿足 P(b(δ))= a(ρ1),使得對(duì) ?t0∈R+,當(dāng)|x0|＜δ時(shí),有|x(t)|≤ρ1,且V(t)≤P(b(δ)),t＞t0.對(duì) ?ε:0＜ε＜ρ1,由 P(s)＞s, s＞0知,?d= d(ε)＞0,滿足,

設(shè)N為滿足P(b(δ))≤a(ε)+Nd的最小正整數(shù),下證,?ri∈[tk+i,tk+i+τ],使得

顯然,式(9)0成立.設(shè)式(9)i對(duì)某個(gè)i:0≤i＜N成立,須證,?ri+1∈[tk+i+1,tk+i+1+τ]有,

首先證明,?ri+1∈[tk+i+1,tk+i+1+τ],使得,

若不然,對(duì)所有 t∈[tk+i+1,tk+i+1+τ]有,

則,P(V(t))＞V(t)+d＞a(ε)+(N-i-1)d+d= a(ε)+(N-i)d≥V(s),ri≤s≤t, t∈[tk+i+1,tk+i+1+τ].

由(iii)有,

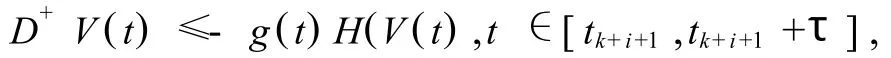
則,

又,

于是,

故,

與(iv)矛盾,故式(10)成立.

下面再證明,

若不然,?t—∈(ri+1,tk+i+2)使,

則,?t＊∈[ri+1,—t)及—t∈(t＊,—t)使,V(t＊) =a(ε)+(N-i-1)d,D+V(—t )＞0,且V(t＊)＜V(—t),于是,

由(iii)知,D+V(t—)≤0,矛盾,故式(11)成立.

然后再證 ?r＊

i+1∈[ri+1,tk+i+2)使,

若不然,對(duì)所有 t∈[ri+1,tk+i+2)有,

由式(11)有,

V(s)≤P(V(t)),ri+1≤s≤t,t∈[ri+1,tk+i+2),則由(iii)知,D+V(t)≤-g(t)H(V(t)),t∈[ri+1,tk+i+2),于是,

又由式(11)及式(13),

故,

從而,

與(iv)矛盾,故式(12)成立.

最后,證明,

若不然,?t⌒∈(r＊

i+1,tk+i+2)使,

則,?～t ∈ [ri＊+1,ti+i+2) 及∧t∈ (～t ,⌒t]使, P(V(～t))=a(ε)+(N-i-1)d,D+V(∧t)＞0,且V(～t)＜V(∧t).由,式(11)有,

由(iii)知,D+V(∧t)≤0,矛盾,故式(14)成立.

由式(14)及(ii)有,

又由式(11)知,

同理可證,

由數(shù)學(xué)歸納法知,對(duì)于j=2,3,…,有,

即式(9)i+1成立.

從而式(9)i對(duì)所有i=0,1,…,N均成立.

當(dāng)i=N時(shí),

于是,|x(t)|≤ε,t≥tk+N+1.令,T=T(ε)= (N+2)λ,則,t0+T=t0+(N+2)λ＞tk-1+(N +2)λ≥tk+N+1,因此,

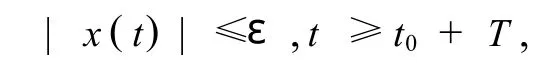
即系統(tǒng)(1)的零解是一致漸近穩(wěn)定的.

[1]傅希林,閻寶強(qiáng),劉衍勝.脈沖微分系統(tǒng)引論[M].北京:科學(xué)出版社,2004.

[2]Fu X L,Zhang L Q.On Boundedness of Solutions of Impulsive Integre-differential Systems with Fixed Moments of Impulsive Effects[J].Acta Mathematica Scientia,1997,17(2):219-229.

[3]Shen J H,Yan J R.Razumikhin-type Stability Theorems for Impulsive Functional Differential Equations[J].Nonlinear Analysis, 1998,33(1):519-537.

[4]呂濯纓,傅希林.脈沖積分微分方程的有界性與Lagrange穩(wěn)定性[J].科學(xué)技術(shù)與工程,2005,5(16):1121-1122.

[5]呂濯纓,董斌,李曉迪.脈沖積分—微分系統(tǒng)解的有界性[J].成都大學(xué)學(xué)報(bào)(自然科學(xué)版),2008,27(2):109-111.