ANALYSIS OF EDL EFFECTS ON THE FLOW AND FLOW STABILITY IN MICROCHANNELS*

YOU Xue-yi, GUO Li-xiang

School of Environmental Science and Engineering, Tianjin University, 300072, Tianjin, China, E-mail: xyyou@tju.edu.cn

ANALYSIS OF EDL EFFECTS ON THE FLOW AND FLOW STABILITY IN MICROCHANNELS*

YOU Xue-yi, GUO Li-xiang

School of Environmental Science and Engineering, Tianjin University, 300072, Tianjin, China, E-mail: xyyou@tju.edu.cn

(Received April 16, 2010, Revised July 15, 2010)

The effects of the Electrical Double Layer (EDL) on the liquid mean flow and the flow stability in microchannels are investigated by solving the Poisson-Boltzmann equation. The models of the traditional streaming Electrical Current Balance (ECB) and the newly introduced streaming Electrical Current Density Balance (ECDB) are applied to determine the electrical streaming current. The numerical results show that the electrical streaming current backflow in the ECB model near the wall can be removed by using the ECDB model, which is suitable to study the effects of the EDL on the mean flow and the flow stability in microchannels. The flow is found more unstable if the ECDB model is applied.

electrical double layer, Poisson-Boltzmann equation, electrical streaming current balance, flow stability, microchan

1. Introduction

With the rapid development of MEMS technology, there has been a growing interest in the study of microfluidicss involved in lab-on-a-chip and microreactor systems. Microfluidics, which deals with flows with hydraulic diameter ranging from 10-6m to 10-3m, is theoretically very complicated. A fundamental understanding of the behavior of fluids in microchannels is very important.

The effects of solid-liquid interface that can be ignored safely in macro flows become important in microchannel flows because of the large ratio of interfacial layer thickness to channel height. The important microscale effects include the variation of electric potential near a surface (Electrical Double Layer (EDL))[1,2], boundary slip[3,4], roughness[5,6], apparent viscosity[7]. In this article, the effects of EDL on the flow and the flow stability are studied.

Ren et al.[8,9]studied the effects of EDL on the velocity distribution, friction coefficient, apparent viscosity and heat transfer in microflows. It is found that the analytical and experimental results of volume flow rates through parallel plates and rectangular microchannels are significantly lower than those predicted by classical theories. They attributed this discrepancy to the influence of EDL.

Although the electrical potential distribution described by Poisson-Boltzmann equation in the diffuse layer is deduced for the case of resting fluid, this theory is always applied for considering the effect of EDL on the fully developing flow[8-10]. Nernst-Planck equation is employed to describe the anion and cation distributions for the fully developed flow. It was reported that the ion concentration distribution predicted by Nernst-Planck equation is more appropriate for developed microchannel flows[11,12]. But for low Reynolds flows, Poisson-Boltzmann equation is also suitable to describe the electrical potential distribution[13].

The stability of the microchannel flow is of importance. In biotechnology and biochemistry, it was reported that the droplets could be used as micro-reactors to control the mixing and dispersion of chemical reagents[14]or to help protein crystallization[15]. The stability of flow is required to be under control in these processes. The prediction ofthe critical Reynolds number is indispensable. There were some reports concerning the effects of apparent viscosity and boundary slip on the stability of mocroflows[16,17]. The effects of EDL on the flow stability and the heat transfer were studied by Tardu in microchannel Poiseuille flow[18,19]. It was found that the critical Reynolds number is decreased considerably and the laminar mode is destabilized easily when the thickness of EDL is comparable to the channel diameter.

The influence of the electrokinetic process of EDL charges on the velocity distribution and the stability of the microchannel flow is very complicated. Specifically, in the absence of an applied electrical field, when a liquid is forced to flow through a microchannel under an applied hydrostatic pressure difference, the ions in the diffuse layer (the mobile part) of EDL are carried to move towards the downstream end, resulting in an electrical current in the pressure-driven flow direction. This current is called the streaming current. The accumulation of ions downstream sets up an electrical field with a streaming potential, which would induce a conduction current, to flow back in the opposite direction. At a steady state, the streaming current is balanced by the conduction current, and hence the net current in microchannel is zero. To determine the conduction current, the current balancing model, which is called the Electrical Current Balance (ECB), is widely used. In this model, the mean flow is obtained by solving both Poisson-Boltzmann and EDL-modified N-S equations[8-10,18,19].

However, there is an ambiguity point about a backflow in the liquid velocity distribution near the channel wall by applying the ECB model. The backflow cannot be confirmed by experimental results[20,21]. Recently, Gong and Wu[22]found that the backflow comes from the application of the average streaming potential in determining the conduction current in the ECB model. To overcome the problem of backflow, a streaming Electrical Current Density Balance (ECDB) model was proposed. In the new model, it is assumed that the streaming electrical current and the conduction current are balanced at all points across the microchannel. A new mean flow velocity without the backflow could be obtained by applying the ECDB model.

It is well known that the shape of the mean flow velocity is very important to the flow stability. The study of the flow stability in a microchannel by the newly proposed ECDB model is desirable. Firstly, the EDL effects on the mean flow distribution are studied by applying the ECDB model in this article. Then the stability analysis of the microchannel flow is carried out by usingthe ECDB model. A comparison of the results obtained by using the ECB and ECDB models is made.

2. Mathematical model

2.1 Description of EDL

The electrically neutral solution contains an equal number of positively charged ions and negatively charged ions. While contacting an aqueous solution, most solid surfaces carry electrostatic charges or have an electrical surface potential. However, the electrostatic charges on the solid surface attract the counter-ions in the liquid. The concentration of counter-ions near the solid surface is higher than that in the bulk liquid far away from the surface. The concentration of co-ions near the surface is lower than that in the bulk liquid far away from the surface due to the electrical repulsion. Therefore, there is a net charge in the region close to the surface. This net charge balances that on the surface. The surface and the layer of liquid containing the balancing charge is called the electrical double layer, as illustrated in Fig.1.

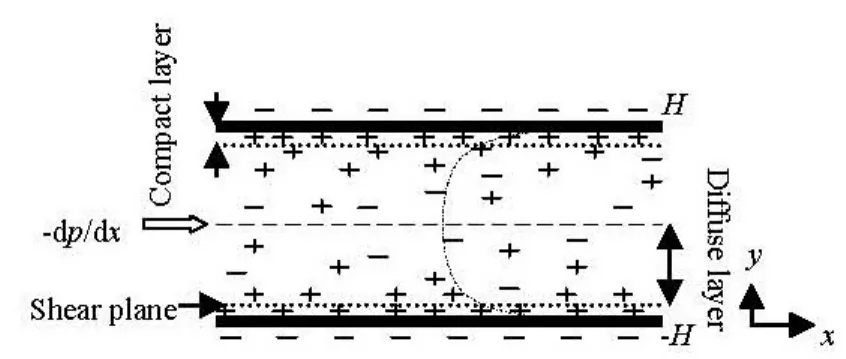
Fig.1 The EDL and the compact and diffuse layers in parallel microchannel

Next to the charged surface, there is a layer of immobile ions that are strongly attracted to the surface. This layer is called the compact layer, normally about several Angstroms thick. The potential distribution in the compact layer is mainly determined by the geometrical restrictions of the ion and molecule sizes, the short-range interactions between ions, and the wall and the adjoining dipoles. From the compact layer to the channel central line, the net charge density is gradually decreased to zero. The mobile ions in this region are less affected by the electrostatic interaction. This region is called the diffuse layer. The thickness of the diffuse layer depends on the bulk ionic concentration and electrical properties of the liquid, usually ranging from several nanometers for high ionic concentration solutions up to several microns for pure water and pure oils. The boundary between the compact layer and the diffuse layer is called the shear plane. Generally, the electrical potential at the solid-liquid interface is difficult to be measured directly. The electrical potential called the ζ potential at the shear plane can be measured experimentally, which is considered as an approximation of the surface potential in most electrokinetic models.

2.2 Poisson-Boltzmann (P-B) equation

Figure 1 shows a fully developed liquid microchannel flow between two parallel plates separated by a height of 2H. According to electrokinetics, the relationship between the electrostatic potentialψ and the local net charge density ρeis described by Poisson equation in y-direction and expressed as

where ε is the dielectric constant of the solution,ε0is the permittivity of vacuum. The net charge density ρeis given by

where Z is the ionic valence, e is the fundamental charge of an electron (1.6021×10?19C), n+and nare the concentrations of positive and negative ions, respectively.

Assuming that the system is in the steady state and the ions in the solution do not move macroscopically, the distribution of ions at a certain point near the charged wall is described by Boltzmann equation

where kbis the Boltzmann constant (1.3805× 10?23Jmol?1K?1), T is the absolute temperature of the fluid in the microchannel ( K).

From Eqs.(1)-(3), we may obtain P-B equation as

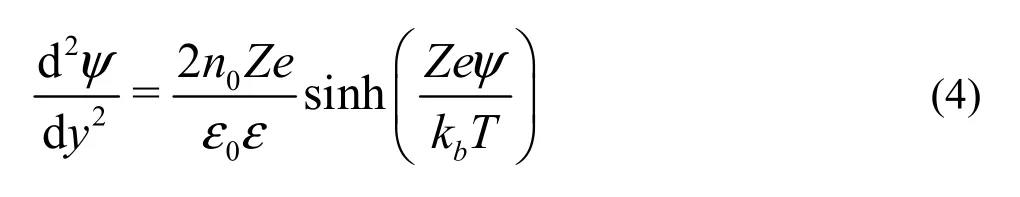
With y =y/ H and ψ = Zeψ / kbT, the nondimensional P-B equation is

where κ= Hk =H (2 n Z2e2/k Tε ε)1/2, which is

0

b0 the Debye-Huckel parameter and whose inversion 1/kis normally referred as the characteristic thickness of EDL. The dimensionless boundary condition of Eq.(5) is

where the dimensionless ζ potential is= Zeζ /kbT. On the wall, the electrical potential at the interface can be approximately considered to be equal to the shear plane potential, i.e.,. The ζ value depending on the system materials is determined by experiment. When the electrical potential is much smaller than the thermal energy of ions (Eq.(5) can be linearized as

The analytical solution of the above electrical potential with its boundary conditions is found in Ref.[18].

2.3 ECB and ECDB models

In a fully developed microchannel liquid flow between two parallel plates, the N-S equation of laminar flow modified by EDL effect takes the form[18]

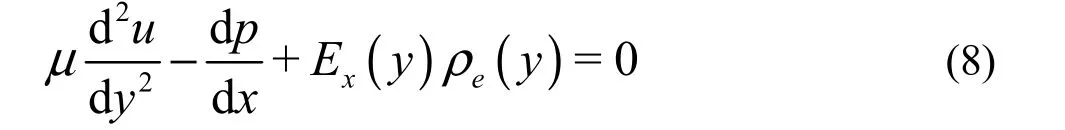
where u is the streamwise mean flow velocity,μ is the fluid viscosity, dp/dx is the pressure gradient and the term Ex(y) ρe(y) is the electrical body force. The boundary condition on the wall is

As explained previously, in the ECB model, it is assumed that the total streaming current in the microchannel is balanced by the conduction current with the same magnitude but the opposite direction in the steady state. The ECB model is expressed as

where I =2 ∫Huρ(y )dy and I =λH E (y ) are

s 0e c x the total streaming and conduction currents in the channel, respectively. λ and Exare the electrical conductivity of the liquid and the average conduction electrical field, respectively. With the ECB model, the N-S equation can be rewritten as

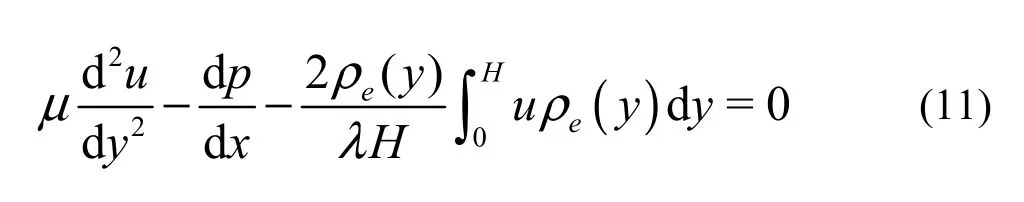
The analytical solution of velocity is found in Ref.[18,19]. However, an unexpected backflow near the walls appears in the distribution of velocity.

The ECDB model is developed to deal with the problem of backflow. In this model, instead of balancing the total streaming current and the conduction current, the streaming electrical current and the conduction current are balanced at all points across the microchannel, which means that[22]

where Jsand Jcare the streaming electrical current density and the conduction current density, respectively, and are expressed as

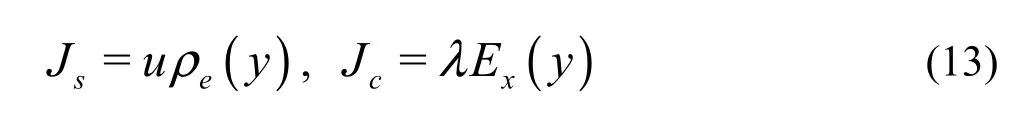
From Eq.(12), we obtain

Substituting Eq.(14) into Eq.(8), we have

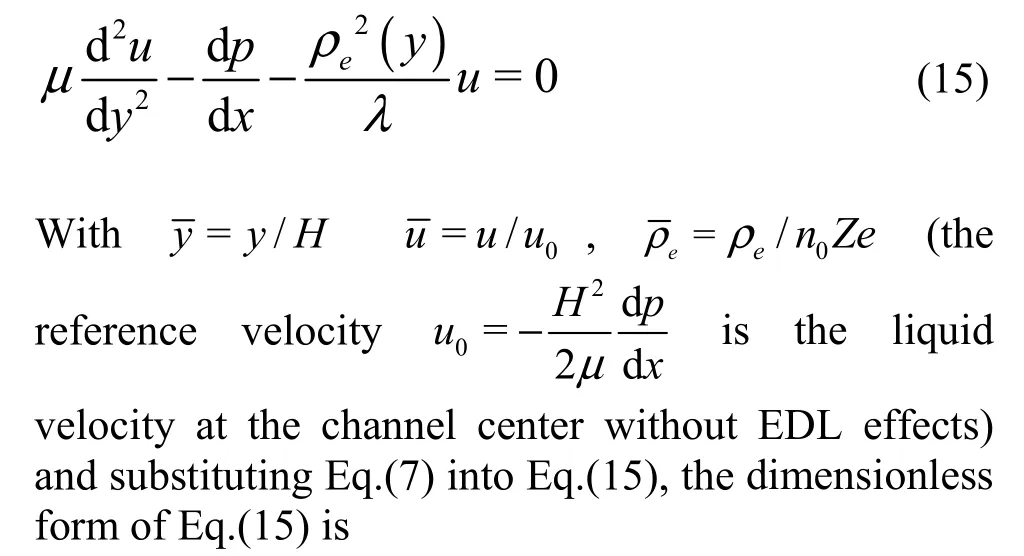
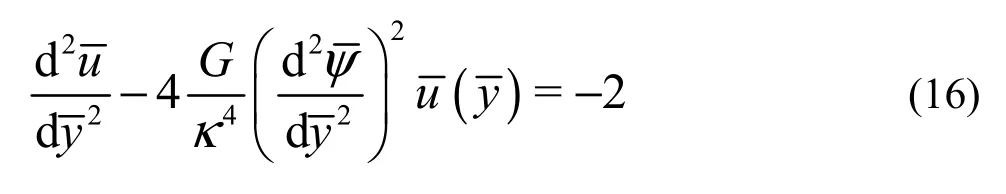
where G =(n0ZeH )2/μλ is the nondimensional surface charge. The boundary condition Eq.(9) is nondimensionalized as

For brevity, the superscript “-” for dimensionless variables will be dropped off. κ,ζ, G are the known parameters. The electrical potentialψ (see Eq.(7)) and the mean velocity u (see Eq.(16)) are solved with their boundary conditions by Chebyshev collocation method described in Ref.[23].

2.4 Stability analysis

The interfacial effects of the wall play an important role in the transition mechanism. In previous approaches, in view of the weakness of the disturbance of electric potential ψ , it is neglected[18,19]. In the linear stability theory, the velocity field is separated into the sum of the mean flow and the superposed disturbance as

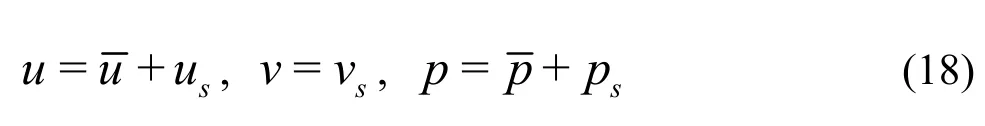
The superscript “-” and the subscript “s” represent the variables of the mean and the superposed disturbance fields, respectively. Substituting Eq.(18) into the dimensionless continuity equation and the EDL modified N-S equation and introducing the disturbance stream functionsφ as

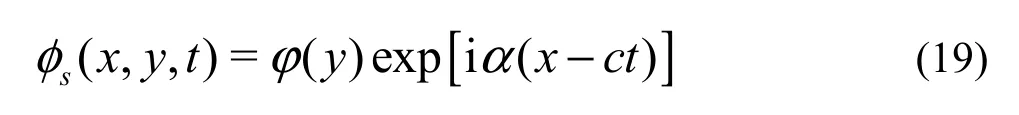
O-S equation is obtained as

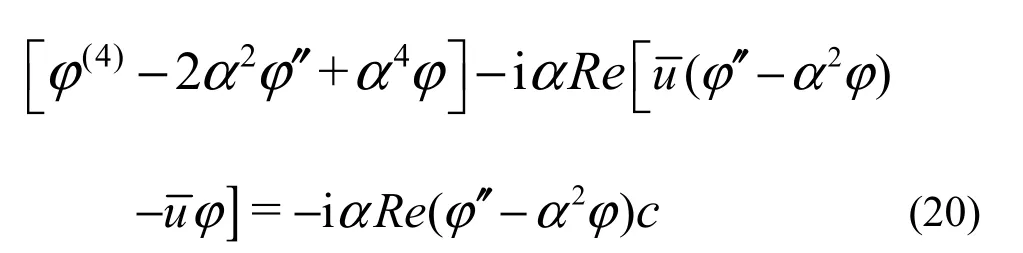
where α , c are the wave number and the phase velocity, respectively.Re =ρu0H/μis Reynolds number. The superscript “'” represents the derivative with respect to y. In the temporal mode, the wave number α is real and the wave speed c is complex. When α ci＞0, the disturbance grows with time and the flow is unstable. When α ci＜0, the disturbance decays with time and the flow is stable. When αci=0, the flow is neutral.

The boundary conditions of Eq.(20) are:

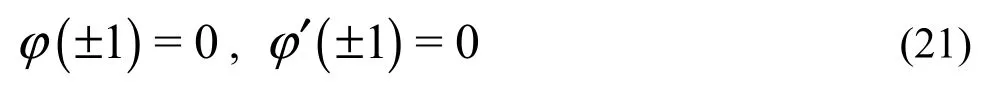
Equation (20) with its boundary conditions describes a generalized eigenvalue problem. The equation is solved by the Chebyshev collocation method and the QR algorithm is applied to determine the eigenvalue c.

3. Results and discussion

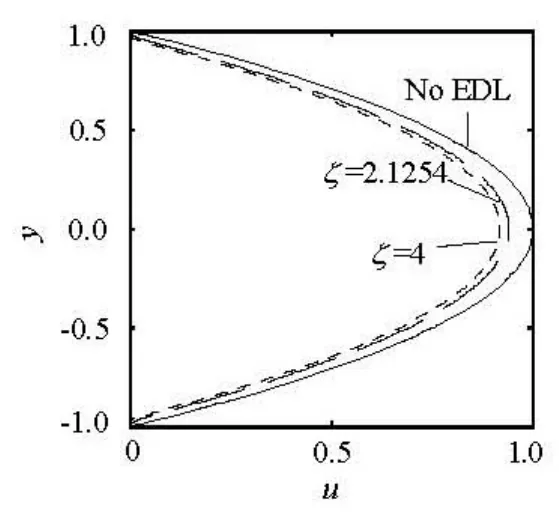
Fig.2 Mean velocity obtained by using the ECB model with different ζ potential, κ =41,G =12 720

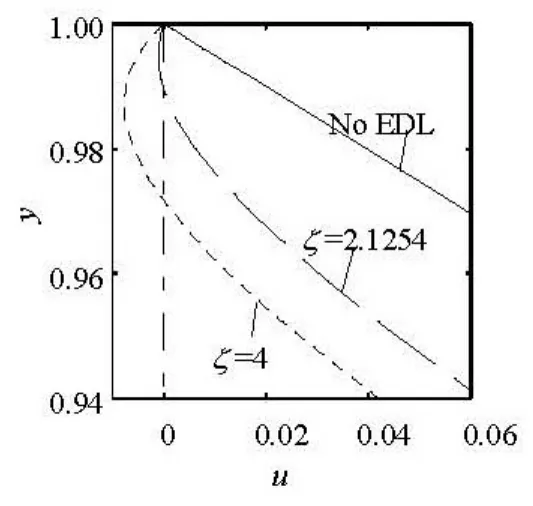
Fig.3 Velocity profiles near the channel wall obtained by using the ECB model with different ζ potential, κ=41, G=12 720

Figure 3 shows the amplificatory local velocity profiles close to the wall in Fig.2. Apparently, there is a backflow close to the channel wall. The intensity of the backflow increases with the increase of ζ potential. One may ask if the backflow is real. Due to the difficulty of measurement, there are few experimental evidences concerning the velocity distribution near a wall. Without experimental results on microchannel flows available, the experimental results of the microtube flow are taken as a reference. Sugii and Okamoto[20]visualized quantitatively the microtube flow using micro-PIV with a spatial resolution of 1.8 μm × 1.8μm . The inner diameter of the microtube is 100 μm. From the velocity distribution near the wall, it is found that, as a Newtonian fluid of laminar flow in a round tube, the velocity distribution conforms generally to Poiseuille’s law. However, the velocities near the wall are slightly smaller than the theoretical values, as shown in Fig.4 of Ref.[20]. There is no near-wall backflow as far as experimental results are concerned. It means that the near-wall backflow obtained by using the ECB model is not reasonable.

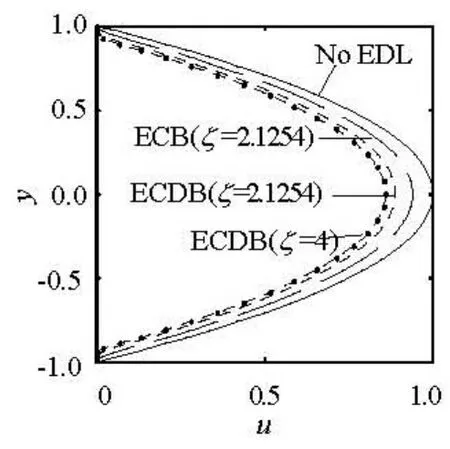
Fig.4 Comparison of the mean velocity in the ECB and ECDB models, κ =41,G=12 720

We may make an analysis of the near-wall backflow as obtained by the ECB model. In the model, it is assumed that the average streaming current across the microchannel is balanced by the conduction current, as represented by Eq.(10). With this assumption, the conduction current near the wall is larger than the actual one. The large conduction current near the wall induces a large velocity opposite to the main flow direction.

Figure 4 shows the mean velocity profiles in the ECDB model with different ζ potentials. It can be seen that the velocity obtained by the ECDB model is smaller than that obtained by the ECB model in places far away from the wall to the middle of channel. This is because the ECDB model assumes the local balance of the streaming current with the conduction current across the microchannel, as indicated by Eq.(12). The smaller velocity makes the opposite conduction current also smaller, which reduces the effect of EDL. Thus, the unreasonable near-wall backflow disappears in the ECDB model. Meanwhile, the larger velocity in the middle of channel increases the opposite conduction current and the effect of EDL, which reduces the corresponding flow velocity. For the same ζ potential, the restrained influence on the flow is larger in the ECDB model than that in the ECB model.

A qualitatively different illustration about the mean velocity profiles as related with the ECB and ECDB models is obtained in this article, which differsfrom that of Gong and Wu[22], where the flow velocities in the ECB and ECDB models are totally detached, and the velocity in the ECB model is always smaller than that in the ECDB model across the microchannel. The above discussion shows that their result is inconsistent with the assumption of the ECDB model.

Figure 5 compares the local velocity profiles obtained by using the ECB and ECDB models near the channel wall. Clearly, the backflow disappears in the ECDB model. The unreasonable backflow is removed by applying the ECDB model instead of the ECB model.

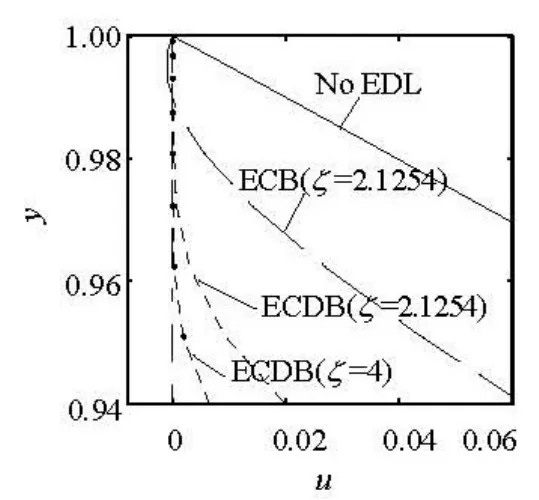
Fig.5 Velocity profiles near channel wall obtained by using the ECB and ECDB models, κ =41,G =12 720

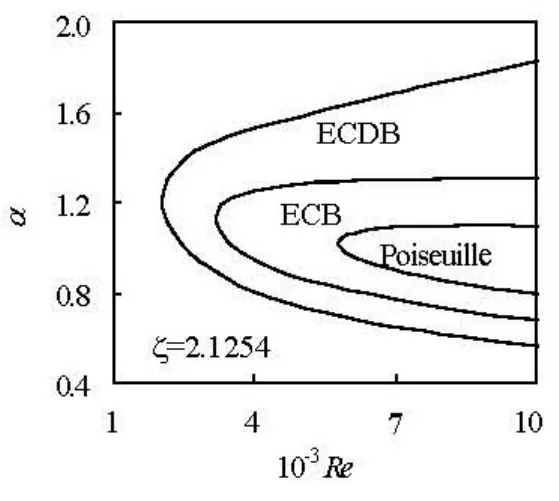
Fig.6 Neutral curves of plane Poiseuille microchannel flow with and without EDL effects, ζ =2.1254, κ=41, G=12 720

3.2 Stability analysis

Figure 6 shows the neutral curves (α ci=0) of stability of the plane Poiseuille microchannel flow with and without EDL effects. The EDL effects are considered by the ECB and ECDB models, separately. The critical wave number and the Reynolds number without EDL effects are α=1.02, Rec=5772, which agree with those of other researchers. Considering EDL effects by using the ECB model, the critical wave number and Reynolds number are α=1.15, Rec=3202 whenζ =2.1254, κ=41, G=12 720, which agree well with those of Tardu[18]. For the same case, the critical wave number and the Reynolds number are α=1.21, Rec=2 051 if EDL effects are considered by using the ECDB model. It can be found that the ECDB model would predict a weaker stability of the flow than the ECB model, i.e., the ECDB model forecasts an early transition in the microchannel flow.

Figure 7 gives the neutral curves of Poiseuille and EDL modified flows (ζ=1) in microchannels. Comparing with Fig.6, it is found that the critical Reynolds number is increased and the wave number is decreased with the decrease of ζ potential.

Fig.7 Neutral curves of plane Poiseuille microchannel flow with and without EDL effects, ζ=1,κ =41, G=12 720

4. Conclusion

The article studies the effects of EDL on the developed laminar flow velocity distribution and the flow stability in microchannels. A careful comparison of EDL effects described by the ECDB and ECB models on the microchannel flow and it’s the flow stability is made. The two models give quite different results. The unreasonable backflow near the channel wall as related with the ECB model is removed by using the ECDB model. It is also found that the ECDB model forecasts an early transition in microchannel flows.

[1] DAS S., CHAKRABORTY S. Effect of conductivity variations within the electric double layer on the streaming potential estimation in narrow fluidic confinements[J]. Langmuir, 2010, 26(13): 11589-11596.

[2] ZHANG Kai, LIN Jian-zhong. The effect of temperature distribution on the mass species transport in micro-channels driven by electroosmosis[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(3 Suppl.): 65-70.

[3] YANG Xiao-fan, ZHENG Zhong-quan. Effects of Channel Scale on Slip Length of Flow in Micro/Nanochannels[J]. Journal of Fluids Engineering-Transactions of the ASME, 2010, 132(6):061201.

[4] GU Chun-yuan, DI Qin-feng and FANG Hai-ping. Slip velocity model of porous walls absorbed by hydrophobic nanoparticles SiO2[J]. Journal of Hydrodynamics, Ser. B,2007, 19(3): 365-371.

[5] YOU Xue-yi, LI Sheng-hua and XIAO hou-peng. The effects of surface roughness on drag reduction and control of laminar plane microchannel flows[J]. Chemical Engneering (China), 2008, 36(8): 25-27(in Chinese).

[6] ZHANG Ren-liang, DI Qin-feng and WANG Xin-liang et al. Numerical study of wall wettabilities and topography on drag reduction effect in micro-channel flow by lattice Boltzmann method[J]. Journal of Hydrodynamics, 2010, 22(3): 366-372.

[7] YOU Xue-yi, ZHENG Xiang-jun and ZHENG Jing-ru. Molecular theory of liquid apparent viscosity in microchannels[J]. Acta Physica Sinica, 2007, 56(4): 2323-2329(in Chinese).

[8] REN Li-qing, QU Wei-lin and LI Dong-qing. Interfacial electrokinetic effects on liquid flow in microchannels[J]. International Journal of Heat and Mass Transfer, 2001, 44(16): 3125-3134.

[9] REN C. L., LI D. Q. Improved understanding of the effect of electrical double layer on pressure-driven flow in microchannels[J]. Analytica Chimica Acta, 2004, 531(1): 15-23.

[10] SHI Yong, ZHAO T. S. and GUO Zhao-li. Simplified model and lattice Boltzmann algorithm for microscale electro-osmotic flows and heat transfer[J]. Internationl Journal of Heat and Mass Transfer, 2008, 51: 586-596.

[11] CHEN X. Y., TOH K. C. and CHAI J. C. et al. Developing pressure-driven liquid flow in microchannels under the electrokinetic effect[J]. Internationl Journal of Mechanical Science, 2004, 42(5-6): 609-622.

[12] NG E. Y. K., TAN S. T. Study of EDL effect on 3-D developing flow in microchannel with Poisson-Boltzmann and Nernst-Planck models[J]. Internationl Journal of Numerical Methods in Engineering, 2007, 71(7): 818-836.

[13] LI Dong-qing. Electrokinetics in microfluidics[M]. Oxford, UK: Academic Press, 2004.

[14] SONG H., TICE J. D. and ISMAGILOV R. F. A microfluidic system for controlling reaction networks in time[J]. Angewandte Chemie International Edition English, 2003, 42(7): 768-772.

[15] ZHENG Bo, ROACH L. S. and ISMAGILOV R. F. Screening of protein crystallization conditions on a microfluidic chip using nanoliter-size droplets[J]. Journal of American Chemical Society, 2003, 125(37): 11170-11171.

[16] MIN T., KIM J. Effects of hydrophobic surface on stability and transition[J]. Physics Fluids, 2005, 17(10): 108106.

[17] YOU Xue-yi, ZHENG Jing-ru and JING Qi. Effects of boundary slip and apparent viscosity on the stability of microchannel flow[J]. Forschung im Ingenieurwesen, 2007, 71(2): 99-106.

[18] TARDU S. The electric double layer effect on the microchannel flow stability and heat transfer[J]. Superlattices and Microstructures, 2004, 35(3-6): 513-529.

[19] TARDU S. Interfacial electrokinetic effect on the microchannel flow linear stability[J]. Journal of Fluids Engineering-Transactions of the ASME, 2004, 126(1): 10-13.

[20] MALA G. M., LI Dong-qing. Flow characteristics of water through a microchannel between two parallel plates with electrokinetic effects[J]. International Journal of Heat and Fluid Flow, 1997, 18(5): 489-496.

[21] SUGII Y., OKAMOTO K. Quantitative visualization of micro-tube flow using micro-PIV[J]. Journal of Visualization, 2004, 7(1): 9-16.

[22] GONG Lei, WU Jian-kang. Resistance effect of electric double layer on liquid flow in microchannel[J]. Applied Mathematics and Mechanics (English Edition), 2006, 27(10): 1391-1398.

[23] YOU Xue-yi. Feedback control of the instability of a fluid layer flowing down a vertical cylinder[J]. International Journal of Heat and Mass Transfer, 2002, 45(22): 4537-4542.

10.1016/S1001-6058(09)60109-8

* Project supported by the National Natural Science Foundation of China (Grant No. 20676093).

Biography: YOU Xue-yi (1964-), Male, Ph. D., Professor