VIBRATION CHARACTERISTICS OF FLUID-STRUCTURE INTERACTION OF CONICAL SPIRAL TUBE BUNDLE*

YAN Ke, GE Pei-qi, BI Wen-bo, SU Yan-cai, HU Rui-rong

Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering, Shandong University, Jinan 250061, China, Email: wssy@mail.sdu.edu.cn

(Received May 25, 2009, Revised August 17, 2009)

VIBRATION CHARACTERISTICS OF FLUID-STRUCTURE INTERACTION OF CONICAL SPIRAL TUBE BUNDLE*

YAN Ke, GE Pei-qi, BI Wen-bo, SU Yan-cai, HU Rui-rong

Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering, Shandong University, Jinan 250061, China, Email: wssy@mail.sdu.edu.cn

(Received May 25, 2009, Revised August 17, 2009)

Heat transfer enhancement is achieved by flow-induced vibration in elastic tube bundles heat exchangers. For a further understanding of heat transfer enhancement mechanism and tube structure optimization, it is of importance to study the vibration characteristics of fluid-structure interaction of tube bundles. The finite element method is applied in the study of fluid-structure interaction of a new type elastic heat transfer element, i.e., the dimensional conical spiral tube bundle. The vibration equation and element matrix for the tube are set up by the regulation of different helical angles and coordinate transformation, together with the simplification of the joint body of the two pipes. The vibration characteristics of conical spiral tube bundle are analyzed at different velocities of the tube-side flow, and the critical velocity of vibration buckling is obtained. The results show that the natural frequency of the tube bundle decreases as the flow speed increases, especially for the first order frequency, and the critical velocity of vibration buckling is between 1.2665 m/s-1.2669 m/s. The vibration mode of conical spiral tube bundle is mainly z-axial, which is feasible to be induced and controlled.

conical spiral tube, heat exchanger, finite element method, fluid-structure interaction, vibration characteristics

1. Introduction

It has long been recognized that flow-induced vibration causes large damage in heat transfer devices, especially in shell-and-tube heat exchangers. Lots of studies have been conducted on the avoidance of flow-induced vibration in heat exchangers[1-3]. A widelyused heat transfer element is the U-tubes in stream generators for nuclear reactors, the vibration of which was studied by Choi et al.[4]. A theoretical and experimental analysis showed that the turbulenceinduced vibration is the main cause for the vibration damages when the shell-side flow velocity was near a sub-critical value. The remarkable work by Cheng et al.[5-9]proposed a novel approach to deal with the flow-induced vibration, which made use of flow-induced vibration in heat transfer enhancement in shell-and-tube heat exchangers. The planar elastic tube bundles[10]are quite different from the conventional ones. Heat transfer is enhanced via the vibration of two joint bodies which has additional mass to adjust the natural frequency of the tube bundle.

Heat transfer enhancement is achieved via the vibration of elastic tube bundles, which must be reasonably induced and controlled. In fact, the bundle is filled with tube-side flow and shell-side flow in heat exchangers in working condition. The inside and outside flow has a great influence on the natural vibration of the tube bundles, which is prevalently noted as fluid-structure interaction. The work done by Wadham-Gagnon et al.[11-13]showed that the vibration of a cantilever pipe changes while the constraint of thefree end is changed. The influence of additional mass on the free end was also studied in their work. The fluid-structure interaction has a great influence on planar elastic tube bundle. Zheng[14]and Lai[15]in their experimental and numerical simulations independently showed that the tube-side flow has a remarkable influence on the natural vibration characteristic of planar elastic tube bundles. Most natural frequencies were 10% dropped, some even 35% dropped. In this article, a new elastic tube bundle, the dimensional conical spiral tube bundle is presented. Due to its conical and spiral structure, the study of its vibration characteristics is much more complex than planar elastic tube bundle. It is a formidable job to establish the simulation model in FEM software, and in addition, the simulation of fluid-structure interaction of conical spiral tube bundle with software requires computers with good performance. In this article, the finite element method is used to study the natural vibration of this tube bundle with tube-side flow. The mass matrix, the pipe stiffness matrix, the fluid kinetic matrix and the Coriolis damping matrix are also derived via the transformation of helical angle and coordinates. The vibration equation is set up with FEM. The results show that the natural frequency of tube bundle decreases when the flow speed increases, especially to the first order frequency, and the critical velocity of vibration buckling is between 1.2665 m/s-1.2669 m/s. In condition of fluid-structure interaction, the vibration mode of the tube bundle is mainly z-axial, which is feasible to be induced, predicted and controlled.

2. Model of finite element analysis

2.1 Structure of spiral tube bundle

The structure of new elastic tube bundle is shown in Fig.1, which is named as the dimensional conical spiral tube bundle. It consists of two pipes, I and II, which are conical spiral and expanding connected via a joint body M. The joint body has additional mass. The inlet and outlet of the pipe is clamp-supported. Because of its conical spiral structure, different bundles are fixed as a nesting structure in the shell-side of heat exchangers.

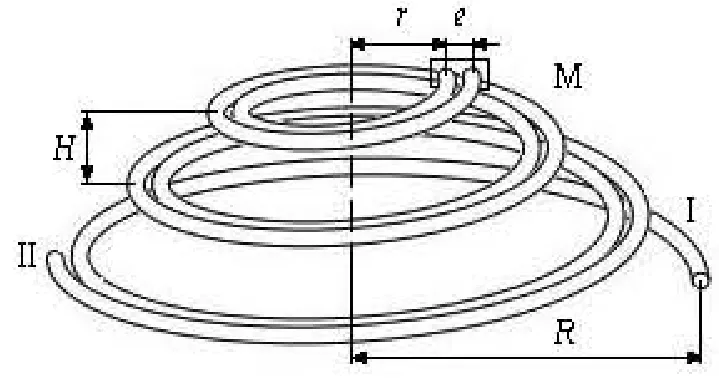
Fig.1 Structure of conical spiral tube bundle

In this article, the finite element method is used to study the vibration characteristics of the tube bundle with tube-side flow, which is simplified as steady flow. The tube bundle is divided into a number of small elements with inside fluid, as shown in Fig.2. The Pipe I is divided into 90 elements and the Pipe II to 83 elements, with a uniform central angle of 12o. The two pipes are connected with two planar curving pipe elements labeled as transition element 01 and 001. The joint body M is simplified with lumped mass method for four elements: 90, 01, 001, 91. The free end of the 1st and the 173rd element is clamped support. In this article, every conical spiral element is approximated as a spiral element. The average radius of conical spiral element is used as its equivalent radius. For example, the average radius of element 75, (R1/2+R2/2), is regard as its equivalent radius.

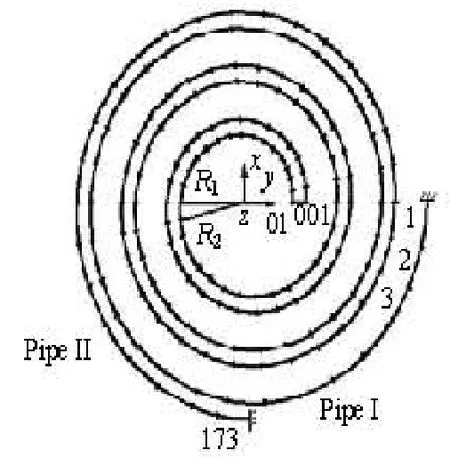
Fig.2 Finite element division of spiral tube bundle

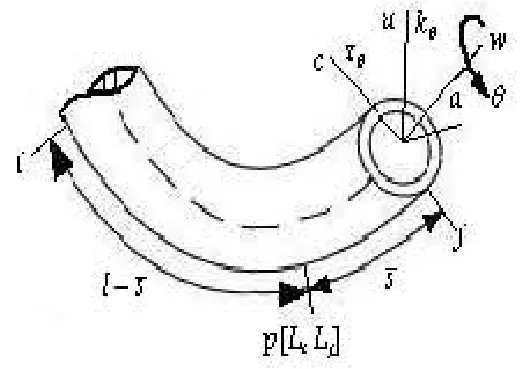
Fig.3 Finite elements of conical spiral pipe with inside flow

The spiral element is shown in Fig.3. w is tangential displacement, u is the first normal displacement, c is the second normal displacement, k0,τ0are the curvature and torsion of spiral element, θ is the sectional twisting angle, and a is the helical angle. Due to the conical structure of tube bundle, every element has different equivalent radius and helical angle a, which influence the curvature and torsion k0,τ0. Take the 75th element as an example:

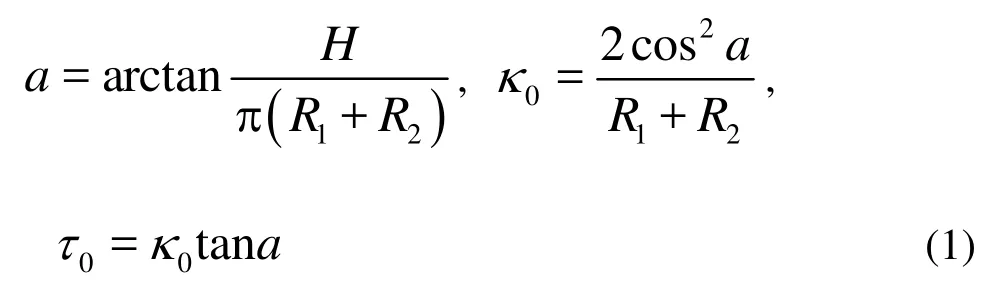
2.2 Coordinate transformation of tube bundle

Due to the conical spiral structure, the helical directions for Pipes I and II are different. For Pipe I, we can see that from the 1st element to the 90th element, the helical directions are uniform. For Pipe II, from the 91st element to the 173rd element, the helical directions are uniform in contrast to Pipe I. For the transition elements 01 and 001, the helical angle is zero because of their planar curving pipe structure. In the study of tube bundle with finite element method, every spiral element is jointed together in sequence, and the vibration equation of the tube bundle is derived with the direct stiffness superposition method, so the natural coordinates and type functions of pipe I and Pipe II must be uniform. Here we suppose that the helical angle of Pipe I is positive, which meansa＞0 for Pipe I, the helical angle of Pipe II is negative, which means a＜0 for Pipe II, we also suppose that the helical angle of transition element is zero.

Before the coordinate transformation, the two nodes of spiral element of Pipe I are denoted as i, j, as shown in Fig.3. The displacement vector at the two nodes is expressed in the determinant form:

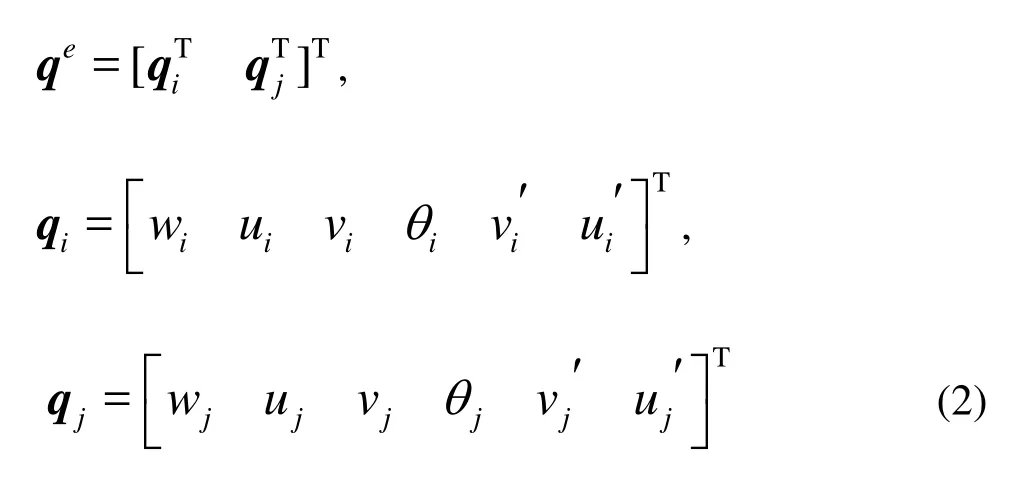
Since its helical direction is opposite to Pipe I, the displacement vector of Pipe II is denoted in an opposite way in order to keep consistant with Pipe I:

To set up the natural coordinate system for the tube bundle, a local coordinate of spiral pipe is defined as=s-si,/ l=ε, as shown in Fig.3, and the natural coordinates as follows:

With arc derivation and natural coordinate integral along the element region, the displacement vector of spiral element can be denoted with the interpolation method as follows:

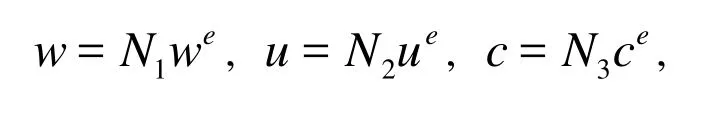
where N1, N2, N3are the type functions of displacement interpolation of spiral element,we, ue, ce,θeare the displacement components of the spiral element:

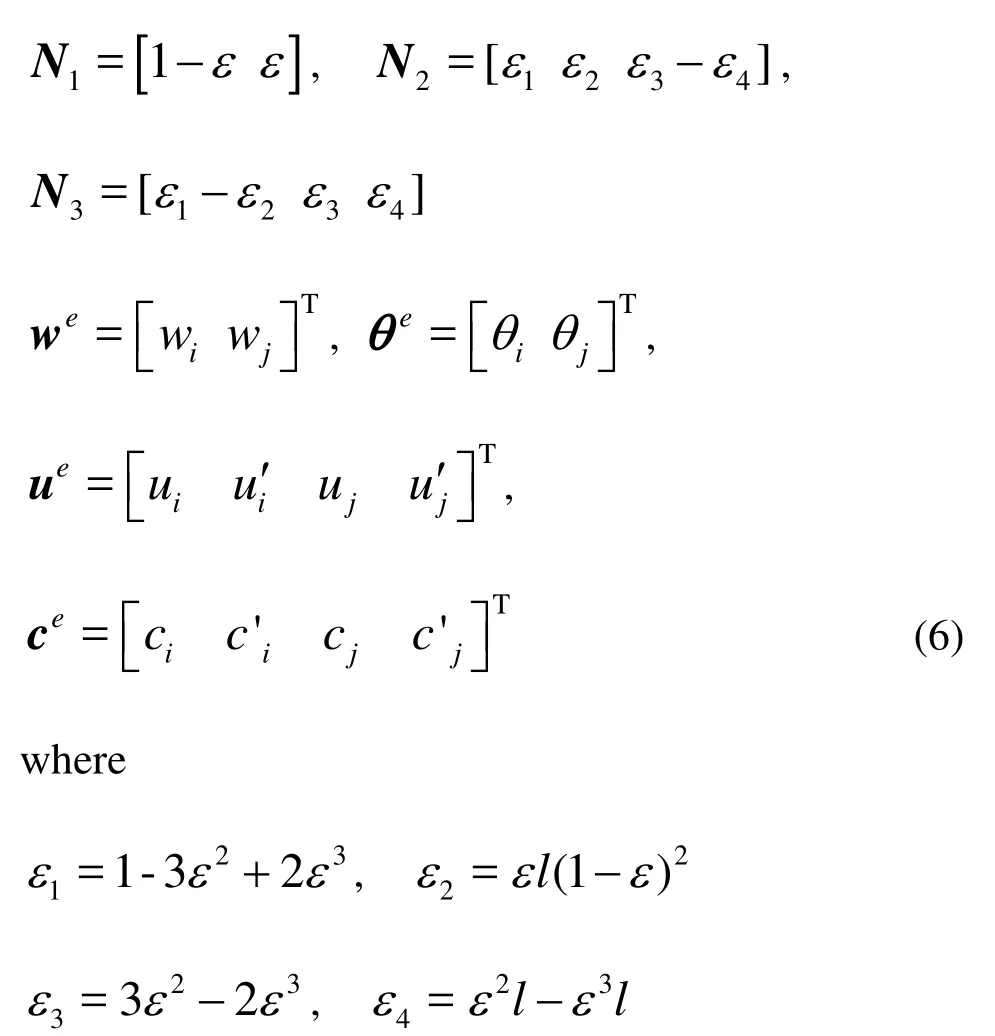
2.3 Modification of spiral element matrix

With the coordinate transformation, the element mass matrix can be derived with the integration method from the Hamilton variational equation of spiral element. From the displacement vector of spiral element it is easy to deduce that the mass matrix of spiral element is a 12×12 one. In order to obtain the general tube bundle matrix, here the mass matrix of spiral element is denoted as

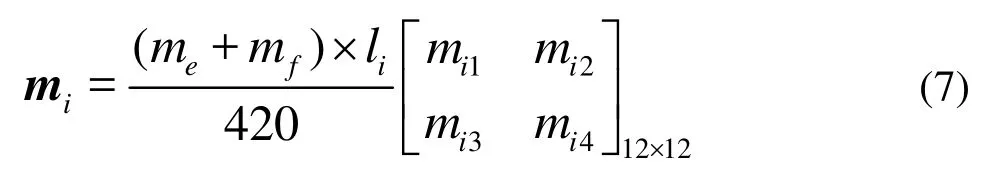
where miis the mass matrix of the ith spiral element, meis spiral pipe mass per unit length,mfis the tube-side fluid per unit length, and liis the ith spiral element length. Because of its conical spiral structure, liis different for each element.

At one end of the spiral elements 90, 91 and the transition elements 01, 001, there is an additional lumped mass M/4, whose influence on the mass matrix can be calculated through its projection in three displacement components.

Take the 90th spiral element as an example. The modified mass matrixis equal to the summation of the element mass matrix and the lumped mass matrix:

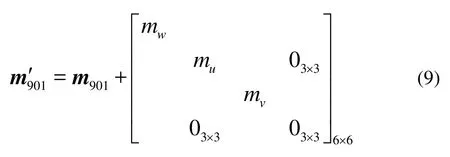
With the direct stiffness superposition method, the general mass matrix of the tube bundle can be given as

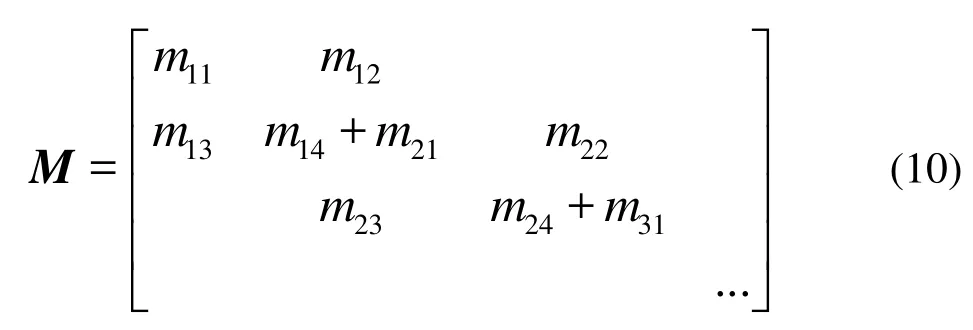
It is easy to figure out that the general mass matrix of the tube bundle is 1056×1056. In fact, the inlet and outlet of the tube bundle are simplified as clamped support, as shown in Fig.2, which means the for the 1st and the 173rd spiral element, the constraint of the displacement vector is

Therefore, the general mass matrix of conical spiral tube bundle is a 1044×1044 one. These matrix of conical element have been deduced by many investigators and the expressions of the fluid-structure interaction could be found in Ni[16]. Due to the variety of helical angle and average radius, each element matrix must be calculated separately through helical angle and coordinate transformation. The helical angle aand the torsion τ0are equal to zero in the calculation of transition elements 01 and element 001. The general stiffness matrix and damp matrix of the tube bundle can be given in the same way as the general mass matrix.

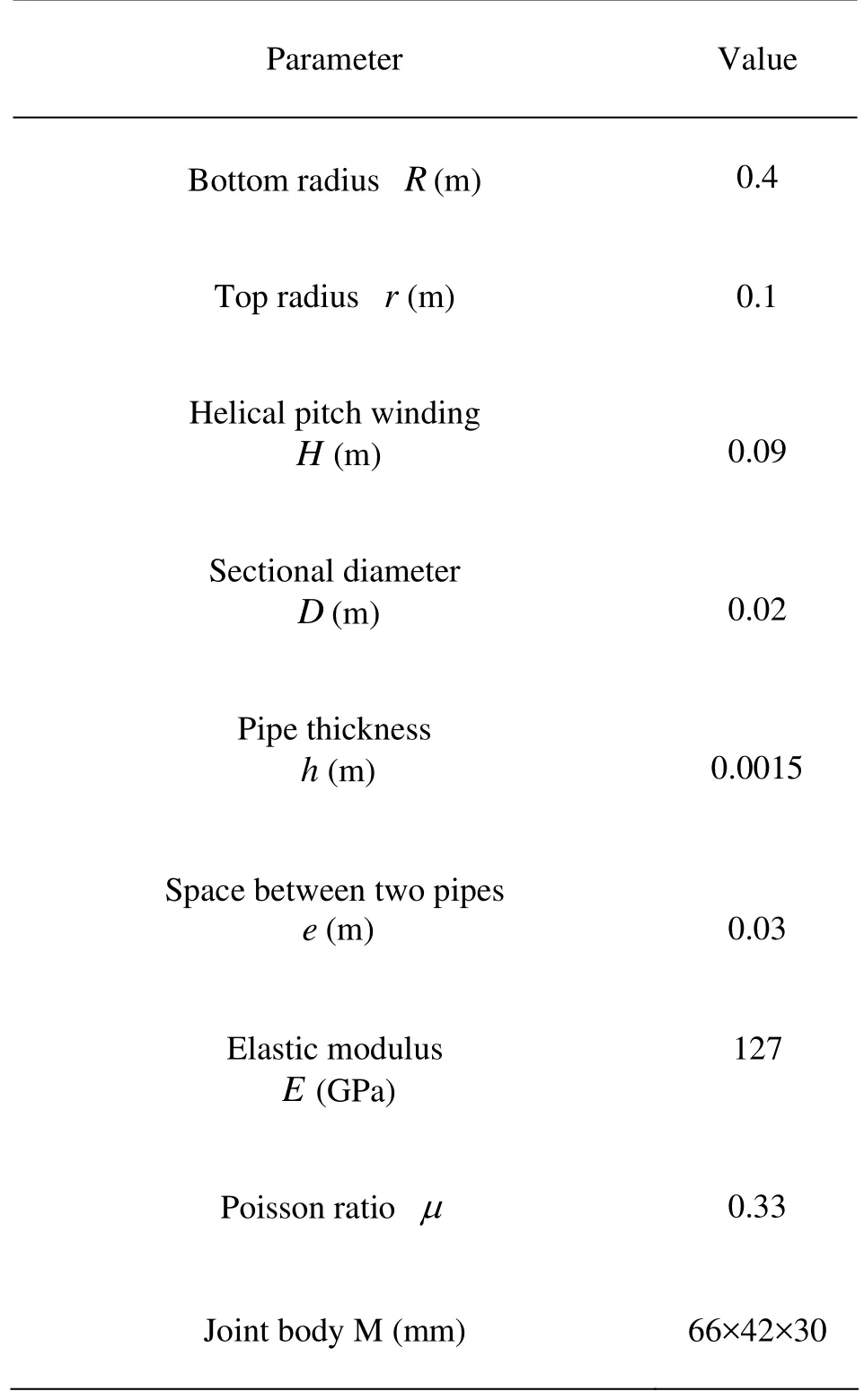
Table 1 structural and material parameter of tube bundle

2.4 Vibration equation of conical spiral tube bundle

The constraint of the inlet and outlet of the conical spiral tube bundle is clumped support, as shown in Fig.2 and Eq.(11), and the modification of damping matrix and fluid kinetic matrix induced by the Coriolis force equals zero. With the direct stiffness superposition method, the vibration equation of conical spiral tube bundle can be given as

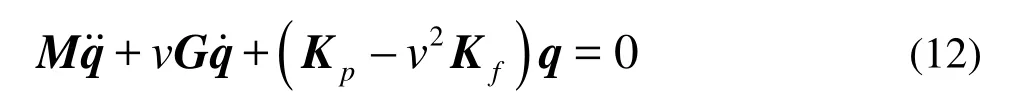
where M is the general mass matrix, v is the flow velocity inside the tube, G is the damping matrix induced by the Coriolis force,Kpis the pipe stiffness matrix, and Kfis the fluid kinetic matrix. The expression of the pipe stiffness matrix Kp, fluid kinetic matrix Kfand Coriolis damping matrixG can be calculated from the Hamilton variationalequation. The inside flow is simplified as steady flow, whose influence on the vibration characteristics is calculated together with the tube element in the element matrix. The additional mass of inside flow is denoted as mfin Eq.(7). The additional damping induced by the Coriolis force is denoted as G and it has been deduced from the Hamilton variational equation. The interaction between the tube and its inside flow is calculated by fluid matrixKf.

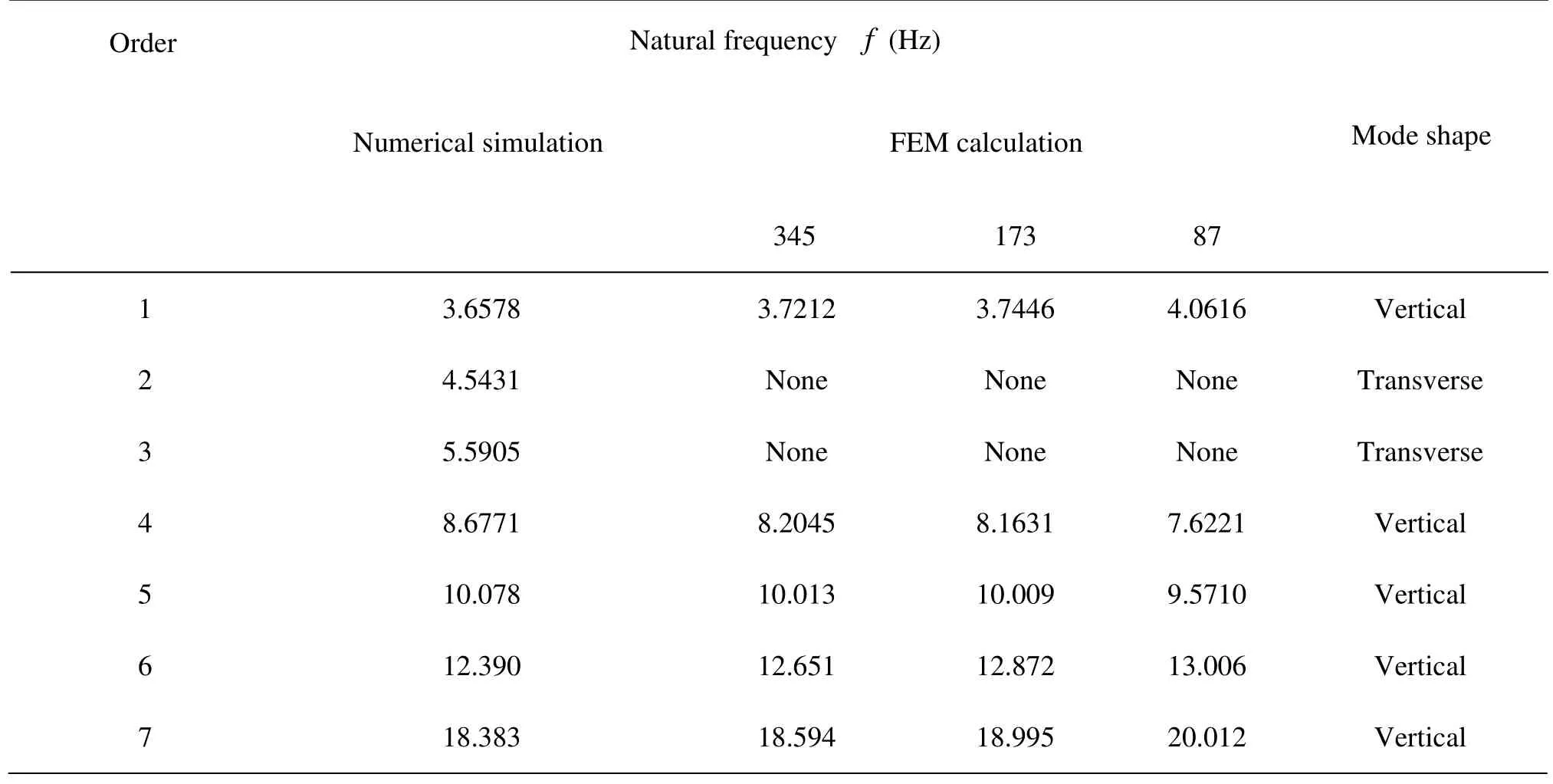
Table 2 Natural frequency of the tube bundle

Numerical simulation is done with the ANSYS software to verify the accuracy of the vibration equation. The natural frequency of the tube bundle, without tube-side flow, is calculated by numerical simulation with linear pipe element. In the simulation, the numerical model of conical spiral tube is constructed with the APDL method, and the sweeping grid is used in the meshing of the model. The cross-section of the tube is meshed with 10 mapped grids and along the tube sweeping grid is used with a length of 5 mm. Table 1 is the structural parameter and material parameter of one type conical spiral tube bundle. In the finite element calculation, the natural frequency can be achieved through the vibration equation when the tube-side flow speed v=0 and the tube-side fluid mass per unit lengthmf=0

The accuracy of the FEM calculation result is affected by the elements number of the tube. In this article, three kinds of divided elements are calculated: 87 elements division with the central angle of 24o, 173 elements with 12o, and 345 elements with 6o. In Table 2, the results for 173 elements division is much better than the 87 elements, and is close to the results for the division 345 elements, which is time-consuming in FEM calculation. So the division of 173 elements is applied in the following analysis because of its accuracy and facility.

The FEM calculation results miss out the 2nd and 3rd modesfor the tube bundle, that is, the transverse vibration, due to the ignorance of the influence of inertia moment and shear deformation on the tube transverse vibration in solving the Hamilton variational equation. The rest orders of natural frequencies are in accordance with the simulation results, and the largest tolerance is 5.92%.

A study on the first to the twentieth modes of tube bundle shows that the modes are mainly vertical vibration, except the 2nd and 3rd modes, which represent transverse vibrations. The vertical vibration means the shape of the conical spiral tube bundle is in the z-direction, and the transverse vibration means the mode is in the x-y plane, as shown in Fig.4. The solid line denotes the mode, and the dashed line the original position of the conical spiral tube bundle. In fact, the vortex shading frequency and the turbulence pulsation frequency[17]in shell-side of heat exchangers in the working condition are much less than the twentieth natural frequency, which equals to 26.74 Hz. Therefore, in the working condition of heat exchangers, the conical spiral tube bundles vibration is mainly in the z-direction, which is proved to be effective in heat transfer enhancement[18-20]. So it is reasonable to ignore the transverse vibration mode in this article.

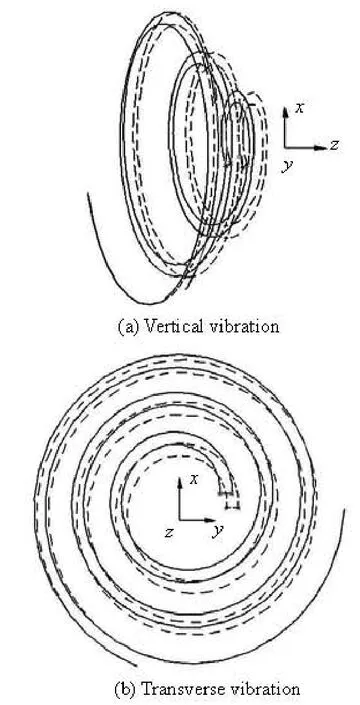
Fig.4 Different mode shape of the tube bundle

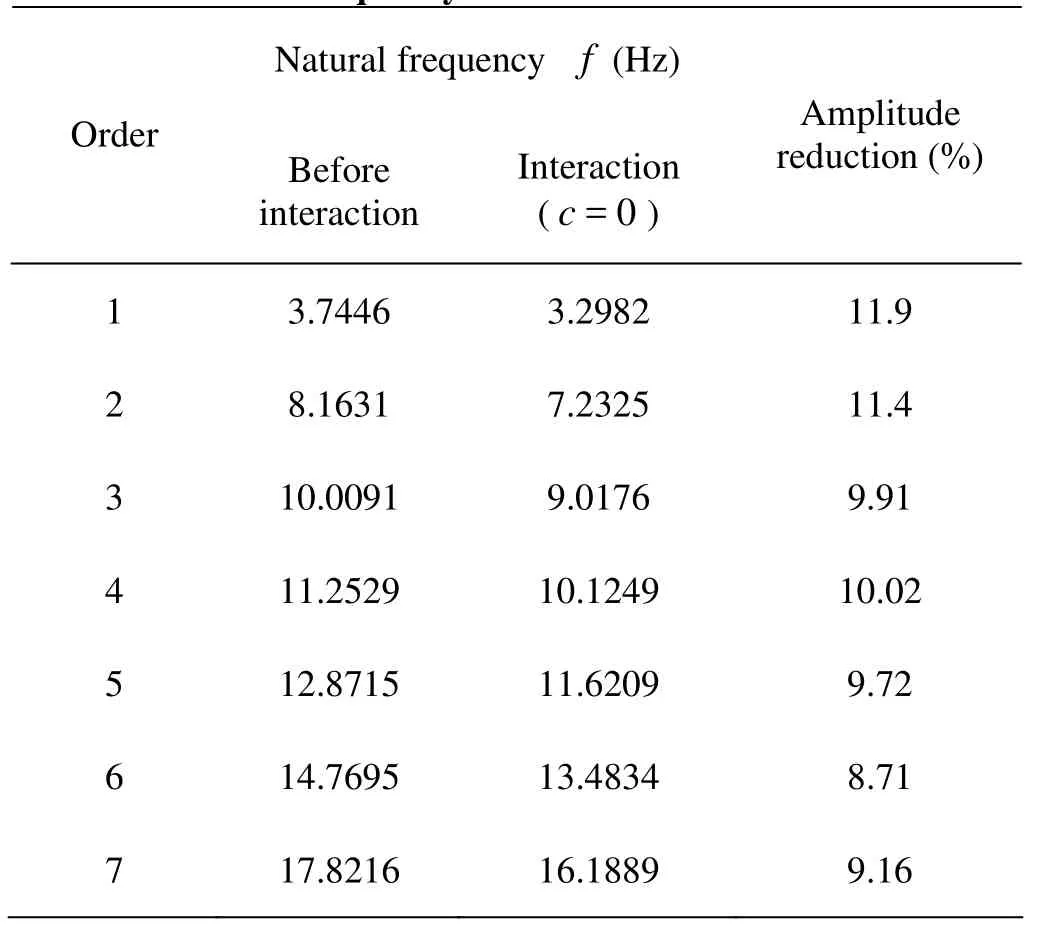
Table 3 Natural frequency of the tube bundle

3. Analysis of results

3.1 Influence of tube-side flow of tube bundle on vibration characteristics

A static inside flow is calculated first to study the influence of fluid-structure interaction on the natural frequency of this tube bundle. The vibration equation is given in Eq.(12), where v =0. The results is shown in Table 3 are the natural frequency of one type tube bundle (Table 1) with and without tube-side fluid interaction. From the comparison it is easy to deduce that the tube-side fluid interaction has a strong influence on the natural vibration of tube bundle. The natural frequencies of tube bundle are all decreased, especially the first order frequency. The reduction in amplitude is about 10%.

The vibration equation can not be solved with the mode decomposition method when the velocity of tube-side flow of tube bundle is taken into account, due to the existence of the asymmetric damping matrix induced by the Coriolis force, showed in Eq.(12). In this circumstance, the vibration equation is turned into standard eigenvalue equation[16]

where λis the eigenvalue,?is corresponding eigenvectors, which are also the displacement vectors of the element nodes, and D is the dynamic matrix of the system, given as

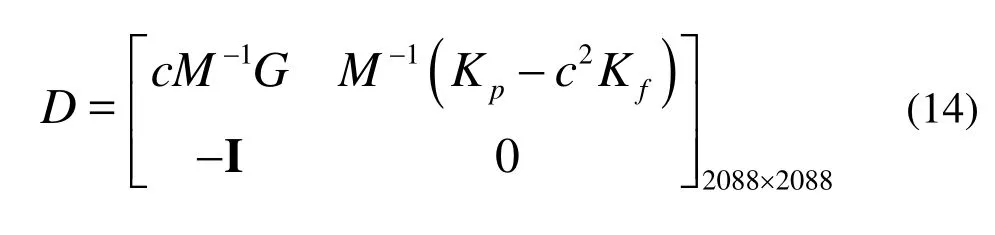
The influence of inside flow speed on the tube vibration characteristics is calculated with Eq.(14). The natural frequency presents complex mode due to the Coriolis force induced by the inside flow. The vibration of the tube bundle is distorted when v>0, it is difficult to identify the mode shape because each mode is a mixing of vertical and transverse vibration, but the vertical vibration is much stronger than the transverse vibration. The low order frequencies decrease rapidly when the inside flow speed increases. The 5th and the higher order frequencies decrease appreciably when the flow speed increases.

Figure 5 shows the variation of natural frequency of tube bundle at different velocities of tube-side flow.It can be deduced that the tube-side flow-structure interaction has significant influence on the vibration characteristic of tube bundle, especially on the lower order mode. The natural frequencies of tube bundle decrease when the velocity of inside flow increase. The influence of velocity on natural frequency becomes larger on the first order. A further study on the mode shape shows that the conical spiral tube bundle is mainly z-axial vibration in the condition of fluid-structure interaction.

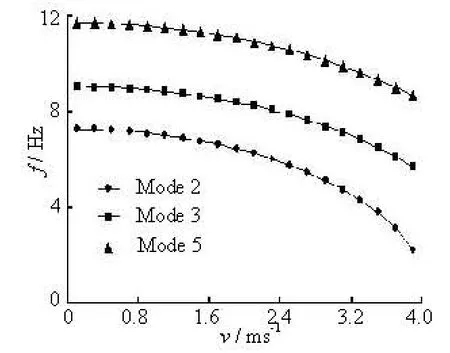
Fig.5 Influence of tube inside flow on natural frequency

In fact, random and irregular turbulence flow exists everywhere in the shell-side of heat exchangers in real working condition. The random and irregular turbulence flow impacts the tube bundles as pulsation through vortex shedding. The vibration characteristic of the widely-used planar elastic tube bundle is complex in work condition due to its special structure. It is hard to predict and control the vibration mode of planar elastic tube bundle in work condition. The dimensional conical spiral tube bundle studied in this article is mainly z-axial vibration even under the influence of inside flow-structure interaction. Because of its simple vibration mode, it is feasible to be induce, predict and control the vibration of conical spiral tube bundle in heat exchangers in real circumstance.

3.2 Critical velocity of vibration buckling

Vibration buckling is a fatal damage to tube bundles in heat exchangers, which induces breakage in tube bundles and hinders the normal circulation in heat exchangers. The vibration buckling of tube bundle happens when the velocity of tube-side flow increases to a critical value, and the first order natural frequency of tube bundle equals to zero. Figure 6 shows the relationship between the first order natural frequency of tube bundle and the tube-side flow velocity. It can be deduced that the velocity of inside flow has a significant influence on the first order natural frequency. The critical inside velocity of vibration buckling is between 1.2665 m/s to 1.2669 m/s. In the real working condition, the inside flow velocity of tube bundle is between 0.01 m/s to 0.3 m/s, which is much smaller than the critical velocity of vibration buckling.

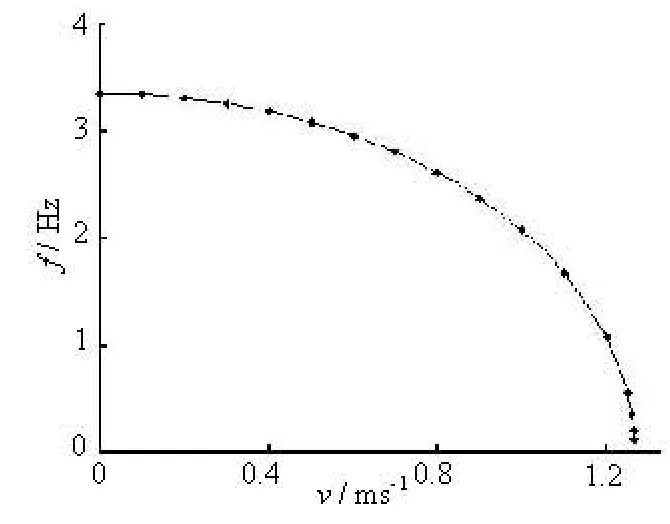
Fig.6 Critical velocity of vibration buckling

4. Conclusions

In this article, the finite element method is used to study the influence of fluid-structure interaction of tube-side flow on the vibration characteristic of conical spiral tube bundle. The relationship between the velocity of tube-side flow and natural frequency are studied, and the critical velocity of vibration buckling is obtained.

(1) The natural frequencies of the conical spiral tube bundle decrease by about 10% due to tube-side fluid flow. The natural frequencies decrease when the tube-side flow velocity increases, especially for the lower order modes of tube bundle.

(2) The critical velocity of vibration buckling of the conical spiral tube bundle is between 1.2265 m/s to 1.2669 m/s, which it much higher than the tube-side flow velocity of heat exchangers in working condition.

(3) In the effect of fluid-structure interaction of tube-side flow, the mode shape of the tube bundle is mainly z-axial, except for the 2nd and 3rd order modes, and it is feasible to induce, predict and control the vibration of tube bundles in heat exchangers.

[1] SHA Yong, WANG Yong-xue. Vortex induced vibrations of finned cylinders[J]. Journal of Hydrodynamics, 2008, 20(2): 195-201.

[2] LIN Li-ming, LING Guo-can. Nonlinear fluid damping in structure-wake oscillators in modeling vortex-induced vibrations[J]. Journal of Hydrodynamics, 2009, 21(1): 1-11.

[3] JONG C. J., MYUNG J. J. Flow-induced vibration and fretting-wear predictions of steam generator helical tubes[J]. Nuclear Engineering and Design, 2008, 238(4): 890-903.

[4] CHOI S. N., YOON K. S. and CHOI T. S. An analytical method to predict fretting-wear damage in the double 90oU-bend tubes[C]. The Fifteenth International Conference on Nuclear Engineering.Nogoya, Japan, 2006, 227-232.

[5] CHENG L., LUAN T. and DU W. J. et al. Heat transfer enhancement by flow-induced vibration in heat exchangers[J]. International Journal of Heat and Mass Transfer, 2009, 52(3): 1053-1057.

[6] TIAN Mao-cheng, CHENG Fei and CHENG Lin et al. Experimental study of enhanced heat transfer by flow-induced vibration of elastic tube bundles[J]. Journal of Hydrodynamics, Ser. B, 2000, 12(3): 103-109.

[7] CHENG Lin, QIU Yan. Complex heat transfer enhancement by fluid induced vibration[J]. Journal of Hydrodynamics, Ser. B, 2003, 15(1): 84-89.

[8] CHENG Lin. Principle and application of elastic tube heat exchanger[M]. Beijing: Science Press, 2001(in Chinese).

[9] JIANG Bo, TIAN Mao-cheng and LENG Xue-li et al. Numerical simulation of flow and heat transfer characteristics outside a periodically vibrating tube[J]. Journal of Hydrodynamics, 2008, 20(5): 629-636.

[10] ZHENG Ji-zhou, CHENG Lin and DU Wen-jing. Dynamic characteristics of elastic tube bundle with component mode synthesis method[J]. Chinese Journal of Mechanical Engineering, 2007, 43(7): 202-206(in Chinese).

[11] WADHAM-GAGNON M., PAIDOUSSIS M. P. and SEMLER C. Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion[J]. Journal of Fluids and Structures, 2007, 23(4): 545-567.

[12] PAIDOUSSIS M. P., SEMLER C. and WADHAMGAGNON M. et al. Dynamics of cantilevered pipes conveying fluid. Part 2: Dynamics of system with intermediate spring support[J]. Journal of Fluids and Structures, 2007, 23(4): 569-587.

[13] MODARRES-SADEGHI Y., SEMLER C. and WADHAMGAGNON M. et al. Dynamics of cantilevered pipes conveying fluid. Part 3: three-dimensional dynamics in the presence of an end-mass[J]. Journal of Fluid and Structure, 2007, 23(4): 589-603.

[14] ZHENG Ji-zhou. Dynamic characteristics of component of elastic tube bundles heat exchanger[D]. Ph. D. Thesis, Jinan: Shandong University, 2007(in Chinese).

[15] LAI Yong-xing, LIU Min-shan and DONG Qi-wu. Dynamic characteristic analysis of heat exchangers tube bundles with internal and external fluid[J]. Journal of Vibration and Shock, 2006, 25(2): 159-162(in Chinese).

[16] NI Zhen-hua, ZHANG Huan. Vibration analysis of spiral tubes conveying fluid by finite element method[J]. Computational Structural Mechanics and Applications, 1992, 9(5): 153-162(in Chinese).

[17] DU Ming-ming, YOU Yun-xiang and WEI Gang. The interaction of water waves with a submerged circular cylinder in a two-layer fluid of finite depth[J]. Journal of Hydrodynamics, Ser. A, 2007, 22(5): 573-582(in Chinese).

[18] YAN Ke, GE Pei-qi and LI Lei. Numerical simulation of fluid flied and resistance characteristics of longitudinal vibrating pipe[J]. Energy Conservation Technology, 2008, 26(5): 387-389(in Chinese).

[19] TAIT S. P., MORY G. Using oscillations to enhance heat transfer for a circular cylinder[J]. International Journal of Heat and Mass Transfer, 2006, 49(17-18): 3190-3210.

[20] YANG Yue-tzu, CHEN Cheng-hua. Numerical simulation of turbulent fluid flow and heat transfer characteristics of heated blocks in the channel with an oscillating cylinder[J]. International Journal of Heat and Mass Transfer, 2008, 51(7-8): 1603-1612.

10.1016/S1001-6058(09)60036-6

* Project supported by the National Basic Research Program of China (973 Program, Grant No. 2007CB206900).

Biography: YAN Ke (1984-), Male, Ph. D. Candidate

GE Pei-qi, E-mail: pqge@sdu.edu.cn