離散廣義系統(tǒng)的區(qū)間矩陣平穩(wěn)振蕩

龔文振

(玉林師范學(xué)院數(shù)學(xué)與計(jì)算機(jī)科學(xué)系,廣西玉林 530004)

離散廣義系統(tǒng)的區(qū)間矩陣平穩(wěn)振蕩

龔文振

(玉林師范學(xué)院數(shù)學(xué)與計(jì)算機(jī)科學(xué)系,廣西玉林 530004)

利用范數(shù)理論和代數(shù)方法,研究了離散廣義系統(tǒng)的區(qū)間平穩(wěn)振蕩問題.給出了兩種區(qū)間矩陣平穩(wěn)振蕩存在的充分條件.提供了可行性的算例.

離散廣義系統(tǒng);穩(wěn)定性;區(qū)間矩陣

1 引言

在實(shí)際的問題中,由于量測和建模的原因,誤差的出現(xiàn)常常是不可避免的,因此研究具有擾動(dòng)性的系統(tǒng)也就是系統(tǒng)的魯棒性問題具有更為實(shí)際的意義.系統(tǒng)的區(qū)間矩陣的相關(guān)問題是魯棒性問題的重要內(nèi)容,關(guān)于區(qū)間矩陣的研究目前已取得了一些成果,如文[1-2]研究了普通狀態(tài)空間系統(tǒng)的區(qū)間矩陣平穩(wěn)振蕩問題,文[3-6]研究了普通狀態(tài)空間系統(tǒng)的區(qū)間矩陣穩(wěn)定性.近年來,在廣義系統(tǒng)區(qū)間矩陣方面的研究也涌現(xiàn)了一些成果,文[8]利用幾何方法研究了廣義區(qū)間動(dòng)力系統(tǒng)的穩(wěn)定性問題,文[9]對系統(tǒng)矩陣E具有特殊形式情況討論了廣義區(qū)間動(dòng)力系統(tǒng)的穩(wěn)定性問題.然而關(guān)于廣義系統(tǒng)的區(qū)間平穩(wěn)振蕩問題研究成果還較少,本文的目的就是研究離散廣義動(dòng)系統(tǒng)區(qū)間平穩(wěn)振蕩的存在性,為廣義系統(tǒng)理論和周期解理論增添新內(nèi)容.

2 定義與引理

考慮如下的正則廣義系統(tǒng)

其中E,A∈Rn×n,rankE=r＜n,x(k)∈Rn

定義1[9]稱系統(tǒng)(1)是正則的,如果存在λ∈C使得|λE?A|/=0.

定義2[9]稱系統(tǒng)(1)是穩(wěn)定的,如果λ∈σ(E,A)={λ|λE?A|=0},都有λ＜0.

定義3[9]稱系統(tǒng)(1)是因果的,如果deg det(λE?A)=rankE.

引理1[12]離散廣義系統(tǒng)(1)是正則的、因果和穩(wěn)定的充要條件是存在可逆對稱矩陣P使得

對于向量x=(x1,…,xn)T∈Rn,其范數(shù)定義如下

對于矩陣A=(aij)n×n,其范數(shù)定義如下

并記L(A)=max{||A||1,||A||∞},λmax(H)表示矩陣H的最大特征值,H＞0(H≥0)表示矩陣H是正定陣(正半定陣).

引理2[11]對于任何矩陣S∈Rn×n,都有|λmax(S)|≤‖S‖∞.

引理3[11]對于對稱矩陣S∈Rn×n,如果|λmax(S)|≤1,則I±S＞0.

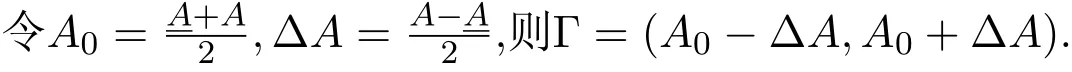
3 主要結(jié)果

3.1 第一種區(qū)間矩陣

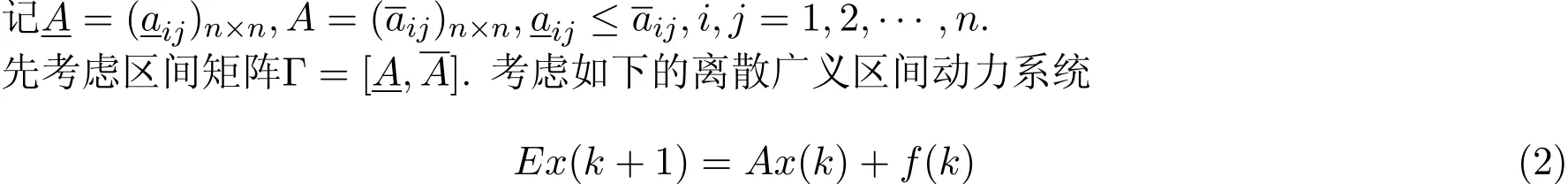
這里A∈Γ.

定理1對于離散廣義區(qū)間動(dòng)力系統(tǒng)(2),設(shè)f(k)是有界函數(shù),如果f(k+m)=f(k)(m是正整數(shù)常數(shù))且存在對稱可逆矩陣P使得

則對于任意的A∈Γ,離散廣義動(dòng)力系統(tǒng)(2)都是正則,因果和穩(wěn)定的且存在以周期為m的平穩(wěn)振蕩.

3.2 第二種區(qū)間矩陣

考慮另一種區(qū)間矩陣.記

由引理1可得,對于任意的A∈G(L,K)離散廣義系統(tǒng)(2)是正則、無脈沖和穩(wěn)定的,類似于定理1的證明,易證離散廣義系統(tǒng)(2)存在周期為m的平穩(wěn)振蕩.

4 例子

例1考慮如下的廣義區(qū)間動(dòng)力系統(tǒng)

容易驗(yàn)證定理2的條件得到滿足,從而對于任意的A∈G(L,K),離散廣義系統(tǒng)(2)都是以周期為2的平穩(wěn)振蕩.

5 結(jié)束語

本文研究了離散廣義動(dòng)力系統(tǒng)的區(qū)間的平穩(wěn)振蕩問題.具體給出了在兩種不同區(qū)間矩陣其平穩(wěn)振蕩存在的充分條件,整個(gè)推導(dǎo)過程簡單,易懂,具有較少的保性.是離散廣義系統(tǒng)理論的有益補(bǔ)充,空間周期解理論的研究又一分支,為離散廣義魯棒控制的研究提供重要的理論基礎(chǔ).當(dāng)導(dǎo)數(shù)矩陣亦為區(qū)間矩陣時(shí)的離散廣義系統(tǒng),其相關(guān)的研究較為復(fù)雜,將另文討論.

[1]王美娟.一類時(shí)變大系統(tǒng)的區(qū)間矩陣平穩(wěn)振蕩[J].應(yīng)用數(shù)學(xué)學(xué)報(bào),1994,17(1):154-159.

[2]王美娟.關(guān)于若干類型大系統(tǒng)周期解的研究[J].應(yīng)用數(shù)學(xué)學(xué)報(bào),1992,15(1):48-56.

[3]Jiang,Chungli.Sufficient condition for the asymptotic stability of interval matrices[J].INT.J.Control., 1987,46(5):1803-1810.

[4]SoH Y C,Evans R J.Stability analysis of interval.Matrices-continuous and discrete systems[J].International Journal of Control,1988,47(1):25-32.

[5]Man Sour M.Simpliyed sufficient Conditions fo the asymptotic Stability of interval Martices[J].International Journal of Control,1989,50(1):443-444.

[6]Wang Qingguo.Necessary and sufficient conditions for stability of a Matrix polytope with Normal Vetex Matrices[J].Automatic,1991,27(5):887-888.

[7]張大慶,何希勤,張慶靈.廣義區(qū)間動(dòng)力系統(tǒng)的穩(wěn)定性的充分條件[J].東北大學(xué)學(xué)報(bào),2003,24(5):412-415.

[8]徐勝元,楊成梧.廣義區(qū)間動(dòng)力系統(tǒng)的穩(wěn)定性分析[J].控制理論與應(yīng)用.2002,17(2):249-250.

[9]Dai L.Singular Control Systems[M].New York:springer-veglag,1989.

[10]Bender D J,Laub A J.The linear-quadratic optimal regulater for descriptor systems[J].IEEE Trans. Automatic Control,1987,32:672-687.

[11]陳景良,陳向暉.特殊矩陣[M].北京:清華大學(xué)出版社,2001.

[12]楊冬梅,張慶靈,姚波.廣義系統(tǒng)[M].北京:科學(xué)出版社,2004.

Internal matrix harmonic oscillation to discrete singular systems

GONG Wen-zhen
(Department of Mathematics and Computer Science,Yulin Normal University, Yulin530004,China)

The norm theory and algebraic method are employed to study the problem of the stability to discrete singular interval systems.The sufficient conditions which there exists interval matrix harmonic oscillation for two kinds interval matriex are presented.Two examples are also given to illustrate the results.

discrete singular systems,stability,interval matrice

O175.12

A

1008-5513(2009)03-0435-07

2008-10-20.

國家自然科學(xué)基金(60564001),教育部“新世紀(jì)優(yōu)秀人才支持計(jì)劃”專項(xiàng)基金(NCET-06-0756).

龔文振(1957-),副教授,研究方向：廣義系統(tǒng)理論和常微分方程理論.

2000MSC:34C05