Challenges in Study of Single Particles and Particle Swarms*
MAO Zaisha (毛在砂) and YANG Chao (楊超)
?
Challenges in Study of Single Particles and Particle Swarms*
MAO Zaisha (毛在砂)**and YANG Chao (楊超)
Key Lab of Green Process and Engineering, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China
Numerical simulation of multiphase flows in processing equipment in industry with two-fluid models and Eulerian-Lagrangian approaches requires the constitutive equations describing the interactions between the dispersed phase of high concentration and the continuous phase. The status of research on the forces on dispersed solid and fluid particles is reviewed in this article. As compared with the knowledge on drag of single solid particles, study on particle swarms and on other forces is not sufficient to meet the demand of reliable and efficient numerical simulation of multiphase flows. Thus, thorough study on the particle swarms becomes the key to accurate multi-scale simulation of multiphase flows. Besides, the development of efficient algorithm dealing with the non-uniformity on both equipment and mesoscopic scales is recognized as an important issue to be resolved. The research topics in the near future are suggested.
particle, drop, bubble, swarm, interphase force, multiphase flow, numerical simulation
1 INTRODUCTION
Numerical simulation is becoming popular in recent years due to great demand in using it as a promising tool in chemical engineering study to partially replace experimental exploration, particularly for the processing equipment design and scale-up. By numerical simulation techniques, more detailed information on the spatial distribution of species concentration, temperature, turbulent strength and chemical reaction rate and their temporal variations may be obtained than sole experimental measurement, so that the chemical engineers can combine the data and experience effectively to optimize the operation of existing facilities and the design of new process equipment.
This involves with the multiscale methodology of chemical reaction engineering study. Two scales are at least relevant, namely the reactor (macroscopic) and particle (including drop and bubble) scales. In multiphase reactors, solid or fluid particles move and react with other reactants through contact on the molecular scale under the influence of the local environment in a macroscopic reactor, and in turn their behaviors in motion, mass and heat transfer and reaction sum up to give the overall performance of the reactor, which is the input to the process flow sheet and the concerns of process engineers. Therefore, deep and quantitative understanding of single particles and that in particle swarms with strong inter-particle action become increasingly important in studying industrial multiphase chemical reactors.
The popularly used numerical method for hydrodynamic properties includes the Eulerian-Lagrangian approach and Eulerian-Eulerian one [1, 2]. The former deals the continuous phase as a spatially averaged field in the whole spatial domain, and is solved based on the Navier-Stokes equation, meanwhile each discrete particle is tracked using the Newton’s 2nd Law by considering all the forces exerted on it. When the number of particles increases as the scale of the task increases gradually to industrial equipment, the computational load becomes overwhelming beyond the computing capacity available to most chemical engineers. In such a case, the Eulerian-Eulerian demonstrate its merits of demanding less computational resources. By this approach, each phase, no matter continuous or dispersed, is treated as a continuous phase filling the whole domain, so that it may be approximated by an equation set of the continuum hydrodynamics. These set of governing equations are coupled together by the interphase force terms appearing in the momentum equations of each phase.
When using a Eulerian-Eulerian two-fluid model to deal with turbulent two-phase flows based on Reynolds time-averaging, the final resulted general model consists of the following continuity and momentum balance equations:
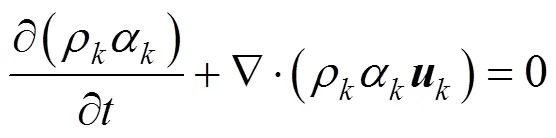

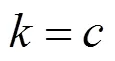
When using a Eulerian-Lagrangian model to deal with two-phase flows, Eqs. (1) and (2) still governs the hydrodynamics of the continuous phase, but each discrete particle is taken as a point mass, and its velocity and position are governed by the Newton’s second law:

whereis the resultant force exerted on a particle.
In either approach,is physically consisted of gravity, buoyancy, other body forces (for example, the magnetic field force) and interphase interacting forces, such as drag, virtual mass force, the Basset force, lift force,. Some authors used the terms such as pressure gradient force, lubrication force to get the gas holdup distribution to match the experimental data. Even the surface force due to interfacial tension may be expressed equivalently as a body force in the level set approach for fluid dispersion [3].
No matter how the multiphase hydrodynamics are formulated, the common element crucial for the successful simulation of multiphase flow is the accurateand convenient constitutive equations for continuum- particle interactions (and probably the interaction between pairs of dispersed phases). That is, we have to fully understand what interphase forces exist on a particle as a result of physical mechanisms, how they are formulated and approximated, and how they are expressed with an accurate and as simple as possible way. Furthermore, the same issues must also be addressed with respect to the interaction among particles, because particles are usually present in high concentration in the process equipment.
This article reviews the status of study on the interphase forces exerted on dispersed solid and fluid particles. As compared with the knowledge on drag of single solid particles, study on particle swarms and on other forces is not sufficient to meet the needs of numerical simulation of multiphase flows. Thus, thorough study on the particle swarms and clusters becomes the key to accurate multi-scale simulation of multiphase flows. Besides, the development of efficient algorithm dealing with the simultaneous non-uniformity on equipment and mesoscopic scales is recognized as an important issue to be resolved. The research topics requiring attention in the near future are also suggested.
2 FORCES ON SINGLE PARTICLES
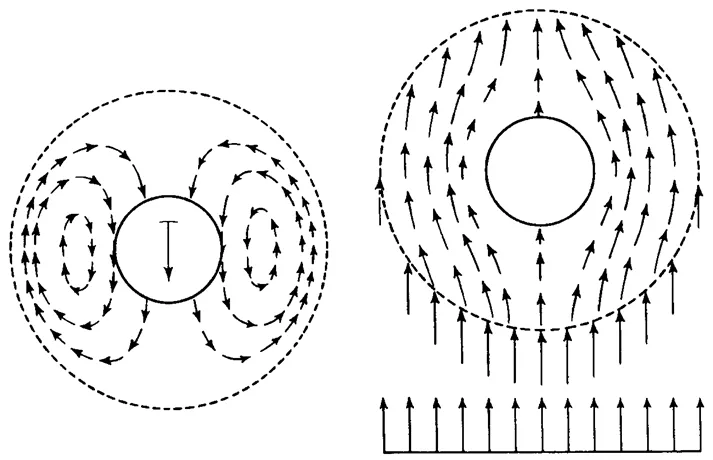
Many terminologies are used in describing the interactions between the particles and the surrounding continuous fluid phase, such as drag, lift, virtual mass force, Basset force, turbulent dispersion force, lubrication force,(Fig. 1). Some of these forces have sound physical basis, but some does not; some forces have been correlated with simple formulae with sufficient accuracy, but some demands further attention. These interphase forces appear in the governing equations as body forces in the Eulerian-Lagrangian model.

Figure 1 Forces arising from the interaction of a particle with continuous fluid phase
2.1 Drag
A moving particle is subjected to drag from the surrounding fluid which is usually calculated by

In fact, this equation is also the definition of the drag coefficient,d, although it applies both to a particle in steady and unsteady motion. However, the term of drag is generally referred to as that in steady motion. A single solid particle in steady motion is the most thoroughly studied case.

2.1.1
Whenpis greater than 0.1, the assumption of creeping flow is no more valid, no analytical solution is available for the flow field around an axisymmetric particle. The only way is the experimental measurement and the subsequent empirical correlation.
For a solid sphere, a simple and popularly used is the Schiller and Naumann correlation [5]:

Although it is based on single spheres moving steadily through quiescent fluid under gravity, it applies to estimate the drag force in turbulent multiphase flows in chemical reactors and pipes with reasonable agreement between numerical simulation results and experimental data. Many works have been devoted to improve it by piece-wise correlation, but they make little difference when used for simulating the solid particles laden engineering multiphase flows, particularly as the time-averaged flow fields are the main concern.
Actually, a solid particle may move zigzagly, in acceleration, spinning or in oscillation, while subjected to turbulence and shear in the fluid field, in processing equipment. These factors have not been systematically studied so that their important effects can be incorporated into the drag coefficient equation. Therefore, Eq. (6) deserves a systematical scrutiny in view of the above factors.
For gas bubbles, it is recognized that the drag coefficient is a function of Reynolds number and bubble shape, and the latter is in turn dependent onand other parameters of gas-liquid systems. Thus, a correlation valid under a wide range of regimes has been proposed by Tomiyama [6]:
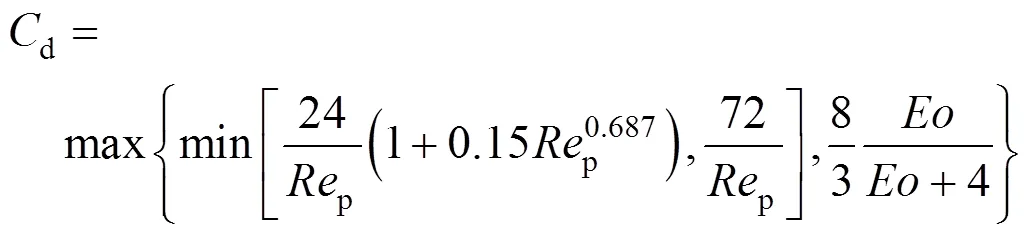
for slightly contaminated systems, and

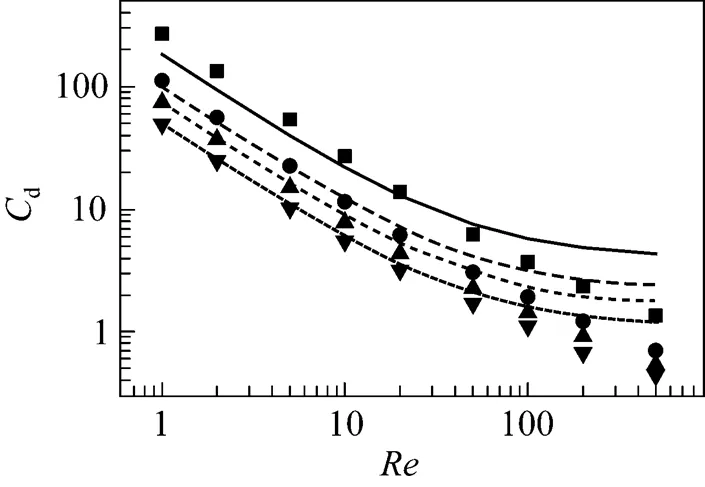
for contaminated systems (10-2<<103, 10-3 Similarly, the drag exerted on single drops is also dependent on drop shape. Whenp<600 and surface tension is relatively large, a drop keeps to be spherical or elliptic. Whenpin the range from 600 to 900, drop velocity reaches the maximum anddgoes to the minimum. Further increase ofpinduces greater change in shape and the drop becomes pulsating, anddincrease sharply along withp. Whenp> 1000~3000, a drop would disintegrate due to the hydrodynamic instability. Hu and Kintner [7] proposed a correlation based on a large amount of experimental data: In summary, the knowledge on single spheres in quiescent fluid is relatively satisfactory, but other situations (turbulence, shear, rotation, oscillation and unsteady motion), particularly for bubbles and drops, have not been understood sufficiently. 2.1.2 Recently the influence of turbulence on the drag enters the scope of research related to computational fluid dynamics (CFD). The motion of single particles is subjected to impact from the pseudo-random vortices present in turbulent flow and the momentum boundary layer changes probably at the characteristic frequency of turbulence. To incorporate such effect into the drag coefficient, Brucato. [8] proposed a correlation ofdbased on the Kolmogorov scaleandd0in laminar flow: For lack of study on the effect of turbulence on bubble motion, Lane. [9] tentatively used the above correlation with the constant adjusted: for simulating gas-liquid flow in stirred tanks and got better agreement with experiment. On the other hand, Khopkar. [10] applied Eq. (10) straightforwardly to gas-liquid stirred tanks. So far no turbulent effect has been considered as the drag coefficient of single drops is concerned. More efforts on the effect of turbulence on the drag of particles, bubbles and drops are desired for better formulation of the drag force exerted on particles in the real engineering situations. 2.1.3 Virtual mass force (or added mass force) and Basset force appear when a particle is in rectilinear unsteady motion. These two forces were clarified as ones with sound physical meanings. 2.2.1 If a particle is accelerating in an ideal fluid, extra force is needed to move the fluid around the particle, and such a force may be calculated by Some issues are not resolved yet. First, the expanded equation for calculating relative acceleration is a difficult choice. Different authors proposed diversified forms of equations. Anderson and Jackson [13] gave two expressions: Homsy. [14] suggested Jakobsen. [15] used after the Basset force deduced according Odar’s formula of Basset force coefficient [19]. In general, no reliable correlation ofvis available. 2.2.2 Basset force is also called the history force, because it is a force related with the history of acceleration of a particle. As compared to a steadily moving particle, an accelerating one at the same slip velocity has thinner momentum boundary layer, which is equivalent to larger friction at the particle surface. It got such a name for Basset in 1988 got a force expressed by the following integral exerted on a solid particle in sinusoidal oscillation in a creeping flow [20]: This force is essentially part of the difference of that to drive an accelerating sphere minus the drag at steady state motion. Although the extension [21], is often used in simulation of single particle motion, many efforts were devoted to developing the equations ofBvalid for more general cases, such as non-oscillating motion and particle of finite,. Because there exists no reliable and simple way to estimate these two unsteady forces, it is desired to know when they are necessary and when ignorable. Sokolichin. [22] declared that virtual mass force may be ignored for the numerical simulation of gas-liquid flow in bubble columns, and it is true for gas-liquid stirred tanks when the pseudo-turbulence is at relatively high frequency. Khopkar. [10] pointed out that virtual mass force is important in the region near the gas sparger, but it is much less than the drag in the bulk flow regions. You. [23] addressed this problem and concluded that Basset force may be ignored when a bubble in unsteady motion with a large or small frequency of oscillation, the Basset force of a solid particle or a drop is negligible, and in other cases it needs a case-specific analysis considering particle size, density ratio, acceleration,. Although virtual mass and Basset forces have definite physical meanings, they are present simultaneously as a particle accelerates in viscous fluid. It is questionable whether it is conceptually sound and feasible to split the unsteady force driving a particle to accelerate into a linear combination of steady motion drag, virtual mass and Basset forces for easier separate correlation, and to sum them linearly when conducting numerical simulation. Since the Navier-Stokes equation governing fluid flow is nonlinear, the above task of splitting seems infeasible. Is it possible to seek approximate correlations with acceptable error for engineering purpose? In viscous flow, may the role of the unsteady force be fully represented by the virtual mass force taking care of the kinetic energy and pressure head of surrounding fluid and the Basset force taking care of the diffusive spreading of viscous boundary layer over the particle surface? A convincing method for their resolution seems to be desired for chemical engineers. Lift force is referred to that exerted on a particle in the direction perpendicular to the particle motion path. Two mechanisms would create the lateral force: the shear in the flow induces the Saffman force, and the rotation of a particle leads to the Magnus force. Such distinction seems to be of theoretical sense, because a particle will rotate in shear flow so that two forces appear together for freely moving particles. The lift force is crucial for obtaining correct spatial distribution of phase holdups, for example, the radial profile of gas holdup in bubble columns. Drew and Lahey [24] gave a general expression for the Saffman force in ideal fluid: with Herebis defined based on the lateral dimension of bubbles. No generally accepted correlation for the lift force is available, and the correlations reported in the literature give wide scattered values ofL. So some authors ignored the lift force as compared with the drag, and sometimes the lift force coefficient is even used as an adjustable parameter to match gas holdup prediction with experimental data. Some other forces are used to describe the interaction between the dispersed and continuous phases, about which argument exists on their physical soundness. For example, the turbulent dispersion force is used to describe the spread of bubbles due to the effect of flow turbulence. This force is partly physical in the sense that turbulent vortices exert impact onto a particle and push it to move in the fluid. In some reports it is expressed as whereis the turbulent kinetic energy [27]. The key problem is to correlate the coefficientTDwith flow conditions. So far no general agreement on the physical basis and the estimation of the coefficient for turbulent dispersion force. It is also puzzling to express a diffusion-like phenomenon in terms of a force. The wall (lubrication) force is conceived as a resistance to the motion of a particle when approaching a solid wall to a certain distance, the flow of continuous phase fluid in the narrow gap between the particle and solid wall creates a net force away from the wall [28]. Different expressions for lubrication force were developed and tested, but no generally accepted one is available. These two forces sometimes are used to compensate the lateral lift forces so that the gas holdup profiles with either wall peak or core peak can be resulted from numerical simulation to match experimental data. Obviously, the physical mechanisms underlying these forces need further thorough investigation. In general, it is better to model these mechanisms based on their physical essences instead of using analog and imitation, so that accurate constitutive equations can be resulted with less empirical constants and wider applicability. In studying the motion of single bubbles in a high viscosity liquid, Zhang. [29] made a successful trial to correlate the total force instead of the individual forces based on the concept of linear splitting of the total force. The unsteady rise of bubbles from shortly after its release from the nozzle to after steady state rise was measured to get the rise velocity and acceleration of bubbles. By defining the total drag coefficientTdby and the total drag is calculated from the gravity, buoyancy and the Newton’s 2nd Law: When a bubble rises at its terminal velocity,Tdwould reduce to the conventional drag coefficient,d. It was found that E?tv?s numberhas little effect in the range of experiment. Therefore, a correlation was proposed based on the combined data set consisting of steady and accelerating bubbles through viscous liquid: in which the dimensionless groups are Similarly, Zhang. [30] succeeded in correlating the total drag coefficient of air bubbles rising steadily or in acceleration through shear-thinning non-Newtonian liquids. Using the modifiedM, the correlation also covers accelerating bubbles: Instead of splitting the total force exerted on a single particle into drag, unsteady force and lateral lift, the above alternative to correlate the total force which drives a particle move transiently through the continuous phase seems to be successful. If a particle accelerates in a shear flow, the drag, virtual mass and Basset forces plus lift would be enwound together, making their linear splitting of the total unsteady force almost impossible. More efforts are certainly required to explore the new route of correlation. In practical multiphase processes, the dispersed phase is often present as small particles, bubbles and drops so that the generated large specific surface area will result in high interphase mass and heat transfer rate and high process efficiency. Therefore, the interactions between particles must be included when estimating the interphase forces between the dispersed and continuous phases. What is really needed is the correlations for interphase forces of particles in a swarm or assemblage for macroscopic numerical simulation of process equipments. It is necessary to establish the correlations in a swarm corresponding to those for single particles. Unfortunately, the work concerned with particle swarms is not sufficient as compared with the counterpart on single particles. On the one hand, we can conduct experiments on particle swarms and get the data and empirical correlations. On the other hand, theoretical and numerical work may help for this goal. For example, we may correct the correlations for single particles with introducing the phase fraction as an additional parameter, if we can find the functional relationship between the properties of single particles and those in a swarm. Theoretical and numerical efforts to this task include roughly two approaches. The first one is direct numerical simulation of multi-particle systems, from two-particle system (tandem or side-by-side configurations) way up to thousands of particles. Due to the rapid progress in computer technique and numerical methods, the hydrodynamics of thousand plus solid particles [31, 32], and 125 drops (boundary element method [33] have been simulated satisfactorily. However, these numbers of particles are too small than a large-scale commercial chemical reactor (up to 1010 particles) to get reliable simulation results. The second approach is more simple and computationally efficient. The so-called cell model takes the particle swarm as composed of the same average cells, and deals with a typical cell constituted by a central particle and the surrounding shell of the continuous phase in accordance to the average phase fraction [34, 35] as illustrated in Fig. 4. Because treating only an average cell, the cell model enjoys the advantages of simple formulations and low computational load. The weakness is that to accurately express the interparticle actions is difficult because the means available for such manipulation are the outer cell boundary conditions only. Nevertheless, the cell models are widely used in chemical engineering, not only for studying multiphase dispersed flows but also for the permeation through porous media and the hydrodynamics in packed and fluidized beds [35]. It is also extended to study diversified phenomena involved with non-Newtonian fluids [36]. Figure 4 Spherical cell model in fixed and moving coordinate systems [35] Figure 5 Drag coefficients of drops predicted by the cell model [42] with the Happel boundary conditionthe correlation [43]:■?0.5;●?0.7;▲?0.8;▼?0.9 By the cell model, the only way to express the interparticle effect is the adoption of correct boundary conditions. In the literature, (1) the external uniform flow, (2) the free-shear condition or (3) the zero vorticity condition were adopted for the outer cell boundary. These conditions do not reflect the real flow conditions. Some improvements of cell models were suggested [37]. The above 3 conditions are all biased from the real flow through particle swarms, and refinement is necessary. To name a few from potential issues, the cell shape and the position of the particle inside the cell need more stringent justification, so that the cell models can express the interaction between particles with reasonable accuracy. The turbulence in the swarm is also an issue to be addressed, if the cell model is to be extended to study commercial unit operations as an effective tool. Most of correlations for particle swarms are some kinds of extension with the phase fraction incorporated into ones for single particles. In general, the following form of correlation is so far preferred: in whichd0is the drag coefficient of single particles. The function(p) differs from case to case. For solid spheres, a popular function is from Wen and Yu [44]: which is even used for simulating gas-liquid flows by several authors [45]. Koch and Hill [46] used lattice Boltzmann simulation to derive a more complex formula: with Li and Kuipers [32] examined these correlations and recommended to use Koch-Hill’s correlation for the numerical simulation of gas-particle flows. The case of bubbles is more complicated due to their deformation, breakage and coalescence, and empirical equations similar to Eq. (29) is used to correlate the drag coefficient in bubble swarms to that of a single bubble. However, the reported functional forms of(g) are diversified, and the correlations from different sources are applicable only in their respective limited range. Pan. [47] redefined the gas Reynolds number in a swarm to express the effect of gas fraction and transformed the correlation for contaminated single bubbles by Tomiyama [6] to a bubble swarm based on a modified Reynolds number: with average relative error of 8.8%. It is thought that no sufficient and systematical studies exist on the constitutive equations for other forces, particularly for liquid drops, in the existing literature. The constitutive equations on drag, heat and mass transfer coefficients in particle swarms as simple function of,and the physical properties of the systems are the desired form to chemical engineers, although such functional dependence is in reality very complex. The data base for correlations can be compiledeither from experimental measurements or from numerical simulation based on the cell models with suitable verification. Each way requires our laborious efforts. Figure 6 Dependence of average drag coefficient on uniformity of particle distribution [48] To date most studies treat particle swarms as a uniform entity. In fact, the non-uniform spatial distribution in particle dispersions has been known for many years. In conventional gas-solid fluidized beds, bubbles, bubble wakes and bulk emulsion with quite different particle concentrations exist in the same bed. In fast circulating fluidized beds, the core-annulus structure symbolizes the substantial radial variation in particle concentration. Therefore, the state of uniformity of particle concentration must be taken as an important factor in the numerical simulation of multiphase flows. The key problem is that the knowledge of the local holdup of a cell only is not enough for us to calculate the total force that is exerted on a particle. In Fig. 7, the particles in cell B are in a dense swarm, and moreover, the swarm is surrounded by those in neighboring cells and an approximately uniform environment is identified. However, cell C and its neighboring cells constitute the situation of a non-uniform environment. Even if cells B and C have the same local holdup, the drag for particles in these two cells must be calculated with different correlations, because a swarm will fall faster in dilute suspension than in the environment of dense one. Thus, it is necessary to rely on the drag coefficient correlation which takes account of local phase holdup and its local uniformity in the numerical procedure for simulating two-phase flows, no matter the model of solid phase isan Eulerian or Lagrangian approach. Unfortunately, this kind of correlation is to date not available for solid particles, not to say fluid particles, and other kinds of forces expressing the interphase interactions. Tremendous efforts have to be devoted in this direction. Figure 7 Non-uniform particle dispersion on a computational grid No mater whichever numerical approach is used for simulating dispersed two-phase flows, the need for accurate constitutive equations of interphase forces is inevitable, which are applicable to a wide range covering turbulent, accelerating motion subject to breakage and coalescence of fluid particles. Therefore, more systematic efforts in experimental, theoretical and simulation studies are necessary. More efforts should be paid to these forces whose physical mechanisms have been recognized, such as drag, lift, virtual mass force, Basset force,. The present research results on them are far from being sufficient to meet the need of the numerical simulation of dispersed two-phase flows, particularly as lift, virtual mass force, and Basset force. Some forces (pressure gradient force, turbulent dispersion force, lubricating force,.) lack sound physical basis but indeed plays certain roles in the current numerical simulation. In a long run, their tentative roles should be replaced by reliable constitutive equations with solid physical basis, after thorough understanding of the respective physical mechanisms is achieved. The particle-particle interaction has to be included when deriving the corresponding constitutive equations, which means we have to pay sufficient attention to resolution of the effect of phase holdup and its spatial uniformity on the forces of individual particles. Both the cell models and the direct numerical simulation of multi-particle systems can contribute to constitutive equations with better accuracy. However, the effects of non-uniformity of phase holdup on the constitutive equations and the numerical procedures have not received enough attention so far. The above observations also apply to the numerical simulation of heat and mass transfer processes in process equipment. It is expected that fundamental study on the particle (and particle swarm) scale will eventually contribute to the accurate numerical simulation of macroscopic multiphase process equipment, so that the operation optimization, renovation and scale-up of process equipment can be done primarily on the basis of accurate and efficient numerical simulation with reduced cost and time of computation. acceleration, m·s-2 coefficient ddrag coefficient vessel diameter, m pequivalent diameter, m body force, N·m-3 acceleration of gravity (9.81 m·s-2) turbulent kinetic energy, m2·s-2 particle mass, kg pressure, Pa radial coordinate, m source term time, s terminal velocity, m·s-1 velocity, m·s-1 particle volume, m3 ,physical coordinates, m phase holdup rate of energy dissipation, m2·s-3 Kolmogorov scale, m viscosity, Pa×s kinematic viscosity, m2×s-1 density, kg·m-3 interfacial tension, N·m-1 stress tensor, virtual time B Basset force b bubble c continuous phase d drag, drop g gas phase index L liquid, lift p particle, dispersed phase r radial slip slip between phase TD turbulent dispersion force Td total drag v virtual mass 0 single particle, initial value 1 Sokolichin, A., Eigenberger, G., Lapin, A., Lübert, A., “Dynamic numerical simulation of gas-liquid two-phase flows Euler/EulerEuler/Lagrange”,..., 52 (4), 611-626 (1997). 2 Jakobsen, H.A., Lindborg, H., Dorao, C.A., “Modeling of bubble column reactors, progress and limitations”,...., 44 (14), 5107-5151 (2005). 3 Brackbill, J.U., Kothe, D.B., Zemach, C., “A continuum method for modeling surface tension”,..., 100 (2), 335-354 (1992). 4 Clift, R., Grace, J.R., Weber, M.E., Bubbles, Drops, and Particles, Academic Press, New York, 30-33 (1978). 5 Kwauk, M.S., Li, H.Z., Handbook of Fluidization, Chemical Industry Press, Beijing, 106 (2008). (in Chinese) 6 Tomiyama, A., “Struggle with computational bubble dynamics”,.., 10, 369-405 (1998). 7 Hu, S., Kintner, R.C., “The fall of single liquid drops through water”,., 1 (1), 42-48 (1955). 8 Brucato, A., Grisafi, F., Montante, G., “Particle drag coefficients in turbulent fluids”,..., 53 (18), 3295-3314 (1998). 9 Lane, G.L., Schwarz, M.P., Evans, G.M., “Modeling of the interaction between gas and liquid in stirred vessels”, In: Proc. 10th Eur. Conf. on Mixing, van den Akker, H.E.A., Derksen, J.J., eds., Elsevier, Amsterdam, 197-204 (2000). 10 Khopkar, A.R., Rammohan, A.R., Ranade, V.V., Dudukovic, M.P., “Gas-liquid flow generated by a Rushton turbine in stirred vessel: CARPT/CT measurements and CFD simulations”,..., 60 (8/9), 2215-2229 (2005). 11 Blumberg, P.N., Mohr, C.M., “Effect of orientation on the settling characteristics of cylindrical particles”,., 14 (2), 331-334 (1968). 12 Fan, L., Mao, Z.S., Yang, C., “Experiment on sedimentation of slender particles with large aspect ratio and correlation of drag coefficient”,...., 43 (23), 7664-7670 (2004). 13 Anderson, T.B., Jackson, R., “A fluid mechanical description of fluidized beds”,...., 6 (11), 527-539 (1967). 14 Homsy, G.M., El-Kaissy, M.M., Didwania, A., “Instability waves and the origin of bubbles in fluidized beds-II”,.., 6 (4), 305-318 (1980). 15 Jakobsen, H.A., Sanns, B.H., Grevskott, S., Svendsen, H.F., “Modeling of vertical bubble-driven flows”,...., 36 (10), 4052-4074 (1997). 16 Kuo, J.T., Walls, G.B., “Flow of bubbles through nozzles”,.., 14 (5), 547-564 (1988). 17 Sankaranarayanan, K., Shan, X., Kevrekidis, I.G., Sundaresan, S., “Analysis of drag and virtual mass forces in bubbly suspensions using an implicit formulation of the lattice Boltzmann method”,.., 452, 61-96 (2002). 18 Kendoush, A.A., Sulaymon, A.H., Mohammed, S.A.M., “Experimental evaluation of the virtual mass of two solid spheres accelerating in fluids”,..., 31 (7), 813-823 (2007). 19 Odar, F., “Verification of the proposed equation for calculation of the forces on a sphere accelerating in a viscous fluid”,.., 25 (3), 591-592 (1966). 20 Zapryanov, Z., Tabakova, S., Dynamics of Bubbles, Drops and Rigid Particles, Kluwer Academic, Dordrecht, 338, 343 (1999). 21 Reeks, M.W., McKee, S., “The dispersive effects of basset history forces on particle motion in a turbulent flow”,., 27 (7), 1573-1582 (1984). 22 Sokolichin, A., Eigenberger, G., Lapin, A., “Simulation of buoyancy driven bubbly flow: Established simplifications and open questions”,., 50 (1), 24-45 (2004). 23 You, C.F., Qi, H.Y., Xu, X.C., “Progress in the Basset force research and its application”,, 19 (2), 31-33 (2002). (in Chinese) 24 Drew, D.A., Lahey, R.T. Jr., “The virtual mass and lift force on a sphere in rotating and straining flow”,.., 13 (1), 113-121 (1987). 25 Tomiyama, A., Sou, A., Zun, I., Kanami, N., Sakaguchi, T., “Effects of E?tv?s number and dimensionless liquid volumetric flux on lateral motion of a bubble in a laminar duct flow”, In: Proceedings of the 2nd International Conference on Multiphase Flow Serizawa, A., Fukano, T., Bataille, J., eds., Elsevier, Amsterdam, 3-15 (1995). 26 Tomiyama, A., Tamai, H., Zun, I., Hosokawa, S., “Transverse migration of single bubbles in simple shear flows”,..., 57 (11), 1849-1858 (2002). 27 Lahey, Jr. R.T., Lopez de Bertodano, M., Jones, Jr. O.C., Buscaglia, G., “Phase distribution in complex geometry conduits”,.., 141 (1/2), 177-201 (1993). 28 Antal, S.P., Lahey, Jr. R.T., Flaherty, J.E., “Analysis of phase distribution in fully developed laminar bubbly two-phase flow”,.., 17 (5), 635-652 (1991). 29 Zhang, L., Yang, C., Mao, Z.S., “Unsteady motion of a single bubble in highly viscous liquid and empirical correlation of drag coefficient”,..., 63 (8), 2099-2106 (2008). 30 Zhang, L., Yang, C., Mao, Z.S., “Unsteady motion of a single bubble in non-Newtonian liquids and empirical correlation of drag coefficient”,...., 47 (23), 9767-9772 (2008). 31 Pan, T.W., Joseph, D.D., Bai, R., Glowinski, R., Sarin, V., “Fluidization of 1204 spheres: Simulation and experiment”,.., 451, 169-191 (2002). 32 Li, J., Kuipers, J.A.M., “Gas-particle interactions in dense gas-fluidized beds”,..., 58 (3-6), 711-718 (2003). 33 Zinchenko, A.Z., Davis, R.H., “An efficient algorithm for hydrodynamical interaction of many deformable drops”,..., 157 (2), 539-587 (2000). 34 Happel, J., “Viscous flow in multi-particle systems: Slow motion of fluids relative to beds of spherical particles”,., 4 (2), 197-201 (1958). 35 Happel, J., Brenner, H., Low Reynolds Number Hydrodynamics, 2nd edition, Noordhoff, Leydon the Netherlands (1973). 36 Chhabra, R.P., Bubbles, Drops, and Particles in Non-Newtonian Fluids, 2nd edition, Taylor Francis, 300-303 (2007). 37 Mao, Z.S., “Numerical simulation of viscous flow through spherical particle assemblage with the modified cell model”,...., 10 (2), 149-162 (2002). 38 Mao, Z.S., Wang, Y.F., “Numerical simulation of mass transfer in a spherical particle assemblage with the cell model”,., 134 (1/2), 145-155 (2003). 39 LeClair, B.P., Hamielec, A.E., “Viscous flow through particle assemblages at intermediate Reynolds numbers—A cell model for transport in bubbles swarms”,...., 49 (6), 713-720 (1971). 40 Sankaranarayanan, K., Sundaresan, S., “Lift force in bubbly suspensions”,..., 57 (17), 3521-3542 (2002). 41 Mao, Z.S., Chen, J.Y., “Numerical approach to the motion and external mass transfer of a drop swarm by the cell model”, In: International Solvent Extraction Conference (ISEC’2002), Sole, K.C., Cole, P.M., Preston, J.S., Robinson, D.J., eds., South African Institute of Mining and Metallurgy, Johannesburg, South Africa, 227-232 (2002). 42 Mao, Z.S., Chen, J.Y., “An attempt to improve the cell model for motion and external mass transfer of a drop in swarms at intermediate Reynolds numbers”, In: International Solvent Extraction Conference (ISEC’2005), Fei, W.Y., Liu, H.Z., Yan, C.H., eds., Beijing, A417 (2005). 43 Kumar, A., Hartland, S., “Gravity settling in liquid/liquid dispersions”,...., 63 (3), 368-376 (1985). 44 Wen, C.Y., Yu, Y.H., “Mechanics of fluidization”,....., 62, 100-111 (1966). 45 Oey, R.S., Mudde, R.F., van den Akker, H.E.A., “Sensitivity study on interfacial closure laws in two-fluid bubbly flow simulations”,., 49 (7), 1621-1636 (2003). 46 Koch, D.L., Hill, R.J., “Inertial effects in suspension and porous-media flows”,..., 33, 619-647 (2001). 47 Pan, Y., Dudukovic, M.P., Chang, M., “Numerical Investigation of gas-driven flow in 2-D bubble columns”,., 46 (3), 434-449 (2000). 48 Li, J.H., Kwauk, M.S., “Exploring complex systems in chemical engineering—The multi-scale methodology”,..., 58 (2), 521-535 (2003). 2009-06-08, 2009-07-12. the National Natural Science Foundation of China (20490206, 20676134), the National Basic Research Program of China (2009CB623406, 2004CB217604), the National Project of Scientific and Technical Supporting Program (2008BAF33B03) and the National High Technology Research and Development Program of China (2007AA060904). ** To whom correspondence should be addressed. E-mail: zsmao@home.ipe.ac.cn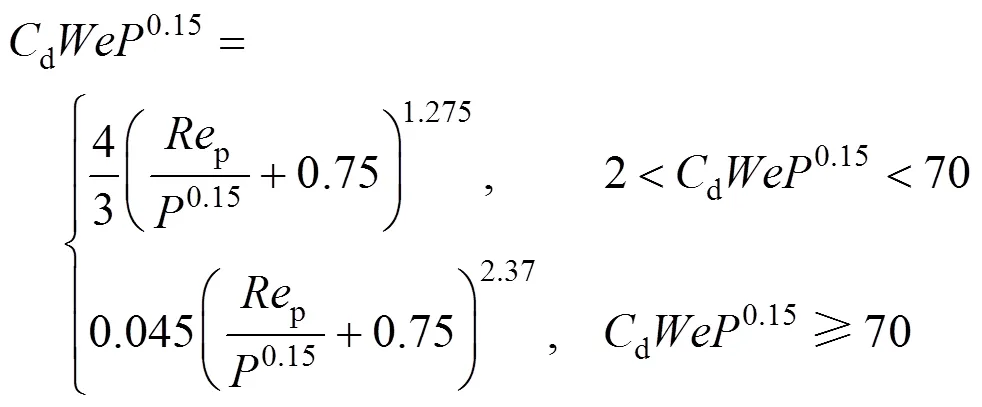
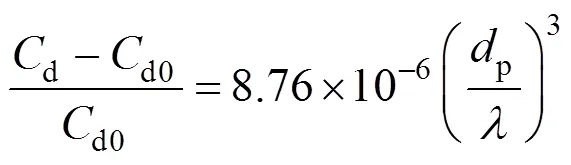

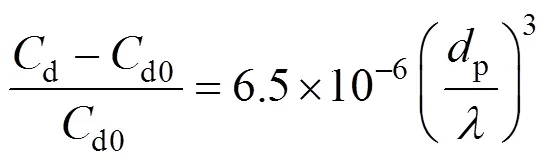
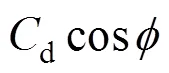
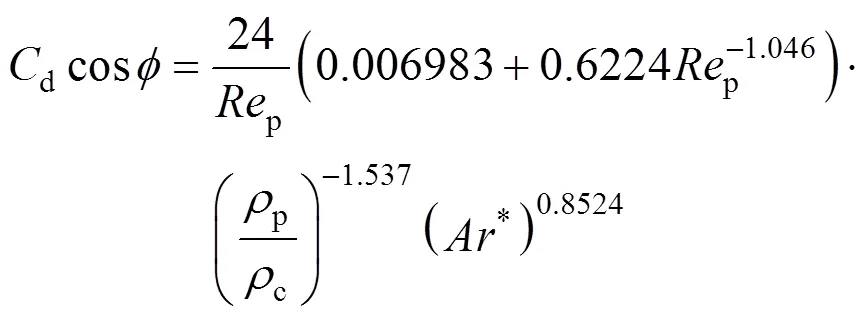
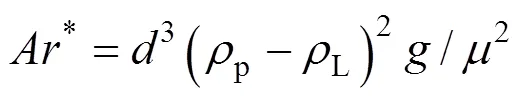
2.2 Unsteady forces

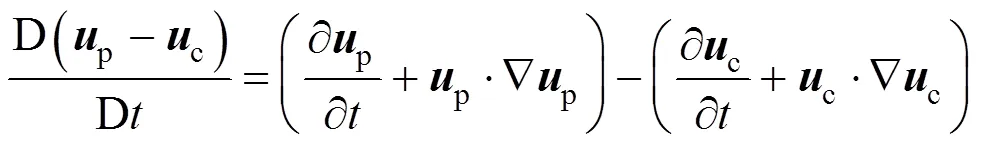

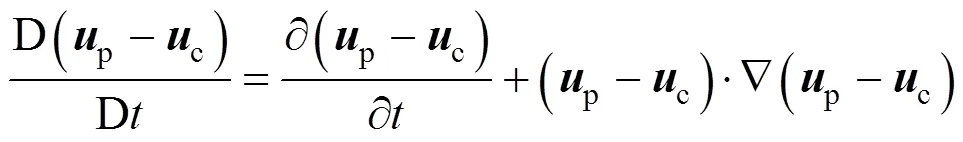
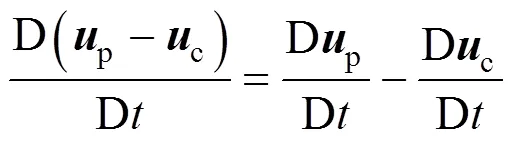

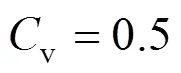


2.3 Lift force
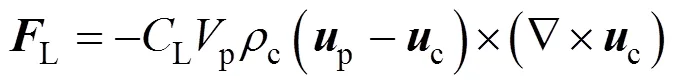
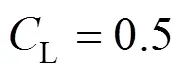
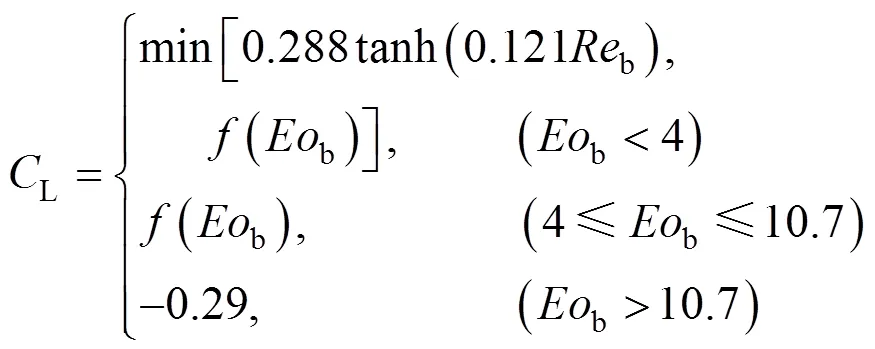

2.4 Other forces
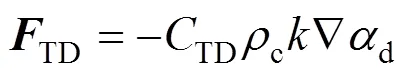
2.5 Modeling total drag
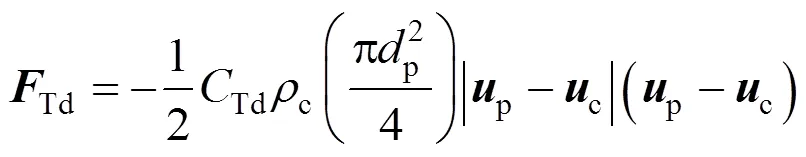
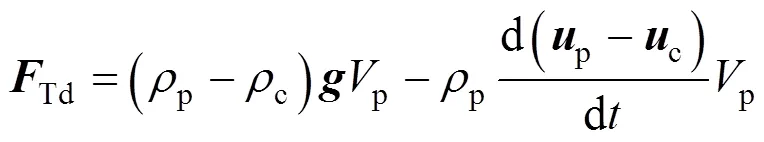
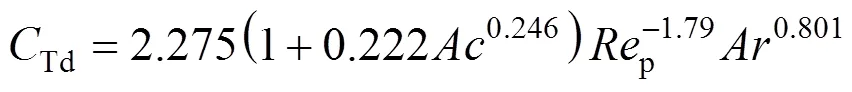
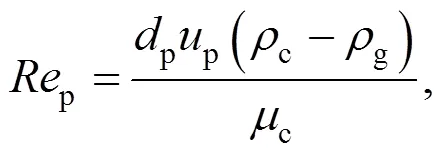



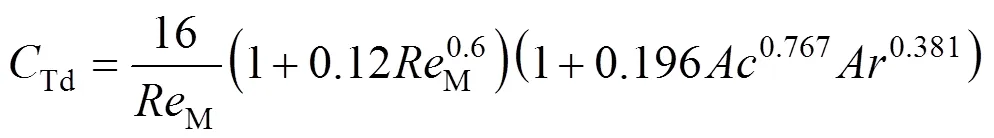
3 FORCES IN PARTICLE SWARMS
3.1 Two approaches
3.2 Effect of dispersed phase fraction

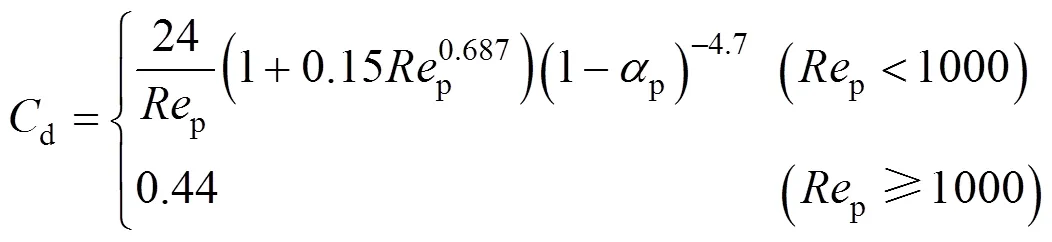
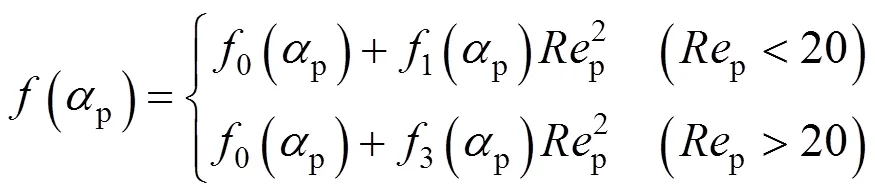
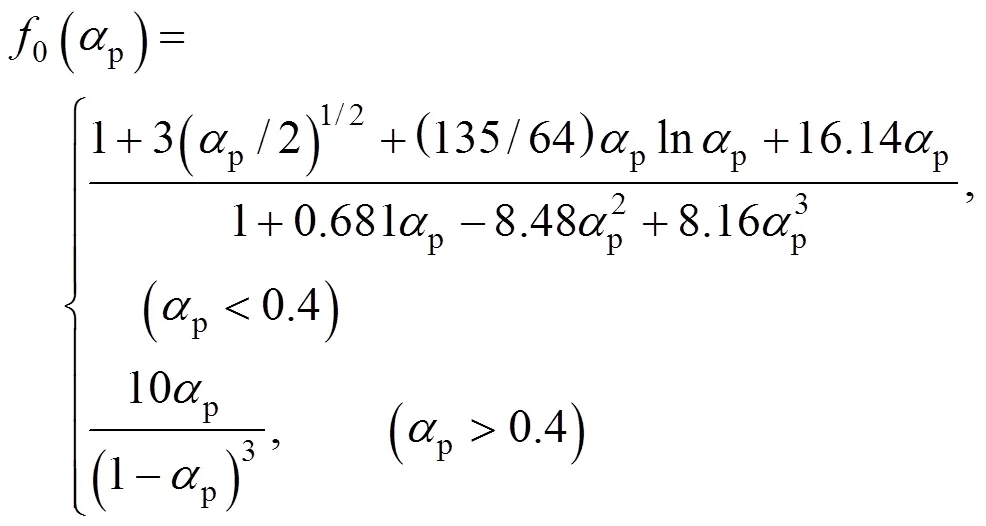
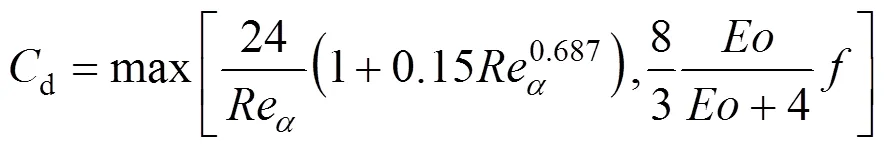

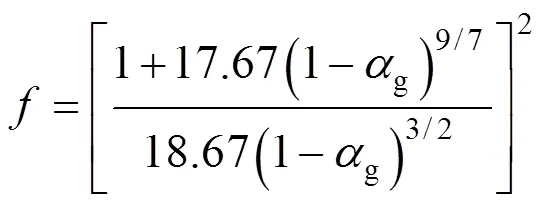
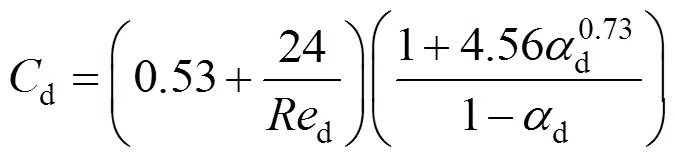

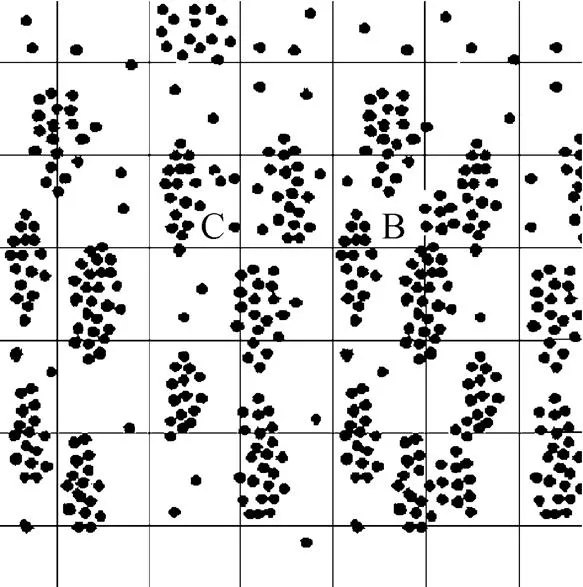
4 SPATIAL NON-UNIFORMITY OF PARTICLE DISTRIBUTION
5 SUMMARY
NOMENCLATURE
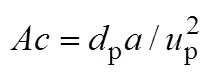
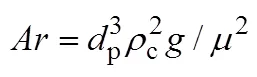
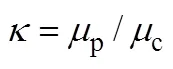
Subscripts
 Chinese Journal of Chemical Engineering2009年4期
Chinese Journal of Chemical Engineering2009年4期
- Chinese Journal of Chemical Engineering的其它文章
- Removal of Uranium (VI) by Fixed Bed Ion-exchange Column Using Natural Zeolite Coated with Manganese Oxide*
- Phase Equilibrium of Isobutanol in Supercritical CO2
- Conversion of Methane by Steam Reforming Using Dielectric-barrier Discharge*
- Permeability and Selectivity of Sulfur Dioxide and Carbon Dioxide in Supported Ionic Liquid Membranes*
- Hydroxyapatite Coatings on Titanium Prepared by Electrodeposition in a Modified Simulated Body Fluid*
- Model Study on a Submerged Catalysis/Membrane Filtration System for Phenol Hydroxylation Catalyzed by TS-1*
